Prediction of phases and mechanical properties of magnesium-based high-entropy alloys using machine learning

2.1 Classification framework

Framework for analysis used in this research was based on Fig. 1. Computational framework was anchored on four platforms as suggested by (Machaka, 2021). Data collection, filtering, and wrangling yielded four crystal structures, 20 phases, and 29 features. Data was processed, segmented, and split into 75% training and 25% testing. Feature selection and validation followed, with model performance tested.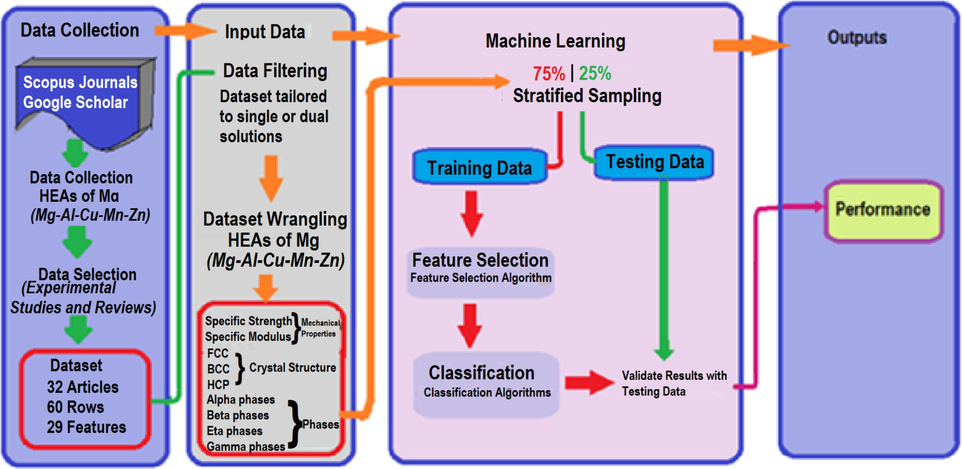

Close

Fig. 1

Phase and mechanical properties classification framework for ML. The figure illustrates the steps used in the ML classification including data collection, details of input data, machine learning process, outputs and performance.

Export to PPT

2.2 Collection and selection of data

Data from research on magnesium alloys (Mg-Al-Cu-Mn-Zn) was cleaned, checked for missing data, encoded, and transformed for machine learning. Feature selection used backward elimination, forward selection, and regularization to identify significant features. New features such as density (Density_calc), change of entropy of mixing (dSmix), atomic size difference (Atom_Size_Diff), electronegativity difference (Elect_Diff) and valence electron concentration (VEC) were created using feature engineering (Bhandari et al., 2020; Machaka, 2021). dSmix was calculated based on Equation 1.

Change in enthalpy of mix was calculated using Equation 2.

Atomic size difference was calculated using Equation 3

Average atomic radius was given by Equation 4.

Valence electron concentration (VEC) was calculated based on Equation 5.

Electronegativity difference, $\chi$ , was calculated based on Equation 6.

Where, in Equations 1 – 6.

R= Ideal gas constant;

$x_i$ and $x_j$ = atomic percentages of the $i^{\mathit{th}}$ and $j^{\mathit{th}}$ elements, respectively

$r_i$ = Radius of the $i^{\mathit{th}}$ element;

$\overline{r}$ = Average atomic radius;

${\chi }_i$ = Pauling electronegativity of the i^th component;

$\overline{\chi }$ = Mean electronegativity for alloy system;

$C_i$ = atomic percentage; and

${\left(VEC\right)}_i$ = Valence electron concentration of the $i^{\mathit{th}}$ element.

Iterative testing evaluated the impact of engineered features on model performance, leading to optimized results. The final data had 60 observations and 29 variables. Multicollinearity tests showed that no Variance Inflation Factor (VIF) values exceeded 5 (see Table 1). There was moderate correlation for Atom_Size_Diff and Elect_Diff. VEC had low multicollinearity (VIF=1.27). There was no multicollinearity between the features that could affect the reliability of the predictive models as no VIF value exceeded the threshold of 5. This implied that each predictor variable, such as Atom_Size_Diff and Elect_Diff, provided unique and valuable information for the prediction without being overshadowed by correlations with other variables. The low VIF of 1.27 indicated that VEC was a stable predictor.

Though the current dataset was small, it had more features compared to other datasets of magnesium-based alloys used in machine learning (He et al., 2023; Mi et al., 2022). The research used 29 features to improve ML model predictions despite a small dataset (Chen et al., 2021). Feature engineering technique proposed by Machaka (2021) was used to refactor the original dataset in order to fit the learning algorithm.

2.3 Feature selection and reduction of dimensions

This study used five stages of experiments as shown in Fig. 2. The first stage used all 29 features of the dataset as the baseline feature set. The second stage created four smaller feature sets by applying Boruta algorithm with the RF algorithm (Machaka, 2021). It also used recursive feature elimination based on RF regression. The third stage ordered the features by declined importance applying majority-vote ranking technique for better outcomes. The fourth stage grouped the ordered-features into seven sets with the top 5, 7, 10, 13, 15, 20, 25 feature sub-sets as proposed by (Machaka, 2021). The fifth stage involved determining and validating performance of different classifiers.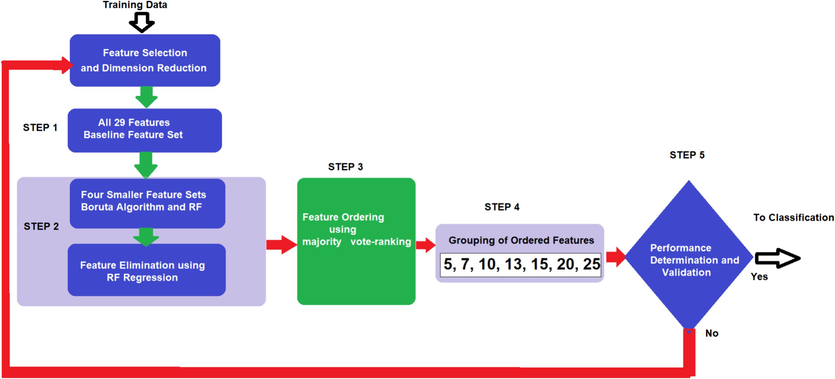

Close

Fig. 2

Feature selection. This illustrates the selection process across 5 steps. Output of the process becomes input to classification. A feedback loop in case the performance and validation are not satisfactory is also illustrated.

Export to PPT

2.4 ML classifiers and performance evaluation criteria

In literature, several ML classifiers have been used in prediction of alloy phases and mechanical properties but only a few are applicable in small datasets which are associated with model over fitting or under fitting as well as and too high or too low feature dimensions (Xu et al., 2023). Algorithms for small datasets such as support vector machine (SVM), Gaussian process regression (GPR), gradient boosting decision tree (GBDT) and XGBoost though robust, have problems of inherent complexity, potential overfitting, and computational intensity. They falter with high dimensions and complex alloy data interactions. Conversely, RF, LDA, and kNN are more apt, with RF excelling in modelling non-linearities and preventing overfitting (Xu et al., 2023). LDA maximizes class separability in limited data and helps in dimensionality reduction (see Table 3). ANN was used to model non-linear relationships and transfer learning helped to leverage it to improve performance with the small dataset. k-NN was used to classify features based on similarity measures and its problems of dimensionality was addressed using principal component analysis (PCA). RF struggles with high-dimensional data, but feature selection helped to mitigate this. LDA may oversimplify, regularization was used to enhance robustness. Models were trained to identify high discriminant power features. A function was defined to calculate accuracy and kappa index using a confusion matrix. Classifier performance was evaluated with three magnesium-based alloys: Mg-80-Al-10-Cu-5-Mn-5-Zn-0, Mg-80-Al-5-Cu-5-Mn-5-Zn-5, and Mg-91.2-Al-8.3-Cu-0-Mn-0.15-Zn-0.35.

2.5 Simulation in MatCalc Software

Optimal values of density, yield strength, ultimate tensile strength and stiffness were obtained from the values of percentages generated from the objective functions. MatCalc 6.04 used classical nucleation theory to estimate alloy precipitates' development and granularity, based on the Svoboda–Fischer–Fratzl–Kozeschnik (SFFK) model. Alloy composition (Mg, Al, Cu, Mn, Zn) was optimized using genetic algorithms and Generalized Reduced Gradient (GRG) non-linear programming in Matlab R2023b for optimal properties.

Density of Mg is given by ${\rho }_{\mathit{Mg}}=1.738$ g/cm³, of Al is ${\rho }_{\mathit{Al}}=2.7$ g/cm³, Cu is ${\rho }_{\mathit{Cu}}=8.96$ g/cm³, Mn is ${\rho }_{\mathit{Mn}}=7.26$ g/cm³ and Zn is ${\rho }_{\mathit{Zn}}=7.133$ g/cm³. Masses of the components were $m_{\mathit{Mg}}$ , $m_{\mathit{Al}}$ , $m_{\mathit{Cu}}$ , $m_{\mathit{Mn}}$ and $m_{\mathit{Zn}}$ for magnesium, aluminium, copper, manganese and zinc. Density estimation was done using alloy formula in Equation 7 and 8 based on density of components.

$m$ =mass of alloy in grams;

$v$ =volume of alloy, cm³,

But $v$ is the sum of volumes of the components of the alloy. Meaning volume of magnesium, $v_{\mathit{Mg}}=\frac{m_{\mathit{Mg}}}{{\rho }_{\mathit{Mg}}}$ , aluminium, $v_{\mathit{Al}}=\frac{m_{\mathit{Al}}}{{\rho }_{\mathit{Al}}}$ , copper, $v_{\mathit{Cu}}=\frac{m_{\mathit{Cu}}}{{\rho }_{\mathit{Cu}}}$ , manganese, $v_{\mathit{Mn}}=\frac{m_{\mathit{Mn}}}{{\rho }_{\mathit{Mn}}}$ and $v_{\mathit{Zn}}=\frac{m_{\mathit{Zn}}}{{\rho }_{\mathit{Zn}}}$ . $${\rho }_{\mathit{alloy}}=\frac{m}{v_{\mathit{Mg}}+v_{\mathit{Al}}+v_{\mathit{Cu}}+v_{\mathit{Mn}}+v_{\mathit{Zn}}}$$

Percentages of the components by weight were $p_{\mathit{Mg}}=\frac{m_{\mathit{Mg}}}{m}\ast 100\%$ , $p_{\mathit{Al}}=\frac{m_{\mathit{Al}}}{m}\ast 100\%$ , $p_{\mathit{Cu}}=\frac{m_{\mathit{Cu}}}{m}\ast 100\%$ , $p_{\mathit{Mn}}=\frac{m_{\mathit{Mn}}}{m}\ast 100\%$ , and $p_{\mathit{Zn}}=\frac{m_{\mathit{Zn}}}{m}\ast 100\%$ for magnesium, aluminium, copper, manganese and zinc

The specific strength at yield, $\frac{\mathit{YS}}{{\rho }_{\mathit{alloy}}}$ , $\frac{\mathit{UTS}}{{\rho }_{\mathit{alloy}}}$ and specific modulus $\frac{E}{{\rho }_{\mathit{alloy}}}$ became the objective functions for genetic algorithm implementation of multi-objective. The aim was to maximize each as shown in Equation 11.

Substituting for percentage components from Equation 10 into Equation 11, the objective functions were as shown in Equation 12.

Additional parameters were essential for the kinetic simulations of precipitation, which included microstructural details and nucleation configurations. The kinetic simulation parameters encompassed thermal treatments, specifying formation at 1300°C and normalization at 400°C for one hour, alongside grain size and dislocation density considerations.

MatCalc 6.04 was used to capture precipitation domains for Mg, Al, Cu, Mn, and Zn solutes with specific trapping enthalpies. It identified precipitates like MgZn, Mg₂Cu, and MnAl phases. The thermal protocols were set to begin with casting at 1300°C, then cooling to 400°C at −0.75°C/s. Homogenization was at 400°C to reduce grain sizes, followed by quenching to 25°C at −100°C/s aimed at enhancing strength and stabilize properties.

2.6 Mechanical tests

Mg-89.43-Al-8.16-Cu-0.34-Mn-0.25-Zn-1.81 alloy obtained from optimization results was produced using stir casting technique from source material AZ91D to which quantities of pure copper, zinc and manganese powders were added. The alloy was prepared in inert argon gas atmosphere with melt heated to 1300°C for about 20 min. Pouring was done in graphite coated pre-heated steel mould. The melt was left to homogenize at 400°C for one hour after which quenching was done in oil. The casting products were age-hardened for seven days, machined into six test samples, and prepared for tensile tests per ASTM E8. Tests in a Universal Testing Machine determined yield strength, ultimate tensile strength, and Young’s Modulus, compared to predicted values.

2.7 Scanning electron microscopy and EDS analysis

The microstructure of the Mg-89.43-Al=8.16-Cu-0.34-Mn-0.25-Zn-1.81 alloy was characterized using scanning electron microscope (SEM) (Tun et al., 2019). Sample preparation involved polishing, embedding, mounting, dehydration, and cleaning. Samples were made electrically conductive for SEM analysis. Images formed from backscattered and secondary electrons. 50mm diameter, 4mm thick samples were prepared using nitric acid and ethanol, adhered to stubs with carbon tape, and vacuum-dried for 30 min.

3.1 Results of ML prediction

The results revealed that homogenization temperatures and time were weakly correlated with the mechanical properties and phases while electronegativity difference and VEC had significant positive correlation. Linear discriminant analysis (LDA) results in Table 2 showed that synthesis methods significantly affected alloy properties. The properties affected included yield strength, UTS, elastic modulus (E), VEC, atomic size difference (Atom_Size_Diff), and enthalpy of mixing (dHmix). Die casting (DC) had a high probability of 0.78889, solution treatment (ST_4) had probability of 0.66667 and solution treatment with age-hardening (ST_6) had highest probability of 0.86667. Induction melting (IM) and disintegrated melt deposition (DMD) had probabilities of 0.75556 and 0.82222, respectively. Yield strength had negative coefficients in all discriminant functions, aiding class differentiation. LD1, LD2, LD3, and LD4 maximized separation between different phases or compositions. Each LD represented a direction in feature space along which the data was projected to achieve maximum separation. LD1 showed the direction that maximized the separation between the most distinct classes, often capturing the most variance. LD2 was orthogonal to LD1 and would maximize separation not captured by LD1. This process continued with each subsequent LD (LD3, LD4, LD5) being orthogonal to the previous ones and capturing the maximum separation possible.

UTS was positively correlated with LD2 and LD3, while Young’s modulus had mixed effects on LD1 and LD2 (See Table 3). VEC significantly influenced LD1 and LD3, but not LD2. Atom_Size_Diff impacted LD1, and to a lesser extent LD3 and LD4. dHmix minimally affected class differentiation. LDA highlighted phase distinctions, with LD1 explaining 42.97% variance, significant for phase identification, contrasting with minimal 3.71% of LD5. Negative coefficients of VEC in LD1 and LD2 underscored its importance, with a positive impact in LD1. High dHmix suggested distinct phase formation in magnesium alloys. Beta-Mg₁₇Al₁₂ was likely to be in group 5 (75.6%) or group 4 (82.2%), while Gamma-Mg₂Si and Mg₂Cu had a 40% chance of classification in group 1. Similar results were found with magnesium alloys that were studied by Machaka (2021) and Tun et al. (2019).

Random forest regression yielded near-perfect categorization with negligible OOB error, predicting alloy synthesis pathways. ANN with a 6–10-5 model structure effectively predicted synthesis techniques, avoiding overfitting. Results in Fig. 3 showed that ANN outperformed other models with prediction accuracy of 98.70%, precision of 98.41%, recall of 98.12%, and an F1-score of 98.70% with the proposed framework. k-NN algorithm followed closely, with slightly lower metrics across the board. The resuls that ANN had highest accuracy corroborate findings of Machaka (2021). LDA showed exceptional precision at 99.55% but lagged slightly in other areas. RF algorithm demonstrated consistent performance, though it had the lowest metrics among the evaluated algorithms. Therefore, ANN algorithm demonstrated the most balanced performance, suggesting its suitability.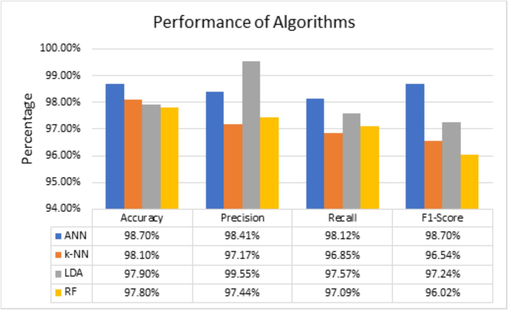

Close

Fig. 3

Performance of the algorithms. It illustrates that ANN was the best followed by k-NN in terms of prediction accuracy. LDA performed best followed by ANN in terms of precision.

Export to PPT

3.2 Results of MatCalc simulation

Simulation results in MatCalc 6.04 showed a high number of fine precipitates with a uniform distribution suggested consistent mechanical properties. Gamma-Mg₁₇Al₁₂ had an extremely low mean phase fraction and low precipitate number, implying it was residual or undeveloped. The Q-AlCuMg phase (Q_ALCUMG_P0) had a higher mean phase fraction, indicating significant presence. Other phases included Mg₂Si, MgZn, and MgZn₂. Thes results confirm findings of Bilbao et al. (2022) and Tayyebi et al. (2021) on intermetallic phases.

3.3 Results of SEM/EDS analysis

At magnifications of X500 and X10,000, the microstructure in Fig. 4 exposed the intricate details of the grain boundary nucleation. It showcased the presence of Mg₁₇Al₁₂, alpha_Mg, and Q_AlCuMg clusters. The white regions denoted the Mg₁₇Al₁₂ phase. The grey regions represented the alpha-Mg matrix and the dark grey areas correspond to the Q_AlCuMg intermetallic clusters. The clarity in grain boundary nucleation of the same phases in Fig. 4 suggested a repeatable and reliable microstructural pattern.

Close

Fig. 4

Tested alloy showing grain boundaries at X500 and X10,000.

Export to PPT

Spectrum 1 and EDS in Fig. 5 showed that magnesium was predominant, with traces of oxygen. Fig. 6 confirmed no peaks were omitted, representing all elements present. The EDS analysis in Fig. 7 showed magnesium as the main element in Spectrum 3, with 70.96% weight and 72.91% atomic percentage. Aluminium was 20.11% by weight and 18.62% atomic percentage. The MgZn phase (6.37 wt%) indicated strengthening. Presence of 10.83 wt% MgO was due to surface oxidation, serving as a protective barrier against further corrosion.

Close

Fig. 5

EDS Spectrum 1 and point of its collection.

Export to PPT

Close

Fig. 6

EDS Spectrum 2 and point of its collection.

Export to PPT

Close

Fig. 7

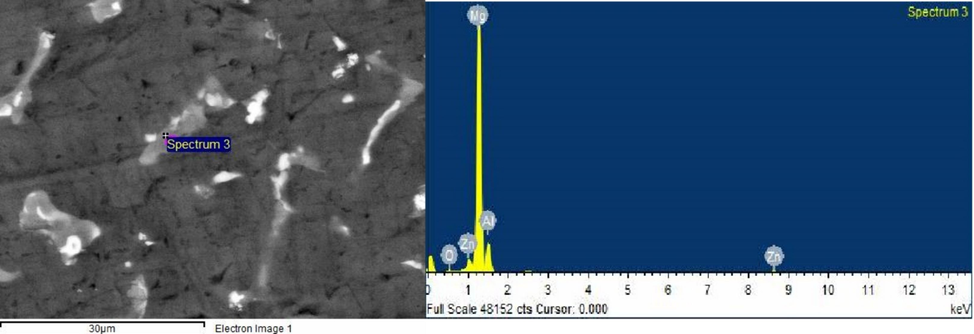
EDS Spectrum 3 and point of its collection.

Export to PPT

3.4 Results of tensile test

The predicted and experimental values for the mechanical properties of the alloy closely matched, with slight variances in yield strength and Young’s Modulus. The UTS showed a broader experimental range, with significant deviations at the lower end. Specific strength and modulus had more discrepancies, likely due to alloy composition, microstructure, or testing conditions. Six samples were tested, all fracturing in the middle, indicating material consistency. Extensions at yield and fracture were 0.102439mm and 1.03mm, respectively, indicating low ductility. The predictions were reliable but could be refined for better accuracy.