Solving singular convection–diffusion equation by exponentially-fitted trial functions and adjoint Trefftz test functions

Chein-Shan Liu

doi:10.1016/j.jksus.2016.09.011

Solving singular convection–diffusion equation by exponentially-fitted trial functions and adjoint Trefftz test functions

Chein-Shan Liu

Center for Numerical Simulation Software in Engineering and Sciences, College of Mechanics and Materials, Hohai University, Nanjing, Jiangsu 210098, China

Received: 2016-3-10, Accepted: 2016-9-25, Published: 2016-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

The paper develops a weak-form integral equation method (WFIEM) for solving the singularly perturbed convection–diffusion equation, which is too ill-posed to find the singular solution using conventional methods. We use Green’s second identity to generate integral equation, which includes a source term and boundary functions on the space-time boundary, and the derived adjoint Trefftz test functions. Then the singular solution is expressed in terms of a set of exponentially-fitted trial functions, which automatically satisfy the boundary conditions. The numerical algorithm deduced from the WFIEM is effective and accurate in the numerical solutions of highly singular parabolic type problems as will be observed by numerical examples.

Keywords

Singular convection–diffusion equation

Adjoint Trefftz test functions

Exponentially-fitted trial functions

Show Related Articles from PubMed

1 Introduction

The mathematical models that involve a combination of convective, diffusive and reactive terms are widespread in many engineering and scientific branches. Often we may encounter the problem that the boundary layers are presented when the convective term dominates than the diffusive term. When the Péclet number is large, the difficulty might appear in the numerical approximations. Thus a vast literature has built up over the last few decades on a variety of techniques for analyzing and overcoming these difficulties (Morton, 1996).

Our problem is to find $u (x, t)$ in the following singular convection–diffusion equation:

(1)

u_{t} (x, t) = ε u_{xx} (x, t) - {cu}_{x} (x, t) + au (x, t) + S (x, t),

(2)

u (0, t) = u_{0} (t),

(3)

u (ℓ, t) = u_{ℓ} (t),

(4)

u (x, 0) = f (x),

where

(x, t) \in Ω : {0 < x < ℓ, 0 < t ⩽ t_{f}}, ε > 0

is a small diffusion coefficient, c is the transport velocity, a is a constant reaction rate,

ℓ

is the length,

t_{f}

is the final time, and

S (x, t)

is the source term. We suppose that the boundary values

u_{0} (t) \neq u_{ℓ} (t)

. For a given problem if

u_{0} (t) = u_{ℓ} (t)

we can transform it by

w (x, t) = u (x, t) + xt

to a new problem for

w (x, t)

with the new boundary conditions

w (0, t) = u_{0} (t)

and

w (ℓ, t) = u_{ℓ} (t) + ℓ t \neq w (0, t)

Because the highest order term $u_{xx}$ is multiplied by a small parameter $ε$ , Eq. (1) is one of the singularly perturbed problems of parabolic type partial differential equations (PDEs), which exhibits boundary layers near to $x = 0$ and $x = ℓ$ . The singularly perturbed parabolic type problems have been an interesting subject for many applications, of which a lot of numerical methods were proposed to solve them (Boglaev, 1998; Clavero and Gracia, 2005, 2010; Hemker et al., 2000; Kopteva, 1997; Linß and Madden, 2007; Mukherjee and Natesan, 2011; Ng-Stynes et al., 1988; Shishkin, 1997 ). The numerical methods to treat the singularly perturbed problems were surveyed by Kadalbajoo and Patidar (2002), Kadalbajoo and Gupta (2010). More difficult asymptotic behavior at small diffusivity of the solutions in a rectangle with corner layers was analyzed by Gie et al. (2013) and Hamouda et al. (2016). Recently, Temam et al. (2015) have explored the recent progresses in boundary layer theory, where the boundary layer analysis is performed on a curved boundary, and also the interior transition layers at the turning point characteristics in an interval domain and classical (ordinary), characteristic (parabolic) and corner (elliptic) boundary layers in a rectangular domain are provided using the technique of correctors and the tools of functional analysis.

It is known that the singularly perturbed convection–diffusion Eq. (1) is highly ill-posed (Rajan and Reddy, 2016), and as mentioned there the discretization of the singularly perturbed convection–diffusion equation often leads to a highly ill-conditioned system which results in an unstable numerical solution. Due to the presence of boundary layers phenomena we have to seek more suitable trial functions and test functions in the weak-form methods, which lead to stable and robust numerical methods to give stable solution for any value of the diffusion parameter.

The remaining portion is arranged as follows. In Section 2 we introduce a weak-form integral equation method based on Green’s second identity and the adjoint operator. In Section 3 we derive the spectral functions to simplify the weak-form integral equation derived in Section 2. Using the exponentially-fitted trial functions to expand the singular solution and using the adjoint Trefftz test functions, we can derive a quite simple linear system in Section 4, which is then solved using the conjugate gradient method (CGM) to determine the expansion coefficients. Numerical examples are given in Section 5, and the conclusions are drawn in Section 6.

2 A weak-form integral equation method

The idea of weak-form integral equation method with inserting the adjoint Trefftz functions as test functions has been successfully developed by Liu (2016a), Liu and Chang (2016) and Liu and Wang (2016) to solve the direct and inverse problems of elliptic and parabolic PDEs. In order to explore the new method we first derive the following results.

Theorem 1

Green’s second identity) Let $Ω$ be a bounded region in the plane $(x, t)$ with a counter-clockwise contour $Γ$ consists of finitely many smooth curves. Let $u (x, t)$ and $v (x, t)$ be functions that are differentiable in $Ω$ and continuous on $\bar{Ω}$ . Then

(5)

\int \int_{Ω} (u H^{*} v + v H u) dxdt = \oint_{Γ} [ε ({uv}_{x} - {vu}_{x}) + cuv] dt - uvdx,

where

(6)

H (u) = \frac{\partial u}{\partial t} - ε \frac{\partial^{2} u}{\partial x^{2}} + c \frac{\partial u}{\partial x} - au,

(7)

H^{*} (v) = \frac{\partial v}{\partial t} + ε \frac{\partial^{2} v}{\partial x^{2}} + c \frac{\partial v}{\partial x} + av

are, respectively, the linear parabolic operator and its adjoint operator.

Proof

Inserting $\begin{matrix} \int \int_{Ω} u_{t} vdxdt = - \oint_{Γ} uvdx - \int \int_{Ω} v_{t} udxdt, \\ - ε \int \int_{Ω} u_{xx} vdxdt = - ε \oint_{} Γ u_{x} vdt + ε \oint_{Γ} {uv}_{x} dt - ε \int \int_{Ω} {uv}_{xx} dxdt, \\ c \int \int_{Ω} u_{x} vdxdt = c \oint_{Γ} uvdt - c \int \int_{Ω} {uv}_{x} dxdt, \\ - a \int \int_{Ω} uvdxdt = - a \int \int_{Ω} vudxdt \end{matrix}$ into the first integral term in left-hand side of Eq. (5) and moving the double integral terms to the left-hand side we can prove this theorem. □

Theorem 2

For the singular problem (1) we have the following integral relation:

(8)

\begin{matrix} \int_{0}^{t_{f}} \int_{0}^{ℓ} S (x, t) v (x, t) dxdt = \int_{0}^{ℓ} [u (x, t_{f}) v (x, t_{f}) - u (x, 0) v (x, 0)] dx \\ + \int_{0}^{t_{f}} ε [u (ℓ, t) v_{x} (ℓ, t) - u (0, t) v_{x} (0, t)] dt \\ - \int_{0}^{t_{f}} ε [u_{x} (ℓ, t) v (ℓ, t) - u_{x} (0, t) v (0, t)] dt \\ + \int_{0}^{t_{f}} c [u (ℓ, t) v (ℓ, t) - u (0, t) v (0, t)] dt \end{matrix}

for any function

v (x, t)

with

H^{*} v = 0

, where

u (x, 0) = f (x)

u (0, t) = u_{0} (t)

and

u (ℓ, t) = u_{ℓ} (t)

are given functions.

Proof

Inserting $H u = S (x, t)$ and $H^{*} v = 0$ into Eq. (5), integrating along the contour $Γ = Γ_{1} \cup Γ_{2} \cup Γ_{3} \cup Γ_{4} = {0 ⩽ x ⩽ ℓ, t = 0} \cup {x = ℓ, 0 ⩽ t ⩽ t_{f}} \cup {0 ⩽ x ⩽ ℓ, t = t_{f}} \cup {x = 0, 0 ⩽ t ⩽ t_{f}}$ , and inserting the corresponding conditions in Eqs. (2)–(4) we can prove this theorem. □

3 The adjoint Trefftz test functions

In order to simplify the weak-form integral Eq. (8), we need to find the adjoint Trefftz test function $v (x, t)$ , which satisfies the following adjoint PDE as well as the adjoint boundary conditions:

(9)

H^{*} v = \frac{\partial v}{\partial t} + ε \frac{\partial^{2} v}{\partial x^{2}} + c \frac{\partial v}{\partial x} + av = 0,

(10)

v (0, t) = v (ℓ, t) = 0 .

Theorem 3

For the singular problem, the adjoint Trefftz test functions which satisfy Eqs. (9) and (10) are given by

(11)

v^{j} (x, t) = \exp [(λ_{j} - a) (t - t_{f})] G (x, j),

(12)

G (x, j) = \exp (\frac{- cx}{2 ε}) \sin \frac{j π x}{ℓ},

where

(13)

λ_{j} = \frac{c^{2}}{4 ε} + \frac{ε j^{2} π^{2}}{ℓ^{2}}, j \in N .

Proof

Let

(14)

I (t) = e^{at}

be the integrating factor, and multiplying Eq. (9) by

I (t)

we have

(15)

\frac{\partial I (t) v}{\partial t} + ε \frac{\partial^{2} I (t) v}{\partial x^{2}} + c \frac{\partial I (t) v}{\partial x} = 0 .

By letting

(16)

w (x, t) : = I (t) v (x, t),

a simpler PDE for

w (x, t)

follows:

(17)

w_{t} (x, t) = - {cw}_{x} (x, t) - ε w_{xx} (x, t) .

Upon taking

(18)

w (x, t) = y (x) Λ (t),

and using the method of separation of variables it follows that

(19)

\frac{\dot{Λ} (t)}{Λ (t)} = \frac{- {cy}^{'} (x) - ε y^{″} (x)}{y (x)} = λ,

where the eigenvalue

λ

is to be determined.

In order to satisfy the boundary conditions $v (0, t) = v (ℓ, t) = 0$ in Eq. (10) we impose

(20)

y (0) = y (ℓ) = 0,

such that by Eqs. (19) and (20) we can derive Eq. (13). As a consequence we have the following solutions:

(21)

Λ (t) = {De}^{λ_{j} t},

(22)

y (x) = C \exp (\frac{- cx}{2 ε}) \sin \frac{j π x}{ℓ},

where C and D are constants. Therefore, by Eqs. (16), (18) and (14) we can derive Eqs. (11) and (12), of which

v^{j} (x, t)

are closed-form spectral solutions of the adjoint equation

H^{*} v = 0

, and automatically satisfy the boundary conditions

v (0, t) = v (ℓ, t) = 0

in Eq. (10) due to

(23)

G (0, j) = G (ℓ, j) = 0 .

We may call $v^{j} (x, t), j \in N$ the adjoint Trefftz test functions, because they satisfy the adjoint equation automatically; moreover, $v^{j} (x, t), j \in N$ are spectral functions. □

Inserting Eq. (11) into Eq. (8) we can derive a quite simple integral relation between $S (x, t)$ and other boundary functions.

Theorem 4

For the singular convection–diffusion Eq. (1), the solution $u (x, t_{f}) = g (x)$ at any time $t_{f}$ , the given source function $S (x, t)$ , and the given conditions $u (x, 0) = f (x), u (0, t) = u_{0} (t), u (ℓ, t) = u_{ℓ} (t)$ satisfy the following weak-form integral relation:

(24)

\begin{matrix} \int_{0}^{ℓ} g (x) v^{j} (x, t_{f}) dx = \int_{0}^{t_{f}} \int_{0}^{ℓ} S (x, t) v^{j} (x, t) dxdt \\ + \int_{0}^{ℓ} f (x) v^{j} (x, 0) dx - \int_{0}^{t_{f}} ε [u_{ℓ} (t) v_{x}^{j} (ℓ, t) - u_{0} (t) v_{x}^{j} (0, t)] dt, \end{matrix}

where

v^{j} (x, t), j \in N

are the adjoint Trefftz test functions.

Proof

This theorem follows from Eq. (8) using $v (0, t) = v (ℓ, t) = 0$ . □

4 Numerical algorithm of WFIEM

To prompt the introduction of the exponentially-fitted trial functions, let us consider

(25)

\begin{matrix} ε y^{″} (x) + y^{'} (x) = 0, 0 < x < 1, \\ y (0) = 0, y (1) = 1, \end{matrix}

which has a closed-form solution:

(26)

y (x) = \frac{e^{- x / ε} - 1}{e^{- 1 / ε} - 1} .

It can be seen that the singular solution is of the exponential type function.

There are two basic trial functions we need:

(27)

\begin{matrix} ϕ_{j} (x) = \frac{e^{jx} - 1}{e^{j ℓ} - 1}, ϕ_{j} (0) = 0, ϕ_{j} (ℓ) = 1, \end{matrix}

(28)

\begin{matrix} ϕ_{j} (x) = \frac{e^{j ℓ} - e^{jx}}{e^{j ℓ} - 1}, ϕ_{j} (0) = 1, ϕ_{j} (ℓ) = 0, \end{matrix}

and via a linear superposition they can generate other trial functions, which automatically satisfy the given boundary conditions.

Then we describe a simple algorithm to solve $g (x)$ in the integral Eq. (24). For the solution of the singular convection–diffusion Eq. (1) we may consider

(29)

\begin{matrix} g (x) = \sum_{j = - m_{1}}^{m_{2}} a_{j} s_{j} ϕ_{j} (x), \end{matrix}

(30)

\begin{matrix} ϕ_{j} (x) = \frac{(β_{2} - β_{1}) e^{jx} - β_{2} + β_{1} e^{j ℓ}}{e^{j ℓ} - 1}, \end{matrix}

(31)

\begin{matrix} ϕ_{0} (x) = \frac{1}{ℓ} [(β_{2} - β_{1}) x + β_{1} ℓ], \end{matrix}

where

m_{1}

and

m_{2}

are integers chosen by the user,

s_{j}

are multiple-scales, and

β_{1} = u_{0} (t_{f})

and

β_{2} = u_{ℓ} (t_{f})

. In the trial functions

ϕ_{j} (x), β_{1}

and

β_{2}

must be different constants; otherwise,

ϕ_{j} (x)

will be constants. We impose an extra moment equation:

(32)

\sum_{j = - m_{1}}^{m_{2}} a_{j} = 1

to guarantee that the boundary conditions are satisfied. The new idea of using the exponentially and polynomially fitted trial functions as the bases for a trial solution was first developed by Liu (2016b) to solve the third-order singular boundary value problems.

Inserting Eq. (29) with $s_{j} = 1$ into Eq. (24) and integrating, and letting $j = 1, \dots, n_{q} - 1$ we can derive a linear system:

(33)

Ac = e

to determine the expansion coefficients

c : = {a_{j}}

whose number is

n = m_{1} + m_{2} + 1

. The dimension of

A

n_{q} \times n

, including Eq. (32). According to the idea of equilibrated matrix method (Liu, 2012), the multiple-scales

s_{j}

are given by

(34)

s_{j} = \frac{‖ a_{1} ‖}{‖ a_{j} ‖},

where

a_{j}

is the jth column vector of the coefficient matrix

A

, and

s_{1} = 1

Instead of Eq. (33), we can solve a normal linear system:

(35)

Dc = b_{1},

where

(36)

b_{1} : = A^{T} e, D : = A^{T} A > 0 .

The algorithm of conjugate gradient method (CGM) for solving Eq. (35) is summarized as follows.

Give an initial $c_{0}$ and then compute $r_{0} = {Dc}_{0} - b_{1}$ and set $p_{0} = r_{0}$ .
For $k = 0, 1, 2, \dots$ , we repeat the following iterations:

(37)

\begin{matrix} η_{k} = \frac{‖ r_{k} ‖^{2}}{p_{k}^{T} {Dp}_{k}}, \\ c_{k + 1} = c_{k} - η_{k} p_{k}, \\ r_{k + 1} = {Dc}_{k + 1} - b_{1}, \\ α_{k + 1} = \frac{‖ r_{k + 1} ‖^{2}}{‖ r_{k} ‖^{2}}, \\ p_{k + 1} = α_{k + 1} p_{k} + r_{k + 1} . \end{matrix}

If $c_{k + 1}$ converges according to a given stopping criterion $‖ r_{k + 1} ‖ < ε_{1}$ , then stop; otherwise, go to step (ii).

There are many different methods to choose the test functions and trial functions. Here, the method of adjoint Trefftz test functions transforms the strong form in Eq. (1) into the most weak-form integral Eq. (24). Moreover, the test functions can be solved in closed-form by Eq. (11), which significantly enhance the efficiency of the presented method in the solution of the singular problems at hand. From Eqs. (11) and (12) we can observe that the singular behavior of the singular problems is reflected in the test functions. On the other hand, in order to simulate the singular behavior of the singular problems we have used the exponentially-fitted functions as the trial functions, which automatically satisfy the boundary conditions. When we take enough bases and generate enough algebraic equations using many linearly independent test functions $v^{j} (x, t)$ , we can solve the singular problems effectively and accurately. The above two points using the adjoint Trefftz test functions and the exponentially-fitted trial functions are highly original and sufficiently novel.

5 Numerical examples

In this section we apply the weak-form integral equation method (WFIEM) to solve Eq. (1). Sometimes we may want to find all the time histories of $u (x, t)$ in a time interval $t \in (0, t_{f}]$ . For this purpose we rewrite Eqs. (11), (12) and (24) to $\begin{matrix} v^{j} (x, s; t) = \exp [(λ_{j} - a) (s - t)] \exp (\frac{- cx}{2 ε}) \sin \frac{j π x}{ℓ}, \\ G (x, j) = \exp (\frac{- cx}{2 ε}) \sin \frac{j π x}{ℓ}, \end{matrix}$

(38)

\begin{matrix} \int_{0}^{ℓ} g (x) G (x, j) dx = \int_{0}^{t} \int_{0}^{ℓ} S (x, s) v^{j} (x, s; t) dxds \\ + \int_{0}^{ℓ} f (x) v^{j} (x, 0; t) dx - \int_{0}^{t} ε [u_{ℓ} (s) v_{x}^{j} (ℓ, s; t) - u_{0} (s) v_{x}^{j} (0, s; t)] ds . \end{matrix}

Reminding that the linear system (33) has a constant coefficient matrix $A$ , while the right-hand side is a time-varying input vector for $t \in (0, t_{f}]$ . Hence, we can obtain

(39)

c (t) = {(A^{T} A)}^{- 1} A^{T} e (t) .

Upon substituting the time-varying coefficients $c (t) = {a_{j} (t)}$ into Eq. (29) we can obtain the time-varying singular solution $u (x, t) = g (x; t)$ .

Example 1

In order to assess the accuracy of the new method, we consider an exact solution:

(40)

u (x, t) = \exp (- t - \frac{x}{\sqrt{ε}})

of Eq. (1), where we take

ε = 0.005, a = 0.1

and

c = - (2 + a) \sqrt{ε}

, such that

S (x, t) = 0

In the WFIEM we take $m_{1} = 12, m_{2} = 0$ , and $n_{q} = 31$ , which is convergence with 37 steps as shown in Fig. 1(a), where the convergence criterion is given by $ε_{1} = 10^{- 10}$ . In Fig. 1(b) we plot the numerical and exact solutions at $t_{0} = 1$ , whose maximum error is $1.77 \times 10^{- 4}$ .

In Fig. 2 we plot the numerical errors in a time interval $t \in (0, 1]$ , whose maximum error in the whole domain is $1.91 \times 10^{- 4}$ . It can be seen that the WFIEM is very accurate and has no problems of error propagation and error amplified.

Example 2

Next we consider a more complex exact solution with two boundary layers at $x = 0$ and $x = 1$ :

(41)

u (x, t) = t (1 - x) + t [1 + (x - 1) \exp (- \frac{x}{\sqrt{ε}}) - x \exp (\frac{x - 1}{\sqrt{ε}})],

where we take

ε = 0.01, a = - 0.1

and

c = - 0.19

, and accordingly the exact

S (x, t)

can be computed from Eq. (1).

In Fig. 3(a) we plot the numerical solution, while in Fig. 3(b) the exact solution in a time interval $t \in (0, 2]$ , whose maximum error in the whole domain is $2.88 \times 10^{- 4}$ . It can be seen that the numerical solution is very close to the exact one. Again we can observe that the error is not being amplified.

Example 3

Finally we consider

(42)

\begin{matrix} w_{t} (x, t) - ε w_{xx} (x, t) + \frac{w (x, t)}{2} = e^{t} - 1 + \sin (π x), (x, t) \in (0, 1) \times (0, 1], \\ w (0, t) = w (1, t) = 0, \\ w (x, 0) = 0, \end{matrix}

which is a variant of Eq. (32) in Clavero and Gracia (2010).

In order to apply the exponentially-fitted trial functions in Eqs. (30) and (31) to solve the above problem we need to consider the following variable transformation:

(43)

u (x, t) = w (x, t) + xt,

such that Eq. (42) becomes

(44)

\begin{matrix} u_{t} (x, t) - ε u_{xx} (x, t) + \frac{u (x, t)}{2} = x + \frac{xt}{2} + e^{t} - 1 + \sin (π x), \\ u (0, t) = 0, u (1, t) = t, \\ u (x, 0) = 0 . \end{matrix}

Solving $u (x, t)$ by the WFIEM, one can obtain $w (x, t) = u (x, t) - xt$ .

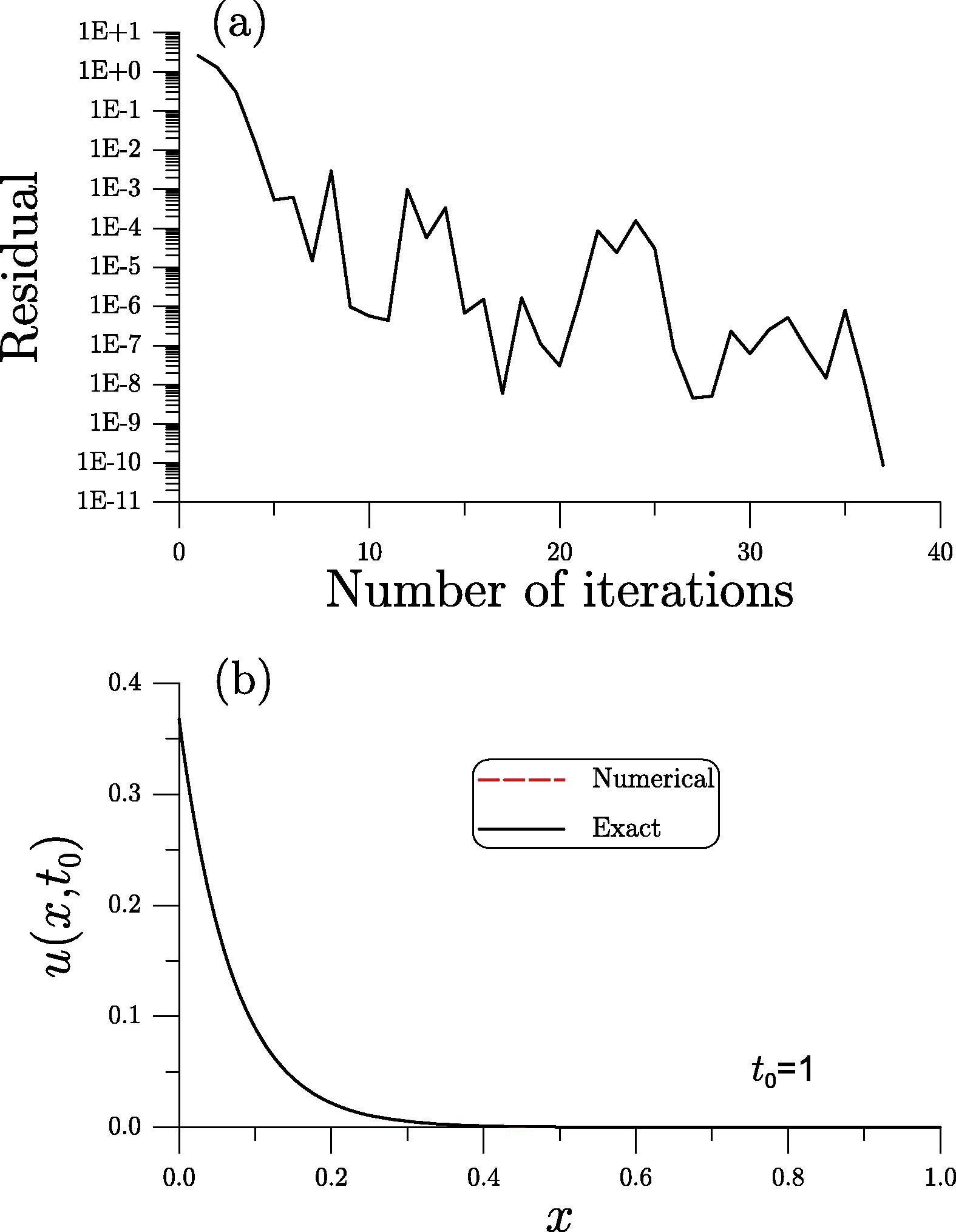
For the singular problem of example 1 solved by the WFIEM, (a) showing the convergence iterations, and (b) comparing numerical and exact solutions.

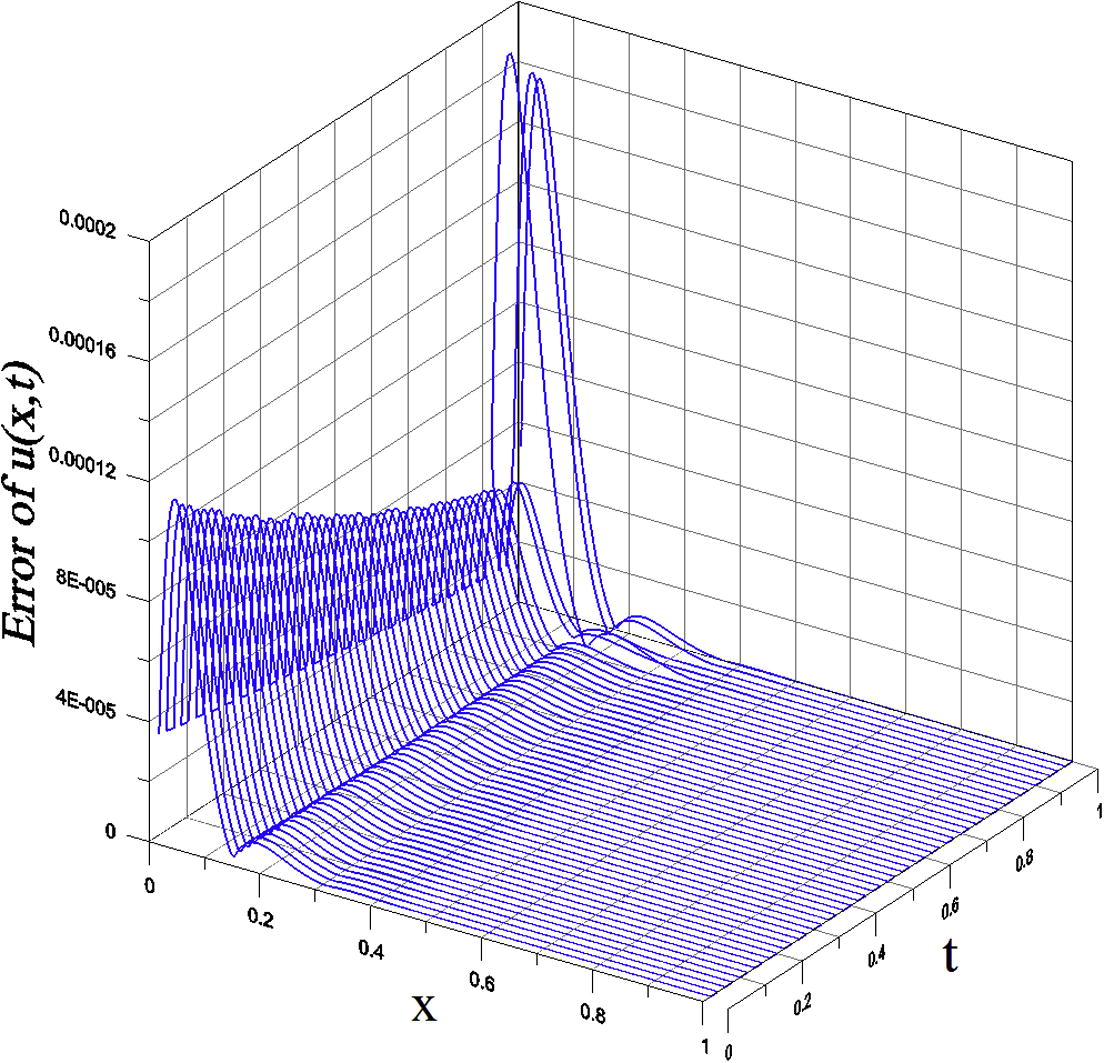
For the singular problem of example 1 solved by the WFIEM, showing the numerical errors in a time interval.

For the singular problem of example 2 solved by the WFIEM, comparing the numerical and exact solutions in a time interval.

We take $ε = 10^{- 4}$ for a highly singular problem. We take $m_{1} = m_{2} = 100$ , and $n_{q} = 31$ in the WFIEM, which converges after 448 steps under the convergence criterion $ε_{1} = 10^{- 10}$ , as shown in Fig. 4(a). In Fig. 4(b) we plot the numerical solutions at two different times.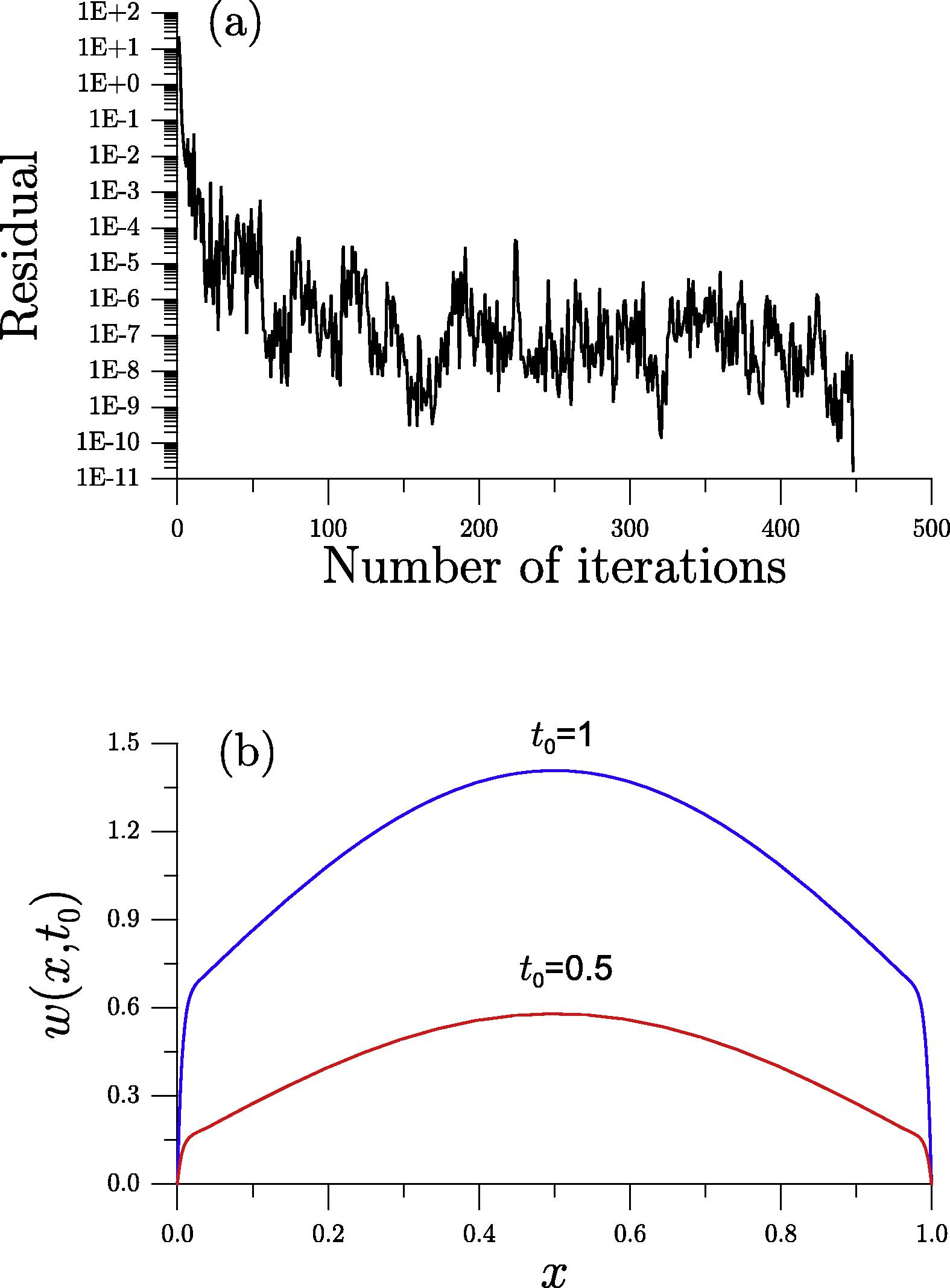

For the singular problem of example 3 solved by the WFIEM, (a) showing the convergence iterations and (b) showing numerical solutions at two different times.

6 Conclusions

In this paper we have derived a weak-form integral equation method to tackle the highly singular problem of the one-dimensional convection–diffusion equation. Because the closed-form spectral functions were used as the adjoint Trefftz test functions in the integral equation, we can easily find the singular solution at any time. The use of exponentially-fitted trial functions as solution bases can faithfully capture the singular behavior in the boundary layers. Through numerical experiments, we have confirmed that the proposed algorithm is applicable to the singular convection–diffusion equation. Moreover, the WFIEM is very accurate and no error propagation and amplification.

Acknowledgements

The Chair Professor of Hohai University and the Thousand Talents Programme of China granted to the author are highly appreciated.

References

Boglaev I.P., . Finite difference domain decomposition algorithms for a parabolic problem with boundary layers. Comput. Math. Appl.. 1998;36:25-40.
[Google Scholar]
Clavero C., Gracia J.L., . High order methods for elliptic and time dependent reaction-diffusion singularly perturbed problems. Appl. Math. Comput.. 2005;168:1109-1127.
[Google Scholar]
Clavero C., Gracia J.L., . On the uniform convergence of a finite difference scheme for time dependent singularly perturbed reaction-diffusion problems. Appl. Math. Comput.. 2010;216:1478-1488.
[Google Scholar]
Gie G.M., Jung C.Y., Temam R., . Analysis of mixed elliptic and parabolic boundary layers with corners. Int. J. Diff. Eqs.. 2013;2013:13. Article ID 532987
[Google Scholar]
Hamouda M., Jung C.Y., Temam R., . Boundary layers for the 3D primitive equations in a cube: the supercritical modes. Nonlinear Anal.. 2016;132:288-317.
[Google Scholar]
Hemker P.W., Shishkin G.I., Shishkina L.P., . $ε$ -uniform schemes with high-order time accuracy for parabolic singular perturbation problems. IMA J. Numer. Anal.. 2000;20:99-121.
[Google Scholar]
Kadalbajoo M.K., Patidar K.C., . A survey of numerical techniques for solving singularly perturbed ordinary differential equations. Appl. Math. Comput.. 2002;130:457-510.
[Google Scholar]
Kadalbajoo M.K., Gupta V., . A brief survey on numerical methods for solving singularly perturbed problems. Appl. Math. Comput.. 2010;217:3641-3716.
[Google Scholar]
Kopteva N., . On the uniform in small parameter convergence of a weighted scheme for the one dimensional time dependent convection-diffusion equation. Comput. Math. Math. Phys.. 1997;37:1173-1180.
[Google Scholar]
Linß T., Madden N., . Parameter uniform approximations for time-dependent reaction-diffusion problems. Numer. Methods Partial Differ. Eq.. 2007;23:1290-1300.
[Google Scholar]
Liu C.-S., . An equilibrated method of fundamental solutions to choose the best source points for the Laplace equation. Eng. Anal. Boundary Elem.. 2012;36:1235-1245.
[Google Scholar]
Liu C.-S., . A BIEM using the Trefftz test functions for solving the inverse Cauchy and source recovery problems. Eng. Anal. Boundary Elem.. 2016;62:177-185.
[Google Scholar]
Liu C.-S., . Solving third-order singularly perturbed problems: exponentially and polynomially fitted trial functions. J. Math. Research. 2016;8(2):16-24.
[Google Scholar]
Liu C.-S., Chang C.W., . A global boundary integral equation method for recovering space-time dependent heat source. J. Heat Mass Transfer. 2016;92:1034-1040.
[Google Scholar]
Liu C.-S., Wang P., . An analytic adjoint Trefftz method for solving the singular parabolic convection-diffusion equation and initial pollution profile problem. J. Heat Mass Transfer. 2016;101:1177-1184.
[Google Scholar]
Morton K.W., . Numerical Solution of Convection-Diffusion Problems. New York: Academic Chapman & Hall; 1996.
Mukherjee K., Natesan S., . Richardson extrapolation technique for singularly perturbed parabolic convection-diffusion problems. Computing. 2011;92:1-32.
[Google Scholar]
Ng-Stynes M.J., O’Riordan E., Stynes M., . Numerical methods for time-dependent convection-diffusion equations. J. Comput. Appl. Math.. 1988;21:289-310.
[Google Scholar]
Rajan M.P., Reddy G.D., . An iterative technique for solving singularly perturbed parabolic PDE. J. Appl. Math. Comput.. 2016;50:199-225.
[Google Scholar]
Shishkin G.I., . On finite difference fitted schemes for singularly perturbed boundary value problems with a parabolic boundary layer. J. Math. Anal. Appl.. 1997;208:181-204.
[Google Scholar]
Temam R., Jung C.Y., Gie G.M., . Recent progresses in boundary layer theory. Discr. Contin. Dyna. Sys.. 2015;36:2521-2583.
[Google Scholar]