Translate this page into:
Short-term wind power prediction based on IBOA-AdaBoost-RVM
⁎Corresponding author. 18738309135@163.com (Kunpeng Li)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
This study introduces an innovative model, namely IBOA-AdaBoost-RVM, which leverages the Improved Butterfly Optimization Algorithm (IBOA), Adaptive Boosting (AdaBoost), and Relevance Vector Machine (RVM). This model is used to solve the problem of low precision of wind power prediction. Initially, normalization is applied to reduce the influence of varying data dimensions. Subsequently, input variables are determined through the Pearson correlation method. Lastly, the efficacy of the introduced model is assessed across four distinct seasonal monthly data sets. The observed outcomes indicate that the proposed model outperforms other models in terms of evaluation metrics, with the average R2, RMSE, MAE, and MAPE values across the four datasets being 0.954, 10.403, 7.032, and 0.645, respectively, show that the proposed method has potential in the field of wind power prediction.
Keywords
Wind power forecasting
BOA
AdaBoost
RVM
1 Introduction
The surge in worldwide economic growth coupled with a steady increase in population figures has led to a growing need for energy, historically satisfied by the consumption of fossil fuels (He et al., 2024a). However, the widespread utilization of conventional energy sources in recent years has engendered increasingly severe issues such as environmental degradation and climate change (Abou et al., 2023). Consequently, promoting the development of clean energy has become a global consensus. Clean energy refers to forms of energy production and utilization that generate minimal to no pollutants, with wind energy being a notable example. Owing to its renewable nature, environmental friendliness, and abundant availability, the advancement of wind power has garnered significant attention worldwide (Tan et al., 2024).
Numerous researchers have explored various methodologies to strengthen the exactness of short-term wind power prediction, including physical, statistical, and artificial intelligence methods (Carpinone et al., 2015). While physical prediction methods necessitate solving complex partial differential equations, rendering them computationally intensive (Ye et al., 2017), statistical methods entail simpler modeling through statistical regression fitting of historical data but exhibit significant prediction errors when confronted with nonlinear and non-stationary wind power series (Sopeña et al., 2023). Artificial intelligence, particularly deep learning methods rooted in machine learning, has arisen as a promising avenue [Sait et al., 2024a]. Techniques like Convolutional Neural Networks (CNN) [Sait et al., 2024b; Ma et al., 2024] and Recurrent Neural Networks (RNN) [Mehta et al., 2024; Yuan et al., 2024a] within deep learning have gained extensive usage in the field of short-term wind energy forecasting.
In the field of machine learning, bias-variance tradeoff is a significant concept to explain the generalization effectiveness of an algorithm (Doroudi and Rastegar, 2023). The emergence of ensemble learning makes it possible to guarantee good generalization performance on complex monitoring data of wind power. As one of the popular ensemble learning algorithms, the AdaBoost algorithm stands out for its capacity to mitigate bias and variance by combining multiple weak learners, thereby improving the model’s capacity for generalization. The adaBoost method has been commonly applied in various fields and has shown excellent capabilities in classification and regression problems (Zounemat-Kermani et al., 2021). An et al. (2021) introduced a wind power forecasting model (AdaBoost-PSO-ELM), and verified it through the data of wind turbines in Turkey. The findings from the experiment indicate that AdaBoost-PSO-ELM achieves a superior accuracy rate. Ren et al. (2022) introduced an improved genetic algorithm-assisted AdaBoost double-layer learner (GA-ADA-RF) for predicting the oil temperature of tunnel boring machines, and the experiment revealed that the GA-ADA-RF has better predictive capability.
While the aforementioned evidence highlights the efficacy of the AdaBoost algorithm, it also underscores its inherent limitations, notably susceptibility to overfitting and its constrained capability to address nonlinear challenges (Vincent and Duraipandian, 2024). Hence, this study introduces the Relevance Vector Machine (RVM) as a solution to mitigate these drawbacks. RVM, a variant of SVM, exhibits inherent sparsity, thereby mitigating overfitting during training (Qiu et al., 2024). Furthermore, RVM's utilization of kernel functions enables effective handling of nonlinear problems, thereby compensating for AdaBoost's deficiencies.
Given the AdaBoost algorithm's capacity to diminish both variance and bias while enhancing model generalization, coupled with the intrinsic strengths of RVM that can compensate for AdaBoost's limitations, this research integrates RVM as a weak learner within the AdaBoost framework to advance model efficacy. Moreover, the selection of hyperparameters holds paramount importance in influencing the performance of machine learning algorithms, with an optimal combination significantly enhancing model performance. Swarm intelligence optimization algorithms, simulating population hunting behaviors in nature, demonstrate remarkable prowess in optimizing hyperparameters and are frequently employed for this purpose (El-Kenawy et al., 2024a; Yuan et al., 2023a; Abdollahzadeh et al., 2024; Yuan et al., 2024b). However, swarm intelligence algorithms frequently suffer from the drawbacks of a skewed distribution in the initial population and a tendency to converge to local optima rather than global solutions (El-Kenawy et al., 2024b; Duzgun et al., 2024; Chu et al., 2024). Therefore, this study proposes an improved butterfly optimization algorithm to determine the best combination of hyperparameters for the prediction model.
2 Related algorithms
2.1 Adaptive boosting (AdaBoost)
AdaBoost is a renowned ensemble algorithm (Freund and Schapire, 1997). During each iteration, AdaBoost adjusts the weight of individual samples, assigning higher weights to previously misclassified samples to emphasize their importance in subsequent iterations. Consequently, the new learner focuses more on these challenging instances. Ultimately, AdaBoost combines these learners through weighted voting to yield predicted sample values, thereby enhancing the overall learner's performance.
2.2 Relevance vector machine (RVM)
RVM, a machine learning algorithm rooted in Bayesian theory (Tipping, 2001), serves as a sparse probability model utilized for both classification and regression analyses. Notably, the sparsity of the RVM algorithm is a key characteristic: during training, most weights tend towards infinity, effectively nullifying the contribution of corresponding features to the model. Consequently, RVM automatically identifies and emphasizes the most crucial features for the prediction task while disregarding irrelevant ones.
2.3 Butterfly optimization algorithm (BOA)
Butterfly optimization algorithm (BOA) (Arora and Singh, 2019) is a meta-heuristic algorithm for global optimization inspired by natural heuristics, initially introduced by Arora and Singh in 2019. It emulates the cooperative movement of butterflies towards a food source, a behavior observed in nature. Butterflies navigate by receiving, sensing, and analyzing odors in the air to locate potential food sources or mates.
3 The proposed algorithm (IBOA-AdaBoost-RVM)
3.1 Improved butterfly optimization algorithm (IBOA)
Chaotic mapping, characterized by attributes such as good ergodicity, non-repeatability, unpredictability, and non-periodicity, is leveraged to enrich population diversity and enhance algorithm performance (Peng et al., 2023; Xing et al., 2024). In the original butterfly optimization algorithm, butterfly diversity suffers due to random initialization of the population. Therefore, this study introduces Tent chaotic mapping to uniformly distribute the butterfly population and broaden its search range. It is defined as:
The search step length of a single butterfly is not set in the original BOA algorithm. During the operation of the algorithm, due to the high degree of freedom of individuals, the search step length is not limited, resulting in fast search speed in the early stage of the search, low search accuracy in the late stage, and easy-to-fall into the local optimum or far from the global optimum. To avoid the restriction of butterfly individual search step size due to this situation, this study proposes a weight coefficient that adaptively adjusts according to individual fitness value, and the formula is as follows:
If the fitness value of the current individual is nearly equivalent to the worst global fitness, the higher the weight coefficient assigned to that individual, the greater the step size they will take in their movement, aimed at avoiding entrapment in a local optimum. If the current individual fitness value is much different from the global worst value, that is, it is nearer to the global optimal value, then the weight coefficient of the individual is smaller, and the smaller moving step size ensures the high-precision search of the population in the later stage of the algorithm, and avoids the individual skipping the global optimal value, which reduces the performance of the algorithm.
Furthermore, following the “No free lunch” theorem (Rashki and Faes, 2023; Yuan et al., 2023b), a single algorithm cannot be fully applicable to all problems, so this work introduces a sine–cosine algorithm to improve the search phase of butterfly optimization algorithm. Combined with the adaptive weight coefficient, the formula of the global search stage and the local search stage of butterfly optimization algorithm can be updated as:
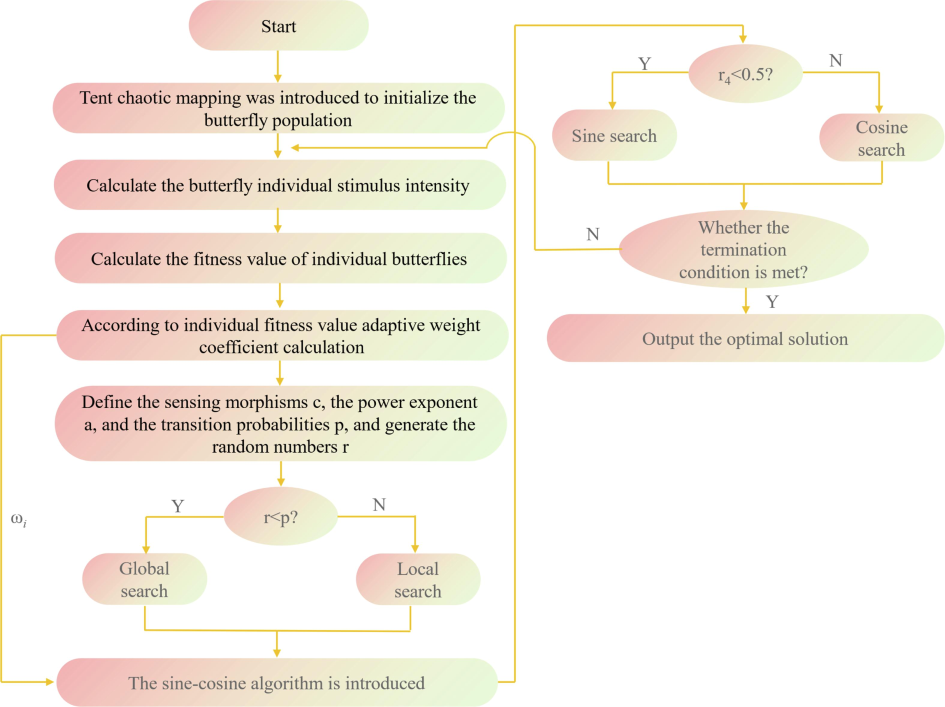
IBOA frame diagram.
3.2 Adaptive boosting based on relevance vector machine (AdaBoost-RVM)
Traditional AdaBoost uses decision trees as weak learners (Zhan et al., 2024). However, decision tree models are susceptible to overfitting, diminishing the model's generalization capacity, and they have limited efficacy in addressing nonlinear problems (He et al., 2024b). The inherent sparsity of the RVM model aids in enhancing the model's generalization ability and mitigating the risk of overfitting. Additionally, RVM can be extended to handle nonlinear problems through kernel techniques, enabling it to tackle more intricate datasets (Zhang et al., 2023). Hence, this study capitalizes on the strengths of both RVM and AdaBoost by utilizing RVM as a weak learner within the AdaBoost framework. The model structure is shown in Fig. 2.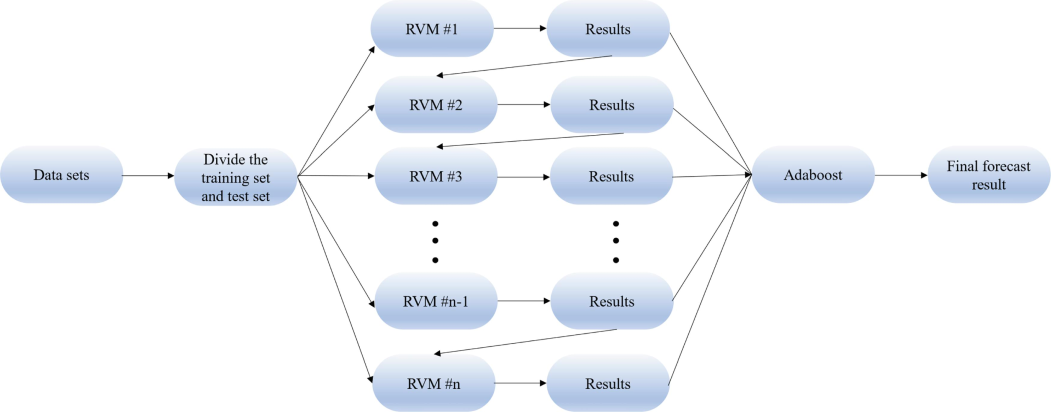
AdaBoost-RVM frame diagram.
3.3 The IBOA-AdaBoost-RVM prediction model
To sum up, the flow of the IBOA-AdaBoost-RVM model introduced in this work is shown in Fig. 3.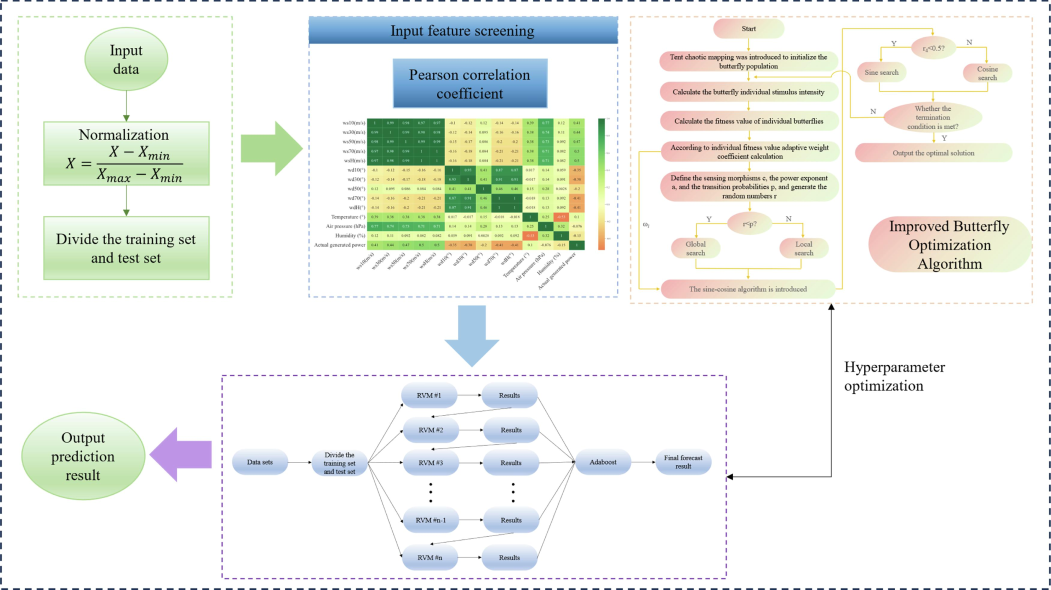
IBOA-AdaBoost-RVM prediction flow chart.
Step 1: Acquire the power production data of the wind farm, and normalize the data to prepare for the subsequent research.
Step 2: Calculate the Pearson correlation coefficient of each input and output variable, and select the appropriate input variable.
Step 3: Weather and power data are used for short-term wind power prediction, and the improved butterfly optimization algorithm optimizes the model's hyperparameters.
Step 4: Output final model prediction results.
4 Experimental simulation and result discussion
4.1 Data description
The dataset comprises measurements taken at a frequency of 15 min. The division between the training and test sets adheres to a ratio of 7:3. The input variables encompass measurements of wind speed, wind direction, temperature, air pressure, and humidity. The validity and reliability of the model are verified by real wind power data. Moreover, to alleviate the impact stemming from the differing scales of the data and augment the precision of the prediction outcomes, this study implements normalization (Hu et al., 2018) as part of the data preprocessing stage.
4.2 Input feature selection
The Pearson method is a common way to measure the degree of correlation between two variables (Zhao et al., 2024). From Fig. 4 (refer to Table 1 for details), it is evident that characteristics highly correlated with actual power generation primarily include wind speed and wind direction attributes. Consequently, wind speed and direction characteristics (excluding the 50-meter wind direction of the wind tower) are chosen as input features for the model in this study.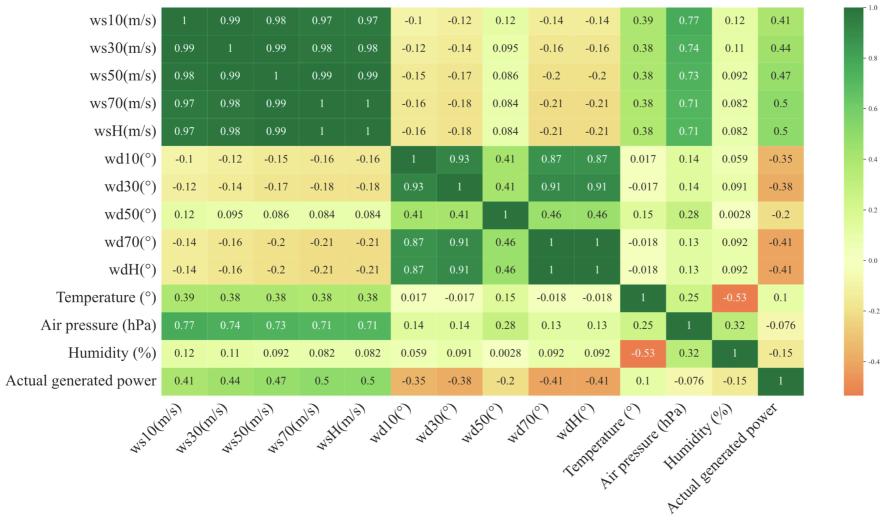
The correlation between various characteristics and actual power generation.
Abbreviations
Parameters
ws10 (m/s)
Wind tower 10 m wind speed (m/s)
ws30 (m/s)
Wind tower 30 m wind speed (m/s)
ws50 (m/s)
Wind tower 50 m wind speed (m/s)
ws70 (m/s)
Wind tower 70 m wind speed (m/s)
wsH (m/s)
Hub height Wind speed (m/s)
wd10 (°)
Wind tower 10 m Wind direction (°)
wd30 (°)
Wind tower 30 m Wind direction (°)
wd50 (°)
Wind tower 50 m Wind direction (°)
wd70 (°)
Wind tower 70 m Wind direction (°)
wdH (°)
Hub height Wind direction (°)
4.3 Evaluation indicators
This article selects the coefficient of determination (R2), root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute percentage error (MAE) to evaluate the accuracy of the model's prediction results.
4.4 Experimental comparison
4.4.1 Experimental comparison in March
Table 2 displays the results of the four evaluation indicators for the introduced model and other comparative models using the spring March dataset. Furthermore, Model1 to Model6 represent the performance of the following models: IBOA-AdaBoost-RVM, BOA-AdaBoost-RVM, AdaBoost-RF, AdaBoost-CNN, AdaBoost-BiLSTM, and AdaBoost-CNN-BiLSTM, respectively.
Mdoel1
Model2
Model3
Model4
Model5
Model6
R2
0.971
0.953
0.944
0.918
0.950
0.960
RMSE
11.060
14.167
15.366
18.604
14.437
13.076
MAE
7.047
9.300
10.197
13.479
10.341
8.821
MAPE
0.418
0.505
0.426
0.897
0.920
0.525
Compared with BOA-AdaBoost-RVM, the IBOA-AdaBoost-RVM model exhibits a 1.8 % increase in the R2 value, a 21.9 % decrease in RMSE, a 24.2 % decrease in MAE, and a 17.2 % decrease in MAPE. Furthermore, employing Random Forest (RF), Convolutional Neural Network (CNN), Bidirectional Long Short-Term Memory Neural Network (BiLSTM), etc., as weak learners for AdaBoost results in weaker performance across all four-evaluation metrics compared to AdaBoost-RVM. From Fig. 5, it is evident that all six models demonstrate satisfactory fitting results for wind power data in March of spring. Nevertheless, upon closer inspection of the locally enlarged graph, it becomes apparent that the IBOA-AdaBoost-RVM model exhibits the most favorable fitting effect, closely aligning with the actual wind power values.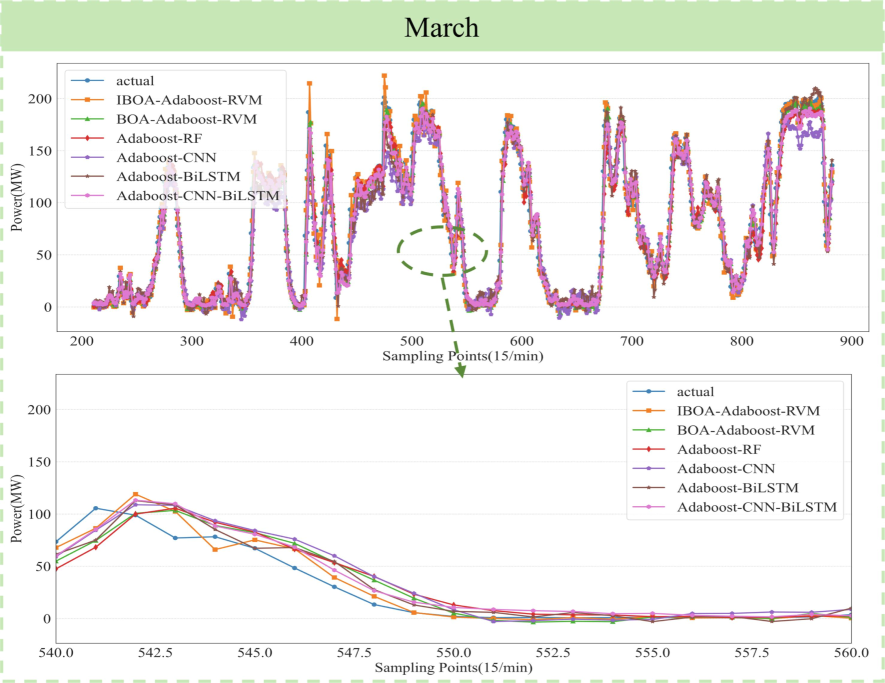
Prediction curves of different models in March.
4.4.2 Experimental comparison in June
Table 3 shows four evaluation indicators of different models on the summer June data set. The four evaluation indicators of the introduced method outperformed the comparative models, with the R2 values increasing by 2.0 %, 6.7 %, 6.9 %, 2.3 %, and 1.5 %, respectively. Additionally, the RMSE values decreased by 17.9 %, 37.3 %, 38.1 %, 19.9 %, and 14.6 %, while the MAE values decreased by 15.9 %, 32.7 %, 42.2 %, 23.1 %, and 13.4 %, and the MAPE values decreased by 12.2 %, 56.1 %, 53.5 %, 22.9 %, and 14.3 %, respectively. Fig. 6 provides further support for the proposed improvement strategy and demonstrates the accuracy of the proposed model.
Mdoel1
Model2
Model3
Model4
Model5
Model6
R2
0.962
0.943
0.902
0.900
0.940
0.948
RMSE
7.905
9.625
12.612
12.771
9.878
9.254
MAE
5.503
6.543
8.178
9.515
7.160
6.354
MAPE
0.776
0.884
1.768
1.668
1.006
0.906
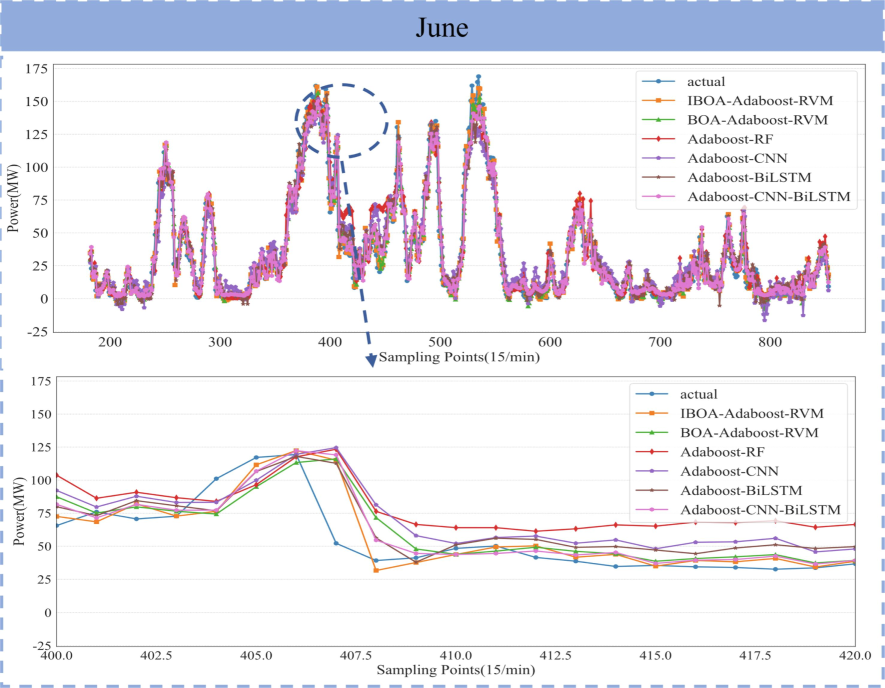
Prediction curves of different models in June.
4.4.3 Experimental comparison in September
As depicted in Table 4, on the autumn September dataset, the R2, RMSE, and MAE values of IBOA-AdaBoost-RVM outperform those of the comparison model. Although the proposed method did not achieve optimal results for all four-evaluation metrics, BOA-AdaBoost-RVM obtained the optimal MAPE value. This outcome further substantiates the feasibility of utilizing RVM as a weak learner for AdaBoost in this study. Moreover, upon examining the image in Fig. 7, it was observed that the introduced method can better capture the trend of changes in true values.
Mdoel1
Model2
Model3
Model4
Model5
Model6
R2
0.961
0.926
0.915
0.909
0.932
0.931
RMSE
8.069
11.141
11.972
12.370
10.680
10.749
MAE
4.722
5.974
6.616
7.452
6.413
6.877
MAPE
0.948
0.726
0.827
1.735
1.420
1.512
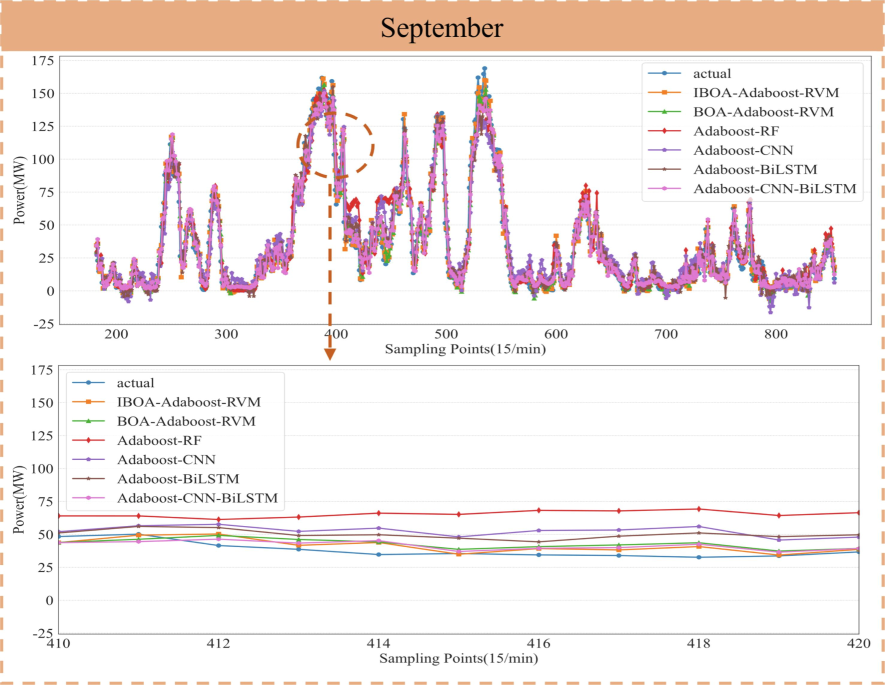
Prediction curves of different models in September.
4.4.4 Experimental comparison in December
As can be seen from Table5, among the six models, only the R2 values of IBOA-AdaBoost-RVM and BOA-AdaBoost-RVM exceed 0.9, with BOA-AdaBoost-RVM reaching 0.92. When compared to AdaBoost-RF, the proposed method demonstrates a 21.5 % increase in R2 value, a 42.6 % reduction in RMSE, a 36.7 % decrease in MAE, and a 45.9 % decrease in MAPE. This further underscore the advanced nature of the method proposed in this study. Fig. 8 provides additional evidence supporting this conclusion.
Mdoel1
Model2
Model3
Model4
Model5
Model6
R2
0.920
0.910
0.757
0.853
0.891
0.819
RMSE
14.576
15.383
25.410
19.763
16.988
21.897
MAE
10.854
11.371
17.140
14.976
12.811
16.259
MAPE
0.438
0.499
0.811
0.585
0.521
0.619
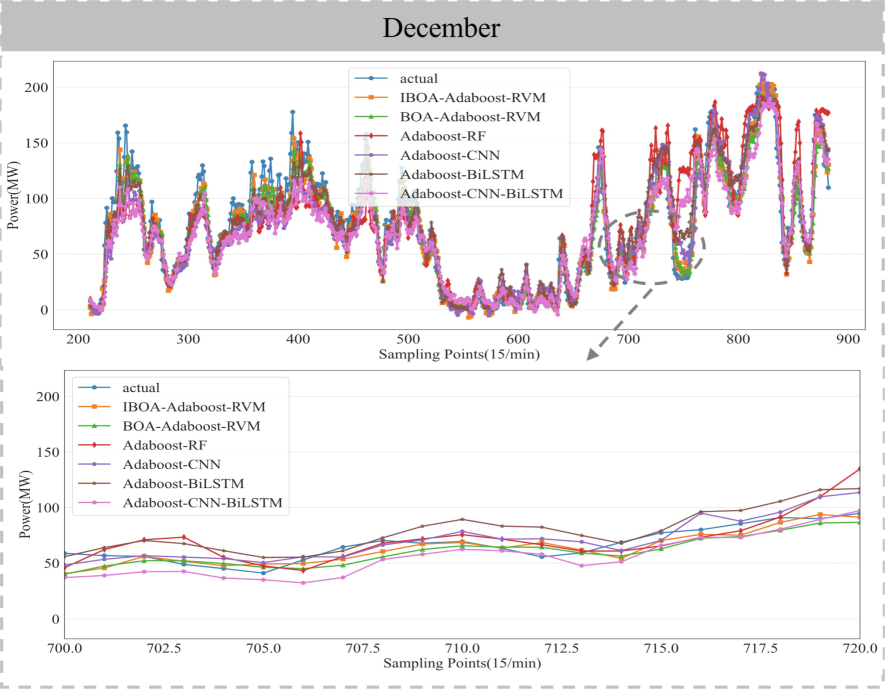
Prediction curves of different models in December.
5 Conclusions
In this study, an innovative model, named IBOA-AdaBoost-RVM, is proposed. The performance of the IBOA-AdaBoost-RVM is verified by four distinct seasonal monthly data sets. Results demonstrate that IBOA-AdaBoost-RVM achieves high forecasting accuracy. The model's prediction results across four different seasons and months consistently yield optimal outcomes, indicative of its robust generalization ability and applicability.
In the future work, data from different geographic locations are considered and compared with more advanced algorithms to further validate the model's excellence. In addition, future studies need to consider applying the model to different forms of renewable energy, such as solar energy, hydrogen energy, and so on.
CRediT authorship contribution statement
Yongliang Yuan: Writing – review & editing, Writing – original draft, Validation, Resources, Methodology, Funding acquisition. Qingkang Yang: Writing – original draft, Methodology, Investigation. Jianji Ren: Writing – review & editing, Supervision, Resources. Kunpeng Li: Writing – review & editing, Supervision, Methodology. Zhenxi Wang: Formal analysis, Conceptualization. Yanan Li: Supervision, Resources. Wu Zhao: Supervision, Formal analysis. Haiqing Liu: Resources.
Acknowledgments
This research work was supported by the National Natural Science Foundation of China (No. 52404163), Fundamental Research Funds for the Universities of Henan Province (No. NSFRF220415), Henan Natural Science Foundation (No. 222300420168), the Natural Science Foundation of Henan Polytechnic University (No. B2021-31), Scientific Studies of Higher Education Institution of Henan province (23B520006), the Fundamental Research Funds for the Universities of Henan Province (NSFRF230503).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Cluster. Comput. 2024:1-49.
- [Google Scholar]
- COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Appl. Energ.. 2023;349:121638
- [Google Scholar]
- Short-term wind power prediction based on particle swarm optimization-extreme learning machine model combined with AdaBoost algorithm. IEEE Access.. 2021;9:94040-94052.
- [Google Scholar]
- Butterfly optimization algorithm: a novel approach for global optimization. Soft. Comput.. 2019;23:715-734.
- [Google Scholar]
- Markov chain modeling for very-short-term wind power forecasting. Electr. Pow. Syst. Res.. 2015;122:152-158.
- [Google Scholar]
- Ship rescue optimization: A new metaheuristic algorithm for solving engineering problems. J. Internet Technol.. 2024;25(1):61-78.
- [Google Scholar]
- The bias–variance tradeoff in cognitive science[J] Cognitive Sci.. 2023;47(1) e13241
- [Google Scholar]
- A novel chaotic artificial rabbits algorithm for optimization of constrained engineering problems[J] Mater. Test. 2024
- [Google Scholar]
- Greylag goose optimization: nature-inspired optimization algorithm. Expert. Syst. Appl.. 2024;238:122147
- [Google Scholar]
- Football optimization algorithm (FbOA): A novel metaheuristic inspired by team strategy dynamics. J. Artif. Intell. Meta.. 2024;1 21-1-38
- [Google Scholar]
- A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci.. 1997;55(1):119-139.
- [Google Scholar]
- A short-term wind power prediction approach based on an improved dung beetle optimizer algorithm, variational modal decomposition, and deep learning. Comput. Electr. Eng.. 2024;116:109182
- [Google Scholar]
- Research and application of a hybrid model based on Meta learning strategy for wind power deterministic and probabilistic forecasting. Ene. Convers. Manage.. 2018;173:197-209.
- [Google Scholar]
- A novel method for remaining useful life of solid-state lithium-ion battery based on improved CNN and health indicators derivation. Mech. Syst. Signal Pr.. 2024;220:111646
- [Google Scholar]
- A new enhanced mountain gazelle optimizer and artificial neural network for global optimization of mechanical design problems. Mater. Test.. 2024;66(4):544-552.
- [Google Scholar]
- An intelligent hybrid approach for photovoltaic power forecasting using enhanced chaos game optimization algorithm and Locality sensitive hashing based Informer model. J. Build. Eng.. 2023;78:107635
- [Google Scholar]
- A hybrid PV cluster power prediction model using BLS with GMCC and error correction via RVM considering an improved statistical upscaling technique. Appl. Energ.. 2024;359:122719
- [Google Scholar]
- No-free-lunch theorems for reliability analysis. Asce-Asme J. Risk U A.. 2023;9(3) 04023019
- [Google Scholar]
- Genetic algorithm-assisted an improved AdaBoost double-layer for oil temperature prediction of TBM. Adv. Eng. Inform.. 2022;52:101563
- [Google Scholar]
- Artificial neural network infused quasi oppositional learning partial reinforcement algorithm for structural design optimization of vehicle suspension components. Mater. Test. 2024
- [Google Scholar]
- Optimal design of structural engineering components using artificial neural network-assisted crayfish algorithm. Mater. Test. 2024
- [Google Scholar]
- A benchmarking framework for performance evaluation of statistical wind power forecasting models. Sustain Energy. Techn.. 2023;57:103246
- [Google Scholar]
- Research on the short-term wind power prediction with dual branch multi-source fusion strategy. Energy.. 2024;291:130402
- [Google Scholar]
- Sparse bayesian learning and the relevance vector machine. J. Mach. Learn. Res.. 2001;1(Jun):211-244.
- [Google Scholar]
- Detection and prevention of sinkhole attacks in MANETS based routing protocol using hybrid AdaBoost-Random Forest algorithm. Expert Syst. Appl.. 2024;249:123765
- [Google Scholar]
- Improving teaching-learning-based optimization algorithm with golden-sine and multi-population for global optimization. Math. Comput. Simulat.. 2024;221:94-134.
- [Google Scholar]
- Short-term wind power prediction based on spatial model. Renew Energ.. 2017;101:1067-1074.
- [Google Scholar]
- Yuan, Y., Yang, Q., Wang, G., Ren, J., Wang, Z., Qiu, F., Liu, H., 2024. Combined improved tuna swarm optimization with graph convolutional neural network for remaining useful life of engine[J]. Qual. Reliab. Eng. Int.
- Coronavirus mask protection algorithm: A new bio-inspired optimization algorithm and its applications. J. Bionic. Eng.. 2023;20(4):1747-1765.
- [Google Scholar]
- Multidisciplinary design optimization of dynamic positioning system for semi-submersible platform. Ocean Eng.. 2023;285:115426
- [Google Scholar]
- Attack-defense strategy assisted osprey optimization algorithm for PEMFC parameters identification. Renew. Energ.. 2024;225:120211
- [Google Scholar]
- Reconstructing historical forest spatial patterns based on CA-AdaBoost-ANN model in northern Guangzhou China. Landscape Urban Plan.. 2024;242:104950
- [Google Scholar]
- Prediction of surface settlement in shield-tunneling construction process using PCA-PSO-RVM machine learning. J. Perform Constr. Fac.. 2023;37(3) 04023012
- [Google Scholar]
- Refined landslide susceptibility mapping in township area using ensemble machine learning method under dataset replenishment strategy. Gondwana Res.. 2024;131:20-37.
- [Google Scholar]
- Ensemble machine learning paradigms in hydrology: A review. J Hydrol.. 2021;598:126266
- [Google Scholar]
Appendix A
Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jksus.2024.103550.
Appendix A
Supplementary data
The following are the Supplementary data to this article:







