Translate this page into:
Time-fractional telegraph equation for hydrogen diffusion during severe accident in BWRs
⁎Corresponding author. Tel.: +52 55 5804 4645; fax: +52 55 5804 4900. gepe@xanum.uam.mx (G. Espinosa-Paredes)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
The aim of this work is to study the behavior of heat and mass transfer during hydrogen generation in the core of the boiling water reactor (BWR). The core of the BWR is a system highly heterogeneous where the transport processes are complex. The core is considered as an average channel of the fuel assembly, which consists of arrays of in-line fuel rod. This study considers diffusion and reaction due to generation of hydrogen during severe accident in a nuclear power plant with reactor type BWR. The temperature distribution in the nuclear fuel is obtained with a normal diffusion model, whereas that of the distribution of the hydrogen concentration is obtained with a time-fractional telegraph equation (TFTE). The TFTE allows consider the anomalous diffusion processes (non-Fickian effects), which govern the transport in heterogeneous systems.
The numerical experiments were performance in an averaging channel that represents a core reactor with the fuel rod with its gap and cladding and cooling steam, in order to establish the importance of the effects of hydrogen diffusion in a severe accident scenario. The initial conditions of this scenario correspond to 100% of rated power, with scram of the reactor, and without cooling flow. The temperature of the fuel is incremented due to decay heat, and due to lack of cooling the fuel temperature increases, which eventually causes fuel cladding oxidation and hydrogen generation.
The hydrogen concentration results in a reaction due to oxidation for different values of fractional coefficient, at and short times were obtained. The physical meaning is discussed when the fractional coefficient tends to a value of 1 and when it tends to a value of 0.5, i.e., within the limits of validity of the fractional model proposed. According to the results obtained the hydrogen concentration is inversely proportional to the fractional coefficient. These results are relevant for decision making in terms of risk analysis in nuclear power plant with BWR.
Keywords
Fractional mass transport
Hydrogen generation
Severe accident
Zircaloy oxidation
Decay heat
Reactor BWR
1 Introduction
Safety of nuclear power plants is essential and safety standards are continuously reviewed and upgraded as new developments and research are performed. Continuous research regarding this subject is fundamental for the nuclear industry. Although severe accident analysis and research have been performed throughout the evolution of nuclear industry, it has not yet considered all plausible scenarios (Espinosa-Paredes et al., 2012a). Adequate analyses are needed for all phases of severe accidents in order to maintain or improve safety margins.
Severe core damage of a boiling water reactor (BWR) is produced during a nuclear accident by the critical oxidation of the Zircaloy components in the core by steam (Olander, 1994). A large review on Zry-4 fuel cladding behavior in a loss-of-coolant accident (LOCA) was reported by Erbacher and Leistikow (1985), which studied the chemical reactions between reactor zirconium alloy cladding and high temperature steam during a topical subject in the severe accident program for long time. Overheating of the fuel elements in a BWR would be caused by a loss of coolant accident or a power excursion, which led in a violent chemical reaction of the cladding with steam. During a station blackout with early loss of cooling with a typical heating rate, the feed of water can result in the accelerated oxidation of Zry-4 cladding and a significant increase in hydrogen production and the accelerated liquefaction and slumping of {U–Zr} – O2 (Allison et al., 2012).
The oxidation is a very large exothermic reaction with a great heat release, and it is made under high temperature accident conditions, it determines the hydrogen rate production and the cladding brittleness degradation (Fichot et al., 2004). The Zry-4 oxidation in steam is bitter and more than a half of the heat released during oxidation in air causes a higher rise in the temperature (Beuzet et al., 2011). The last two decades, has seen a higher interest in the phenomena during a hypothetical severe nuclear accident and it was intensified by the Fukushima Daiichi station blackout accident.
To design a nuclear power plant it is very important to make the safety evaluation in order to prove safety features of systems and install equipment to prevent any kind of accidents. For this reason the analysis of design based accident is considered as reference, whose main differences with the modeling of severe accident are related to the fact that the modeled system itself is not well defined due to the that molten core material having constants changes of geometrical factors, composition and its properties.
Typical codes for severe accident analysis at nuclear reactor are MELCOR (Methods for Estimation of Leakages and Consequences of Releases, Gauntt et al. 2000), MAAP (Modular Accident Analysis Program, MAAP4, 1994), and SCDAP/RELAP5 (SCDAP: Severe Core Damage Analysis Package, Siefken et al., 2001a,b), which are widely used for the integral analysis of core melt accident progression and the resultant lower head response expected at the reactor lower plenum. However, these codes consider diffusion normal in the mass transfer processes, where this theory fails for the complexity of the phenomena in highly heterogeneous systems being crucial in severe accidents. Then, an alternative for considering anomalous diffusion is with differential equations of fractional order.
In this work the behavior of the temporal evolution of the distributions of the hydrogen concentration and temperatures in the core of the boiling water reactor (BWR) during a severe accident, is analyzed numerically. The core of the BWR is a system highly heterogeneous where the simultaneous heat and mass transport is. This study considers diffusion and reaction due to generation of hydrogen during severe accidents in a nuclear power plant with reactor type BWR. The fractional-time diffusion equation or the so called time-fractional telegraph equation (TFTE) for hydrogen diffusion was applied in order to consider the anomalous diffusion processes (non-Fickian effects), and normal diffusion for heat transfer in the nuclear fuel. The hydrogen concentration results in a reaction due to oxidation for different values of fractional coefficient, at t = 0 and short times were obtained. These results are relevant for decision making in terms of risk analysis in nuclear power plant with BWR.
Differential equations of fractional order have recently proved to be valuable tools in the modeling of many phenomena in various fields of science and engineering (e.g., Fellah et al., 2002; Soczkiewicz, 2002; Zhou and Selim, 2003; Magin and Ovadia, 2008; Scherer et al. 2008). Fractional space derivatives are used to model anomalous diffusion or dispersion (e.g., Wu et al., 2015a,b; Yang et al., 2015), i.e., non-Fickian effects for mass transfer where a particle plume spreads at a rate inconsistent with the classical Brownian motion model, and the plume may be asymmetric. When a fractional derivative replaces the second derivative in a diffusion or dispersion model, it leads to enhanced diffusion (Meerschaert et al., 2006).
The analytical solution of the TFTE in a bounded-space domain derived by Huang (2009) is applied in this work.
2 BWR description
The BWR configuration and the flow paths are illustrated in Fig. 1 (BWR, 1975). The reactor water recirculation system consists of two external loops to the reactor vessel. Each loop contains a pump with a directly coupled motor, a flow control valve, and two shut-off valves. The jet pump located within the reactor vessel provides a continuous internal circulation path for a major portion of the core coolant flow. The recirculation pumps take the suction from the downward flow in the annulus between the core shroud and the vessel wall. The core flow is taken from the vessel through two recirculation nozzles. Into this site, the flow is pumped to a higher pressure, distributed through a manifold to which a number a riser pipes are connected, and returned to the vessel inlet nozzles.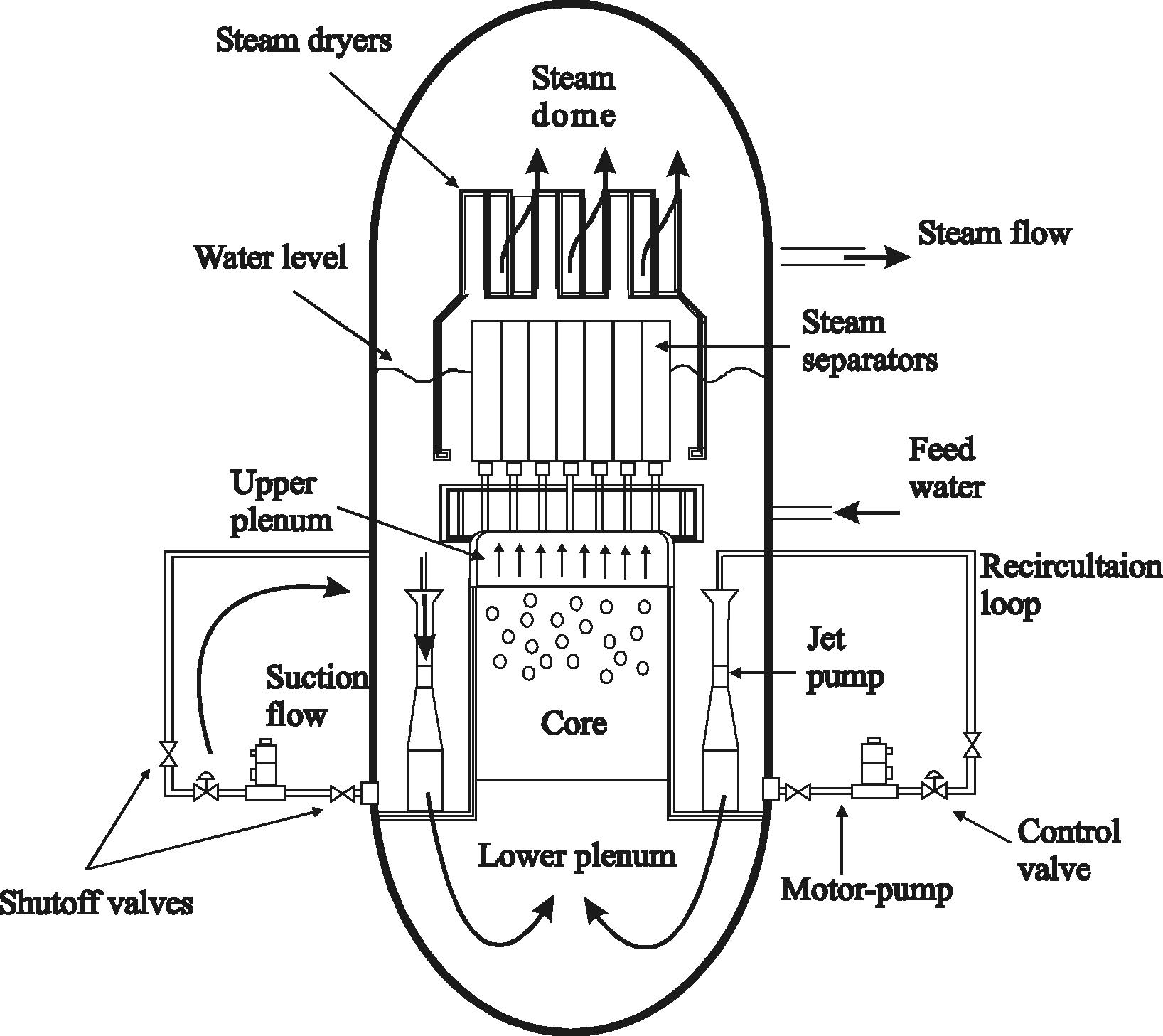
BWR configuration and flow paths.
The coolant water passes along the individual fuel rods inside the fuel channel where it boils and becomes a two-phase steam and water mixture. In the core, the two-phase fluid generates upward flows through the axial steam separators while the steam continues through the dryers and flows directly out through the steam lines into the turbine-generator. The condensate flow is then returned through the feedwater heaters by the condensate-feedwater pumps into the vessel.
3 Core damage progression and phenomenology
During a severe accident is exceeded the design basis of the nuclear power plant (NPP) sufficiently to cause failure of structures, materials and systems, i.e., core damage and hydrogen production, fission products released, and debris bed. In this sense it is necessary to understand fully the progression of core damage, since the action mitigation has effects that may be decisive in accident progression (Espinosa-Paredes et al., 2012b).
As a result of heat produced by radioactive decay of the active elements, known as the decay energy, the fuel temperature begins to rise, even when the reactor is in stop if the core cooling is inadequate (Todreas and Kazimi, 1990).Then, to the extent that the core loses its cooling, the core will be damaged by overheating and release radioactive elements.
At temperatures of 1073 K, molten occurs of the alloy Ag–In–Cd of the control rod. The guide tube failure will cause the attack of the alloy Zircaloy of the fuel element. The liquid mixture may fall by gravity effects and move into the nucleus, causing localized damage in the fuel cladding. Eventually re-solidify and may produce block in cold areas of the lower region of the nucleus. At temperatures around 1173 K, the zirconium in the cladding of the fuel begins to react chemically with steam, which produces hydrogen and reaction heat. At temperatures above 1500 K, the reaction becomes very large, accelerating overheating of the fuel, the oxidation of Zircaloy of the fuel cladding by steam effects, it becomes important. This reaction is exothermic and the temperature increases the rate of oxidation increases, the energy release as well as the generation of hydrogen is large.
The degree to which hydrogen is produced depends on the temperature of zirconium in the core and the amount of steam available. When the temperature rises about 1500 K the following reaction is presented:
On the other hand the heating of the fuel elements results in a loss of mechanical properties with consequent ballooning that can lead to breakage. The deformation occurs due to the difference in pressure between the inside of the fuel element and reactor pressure. The internal pressure of the fuel element is a function of fuel temperature on the thermodynamic process of heating at constant volume.
Experiments have shown that the rupture of the fuel does not block the flow of steam but it deviates by reducing the natural flow in the core. The fuel temperature increases and most of the hydrogen generated in the accident occurs during this early stage. At intermediate temperatures (2033 and 2273 K), if the thickness of the oxide layer is sufficiently large, will retain the Zr oxide inside molten metal, preventing the fall by gravity and staying in touch with the pellets dioxide uranium (UO2) which, will remain until the outer layer of oxide loses its strength due to its dissolution by molten Zr or due to mechanical failure or because it reaches the melting temperature (2963 K) of ZrO2.
After a severe accident, when fuel rod cladding has disappeared, the fuel pellets may collapse and form a debris bed, which is difficult to cool due to complex flow path between the solid fragments. Then the debris bed cannot cooling the temperature rises up to the fuel melting point and a large curium pool grows through the core, and finally relocates down into lower plenum (Li and Ma, 2011).
4 Mathematical model
The problem under consideration is depicted in Fig. 2, which consists of an array of fuel cylinder rods, each coated with a cladding and a current of steam flowing outside the cylinders. In the same figure we also show a representative periodic unit cell where the initial and boundary-value problems for heat and mass transfer are to be solved.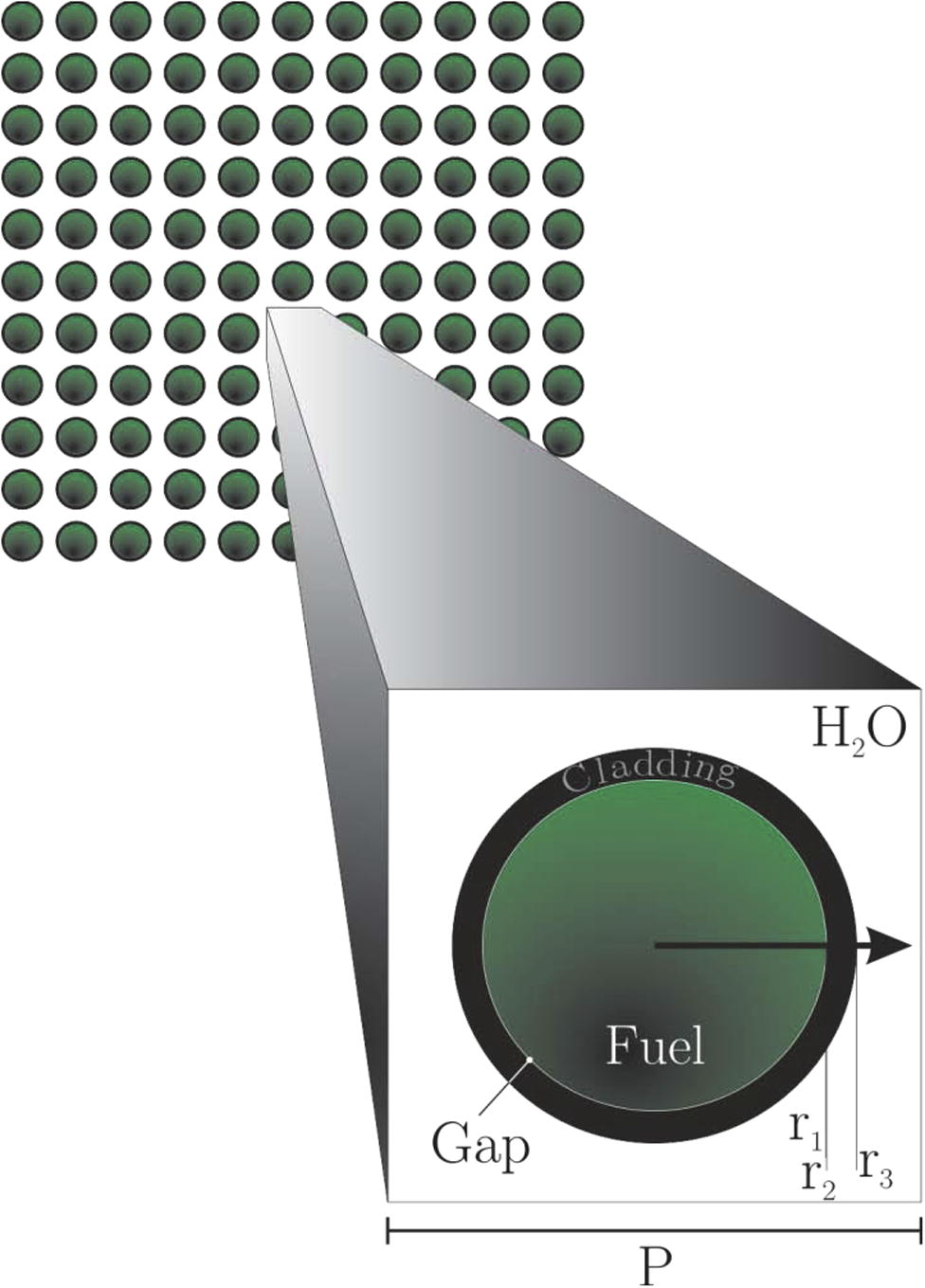
Fuel assemblies; consisting of arrays of in-line fuel rods. Characteristic geometric r1 = 5.207 mm, r2 = 5.321 mm, r3 = 6.234 mm and P = 16.2 mm.
In this way, we can identify four regions of interest, where the problem under study has a characteristic length of the order of P, i.e., 16.2 mm, in contrast with the fuel assembly that is the order of ten times larger as is illustrated in Fig. 3b (large scale). Accordingly, the unit cell regarding the core of the BWR is hundreds of times smaller (Fig. 3a). Then, we can say that the study presented in this work takes place in a small length scale (Fig. 3c).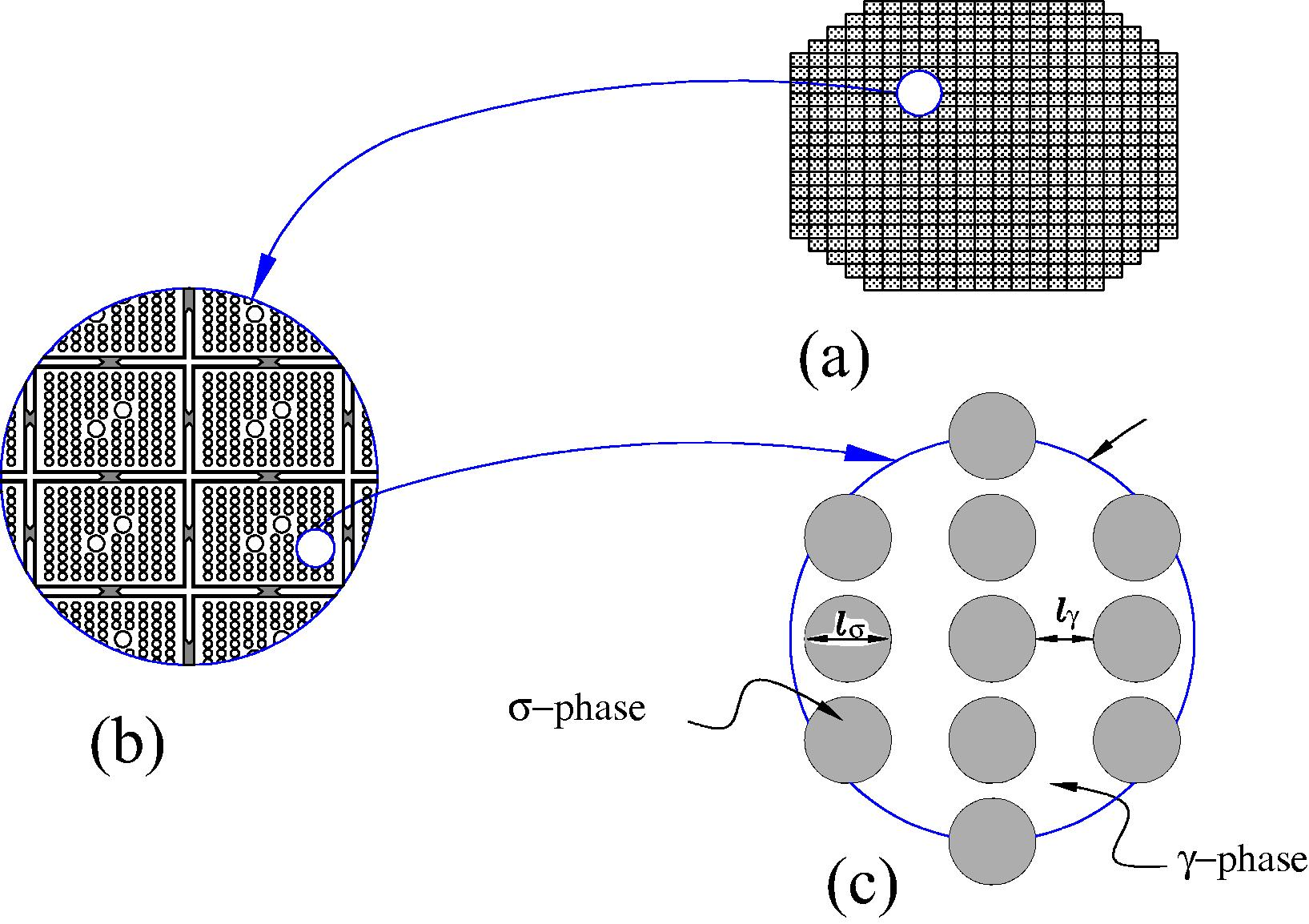
Characteristic lengths of the system (Espinosa-Paredes et al., 2008). (a) Nuclear reactor core; (b) large scale (showing four fuel assemblies); (c) small scale;
-phase is the fuel element and
-phase is the coolant.
4.1 Fractional mass transfer
During the heat up of the fuel and core damage, hydrogen production is a very important parameter, because it represents an integrated effect of different models on the core degradation progress, including the metal oxidation model, the availability of coolant for chemical reaction and the fraction of metal surface exposed to coolant (Vierow et al., 2004).
The mass transfer phenomena consider that hydrogen generated diffuses in the coolant by diffusion. In this work the mass transport with diffusion and reaction was approximate with time-fractional telegraph equation
The initial and boundary conditions are given by:
4.1.1 Reaction rate ( )
According to Veshchunov et al. (1997) the oxide layer consists of two sub layers in the temperature range of 1800–2650 K: the tetragonal phase outside and the cubic phase inside. Later, the best-fitted correlations were made at a high temperature
K and the applicability was verified to different temperature transients based on experiments (Fichot et al., 2004) and also reported by Xingwei and Xinrong (2011). Then the next equations can be applied to compute the
kinetics parameter for the superficial oxidation that is predominant in these phenomena:
The kinetic parameter is a function of average fuel temperature evaluated in the interface between fuel and coolant fluid ( ), which is obtained with the heat transfer equation.
The early phase of a severe accident is dominated by thermal–hydraulic phenomena. Then, sophisticated thermal–hydraulic modeling is important for accurate prediction of the early reactor response and timing of events. On the other hand, the later phases of severe accidents are dominated by additional complicated phenomena in addition to the thermal–hydraulics. Severe accident models of the codes are more diversified, less validated, and hence have more uncertainties (Vierow et al., 2004). The thermal–hydraulic model is presented in following section.
4.2 Heat transfer in the fuel ( )
The fuel element is represented by a one-dimensional mesh-centered grid consisting of a variable number of radial elements at each axial position (
). The differential equation given by Eq. (9) is transformed into discrete equations using the control volume formulation technique in implicit form (Patankar, 1980):
4.2.1 Decay heat ( )
Evaluation of the heat generated in a reactor after shutdown is important for determining cooling requirements under normal conditions and accident consequences. Reactor shutdown heat generation is the sum of heat produced from fission due to delayed neutron or photoneutron emissions, and decay of fission products fertile materials, and activation products. The heat decay level used in this work is given by Todreas and Kazimi (1990):
4.2.2 Reaction heat ( )
The heat generated at the solid–fluid interface due to reaction heat, which applies to Eq. (9) is given by:
The transition solid phase enthalpy is: at 1445 K.
4.2.3 Heat Flux ( )
The heat flux is required in Eq. (9) and for evaluation Newton’s law of cooling was applied:
The enthalpy (
) is obtained with energy balance in the fluid:
The mass flux is obtained with a momentum balance:
5 Numerical solution
The fractional telegraph equation has been considered by many authors (e.g., Anh and Leonenko, 2001, 2002; Cascaval et al., 2002; Orsingher and Zhao, 2003; Orsingher and Beghin, 2004; Momani, 2005; Chen et al., 2008; Camargo et al., 2008). Anh and Leonenko (2001, 2002) considered the fractional diffusion–wave equation under some random initial conditions and obtained their renormalized solutions. Cascaval et al. (2002) analyzed the time-fractional telegraph equations, dealing with wellposedness and presenting a study involving asymptotic by using the Riemann–Liouville approach. Orsingher and Zhao (2003) considered the space-fractional telegraph equations, obtaining the Fourier transform of its fundamental solution and presenting a symmetric process with discontinuous trajectories, whose transition function satisfies the space-fractional telegraph equation. Orsingher and Beghin (2004) discussed the time-fractional telegraph equation and telegraph processes with Brownian time, showing that some processes are governed by time-fractional telegraph equations. Momani (2005) discussed analytic and approximate solutions of the space- and time-fractional telegraph differential equations by means of the so-called adomian decomposition method. Chen et al. (2008) also discussed and derived the solution of the time-fractional telegraph equation with three kinds of nonhomogeneous boundary conditions, by the method of separating variables. Camargo et al. (2008) proposed the so-called general space–time fractional telegraph equations by the methods of differential and integral calculus, discussing the solution by means of the Laplace and Fourier transforms in variables t and x, respectively.
The time-fractional telegraph equation (TFTE) given by Eq. (1) with initial and boundary conditions (Eqs. (3) and (4)) consists of an analytical solution derived by Huang (2009). The solution in the form of a series for the boundary problem (Eqs. (1), (3) and (4)) in a bounded-space domain is derived by the Sine-Laplace transforms method:
The parameters to evaluate this solution are and .
Other studies without the forcing term , and with , Eq. (1) is known as the fractional diffusion–wave equation studied in Schneider and Wyss (1989), Mainardi (1996), and Agrawal (2002).
6 Results and discussions
The numerical experiments were performance in an averaging channel that represents a core reactor with the fuel rod with its gap and cladding and cooling steam of a BWR, in order to establish the importance of the effects of hydrogen diffusion in a severe accident scenario. The initial conditions of this scenario correspond to 100% of rated power, with scram of the reactor without cooling flow, i.e., without mitigation effects. The temperature of the fuel is incremented due to decay heat, which follows the transient behavior given by Eq. (13). Then, due to lack of cooling the fuel temperature increases. Eventually the temperature rise causes fuel cladding oxidation and hydrogen generation.
Figs. 4 and 5 show the initial conditions of concentration and reaction rate, respectively. These initial conditions were obtained with the normal diffusion model. In Fig. 4 can be see that the concentration that apparently asymptotically it approaches a state of equilibrium, the trend of behavior is expected due to the presence of clad oxidation in the range
, as is shown in Fig. 5.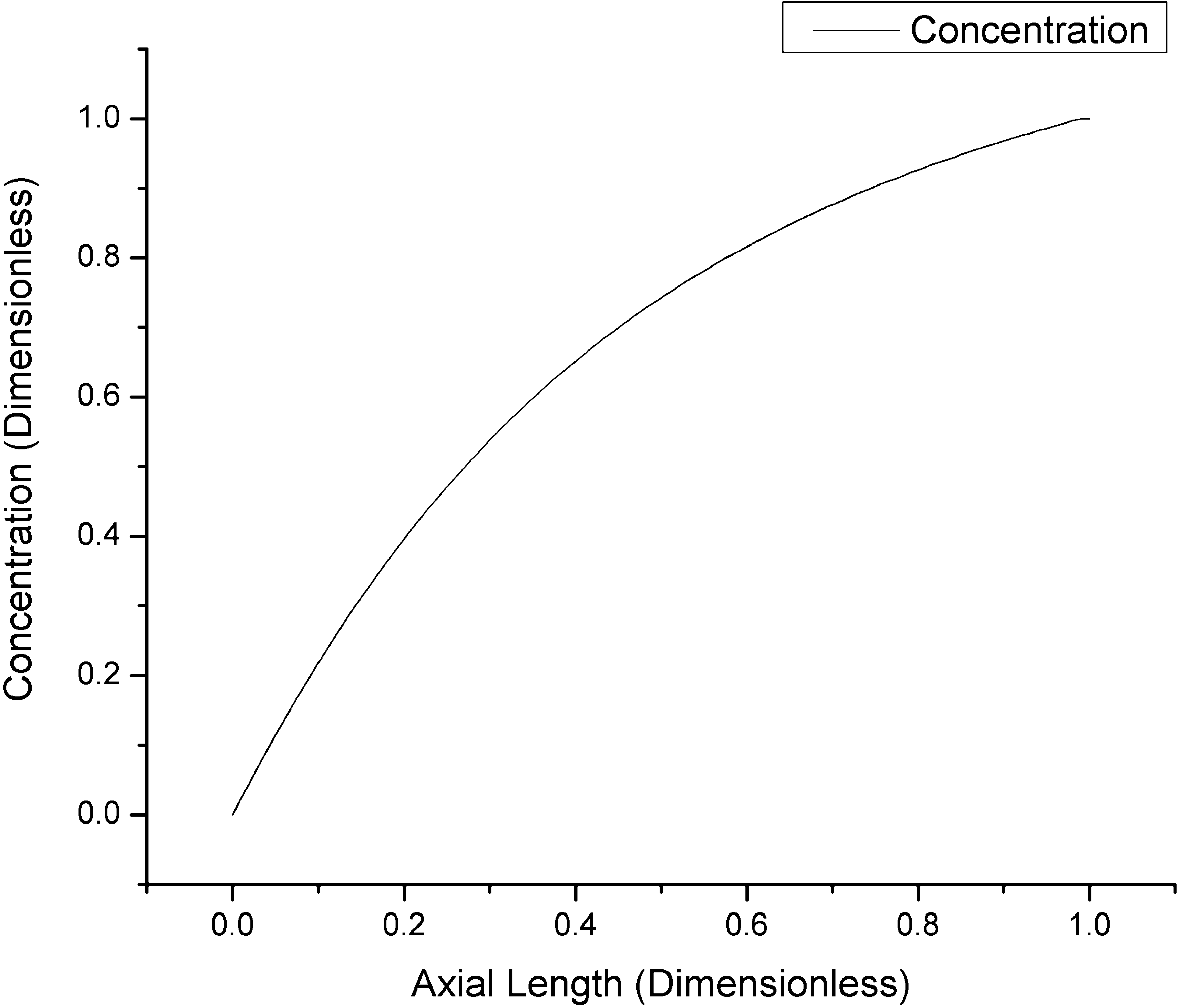
Initial condition
, for
, for any value of fractional coefficient.
Initial condition
, for
.
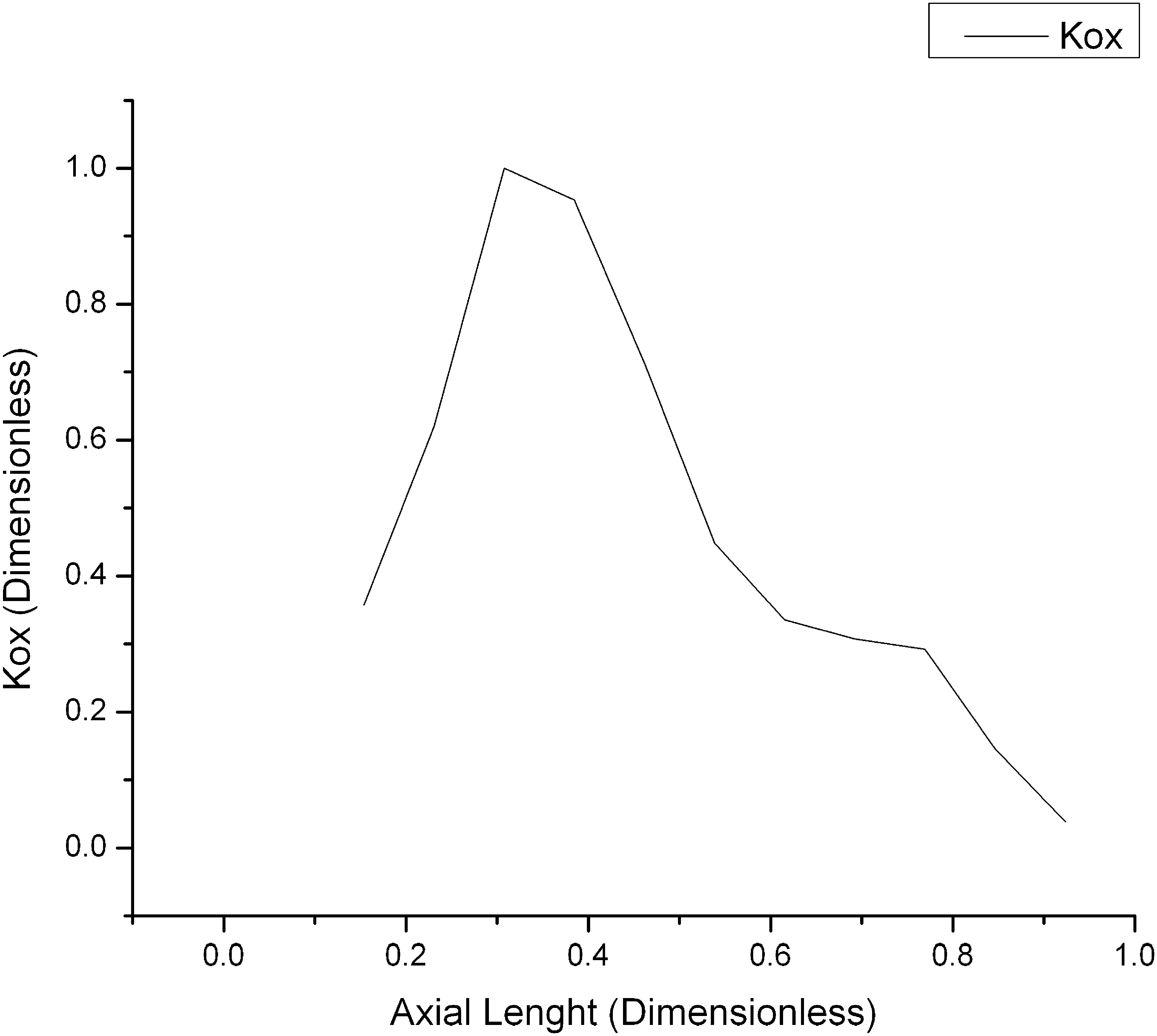
The trend of reaction rate shown in Fig. 5 follows the behavior non-uniform power generated by the residual heat in the reactor core. Under these conditions the clad temperature distribution is presented in Fig. 6. As you can see in this figure, the clad temperature is not uniform in the axial direction of the nuclear fuel, and therefore the reaction rate follows the behavior of clad temperature.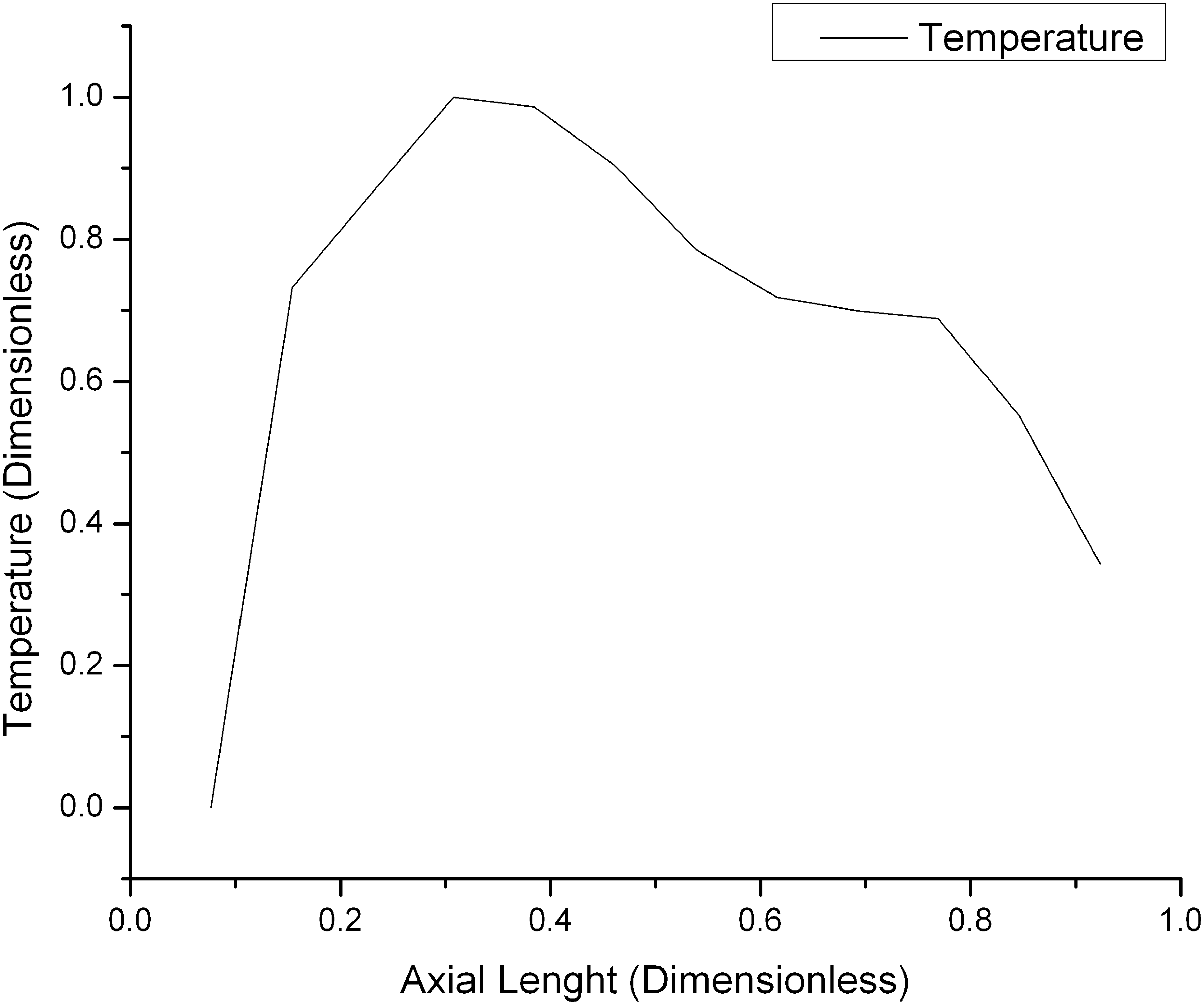
Clad temperature distributions in axial direction.
The behavior of the fractional model of the mass transfer with reaction for different values of
is shown in Fig. 7, where the coefficient value
is 0.03. In each of these cases the hydrogen density is analyzed by different values of the anomalous diffusion order, namely
.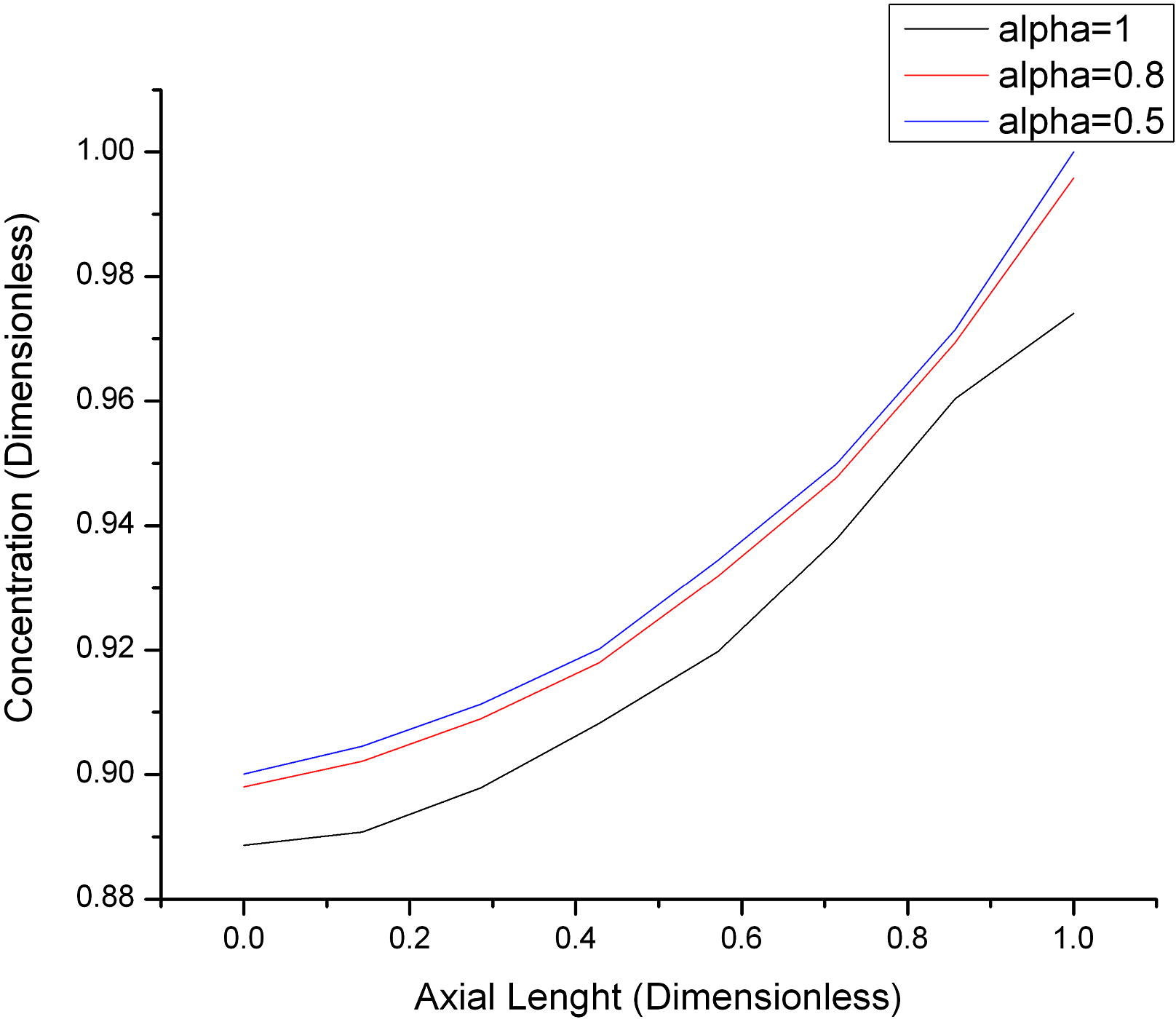
Behavior fractional of hydrogen concentration for different values of
at of
.
The hydrogen concentration results for different values of , at for are presented in Fig. 4, and under these conditions the hydrogen concentration is the same for any value of , as expected.
The hydrogen concentration results for different values of
, at
is presented in Fig. 7, i.e., for short times. In this figure can be observed that the hydrogen concentration is increased with decreasing value of
. The physical meaning of this phenomenon is that when
, the mass transfer resistance is greater than for
, due to sub-diffusive effects characteristic of the FFTE for the range of
. Then, when the
, Eq. (1) leads to:
The second term on left hand side generates sub-diffusive effects.
Now, when
, Eq. (1) leads to
Then, the resistance to mass transfer is less than with respect to , due to the transport phenomena is propagative, and the diffusive effects are negligible.
The behavior of hydrogen concentration in the range , can be inferred of the Fig. 7 between the limits of and .
7 Conclusions
In this work the time-fractional telegraph equation (TFTE) to study the behavior transient of the distributions of the hydrogen concentration in the core of the boiling water reactor (BWR) during a severe accident was applied. The problem considers diffusion and reaction or generation of hydrogen during severe accident in a nuclear power plant with reactor type BWR. The data, parameters and operating conditions correspond to this type of reactors.
The hydrogen concentration results with reaction due to oxidation for different values of fractional coefficient, at (Fig. 4) and short times (Fig. 7) were obtained. According with results obtained with the TFTE, the hydrogen concentration is inversely proportional to the fractional order coefficient . These results are relevant for decision making in terms of risk analysis in nuclear power plant with BWR.
Acknowledgements
The authors acknowledge the support given by the Universidad Autónoma Metropolitana (UAM) through a scholarship at the Graduate Program in Energy and Environment at the UAM-Iztapalapa.
References
- Solution for a fractional diffusion–wave equation defined in a bounded domain. Nonlinear Dyn.. 2002;29:145-155.
- [Google Scholar]
- Preliminary assessment of the possible BWR core/vessel damage states for Fukushima Daiichi station blackout scenarios using RELAP/SCDAPSIM. Sci. Technol. Nucl. Ins.. 2012;2012
- [Google Scholar]
- Spectral analysis of fractional kinetic equations with random data. J. Stat. Phys.. 2001;104:1349-1387.
- [Google Scholar]
- Renormalization and homogenization of fractional diffusion equations with random data. Probab. Theory Related Fields. 2002;124:381-408.
- [Google Scholar]
- Modelling of Zry-4 cladding oxidation by air, under severe accident conditions using the MAAP4 code. Nucl. Eng. Des.. 2011;241:1217-1224.
- [Google Scholar]
- Differentiation to fractional orders and the fractional telegraph equation. J. Math. Phys.. 2008;49(2008):1-12.
- [Google Scholar]
- Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl.. 2008;338:1364-1377.
- [Google Scholar]
- A review of zircaloy fuel cladding behavior in a loss-of-coolant accident.Kernforschungszentrum Karlsruhe. September 1985. KFK 3973, pp. 3–4. Cited by Xingwei et al. (2011)
- Constitutive laws for the neutron density current. Ann. Nucl. Energy. 2008;35:1963-1967.
- [Google Scholar]
- Severe accident analysis in nuclear power plants. Sci. Technol. Nucl. Ins.. 2012;2012
- [Google Scholar]
- Severe accident simulation of the Laguna Verde nuclear power plant. Sci. Technol. Nucl. Ins.. 2012;2012
- [Google Scholar]
- Application of fractional calculus to the sound waves propagation in rigid porous materials: validation via ultrasonic measurements. Acta Acoust. United Ac.. 2002;88(1):34-39.
- [Google Scholar]
- Advanced treatment of zircaloy cladding high-temperature oxidation in severe accident code calculations: Part III. Verification against representative transient tests. Nucl. Eng. Des.. 2004;232:97-109.
- [Google Scholar]
- Gauntt, R.O., Cole, R.K., Erickson, C.M., Gido, R.-G., Gasser, R.D., Rodriguez, S.B., Young, M.F., 2000. NUREG/CR-6119, Rev. 2, MELCOR Computer Code Manuals Primer and User’s Guide, Version 1.8.5, vol. 1. Prepared by Sandia National Laboratories for the U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research.
- Analytical solution for the time-fractional telegraph equation. J. Appl. Math.. 2009;2009:890158:1-9.
- [Google Scholar]
- Experimental characterization of the effective particle diameter of a particulate bed packed with multi-diameter spheres. Nucl. Eng. Des.. 2011;241:1736-1745.
- [Google Scholar]
- MAAP4, 1994. MAAP4: Modular Accident Analysis Program for LWR Plants, Code Manual Vols. 1–4. Prepared by Fauske & Associates Inc, Burr Ridge, IL, USA for the EPRI, Palo Alto, CA, USA.
- Modeling the cardiac tissue electrode interface using fractional calculus. J. Vib. Control. 2008;14(9–10):1431-1442.
- [Google Scholar]
- The fundamental solutions for the fractional diffusion–wave equation. Appl. Math. Lett.. 1996;9(1996):23-28.
- [Google Scholar]
- Finite difference methods for two-dimensional fractional dispersion equation. J. Comput. Phys.. 2006;211(1):249-261.
- [Google Scholar]
- Analytic and approximate solutions of the space- and time-fractional telegraph equations. Appl. Math. Comput.. 2005;170:1126-1134.
- [Google Scholar]
- Materials chemistry and transport modeling for severe accident analyses in light-water reactors I: external cladding oxidation. Nucl. Eng. Des.. 1994;148:253-271.
- [Google Scholar]
- Time-fractional telegraph equations and telegraph processes with brownian time. Probab. Theory Relat. Fields. 2004;128:141-160.
- [Google Scholar]
- The space-fractional telegraph equation and the related fractional telegraph process. Chin. Ann. Math. Ser. B. 2003;24:45-56.
- [Google Scholar]
- Numerical Heat Transfer and Fluid Flow. New York: McGraw-Hill; 1980.
- Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, To Methods of Their Solution and Some of Their Applications. Vol vol. 198. San Diego, Calif., USA: Academic press; 1998.
- Numerical treatment of fractional heat equations. Appl. Numer. Math.. 2008;58(8):1212-1223.
- [Google Scholar]
- Siefken, L.J., Coryell, E.W., Harvego, E.A., Hohorst, J.K., 2001. SCDAP/RELAP5/MOD 3.3 Code Manual, Code Architecture and Interface of Thermal-Hydraulic and Core Behavior Models. NUREG/CR-6150, vol. 1, Rev. 2, INEL-96/0422. Idaho National Engineering and Environmental Laboratory.
- Siefken, L.J., Coryell, E.W., Harvego, E.A., Hohorst, J.K., 2001. SCDAP/RELAP5/MOD 3.3 Code Manual, Modeling of Reactor Core and Vessel Behavior During Severe Accidents. NUREG/CR-6150, vol. 2, Rev. 2, INEL-96/0422. Idaho National Engineering and Environmental Laboratory.
- Application of fractional calculus in the theory of viscoelasticity. Mol. Quantum Acoust.. 2002;23:397-404.
- [Google Scholar]
- Nuclear Systems I: Thermal Hydraulic Fundamentals. Hemisphere Publishing Corporation; 1990.
- Physico-Chemical Behavior of Zircaloy Fuel Rod Cladding Tubes During LWR Severe Accident Reflood Part II: Modelling of quench phenomena. Forschungszentrum Karlsruhe; 1997. FZKA 5864
- Severe accident analysis of a PWR station blackout with the MELCOR, MAAP4 and SCDAP/RELAP5 codes. Nucl. Eng. Des.. 2004;234:129-145.
- [Google Scholar]
- Lattice fractional diffusion equation in terms of a Riesz-Caputo difference. Physica A. 2015;438:335-339.
- [Google Scholar]
- Xingwei, S., Xinrong, C., 2011. Study and assessment of Zry cladding oxidation model under severe accident in PWR. In: Power and Energy Engineering Conference (APPEEC) Asia-Pacific, pp. 1–5.
- Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett.. 2015;47:54-60.
- [Google Scholar]
- Application of the fractional advection-dispersion equation in porous media. Soil Sci. Soc. Am. J.. 2003;67(4):1079-1084.
- [Google Scholar]







