On two-dimensional diffusion with integral condition

Syed Tauseef Mohyud-Din; Ahmet Yıldırım

doi:10.1016/j.jksus.2010.06.003

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

23 (

); 121-125

doi:

10.1016/j.jksus.2010.06.003

On two-dimensional diffusion with integral condition

Syed Tauseef Mohyud-Din^a,⁎, Ahmet Yıldırım^b

a HITEC University Taxila Cantt, Pakistan

b Ege University, Department of Mathematics, 35100 Bornova – İzmir, Turkey

⁎Corresponding author. Tel.: +92 333 5151290. syedtauseefs@hotmail.com (Syed Tauseef Mohyud-Din)

Received: 2010-5-29, Accepted: 2010-6-10, Published: 2010-04-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 13 June 2010

Peer-review under responsibility of King Saud University.

Abstract

In this paper, homotopy analysis method (HAM) is used to obtain numerical and analytical solutions for two-dimensional diffusion with an integral condition. Comparisons with exact solution show that the HAM is a powerful method for the solution of non-linear equations.

Keywords

Homotopy analysis method

Parabolic PDEs

Non-classical boundary conditions

Show Related Articles from PubMed

1 Introduction

Parabolic partial differential equations with non-classic boundary conditions arise in modelling of various physical phenomena occurring in areas such as chemical diffusion, thermoelasticity, heat conduction processes, control theory and medical science (Capasso and Kunisch, 1988; Day, 1982; Cannon and Yin, 1989; Wang and Lin, 1989 ). The one-dimensional diffusion (or parabolic) problem was studied by Cannon et al. (1990), Liu (1999) and Ang (2002). In this paper, we consider the two-dimensional diffusion problem.

(1)

u_{t} = u_{xx} + u_{yy} .

The existence, uniqueness and continuous dependence on data of solution of this initial-boundary value problem have been considered in Day (1982), Cannon and Yin (1989) and Lin (1988). A number of numerical methods for solving several types of two dimensional diffusion problems were given in Dehghan (2000), Dehghan (2002), Cannon et al. (1993) and Hashim (2006). In particular, Dehghan (2002) presented a fourth-order finite-difference method for solving (1) subject to some standard boundary conditions, together with another condition in the form of the integral,

(2)

\int_{0}^{1} \int_{0}^{s (x)} u (x, y, t) dxdy = m (t), 0 \leq x, y \leq 1,

where s and m are known functions.

Recently, Dehghan (2004a) and Dehghan (2004b) applied the Adomian decomposition method (ADM) to the one-dimensional parabolic and hyperbolic problems with non-local boundary specifications, respectively. The application of the ADM was extended to a specific two-dimensional diffusion problem subject to non-standard boundary conditions by Dehghan (2004c). The present work is motivated by the desire to obtain approximate analytical and numerical solutions to two-dimensional diffusion problems with an integral boundary condition using the homotopy analysis method (HAM) and to compare its reliability and efficiency with exact solution.

The HAM is developed in 1992 by Liao (1992, 1995, 1997, 1999, 2003a,b, 2004) and Liao and Campo (2002). This method has been successfully applied to solve many types of non-linear problems in science and engineering by many authors (Ayub et al., 2003; Hayat et al., 2004a; Hayat et al., 2004b; Abbasbandy, 2007a; Abbasbandy, 2007b; Abbasbandy, 2007c; Bataineh et al., in press ), and references therein. By the present method, numerical results can be obtained with using a few iterations. The HAM contains the auxiliary parameter $ℏ,$ which provides us with a simple way to adjust and control the convergence region of solution series for large values of t. Unlike, other numerical methods are given low degree of accuracy for large values of t. Therefore, the HAM handles linear and non-linear problems without any assumption and restriction.

2 Homotopy analysis method (HAM)

We apply the HAM (Liao, 1992, 1995, 1997, 1999, 2003,a,bLiao, 2004; Liao and Campo, 2002 ) to two-dimensional diffusion with an integral condition (1). We consider the following differential equation

(3)

N [u (x, y, t)] = 0,

where N is a non-linear operator for this problem, x, y and t denote an independent variables,

u (x, y, t)

is an unknown function.

In the frame of HAM (Liao, 1992, 1995, 1997, 1999, 2003a,b, 2004; Liao and Campo, 2002 ), we can construct the following zeroth-order deformation:

(4)

(1 - q) L (U (x, y, t; q) - u_{0} (x, y, t)) = q ℏ H (x, y, t) N (U (x, y, t; q)),

where

q \in [0, 1]

is the embedding parameter,

ℏ \neq 0

is an auxiliary parameter,

H (x, y, t) \neq 0

is an auxiliary function, L is an auxiliary linear operator,

u_{0} (x, y, t)

is an initial guess of

u (x, y, t)

and

U (x, y, t; q)

is an unknown function on the independent variables x, y, t and q.Obviously, when

q = 0

and

q = 1,

it holds

U (x, y, t; 0) = u_{0} (x, y, t),

(5)

U (x, y, t; 1) = u (x, y, t), U (x, y, t; 1) = u (x, y, t),

respectively. Using the parameter q, we expand

U (x, y, t; q)

in Taylor series as follows:

(6)

U (x, y, t; q) = u_{0} (x, y, t) + \sum_{m = 1}^{\infty} u_{m} (x, y, t) q^{m},

where

(7)

u_{m} = \frac{1}{m!} {\frac{\partial^{m} U (x, y, t; q)}{\partial^{m} q}|}_{q = 0}

Assume that the auxiliary linear operator, the initial guess, the auxiliary parameter $ℏ$ and the auxiliary function $H (x, y, t)$ are selected such that the series (6) is convergent at $q = 1$ , then due to (5) we have

(8)

u (x, y, t) = u_{0} (x, y, t) + \sum_{m = 1}^{\infty} u_{m} (x, y, t)

Let us define the vector

(9)

{\vec{u}}_{n} (x, y, t) = \{u_{0} (x, y, t), u_{1} (x, y, t), . . ., u_{n} (x, y, t)\}

Differentiating (4) m times with respect to the embedding parameter q, then setting $q = 0$ and finally dividing them by $m!,$ we have the so-called mth-order deformation equation

(10)

L [u_{m} (x, y, t) - χ_{m} u_{m - 1} (x, y, t)] = ℏ H (x, y, t) R_{m} ({\vec{u}}_{m - 1}),

where

(11)

R_{m} ({\vec{u}}_{m - 1}) = {\frac{1}{(m - 1)!} \frac{\partial^{m - 1} N (U (x, y, t; q))}{\partial^{m - 1} q}|}_{q = 0}

and

(12)

χ_{m} = \{\begin{matrix} 0 m \leq 1, \\ 1 m > 1 . \end{matrix}

Finally, for the purpose of computation, we will approximate the HAM solution (8) by the following truncated series:

(13)

ϕ_{m} (x, y, t) = \sum_{k = 0}^{m - 1} u_{k} (x, y, t) .

3 Illustrative examples

In this section we demonstrate the feasibility and efficiency of the HAM through two examples with closed form solutions. Comparisons with exact solutions are also made.

3.1

3.1 Example 1

Consider the two-dimensional diffusion problem (1) subject to the initial condition

(14)

u (x, y, 0) = (1 - y) e^{x}, 0 \leq x \leq 1, 0 \leq y \leq 1,

and boundary conditions

(15)

u (0, y, t) = (1 - y) e^{t}, 0 \leq t \leq 1, 0 \leq y \leq 1,

(16)

u (1, y, t) = (1 - y) e^{1 + t}, 0 \leq t \leq 1, 0 \leq y \leq 1,

(17)

u (x, 1, t) = 0, 0 \leq t \leq 1, 0 \leq x \leq 1,

(18)

u (x, 0, t) = e^{x} e^{t}, 0 \leq t \leq 1, 0 \leq x \leq 1,

and the integral condition

(19)

\int_{0}^{1} \int_{0}^{x (1 - x)} u (x, y, t) dxdy = 2 (11 - 4 e) e^{t}, 0 \leq x \leq 1, 0 \leq y \leq 1 .

According to (4), the zeroth-order deformation can be given by

(20)

(1 - q) L (U (x, y, t; q) - u_{0} (x, y, t)) = q ℏ H (x, y, t) (U_{t} - U_{xx} - U_{yy})

We can start with an initial approximation $u_{0} (x, y, t) = (1 - y) e^{x},$ and we choose the auxiliary linear operator $L (U (x, y, t; q)) = \frac{\partial U (x, y, t; q)}{\partial t},$ with the property $L (C) = 0,$ where C is an integral constant. We also choose the auxiliary function to be $H (x, y, t) = 1 .$ Hence, the mth-order deformation can be given by $L [u_{m} (x, y, t) - χ_{m} u_{m - 1} (x, y, t)] = ℏ H (x, y, t) R_{m} ({\vec{u}}_{m - 1}),$ where

(21)

R_{m} ({\vec{u}}_{m - 1}) = \frac{\partial (u_{m - 1})}{\partial t} - \frac{\partial^{2} (u_{m - 1})}{\partial x^{2}} - \frac{\partial^{2} (u_{m - 1})}{\partial y^{2}}

Now the solution of the mth-order deformation equations (21) for $m \geq 1$ become

(22)

u_{m} (x, t) = χ_{m} u_{m - 1} (x, t) + ℏ L^{- 1} [R_{m} ({\vec{u}}_{m - 1})] .

Consequently, the first few terms of the HAM series solution are as follows: $u_{0} (x, y, t) = (1 - y) e^{x},$ $u_{1} (x, y, t) = - ℏ (1 - y) e^{x} t,$ $u_{2} (x, y, t) = - ℏ (1 - y) e^{x} t - ℏ^{2} (1 - y) e^{x} t + \frac{ℏ^{2}}{2} (1 - y) e^{x} t^{2},$ and so on. Hence, the HAM series solution (for $ℏ = - 1)$ is $u (x, y, t) = u_{0} (x, y, t) + u_{1} (x, y, t) + u_{2} (x, y, t) + u_{3} (x, y, t) + u_{4} (x, y, t) + u_{5} (x, y, t) + \dots$

(23)

= (1 - y) e^{x} + (1 - y) e^{x} t + \frac{1}{2} (1 - y) e^{x} t^{2} + \frac{1}{6} (1 - y) e^{x} t^{3} + \frac{1}{24} (1 - y) e^{x} t^{4} + \frac{1}{120} (1 - y) e^{x} t^{4} + \dots

In the same manner, the rest of the components of the iteration formulae (23) can be obtained using the Maple Package.

Using Taylor series into (23), we have the closed form solution

(24)

u (x, y, t) = (1 - y) e^{x + t} .

This is exact solution of 1 with (14)–(19) conditions.

In Fig 1c, we present the absolute error between the exact solution and 10-iterate of HAM. Fig. 1a and b show the comparison between the exact solution and 10-iterate of HAM.

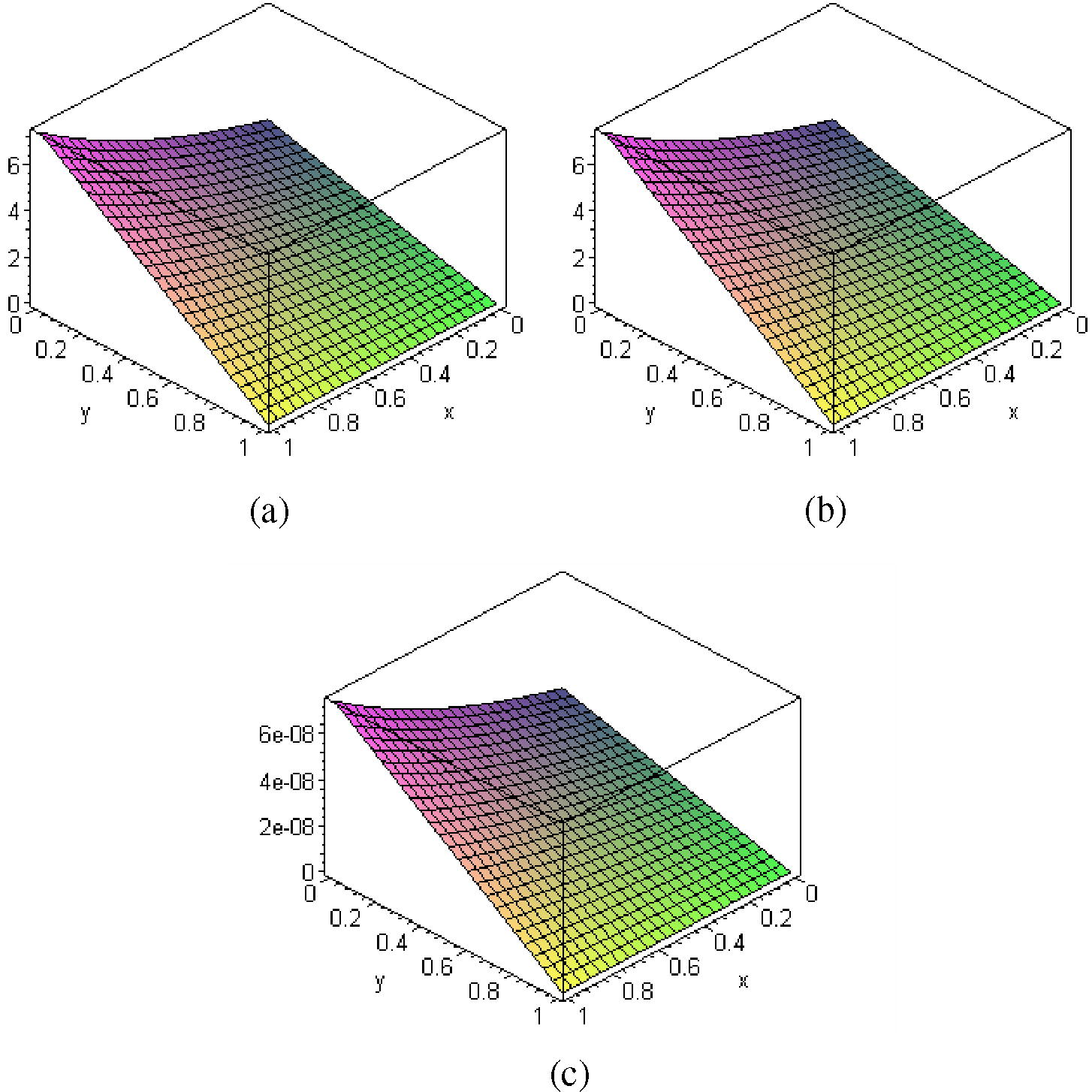
The surface shows the solution u(x, y, t) for Eqs. (1), (14)–(19) when t = 1: (a) exact solution (24) (b) approximate solution (10-iterate of HAM) (c) u ex - u app .

3.2

3.2 Example 2

Consider the two-dimensional diffusion problem (1) subject to the initial condition

(25)

u (x, y, 0) = e^{x + y}, 0 \leq x \leq 1, 0 \leq y \leq 1,

and boundary conditions

(26)

u (0, y, t) = e^{y + 2 t}, 0 \leq t \leq 1, 0 \leq y \leq 1,

(27)

u (1, y, t) = e^{1 + y + 2 t}, 0 \leq t \leq 1, 0 \leq y \leq 1,

(28)

u (x, 1, t) = e^{1 + x + 2 t}, 0 \leq t \leq 1, 0 \leq x \leq 1,

(29)

u (x, 0, t) = e^{x} e^{2 t}, 0 \leq t \leq 1, 0 \leq x \leq 1,

and the integral condition

(30)

\int_{0}^{1} \int_{0}^{e^{x / 4}} u (x, y, t) dxdy = (4 e^{e / 4} - 4 e^{1 / 4} - e + 1) e^{2 t}, 0 ⩽ x ⩽ 1, 0 ⩽ y ⩽ 1 .

3.3

3.3 We can start with an initial approximation

(31)

u_{0} (x, y, t) = e^{x + y},

We can use similar procedures which was used in example 1 and the first few terms of the HAM series solution are as follows: $u_{0} (x, y, t) = e^{x + y},$ $u_{1} (x, y, t) = - 2 ℏ e^{x + y} t,$ $u_{2} (x, y, t) = - 2 ℏ e^{x + y} t - 2 ℏ^{2} e^{x + y} t + 2 ℏ^{2} e^{x + y} t^{2},$ and so on. Hence, the HAM series solution (for $ℏ = - 1)$ is $u (x, y, t) = u_{0} (x, y, t) + u_{1} (x, y, t) + u_{2} (x, y, t) + u_{3} (x, y, t) + u_{4} (x, y, t) + u_{5} (x, y, t) + \dots$

(32)

= e^{x + y} + 2 e^{x + y} t + 2 e^{x + y} t^{2} + \frac{4}{3} e^{x + y} t^{3} + \frac{2}{3} e^{x + y} t^{4} + \frac{4}{15} e^{x + y} t^{5} + \dots

In the same manner, the rest of the components of the iteration formulae (32) can be obtained using the Maple Package.

Using Taylor series into (32), we have the closed form solution

(33)

u (x, y, t) = e^{x + y + 2 t} .

This is exact solution of (1) with (25–30) conditions.

In Fig 2c, we present the absolute error between the exact solution and 10-iterate of HAM. Fig. 2a and b show the comparison between the exact solution and 10-iterate of HAM.

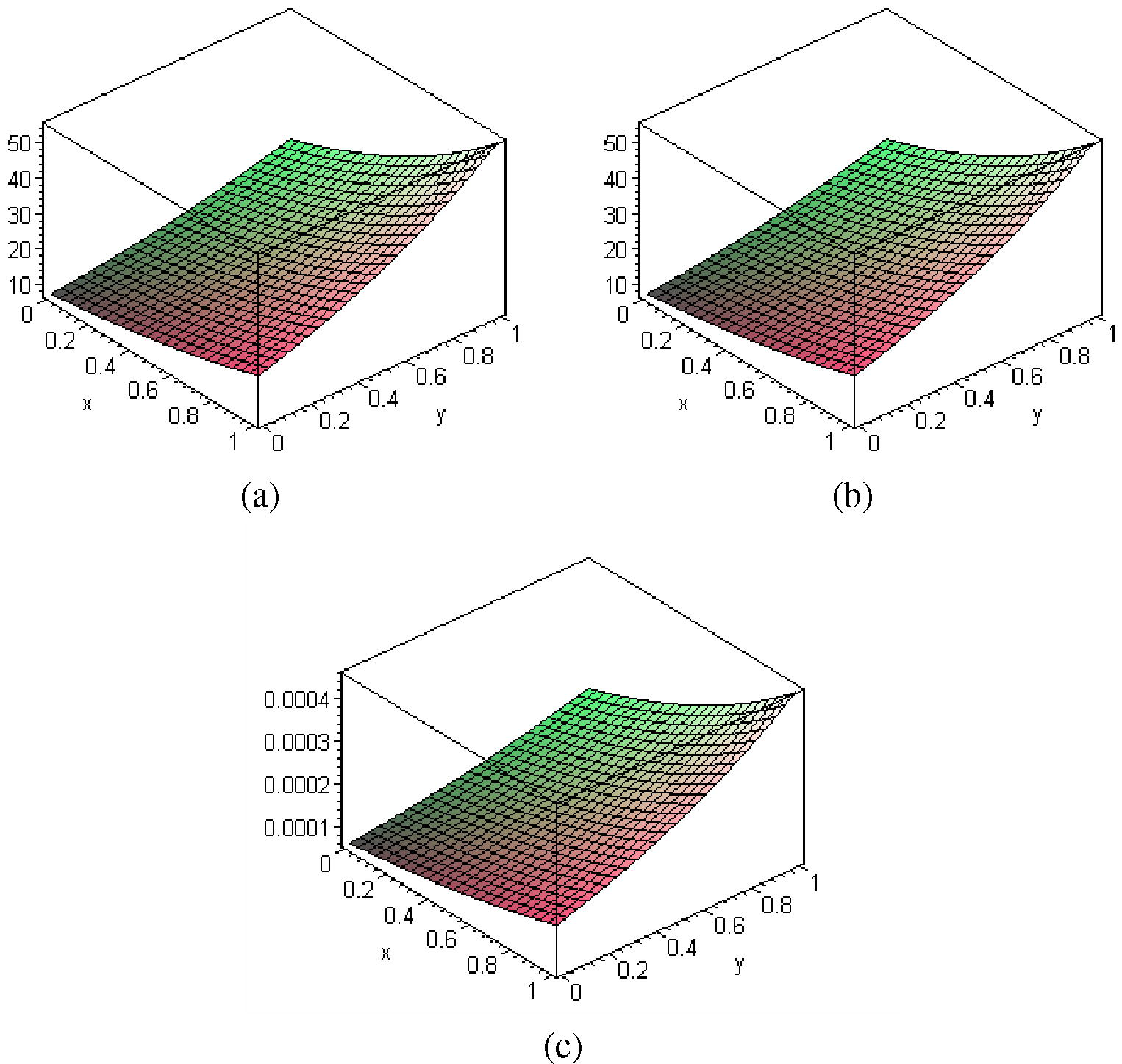
The surface shows the solution u(x, y, t) for Eqs.(1), (25)–(30) when t = 1: exact solution (33) (b) approximate solution (10-iterate of HAM) (c) u ex - u app .

4 Conclusions

In this work, we employed the HAM for the solutions of two-dimensional diffusion equations subject to non-standard boundary specifications. Unlike the traditional techniques used by other numerical algorithms, the solutions here are given in series forms which can lead to exact closed form solutions. The approximate solutions to the equations were computed without any need for transformation techniques, linearization and discretization, and then compared with exact solutions. It was shown that the method is reliable, efficient and requires less computations.

References

Abbasbandy S., . Homotopy analysis method for heat radiation equations. Int. Comm. Heat Mass Transfer. 2007;34:380-387.
[Google Scholar]
Abbasbandy S., . The application of homotopy analysis method to solve a generalized Hirota–Satsuma coupled KdV equation. Phys. Lett. A. 2007;361:478-483.
[Google Scholar]
Abbasbandy S., . Approximate solution for the nonlinear model of diffusion and reaction in porous catalysts by means of the homotopy analysis method. Chem. Eng. J. 2007
[CrossRef] [Google Scholar]
Ang W.T., . A method of solution for the one-dimensional heat equation subject to a non-local condition. SEA Bull. Math.. 2002;26:197-203.
[Google Scholar]
Ayub M., Rasheed A., Hayat T., . Exact flow of a third grade fluid past a porous plate using homotopy analysis method. Int. J. Eng. Sci.. 2003;41:2091-2103.
[Google Scholar]
Bataineh, A.S., Noorani, M.S.M., Hashim, I. Solving systems of ODEs by homotopy analysis method, Commun. Nonlinear Sci. Numer. Sim. doi:10.1016/j.cnsns.2007.05.026. in press.
Cannon J.R., Yin H.M., . On a class of non-classic parabolic problems. J. Differen. Equat.. 1989;79:266-288.
[Google Scholar]
Cannon J.R., Lin Y., Wang S., . An implicit finite difference scheme for the diffusion equation subject to mass specification. Int. J. Eng. Sci.. 1990;28:573-578.
[Google Scholar]
Cannon J.R., Lin Y., Matheson A.L., . The solution of the diffusion equation in two-space variables subject to the specification of mass. J. Appl. Anal.. 1993;50:1-19.
[Google Scholar]
Capasso V., Kunisch K., . A reaction–diffusion system arising in modelling man–environment diseases. Quart. Appl. Math.. 1988;46:431-449.
[Google Scholar]
Day W.A., . Existence of a property of solutions of the heat equation subject to linear thermoelasticity and other theories. Quart. Appl. Math.. 1982;40:319-330.
[Google Scholar]
Dehghan M., . A finite difference method for a non-local boundary value problem for two-dimensional heat equation. Appl. Math. Comput.. 2000;112:133-142.
[Google Scholar]
Dehghan M., . Fully explicit finite-difference methods for two-dimensional diffusion with an integral condition. Nonlinear Anal.. 2002;48:637-650.
[Google Scholar]
Dehghan M., . The use of Adomian decomposition method for solving the one-dimensional parabolic equation with non-local boundary specifications. Int. J. Comput. Math.. 2004;81:25-34.
[Google Scholar]
Dehghan M., . The solution of a nonclassic problem for one-dimensional hyperbolic equation using the decomposition procedure. Int. J. Comput. Math.. 2004;81:979-989.
[Google Scholar]
Dehghan M., . Application of the Adomian decomposition method for two-dimensional parabolic equation subject to nonstandard boundary specifications. Appl. Math. Comput.. 2004;157:549-560.
[Google Scholar]
Hashim I., . Comparing numerical methods fort he solutions of two-dimensional diffusion with an integral condition. Appl Math Comput.. 2006;181:880-885.
[Google Scholar]
Hayat T., Khan M., Asghar S., . Homotopy analysis of MHD flows of an Oldroyd 8-constant fluid. Acta Mech.. 2004;168:213-232.
[Google Scholar]
Hayat T., Khan M., Asghar S., . Magnetohydrodynamic flow of an Oldroyd 6-constant fluid. Appl. Math. Comput.. 2004;155:417-425.
[Google Scholar]
Liao, S.J. The proposed homotopy analysis technique for the solution of nonlinear problems, Ph.D Thesis, Shanghai Jiao Tong University, 1992.
Liao S.J., . An approximate solution technique which does not depend upon small parameters: a special example. Int. J. Nonlinear Mech.. 1995;30:371-380.
[Google Scholar]
Liao S.J., . An approximate solution technique which does not depend upon small parameters (II): an application in fluid mechanics. Int. J. Nonlinear Mech.. 1997;32:815-822.
[Google Scholar]
Liao S.J., . An explicit, totally analytic approximation of Blasius viscous flow problems. Int. J. Nonlinear Mech.. 1999;34(4):759-778.
[Google Scholar]
Liao S.J., . Beyond Perturbation: Introduction to the Homotopy Analysis Method. Boca Raton: Chapman & Hall, CRC Press; 2003.
Liao S.J., . On the analytic solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J. Fluid Mech.. 2003;488:189-212.
[Google Scholar]
Liao S.J., . On the homotopy analysis method for non-linear problems. Appl. Math. Comput.. 2004;147:499-513.
[Google Scholar]
Liao S.J., Campo A., . Analytic solutions of the temperature distribution in Blasius viscous flow problems. J. Fluid Mech.. 2002;453:411-425.
[Google Scholar]
Lin, Y. Parabolic partial differential equations subject to non-local boundary conditions, Ph.D. Thesis, Washington State University, 1988.
Liu Y., . Numerical solution of the heat equation with non-local boundary conditions. J. Comput. Appl. Math.. 1999;110:115-127.
[Google Scholar]
Wang S., Lin Y., . A finite difference solutions to an inverse problem determining a control function in a parabolic partial differential equations. Inverse Probl.. 1989;5:631-640.
[Google Scholar]