Translate this page into:
Two-point block variable order step size multistep method for solving higher order ordinary differential equations directly
⁎Corresponding author. mohdhasan@upm.edu.my (Mohammad Hasan Abdul Sathar)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The current research aims to provide a viable numerical method for solving difficult engineering and science problems which are in the form of higher order ordinary differential equations. The proposed method approximates these ordinary differential equations using Newton-Gregory backward difference polynomial in predictor–corrector mode. The predictor–corrector algorithm is then fitted with a variable order step size algorithm to reduce computational cost. The variable order stepsize algorithm allows the method to predetermine the preferred level of accuracy with the added advantage of less computational cost. The method is subsequently programmed with a two-point block formulation which can be altered for parallel programming. This research also discusses order and stepsize strategies of the variable order stepsize algorithm. Stability and convergence estimations of the method are also established. Numerical results obtained will validate the accuracy and efficiency of the method using various types of linear and nonlinear higher order ordinary differential equations.
Keywords
Ordinary differential equations
Block
Multistep method
Variable order stepsize
34A12
34A34
65L06
65L05

1 Introduction
Problems in science and engineering are often modeled in the form of ordinary, partial and fractional differential equations depending on the type of problem. These problems may range from various field such as the interaction between chemicals as found in chemical kinetics to the mechanics of fluids which are often modelled in medicine and engineering. For recent analytical and numerical methods established for solving these differential applications, readers may refer to literature by Al-Jawary et al. (2020), Khataybeh et al. (2019), Mohd Ijam et al. (2020), Zhang et al. (2020) and Rasedee et al. (2021) for ordinary differential equations, Colbrook et al. (2019), Fu et al. (2019) and Lehrenfeld and Olshanskii (2019) for partial differential equations and Goswami et al. (2019), Singh et al. (2019), Srivastava et al. (2020) and Veeresha et al. (2020) for fractional differential equations. The algorithm development provided in this research is to specifically cater a numerical method for solving higher order ordinary differential equations directly using variable order step size formulations. We begin the study with the evolution of the variable order step size algorithm based on the multistep method.
Previous numerical methods used to solve these higher order ordinary differential equations (ODEs) by reducing them to systems of first order ODEs were so efficient such that methods for solving ODEs directly were considered as robust. These methods were almost overlooked until (Krogh, 1968) revived the field of study with a modified version of the divided difference approach. He proposed that the back values of any point of the derivative were to be interpolated. In a order ODE, the method used to interpolate the highest derivative value was referred as the Direct Integration (DI). Krogh (1968) provide a comparison for two second order problems which was similar to Gear (1967) whom used a Nordsieck version of the multistep method. Suleiman (1979) extended works of Krogh by adapting the DI for estimating higher order derivatives ( h order) which corresponds with nonstiff problems and a generalized backward differentiation method (GBDF) method for lower derivatives which corresponds with stiff problems. Omar and Suleiman (2005) adapted Suleiman’s DI algorithm with a two-point explicit block algorithm. By doing so, Omar was able to reduce computational cost by providing a more efficient divided difference code. In efforts of solving higher order ODEs directly, Rasedee (2009) proposed a direct method for solving these higher order derivatives using a backward difference formulation. The backward difference method suggested by Rasedee was in effort to overcome the drawback of the DI method, as it requires calculating the integration coefficients at every step change which proves to be costly. The method proposed by Rasedee (2009) requires calculating the integration coefficients only once in the beginning of the algorithm and once more at the end, if deemed necessary.
This article is part of a research series influenced by the works of Suleiman (1979). He initiated a series of research based on Adams type difference formulation for solving ordinary differential equations (ODEs). In his research, Suleiman established the Direct Integration method (DI) for solving both, stiff and nonstiff initial value higher order ODEs directly. This method was formulated using a multistep method in divided difference form combined with variable order stepsize (VOS) capability. Using works by Suleiman as their foundation, authors such as Omar and Suleiman (2005), Majid and Suleiman (2006, 2007), Suleiman et al. (2011), Mohd Ijam et al. (2014) and Waeleh and Abdul Majid (2016) and Rasedee et al. (2016) have produced an extended variation for solving various types of differential problems.
The current research proposes a two-point block formulation in backward difference form (2PVOSBD) for solving both artificial and real life higher order ODE problems. Equipped with a VOS algorithm similar to Rasedee et al. (2014), the proposed method calculates the integration coefficients only once at the beginning and once at the end (if required) in contrast to the DI which requires calculating integration coefficients at every step change. The 2PVOSBD only requires calculating the integration coefficients a second time if , where H as the current stepsize, as the last point of the interval, and as the current point.
When implementing a variable order stepsize strategy, the acceptance criteria is key. An unsuitable criteria may result in an increase in the total of steps or the loss of accuracy. The selection criteria is discussed in the upcoming sections. Following the appropriate selection criteria, strategies suggested by Lambert (1973) are used and integrated with the variable step size code proposed by Krogh (1973).
The current research also provides the discussion on the order, stability and convergence of the proposed method. For the variable order step size techniques and selection criterion implemented in this research, authors adapted techniques suggested by Gear (1967), Krogh (1968), Lambert (1973), Hall and Watt (1976) and Suleiman (1979). And in more recent works for solving higher order ODEs found in Zainuddin et al. (2016), Rasedee et al. (2017b, 2018a), Ibrahim et al. (2019) and Asnor et al. (2019) and others. The following are preliminary definitions that are used to determine order, stability and convergence of the 2PVOSBD.
2 Preliminaries
This section entails definitions used to determine the order, stability and convergence of the method.
The general linear multistep method is denoted by
The linear differential operator L associated with the linear multistep method is defined where is an arbitary function in .
Choose a function to be differentiable as often as needed, and expand and with respect to t, and arrange as where are constants.
The linear multistep method and associated difference operator L defined are said to be of order p if in, where
The block method is zero stable if the roots of the first characteristic polynomial is denoted by which satisfies the conditions and the roots with , where the multiplicity does not exceed 2.
A Linear Multistep Method (LLM) is said to be consistent if the LLM is of order .
3 The higher order ordinary differential equation
Differential equations have been widely used to model various types of real-life applications, from natural phenomenon to man-made machinery. Examples of these higher order ODEs can found in classical mechanics of the two-body problem, chaotic motions in periodic-self exited oscillators to the elasticity of thin clamp plates.
The focus of this research is to establish a numerical method for solving higher order initial value ordinary differential equations. For the purpose of this research, consider the following higher order ODE
Direct methods versus reduction to first order systems have been extensively discussed by Rutishauser (1960), Collatz (1960), Henrici (1962) and Gear (1967). These opinions may vary based on individual preferences. In the case of Henrici (1962), the author favours reduction methods due to the large global error of direct methods even though lower order derivatives have small local truncation error, whereas Collatz (1960) and Gear (1967) prefer direct methods. Rutishauser (1960) provided proof that the nth linear order ODE was solved using a direct method (Euler extended method) had a global error of order 1, which was equal to the global error of the reduction method (Euler method). A N order direct method algorithm requires only storing and updating one set of back values, where a N reduction method needs N set of back values. Due to the fact that the accuracy of each derivative is of the same order thus, the direct method requires controlling the local error of only derivative because it offers the lowest accuracy opposed to controlling the local error of each derivative as required by the reduction method.
The method proposed in this research approximates (3.1) directly with minimal loss of accuracy, if not any. The succeeding section will provide detailed derivation of the proposed method.
4 The two-point block method
This section explains derivation of both first and second point of the two-point block method. To formulate a two-point predictor–corrector (PeCe) block method with a variable order step size backward difference algorithm, elements such as explicit–implicit integration coefficients and order stepsize strategy are necessary.
Firstly, note that the 2PVOSBD method is formulated in predictor–corrector mode similar to the Adam-Basthforth-Moulton formulation. The derivation begins with integrating the higher order ODE as defined in (3.1). By integrating (3.1) once,
becomes
Predictor:
Corrector:
Explicit:
Implicit:
5 Integration coefficients
The current section provides derivation for explicit and implicit coefficients. Firstly, let the first order explicit,
and implicit
generating functions as
and
Next, by substituting
into
, the explicit generating function can be rewritten as
which can be simplified as
Explicit Coefficients:
Implicit Coefficients:
Inline with the aim of this research to reduce computational cost, a recursive relationship between explicit and implicit coefficients is established. The relationship obtained begins in terms of the generating functions. Referring to Eqs. (5.10) and (5.11), which are the first order generating functions
k
0
1
2
3
4
5
6
7
1
2
2
k
0
1
2
3
4
5
6
7
1
2
0
6 Order and stability
Various researchers have studied conditions of zero stability and the order of a block method which can be found in works of Watts and Shampine (1972), Mohd Ijam et al. (2018), Mohd Ijam and Ibrahim (2019) and Rasedee et al. (2021a) and etc. Discussions on order and stability of the proposed method applies definitions which are similar to Ola Fatunla (1991).
6.1 Order
The current section will show how the order of the method is established for the predictor in (4.7) and corrector in (4.8) when the given
. For the purpose of this research, let consider the case where
. The derivation begins with establishing the order method for the predictor. By extracting the explicit coefficients, the predicted first and second point can be expanded and written as
6.2 Stability
The viability of a linear multistep method is subject to certain conditions governed by zero stability. Similarly to works discussed in Hall and Watt (1976), the stability of the two-point predictor can be obtained by applying Eqs. (6.16) and (6.17) to the standard linear test problem,
Firstly, the predictor formula is amended in the form of block matrices which is substituted into the standard linear test problem which then expressed as
Whereas for the corrector, the stability polynomial is established as follows
7 Convergence of the backward difference method
As previously shown by Suleiman (1993), there are certain conditions that need to be met to show the convergence of the backward difference method.
The necessary conditions for the linear multistep method (4.7) and (4.8) to be convergent are
i) the method must be zero.
ii) the method must be consistent.
In the previous section, both the predictor and corrector satisfies conditions in Definition 2.4, making the method zero stable; whereas the order method as previously shown in Definition 2.3, with the predictor and the corrector are consistent with Definition 2.5 of order of 8 and 9 respectively. Satisfying both conditions and of Theorem 7.1 shows that the method to be convergent.
8 Variable order step size strategies
The literature on the variable order stepsize codes show an incomplete theory with numerous strategies of order and stepsize selection are given. Firstly, varying the order. The variable strategies are dependent on the amount of back values stored. With the appropriated amount of back values, the order can simply be increased by retaining the values of previous steps and can be decreased by disregarding unnecessary values. Previous researches have shown that the order strategies which are unbiased to lower order is efficient in an Adams based code for solving nonstiff problems.
As mentioned earlier, the acceptance criteria in a variable order strategy is crucial. In this article, the second step evaluation is determined on whether the estimated error, satisfies the local accuracy requirement, where A and B determine the type of error test, which is discussed later in the numerical results section. For reason of simplicity, the error estimate is denoted as , where . The order condition is set for and if both conditions and are satisfied, the order is reduced by 1. If is available, the condition to reduce the order is when and is satisfied. For the latter, the algorithm must first complete successful steps in constant stepsize, only then for where , and both and are satisfied will the order be increased.
As for varying the stepsize, this research adopts the halving and doubling of the stepsize algorithm suggested by Krogh (1973). Although doubling the stepsize might seem necessary because the previous back values of
can be used, Krogh argues that such technique will contribute to the loss of accuracy. In fact, doubling the stepsize after every evaluation may also have a toll on the accuracy. This is when halving the stepsize is required. In halving the step size algorithm, new back values are obtained. The use of back values in the form of
has shown to be more accurate. For more details on the algorithm, reader may refer to Rasedee (2009) and Rasedee et al. (2014). Fig. 1 illustrates the general flow of the proposed 2PVOSBD algorithm.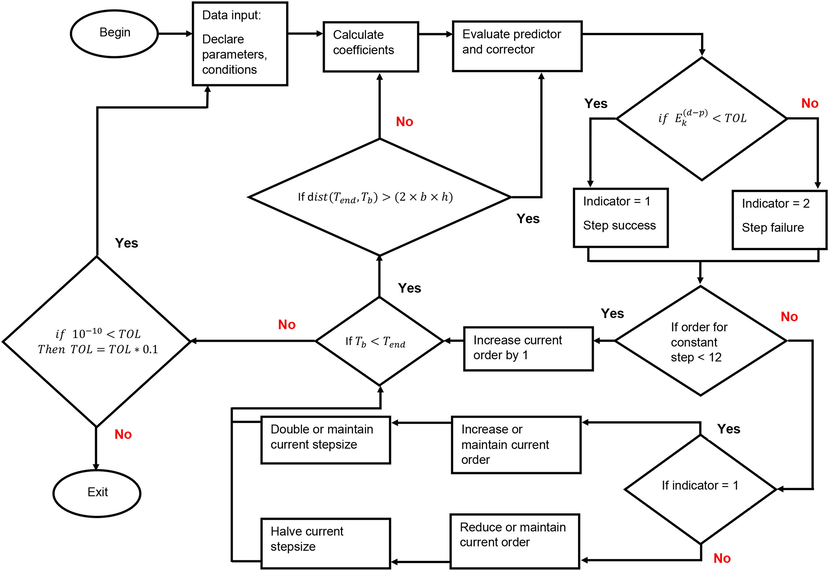
The general flowchart for the 2PVOSBD algorithm.
9 Numerical results and discussions
As numerical method becomes more robust, the accuracy of a method alone is no longer sufficient hence, the need for efficiency. When dealing with complex problems that require massive calculation, computational cost becomes a concern. The current research highlights the efficiency of proposed method. With little to none loss of accuracy, the 2PVOSBD offers an accuracy to total step ratio which proves to be efficient, similar as proposed in Rasedee (2009).
The 2PVOSBD method is tested with a combination of linear and nonlinear higher order initial value ODEs. The selected test problems are also inclusive of artificial and real-life, practical ODEs. The approximation obtained by the 2PVOSBD was compared with approximations of 1PVOSBD and DI methods which were reconstructed for the purpose of this research. Due to its divided difference based algorithm, the DI method was considered as a suitable counterpart of the 2PVOSBD backward difference based algorithm. The comparison is based on accuracy, total steps and efficiency of the methods. To compare approximated solution, the error solution in this research is defined by
where
is the
component of the exact solution and
is the
component of the approximated solution of f. There are 3 types of error test provided in the algorithm, where the most suitable estimation is selected. The choice of error tests are, absolute error when the corresponding
, relative error when
. and mixed error when
. For the current research, the mixed error test was deemed best suited. On the other hand, the maximum error (MaxErr) is defined as
and the average error (AvErr)
with N as the number of equations and B as the number of blocks. Contrary, the efficiency of the methods is defined as the ratio of accuracy compared to the corresponding total steps. These are the abbreviations that are used in the current section:
PeCe
predictor–corrector
ODE
ordinary differential equation
TOL
tolerance level
H
stepsize
TStep
total steps
MaxErr
overall maximum error
AvErr
average error
MTD
method used
DI
Direct Integration method
1PVOSBD
One-Point Block VOS backward difference method
2PVOSBD
Two-Point Block VOS backward difference method
The following are test problems that were selected for comparisons.
(Non linear 5th order ODE): The equation for with initial value conditions and as the exact solution. Source: Waeleh and Abdul Majid (2016).
(Non linear 5th order ODE): The equation for with initial value conditions and as the exact solution. Source: Waeleh and Abdul Majid (2016).
(Artificial problem): The equation for with initial value conditions and as the exact solution. Source: Suleiman (1979).
(4th order ODE) The equation for with initial value conditions where and as the exact solution.
(Van Der Pol equation): The equation for with initial value conditions .
Tables 3 and 4 are the approximated results for Problems 1–4 using the 2PVOSBD, but with the absence of the variable order stepsize component. The result presented compare the constant stepsizes, H
, H
, H
, H
and H
. Starting with Euler’s method, the algorithm increase the back values (order) each step until the total of 12 back values were obtained. Then, the algorithm completed its estimation using 12 back values for the remaining steps.
Table 5 presents the numerical approximation of the DI, 1PVOSBD and 2PVOSBD methods for the 5th order ODEs (Problems 1 and 2). Problems 1 and 2 were selected to test the 2PVOSBD method in approximating nonlinear ODEs. For Problem 1, the DI method out performed both 1PVOSBD and 2PVOSBD method in terms of accuracy and total steps. The non-homogeneous nature of the problems requires additional steps adjustments which affected the accuracy and total steps of proposed 2PVOSBD. Whereas for Problem 2, the proposed method shows better accuracy for almost every TOL level. It is also shown that in Problem 2, the 2PVOSBD method required less steps as compared to its counterpart when finer TOL is applied.
Next, Table 6 compares the numerical results of the 8th (Problem 3) and 6th (Problem 4) orders ODE. These problems were selected due to the order of the problems and large intervals. Problem 3 is an artificial problem obtained from Suleiman (1979). The accuracy of 2PVOSBD shows to be superior compared to latter methods. The 2PVOSBD out performs the accuracy of the other methods at every TOL. In terms of total steps, the 2PVOSBD and DI method shows to be competitive. Whereas for Problem 4, displays the rivaling nature of accuracy between the 1PVOSBD and 2PVOSBD. To avoid unbiasness, all methods used for comparison are structured with similar order stepsize conditions. Due to the characteristics of the DI method, certain criteria are not able to be met causing the DI method to be ineffective when dealing with large TOL for this particular problem. This becomes evident at TOL
. Due too many steps failures, the DI is forced to make an early exit from the program.
The accuracy to the total step ratio can be emphasized clearer by using illustrations. The efficiency of Problems 1 to 4 are presented in Fig. 1(a)–(d). To determine their efficiency, the accuracy to the stepsize ratio could be illustrated in the graphical form where the most efficient method is defined in Rasedee (2009) as the undermost curve. Fig. 1 exemplifies the efficiency of the DI for Problem 1(a) whereas the efficiency displayed in Figs. 1(b) and (c) favours the 2PVOSBD. On the other hand, the competitive efficiency between 2PVOSBD and DI is provided in Fig. 1(d), where the DI method is more efficient for large TOL and the 2PVOSBD is more efficient for finer TOL.
Finally, the approximation of Van Der Pol’s equation by 2PVOSBD method. Since the Van Der Pol equation is a nonlinear ODE without any known exact solution, the authors decided that it is best to represent the 2PVOSBD’s approximation in graphical form. Figs. 2 and 3 are provided to illustrate the approximation capability of the 2PVOSBD when faced with a non-linear oscillatory equation such as the Van Der Pol’s equation. See Fig. 4.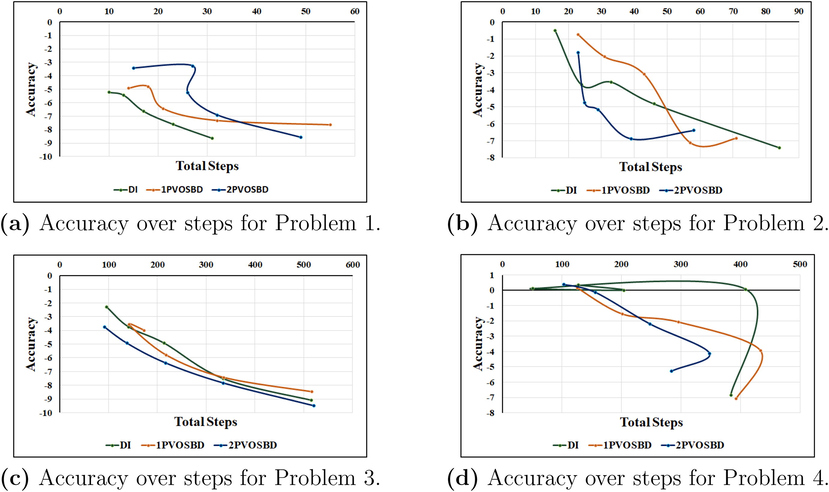
Efficiency of the DI, 1PVOSBD and 2PVOSBD methods.
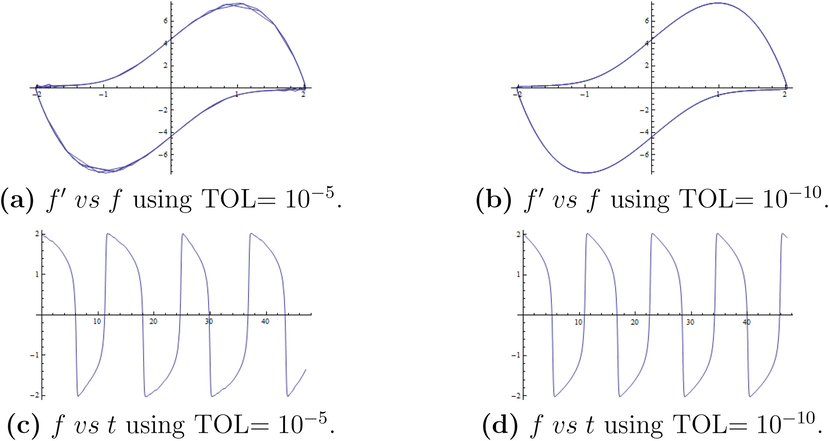
Van Der Pol Problem
using different TOL levels.
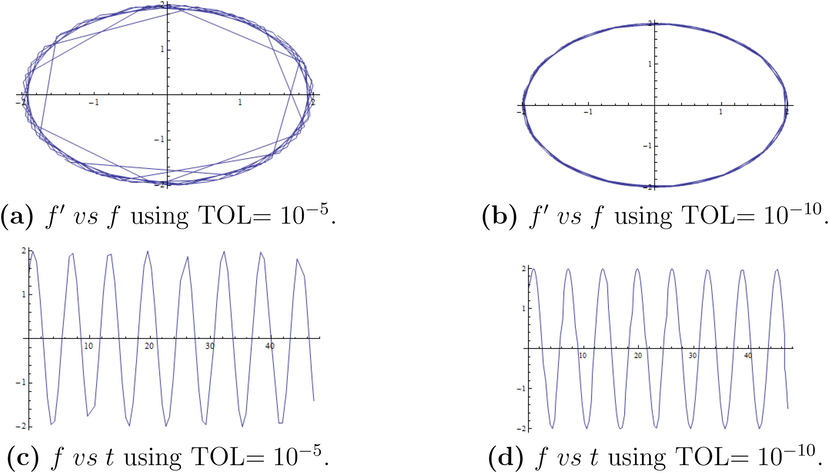
Van Der Pol Problem
using different TOL levels.
Fig. 2(a)–(d) are the approximated solution for Van Der Pol’s equation given using two separate TOL, and . It can be easily seen that Fig. 2(b) and (d) provide a smoother approximation as compared to Fig. 2(a) and (c). This shows the effectiveness of the 2PVOSBD method when using finer TOL. This becomes evident in Fig. 3(a)–(d) (given ).
The rapid stepsize increase which is due to a large TOL level, clearly has a more obvious effect in the accuracy of the approximation as shown in Fig. 3(a) and (c). By implementing a finer TOL level, Fig. 3(b) and (d) shows a smoother approximation for the current problem.
In conclusion, the proposed 2PVOSBD method is a viable instrument for solving higher order ODEs. This is contributed to the formulation of its algorithm. With a recursive relationship between different orders, each set of coefficients can be expressed in terms of the previous order. This eliminates the need to reformulate the integration coefficients for different orders but can simply be obtained using the recursive algorithm which reduces computational cost significantly. The efficiency of the algorithm is then elevated with the relationship between the explicit and implicit coefficients which allows the corrector code to be written in terms of the predictor, eliminates the need for tedious to obtain the corrector form scratch.
An extra advantage of the 2PVOSBD method is its adaptability to parallel programming because even with the current accuracy per step, there is an obvious difference between the constant and variable approaches. Problems selected for this research is to challenge the 2PVOSBD method’s capabilities. The method has also been tested against the second order systems of ODEs which readers may refer to in the works of Rasedee et al. (2017a, 2018b). The authors are currently working in effort of refine the order and step change for both selection criteria and algorithm to overcome any shortcomings in order to provide a more consistent and optimum approximation for every TOL level selected regardless of the type of ODE. For future works, the 2PBVOS method can modified for parallel programming and where reduced computational time can be observed. The proposed method can be extended to a three, four and eventually a N block algorithm.
Acknowledgment
This research has been supported by the Ministry of Education Malaysia (MoE) under the Fundamental Research Grant Scheme (FRGS), project number USIM/FRGS/FEM/ 055002/51517 and Universiti Putra Malaysia under the Putra Grant Scheme, project number GP-IPM95859600.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Three iterative methods for solving second order nonlinear odes arising in physics. Journal of King Saud University-Science. 2020;32(1):312-323.
- [Google Scholar]
- Solving directly higher order ordinary differential equations by using variable order block backward differentiation formulae. Symmetry. 2019;11(10):1289.
- [Google Scholar]
- A hybrid analytical-numerical technique for elliptic pdes. SIAM Journal on Scientific Computing. 2019;41(2):1066-1090.
- [Google Scholar]
- The numerical treatment of differential equations. 1960.
- A robust kernel-based solver for variable-order time fractional pdes under 2d/3d irregular domains. Applied Mathematics Letters. 2019;94:105-111.
- [Google Scholar]
- The numerical integration of ordinary differential equations. Mathematics of Computation. 1967;21(98):146-156.
- [Google Scholar]
- An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Physica A: Statistical Mechanics and its Applications. 2019;524:563-575.
- [Google Scholar]
- Modern Numerical Methods for Ordinary Differential Equations. Oxford: Claredon Press; 1976.
- Discrete Variable Methods in Ordinary Differential Equations. New York: Wiley; 1962.
- Variable order block method for solving second order ordinary differential equations. Sains Malaysiana. 2019;48(8):1761-1769.
- [Google Scholar]
- Solving directly third-order odes using operational matrices of bernstein polynomials method with applications to fluid flow equations. Journal of King Saud University-Science. 2019;31(4):822-826.
- [Google Scholar]
- A variable-step, variable-order multistep method for the numerical solution of ordinary differential equations. IFIP Congress. 1968;1:194-199.
- [Google Scholar]
- Algorithms for changing the step size. SIAM Journal on Numerical Analysis. 1973;10(5):949-965.
- [Google Scholar]
- Lambert, J. (1973). Computational methods in ordinary differential equations. Chichester, New York.
- An eulerian finite element method for pdes in time-dependent domains. ESAIM: Mathematical Modelling and Numerical Analysis. 2019;53(2):585-614.
- [Google Scholar]
- Direct integration implicit variable steps method for solving higher order systems of ordinary differential equations directly. Sains Malaysiana. 2006;35(2):63-68.
- [Google Scholar]
- Two point fully implicit block direct integration variable step method for solving higher order system of ordinary differential equations. World Congress on Engineering 2007:812-815.
- [Google Scholar]
- Diagonally implicit block backward differentiation formula with optimal stability properties for stiff ordinary differential equations. Symmetry. 2019;11(11):1342.
- [Google Scholar]
- Stability analysis of a diagonally implicit scheme of block backward differentiation formula for stiff pharmacokinetics models. Advances in Difference Equations. 2020;2020(1):1-22.
- [Google Scholar]
- Solving nonstiff higher-order ordinary differential equations using 2-point block method directly. Abstract and Applied Analysis. 2014;2014:1-13.
- [Google Scholar]
- Mohd Ijam, H., Ibrahim, Z.B., Senu, N., Suleiman, M., Rasedee, A.F.N. (2018). Order and stability of 2-point block backward difference method. In: AIP Conference Proceedings, vol. 1974, AIP Publishing LLC, p. 020054.
- Block methods for second order odes. International Journal of Computer Mathematics. 1991;41(1–2):55-63.
- [Google Scholar]
- Solving higher order ordinary differential equations using parallel 2-point explicit bock method. Matematika. 2005;21(1):15-23.
- [Google Scholar]
- Direct method using backward difference for solving higher order ordinary differential equations. Selangor: University Putra of Malaysia; 2009.
- Solving nonstiff higher order odes using variable order step size backward difference directly. Mathematical Problems in Engineering. 2014;2014:1-11.
- [Google Scholar]
- Rasedee, A.F.N. b., Sathar, M.H. b. A., Deraman, F., Ijam, H.M., Suleiman, M. b., Saaludin, N. b., Rakhimov, A. (2016). 2 point block backward difference method for solving riccati type differential problems. In: AIP Conference Proceedings, vol. 1775, AIP Publishing LLC, p. 030005.
- Numerical Solution for Duffing-Van Der Pol Oscillator Via Block Method. Plos One. 2021;10(1):19-28.
- [Google Scholar]
- Numerical Solutionf Duffing-Van Der Pol Oscillator Via Block Method. Advances in Mathematics: Scientific Journal. 2021;10(1):19-28.
- [Google Scholar]
- Variable order variable stepsize algorithm for solving nonlinear duffng oscillator. Journal of Physics: Conference Series. 2017;890 012045
- [Google Scholar]
- Solution for nonlinear duffing oscillator using variable order variable stepsize block method. MATEMATIKA: Malaysian Journal of Industrial and Applied Mathematics. 2017;33(2):165-176.
- [Google Scholar]
- Rasedee, A.F.N., Ijam, H.M., Sathar, M.H.A., Ishak, N., Hamzah, S.R., Sahrim, M., Ismail, I. (2018a). Solution for nonlinear riccati equation by block method. In: AIP Conference Proceedings, vol. 1974, AIP Publishing LLC, p. 020071.
- A numerical solution for duffing-van der pol oscillators using a backward difference formulation In AIP Conference Proceedings, vol. 2016. AIP Publishing LLC.; 2018. 020120
- Bemerkungen zur numerischen integration gewöhnlicher differentialgleichungen n-ter ordnung. Numerische Mathematik. 1960;2(1):263-279.
- [Google Scholar]
- A reliable numerical algorithm for the fractional klein-gordon equation. Engineering Transactions. 2019;67(1):21-34.
- [Google Scholar]
- An efficient computational approach for a fractional-order biological population model with carrying capacity. Chaos, Solitons & Fractals. 2020;138:1-13.
- [Google Scholar]
- Suleiman, M., 1979. Generalized multistep adams and backward differentiation methods for the solution of stiff and non-stiff ordinary differential equations. Ph. D. thesis, University of Manchester.
- Suleiman, M.B., 1993. Some necessary conditions for convergence of the gbdf methods. Mathematics of Computation 60(202) 635–649.
- Suleiman, M., Binti Ibrahim, Z.B., Bin Rasedee, A.F.N., 2011. Solution of higher-order odes using backward difference method. Mathematical Problems in Engineering, 2011.
- An efficient computational technique for fractional model of generalized hirota-satsuma coupled kdv and coupled mkdv equations. Journal of Computational and Nonlinear Dynamics. 2020;15(7):1-14.
- [Google Scholar]
- Waeleh, N. and Abdul Majid, Z., 2016. A 4-point block method for solving higher order ordinary differential equations directly. International Journal of Mathematics and Mathematical Sciences, 2016.
- A-stable block implicit one-step methods. BIT Numerical Mathematics. 1972;12(2):252-266.
- [Google Scholar]
- Direct fifth order block backward differentation formulas for solving second order ordinary differential equations. Chiang Mai J. Sci.. 2016;43:1171-1181.
- [Google Scholar]
- Novel high-order energy-preserving diagonally implicit runge–kutta schemes for nonlinear hamiltonian odes. Applied Mathematics Letters. 2020;102:1-9.
- [Google Scholar]
Appendix A
Supplementary data
Supplementary data associated with this article can be found, in the online version, athttps://doi.org/10.1016/j.jksus.2021.101376.
Supplementary data
The following are the Supplementary data to this article:






