Traveling wave solutions of conformable time-fractional Klien-Fock-Gordon equation by the improved
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This paper considers the improved
Keywords
Improved tan(α(Ψ)/2)-expansion method
Conformable derivative
Time-fractional Klien-Fock-Gordon equation
Trigonometric solutions
Exponential solutions
Hyperbolic solutions
Rational solutions
1 Introduction
The Klien-Fock-Gordon equation (KFG) models various physical phenomena in quantum field theory, condensed matter physics, nonlinear equations, correlation of solitons, collisionless plasma and theory of relativity etc. It was established by Osker Klien, Viladimir Fock and Walter Gordon for determining relativistic electrons. This equation is calibrated version of the relativistic energy–momentum correspondence. It is associated with Schr
In recent times, various research scholars of science and telecommunication have taken fractional order mathematical models under consideration. Fractional calculus has become a preeminent tool to analyze and characterize the nonlinear complex phenomena. Many partial differential equations (PDEs) that exhibit different physical phenomena are remodeled in terms of fractional derivative and their behavior is observed along with their solutions by developed methods (Akgül, 2018; Mamun et al., 2021). Fractional differential equations are widely studied in engineering mathematics and their fractional effects are observed for particular choices of fractional order parameters (Shahen et al., 2020; Shahen et al., 2021; Mamun et al., 2021; Hosseini et al., 2020).
This study considers the conformable time-fractional form of the Klein-Fock-Gordon equation (Alam et al., 2021)
Keeping in view the importance of fractional effects, the conformable time-fractional Klien-Fock-Gordon equation is solved to construct solitary wave solutions by
Various mathematical techniques have been developed to construct the traveling wave solutions of nonlinear evolution equations (NLEEs). Some recently proposed methods include
This article appraises the
This paper is coordinated as follows: In Section 2, the proposed model is introduced. In Section 3, the improved
2 Governing model
The quadratic conformable time-fractional KFG equation is considered, as
Conformable Derivative A new definition of conformable fractional derivative was proposed by Khalil et al. (2014) in 2014.
The conformable derivative of function
Properties Following properties are satisfied:
Theorem The following property is satisfied by conformable differentiable function
3 Description of Improved
In this section, the improved
Step
Step
Eq. (3.5) provides the following families of solutions (Akram et al., 2021).
Family 1: If
Family 2: If
Family 3: If
Family 4: If
Family 5: If
Family 6: If
Family 7: If
Family 8: If
Family 9: If
Family 10: If
Family 11: If
Family 12: If
Family 13: If
Family 14: If
Family 15: If
Family 16: If
Family 17: If
Family 18: If
Step
Substitute Eq. (3.24) in Eq. (3.3), to determine the value of k using homogeneous balance rule.
Inserting Eq. (3.25) into Eq. (3.3), the value of k is determined by homogeneous balance rule.
Step
Step
4 Exact solutions of quadratic time-fractional KFG equation
The reduced differential equation form of Eq. (2.1) is acquired by the complex-wave transform
The application of Eq. (4.1) on Eq. (2.1) yields
Using homogeneous balance rule, the integer
Eq. (4.3) is inserted into Eq. (4.1) and the coefficients of
Set
By Eq. (4.5), the Families 1, 2, 3, 4, 5, 6 and 7 are written respectively, as
The above solutions are valid for
Using Eq. (4.5), the Families 9, 10, 11, 12, 13 and 14 can be presented respectively, as
All the above solutions hold true for
Using Eq. (4.5), Family 18 is reported, as
The constraint condition to be satisfied by the above solution is
Set
By Eq. (4.21), the Families 1, 2, 3, 4, 5, 6 and 7 are respectively given, as
All the above solutions are valid for
By Eq. (4.21), the Families 9, 10, 11, 12, 13 and 14 can be written respectively, as
The above solutions are true for
Using Eq. (4.21), Family 18 is given, as
The above extracted solutions are valid for
Set
By Eq. (4.37), the Families 1, 2, 3, 4, 5, 6 and 7 can be presented respectively, as
All the above solutions are valid for
With the help of Eq. (4.21), the Families 9, 10, 11, 12, 13 and 14 can be respectively noted, as
All the above solutions are valid for
Using Eq. (4.37), Family 18 is reported, as
The above solution holds true for
Set
Using Eq. (4.53), the Families 1, 2, 3, 4, 5, 6 and 7 can be written respectively, as
All the preceding solutions are valid for
By Eq. (4.53), the Families 9, 10, 11, 12, 13 and 14 can be respectively reported, as
All the above solutions hold true for
Using Eq. (4.53), Family 18 is noted, as
The above extracted solution is valid for
5 Graphical representations of the obtained solutions
The graphical representation of solutions retrieved by the proposed method is usually as significant as the computation. It helps the reader to grab maximum amount of information of the model. In this section, the behavior of some solutions under fractional effect has been examined using their 3D plots and line plots. The graphical illustration of solutions is given for suitable choices of parameters
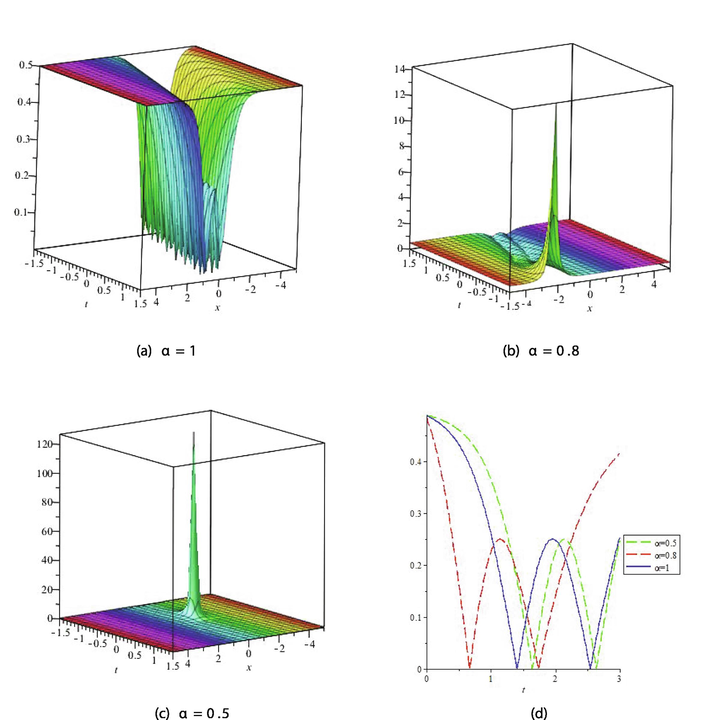
- The Graph for
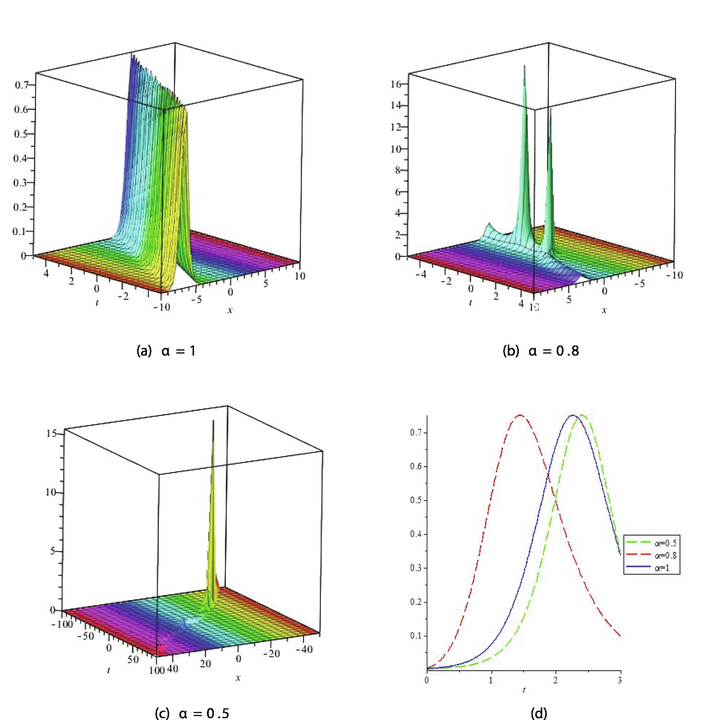
- The Graph for
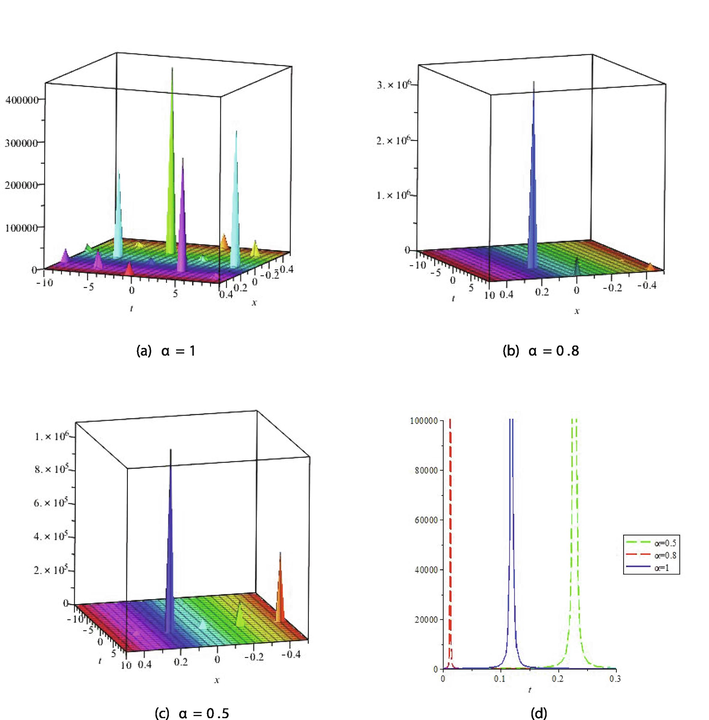
- The Graph for
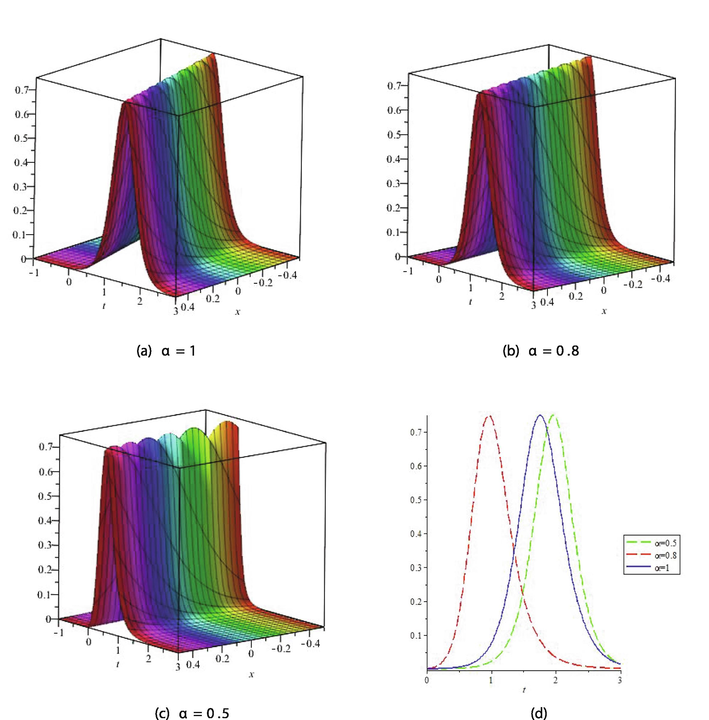
- The graph for
6 Conclusion
This paper addressed the conformable time-fractional Klien-Fock-Gordon equation. The proposed model was examined for quadratic nonlinearity. The conformable derivative was applied on the proposed model for investigating the fractional effects. The conformable derivative opens new horizons for the researchers and scientists to obtain analytical and numerical solutions of problems in science and engineering. The traveling wave transformation along with fractional operator was applied, for transforming the proposed fractional model into an ODE. After obtaining ODE, the improved
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Functionally invariant solutions of nonlinear Klein-Fock-Gordon equation. Appl. Math. Comput.. 2013;223:160-166.
- [Google Scholar]
- A novel method for a fractional derivative with non-local and non-singular kernel. Chaos Solitons Fractals. 2018;114:478-482.
- [Google Scholar]
- Bright, dark, kink, singular and periodic soliton solutions of Lakshmanan-Porsezian-Daniel model by generalized projective Riccati equations method. Optik: Int. J. Light Electron Optics. 2021;241:167051
- [Google Scholar]
- Kink, periodic, dark and bright soliton solutions of Kudryashov-Sinelshchikov equation using the improved
- [Google Scholar]
- Exact and explicit travelling traveling wave solution to the time-fractional phi-four and
- [Google Scholar]
- Stable and functional solutions of the Klein-Fock-Gordon equation with nonlinear physical phenomena. Phys. Scr.. 2021;96(5):055207
- [Google Scholar]
- Some exact solutions for a Klein-Gordon equation. Ingeniería y Ciencia. 2012;8(16):57-70.
- [Google Scholar]
- Solution of Volterra’s integro-differential equations by using variational iteration method. Int. J. Sci. Eng. Res.. 2020;11(3):1-9.
- [Google Scholar]
- Two-dimensional differential transform method and modified differential transform method for solving nonlinear fractional Klein-Gordon equation. National Acad. Sci. Lett.. 2014;37(2):163-171.
- [Google Scholar]
- Fixed point theorem based solvability of
- [Google Scholar]
- Optical solitons for complex Ginzburg-Landau model with Kerr, quadratic-cubic and parabolic law nonlinearities in nonlinear optics by the
- [Google Scholar]
- Soliton solutions of the Sasa-Satsuma equation in the monomode optical fibers including the beta-derivatives. Optik: Int. J. Light Electron Optics. 2020;224:165425
- [Google Scholar]
- A high-order nonlinear Schrödinger equation with the weak non-local nonlinearity and its optical solitons. Results Phys.. 2021;23:104035
- [Google Scholar]
- The
- [Google Scholar]
- Differential transform method for solving the linear and nonlinear Klein-Gordon equation. Comput. Phys. Commun.. 2009;180(5):708-711.
- [Google Scholar]
- Analytical solutions of linear and nonlinear Klein-Fock-Gordon equation. Nonlinear Eng.. 2015;4(1):43-48.
- [Google Scholar]
- Improved
- [Google Scholar]
- Equation with the many fathers. The Klein-Gordon equation in 1926. Am. J. Phys.. 1984;52(11):1024-1033.
- [Google Scholar]
- The first integral method for some time-fractional differential equations. J. Math. Anal. Appl.. 2012;395(2):684-693.
- [Google Scholar]
- Exact solitary wave solutions by extended rational sine-cosine and extended rational sinh-cosh techniques. Phys. Scr.. 2019;94(11):115212
- [Google Scholar]
- A study on an analytic solution 1D heat equation of a parabolic partial differential equation and implement in computer programming. Int. J. Sci. Eng. Res.. 2018;9:913-921.
- [Google Scholar]
- Exact and explicit travelling-wave solutions to the family of new 3D fractional WBBM equations in mathematical physics. Results Phys.. 2020;19:103517
- [Google Scholar]
- Dynamical behavior of travelling wave solutions to the conformable time-fractional modified Liouville and mRLW equations in water wave mechanics. Heliyon. 2021;7(8):e07704.
- [Google Scholar]
- Periodic and solitary wave solutions to a family of new 3D fractional WBBM equations using the two-variable method. Partial Differ. Eqs. Appl. Math.. 2021;3:100033.
- [Google Scholar]
- Solution of seventh order boundary value problem by using variational iteration method. Int. J. Math. Comput. Sci.. 2019;5(1):6-12.
- [Google Scholar]
- Solution of eighth order boundary value problem by using variational iteration method. Int. J. Math. Comput. Sci.. 2019;5(1):13-23.
- [Google Scholar]
- Solitary and periodic wave solutions to the family of new 3D fractional WBBM equations in mathematical physics. Heliyon. 2021;7(7):e07483.
- [Google Scholar]
- Application of
- [Google Scholar]
- New improvement of the expansion methods for solving the generalized Fitzhugh-Nagumo equation with time-dependent coefficients. Int. J. Eng. Math.. 2015;2015:107978
- [Google Scholar]
- Application of
- [Google Scholar]
- Optical soliton solutions for the Gerdjikov-Ivanov model via
- [Google Scholar]
- On the exact solutions of nonlinear evolution equations by the improved
- [Google Scholar]
- A Legendre-homotopy method for the solutions of higher order boundary value problems. J. King Saud Univ.-Sci.. 2020;32(1):537-543.
- [Google Scholar]
- Novel solutions of Biswas-Arshed equation by newly
- [Google Scholar]
- Solitary dynamics of longitudinal wave equation arises in magneto-electro-elastic circular rod. Mod. Phys. Lett. B. 2021;35(5):2150086.
- [Google Scholar]
- Interaction among lump, periodic, and kink solutions with dynamical analysis to the conformable time-fractional Phi-four equation. Partial Differential Equations. Appl. Math.. 2021;4:100038
- [Google Scholar]
- Dynamical analysis of long-wave phenomena for the nonlinear conformable space-time fractional
- [Google Scholar]
- An efficient technique for nonlinear time-fractional Klein-Fock-Gordon equation. Appl. Math. Comput.. 2020;364:124637
- [Google Scholar]







