The influence of pathological conditions on vocal cord’s displacement: A numerical method and data analysis

Nur Fatin Amirah Mohd Rodzi; Shazalina Mat Zin; Syatirah Mat Zin

doi:10.1016/j.jksus.2024.103545

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Full Length Article

12 2024

:36;

103545

doi:

10.1016/j.jksus.2024.103545

The influence of pathological conditions on vocal cord’s displacement: A numerical method and data analysis

Nur Fatin Amirah Mohd Rodzi^{^a}, Shazalina Mat Zin^{^a,⁎}, Syatirah Mat Zin^{^b}

a Institute of Engineering Mathematics, Universiti Malaysia Perlis (UniMAP), 02600 Arau, Perlis, Malaysia

b School of Technology and Engineering Sciences, Wawasan Open University, Jalan Sultan Ahmad Shah, 10050, Penang, Malaysia

⁎Corresponding author. shazalina@unimap.edu.my (Shazalina Mat Zin),

Received: 2024-8-16, Accepted: 2024-11-14,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Abstract

In this study, one-mass model of vocal cord is solved by using cubic trigonometric B-spline (CTBS) in order to generate displacements of healthy and pathological vocal cord. By utilizing CTBS, this work aims to investigate the relationship between five vocal cord conditions and its displacements generation throughout phonation process. The approximate displacements derived from CTBS are then compared to displacement generated by ode45 built-in solver through MATLAB software. The errors from both methods are then calculated which represented the effectiveness of the CTBS method in generating vocal cord displacements. Any discrepancies between the results generated by using CTBS and ode45 can be analysed to prove the reliability of CTBS method. Besides, an error analysis is demonstrated in order to quantitatively evaluate the accuracy of the approximate solutions. The generated approximate displacements of CTBS have shown to be approximately close to ode45 results. Thus, it can be concluded that CTBS is a reliable numerical method. The relationship between vocal cord conditions and its generated displacements has represented the distinction between healthy and pathological vocal cord outcomes. Healthy vocal cord has generated a steady decline displacements value while vocal cords with pathological condition have generated fluctuated displacement values throughout the phases of phonation process. The fluctuation trend of displacements value has revealed the irregular displacements value generation which is one of pathological vocal cord feature caused by low stiffness.

Keywords

Displacements of vocal cords

Cubic trigonometric B-spline

One-mass model of vocal cord

Show Related Articles from PubMed

1 Introduction

Speech production involves a complex interplay of physiological processes, with the vocal cords playing a crucial role in sound generation. The vocal cords, also known as vocal folds, are essential components of the larynx responsible for producing voice sounds. The vocal cords vibrate as the air passes through the larynx from lungs, which then form the basis of speech created by the sound waves. The larynx, also known as the voice box, is a structure located at the top of the trachea that involved in sound production process, breathing, and swallowing. The larynx contains the vocal cords, which are fold-like soft tissue that vibrates to produce sound. The distance between the opening of vocal cords is called glottis, that function to opens and closes, during breathing, swallowing and sound production process. Lot of researches have been conducted to study the movements of vocal cord through experiment and mathematical modelling approach.

The evolution of mechanical models of vocal cords has progressed from the basic one-mass model (Flanagan and Landgraf, 1968) to more complex multi-mass models (Drioli and Aichinger, 2021), as discussed in various research papers. Initially, the one-mass nonlinear oscillator system was accepted as the fundamental model for describing voice production. Over time, this model has been extended into three (Story and Titze, 1993), five (Yang et al., 2010), and more mass systems, incorporating time variable parameters (Cveticanin, 2015) and three-dimensional aspects (Lan, 2006), as well as simplified into systems with coupled deflection (Zheng et al., 2011) and damping functions (Fulcher et al., 2006). These advancements have allowed for more detailed description of the vibrations of symmetric (Tao et al., 2007) and asymmetric vocal cords (Erath et al., 2019), providing insights into regular and irregular motions like bifurcation (Mehdi and Mohammad, 2019) and deterministic chaos (Jiang and Zhang, 2002) in vocal cords. The progression from simpler one-mass models to more intricate multi-mass systems has significantly enhanced our understanding of the mechanical behaviour of vocal cords and their role in voice production.

The one-mass model of vocal cords by Flanagan is a significant advancement in vocal cord modelling, particularly in understanding the nonlinear interaction between vocal cord displacement and airflow. This model describes the system's behaviour qualitatively similar to higher-dimensional models like the two-mass Ishizaka‐Flanagan model (Ishizaka and Flanagan, 1972), showcasing its effectiveness in capturing essential dynamics of vocal cord vibration (Mcgowan and Howe, 2010). The one-mass model simplifies the complex mechanics of vocal cord oscillation into a more manageable framework, aiding in the study of voice production and pathology detection (Perrine et al., 2020). By incorporating the one-mass model, researchers can simulate vocal cord vibrations accurately and efficiently, enhancing the understanding of vocal physiology and potential disorders. Further, this work aims to generate displacements of vocal cord by solving one-mass model of vocal cord.

Numerical methods play an important role in solving various problems (Abd El-Hady & El-shenawy, 2024; Shirokova & El-Shenawy, 2018) such as mechanical models, (El-shenawy, El-Gamel, & Teba, 2024) and also to solve mechanical model of vocal cords. A numerical model called simVoice is introduced, which includes experimentally obtained vocal cord motion to simplify computational expenses and enhance efficiency (Maurerlehner et al., 2021). The numerical simulation of vocal cord vibrations excited by compressible viscous flow for flow and elasticity problems which involves space–time discontinuous Galerkin method and the backward difference formula in time and discontinuous Galerkin method in space (Balázsová et al., 2021). Furthermore, the mathematical model and numerical simulation of flow-induced vibrations of human vocal cords model employ the finite element method with SUPG and PSPG stabilization methods for fluid flow approximation, emphasizing the importance of inlet boundary conditions (Sváček and Horáček, 2018). Lastly, a study on vocal cord asymmetric collision presents a position-based contact model with variational methods for contact enforcement and highlights the impact of contact on vocal cord dynamics and oscillations (Granados et al., 2017).

The B-spline collocation method is a powerful numerical technique used in solving both initial value problems (IVPs) (Islam, 2015) and boundary value problems (BVPs) (Goh et al., 2012) efficiently. Various studies have highlighted the effectiveness of this method in providing accurate approximations for a wide range of problems. For instance, the uniform cubic B-spline collocation method has been successfully applied to linear (Goh, 2013) and nonlinear fractional IVPs (Rabah et al., 2022), demonstrating its validity and applicability (Tayebi et al., 2022). Additionally, the quintic B-spline collocation method has shown fourth-order convergence results when solving non-linear BVPs, showcasing its proficiency in handling such problems (Tok Onarcan et al., 2023). Moreover, the orthogonal cubic spline collocation technique has been utilized for two-point interface BVPs, emphasizing its computational superiority and stability over other methods (Bhal and Panda, 2022). There are few types of B-spline basis function such as B-spline, trigonometric B-spline (Chawla et al., 2023; Yaseen et al., 2017) and hybrid B-spline (Zin, 2016) that has widely used to solve various mathematical problems.

Since one-mass model of vocal cord is an initial value problem, cubic trigonometric B-spline (CTBS) (El-El-shenawy et al., 2024b) is chosen to solve this model and generate approximate displacements of vocal cord. Besides, CTBS is a simple and straightforward (Abbas et al., 2014) method to generate displacements of vocal cord. Abbas et al. state that the benefit of employing the suggested method is that, compared to the finite difference approach, which only provides the solution at specific points, it generates a spline function on each new time line that can be utilized to get the solutions of any intermediate point in the space direction. Subsequently, in order to prove the reliability of the proposed method, the error obtained by the proposed method will be calculated by comparing the generated displacements to ode45. Ode45 is a built-in solver through MATLAB software that has been widely used to solve various problems (Anyigor & Afiukwa, 2013; Postawa et al., 2020).

In conclusion, this study will generate the approximate displacements of one-mass model for healthy and pathological vocal cord using CTBS and verified by the ode45. Any discrepancies between both results can be analysed and proved the reliability of CTBS method. Besides, an error analysis is done in order to quantitatively evaluate the accuracy of the approximate solutions. This study will also investigate the relationship between vocal cord conditions and its displacements generation throughout phonation process.

2 Parameters

In this work, one-mass mechanical model of vocal cord is solved to generate displacements of vocal cord. The equation of the model is given by (Flanagan and Landgraf, 1968)

(1)

m x^{″} (t) + b x^{'} (t) + k x (t) = F (t),

with the following initial conditions

(2)

x (t_{0}) = α and x^{'} (t_{0}) = β,

where

x (t)

is displacement of vocal cord,

m

is mass,

b

is damping,

k

is spring constant while

F (t)

is forcing function. The value of mass, damping and spring constant can be calculated by

(3)

mass, m = \frac{1}{4} σ l^{2} d,

(4)

damping, b = 2 \sqrt{mk},

and

(5)

springconstant, k = 4 π^{2} m {(f_{0})}^{2},

where

σ

is the density of vocal cord flesh,

l

is the cord length,

d

is the vocal cord thickness, and

f_{0}

is fundamental frequency. The forcing function is calculated by

F (t) = \frac{1}{2} (P_{1} + P_{2}) (ld)

where

P_{1}

and

P_{2}

are the acoustic pressures at the inlet and outlet of the glottal orifice, and can be obtained by

P_{1} = P_{s} - 1.37 P_{B}

and

P_{2} = - 0.50 P_{B} .

P_{s}

is subglottal pressure and

P_{B}

is Bernoulli pressure and can be calculated by

P_{B} = \frac{1}{2} ρ {|U_{g}|}^{2} A g^{- 2}

while the value of displacements and fundamental frequencies will be calculated in the next section.

3 Methodology

This section explained methodology in finding fundamental frequencies, $f_{0}$ and approximate displacements of five vocal cord conditions. The conditions are healthy, laryngitis, hyperfunctional dysphonia, functional dysphonia and recurrent laryngeal nerve paralysis. Subsection 3.1 discussed the method used to generate fundamental frequency. Then, subsection 3.2 and 3.3 discussed the generation of displacements by using CTBS and ode45 respectively.

3.1

3.1 Fundamental frequency

Origin is a data analysis and graphing software that also offered analysis tools and apps for signal processing. The software is used to obtain fundamental frequencies. The fundamental frequencies are obtained by the following steps:

100 voice recordings of each vocal cord conditions are gathered from Saarbruecken Voice Database (Barry and Pützer, 2007).
The recordings are then, imported into Origin, in order to generate the frequencies, providing the magnitude, amplitude, phase, one/two-sided power density, and other computation results.
From the frequency values, fundamental frequencies of the recording can be obtained to find the value of $k$ from Eq. (5) as follows:
(6)
$f_{0} = Index of the largest power \times F_{s} + F 0,$ where the index of the largest power can be obtained from FFT result, $f_{0}$ is frequency resolution and $F 0$ is the starting frequency value.
Further, the average fundamental frequency of each condition is calculated and used in proposed method.

3.2

3.2 Cubic trigonometric B-spline (CTBS)

This subsection discusses CTBS method in generating approximate displacements of vocal cord by solving Eq. (1). In CTBS, the knot with non-decreasing sequence is considered as $\{t_{0}, t_{1}, \dots t_{j - 1}, t_{j}, t_{j + 1}, \dots t_{n}\}$ where $t_{j - 1} ⩽ t_{j} ⩽ t_{j + 1}$ for $j = 0, 1, \dots n$ . The $j - th$ basis of trigonometric B-spline, $T_{j}^{k} (t)$ of order $k$ can be calculated using (Walz, 1997)

(7)

T_{j}^{k} (t) = \frac{\sin (\frac{t - t_{j}}{2})}{\sin (\frac{t_{j + k - 1} - t_{j}}{2})} T_{j}^{k - 1} (t) + \frac{\sin (\frac{t_{j + k} - t}{2})}{\sin (\frac{t_{j + k} - t_{j + 1}}{2})} T_{j + 1}^{k - 1} (t),

where CTBS basis of order one is defined as

(8)

T_{j}^{1} (t) = \{\begin{matrix} 1, & t \in [t_{j}, t_{j + 1}], \\ 0, & otherwise . \end{matrix}

Then, the CTBS basis of order four is defined as

(9)

T_{j}^{4} (t) = \frac{1}{θ} \{\begin{matrix} σ^{3} (t_{j}), & t \in [t_{j}, t_{j + 1}], \\ \begin{matrix} σ (t_{j}) [σ (t_{j}) ϛ (t_{j + 2}) + ϛ (t_{j + 3}) σ^{2} (t_{j + 1})] \\ + ϛ (t_{j + 4}) σ^{2} (t_{j + 1}), \end{matrix} & t \in [t_{j + 1}, t_{j + 2}], \\ \begin{matrix} σ (t_{j}) ϛ^{2} (t_{j + 3}) + ϛ (t_{j + 4}) \\ [σ (t_{j + 1}) ϛ (t_{j + 3}) + ϛ (t_{j + 4}) σ (t_{j + 2})], \end{matrix} & t \in [t_{j + 2}, t_{j + 3}], \\ ϛ^{3} (t_{j + 4}), & t \in [t_{j + 3}, t_{j + 4}], \\ 0, & otherwise, \end{matrix}

where

σ (t_{j}) = \sin (\frac{t - t_{j}}{2}),

ϛ (t_{j}) = (\frac{t_{j} - t}{2})

and

θ = \sin^{2} (\frac{h}{2}) \csc (h) \csc (\frac{3 h}{2}) .

CTBS function, $x^{*} (t)$ is an approximate displacement generated from a linear combination of the CTBS basis, as in

(10)

x^{*} (t) = \sum_{j = - 3}^{n - 1} C_{j} T_{j}^{4} (t),

where

C_{j}

are unknowns to be evaluated and

T_{j}^{4}

is CTBS basis and can be simplified to

(11)

x^{*} (t_{j}) = C_{j - 3} T_{j - 3}^{4} (t) + C_{j - 2} T_{j - 2}^{4} (t) + C_{j - 1} T_{j - 1}^{4} (t) + C_{j} T_{j}^{4} (t),

(12)

x^{*'} (t_{j}) = C_{j - 3} T_{j - 3}^{4'} (t) + C_{j - 2} T_{j - 2}^{4'} (t) + C_{j - 1} T_{j - 1}^{4'} (t) + C_{j} T_{j}^{4'} (t),

(13)

x^{* ″} (t_{j}) = C_{j - 3} T_{j - 3}^{4 ″} (t) + C_{j - 2} T_{j - 2}^{4 ″} (t) + C_{j - 1} T_{j - 1}^{4 ″} (t) + C_{j} T_{j}^{4 ″} (t),

Three nonzero basis functions of $T_{j - 3}^{4} (t_{j}),$ $T_{j - 2}^{4} (t_{j})$ and $T_{j - 1}^{4} (t_{j})$ are included over $[t_{j}, t_{j + 1}]$ subinterval. By considering the nonzero basis functions, Eq. (11) and its derivatives can be simplified and returned as

(14)

\begin{matrix} x^{*} (t_{j}) = ϛ_{1} C_{j - 3} + ϛ_{2} C_{j - 2} + ϛ_{1} C_{j - 1}, \\ x^{*'} (t_{j}) = - ϛ_{3} C_{j - 3} + ϛ_{3} C_{j - 1}, \\ x^{* ″} (t_{j}) = ϛ_{4} C_{j - 3} + ϛ_{5} C_{j - 2} + ϛ_{4} C_{j - 1} \end{matrix}

with

ϛ_{1} = \sin^{2} (\frac{h}{2}) \csc (h) \csc (\frac{3 h}{2})

ϛ_{2} = \frac{2}{1 + 2 \cos (h)},

ϛ_{3} = - \frac{3}{4} \csc (\frac{3 h}{2}),

ϛ_{4} = \frac{3 (1 + 3 \cos (h)) \csc^{2} (\frac{h}{2})}{16 (2 \cos (\frac{h}{2}) + \cos (\frac{3 h}{2}))},

and

ϛ_{5} = - \frac{3 \cot^{2} (\frac{h}{2})}{2 + 4 \cos (h)} .

Eq. (14) is then substituted into the equation to produce a matrix system of order $(n + 1)$ equation with $(n + 3)$ unknown to solve Eq. (1). Next, two equations are needed in order to generate a unique solution. Subsequently, initial condition which given in Eq. (2) is approximated and represented as

(15)

\begin{matrix} x^{*} (t_{0}) = ϛ_{1} C_{j - 3} + ϛ_{2} C_{j - 2} + ϛ_{1} C_{j - 1} = α, \\ x^{*'} (t_{0}) = - ϛ_{3} C_{j - 3} + ϛ_{3} C_{j - 1} = β . \end{matrix}

Eq. (15) is added to the system and become

(16)

{[A]}_{(n + 3) \times (n + 3)} . {[C]}_{(n + 3) \times 1} = {[R]}_{1 \times (n + 3)},

where

$A = [\begin{matrix} ϛ_{1} & ϛ_{2} & ϛ_{1} & 0 & \dots & \dots & \dots & 0 \\ ω_{1} & ω_{2} & ω_{3} & 0 & \dots & \dots & \dots & 0 \\ 0 & ω_{1} & ω_{2} & ω_{3} & 0 & \dots & \dots & 0 \\ ⋮ & 0 & ω_{1} & ω_{2} & ω_{3} & 0 & \dots & 0 \\ 0 & \dots & ⋱ & ⋱ & ⋱ & \dots & \dots & 0 \\ 0 & \dots & \dots & \dots & 0 & ω_{1} & ω_{2} & ω_{3} \\ ϛ_{3} & 0 & ϛ_{3} & 0 & \dots & \dots & \dots & 0 \end{matrix}],$ $C = [\begin{matrix} C_{- 3} \\ C_{- 2} \\ C_{- 1} \\ ⋮ \\ C_{n - 1} \end{matrix}]$ and $F = [\begin{matrix} α \\ F \\ ⋮ \\ ⋮ \\ F \\ β \end{matrix}]$ ,

and $\begin{matrix} ω_{1} = m (ϛ_{4}) - b (ϛ_{3}) + k (ϛ_{1}), \\ ω_{2} = m (ϛ_{5}) + k (ϛ_{2}), \\ ω_{3} = m (ϛ_{4}) + b (ϛ_{3}) + k (ϛ_{1}) . \end{matrix}$

By solving the matrix system, $C$ is evaluated and substituted into Eq. (10) to obtain the approximate solution for Eq. (1).

3.3

3.3 Ode45

Ode45 is a build-in solver in MATLAB’s standard solver for ordinary differential equations (ODEs). By using the same parameter as CTBS, Eq. (1) is also solved by using the following algorithm.

Algorithm 1. Code for solving Eq. (1) by using ode45
f = @(t,x) [x(2); (F-r*x(2)-k*x(1))/m];
tspan = t0:(0.05–0)/(n):tN;
ts = zeros(1,n); xs = zeros(1,n);
[ts,xs] = ode45(f,tspan,[0;0]);

4 Error analysis

The estimation of a truncation error for the proposed method is presented in this section. From approximate displacement in Eq. (14), the relationships can be obtained as follows:

(17)

h [x^{*'} (t_{j - 1}) + 4 x^{*'} (t_{j}) + x^{*'} (t_{j + 1})] = 3 [x^{*'} (t_{j + 1}) - x^{*'} (t_{j - 1})],

(18)

h^{2} x^{* ″} (t_{j}) = 6 [x^{*} (t_{j}) - x^{*} (t_{j + 1})] - 2 h [x^{*'} (t_{j}) + x^{*'} (t_{j + 1})],

(19)

h^{3} x^{* ‴} (t_{j +}) = 12 [x^{*} (t_{j}) - x^{*} (t_{j + 1})] + 6 h [x^{*'} (t_{j}) + x^{*'} (t_{j + 1})],

(20)

h^{3} x^{* ‴} (t_{j -}) = 12 [x^{*} (t_{j - 1}) - x^{*} (t_{j})] + 6 h [x^{*'} (t_{j - 1}) + x^{*'} (t_{j})] .

Then,

x^{* ‴} (t_{j +})

and

x^{* ‴} (t_{j -})

are the approximate values of

x^{* ″'} (t)

[t_{j}, t_{j + 1}]

and

[t_{j - 1}, t_{j}],

respectively. By using the operator notation

E (x^{*} (t_{j})) = x^{*} (t_{j}),

Eq. (17) can be written as

(21)

h (E^{- 1} + 4 + E) x^{*'} (t_{j}) = 3 (E - E^{- 1}) x^{*} (t_{j}) .

Since

E = e^{hD}

where

D = \frac{d}{dx},

operator

E

can be written in an expression form in powers of

hD

e^{hD} = 1 + h D + \frac{h^{2} D^{2}}{2!} + \frac{h^{3} D^{3}}{3!} + \frac{h^{4} D^{4}}{4!} + \frac{h^{5} D^{5}}{5!} + \dots

e^{- h D} = 1 - h D + \frac{h^{2} D^{2}}{2!} - \frac{h^{3} D^{3}}{3!} + \frac{h^{4} D^{4}}{4!} - \frac{h^{5} D^{5}}{5!} + \dots

Next, Eq. (21), can be written as

(22)

h (e^{- h D} + 4 + e^{hD}) x^{*'} (t_{j}) = 3 (e^{hD} - e^{- h D}) x^{*} (t_{j}) .

Hence, can be given by

(23)

x^{*'} (t_{j}) = x^{*'} (t_{j}) - \frac{1}{180} h^{4} x^{* (5)} (t_{j}) + O (h^{6}) .

By using the same approach for Eq. (17)-(20), we can derive the following relations:

(24)

x^{* ″} (t_{j}) = x^{* ″} (t_{j}) - \frac{1}{12} h^{2} x^{* (4)} (t_{j}) + \frac{1}{360} h^{4} x^{* (6)} (t_{j}) + O (h^{6}),

(25)

x^{* ″'} (t_{j +}) = x^{* ″'} (t_{j}) + \frac{1}{2} h x^{* (4)} (t_{j}) + \frac{1}{12} h^{2} x^{* (5)} (t_{j}) - \frac{1}{360} h^{4} x^{* (7)} (t_{j}) - \frac{1}{1440} h^{5} x^{* (8)} (t_{j}) + O (h^{6}),

(26)

x^{* ″'} (t_{j -}) = x^{* ″'} (t_{j}) - \frac{1}{2} h x^{* (4)} (t_{j}) + \frac{1}{12} h^{2} x^{* (5)} (t_{j}) - \frac{1}{360} h^{4} x^{* (7)} (t_{j}) - \frac{1}{1440} h^{5} x^{* (8)} (t_{j}) + O (h^{6}) .

Then, Eq. (25)-(26) can be written as

(27)

\frac{1}{2} [x^{* ″'} (t_{j +}) + x^{* ″'} (t_{j -})] = x^{* ″'} (t_{j}) + \frac{1}{12} h^{2} x^{* (5)} (t_{j}) + O (h^{4})

and

(28)

x^{* ″'} (t_{j +}) + x^{* ″'} (t_{j -}) = h x^{* (4)} (t_{j}) - \frac{1}{720} h^{5} x^{* (8)} (t_{j}) + O (h^{7}) .

Afterwards,

e (t)

is defined as

e (t) = x^{*} (t_{j}) - x^{*}

and the equations of (23)-(26) are substituted into

e (t_{j} + θ h)

to obtain

(29)

e (t_{j} + θ h) = \frac{θ^{2} {(θ - 1)}^{2}}{24} h^{4} x^{* (4)} (t_{j}) + \frac{θ (θ^{2} - 1) (3 θ^{2} - 2)}{360} h^{5} x^{* (5)} (t_{j}) + O (h^{6}) .

Subsequently, the cubic uniform trigonometry B-spline is

O (h^{4})

accurate.

5 Results and discussions

This section represented the approximate displacements generated by healthy and four pathological conditions of vocal cords, and then analysed accordingly. 100 recordings of each vocal cord condition which is healthy, hyperfunctional dysphonia (HD), laryngitis, functional dysphonia (FD) and recurrent laryngeal nerve paralysis (RLNP) were synthesized to obtained average of fundamental frequencies. Table 1 and Table 2 tabulated the parameters, and the average of fundamental frequencies for healthy and the pathological conditions of vocal cords. Three phases of phonation process will be considered; (i) early phase at 0.01 s, (ii) middle phase at 0.03 s and (iii) end phase at 0.05 s. The errors between CTBS and ode45 of each vocal cord condition will be evaluated as $Error = |x (t) - x^{*} (t)|$ .

Table 1 Parameters used in solving Eq. (1) (Cataldo et al., 2006; Flanagan and Landgraf, 1968).

Parameter	Value
m	0.240 × 10^-3 kg
b	0.667 Ns/m
k	4.925 × 10⁵ Ns/m
t	0.050 s
P_s	783 Pa
ρ	1.300 × 10³ kg/m³
l	1.800 × 10^-2 m
d	0.300 × 10^-3 m
h	1.000 × 10^-4

Table 2 Average fundamental frequencies of healthy and pathological conditions of vocal cords.

Vocal cord conditions	Fundamental frequency, $f_{0}$ (Hz)
Healthy	453.7542
Hyperfunctional dysphonia	426.1522
Laryngitis	383.8566
Functional dysphonia	433.9783
Recurrent laryngeal nerve paralysis	418.1722

Fig. 1 illustrated the generated displacements of (a) healthy, (b) HD, (c) laryngitis, (d) FD and (e) RLNP. Numerically, the displacements and the errors of each condition obtained by comparing the approximate displacements between CTBS and ode45 are tabulated in Table 3 and 4. It can be seen that CTBS and ode45 has generated slightly equal displacement within 0.05 s. The figure and numerical values revealed that CTBS is a reliable method in generating displacement of vocal cord when compared to ode45.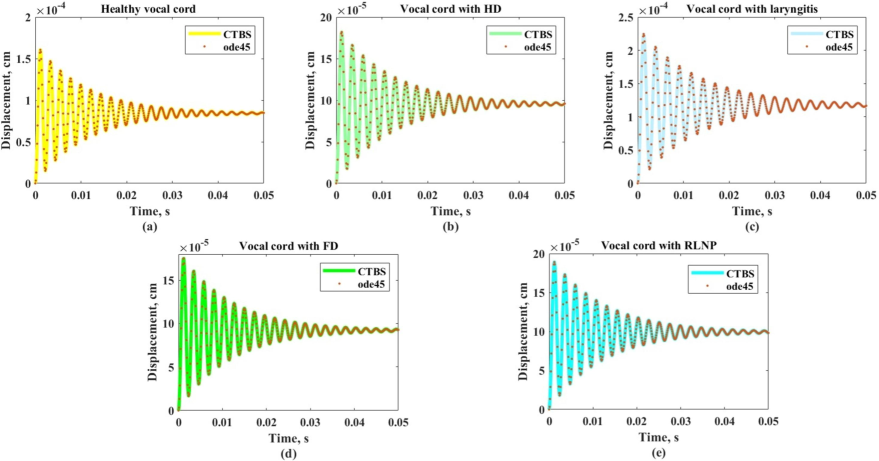

Displacements of (a) healthy vocal cord, vocal cord with (b) HD, (c) laryngitis, (d) FD and (e) RLNP generated by using CTBS and ode45 within 0.05 s.

Table 3 Displacements of each vocal cords condition obtained by using CTBS and ode4 within 0.05 s.

Time (s)	Displacements (cm)
	Healthy		HD		Laryngitis		FD		RLNP
	CTBS	ode45	CTBS	ode45	CTBS	ode45	CTBS	ode45	CTBS	ode45
0.010	1.1878 $\times$ 10^-4	1.1847 $\times$ 10^-4	9.3446 $\times$ 10^-5	9.2517 $\times$ 10^-5	9.3431 $\times$ 10^-5	9.5274 $\times$ 10^-5	1.0876 $\times$ 10^-4	1.0790 $\times$ 10^-4	1.0876 $\times$ 10^-4	1.0790 $\times$ 10^-4
0.015	8.0780 $\times$ 10^-5	8.1291 $\times$ 10^-5	1.1362 $\times$ 10^-4	1.1269 $\times$ 10^-4	1.2106 $\times$ 10^-4	1.2295 $\times$ 10^-4	1.1767 $\times$ 10^-4	1.1724 $\times$ 10^-4	1.1767 $\times$ 10^-4	1.1724 $\times$ 10^-4
0.020	7.0404 $\times$ 10^-5	7.0602 $\times$ 10^-5	1.1345 $\times$ 10^-4	1.1308 $\times$ 10^-4	1.3308 $\times$ 10^-4	1.3429 $\times$ 10^-4	1.0253 $\times$ 10^-4	1.0288 $\times$ 10^-4	1.0253 $\times$ 10^-4	1.0288 $\times$ 10^-4
0.025	8.6857 $\times$ 10^-5	8.6491 $\times$ 10^-5	1.0455 $\times$ 10^-4	1.0479 $\times$ 10^-4	1.3420 $\times$ 10^-4	1.3449 $\times$ 10^-4	8.8370 $\times$ 10^-5	8.8979 $\times$ 10^-5	8.8370 $\times$ 10^-5	8.8979 $\times$ 10^-5
0.030	8.9785 $\times$ 10^-5	8.9697 $\times$ 10^-5	9.6264 $\times$ 10^-5	9.6773 $\times$ 10^-5	1.2988 $\times$ 10^-4	1.2994 $\times$ 10^-4	8.5128 $\times$ 10^-5	8.5408 $\times$ 10^-5	8.5128 $\times$ 10^-5	8.5408 $\times$ 10^-5
0.035	8.2788 $\times$ 10^-5	8.3004 $\times$ 10^-5	9.2327 $\times$ 10^-5	9.2744 $\times$ 10^-5	1.2427 $\times$ 10^-4	1.2348 $\times$ 10^-4	8.8951 $\times$ 10^-5	8.8813 $\times$ 10^-5	8.8951 $\times$ 10^-5	8.8813 $\times$ 10^-5
0.040	8.2152 $\times$ 10^-5	8.2182 $\times$ 10^-5	9.2217 $\times$ 10^-5	9.2373 $\times$ 10^-5	1.1972 $\times$ 10^-4	1.1894 $\times$ 10^-4	9.2952 $\times$ 10^-5	9.2685 $\times$ 10^-5	9.2952 $\times$ 10^-5	9.2685 $\times$ 10^-5
0.045	8.5079 $\times$ 10^-5	8.4962 $\times$ 10^-5	9.3819 $\times$ 10^-5	9.3753 $\times$ 10^-5	1.1701 $\times$ 10^-4	1.1646 $\times$ 10^-4	9.4061 $\times$ 10^-5	9.3929 $\times$ 10^-5	9.4061 $\times$ 10^-5	9.3929 $\times$ 10^-5
0.050	8.5102 $\times$ 10^-5	8.5097 $\times$ 10^-5	9.5372 $\times$ 10^-5	9.5219 $\times$ 10^-5	1.1596 $\times$ 10^-4	1.1571 $\times$ 10^-4	9.3113 $\times$ 10^-5	9.3154 $\times$ 10^-5	9.3113 $\times$ 10^-5	9.3154 $\times$ 10^-5

Table 4 Errors of each vocal cords condition obtained within 0.05 s.

Time (s)	Errors
Time (s)	Healthy	HD	Laryngitis	FD	RLNP
0.010	3.0474 $\times$ 10^-7	9.2841 $\times$ 10^-7	1.8423 $\times$ 10^-6	8.6056 $\times$ 10^-7	8.6056 $\times$ 10^-7
0.015	5.1106 $\times$ 10^-7	9.2687 $\times$ 10^-7	1.8877 $\times$ 10^-6	4.2781 $\times$ 10^-7	4.2781 $\times$ 10^-7
0.020	1.9810 $\times$ 10^-7	3.6930 $\times$ 10^-7	1.2091 $\times$ 10^-6	3.4659 $\times$ 10^-7	3.4659 $\times$ 10^-7
0.025	3.6570 $\times$ 10^-7	2.4035 $\times$ 10^-7	2.9217 $\times$ 10^-7	6.0949 $\times$ 10^-7	6.0949 $\times$ 10^-7
0.030	8.8213 $\times$ 10^-8	5.0958 $\times$ 10^-7	4.3992 $\times$ 10^-7	2.8026 $\times$ 10^-7	2.8026 $\times$ 10^-7
0.035	2.1665 $\times$ 10^-7	4.1664 $\times$ 10^-7	7.8928 $\times$ 10^-7	1.3728 $\times$ 10^-7	1.3728 $\times$ 10^-7
0.040	2.9324 $\times$ 10^-8	1.5561 $\times$ 10^-7	7.7928 $\times$ 10^-7	2.6748 $\times$ 10^-7	2.6748 $\times$ 10^-7
0.045	1.1605 $\times$ 10^-7	6.5709 $\times$ 10^-8	5.4700 $\times$ 10^-7	1.3223 $\times$ 10^-7	1.3223 $\times$ 10^-7
0.050	5.1934 $\times$ 10^-9	1.5306 $\times$ 10^-7	2.5222 $\times$ 10^-7	4.0653 $\times$ 10^-8	4.0653 $\times$ 10^-8

The phases of the phonation process of each vocal cord condition can be observed from Table 3. It is apparent from Table 3 that the value of displacements generated by healthy vocal cord steadily declined throughout the process. Nevertheless, the displacement of vocal cord with HD, laryngitis, FD and RLNP are fluctuated throughout the early, middle and end phases. The HD, laryngitis and RLNP condition have developed the fluctuation increase–decrease displacements while FD condition has formed decrease-increase displacements of phonation process.

Based on the trend which can be observed from Table 5, it can be assumed that healthy vocal cord has the widest opening at early phase of phonation process, which then decreased at the middle and more narrowed at the end phase. However, the fluctuated trend of the vocal cord with pathological conditions such as HD, laryngitis and RLNP have shown that they have wider opening at the middle phase than at the early phase. The opening of these vocal cords are then decreased at the end phase but still wider than at the early phase. Aside from that, vocal cord with FD has demonstrated a different fluctuation trend than other pathological condition. It can be deducted that vocal cord with FD’s opening has decreased at the middle phase than at the early phase, but unexpectedly increased at the end phase.

Table 5 Displacements generated by each condition throughout phonation process.

Conditions	Displacements throughout phonation process (cm)
Conditions	Early phase, 0.010 s	Middle phase, 0.030 s	End phase, 0.050 s
Healthy	1.1878 $\times$ 10^-4	8.9785 $\times$ 10^-5	8.5102 $\times$ 10^-5
HD	9.3446 $\times$ 10^-5	9.6264 $\times$ 10^-5	9.5372 $\times$ 10^-5
Laryngitis	9.3431 $\times$ 10^-5	1.2988 $\times$ 10^-4	1.1596 $\times$ 10^-4
FD	1.0876 $\times$ 10^-4	8.5128 $\times$ 10^-5	9.3113 $\times$ 10^-5
RLNP	7.6495 $\times$ 10^-5	1.0769 $\times$ 10^-4	9.8421 $\times$ 10^-5

6 Conclusion

In this work, the approximate displacements of five types of vocal cord conditions have been generated by using CTBS and ode45. Overall, it is evident that the generated approximate displacements by CTBS are approximately close to ode45. It can be concluded from the calculated error that CTBS is reliable method in generating displacements of vocal cord. The generated displacements also have been utilized to investigate the phases of phonation process. It can be pointed from the outcomes illustrated in Fig. 2 and Table 5, that healthy vocal cord presents the steadily decline phonation process. In contrast, another five pathological conditions have developed fluctuated displacement. Fluctuation of displacements value revealed the irregular displacements value generation that is a characteristic of pathological vocal cord (Bonilha and Deliyski, 2008) which caused by low stiffness. It may be the case therefore that vocal cord with pathological condition has lower stiffness than healthy vocal cord. Therefore, this work offers new insights into the speech production of healthy and pathological vocal cord through numerical results. Future researches are encouraged to investigate the effect of various pathological conditions towards the stiffness of vocal cord. This could aid in determining the relationship between vocal cord conditions towards its stiffness and the effect towards vocal cord displacements value.

Displacements generated by each vocal cord conditions throughout the phases of phonation process.

CRediT authorship contribution statement

Nur Fatin Amirah Mohd Rodzi: Writing – original draft, Visualization, Software, Methodology, Investigation, Formal analysis, Data curation. Shazalina Mat Zin: Writing – review & editing, Project administration, Validation, Supervision, Resources, Data curation, Conceptualization. Syatirah Mat Zin: Formal analysis, Supervision, Validation, Visualization.

Acknowledgments

The authors would like to acknowledge the support from the Fundamental Research Grant Scheme (FRGS) under a grant number of FRGS/1/2019/STG06/UNIMAP/03/2 from the Ministry of Higher Education of Malaysia.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Abbas M., Majid A.A., Ismail A.I.M., Rashid A., . Numerical Method Using Cubic Trigonometric B-Spline Technique for Nonclassical Diffusion Problems. Abstr. Appl. Anal.. 2014;2014(1):849682
[CrossRef] [Google Scholar]
Abd El-Hady M., El-shenawy A., . Jacobi polynomials and the numerical solution of ray tracing through the crystalline lens. Opt. Quant. Electron.. 2024;56(8):1-20.
[CrossRef] [Google Scholar]
Anyigor C., Afiukwa J., . Application of matlab ordinary differential equation function solver (ode45) in modelling and simulation of batch reaction kinetics. American Journal of Scientific and Industrial Research. 2013;4(3):285-287.
[CrossRef] [Google Scholar]
Balázsová M., Feistauer M., Horáček J., Kosík A., . Discontinuous Galerkin Method for the Solution of Fluid-Structure Interaction Problems with Applications to the Vocal Folds Vibration. Lecture Notes in Mechanical Engineering.. 2021;58:401-419.
[CrossRef] [Google Scholar]
Barry W., Pützer M., . Saarbrucken voice database. Institute of Phonetics: University of Saarland; 2007. https://stimmdb.coli.uni-saarland.de/
Bhal S.K., Panda P.K., . A fourth order orthogonal spline collocation method Interface boundary. Indian J. Sci. Technol.. 2022;15(4):184-190.
[Google Scholar]
Bonilha H.S., Deliyski D.D., . Period and Glottal Width Irregularities in Vocally Normal Speakers. J. Voice. 2008;22(6):699-708.
[CrossRef] [Google Scholar]
Cataldo E., Leta F.R., Lucero J., Nicolato L., . Synthesis of voiced sounds using low-dimensional models of the vocal cords and time-varying subglottal pressure. Mech. Res. Commun.. 2006;33(2):250-260.
[CrossRef] [Google Scholar]
Chawla R., Deswal K., Kumar D., Chawla R., Deswal K., Kumar D., . A new numerical approach of solving fractional mobile-immobile transport equation using Atangana-Baleanu derivative. Journal of Applied Analysis & Computation. 2023;13(5):2874-2895.
[CrossRef] [Google Scholar]
Cveticanin L., . A solution procedure based on the Ateb function for a two-degree-of-freedom oscillator. J. Sound Vib.. 2015;346(1):298-313.
[CrossRef] [Google Scholar]
Drioli C., Aichinger P., . Modelling sagittal and vertical phase differences in a lumped and distributed elements vocal fold model. Biomed. Signal Process. Control. 2021;64:102309
[CrossRef] [Google Scholar]
El-shenawy A., El-Gamel M., Reda D., . Troesch’s problem: A numerical study with cubic trigonometric B-spline method. Partial Differ. Equations Appl. Math.. 2024;10:100694
[CrossRef] [Google Scholar]
El-shenawy A., El-Gamel M., Teba A., . Simulation of the SIR dengue fever nonlinear model: A numerical approach. Partial Differ. Equations Appl. Math.. 2024;11:100891
[CrossRef] [Google Scholar]
Erath B.D., Peterson S.D., Weiland K.S., Plesniak M.W., Zañartu M., . An acoustic source model for asymmetric intraglottal flow with application to reduced-order models of the vocal folds. PLoS One. 2019;14(7)
[CrossRef] [Google Scholar]
Flanagan J.L., Landgraf L.L., . Self Oscillating Source for Vocal Tract Synthesizers. IEEE Trans. Audio Electroacoust.. 1968;16(1):57-64.
[Google Scholar]
Goh J.Y.R., . B-splines for initial and boundary value problems. Universiti Sains Malaysia; 2013.
Goh J., Abd. Majid, A., & Ahmad, A. I., . A quartic B-spline for second-order singular boundary value problems. Comput. Math. Appl.. 2012;64(2):115-120.
[CrossRef] [Google Scholar]
Granados A., Misztal M.K., Brunskog J., Visseq V., Erleben K., . A numerical strategy for finite element modeling of frictionless asymmetric vocal fold collision. International Journal for Numerical Methods in Biomedical Engineering.. 2017;33(2)
[CrossRef] [Google Scholar]
Ishizaka K., Flanagan J.L., . Synthesis of Voiced Sounds From a Two‐Mass Model of the Vocal Cords. Bell Syst. Tech. J.. 1972;51(6):1233-1268.
[CrossRef] [Google Scholar]
Islam M.A., . Accurate Solutions of Initial Value Problems for Ordinary Differential Equations with the Fourth Order Runge Kutta Method. Journal of Mathematics Research.. 2015;7(3):41-45.
[CrossRef] [Google Scholar]
Jiang J.J., Zhang Y., . Chaotic vibration induced by turbulent noise in a two-mass model of vocal folds. J. Acoust. Soc. Am.. 2002;112(5):2127-2133.
[CrossRef] [Google Scholar]
Lan, H., 2006. An Investigation into the Dynamic Response of Vocal Folds. Auckland University of Technology Auckland. May. DOI: 10.1115/1.802755.ch10.
Maurerlehner P., Schoder S., Freidhager C., Wurzinger A., Hauser A., Kraxberger F., Falk S., Kniesburges S., Echternach M., Döllinger M., Kaltenbacher M., . Efficient numerical simulation of the human voice: simVoice – a three-dimensional simulation model based on a hybrid aeroacoustic approach. Elektrotechnik Und Informationstechnik.. 2021;138(3):219-228.
[CrossRef] [Google Scholar]
Mcgowan R.S., Howe M.S., . Comments on single-mass models of vocal fold vibration. J. Acoust. Soc. Am.. 2010;127:3003.
[CrossRef] [Google Scholar]
Perrine B.L., Scherer R.C., Fulcher L.P., Zhai G., Scherer R.C., Waddle J.M., Perrine B.L., Scherer R.C., Fulcher L.P., Zhai G., . Phonation threshold pressure and the elastic shear modulus: Comparison of two-mass model calculations with experiments. J. Acoust. Soc. Am.. 2020;147(3):1727-1737.
[CrossRef] [Google Scholar]
Postawa K., Szczygieł J., Kułażyński M., . A comprehensive comparison of ODE solvers for biochemical problems. Renew. Energy. 2020;156:624-633.
[CrossRef] [Google Scholar]
Rabah A.B., Momani S., Arqub O.A., . The B-spline collocation method for solving conformable initial value problems of non-singular and singular types. Alex. Eng. J.. 2022;61:963-974.
[CrossRef] [Google Scholar]
Shirokova E.A., El-Shenawy A., . A Cauchy integral method of the solution of the 2D Dirichlet problem for simply or doubly connected domains. Numer. Methods Partial Differential Equations. 2018;34(6):2267-2278.
[CrossRef] [Google Scholar]
Story B.H., Titze I.R., . Voice simulation with a three‐mass model of the vocal folds. The Journal of the Acoustical Society of America.. 1993;94(3):1762.
[CrossRef] [Google Scholar]
Sváček P., Horáček J., . Finite element approximation of flow induced vibrations of human vocal folds model: Effects of inflow boundary conditions and the length of subglottal and supraglottal channel on phonation onset. Appl. Math. Comput.. 2018;319:178-194.
[CrossRef] [Google Scholar]
Tao C., Zhang Y., Hottinger D.G., Jiang J.J., . Asymmetric airflow and vibration induced by the Coanda effect in a symmetric model of the vocal folds. J. Acoust. Soc. Am.. 2007;122:2270-2278.
[CrossRef] [Google Scholar]
Tayebi S., Momani S., Abu Arqub O., . The cubic B-spline interpolation method for numerical point solutions of conformable boundary value problems. Alex. Eng. J.. 2022;61(2):1519-1528.
[CrossRef] [Google Scholar]
Tok Onarcan A., Adar N., Dag İ., . Numerical Solutions of Reaction-Diffusion Equation Systems With Trigonometric Quintic B-Spline Collocation Algorithm. Eskişehir Technical University Journal of Science and Technology A - Applied Sciences and Engineering.. 2023;24(2):121-140.
[CrossRef] [Google Scholar]
Walz G., . Identities for trigonometric B-splines with an application to curve design. BIT Numer. Math.. 1997;37(1):189-201.
[Google Scholar]
Yang A., Lohscheller J., Berry D.A., Becker S., Eysholdt U., Voigt D., Döllinger M., . Biomechanical modeling of the three-dimensional aspects of human vocal fold dynamics. J. Acoust. Soc. Am.. 2010;127(2):1014-1031.
[CrossRef] [Google Scholar]
Yaseen M., Abbas M., Ismail A.I., Nazir T., . A cubic trigonometric B-spline collocation approach for the fractional sub-diffusion equations. Appl. Math Comput.. 2017;293:311-319.
[CrossRef] [Google Scholar]
Zheng X., Mittal R., Xue Q., Bielamowicz S., . Direct-numerical simulation of the glottal jet and vocal-fold dynamics in a three-dimensional laryngeal model. J. Acoust. Soc. Am.. 2011;130(1):404-415.
[CrossRef] [Google Scholar]
Zin S.M., . Hybrid cubic B-spline collocation method for solving one-dimensional wave equation. AIP Conf. Proc.. 2016;1775(2016)
[CrossRef] [Google Scholar]

Introduction

Parameters

Methodology

Fundamental frequency
Cubic trigonometric B-spline (CTBS)
Ode45

Error analysis

Results and discussions

Conclusion

CRediT authorship contribution statement

Fulltext Views
32

PDF downloads
27

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abbas M., Majid A.A., Ismail A.I.M., Rashid A., . Numerical Method Using Cubic Trigonometric B-Spline Technique for Nonclassical Diffusion Problems. Abstr. Appl. Anal.. 2014;2014(1):849682
[CrossRef] [Google Scholar]

[2] Abd El-Hady M., El-shenawy A., . Jacobi polynomials and the numerical solution of ray tracing through the crystalline lens. Opt. Quant. Electron.. 2024;56(8):1-20.
[CrossRef] [Google Scholar]

[3] Anyigor C., Afiukwa J., . Application of matlab ordinary differential equation function solver (ode45) in modelling and simulation of batch reaction kinetics. American Journal of Scientific and Industrial Research. 2013;4(3):285-287.
[CrossRef] [Google Scholar]

[4] Balázsová M., Feistauer M., Horáček J., Kosík A., . Discontinuous Galerkin Method for the Solution of Fluid-Structure Interaction Problems with Applications to the Vocal Folds Vibration. Lecture Notes in Mechanical Engineering.. 2021;58:401-419.
[CrossRef] [Google Scholar]

[5] Barry W., Pützer M., . Saarbrucken voice database. Institute of Phonetics: University of Saarland; 2007. https://stimmdb.coli.uni-saarland.de/

[6] Bhal S.K., Panda P.K., . A fourth order orthogonal spline collocation method Interface boundary. Indian J. Sci. Technol.. 2022;15(4):184-190.
[Google Scholar]

[7] Bonilha H.S., Deliyski D.D., . Period and Glottal Width Irregularities in Vocally Normal Speakers. J. Voice. 2008;22(6):699-708.
[CrossRef] [Google Scholar]

[8] Cataldo E., Leta F.R., Lucero J., Nicolato L., . Synthesis of voiced sounds using low-dimensional models of the vocal cords and time-varying subglottal pressure. Mech. Res. Commun.. 2006;33(2):250-260.
[CrossRef] [Google Scholar]

[9] Chawla R., Deswal K., Kumar D., Chawla R., Deswal K., Kumar D., . A new numerical approach of solving fractional mobile-immobile transport equation using Atangana-Baleanu derivative. Journal of Applied Analysis & Computation. 2023;13(5):2874-2895.
[CrossRef] [Google Scholar]

[10] Cveticanin L., . A solution procedure based on the Ateb function for a two-degree-of-freedom oscillator. J. Sound Vib.. 2015;346(1):298-313.
[CrossRef] [Google Scholar]

[11] Drioli C., Aichinger P., . Modelling sagittal and vertical phase differences in a lumped and distributed elements vocal fold model. Biomed. Signal Process. Control. 2021;64:102309
[CrossRef] [Google Scholar]

[12] El-shenawy A., El-Gamel M., Reda D., . Troesch’s problem: A numerical study with cubic trigonometric B-spline method. Partial Differ. Equations Appl. Math.. 2024;10:100694
[CrossRef] [Google Scholar]

[13] El-shenawy A., El-Gamel M., Teba A., . Simulation of the SIR dengue fever nonlinear model: A numerical approach. Partial Differ. Equations Appl. Math.. 2024;11:100891
[CrossRef] [Google Scholar]

[14] Erath B.D., Peterson S.D., Weiland K.S., Plesniak M.W., Zañartu M., . An acoustic source model for asymmetric intraglottal flow with application to reduced-order models of the vocal folds. PLoS One. 2019;14(7)
[CrossRef] [Google Scholar]

[15] Flanagan J.L., Landgraf L.L., . Self Oscillating Source for Vocal Tract Synthesizers. IEEE Trans. Audio Electroacoust.. 1968;16(1):57-64.
[Google Scholar]

[16] Goh J.Y.R., . B-splines for initial and boundary value problems. Universiti Sains Malaysia; 2013.

[17] Goh J., Abd. Majid, A., & Ahmad, A. I., . A quartic B-spline for second-order singular boundary value problems. Comput. Math. Appl.. 2012;64(2):115-120.
[CrossRef] [Google Scholar]

[18] Granados A., Misztal M.K., Brunskog J., Visseq V., Erleben K., . A numerical strategy for finite element modeling of frictionless asymmetric vocal fold collision. International Journal for Numerical Methods in Biomedical Engineering.. 2017;33(2)
[CrossRef] [Google Scholar]

[19] Ishizaka K., Flanagan J.L., . Synthesis of Voiced Sounds From a Two‐Mass Model of the Vocal Cords. Bell Syst. Tech. J.. 1972;51(6):1233-1268.
[CrossRef] [Google Scholar]

[20] Islam M.A., . Accurate Solutions of Initial Value Problems for Ordinary Differential Equations with the Fourth Order Runge Kutta Method. Journal of Mathematics Research.. 2015;7(3):41-45.
[CrossRef] [Google Scholar]

[21] Jiang J.J., Zhang Y., . Chaotic vibration induced by turbulent noise in a two-mass model of vocal folds. J. Acoust. Soc. Am.. 2002;112(5):2127-2133.
[CrossRef] [Google Scholar]

[22] Lan, H., 2006. An Investigation into the Dynamic Response of Vocal Folds. Auckland University of Technology Auckland. May. DOI: 10.1115/1.802755.ch10.

[23] Maurerlehner P., Schoder S., Freidhager C., Wurzinger A., Hauser A., Kraxberger F., Falk S., Kniesburges S., Echternach M., Döllinger M., Kaltenbacher M., . Efficient numerical simulation of the human voice: simVoice – a three-dimensional simulation model based on a hybrid aeroacoustic approach. Elektrotechnik Und Informationstechnik.. 2021;138(3):219-228.
[CrossRef] [Google Scholar]

[24] Mcgowan R.S., Howe M.S., . Comments on single-mass models of vocal fold vibration. J. Acoust. Soc. Am.. 2010;127:3003.
[CrossRef] [Google Scholar]

[25] Perrine B.L., Scherer R.C., Fulcher L.P., Zhai G., Scherer R.C., Waddle J.M., Perrine B.L., Scherer R.C., Fulcher L.P., Zhai G., . Phonation threshold pressure and the elastic shear modulus: Comparison of two-mass model calculations with experiments. J. Acoust. Soc. Am.. 2020;147(3):1727-1737.
[CrossRef] [Google Scholar]

[26] Postawa K., Szczygieł J., Kułażyński M., . A comprehensive comparison of ODE solvers for biochemical problems. Renew. Energy. 2020;156:624-633.
[CrossRef] [Google Scholar]

[27] Rabah A.B., Momani S., Arqub O.A., . The B-spline collocation method for solving conformable initial value problems of non-singular and singular types. Alex. Eng. J.. 2022;61:963-974.
[CrossRef] [Google Scholar]

[28] Shirokova E.A., El-Shenawy A., . A Cauchy integral method of the solution of the 2D Dirichlet problem for simply or doubly connected domains. Numer. Methods Partial Differential Equations. 2018;34(6):2267-2278.
[CrossRef] [Google Scholar]

[29] Story B.H., Titze I.R., . Voice simulation with a three‐mass model of the vocal folds. The Journal of the Acoustical Society of America.. 1993;94(3):1762.
[CrossRef] [Google Scholar]

[30] Sváček P., Horáček J., . Finite element approximation of flow induced vibrations of human vocal folds model: Effects of inflow boundary conditions and the length of subglottal and supraglottal channel on phonation onset. Appl. Math. Comput.. 2018;319:178-194.
[CrossRef] [Google Scholar]

[31] Tao C., Zhang Y., Hottinger D.G., Jiang J.J., . Asymmetric airflow and vibration induced by the Coanda effect in a symmetric model of the vocal folds. J. Acoust. Soc. Am.. 2007;122:2270-2278.
[CrossRef] [Google Scholar]

[32] Tayebi S., Momani S., Abu Arqub O., . The cubic B-spline interpolation method for numerical point solutions of conformable boundary value problems. Alex. Eng. J.. 2022;61(2):1519-1528.
[CrossRef] [Google Scholar]

[33] Tok Onarcan A., Adar N., Dag İ., . Numerical Solutions of Reaction-Diffusion Equation Systems With Trigonometric Quintic B-Spline Collocation Algorithm. Eskişehir Technical University Journal of Science and Technology A - Applied Sciences and Engineering.. 2023;24(2):121-140.
[CrossRef] [Google Scholar]

[34] Walz G., . Identities for trigonometric B-splines with an application to curve design. BIT Numer. Math.. 1997;37(1):189-201.
[Google Scholar]

[35] Yang A., Lohscheller J., Berry D.A., Becker S., Eysholdt U., Voigt D., Döllinger M., . Biomechanical modeling of the three-dimensional aspects of human vocal fold dynamics. J. Acoust. Soc. Am.. 2010;127(2):1014-1031.
[CrossRef] [Google Scholar]

[36] Yaseen M., Abbas M., Ismail A.I., Nazir T., . A cubic trigonometric B-spline collocation approach for the fractional sub-diffusion equations. Appl. Math Comput.. 2017;293:311-319.
[CrossRef] [Google Scholar]

[37] Zheng X., Mittal R., Xue Q., Bielamowicz S., . Direct-numerical simulation of the glottal jet and vocal-fold dynamics in a three-dimensional laryngeal model. J. Acoust. Soc. Am.. 2011;130(1):404-415.
[CrossRef] [Google Scholar]

[38] Zin S.M., . Hybrid cubic B-spline collocation method for solving one-dimensional wave equation. AIP Conf. Proc.. 2016;1775(2016)
[CrossRef] [Google Scholar]

The influence of pathological conditions on vocal cord’s displacement: A numerical method and data analysis

Abstract

Keywords

Displacements of vocal cords

Cubic trigonometric B-spline

One-mass model of vocal cord

1 Introduction

2 Parameters

3 Methodology

3.1 Fundamental frequency

3.2 Cubic trigonometric B-spline (CTBS)

3.3 Ode45

4 Error analysis

5 Results and discussions

6 Conclusion

CRediT authorship contribution statement

Acknowledgments

Declaration of competing interest

References

Suggested read for related articles: