The effects of pressure and temperature on the energy levels of a parabolic two-electron quantum dot in a magnetic field

Faten Bzour; Mohammad K. Elsaid; Khaled F. Ilaiwi

doi:10.1016/j.jksus.2017.01.001

View/Download PDF

Buy Reprints

PDF

Translate this page into:

30 (

); 83-90

doi:

10.1016/j.jksus.2017.01.001

The effects of pressure and temperature on the energy levels of a parabolic two-electron quantum dot in a magnetic field

Faten Bzour, Mohammad K. Elsaid^⁎, Khaled F. Ilaiwi

Physics Department, Faculty of Science, An-Najah National University, Nablus, West Bank, Palestine

⁎Corresponding author. mkelsaid@najah.edu (Mohammad K. Elsaid)

Received: 2016-10-30, Accepted: 2017-1-2, Published: 2017-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In the present work, we have calculated the energy levels of GaAs parabolic quantum dot under the combined effects of external pressure, temperature and magnetic field. The eigenenergies have been obtained by solving the two electron quantum dot Hamiltonian using the exact diagonalization method. The obtained results show that the energy levels of the quantum dot depend strongly on the pressure and temperature. We have found that the energy levels enhance as the pressure increases for fixed temperature and magnetic field while the quantum dot energy levels decrease as the temperature increases for fixed pressure and magnetic field. The comparisons show that our results are in very good agreement with the reported works.

Keywords

Energy levels

Pressure

Temperature

Quantum dot

Magnetic field

Exact diagonalization

Show Related Articles from PubMed

1 Introduction

Quantum dots (QDs), or artificial atoms, are the subject of interest research due to their physical properties and great potential device applications such as quantum dot lasers, solar cells, single electron transistors and quantum computers (Owji et al., 2016; Boda and Chatterjee, 2016; Ciftja, 2013; Kastner, 1992 ). The application of a magnetic field perpendicular to the dot plane will introduce an additional structure on the energy levels and correlation effects of the interacting electrons that are confined in a quantum dot.

Different approaches were used to study the electronic and thermodynamic properties of the quantum dot .Theoretically, many authors had solved the two electron QD Hamiltonian, including the effect of an applied magnetic field, to obtain the eigenenergies and eigenstates of the QD-system (Wagner et al., 1992; Taut, 1994; Ciftja and Kumar, 2004; Ciftja and Golam Faruk, 2005; Kandemir, 2005; Elsaid, 2000; Elsaid et al., 2008; Nguyen and Peeters, 2008; Nammas et al., 2011; Boyacioglu and Chatterjee, 2012; Helle et al., 2005; Schwarz et al., 2002; Nguyen and Das Sarma, 2011 ) .The results of these studies predicted the oscillations between spin-singlet (S) and spin-triplet (T) ground states. The thermodynamic quantities like: heat capacity $(C_{v})$ , magnetization $(M)$ and magnetic susceptibility $(χ)$ of the quantum dot had also been calculated (Sanjeev Kumar et al., 2016; Avetisyan et al., 2016; Boyacioglu and Chatterjee, 2012; Nguyen and Peeters, 2008 ). The computed results show that the interacting model behaves very differently from non-interacting electrons, and the oscillations in these magnetic and thermodynamic curves of the magnetization and heat capacity were attributed to the spin singlet–triplet transitions in the ground state spectra of the quantum dot. Experimentally, the magnetization of electrons in GaAs/AlGaAs semiconductor QD as function of applied magnetic field at low temperature 0.3 K had been measured (Schwarz et al., 2002). They had observed oscillations in the magnetization. To reproduce the experimental results of the magnetization, they found that the electron–electron interaction should be taken into account in the theoretical model of the QD magnetization. Very recently, the effects of pressure and temperature on the electronic and optical properties of a quantum dot presented in external magnetic and electric fields had been also considered (Owji et al., 2016; Dybalski and Hawrylak, 2005).

In this work, we consider a two electron parabolic quantum dot placed in a magnetic field and study the pressure and temperature effects. We applied the exact diagonalization method to solve the QD Hamiltonian and obtain the energy states for various values of physical parameters: pressure, temperature, parabolic confinement and magnetic field strength.

The rest of this paper is organized as follows: Section 2 presents the Hamiltonian of two interacting electron in a quantum dot, and the diagonalization technique of the interacting quantum artificial atom. We devoted the final section for numerical results and conclusions.

2 Theory

In this section we describe in detail the theory of the two electron QD which consists of two parts, namely: quantum dot Hamiltonian and exact diagonalization method of the GaAs quantum dot.

2.1

2.1 Quantum dot Hamiltonian

In the effective mass approximation the Hamiltonian for two interacting electrons confined in a QD by a parabolic potential in a uniform magnetic field $\vec{B} = B \hat{k}$ can be written in a separable form as:

(1)

\hat{H} = {\hat{H}}_{CM} + {\hat{H}}_{r}

(2)

{\hat{H}}_{CM} = \frac{1}{2 M} {[{\vec{P}}_{R} + \frac{Q}{c} \vec{A} (\vec{R})]}^{2} + \frac{1}{2} M ω_{0}^{2} R^{2}

(3)

{\hat{H}}_{r} = \frac{1}{2 μ} {[{\vec{p}}_{r} + \frac{q}{c} \vec{A} (\vec{r})]}^{2} + \frac{1}{2} μ ω_{0}^{2} r^{2} + \frac{e^{2}}{∊ | \vec{r} |}

where

ω_{0}

M = 2 m^{*}, μ = \frac{m^{*}}{2}

and

∊

are defined as the confining frequency, total mass, reduced mass and the dielectric constant for the GaAs medium, respectively.

\vec{R} = \frac{\vec{r_{1}} + \vec{r_{2}}}{2}

and

\vec{r} = \vec{r_{2}} - \vec{r_{1}}

are the center of mass and relative coordinates, respectively.

ω_{c} = \frac{eB}{m^{*}}

is the cyclotron frequency and

A = \frac{1}{2} B \times r

is the vector potential, (Dybalski and Hawrylak, 2005).

The corresponding energy of the QD Hamiltonian in Eq. (1) is:

(4)

E_{total} = E_{CM} + E_{r}

The center of mass Hamiltonian given by Eq. (2) is a harmonic oscillator type with well-known eigenenergies:

(5)

E_{n_{cm}, m_{cm}} = (2 n_{cm} + | m_{cm} | + 1) ℏ ω + m_{cm} \frac{ℏ ω_{c}}{2}

where

n_{cm}, m_{cm}

are the radial and angular quantum numbers, respectively, while

$ω^{2} = ω_{0}^{2} + \frac{ω_{c}^{2}}{4}$ is the effective confining frequency.

However, the relative motion Hamiltonian part ( $H_{r}$ ), given by Eq. (3) does not have an analytical solution for all ranges of $ω_{0}$ and $ω_{c}$ . In this work, we applied the exact diagonalization method to solve the relative part of the Hamiltonian and obtained the corresponding eigenenergies $E_{r}$ .

The two electron wave function $Ψ (\vec{r_{1}}, \vec{r_{2}}) = ψ (\vec{r_{1}}, \vec{r_{2}}) χ (σ_{1}, σ_{2})$ is a product of the spatial part $ψ (\vec{r_{1}}, \vec{r_{2}})$ and the spin part $χ (σ_{1}, σ_{2})$ . The spatial part can be separated into a CM (2) and relative (3) parts wave functions: ψ( $\vec{r_{1}}, \vec{r_{2}}) = ψ_{CM} (\vec{R}) ψ_{r} (\vec{r})$ .

The relative part $ψ_{r} (\vec{r})$ has a parity : ${(- 1)}^{m}$ , under the particle permutation ( $φ \to φ + 2 π$ . Therefore, the spatial part has an even parity for even m- quantum number, and in this case the spin part must be a singlet state with total spin S = 0.The total two-electron wave function becomes antisymmetric as the Pauli exclusion principle requires. On the other hand, if the spatial relative part has an odd parity for odd m-values, in this case the spin part must be triplet with total spin S = 1. The angular quantum number (m) and the total spin (S) are related by the expression $S = \frac{[1 - {(- 1)}^{m}]}{2}$ , (Wagner et al., 1992).

2.2

2.2 Exact diagonalization method

For non-interacting case the relative Hamiltonian in Eq. (3) is a single particle problem with eigenstates $| n_{r} m_{r} 〉$ known as Fock-Darwin states, (Fock, 1928; Ciftja and Kumar, 2004; Ciftja and Golam Faruk, 2005 ).

(6)

|n_{r} m_{r} 〉 = N_{n_{r} m_{r}} \frac{e^{{im}_{r} ϕ}}{\sqrt{2 π}} {(α r)}^{| m_{r} |} e^{- α^{2} r^{2} / 2} L_{n_{r}}^{| m_{r} |} (α^{2} r^{2})

where the functions

L_{n_{r}}^{| m_{r} |} (α^{2} r^{2})

are the standard associated Laguerre polynomials. We calculated the normalization constant

N_{n_{r} m_{r}}

from the normalization condition of the basis,

〈 n_{r} m_{r} | n_{r} m_{r} 〉 = 1

, which resulted in,

(7)

N_{n_{{rm}_{r}}} = \sqrt{\frac{2 n_{r}! α^{2}}{(n_{r} + | m_{r} |)!}}

We used

α

as a constant which has the dimensionality of an inverse length

(8)

α = \sqrt{\frac{m ω}{h}}

The eigenenergies of the QD Hamiltonian which are given by Eq. (4) consist of the sum of the energies for the center of mass Hamiltonian ( $E_{cm})$ and the eigenenergies $(E_{r})$ which are obtained by direct diagonalization to the relative Hamiltonian part. For interacting case, we applied the exact diagonalization method to solve Eq. (3) and find the corresponding exact eigenenergies for arbitrary values of $ω_{c}$ and $ω_{0}$ .

The matrix element of the relative Hamiltonian part using the basis $| n_{r} m_{r} 〉$ can be written as,

(9)

h_{{nn}^{'}} = 〈 n_{r}, m_{r} | {\hat{H}}_{r} | n_{r}^{'}, m_{r} 〉 = 〈 n_{r} m_{r} | - \frac{ℏ^{2}}{2 μ} \nabla^{2} + \frac{1}{2} μ ω^{2} r^{2} | n_{r}^{'} m_{r} 〉 + 〈 n_{r} m_{r} | \frac{e^{2}}{r} | n_{r}^{'} m_{r} 〉

The first term in the right side of Eq. (9),which represents the kinetic energy, is diagonalized as,

(10)

[(2 n + | m_{r} | + 1) \sqrt[]{(1 + \frac{γ^{2}}{4})} - \frac{γ}{2} | m_{r} |] δ_{{nn}^{'}}

where the coulomb matrix energy can be given as

(11)

\frac{λ}{\sqrt{2}} \sqrt{\frac{n^{'} n!}{(n^{'} + | m_{r} |)! (n + | m_{r} |)!}} \times I_{{nn}^{'}} | m_{r} |

where

γ = \frac{ω_{c}}{ω_{0}}

and

λ = \frac{e^{2} α}{ℏ ω_{0}}

are dimensionless parameters (Ciftja and Kumar, 2004). By changing the coordinate transformation to t-variable upon direct substitution of

r = \frac{\sqrt{t}}{α}

in the integration

I_{{nn}^{'}} = I_{n_{r} n_{r}^{'}}

, we can express the coulomb energy matrix element into the integral form:

(12)

〈 n_{r} m_{r} | \frac{e^{2}}{r} | n_{r}^{'} m_{r} 〉 \propto I_{{nn}^{'} | m_{r} |} = \int_{0}^{\infty} dt t^{| m_{r} |} e^{- t} L_{n}^{| m_{r} |} (t) L_{n^{'}}^{| m_{r} |} (t) \frac{1}{\sqrt{t}}

We evaluated the above coulomb energy matrix element in a closed form by using the Laguerre relation given in the Appendix A (Nguyen and Das Sarma, 2011) .This closed form result of the coulomb energy reduces greatly the computation time needed in the diagonalization process.

In our calculation, we used the basis $| n_{r} m_{r} 〉$ defined by Eq. (6) to diagonalize the relative QD Hamiltonian and obtain its corresponding eigenenergies $E_{r}$ .

To include the effects of the pressure (P) and temperature (T) on the energy states we replace the dielectric constant $∊$ with $∊_{r}$ ( $P, T$ ) and the effective mass $m^{*}$ with $m (P, T)$ in the QD Hamiltonian as given in Eq. (2) and (3), where $∊_{r} (P, T)$ and $m^{*} (P, T)$ are the pressure and temperature dependent dielectric constant and electron effective mass, respectively, (Rezaei and Shojaeian Kish, 2012). For quantum dot made of GaAs the dependency of $∊_{r} (P, T)$ and $m^{*} (P, T)$ is given in Appendix B.

The pressure and temperature effective Rydberg ( $R_{y}^{*} (P, T))$ is used as the energy unit and given as follows:

(13)

R_{y}^{*} (P, T) = \frac{e^{2}}{2 ∊ (P, T) a_{B}^{*} (P, T)}

where

a_{B}^{*} (P, T)

is the effective Bohr radius and given as:

(14)

a_{B}^{*} (P, T) = ∊ (P, T) {\bar{h}}^{2} / (m^{*} (P, T) e^{2})

so the effective Rydberg can be written as:

(15)

R_{y}^{*} (P, T) = \frac{e^{4} m^{*} (P, T)}{2 {(∊ (P, T))}^{2} {\bar{h}}^{2}}

The pressure and temperature values will be changed to study the effects on the ground state energy of the QD Hamiltonian in a zero ( $ω_{c} = 0)$ and finite magnetic field ( $ω_{c})$ . Eventually, the ground state energies of the two electron-quantum dot system will be calculated as function of temperature (T), pressure (P), confining frequency and magnetic field ( $ω_{c})$ .The obtained results are displayed in the next section.

3 Results and conclusions

We present the results for two interacting electrons in a GaAs material (effective Rydberg $R^{*} = 5.825 meV$ ) in Tables 1 and 2 and Figs. 1 to 6 . We have listed in Table 1, for the sake of comparisons, the calculated ground state energy results, for zero pressure, (P = 0.0 Kbar), zero temperature (T = 0.0 K) and zero magnetic field ( $ω_{c}$ = 0.0 tesla) against the corresponding ones given by Ciftja and Kumar (2004) . The results show excellent agreement between both works. For finite magnetic field, and confinement energy strength $ω_{0} = \frac{2}{3} R^{*}$ , we have presented our results, in Table 2, for T = 0.0, P = 0.0 and various magnetic field strength. The energy values, in bold type given in the table actually show the ground state energy of the QD. For example the state with angular momentum m = 0 is the ground state for the QD for the magnetic field strength of range $ω_{c} = 0.0 to 0.6$ . As we continue increasing the magnetic field strength the ground state switches to m = 1 in the magnetic field range $ω_{c} = 0.8 to 1.8$ .

Table 1 The ground state energies of QD (in

R_{y}^{*}

) as a function of dimensionless coulomb coupling parameter (λ) obtained from exact diagonalization method compared with reported work of Ciftja and Kumar (2004).

$λ$	E(Present work)	E (Ciftja and Kumar, 2004)
0	2.00000	2.00000
1	3.000969	3.00097
2	3.721433	3.72143
3	4.318718	4.31872
4	4.847800	4.84780
5	5.332238	5.33224
6	5.784291	5.78429
7	6.211285	6.21129
8	6.618042	6.61804
9	7.007949	7.00795
10	7.383507	7.38351

Table 2 The relative motion energy spectra (in

R_{y}^{*})

of the QD states (m = 0,1,2,3,4) against the magnetic field cyclotron frequency (

ω_{c})

for two interacting electrons for

ω_{o} = \frac{2}{3} R^{*}

(the shaded energy values show the angular momentum transitions of the ground state of the QD).

$ω_{c} [Ry]$	m = 0	m = 1	m = 2	m = 3	m = 4
0	1.69891	2.00014	2.52193	3.10833	3.72267
0.2	1.71352	1.91905	2.34732	2.84068	3.36217
0.4	1.75622	1.87444	2.22178	2.63558	3.07805
0.6	1.82399	1.86272	2.14064	2.48721	2.86328
0.8	1.91275	1.87899	2.09757	2.38761	2.70824
1	2.01822	1.91809	2.08584	2.32833	2.60269
1.2	2.13655	1.97528	2.09923	2.30155	2.53712
1.4	2.2645	2.04659	2.13249	2.30058	2.50342
1.6	2.39955	2.12879	2.18132	2.32002	2.49499
1.8	2.53975	2.21941	2.24239	2.35558	2.50659
2	2.68364	2.31652	2.31308	2.40392	2.53414
2.2	2.83014	2.41866	2.3914	2.46248	2.57448
2.4	2.97845	2.52472	2.4758	2.52924	2.62515
2.6	3.12795	2.63385	2.56507	2.60265	2.68423
2.8	3.27821	2.74538	2.65829	2.68149	2.7502
3	3.42889	2.85879	2.75471	2.7648	2.82187
3.2	3.57975	2.97371	2.85376	2.8518	2.89829
3.4	3.73059	3.0898	2.95497	2.94189	2.97869
3.6	3.88129	3.20683	3.05798	3.03458	3.06246
3.8	4.03174	3.3246	3.16248	3.12945	3.14908
4	4.18187	3.44294	3.26822	3.22618	3.23815

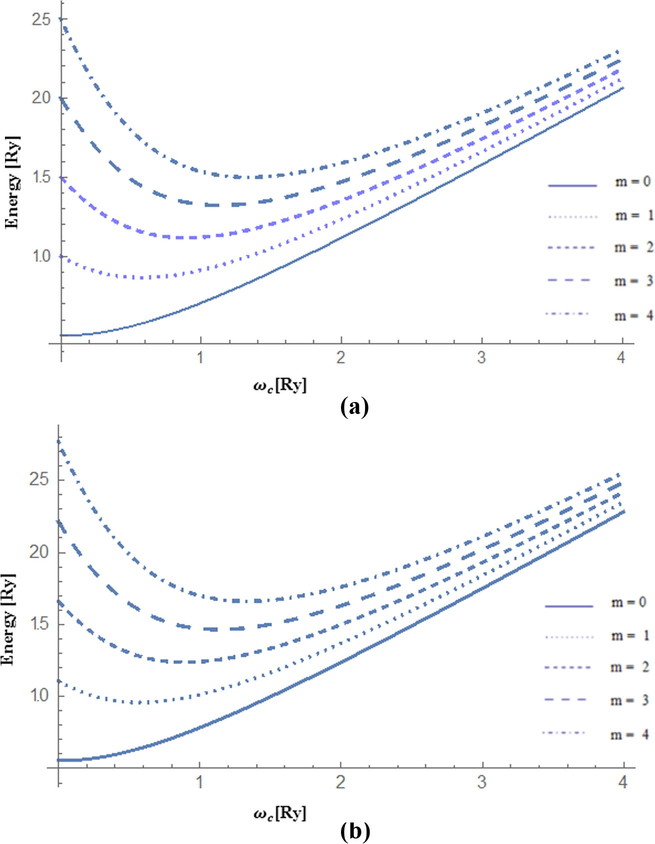
The dependence of the energy spectra of non-interaction electrons on the magnetic field calculated at ω 0 = 2 3 R ∗ for (a) Pressure = 0 and (b) Pressure P = 10 Kbar.

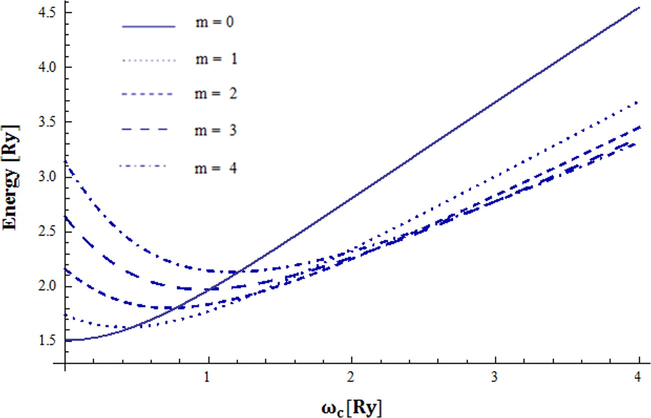
The computed energy spectra of quantum dot versus the strength of the magnetic field for ω 0 = 0.5 R ∗ , T = 0 K, and P = 10.0 Kbar. Angular momentum m = 0 , 1 , 2 , 3 , 4 .

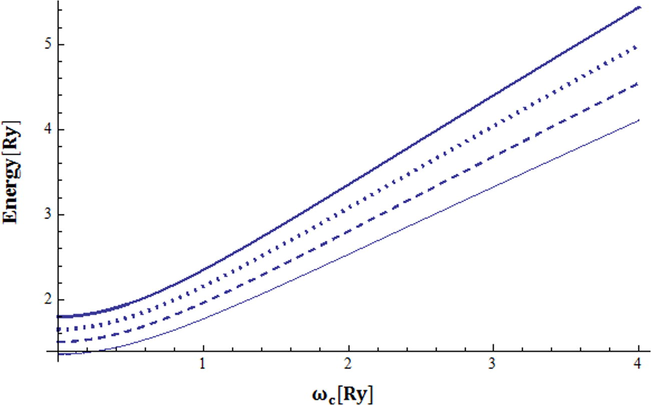
The computed energy spectra of quantum dot versus the strength of the magnetic field for ω 0 = 0.5 R ∗ , T = 0 K, m = 0 and various pressures (P = 0 Kbar, solid; P = 10 Kbar, dashed; P = 20 Kbar, dotted and P = 30 Kbar, thick).

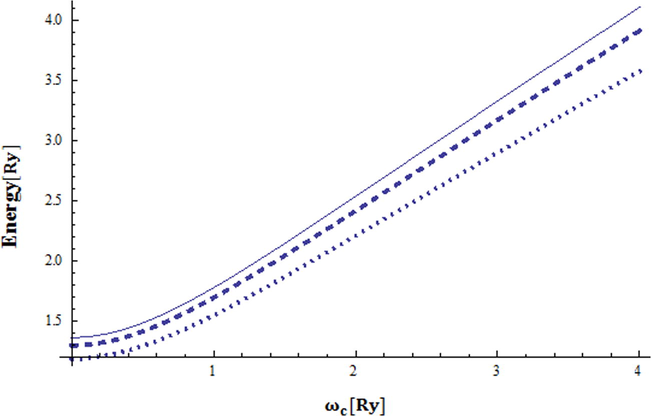
The energy of the quantum dot system versus the magnetic field strength for ω 0 = 0.5 R ∗ , P = 0 Kbar, m = 0 and various temperatures(T = 0 K solid; T = 150 K dashed; T = 350 K dotted).

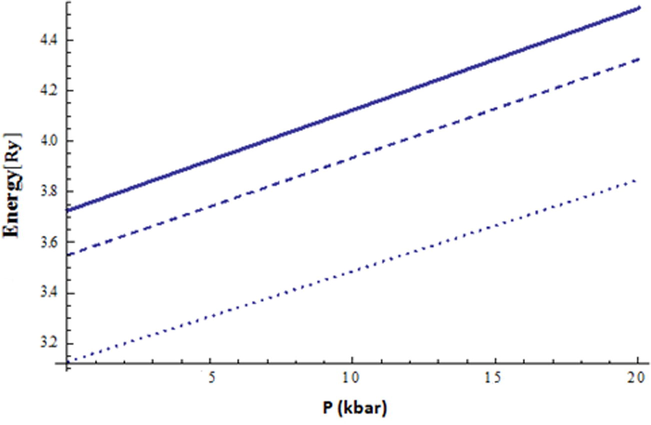
The energy of the QD system against the pressure for ω o = 0.5 R ∗ , ω c = 0 and various temperatures (T = 0 K solid; T = 150 K dashed; T = 350 K dotted).

The energy of the QD system against the temperature for ω o = 0.5 R ∗ , ω c = 0 R ∗ and various pressures (P = 0 Kbar, solid; P = 2 Kbar, dashed; P = 5 Kbar, dotted and P = 7 Kbar, dashed-dotted). [The change of the slope at T = 200 K is not due to any physical reason but a consequence of Eq. (B1)].

To see the effects of the pressure (P) on the energy spectra of the QD, we have plotted the energy levels for non-interacting (Fig. 1a and b) and interacting (Fig. 2) electrons both calculated at P = 10 Kbar. For independent electron case, the comparison of the energy spectra in Figs. 1a (P = 0.0 Kkbar) and Fig. 1b (P = 10Kbar) shows a clear enhancement in the energy of the electron as a function of magnetic field for pressure value P = 10 Kbar. This behavior can be explained by the help of the dependence of the effective mass of the confined electron on the pressure given in Eq. (B2). For fixed values of magnetic field and temperature, as the pressure increases the effective mass of the electron increases also, leading to a reduction in the kinetic energy term $(- \frac{ℏ^{2}}{2 μ^{*}} \nabla^{2})$ while the parabolic confinement $(\frac{1}{2} μ ω_{0}^{2} r^{2})$ energy enhances. In Fig. 2, we have displayed the computed energy states of interacting electrons case against the magnetic field for confinement energy strength $ω_{0} = 0.5 R^{*}$ , pressure P = 10.0 Kbar, and temperature T = 0.0 K. The inclusion of the electron –electron interaction term shows a significant effect on the QD energy spectra. The plot obviously shows the state with m = 0 remains aground state only for small range of magnetic field. As we increase the magnetic field, the m = 0 state rises in energy while the states with $m = - 1, - 2, - 3, \dots$ decrease. As the quantum number, $| m |$ , increases the average separation of the electrons increases also leading to a reduction in the coulomb energy. The transition in the angular momentum of the QD ground state from $m = 0 to m = - 1, - 2, - 3, \dots$ is associated with the total spin oscillations of the ground state between the singlet (S = 0) and the triplet (S = 1) state (Wagner et al., 1992). These transitions manifest themselves as cusps in the heat capacity and magnetization curves of these thermodynamic quantities, as we mentioned earlier in the introduction (Sanjeev Kumar et al., 2016; Avetisyan et al., 2016; Helle et al., 2005 ).

We have plotted, in Fig. 3, the ground state energy, m = 0, against the magnetic field for pressure values (P = 0 Kbar, 10 Kbar, 20 Kbar and 30 Kbar and T = 0 K. The curves clearly show the enhancement in the QD energy state as the pressure increases. This energy-pressure behavior can be understood from the effective mass and dielectric constant pressure-temperature relations. As the pressure increases the dielectric constant, $∊_{(P)}$ , decreases for zero temperature and this leads to an enhancement in the electron–electron coulomb interaction, $V_{c} \approx \frac{1}{∊_{(} p) r}$ , in the QD-Hamiltonian. However, the effective mass increases and thus the kinetic energy term decreases. This coulomb energy and kinetic energy behavior terms lead to an effective increase in the energy levels of the QD spectra. In Fig. 4, we have shown the dependence of the ground state energy m = 0 on the magnetic field and for various temperature values T = 0, T = 150 k T = 350 k and P = 0 Kbar. The energy state shows strong dependence on the temperature. For fixed value of magnetic field, the energy decreases as the temperature increases. In Figs. 5 and 6 we vary both the pressure and the temperature simultaneously while keeping the magnetic field strength unchanged. The energy spectra, in Fig. 5, increases as the pressure increases for low temperature values. On the other hand the energy spectra decrease as the temperature increases for high pressure values. This energy behavior for various pressures as temperature increases is shown in Fig. 6. The exact diagonalization method is used in spanning the total Hamiltonian for the selected single electron basis and extract the lowest eigenvalues (eigenenergies) of the matrix. The procedure of increasing the number of linearly independent eigenstates is converging to the exact results. In each step the new energy results are compared with previous results from a smaller apace, until satisfactory convergence is achieved. The convergence issue is achieved in our numerical calculations. For example the ground state energies were converged to $E_{r} ≅ 1.66 R^{*}$ as we increase the basis numbers from $s_{p}$ = 5 to 20. In the present numerical calculations we diagonalize $20 \times 20$ Hermitian matrix.

In conclusion, we have investigated the effects of pressure and temperature on the energy levels of the QD as a function of magnetic field. The exact diagonalization method is applied to solve the two electron-QD Hamiltonian. The comparisons show that our results are in very good agreement with other reported works.

References

Avetisyan S., Chakraboty T., Pietilainen P., . Magnetization of interacting electrons in anisotropic quantum dots with Rashbaa spin-orbit interaction. Physica. E. 2016;81:334.
[Google Scholar]
Boda A., Chatterjee A., . Transition energies and magnetic properties of a neutral complex in a Gaussian GaAs quantum dot. Superlattices Microstruct.. 2016;97:268.
[Google Scholar]
Boyacioglu B., Chatterjee A., . Heat capacity and entropy of GaAs quantum dot with a Gaussian confinement. J. Appl. Phys.. 2012;112:083514.
[Google Scholar]
Ciftja C., . Understanding electronic systems in semiconductor quantum dots. Phys. Scr.. 2013;72:058302.
[Google Scholar]
Ciftja O., Golam Faruk M., . Two-dimensional quantum dot- helium in a magnetic field: Variational theory. Phys. Rev. B. 2005;72:205334.
[Google Scholar]
Ciftja O., Kumar A.A., . Ground-state of two-dimensional quantum dot helium in zero magnetic field: Perturbation, diagonalization and variational theory. Phys. Rev. B. 2004;70:205326.
[Google Scholar]
Dybalski W., Hawrylak P., . Two electrons in a strongly coupled double quantum dot: from an artificial helium atom to a hydrogen molecule. Phys. Rev. B. 2005;72:205432.
[Google Scholar]
Elsaid M., . Spectroscopic structure of two interacting electrons in a quantum dot by the shifted 1/N expansion method. Phys. Rev. B. 2000;61:13026.
[Google Scholar]
Elsaid M., Al-Naafa M.A., Zugail S.J., . Spin singlet-triplet splitting in the ground state of a quantum dot with a magnetic field: Effects of dimensionality. Comput. Theor. Nanosci.. 2008;5:677.
[Google Scholar]
Fock V., . Bemerkung zur quantellung des harmonischen Ozscillators im Magnetfeld. Z. Phys.. 1928;47:446.
[Google Scholar]
Helle M., Harju A., Nieminen R.M., . Two-electron quantum dot molecule in a magnetic field. Phys. Rev. B. 2005;72:205329.
[Google Scholar]
Kandemir B.S., . Variational study of two-electron quantum dots. Phys. Rev. B. 2005;72:165350.
[Google Scholar]
Kastner M.A., . The single electron transistor. Rev. Mod. Phys. 1992;64:849.
[Google Scholar]
Nammas F.S., Sandouqa A.S., Ghassib H.B., Al Sugheir M.K., . Thermodynamic properties of two-dimensional of few-electrons quantum dot using the static fluctuation approximation (SFA) Phys. B. 2011;406:4671.
[Google Scholar]
Nguyen N.T.T., Das Sarma S., . Impurity effects of semiconductor quantum bits in coupled quantum dots. Phys. Rev. B. 2011;83:235322.
[Google Scholar]
Nguyen N.T.T., Peeters F.M., . Magnetic field dependence of many electron states in a magnetic quantum dot: The ferromagnetic-antiferromagnetic transition. Phys. Rev. B. 2008;78:045321.
[Google Scholar]
Owji E., Keshavarza A., Mokhtari H., . The effects of temperature, hydrostatic pressure and size on optical gain for GaAs spherical quantum dot laser with hydrogen impurity. Superlattices Microstruct.. 2016;98:276.
[Google Scholar]
Rezaei G., Shojaeian Kish S., . Effects of external electric and magnetic fields, hydrostatic pressure and temperature on the binding energy of a hydrogenic impurity confined in a two-dimensional quantum dot. Physica E. 2012;45:56.
[Google Scholar]
Sanjeev Kumar D., Mukhopadhyay S., Chatterjee A., . Magnetization and susceptibility of a parabolic InAs quantum dot with electron-electron interaction and spin-orbit interactions in the presence of a magnetic field at finite temperature. J. Magn. Magn. Mater.. 2016;418:169.
[Google Scholar]
Schwarz M.P., Grundler D., Wilde M., Heyn Ch., Heitmann D., . Magnetization of semiconductor quantum dots. J. Appl. Phys.. 2002;91:6875.
[Google Scholar]
Taut M., . Two electrons in a homogeneous magnetic field: particular analytical solutions. J. Phys. A: Math. Gen.. 1994;27:1045.
[Google Scholar]
Wagner M., Merkt M.U., Chaplik A.V., . Spin-singlet-spin-triple oscillations in quantum dots. Phys. Rev. B. 1992;45:1951.
[Google Scholar]

Appendix A

Properties of the Laguerre polynomials

The following Laguerre relation was used to evaluate the coulomb energy matrix element given by Eq. (12) in a closed form (Nguyen and Das Sarma, 2011):

(A.1)

\int_{0}^{\infty} t^{α - 1} e^{- pt} L_{m}^{λ} (at) L_{n}^{β} (bt) dt = \frac{Γ (α) {(λ + 1)}_{m} {(β + 1)}_{n} p^{- α}}{mn} \sum_{j = 0}^{m} \frac{{(- m)}_{j} {(α)}_{j}}{{(λ + 1)}_{j} j} {(\frac{a}{p})}^{j} \sum_{k = 0}^{n} \frac{{(- n)}_{k} {(α + j)}_{k}}{{(β + 1)}_{k} k} {(\frac{b}{p})}^{k}

Appendix B

The pressure and temperature dependent dielectric constant and electron effective mass

In this Appendix, we give the dependence relations of the physical parameters, like effective mass and dielectric constant, for GaAs quantum dot on the pressure and temperature:

(B.1)

\in_{r} (P, T) = \{\begin{matrix} 12.74 \exp (- 1.73 \times 10^{- 3} P) \exp [9.4 \times 10^{- 5} (T - 75.6)] for T < 200 K \\ 13.18 \exp (- 1.73 \times 10^{- 3} P) \exp [20.4 \times 10^{- 5} (T - 300)] for T ⩾ 200 K \end{matrix}

(B.2)

m^{*} (P, T) = {[1 + 7.51 (\frac{2}{E_{g}^{Γ} (P, T)} + \frac{1}{E_{g}^{Γ} (P, T) + 0.341})]}^{- 1} m_{0}

(B.3)

E_{g}^{Γ} (P, T) = [1.519 - 5.405 \times 10^{- 4} \frac{T^{2}}{T + 204}] + bP + {cP}^{2}

where

m_{0}

is the free electron mass,

E_{g}^{Γ} (P, T)

is the pressure and temperature dependent energy band gap for GaAs quantum dots at г point, b = 1.26

\times 10^{- 1} {eV GPa}^{- 1}

and c = −3.77

\times 10^{- 3} {eV GPa}^{- 2}

, (Rezaei and Shojaeian Kish, 2012).

Introduction

Theory

Quantum dot Hamiltonian
Exact diagonalization method

Results and conclusions

Fulltext Views
28

PDF downloads
13

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Avetisyan S., Chakraboty T., Pietilainen P., . Magnetization of interacting electrons in anisotropic quantum dots with Rashbaa spin-orbit interaction. Physica. E. 2016;81:334.
[Google Scholar]

[2] Boda A., Chatterjee A., . Transition energies and magnetic properties of a neutral complex in a Gaussian GaAs quantum dot. Superlattices Microstruct.. 2016;97:268.
[Google Scholar]

[3] Boyacioglu B., Chatterjee A., . Heat capacity and entropy of GaAs quantum dot with a Gaussian confinement. J. Appl. Phys.. 2012;112:083514.
[Google Scholar]

[4] Ciftja C., . Understanding electronic systems in semiconductor quantum dots. Phys. Scr.. 2013;72:058302.
[Google Scholar]

[5] Ciftja O., Golam Faruk M., . Two-dimensional quantum dot- helium in a magnetic field: Variational theory. Phys. Rev. B. 2005;72:205334.
[Google Scholar]

[6] Ciftja O., Kumar A.A., . Ground-state of two-dimensional quantum dot helium in zero magnetic field: Perturbation, diagonalization and variational theory. Phys. Rev. B. 2004;70:205326.
[Google Scholar]

[7] Dybalski W., Hawrylak P., . Two electrons in a strongly coupled double quantum dot: from an artificial helium atom to a hydrogen molecule. Phys. Rev. B. 2005;72:205432.
[Google Scholar]

[8] Elsaid M., . Spectroscopic structure of two interacting electrons in a quantum dot by the shifted 1/N expansion method. Phys. Rev. B. 2000;61:13026.
[Google Scholar]

[9] Elsaid M., Al-Naafa M.A., Zugail S.J., . Spin singlet-triplet splitting in the ground state of a quantum dot with a magnetic field: Effects of dimensionality. Comput. Theor. Nanosci.. 2008;5:677.
[Google Scholar]

[10] Fock V., . Bemerkung zur quantellung des harmonischen Ozscillators im Magnetfeld. Z. Phys.. 1928;47:446.
[Google Scholar]

[11] Helle M., Harju A., Nieminen R.M., . Two-electron quantum dot molecule in a magnetic field. Phys. Rev. B. 2005;72:205329.
[Google Scholar]

[12] Kandemir B.S., . Variational study of two-electron quantum dots. Phys. Rev. B. 2005;72:165350.
[Google Scholar]

[13] Kastner M.A., . The single electron transistor. Rev. Mod. Phys. 1992;64:849.
[Google Scholar]

[14] Nammas F.S., Sandouqa A.S., Ghassib H.B., Al Sugheir M.K., . Thermodynamic properties of two-dimensional of few-electrons quantum dot using the static fluctuation approximation (SFA) Phys. B. 2011;406:4671.
[Google Scholar]

[15] Nguyen N.T.T., Das Sarma S., . Impurity effects of semiconductor quantum bits in coupled quantum dots. Phys. Rev. B. 2011;83:235322.
[Google Scholar]

[16] Nguyen N.T.T., Peeters F.M., . Magnetic field dependence of many electron states in a magnetic quantum dot: The ferromagnetic-antiferromagnetic transition. Phys. Rev. B. 2008;78:045321.
[Google Scholar]

[17] Owji E., Keshavarza A., Mokhtari H., . The effects of temperature, hydrostatic pressure and size on optical gain for GaAs spherical quantum dot laser with hydrogen impurity. Superlattices Microstruct.. 2016;98:276.
[Google Scholar]

[18] Rezaei G., Shojaeian Kish S., . Effects of external electric and magnetic fields, hydrostatic pressure and temperature on the binding energy of a hydrogenic impurity confined in a two-dimensional quantum dot. Physica E. 2012;45:56.
[Google Scholar]

[19] Sanjeev Kumar D., Mukhopadhyay S., Chatterjee A., . Magnetization and susceptibility of a parabolic InAs quantum dot with electron-electron interaction and spin-orbit interactions in the presence of a magnetic field at finite temperature. J. Magn. Magn. Mater.. 2016;418:169.
[Google Scholar]

[20] Schwarz M.P., Grundler D., Wilde M., Heyn Ch., Heitmann D., . Magnetization of semiconductor quantum dots. J. Appl. Phys.. 2002;91:6875.
[Google Scholar]

[21] Taut M., . Two electrons in a homogeneous magnetic field: particular analytical solutions. J. Phys. A: Math. Gen.. 1994;27:1045.
[Google Scholar]

[22] Wagner M., Merkt M.U., Chaplik A.V., . Spin-singlet-spin-triple oscillations in quantum dots. Phys. Rev. B. 1992;45:1951.
[Google Scholar]

The effects of pressure and temperature on the energy levels of a parabolic two-electron quantum dot in a magnetic field

Abstract

Keywords

Energy levels

Pressure

Temperature

Quantum dot

Magnetic field

Exact diagonalization

1 Introduction

2 Theory

2.1 Quantum dot Hamiltonian

2.2 Exact diagonalization method

3 Results and conclusions

References

Appendix A

Properties of the Laguerre polynomials

Appendix B

The pressure and temperature dependent dielectric constant and electron effective mass

Suggested read for related articles: