Study of fractional order Van der Pol equation

V. Mishra; S. Das; H. Jafari; S.H. Ong

doi:10.1016/j.jksus.2015.04.005

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

28 (

); 55-60

doi:

10.1016/j.jksus.2015.04.005

Study of fractional order Van der Pol equation

V. Mishra^{^a}, S. Das^{^a}, H. Jafari^{^b,⁎}, S.H. Ong^{^c}

a Department of Mathematical Sciences, Indian Institute of Technology (BHU), Varanasi 21005, India

b Department of Mathematics, Faculty of Mathematical Sciences, University of Mazandaran, Babolsar, Iran

c Institute of Mathematical Sciences, University of Malaya, Kuala Lumpur 50603, Malaysia

⁎Corresponding author. jafari@umz.ac.ir (H. Jafari) jafari.ho1@gmail.com (H. Jafari)

Received: 2015-3-9, Accepted: 2015-4-18, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this article, Homotopy analysis method is successfully used to find the approximate solution of fractional order Van der Pol equation. The fractional derivative is described in the Caputo sense.The numerical computations of convergence control parameters for the acceleration of convergence of approximate series solution are obtained by the analysis of minimization of error for different particular cases and the results are depicted through graphs. The salient feature of the article is the graphical presentation of achieving limit cycles for different parameters.

Keywords

Oscillator equation

Damping

Homotopy analysis method

Embedding parameter

Error analysis

Limit cycle

Show Related Articles from PubMed

1 Introduction

Van der Pol oscillator equation was first introduced in 1920 by Vander Pol (1920) who introduced the equation to describe the oscillation of triode in the electrical circuit. The mathematical model for this system is a second order differential equation with third degree of nonlinearity as

(1)

\ddot{u} (t) - ∊ (1 - u^{2} (t) \dot{u} (t) + u (t) = 0,

where

∊ > 0

is a control parameter and

\ddot{u} (t), \dot{u} (t)

are the second and first order derivative of u with respect to time. if

∊ = 0

, Eq. (1) represents the simple linear oscillator and for

∊ ≫ 1

it represents relaxation oscillator. The equivalent state space formulation of the Eq. (1) is

\begin{matrix} \frac{{du}_{1}}{dt} = u_{2}, \\ \frac{{du}_{2}}{dt} = - u_{1} - ∊ (u_{1}^{2} - 1) u_{2}, \end{matrix}

In the Eq. (1) for the small value of

u (t)

, the damping force is negative i.e.,

- ∊ \dot{u} (t)

. Again if

u (t)

is bigger, it becomes dominant and the damping is positive. Van der Pol oscillator is an example of self oscillatory system which is now considered as a very useful mathematical model. Eq. (1) is also known as unforced Van der Pol equation. Van der Pol proposed another version of the above equation by including a periodic forcing term as

(2)

\ddot{u} (t) - ∊ (1 - u^{2} (t)) \dot{u} (t) + u (t) = a \sin wt

In 1945, Cartwright and Littlewood (1945) analyzed the Van der Pol equation with large nonlinearity parameter. In 1949, Levinson (1949) studied the Van der Pol equation and had shown that the equation has singular solution. The equation is considered as basic model for oscillatory process for Physics, Biology, Electronics, and Neurology. Van der Pol himself built a number of electronic circuits to model human heart using the equation.

Many researchers have tried to solve and study the Van der Pol equation in various forms. Mickens (2001) proposed the study of a non-standard finite difference scheme for the unplugged Van der Pol equation. In 2002, Mickens (2002) studied numerically the Van der Pol equation using a non-standard finite-difference scheme . In the same year, Mickens (2002) proposed a step-size dependence of the period for a forward-Euler scheme of the Van der Pol equation. In 2003, Mickens (2003) proposed different forms of Fractional Van der Pol oscillators. Researchers have tried many methods to solve the Van der Pol differential equation using Energy balance method (Mehdipour et al., 2010; Younesian et al., 2010), Parameter expanding method (He, 2006; Xu, 2007) etc.

The Fractional order differential equations have created much interest to the researchers (Atangana and Secer, 2013) due to the non local behavior of the operator which takes into account the fact that future state depends on the present as well as on the history of the previous states. Thus fractional order derivatives are naturally related to the systems with memory which prevails for most of physical and scientific system models. Another advantage is fractional order system response ultimately converges to integer order system response. Leung et al. (2012) have used residue harmonic balance method for fractional order Van der Pol like oscillators. Gafiychuk et al. (2008) have done the analysis of fractional order Bonhoeffer Van der Pol oscillator. Leung and Guo (2011) have used forward residue harmonic balance for autonomous and non autonomous systems with fractional derivative damping. Guo et al. (2011) have given the asymptotic solution of fractional Van der Pol oscillator using the same method. Leung and Guo (2010) have used the method for discontinuous nonlinear oscillator for fractional power restoring force. Sardar et al. (2009) have found the approximate analytical solution of multi term fractionally damped Van der Pol equation. Konuralp et al. (2009) studied numerical solution of Van der Pol equation with fractional damping term. Pereira et al. (2004) have proposed a fractional order Van der Pol equation as

(3)

\frac{d^{λ} u (t)}{{dt}^{λ}} - ∊ (1 - u^{2} (t)) \frac{du (t)}{dt} + u (t) = 0, 1 < λ < 2,

with the state space formulation as

\begin{matrix} \frac{{du}_{1}}{dt} = u_{2}, \\ \frac{d^{λ} u_{2}}{{dt}^{λ}} = - u_{1} - ∊ (u_{1}^{2} - 1) u_{2}, \end{matrix}

which is obtained by introducing a capacitance by a fractance in the nonlinear RLC circuit. Barbosa et al. proposed fractional order Van der Pol equation by introducing a fractional order time derivative in the state space equation of the classical Van der Pol equation as

\begin{matrix} \frac{d^{λ} u_{1}}{{dt}^{λ}} = u_{2}, \\ \frac{{du}_{2}}{dt} = - u_{1} - ∊ (u_{1}^{2} - 1) u_{2}, \end{matrix}

which gives us the Van der Pol equation as

(4)

\frac{d^{1 + λ} u (t)}{{dt}^{λ}} - ∊ (1 - u^{2} (t)) \frac{d^{λ} u (t)}{{dt}^{λ}} + u (t) = 0, 1 < λ < 2,

In the present article authors have considered the two fractional order time derivative in the state space equation as

\begin{matrix} \frac{d^{α} u_{1}}{{dt}^{α}} = u_{2}, \\ \frac{d^{α} u_{2}}{{dt}^{α}} = - u_{1} - ∊ (u_{1}^{2} - 1) u_{2}, 0 < α < 1, \end{matrix}

which generates the fractional order Van der Pol equation as

(5)

\frac{d^{2 α} u (t)}{{dt}^{α}} - ∊ (1 - u^{2} (t)) \frac{d^{α} u (t)}{{dt}^{α}} + u (t) = 0, 1 < α < 2,

with

u (0) = a, \dot{u} (0) = 0

. Eq. (5) represents the classical Van der Pol equation for

α = 1

. In 1992, the Chinese Mathematician Liao (1992) proposed Homotopy Analysis Method (HAM) using the Homotopy, a basic concept in topology. In the method some parameter terms are used viz., auxiliary linear operator, embedding parameter or Homotopy parameter, initial guess, convergence control parameter, auxiliary parameter etc. In the method there are flexibilities to choose the auxiliary linear parameter, initial guess, auxiliary function and the convergence control parameter. Liao showed the advantages of the method are it is independent of any small or large physical parameters and also provides a convenient way to guarantee the convergence for approximation of series solution. Due to these advantages it can overcome the restrictions and limitations of various existing traditional perturbation and non-perturbation methods. The biggest advantage of the method is the smooth construction of so called zero-th order deformation equation, which is a base of HAM to connect a given non-linear problem and a relatively much simpler linear ones. Keeping in mind these advantages and flexibilities of HAM, the authors have made an endeavor to solve the fractional order Van der Pol equation. The convergence of the series solution (Liao, 2012; Atangana, 2014) with the proper choice of optimal values of convergence control parameter and also the stability analysis of the Van der Pol equation for different fractional order time derivatives through numerical and graphical presentations for different particular cases is the striking feature of this scientific contribution. The remarkable contribution of the study is the presentation of oscillations of the system, which are depicted through phase portraits for various values of control parameters and fractional order derivatives.

2 Solution of the Problem by HAM

The Eq. (5) can be rewritten as

(6)

D_{t}^{2 α} u (t) + ∊ u^{2} (t) D_{t}^{α} u (t) - ∊ D_{t}^{α} u (t) + u (t) = 0, 0 < α ⩽ 1,

with

u (0) = a, \dot{u} (0) = 0

The linear auxiliary operator is

(7)

L [ϕ (t, q)] = \frac{\partial^{2 α} ϕ (t, q)}{\partial t^{2 α}}, t > 0, 0 < α ⩽ 1,

with the property that

(8)

L [c] = 0

where c is the integrating constant,

ϕ (t, q)

is an unknown function.

The nonlinear operator is defined as

(9)

N [ϕ (t, q)] = D_{t}^{2 α} ϕ (t, q) + ∊ ϕ {(t, q)}^{2} (t, q) D_{t}^{α} ϕ (t, q) - ∊ D_{t}^{α} ϕ (t, q) + ϕ (t, q) .

Hence the zero-th order deformation equation is

(10)

(1 - q) L [ϕ (t, q) - u_{0} (t)] = q ℏ N [ϕ (t, q)],

where q and

ℏ \neq 0

are the embedding and the convergence control parameters,

u_{0} (t)

is the initial guess of

u (t)

. For

q = 0

and 1 , Eq. (10) gives

ϕ (t, 0) = u_{0} (t), ϕ (t, 1) = u (t)

The m-th order deformation equation is

(11)

L [u_{m} (t) - χ_{m} u_{m - 1} (t)] = ℏ R_{m} ({\vec{u}}_{m - 1} (r, t)),

with initial condition

(12)

u_{m} (0) = 0,

where

χ_{m} = \{\begin{matrix} 0, & m ⩽ 1, \\ 1, & m > 1 . \end{matrix}

Therefore solution of the deformation equation is

(13)

u_{m} (t) = χ_{m} u_{m - 1} (t) + ℏ J_{t}^{2 α} R_{m} [{\vec{u}}_{m - 1} (t)] + c,

where

J_{t}^{2 α} [f (t)] = \frac{1}{Γ (2 α)} \int_{0}^{t} {(t - ξ)}^{2 α - 1} f (ξ) d ξ, c

is the integration constant determined from Eq. (12).

Thus, $R_{m} [{\vec{u}}_{m - 1} (t)] = D_{t}^{2 α} u_{m - 1} (t) + ∊ \sum_{i = 0}^{m - 1} (\sum_{j = 0}^{i} u_{j} u_{i - j}) D^{α} u_{m - 1 - i} - ∊ D_{t}^{α} u_{m - 1} (t) + u_{m - 1} (t)$ .

Taking $u_{0} = a$ , we get

(14)

u_{1} (t) = \frac{ℏ a}{Γ (1 + 2 α)} t^{2 α},

(15)

u_{2} (t) = \frac{ℏ (ℏ + 1) a}{Γ (1 + 2 α)} t^{2 α} + \frac{∊ a (a^{2} - 1) ℏ^{2}}{Γ (1 + 3 α)} t^{3 α} + \frac{ℏ^{2} a}{Γ (1 + 4 α)} t^{4 α},

(16)

u_{3} (t) = \frac{ℏ {(ℏ + 1)}^{2} a}{Γ (1 + 2 α)} t^{2 α} + [2 ∊ a (a^{2} - 1) ℏ (ℏ + 1)] \frac{t^{3 α}}{Γ (1 + 3 α)} + [h^{3} a + ∊^{2} a (a^{2} - 1) ℏ^{3} + ℏ^{2} (ℏ + 1) a] \frac{t^{4 α}}{Γ (1 + 4 α)} + [2 ∊ a ℏ^{3} (a^{2} - 1) + \frac{2 ∊ a^{3} ℏ^{3} Γ (1 + 3 α)}{Γ (1 + 2 α) Γ (1 + α)}] \frac{t^{5 α}}{Γ (1 + 5 α)} + \frac{ℏ^{3} {at}^{6 α}}{Γ (1 + 6 α)},

(17)

u_{4} (t) = \frac{ℏ {(ℏ + 1)}^{3} a}{Γ (1 + 2 α)} t^{2 α} + [2 ∊ a (a^{2} - 1) ℏ^{2} {(ℏ + 1)}^{2} + ℏ^{2} {(1 + ℏ)}^{2} ∊ a (a^{2} - 1)] \frac{t^{3 α}}{Γ (1 + 3 α)} + [ℏ^{3} (ℏ + 1) a + ∊^{2} a {(a^{2} - 1)}^{2} ℏ^{2} (ℏ + 1) + 2 ∊^{2} a {(a^{2} - 1)}^{2} ℏ^{3} (1 + ℏ) + ℏ^{2} {(1 + ℏ)}^{2} a] \frac{t^{4 α}}{Γ (1 + 4 α)} + [2 ∊ ℏ^{3} (ℏ + 1) a (a^{2} - 1) + ∊ a ℏ^{4} (a^{2} - 1) + ∊^{3} a {(a^{2} - 1)}^{3} ℏ^{3} + 2 ∊ a (a^{2} - 1) ℏ^{3} (ℏ + 1) + ℏ^{3} (ℏ + 1) ∊ a (a^{2} - 1) + \frac{2 ∊ a^{3} ℏ^{3} (ℏ + 1) Γ (1 + 3 α)}{Γ (1 + 2 α) Γ (1 + α)} + \frac{2 a^{3} ℏ^{3} (ℏ + 1) Γ (1 + 3 α)}{Γ (1 + α) Γ (1 + 2 α)} + \frac{2 ℏ^{3} (ℏ + 1) a^{3} Γ (1 + 3 α)}{Γ (1 + α) Γ (1 + 2 α)}] \frac{t^{5 α}}{Γ (1 + 5 α)} + [ℏ^{3} (ℏ + 1) a + 2 ∊^{2} a ℏ^{4} {(a^{2} - 1)}^{2} + ℏ^{4} a + a ℏ^{3} + ∊^{2} a ℏ^{3} {(a^{2} - 1)}^{2} + ℏ^{3} (ℏ + 1) a + \frac{2 ∊^{3} ℏ^{4} a^{3} (a + 1) Γ (1 + 3 α)}{Γ (1 + 2 α) Γ (1 + α)} + \frac{2 ∊ a^{3} (a^{2} - 1) ℏ^{4} Γ (1 + 4 α)}{Γ^{2} (1 + 2 α)} + \frac{2 ∊ a^{3} ℏ^{4} (a^{2} - 1) Γ (1 + 4 α)}{Γ (1 + α) Γ (1 + 3 α)}] \frac{t^{6 α}}{Γ (1 + 6 α)} [(a^{2} - 1) ℏ^{4} ∊ a + 2 ∊ ℏ^{4} a (a^{2} - 1) + \frac{2 ∊ a^{3} ℏ^{4} Γ (1 + 3 α)}{Γ (1 + 2 α) Γ (1 + 3 α)} + \frac{2 ∊ ℏ^{4} a^{3} Γ (1 + 5 α)}{Γ (1 + 2 α) Γ (1 + 3 α)} + \frac{2 ∊ ℏ^{4} a^{3} Γ (1 + 5 α)}{Γ (1 + 4 α) Γ (1 + 5 α)} + \frac{∊ ℏ^{3} a^{3} Γ (1 + 5 α)}{Γ^{2} (1 + 2 α) Γ (1 + α)}] \frac{t^{7 α}}{Γ (1 + 7 α)} + \frac{ℏ^{4} a}{Γ (1 + 8 α)} t^{8 α} .

Proceeding in a similar manner, we can calculate the other components

u_{n}, n > 4

and hence we get the series solution of the considered problem as

(18)

u (t) = \lim_{N ⟶ \infty} ϕ_{N} (t),

where

ϕ_{N} (t) = \sum_{n = 0}^{N - 1} u_{n} (t), N ⩾ 1

. As given by Liao (2012), at the m-th order of approximation, one can define the exact square residual error as

(19)

E_{m} = \int_{Ω} {(N [\sum_{i = 0}^{m} u_{i} (t)])}^{2} dt,

During numerical computation the limits of the Eq. (19) will be taken from 0 to 1. The optimal value of

E_{m}

will be obtained by minimizing the so called exact residual error defined by Eq. (19), corresponding to the nonlinear algebraic equation

\frac{{dE}_{m}}{d ℏ} = 0 .

Theorem 2.1

(Convergence theorem) If the series solution defined by the Eq. (18) is convergent then it converges to an exact solution of the nonlinear problem (6).

Proof

See Theorem 4.21 and Theorem 4.22 in the monograph of Liao (2012). □

3 Numerical results and discussion

In this section, the numerical results of $u (t)$ for the considered non-linear fractional Van der Pol oscillator equation have been obtained. The optimal values of $ℏ$ , for comparison of minimum residual errors for $a = 1, ∊ = 1$ and various values of $α$ are provided through Tables 1–3 and are displayed through Figs. 1–3 . It is observed from Tables 1–3 that with increase in the order of approximations, the residual error is decreasing and optimal value of $ℏ$ goes away from $ℏ = - 1$ . Tables 1–3 also depict that with decrease in the value of $α$ , residual error is decreasing for $ℏ = - 1$ . 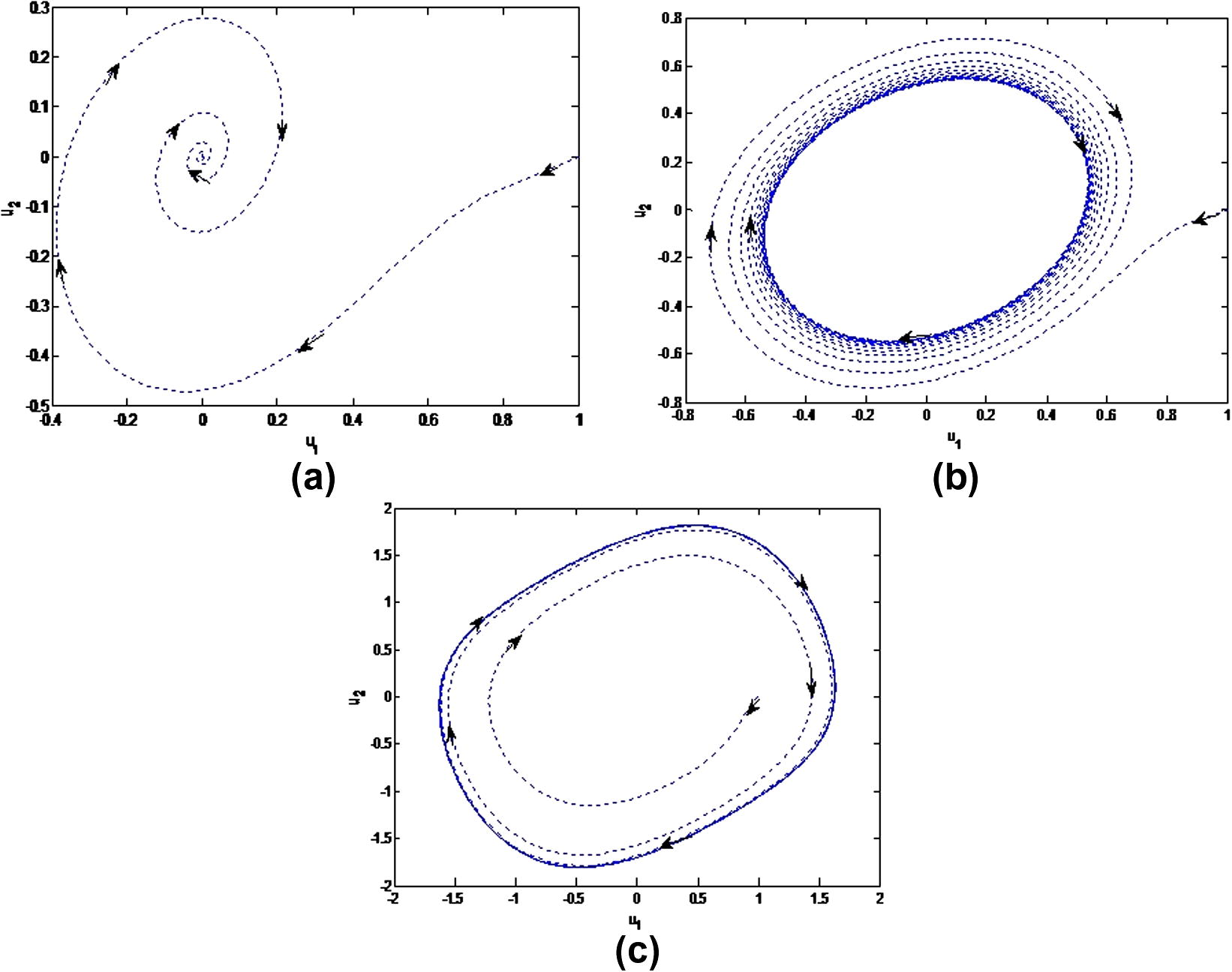The phase portraits between $u_{1}$ and $u_{2}$ are presented through Fig. 4(a)–(c). It is observed that for $∊ = 1$ and $α = 0.5$ , system approaches towards an equilibrium point whereas for $∊ = 1$ and $α = 0.75$ the system gives us a stable limit cycle and with the increase of the values of $α$ from $0.75$ to 1, it is seen from Fig. 4(b) and (c) that amplitude of the limit cycle is increasing. In Fig. 5 drawn for $α = 0.75$ and $∊ = 1 (1) 4$ the same nature is found in the amplitude of the limit cycle. When $∊ = 0.5$ , the system approaches towards the equilibrium point at $α = 0.75$ (Fig. 6(a)). An interesting phenomenon is observed at $∊ = 0.5, α = 0.85$ and $∊ = 0.5, α = 0.95$ . In both occasions limit cycles obtained are displayed through Fig. 6(b) and (c). In the first case the path of the orbit approaches towards the limit cycle from outside whereas in the later one the nature is opposite. Again for $∊ ⩾ 7$ , some strange natures are found in the limit cycles at $α = 0.75$ depicted through Fig. 7 which may be described as bad bands (Guckenheimer, 1980).

Table 1 Comparison of exact residual error for different values of at

α = 1

Order of approximation	$ℏ$	$E_{m}$	$E_{m}$ at $ℏ = - 1$
1	$- 1.02178$	$7.23448 \times 10^{- 3}$	$7.56674 \times 10^{- 3}$
2	$- 0.729311$	$7.59265 \times 10^{- 2}$	$1.09266 \times 10^{- 1}$
3	$- 0.76059$	$1.07886 \times 10^{- 4}$	$5.11962 \times 10^{- 2}$

Table 2 Comparison of exact residual error for different values of at

α = 0.75

Order of approximation	$ℏ$	$E_{m}$	$E_{m}$ at $ℏ = - 1$
1	−1.04575	$1.39174 \times 10^{- 2}$	$1.50387 \times 10^{- 2}$
2	−0.624875	$1.41559 \times 10^{- 1}$	$2.35311 \times 10^{- 1}$
3	−0.758726	$2.03645 \times 10^{- 4}$	$9.34828 \times 10^{- 2}$

Table 3 Comparison of exact residual error for different values of at

α = 0.5

Order of approximation	$ℏ$	$E_{m}$	$E_{m}$ at $ℏ = - 1$
1	−1.09418	$8.14262 \times 10^{- 3}$	$1.21135 \times 10^{- 2}$
2	−0.550819	$1.87993 \times 10^{- 1}$	$3.65587 \times 10^{- 1}$
3	−0.725017	$2.56436 \times 10^{- 3}$	$1.22567$

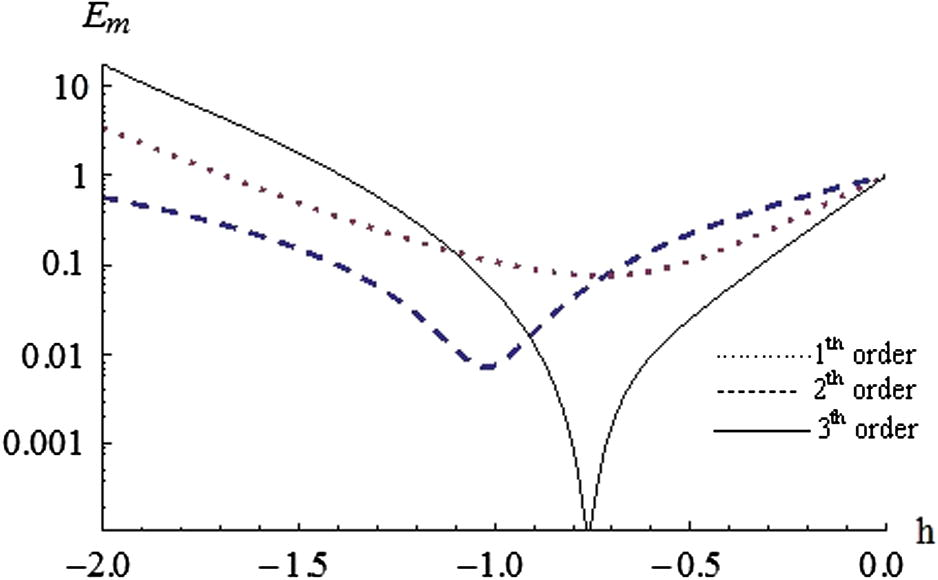
Plots of exact residual error E m versus ℏ for a = 1 , ∊ = 1 and α = 1 .

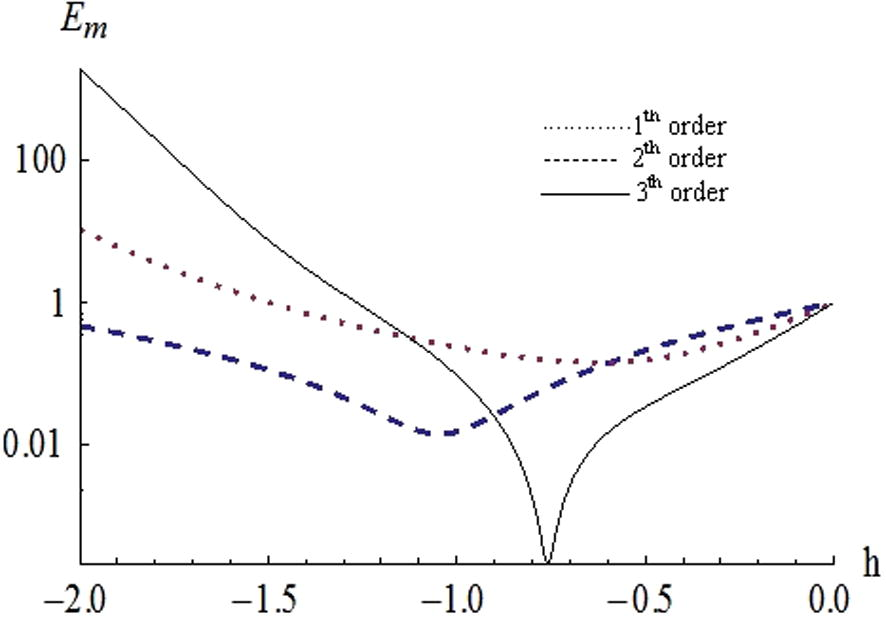
Plots of exact residual error E m versus ℏ for a = 1 , ∊ = 1 and α = 0.75 .

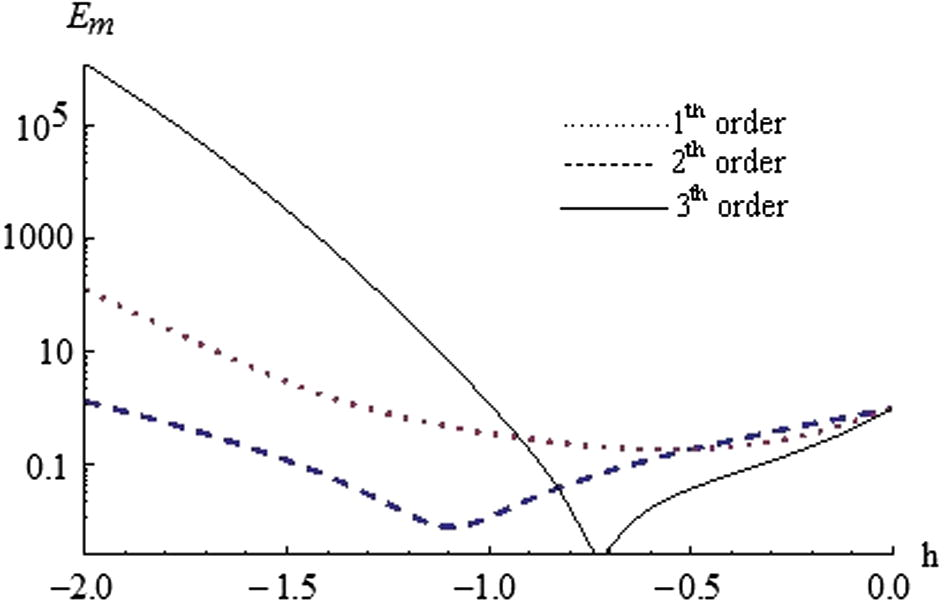
Plots of exact residual error E m versus ℏ for a = 1 , ∊ = 1 and α = 0.5 .

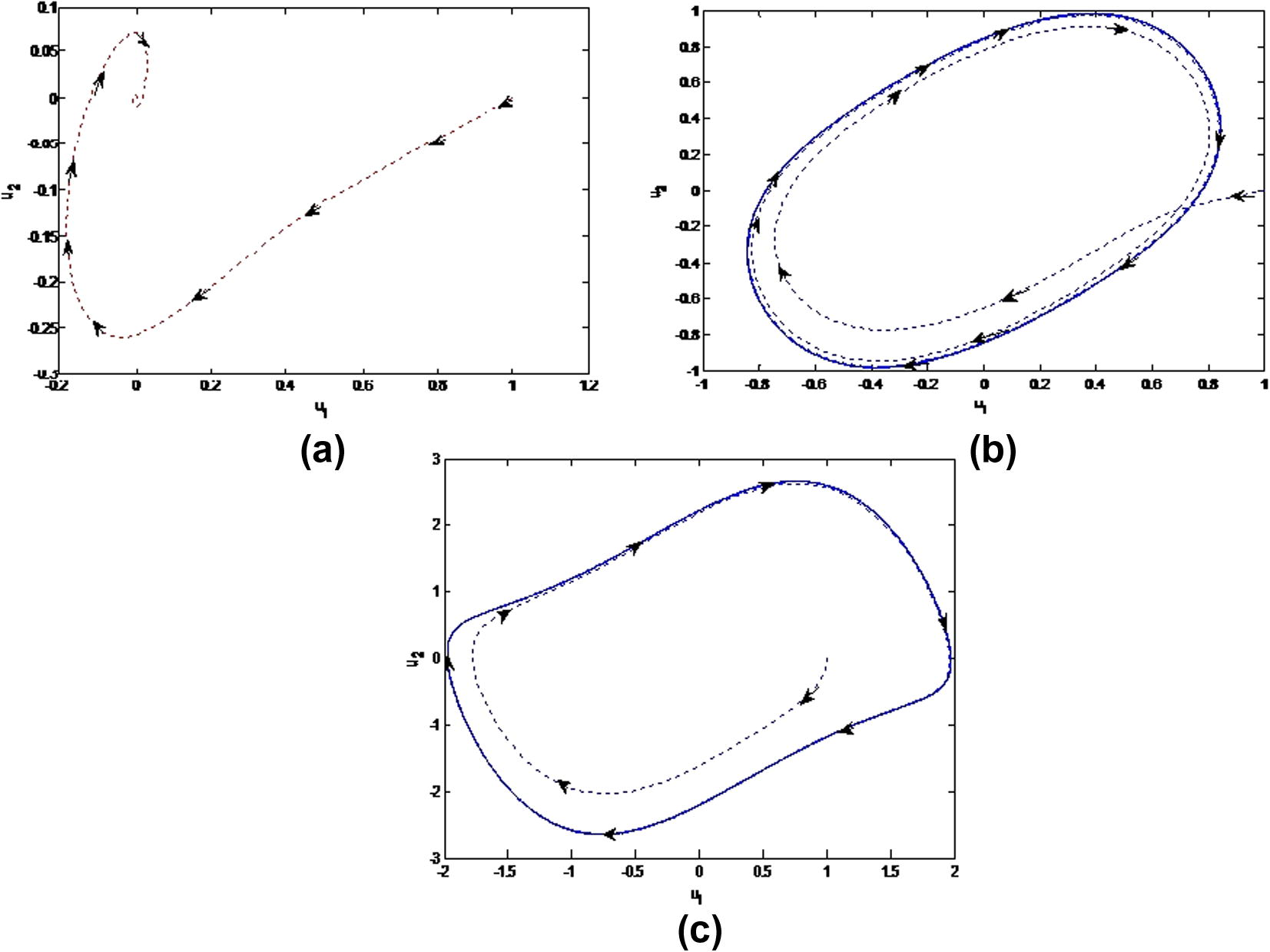
Phase Portrait between u 1 and u 2 (a) for a = 1 , ∊ = 1 and α = 0.5 (b) for a = 1 , ∊ = 1 and α = 0.75 (c) for a = 1 , ∊ = 1 and α = 1 .

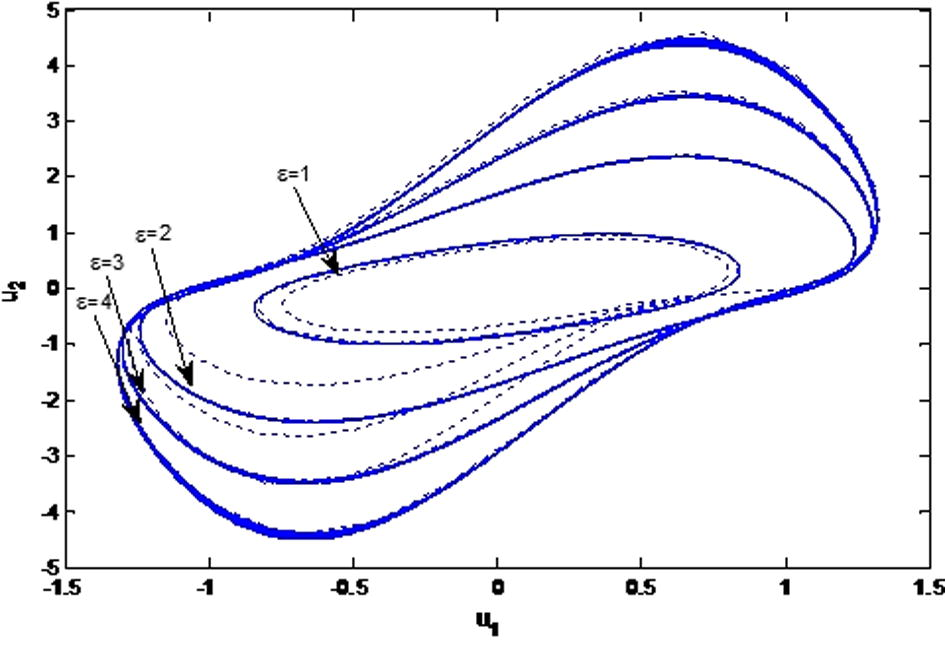
Phase Portrait between u 1 and u 2 for a = 1 , α = 0.5 and ∊ = 1 , 2 , 3 , 4 .

Phase Portrait between u 1 and u 2 (a) for a = 1 , ∊ = 0.5 and α = 0.75 (b) for a = 1 , ∊ = 0.5 and α = 0.85 (c) for a = 1 , ∊ = 0.5 and α = 0.95 .

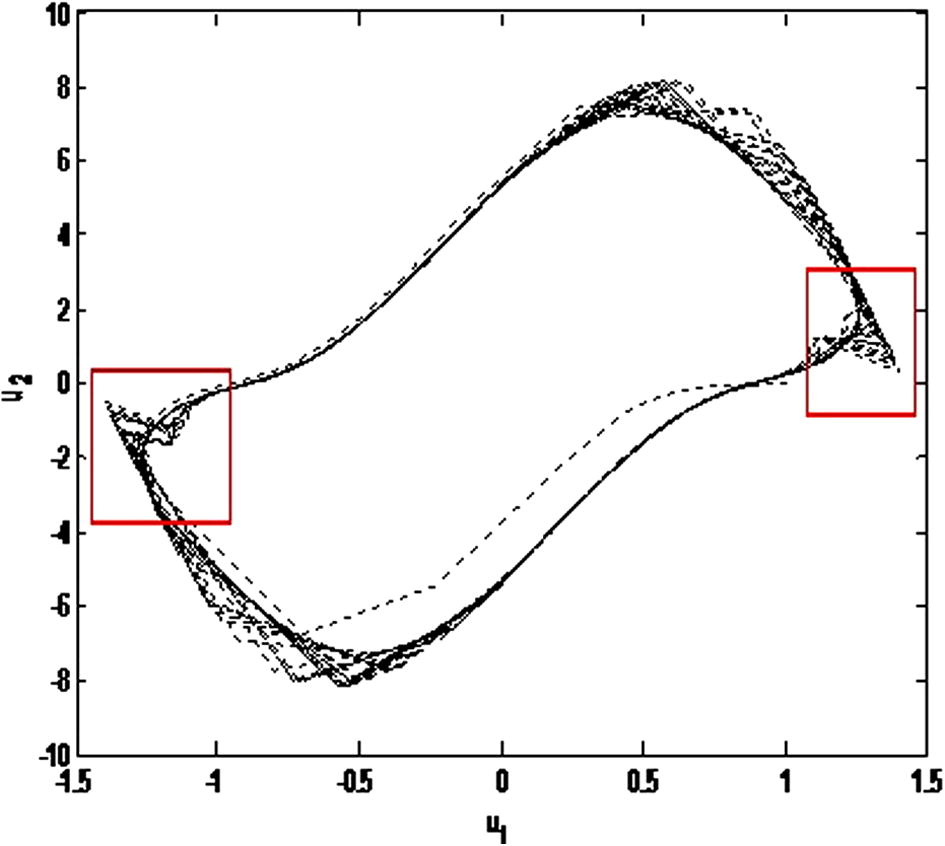
Phase Portrait between u 1 and u 2 for a = 1 , ∊ = 8 and α = 0.75 .

4 Conclusion

There are two important goals that the authors have achieved in the present article. First one is how the convergence of approximate solution can be accelerated using convergence control parameter which demonstrates computationally efficient approximate solutions with low residual errors during the solution of the historical nonlinear equation in fractional order system. This clearly reveals the reliability and potential of the method HAM during the solution of nonlinear partial differential equations even in fractional order system. The second one is the observation of limit cycles for small values of when is close to the standard one, and also the large value of when is close to 0.5, which clearly demonstrate the variations of achieved stable limit cycles of the system with changes in small value of control parameter and higher value of fractional order time derivative to the large value of control parameter and small value of fractional order derivative.

References

Atangana Abdon, . Convergence and stability analysis of a novel iteration method for fractional biological population equation. Neural Comput. Appl.. 2014;25:1021-1030.
[Google Scholar]
Abdon Atangana, Aydin Secer, 2013. A Note on Fractional Order Derivatives and Table of Fractional Derivatives of Some Special Functions, 2013, 1–8.
Barbosa, R.S., Machado, J.A.T., Ferreira, M.I., Tar, K.J., Proceedings of the Second IEEE International Conference on Computational Cybernetics (ICCC₀₄), Vienna University of Technology, 200, 373.
Cartwright M.L., Littlewood J.E., . On non-linear differential equations of the second order. J. London Math. Soc.. 1945;20:180-189.
[Google Scholar]
Gafiychuk V., Datskoc B., Meleshkoc V., . Analysis of fractional order Bonhoeffer-Van der Pol oscillator. Phys. A. 2008;387:418-424.
[Google Scholar]
Guckenheimer, John, 1980. Dynamics of Van der Pol Equation. IEEE Trans. Circ. Syst. Cas-27, 983–989.
Guo Z.J., Leung A.Y.T., Yang H.X., . Oscillatory region and asymptotic solution of Fractional Van der Pol oscillator via residue harmonic balance technique. Appl. Math. Model.. 2011;35:3918-3925.
[Google Scholar]
He J.H., . Some asymptotic methods for strongly nonlinear equations. Int. J. Modern Phys. B. 2006;20(1):1141-1199.
[Google Scholar]
Konuralp A., Konuralp C., Yildirim A., . Numerical solution to the Van der Pol equation with fractional damping. Phys. Scripta. 2009;136:014034-014035.
[Google Scholar]
Leung A.Y.T., Guo Z.J., . Residue harmonic balance for discontinuous nonlinear oscillator with fractional power restoring force. Int. J. Nonlinear Sci. Numer. Simul.. 2010;11:705-723.
[Google Scholar]
Leung A.Y.T., Guo Z.J., . Forward residue harmonic balance for autonomous and non-autonomous systems with fractional derivative damping. Commun. Nonlinear Sci. Numer. Simul.. 2011;16(9):2169-2183.
[Google Scholar]
Leung A.Y.T., Yang H.X., Guo Z.J., . The residue harmonic balance for fractional order Van der Pol like oscillators. J. Sound Vibr.. 2012;331:1115-1126.
[Google Scholar]
Levinson N., . A second order differential equation with singular solutions. Ann. Math.. 1949;50:127-153. (ser. 2nd)
[Google Scholar]
Liao, S.J., 1992. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, Ph.D. Thesis, Shanghai Jiao Tong University.
Liao, S.J., 2012. Homotopy Analysis Method in Nonlinear Differential Equations, Higher Education Press, Beijing and Springer-Verlag Berlin, Heidelberg.
Mehdipour I., Ganji D.D., Mozaffari M., . Application of the energy balance method to nonlinear vibrating equations. Curr. Appl. Phys.. 2010;10:104-112.
[Google Scholar]
Mickens R.E., . Analytical and numerical study of a non-standard finite difference scheme for the unplugged Van der Pol equation. J. Sound Vibr.. 2001;245(4):757-761.
[Google Scholar]
Mickens R.E., . Numerical study of a non-standard finite-difference scheme for the Van der Pol equation. J. Sound Vibr.. 2002;250(5):955-963.
[Google Scholar]
Mickens R.E., . Step-size dependence of the period for a forward-euler scheme of the Van der Pol equation. J. Sound Vibr.. 2002;258(1):199-202.
[Google Scholar]
Mickens R.E., . Fractional Van der Pol equations. J. Sound Vibr.. 2003;259(2):457-460.
[Google Scholar]
Pereira, E., Monje, C.A., Vinagre, B.M., Gordillo, F., 2004. MATLAB tool box for the analysis of fractional order systems with hard nonlinearities. In: Proceedings of the First IFAC Congress on Fractional Differentiation and its Applications, Bordeaux (France), 214–219.
Sardar T., Ray S.S., Bera R.K., Biswas B.B., . The analytical approximate solution of the multi-term fractionally damped Van der Pol equation. Phys. Scripta. 2009;80:025003-025006.
[Google Scholar]
Vander Pol, B.,1920. A theory of the amplitude of free and forced triode vibrations. Radio Rev., 1, 701–710, 754–762.
Xu L., . Determination of limit cycle by He’s parameter-expanding method for strongly nonlinear oscillators. J. Sound Vibr.. 2007;302:178-184.
[Google Scholar]
Younesian D., Askari H., Saadatnia Z., Yazdi M.K., . Frequency analysis of strongly nonlinear generalized Duffing oscillators using He’s frequency amplitude formulation and He’s energy balance method. Comput. Math. Appl.. 2010;59:3222-3228.
[Google Scholar]

Introduction

Solution of the Problem by HAM

Numerical results and discussion

Conclusion

Fulltext Views
2

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Atangana Abdon, . Convergence and stability analysis of a novel iteration method for fractional biological population equation. Neural Comput. Appl.. 2014;25:1021-1030.
[Google Scholar]

[2] Abdon Atangana, Aydin Secer, 2013. A Note on Fractional Order Derivatives and Table of Fractional Derivatives of Some Special Functions, 2013, 1–8.

[3] Barbosa, R.S., Machado, J.A.T., Ferreira, M.I., Tar, K.J., Proceedings of the Second IEEE International Conference on Computational Cybernetics (ICCC₀₄), Vienna University of Technology, 200, 373.

[4] Cartwright M.L., Littlewood J.E., . On non-linear differential equations of the second order. J. London Math. Soc.. 1945;20:180-189.
[Google Scholar]

[5] Gafiychuk V., Datskoc B., Meleshkoc V., . Analysis of fractional order Bonhoeffer-Van der Pol oscillator. Phys. A. 2008;387:418-424.
[Google Scholar]

[6] Guckenheimer, John, 1980. Dynamics of Van der Pol Equation. IEEE Trans. Circ. Syst. Cas-27, 983–989.

[7] Guo Z.J., Leung A.Y.T., Yang H.X., . Oscillatory region and asymptotic solution of Fractional Van der Pol oscillator via residue harmonic balance technique. Appl. Math. Model.. 2011;35:3918-3925.
[Google Scholar]

[8] He J.H., . Some asymptotic methods for strongly nonlinear equations. Int. J. Modern Phys. B. 2006;20(1):1141-1199.
[Google Scholar]

[9] Konuralp A., Konuralp C., Yildirim A., . Numerical solution to the Van der Pol equation with fractional damping. Phys. Scripta. 2009;136:014034-014035.
[Google Scholar]

[10] Leung A.Y.T., Guo Z.J., . Residue harmonic balance for discontinuous nonlinear oscillator with fractional power restoring force. Int. J. Nonlinear Sci. Numer. Simul.. 2010;11:705-723.
[Google Scholar]

[11] Leung A.Y.T., Guo Z.J., . Forward residue harmonic balance for autonomous and non-autonomous systems with fractional derivative damping. Commun. Nonlinear Sci. Numer. Simul.. 2011;16(9):2169-2183.
[Google Scholar]

[12] Leung A.Y.T., Yang H.X., Guo Z.J., . The residue harmonic balance for fractional order Van der Pol like oscillators. J. Sound Vibr.. 2012;331:1115-1126.
[Google Scholar]

[13] Levinson N., . A second order differential equation with singular solutions. Ann. Math.. 1949;50:127-153. (ser. 2nd)
[Google Scholar]

[14] Liao, S.J., 1992. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, Ph.D. Thesis, Shanghai Jiao Tong University.

[15] Liao, S.J., 2012. Homotopy Analysis Method in Nonlinear Differential Equations, Higher Education Press, Beijing and Springer-Verlag Berlin, Heidelberg.

[16] Mehdipour I., Ganji D.D., Mozaffari M., . Application of the energy balance method to nonlinear vibrating equations. Curr. Appl. Phys.. 2010;10:104-112.
[Google Scholar]

[17] Mickens R.E., . Analytical and numerical study of a non-standard finite difference scheme for the unplugged Van der Pol equation. J. Sound Vibr.. 2001;245(4):757-761.
[Google Scholar]

[18] Mickens R.E., . Numerical study of a non-standard finite-difference scheme for the Van der Pol equation. J. Sound Vibr.. 2002;250(5):955-963.
[Google Scholar]

[19] Mickens R.E., . Step-size dependence of the period for a forward-euler scheme of the Van der Pol equation. J. Sound Vibr.. 2002;258(1):199-202.
[Google Scholar]

[20] Mickens R.E., . Fractional Van der Pol equations. J. Sound Vibr.. 2003;259(2):457-460.
[Google Scholar]

[21] Pereira, E., Monje, C.A., Vinagre, B.M., Gordillo, F., 2004. MATLAB tool box for the analysis of fractional order systems with hard nonlinearities. In: Proceedings of the First IFAC Congress on Fractional Differentiation and its Applications, Bordeaux (France), 214–219.

[22] Sardar T., Ray S.S., Bera R.K., Biswas B.B., . The analytical approximate solution of the multi-term fractionally damped Van der Pol equation. Phys. Scripta. 2009;80:025003-025006.
[Google Scholar]

[23] Vander Pol, B.,1920. A theory of the amplitude of free and forced triode vibrations. Radio Rev., 1, 701–710, 754–762.

[24] Xu L., . Determination of limit cycle by He’s parameter-expanding method for strongly nonlinear oscillators. J. Sound Vibr.. 2007;302:178-184.
[Google Scholar]

[25] Younesian D., Askari H., Saadatnia Z., Yazdi M.K., . Frequency analysis of strongly nonlinear generalized Duffing oscillators using He’s frequency amplitude formulation and He’s energy balance method. Comput. Math. Appl.. 2010;59:3222-3228.
[Google Scholar]