Solutions for a fractional diffusion equation: Anomalous diffusion and adsorption–desorption processes

E.K. Lenzi; M.A.F. dos Santos; M.K. Lenzi; D.S. Vieira; L.R. da Silva

doi:10.1016/j.jksus.2015.08.003

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

28 (

); 3-6

doi:

10.1016/j.jksus.2015.08.003

Solutions for a fractional diffusion equation: Anomalous diffusion and adsorption–desorption processes

E.K. Lenzi^{^a,^b}, M.A.F. dos Santos^{^a}, M.K. Lenzi^{^c,⁎}, D.S. Vieira^{^b}, L.R. da Silva^{^d}

a Departamento de Física, Universidade Estadual de Ponta Grossa, Ponta Grossa, PR 84030-900, Brazil

b Departamento de Física, Universidade Estadual de Maringá, Maringá, PR 87020-900, Brazil

c Departamento de Engenharia Qumica, Universidade Federal do Paraná, Curitiba, PR 81531-990, Brazil

d Departamento de Física, Universidade Federal do Rio Grande do Norte, Natal, RN 59072-970, Brazil

⁎Corresponding author. Tel.: +55 41 3361 3590. lenzi@ufpr.br (M.K. Lenzi)

Received: 2015-4-1, Accepted: 2015-8-4, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

We investigate the solutions for a fractional diffusion equation subjected to boundary conditions which can be connected to adsorption–desorption processes. The analytical solutions were obtained using the Green function approach and showed an anomalous spreading which can be connected to an anomalous diffusion.

Keywords

Fractional diffusion equation

Anomalous diffusion

Adsorption–desorption

Show Related Articles from PubMed

1 Introduction

Diffusion is one of the most important phenomena present in nature which has been investigated using several approaches. In general, the description employs stochastic differential equations which are connected to Markovian processes (Crank, 1975) and, consequently, leads us to a linear dependence for the mean square displacement, i.e., 〈(x − 〈x〉)²〉 ∝ t. However, the experimental scenarios characterized by fractality (ben-Avraham and Havlin, 2005; Weigel et al., 2011), molecular diffusion in vivo (Leijnse et al., 2012; Robson et al., 2013), molecular crowding (Sokolov, 2012), chemotaxis diffusion (Langlands and Henry, 2010), and active transport (Caspi et al., 2000; Bruno et al., 2009; Brangwynne et al., 2009; Weber et al., 2012 ) have evidenced the limitations of the Markovian processes in describing situations where memory effects, long-range correlations, and long-range interactions are present. In order to overcome the limitations present in the usual approach several extensions, for example, involving continuous time random walk (Klafter and Sokolov, 2011), generalized Langevin equations, and fractional diffusion equations (Leijnse et al., 2012; Hilfer et al., 2004; Metzler and Klafter, 2000, 2004; Eliazar and Shlesinger, 2013; Bressloff and Newby, 2013; Condamin et al., 2008; Podlubny, 1999 ), have been investigated to establish the appropriated links between the models and the experimental results. It is also worth mentioning that Cantor space-time has been used to analyse the diffusion equation and the reported results show the dependence on the fractal dimension order of the differential equation on Cantor space-time (Yang et al., 2013; Yang et al., 2015a,b; Yan, 2015 ). In these extensions, one of the main points is the nonlinear time dependence exhibited by the mean-square displacement which, in general, is characterized by 〈(x − 〈x〉)²〉 ∝ t^α, where α > 1 and α < 1 correspond to superdiffusion and subdiffusion, respectively (Caputo et al., 2008; Caputo and Cametti, 2009; Kosztolowicz et al., 2012 ). Here, we investigate the solutions for the fractional diffusion equation (Jiang et al., 2013; Barbero and Evangelista, 2006; Garrod, 1995; Lyklema, 1993 )

(1)

\frac{\partial}{\partial t} ρ (x, t) =_{0} D_{t}^{1 - γ} (K_{γ} \frac{\partial^{2}}{\partial x^{2}} ρ (x, t) - F \frac{\partial}{\partial x} ρ (x, t))

where K_γ is the diffusion coefficient, F is an external force which represents a constant field acting on the system, and fractional time operator is the Riemann–Liouville with 0 < γ < 1. For γ = 1 Eq. (1) recovers the usual form of the diffusion equation with a constant external force. This equation is subjected to the boundary conditions: ρ(∞, t) = 0,

(2)

κ τ ρ (0, t^{'}) = τ \frac{d}{dt} Γ_{0} (t) + Γ_{0} (t)

where κ is connected to the characteristics of the surface and

(3)

Γ_{0} (t) + \int_{0}^{\infty} {dx}^{'} ρ (x^{'}, t) = const.

In Eq. (2), Γ₀(t) gives the quantity of particles sorbed by the surface, κ represents the sorption rate of the particles from the bulk to the surface, and τ is the relaxation time connected with the desorption process of particles from the surface to the bulk. The quantity κτ has the dimension of length and represents a thickness which may be related to the interaction of the surface with particles present in the bulk (Garrod, 1995; Lyklema, 1993). Also, Eq. (3) implies that the number of particles in the system is conserved, independently of the nature of surface effects that may occur. In particular, it can be connected to the condition

(4)

D_{t}^{1 - γ} (J (x, t)) |_{x = 0} = - \frac{d}{dt} Γ_{0} (t)

(5)

J (x, t) = - K_{γ} \frac{\partial}{\partial x} ρ (x, t) + F ρ (x, t)

where J(x, t) is the current density. Some changes in Eq. (3) by incorporating source or sink terms (Lenzi et al., 2010) are necessary when the processes present in the system lead us to a non-conservation number of particles.

2 Diffusion equation and adsorption–desorption

Let us start our discussion concerning the solutions for Eq. (1) and the implications of the sorption phenomenon on the surface present at x = 0. For this, we first apply the Laplace transform and, after, use the Green function approach to investigate the behavior of this system. Following, in the Laplace domain, it can be written as

(6)

K_{γ} s^{1 - γ} \frac{\partial^{2}}{\partial x^{2}} ρ (x, s) - s^{1 - γ} F \frac{\partial}{\partial x} ρ (x, s) - s ρ (x, s) = - φ (x),

where the initial condition ρ(x, 0) = φ(x) was considered, subjected to

(7)

κ τ ρ (0, s) = (1 + τ s) Γ_{0} (s) - Γ_{0} (0)

and Eq. (3). The presence of Γ₀(0) in the previous equation shows that the surface may initially contain particles which for t > 0 can be released to the bulk. A similar situation involving desorption phenomenon can be found in the pharmaceutical scenario concerning the behavior of the drug release in a living organism. In particular, a better understanding of how the system behaves in conditions due to geometry, drug concentration, and drug solubility is important to the development of medications (Siepmann and Siepmann, 2008, 2012; Siepmann and Peppas, 2001 ). In terms of the Green function approach, the solution for Eq. (6) can formally be written as

(8)

ρ (x, s) = - \frac{1}{s^{1 - γ}} \int_{0}^{\infty} {dx}^{'} G (x, x^{'}; s) φ (x^{'}) - K_{γ} ρ (0, s) \frac{\partial}{\partial x^{'}} G (x, x^{'}; s) |_{x^{'} = 0}

where the last term represents the surface effect on the spreading of the initial condition, which is represented by the first term of this equation. The Green function is obtained by solving the following equation:

(9)

K_{γ} \frac{\partial^{2}}{\partial x^{2}} G (x, x^{'}; s) + F \frac{\partial}{\partial x} G (x, x^{'}; s) - s^{γ} G (x, x^{'}; s) = δ (x - x^{'})

with

G (0, x^{'}; s) = 0

and

G (\infty, x^{'}; s) = 0

. Before solving this equation for the Green function, it is interesting to perform the change

G (x, x^{'}; s) = e^{- Fx / 2 K_{γ}} G^{'} (x, x^{'}; s)

which leads us to

(10)

K_{γ} \frac{\partial^{2}}{\partial x^{2}} G^{'} (x, x^{'}; s) - (s^{γ} + \frac{F^{2}}{4 K_{γ}}) G^{'} (x, x^{'}; s) = e^{\frac{F}{2 K_{γ}} x} δ (x - x^{'})

By solving Eq. (10) with the previous condition, after some calculations, it is possible to show that the solution can be written as

(11)

G^{'} (x, x^{'}; s) = - \frac{e^{\frac{F}{2 K_{γ}} x^{'}}}{\sqrt{F^{2} + 4 K_{γ} s^{γ}}} (e^{- \frac{\sqrt{F^{2} + 4 K_{γ} s^{γ}}}{2 K_{γ}} | x - x^{'} |} - e^{- \frac{\sqrt{F^{2} + 4 K_{γ} s^{γ}}}{2 K_{γ}} | x + x^{'} |})

Then, the Green function, after performing the inverse Laplace transform, can be written as

(12)

G (x, x^{'}; t) = - \frac{2}{π} t^{γ - 1} e^{- \frac{F}{2 K_{γ}} (x - x^{'})} \int_{0}^{\infty} dk \sin (kx) \sin ({kx}^{'}) E_{γ, γ} [- (K_{γ} k^{2} + \frac{F^{2}}{4 K_{γ}}) t^{γ}]

where E_γ_,_β(x) is the generalized Mittag-Leffler function (see, Fig. 1(a) and (b)) and the distribution is given by

(13)

ρ (x^{'}, t) = - \frac{1}{Γ (1 - γ)} \int_{0}^{t} \frac{{dt}^{'}}{{(t - t^{'})}^{γ}} \int_{0}^{\infty} dx G (x, x^{'}; t^{'}) φ (x^{'}) - K_{γ} \int_{0}^{t} {dt}^{'} ρ (0, t^{'}) \frac{\partial}{\partial x} G (0, x^{'}; t - t^{'})

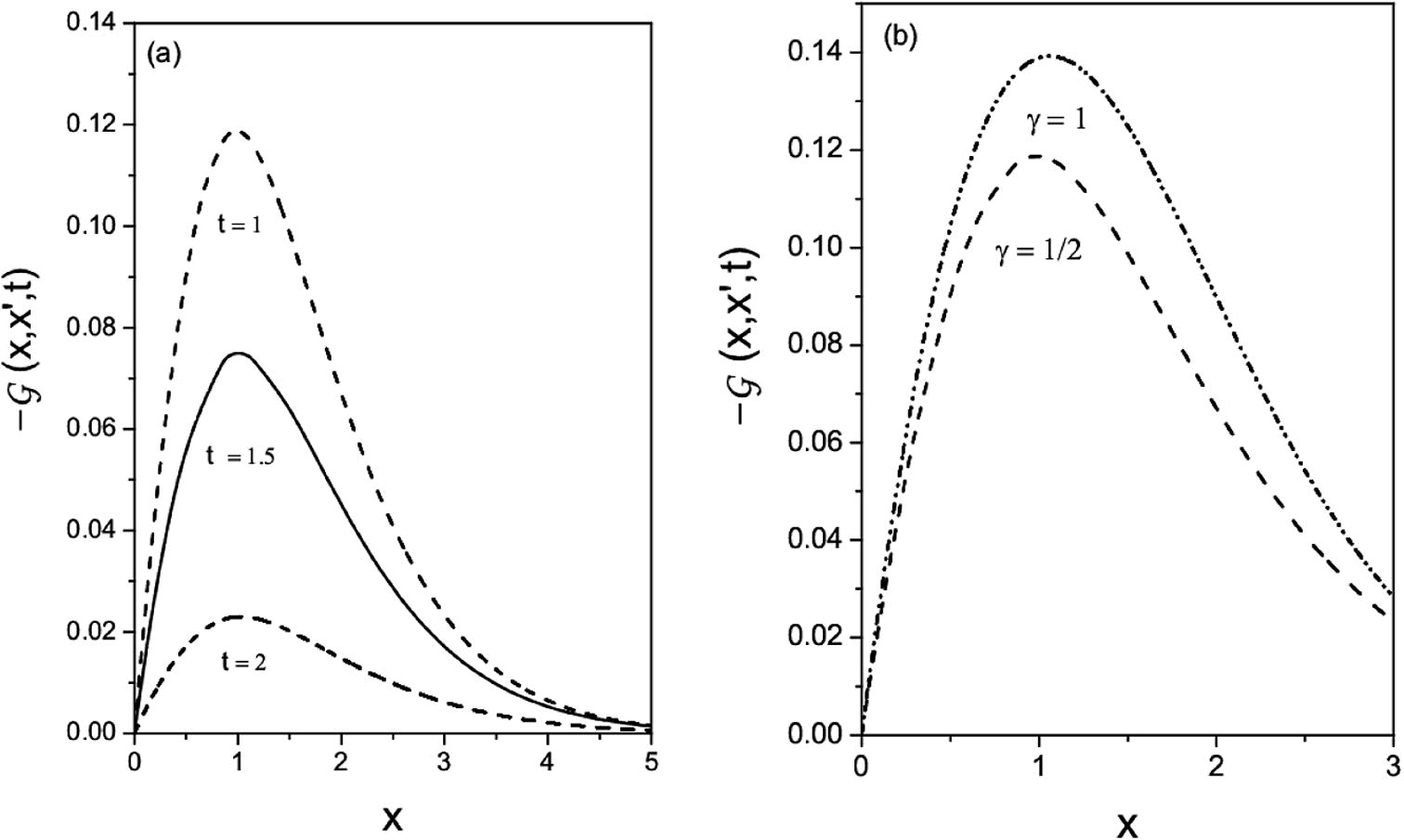
(a and b) shows the behavior of the Green function. (a) Shows the time evolution of the Green function for γ = 1/2 for three different times to illustrate the effect of the external force. (b) Illustrates the behavior of the Green function for different values of γ. For simplicity, Kγ = 1 and F = 1.

using the previous results, it is possible to obtain the quantity of adsorbed particles by the surface. In particular, in the Laplace domain, it is given by

(14)

Γ_{0} (s) = \frac{κ τ (\sqrt{F^{2} + 4 K_{γ} s^{γ}} - F) / s + 2 K_{γ}}{2 K_{γ} (1 + s τ) + κ τ (\sqrt{F^{2} + 4 K_{γ} s^{γ}} - F)} Γ_{0} (0) + \frac{κ τ (\sqrt{F^{2} + 4 K_{γ} s^{γ}} - F)}{2 K_{γ} (1 + s τ) + κ τ (\sqrt{F^{2} + 4 K_{γ} s^{γ}} - F)} \frac{1}{s} \int_{0}^{\infty} d \tilde{x} φ (\tilde{x}) e^{\frac{F}{2 K_{γ}} \tilde{x}} e^{- \frac{1}{2 K_{γ}} \sqrt{F^{2} + 4 K_{γ} s^{γ}} \tilde{x}}

This equation, in the asymptotic limit of |4K_γs^γ/F²| ≪ 1 can be approximated to

(15)

Γ_{0} (s) \frac{F}{(1 + s τ) F + κ τ s^{γ}} Γ_{0} (0) + \frac{κ τ s^{γ}}{(1 + s τ) F + κ τ s^{γ}} \frac{1}{s} (Γ_{0} (0) + \int_{0}^{\infty} d \tilde{x} ϕ (\tilde{x}) e^{- \frac{s^{γ}}{F} \tilde{x}})

and, consequently, for γ ≠ 1 the inverse Laplace transform is given by (Mathai et al., 2009)

(16)

Γ_{0} (t) \approx \int_{0}^{t} {dt}^{'} ϒ (t - t^{'}) (Γ_{0} (0) + \frac{κ τ}{Γ (1 - γ)} \frac{1}{t^{' γ}} Γ_{0} (0) + \int_{0}^{\infty} d \tilde{x} φ (\tilde{x}) H_{1, 1}^{1, 0} [\frac{x}{{Ft}^{' γ}} |_{(0, 1)}^{(1 - γ, γ)}])

with

(17)

ϒ (t) = \frac{1}{τ} e^{- t / τ} + \frac{1}{τ} \sum_{n = 1}^{\infty} \frac{1}{n!} {(- \frac{κ}{F})}^{n} t^{n (1 - γ)} E_{1, 1 - n γ}^{(n)} (- t / τ)

where

E_{α, β}^{(n)} (t) \equiv \frac{d^{n}}{{dt}^{n}} E_{α, β} (t)

is the nth time derivative of the generalized Mittag-Leffler function. Fig. 2 shows the behavior of Eq. (14) for a desorption process by considering two different values of γ and Fig. 3 compares the behavior of the desorption process for the cases γ = 1/2 with F ≠ 0 (obtained from Eq. (16)) and γ = 1 with F = 0 (obtained from Eq. (14)).

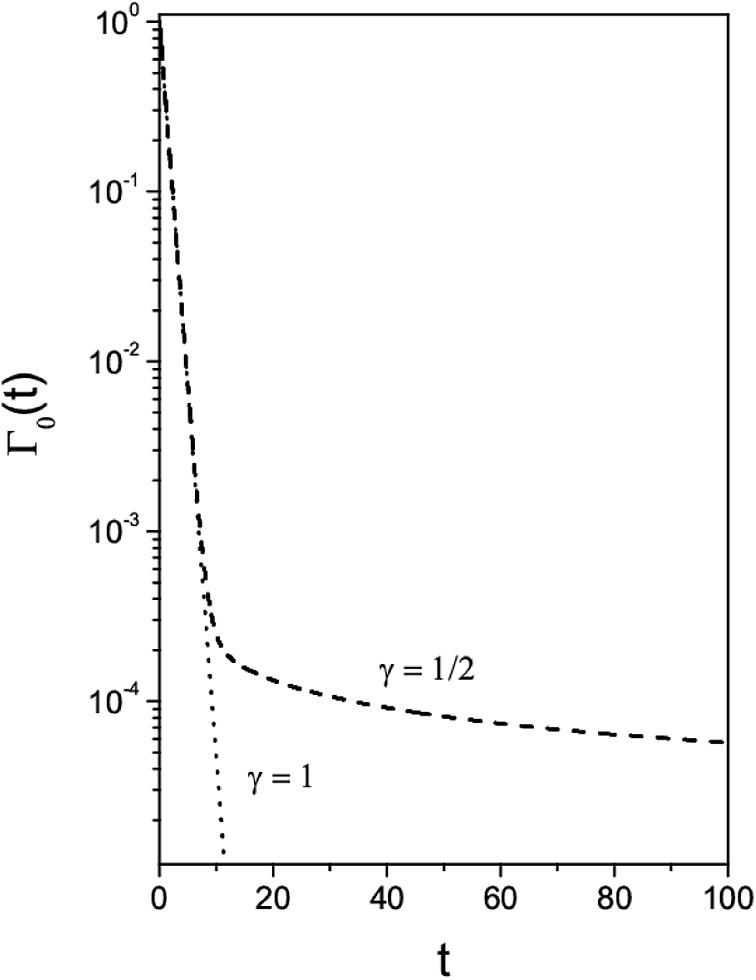
This figure shows the behavior of the Eq. (14) for two different values of γ with Γ0(0) = 1 and φ(x) = 0. For simplicity, Kγ = 1, F = 103, κ = 1, and, τ = 1. Note that the effect of γ ≠ 1 is pronounced for long times.

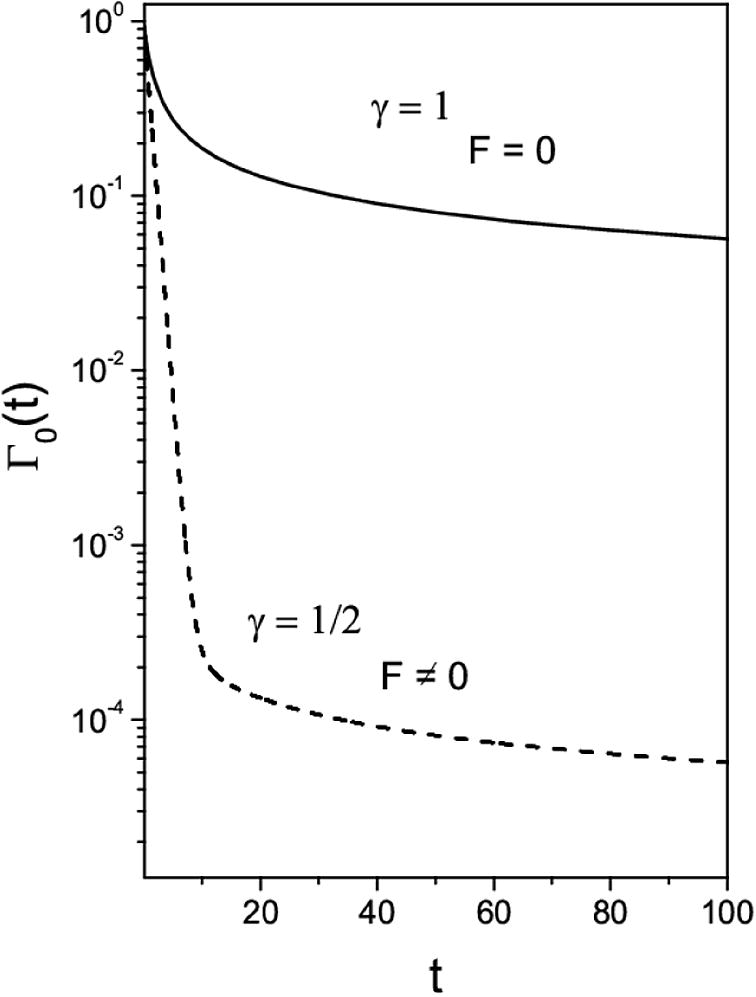
This figure shows the behavior of the Eq. (14) for two different values of γ with Γ0(0) = 1 and φ(x) = 0. For simplicity, Kγ = 1, F = 103, κ = 1, and τ = 1.

3 Discussion and conclusion

We have investigated the solutions for a fractional diffusion equation subjected to a constant external field with nonusual boundary conditions which can be connected to an adsorption and desorption processes. We obtained exact and approximated analytical solutions in the Laplace domain in order to evidence the effect of the external force. In Fig. 2, we illustrated the effect of the index γ on the desorption process, leading us to an asymptotic behavior different from the exponential. Fig. 3 shows the effect of the external field and index γ. The results presented here may be useful to discuss sorption and desorption processes when nonconventional dynamics aspects are present.

Acknowledgement

The authors are thankful to CNPq and CAPES (Brazilian agencies) for financial support.

References

Barbero G., Evangelista L.R., . Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals (first ed.). London: Taylor & Francis; 2006.
ben-Avraham D., Havlin S., . Diffusion and Reactions in Fractals and Disordered Systems (first ed.). Cambridge: Cambridge University Press; 2005.
Brangwynne C.P., Koenderink G.H., MacKintosh F.C., Weitz D.A., . Intracellular transport by active diffusion. Trends Cell Biol.. 2009;19:423-427.
[Google Scholar]
Bressloff P.C., Newby J.M., . Stochastic models of intracellular transport. Rev. Mod. Phys.. 2013;85:135-196.
[Google Scholar]
Bruno L., Levi V., Brunstein M., Desposito M.A., . Transition to superdiffusive behavior in intracellular actin-based transport mediated by molecular motors. Phys. Rev. E.. 2009;80:011912
[Google Scholar]
Caputo M., Cametti C., . The memory formalism in the diffusion of drugs through skin membrane. J. Phys. D: Appl. Phys.. 2009;42:12505
[Google Scholar]
Caputo M., Cametti C., Ruggero V., . Time and spatial concentration profile inside a membrane by means of a memory formalism. Phys. A. 2008;387:2010-2018.
[Google Scholar]
Caspi A., Granek R., Elbaum M., . Enhanced diffusion in active intracellular transport. Phys. Rev. Lett.. 2000;85:5655-5658.
[Google Scholar]
Condamin S., Tejedor V., Voituriez R., Bénichou O., Klafter J., . Probing microscopic origins of confined subdiffusion by first-passage observables. Proc. Natl. Acad. Sci. U.S.A.. 2008;105:5675-5680.
[Google Scholar]
Crank J., . The Mathematics of Diffusion (first ed.). Oxford: Oxford Science Publications; 1975.
Eliazar I.I., Shlesinger M.F., . Fractional motions. Phys. Rep.. 2013;527:101-129.
[Google Scholar]
Garrod C., . Statistical Mechanics and Thermodynamics (first ed.). Oxford: Oxford University Press; 1995.
Hilfer R., Metzler R., Blumen A., Klafter J., . Strange Kinetics, Chemical Physics (first ed.). Amsterdam: Pergamon-Elsevier; 2004.
Jiang H., Cheng Y., Tuan L., An F., Jin K., . A fractal theory based fractional diffusion model used for the fast desorption process of methane in coal. Chaos. 2013;23:033111
[Google Scholar]
Klafter J., Sokolov I.M., . First Steps in Random Walks: From Tools to Applications (first ed.). Oxford: Oxford University Press; 2011.
Kosztolowicz T., Dworecki K., Lewandowska K.D., . Subdiffusion in a system with thin membranes. Phys. Rev. E.. 2012;86:021123
[Google Scholar]
Langlands T.A.M., Henry B.I., . Fractional chemotaxis diffusion equations. Phys. Rev. E.. 2010;81:051102
[Google Scholar]
Leijnse N., Jeon J.-H., Loft S., Metzler R., Oddershede L.B., . Diffusion inside living human cells. Eur. Phys. J. Spec. Top.. 2012;204:75-84.
[Google Scholar]
Lenzi E.K., Yednak C.A.R., Evangelista L.R., . Non-Markovian diffusion and the adsorption–desorption process. Phys. Rev. E. 2010;81:011116
[Google Scholar]
Lyklema J., . Fundamentals of Interface and Colloid Sciences (first ed.). London: Academic Press; 1993.
Mathai A.M., Saxena R.K., Haubold H.J., . The H-Function: Theory and Applications (first ed.). New York: Springer; 2009.
Metzler R., Klafter J., . The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep.. 2000;339:1-77.
[Google Scholar]
Metzler R., Klafter J., . The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A: Math. Gen.. 2004;37:R161-R208.
[Google Scholar]
Podlubny I., . Fractional Differential Equations (first ed.). San Diego: Academic Press; 1999.
Robson A., Burrage K., Leake M.C., . Inferring diffusion in single live cells at the single-molecule level. Philos. Trans. R. Soc. B.. 2013;368:20120029
[Google Scholar]
Siepmann J., Peppas N.A., . Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC) Adv. Drug Delivery Rev.. 2001;48:139-157.
[Google Scholar]
Siepmann J., Siepmann F., . Mathematical model of drug delivery. Int. J. Pharm.. 2008;364:328-343.
[Google Scholar]
Siepmann J., Siepmann F., . Modeling of diffusion controlled drug delivery. J. Controlled Release. 2012;161:351-362.
[Google Scholar]
Sokolov I.M., . Models of anomalous diffusion in crowded environments. Soft Matter. 2012;8:9043-9052.
[Google Scholar]
Weber S.C., Spakowitz A.J., Theriot J.A., . Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc. Natl. Acad. Sci. U.S.A.. 2012;109:7338-7343.
[Google Scholar]
Weigel A.V., Simon B., Tamkun M.M., Krapf D., . Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. U.S.A.. 2011;108:6439-6443.
[Google Scholar]
Yan S.-P., . Local fractional Laplace series expansion method for diffusion equation arising in fractal heat transfer. Therm. Sci.. 2015;19(S1):S131-S135.
[Google Scholar]
Yang X.-J., Baleanu D., Baleanu M.-C., . Observing diffusion problems defined on cantor sets in different co-ordinate systems. Therm. Sci.. 2015;19(S1):S151-S155.
[Google Scholar]
Yang X.-J., Baleanu D., Srivastava H.M., . Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett.. 2015;47:54-60.
[Google Scholar]
Yang X.-J., Baleanu D., Zhong W.-P., . Approximate solutions for diffusion equations on Cantor space-time. Proc. Rom. Acad., Ser. A.. 2013;14(2):127-133.
[Google Scholar]

Introduction

Diffusion equation and adsorption–desorption

Discussion and conclusion

Fulltext Views
2

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Barbero G., Evangelista L.R., . Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals (first ed.). London: Taylor & Francis; 2006.

[2] ben-Avraham D., Havlin S., . Diffusion and Reactions in Fractals and Disordered Systems (first ed.). Cambridge: Cambridge University Press; 2005.

[3] Brangwynne C.P., Koenderink G.H., MacKintosh F.C., Weitz D.A., . Intracellular transport by active diffusion. Trends Cell Biol.. 2009;19:423-427.
[Google Scholar]

[4] Bressloff P.C., Newby J.M., . Stochastic models of intracellular transport. Rev. Mod. Phys.. 2013;85:135-196.
[Google Scholar]

[5] Bruno L., Levi V., Brunstein M., Desposito M.A., . Transition to superdiffusive behavior in intracellular actin-based transport mediated by molecular motors. Phys. Rev. E.. 2009;80:011912
[Google Scholar]

[6] Caputo M., Cametti C., . The memory formalism in the diffusion of drugs through skin membrane. J. Phys. D: Appl. Phys.. 2009;42:12505
[Google Scholar]

[7] Caputo M., Cametti C., Ruggero V., . Time and spatial concentration profile inside a membrane by means of a memory formalism. Phys. A. 2008;387:2010-2018.
[Google Scholar]

[8] Caspi A., Granek R., Elbaum M., . Enhanced diffusion in active intracellular transport. Phys. Rev. Lett.. 2000;85:5655-5658.
[Google Scholar]

[9] Condamin S., Tejedor V., Voituriez R., Bénichou O., Klafter J., . Probing microscopic origins of confined subdiffusion by first-passage observables. Proc. Natl. Acad. Sci. U.S.A.. 2008;105:5675-5680.
[Google Scholar]

[10] Crank J., . The Mathematics of Diffusion (first ed.). Oxford: Oxford Science Publications; 1975.

[11] Eliazar I.I., Shlesinger M.F., . Fractional motions. Phys. Rep.. 2013;527:101-129.
[Google Scholar]

[12] Garrod C., . Statistical Mechanics and Thermodynamics (first ed.). Oxford: Oxford University Press; 1995.

[13] Hilfer R., Metzler R., Blumen A., Klafter J., . Strange Kinetics, Chemical Physics (first ed.). Amsterdam: Pergamon-Elsevier; 2004.

[14] Jiang H., Cheng Y., Tuan L., An F., Jin K., . A fractal theory based fractional diffusion model used for the fast desorption process of methane in coal. Chaos. 2013;23:033111
[Google Scholar]

[15] Klafter J., Sokolov I.M., . First Steps in Random Walks: From Tools to Applications (first ed.). Oxford: Oxford University Press; 2011.

[16] Kosztolowicz T., Dworecki K., Lewandowska K.D., . Subdiffusion in a system with thin membranes. Phys. Rev. E.. 2012;86:021123
[Google Scholar]

[17] Langlands T.A.M., Henry B.I., . Fractional chemotaxis diffusion equations. Phys. Rev. E.. 2010;81:051102
[Google Scholar]

[18] Leijnse N., Jeon J.-H., Loft S., Metzler R., Oddershede L.B., . Diffusion inside living human cells. Eur. Phys. J. Spec. Top.. 2012;204:75-84.
[Google Scholar]

[19] Lenzi E.K., Yednak C.A.R., Evangelista L.R., . Non-Markovian diffusion and the adsorption–desorption process. Phys. Rev. E. 2010;81:011116
[Google Scholar]

[20] Lyklema J., . Fundamentals of Interface and Colloid Sciences (first ed.). London: Academic Press; 1993.

[21] Mathai A.M., Saxena R.K., Haubold H.J., . The H-Function: Theory and Applications (first ed.). New York: Springer; 2009.

[22] Metzler R., Klafter J., . The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep.. 2000;339:1-77.
[Google Scholar]

[23] Metzler R., Klafter J., . The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A: Math. Gen.. 2004;37:R161-R208.
[Google Scholar]

[24] Podlubny I., . Fractional Differential Equations (first ed.). San Diego: Academic Press; 1999.

[25] Robson A., Burrage K., Leake M.C., . Inferring diffusion in single live cells at the single-molecule level. Philos. Trans. R. Soc. B.. 2013;368:20120029
[Google Scholar]

[26] Siepmann J., Peppas N.A., . Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC) Adv. Drug Delivery Rev.. 2001;48:139-157.
[Google Scholar]

[27] Siepmann J., Siepmann F., . Mathematical model of drug delivery. Int. J. Pharm.. 2008;364:328-343.
[Google Scholar]

[28] Siepmann J., Siepmann F., . Modeling of diffusion controlled drug delivery. J. Controlled Release. 2012;161:351-362.
[Google Scholar]

[29] Sokolov I.M., . Models of anomalous diffusion in crowded environments. Soft Matter. 2012;8:9043-9052.
[Google Scholar]

[30] Weber S.C., Spakowitz A.J., Theriot J.A., . Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc. Natl. Acad. Sci. U.S.A.. 2012;109:7338-7343.
[Google Scholar]

[31] Weigel A.V., Simon B., Tamkun M.M., Krapf D., . Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. U.S.A.. 2011;108:6439-6443.
[Google Scholar]

[32] Yan S.-P., . Local fractional Laplace series expansion method for diffusion equation arising in fractal heat transfer. Therm. Sci.. 2015;19(S1):S131-S135.
[Google Scholar]

[33] Yang X.-J., Baleanu D., Baleanu M.-C., . Observing diffusion problems defined on cantor sets in different co-ordinate systems. Therm. Sci.. 2015;19(S1):S151-S155.
[Google Scholar]

[34] Yang X.-J., Baleanu D., Srivastava H.M., . Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett.. 2015;47:54-60.
[Google Scholar]

[35] Yang X.-J., Baleanu D., Zhong W.-P., . Approximate solutions for diffusion equations on Cantor space-time. Proc. Rom. Acad., Ser. A.. 2013;14(2):127-133.
[Google Scholar]