Data availability statement

The data used for this paper analysis has been included and cited within this paper. The digraphs are drawn manually according to the proposed algorithm.

1 Introduction

Utilizing network models is a highly effective approach for addressing various decision-related issues, as many problems can be accurately and efficiently modelled as network optimization problems. Network analysis and network flow theory constitute a well-researched area of optimization, with substantial connections to diverse fields such as combinatorial mathematics, algebraic topology, and circuit theory. Vella (2005) laid the ground work for introducing topological characteristics to graph theory. Aljanabi and Jasim (2015), published a strategy for solving transportation problems using a modified Kruskal's algorithm. Santhi and Eswarasamy (2019), proposed a topological solution to a transportation problem using a topologized graph. Vimala and Kalpana (2017), introduced the Bipartition Graph concept and applied it to graph matching and coloring.

According to Zadeh (1965) fuzzy set theory, each element's level of involvement in an ambiguity problem is represented by a degree of membership function. Smarandache (1998) in neutrosophic logic, a proposition has degrees of membership functions for truth (T), indeterminacy (I), and falsity (F). Smarandache (1998) initially formulated the concept of a neutrosophic probability set and logic. Atanassov and Atanassov (1999), the extension of a fuzzy set and the intuitionistic fuzzy set gives rise to the concept of a neutrosophic set and the concept of a NS serves as a generalization of fuzzy set theory, Atanassov and Gargov (1989), intuitionistic fuzzy set theory, and Turksen (1986) interval-valued intuitionisitic fuzzy set theory. Smarandache (2010), NS involve only truth, indeterminacy, and falsity membership degrees, encapsulated within the standard or non-standard unit interval [−0, 1+]. Dijkstra’s (1959) delivered two problems with solutions using graphs.

In a related context, Ekanayake et al. (2021), utilized the graph contraction technique for balanced transportation problems to identify the shortest path in transportation network problems with limited iterations. Furthermore, Johnson et al. (2018), applied the bipartition graph concept, finding the shortest path for Linear Programming Problems (LPP) by transforming a bipartite graph with both balanced and unbalanced TP.

Kavitha and Pandian (2012), investigated the Type II sensitivity analysis for assignment problems in solid transportation, through illustrative examples. Thamaraiselvi and Santhi (2016), proposed a novel approach to determining the optimal value in a real-world transportation problem within a neutrosophic framework, employing the VAM method. Souhail Dhouib (2021), introduced an innovative method, named as Dhouib matrix-TP1, to address a single-valued NTP where transportation unit costs are represented as trapezoidal neutrosophic numbers, and supply and demand are treated as unit costs. Wang et al. (2010), presented a design for SVNS through theoretical proof. Wang and Zhang (2018), discussed about two SVNS covering rough sets and its application to decision making problems. Broumi et al. (2016a,b,c,d), The characteristics of SVN graphs and score functions, as well as their application in isolated SVN graphs, were elucidated in their works.

Kandasamy et al. (2015), regarding the fundamental definitions, characteristics, and outcomes associated with neutrosophic sets, specifically focusing on the definitions of single-valued neutrosophic sets and bipartite neutrosophic graphs. Broumi et al. (2016a,b,c,d), conducted a theoretical examination in their work, exploring the degree, order, and size of SVN graphs and detailing their determination through score functions and ordering based on fundamental definitions. In another contribution, Broumi et al. (2016a,b,c,d), proposed computational concepts to address various issues in SVN networks, applying these concepts to determine the shortest path using a ranking approach. Additionally, Smarandache (2020), presented a study intended to guide researchers in implementing score, accuracy, and certainty functions, as well as calculating a total order on the set of neutrosophic triplets across various domain and also provided basic information and understanding of score function implementation in NS theory in detail. Kanchana and Kavitha (2024), presented about score functions that can be used for graph algorithms and proposed heuristic incident edge path algorithm for interval valued neutrosophic transportation problem for finding minimum cost in uncertain environment.

Smarandache and Pramanik (2016), New trends in neutrosophic sytems a editorial volume discusses; in practical applications within engineering and scientific fields, implementing the principle of a neutrosophic set proves challenging; The application of the neutrosophic set concept is particularly complex in natural, engineering, and scientific domains. Nevertheless, the neutrosophic set idea provides an effective means of handling uncertain, inadequate, incompatible, and inconclusive data more accurately; Due to this characteristic, neutrosophic set theory implemented in all fields to rectify the uncertainty.

2 Preliminaries

Definition 1 (Dhouib, 2021): Consider $U$ to be a space of objects. The set $\overline{X}$ is neutrosophic, containing an object $x$ defined by $\overline{X}=\{\langle x:T_{\overline{X}},I_{\overline{X}},F_{\overline{X}}\rangle ,x\in U\}$ . The functions representing the degree of truth membership $T_{\overline{X}}$ , degree of indeterminacy $I_{\overline{X}}$ , and degree of falsity membership $F_{\overline{X}}$ , respectively, in relation to set $\overline{X}$ , with the conditions $0\le T_{\overline{X}},I_{\overline{X}},F_{\overline{X}}\le 1$ and $0^{-}\le \langle T_{\overline{X}},I_{\overline{X}},F_{\overline{X}}\rangle \le 3^{+}$ .

Logically, the NS takes into account points from a real non-standard or standard subset. However, for practical applications, especially in technological disciplines, the interval $[0,1]$ is often utilized, because it is more possible to apply in real-life settings such as engineering and scientific network difficulties.

Definition 2 (Atanassov and Gargov, 1989): Consider $U$ as a universe of discourse containing global objects denoted by $x$ . A single-valued neutrosophic set is defined by the global elements of a set $\overline{X}$ . The SVNS is represented as $\overline{X}=\{\langle x:T_{\overline{X}},I_{\overline{X}},F_{\overline{X}}\rangle ,x\in U\}$ , where $T_{\overline{X}},I_{\overline{X}},F_{\overline{X}}$ are the degrees of truth, indeterminacy, and falsity membership respectively.

Definition 3 (Dhouib, 2021): Let $\overline{X}=\langle \left({\overline{X}}_a,{\overline{X}}_b,{\overline{X}}_c,{\overline{X}}_d\right);T_{\overline{X}},I_{\overline{X}},F_{\overline{X}}\rangle$ , be a trapezoidal single-valued neutrosophic number, and the truth, indeterminacy, and falsity membership functions $\overline{X}$ are defined as follows,

Eq. (10) is used to de-neutrosophication of TSVNN to compare the edge weights. The boundedness and monotonicity of Eqs. (10) and (11) are defined as follows;

Monotonicity:

• $S\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)$ increases depending on ${\overline{N}}_a,{\overline{N}}_b,{\overline{N}}_c,{\overline{N}}_d(\because S\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)\propto \left({\overline{N}}_a,+{\overline{N}}_b+{\overline{N}}_c+{\overline{N}}_d\right))$

• $S\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)$ increases as $T_{\overline{N}}$ increases and increases as $I_{\overline{N}},F_{\overline{N}}$ decreases $(\because \left(1-I_{\overline{N}}\right)and\left(1-F_{\overline{N}}\right))$

• $A\left({\overline{c}}_{\mathit{ij}}^{\overline{N}}\right)$ increases as minimum of ${\mu }_{{\overline{c}}_{\mathit{ij}}^{\overline{N}}},{\nu }_{{\overline{c}}_{\mathit{ij}}^{\overline{N}}}and1-{\lambda }_{{\overline{c}}_{\mathit{ij}}^{\overline{N}}}$ increases.

• $A\left({\overline{c}}_{\mathit{ij}}^{\overline{N}}\right)$ increases as $S\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)$ is monotonic.

Boundedness:

• $S\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)\propto \left({\overline{N}}_a,+{\overline{N}}_b+{\overline{N}}_c+{\overline{N}}_d\right)$ and ${\overline{N}}_a,{\overline{N}}_b,{\overline{N}}_c,{\overline{N}}_d$ are not constrained to $\left[0,1\right].$

• $A\left({\overline{c}}_{\mathit{ij}}^{\overline{N}}\right)$ is not naturally bounded since adding up minimum of ${\mu }_{{\overline{c}}_{\mathit{ij}}^{\overline{N}}},{\nu }_{{\overline{c}}_{\mathit{ij}}^{\overline{N}}}and1-{\lambda }_{{\overline{c}}_{\mathit{ij}}^{\overline{N}}}$ which give rise to unbound.

The score and accuracy functions are normalized to make the boundedness within the range [0, 1]. Monotonic behaviour of both score and accuracy remains unchanged before and after normalization. For NS theory it is not strictly necessary that the accuracy must be within [0, 1] range. Since, it involves sum of weights, costs, distance, etc., and the truth, indeterminacy and falsity membership values have the range in total as [0, 3] (refer definition 1).

Example: Consider the following TSVNN, $$\begin{array}{c}\overline{N}=<\left(5,4,6,7\right),0.6,0.8,0.4>\hfill \\ ({\overline{N}}_a=5,{\overline{N}}_b=4,{\overline{N}}_c=6,{\overline{N}}_d=7;T_{\overline{N}}=0.6,I_{\overline{N}}=0.8,F_{\overline{N}}=0.4)\hfill \end{array}$$

The score value and accuracy values as follows,

$S\left(\overline{N}\right)=1.925$ and normalized score value. $S^{\prime }\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)=\frac{1.925}{2}=0.9625\in [0,1]$

$A\left(\overline{N}\right)=2.0\times 1.375=2.75$ for ${\mu }_{\overline{N}}=0.6,{\nu }_{\overline{N}}=0.8,and1-{\lambda }_{\overline{N}}=0.6$ . $$A^{\prime }\left(\overline{N}\right)=0.9167\in [0,1]$$

Throughout this article we use $S\left({{\overline{c}}_{\mathit{ij}}}^{\overline{N}}\right)$ before normalization for changing TSVNN into crisp data only.

Definition 6 (Kandasamy et al., 2015): Let $\overline{N}$ be a neutrosophic graph and $\overline{N}$ is partitioned into two neutrosophic sub graphs ${\overline{N}}_{1}and{\overline{N}}_2$ such that.

${\overline{N}}_1\cap {\overline{N}}_2=\phi$ and $\overline{N}={\overline{N}}_1\cup {\overline{N}}_2$ . A graph $\overline{N}$ is said to a bipartite neutrosophic graph if $\overline{N}$ admits a partition into two sub graphs such that each edge has one end in ${\overline{N}}_1$ and another end in ${\overline{N}}_2$ .

3 Algorithm: Bipartite neutrosophic graph contraction algorithm (BNGCA)

Step 1: Convert the LPP into a balanced transportation table with supply and demand. If it is not balanced, then balance the TP by adding dummy rows or columns to supply or demand, as needed. Use the score function to de-neutrosophicate the trapezoidal single-valued neutrosophic network's edge weights.

Step 2: Draw a bipartite neutrosophic graph for the balanced TP with de-neutrosophicated edge weights connecting supply and demand.

Step 3: Choose two minimum unit transportation costs (edge weights) from the bipartite neutrosophic graph connecting supply and demand.

Step 4: Pick the least edge weight with maximum supply and demand, and allocate to the respective edge depending on which has the minimum supply or demand.

Step 5: Remove edges connected to fully satisfied supply or demand nodes. Ensure the bipartite graph’s structure remains valid after the removal of edges.

Step 6: Repeat the process from Step 4 until all allocations are made and no edges remain.

3.1

3.1 Illustration

3.1.1

3.1.1 Trapezoidal single valued neutrosophic transportation problem

Let us assume a transportation problem in the shoe manufacturing process. Initially, the leather needed for making shoes must be collected from three sources namely $O_1,O_2$ and $O_3$ , delivered to four manufacturing industries located in different areas through transports $F_1,F_2,F_3$ and $F_4$ respectively. The TP involves trapezoidal neutrosophic supply, demand, and unit transportation costs, the problem is to calculate the optimum cost of delivering leather to the manufacturing industries at a minimum transportation cost.

Linear Programming Problem with supply and demand constraints, $$\mathit{Minimize}\overline{Z}={\sum }_{i=1}^3{\sum }_{j=1}^4{\overline{c}}_{\mathit{ij}}^{\overline{X}}{x}_{\mathit{ij}}$$

Supply constraints $$\langle \begin{array}{c}\left(3,5,6,8\right);\\ 0.6,0.5,0.4\end{array}\rangle x_{11}+\langle \begin{array}{c}\left(5,8,10,14\right);\\ 0.3,0.6,0.6\end{array}\rangle x_{12}+\langle \begin{array}{c}\left(12,15,19,22\right);\\ 0.6,0.4,0.5\end{array}\rangle x_{13}+\langle \begin{array}{c}\left(14,17,21,28\right);\\ 0.8,0.2,0.6\end{array}\rangle x_{14}\le 26,$$ $$\langle \begin{array}{c}\left(0,1,3,6\right);\\ 0.7,0.5,0.3\end{array}\rangle x_{21}+\langle \begin{array}{c}\left(5,7,9,11\right);\\ 0.9,0.7,0.5\end{array}\rangle x_{22}+\langle \begin{array}{c}\left(15,17,19,22\right);\\ 0.4,0.8,0.4\end{array}\rangle x_{23}+\langle \begin{array}{c}\left(9,11,14,16\right);\\ 0.5,0.4,0.7\end{array}\rangle x_{24}\le 24,$$ $$\langle \begin{array}{c}\left(4,8,11,15\right);\\ 0.6,0.3,0.2\end{array}\rangle x_{31}+\langle \begin{array}{c}\left(1,3,4,6\right);\\ 0.6,0.3,0.5\end{array}\rangle x_{32}+\langle \begin{array}{c}\left(5,7,8,10\right);\\ 0.5,0.4,0.7\end{array}\rangle x_{33}+\langle \begin{array}{c}\left(5,9,14,19\right);\\ 0.3,0.7,0.6\end{array}\rangle x_{34}\le 30.$$

Demand constraints $$\langle \begin{array}{c}\left(3,5,6,8\right);\\ 0.6,0.5,0.4\end{array}\rangle x_{11}+\langle \begin{array}{c}\left(0,1,3,6\right);\\ 0.7,0.5,0.3\end{array}\rangle x_{21}+\langle \begin{array}{c}\left(4,8,11,15\right);\\ 0.6,0.3,0.2\end{array}\rangle x_{31}\le 17,$$ $$\langle \begin{array}{c}\left(5,8,10,14\right);\\ 0.3,0.6,0.6\end{array}\rangle x_{12}+\langle \begin{array}{c}\left(5,7,9,11\right);\\ 0.9,0.7,0.5\end{array}\rangle x_{22}+\langle \begin{array}{c}\left(1,3,4,6\right);\\ 0.6,0.3,0.5\end{array}\rangle x_{32}\le 23,$$ $$\langle \begin{array}{c}\left(12,15,19,22\right);\\ 0.6,0.4,0.5\end{array}\rangle x_{13}+\langle \begin{array}{c}\left(15,17,19,22\right);\\ 0.4,0.8,0.4\end{array}\rangle x_{23}+\langle \begin{array}{c}\left(5,7,8,10\right);\\ 0.5,0.4,0.7\end{array}\rangle x_{33}\le 28,$$ $$\langle \begin{array}{c}\left(14,17,21,28\right);\\ 0.8,0.2,0.6\end{array}\rangle x_{14}+\langle \begin{array}{c}\left(9,11,14,16\right);\\ 0.5,0.4,0.7\end{array}\rangle x_{24}+\langle \begin{array}{c}\left(5,9,14,19\right);\\ 0.3,0.7,0.6\end{array}\rangle x_{34}\le 12.$$

3.1.2

3.1.2 De-neutrosophicated TSVNTP

The neutrosophic numbers of unit transportation costs are de-neutrosophicated using the following equation $$S\left({\overline{c}}_{\mathit{ij}}^{\overline{N}}\right)=\frac{1}{16}\times (\left({\overline{N}}_a+{\overline{N}}_b+{\overline{N}}_c+{\overline{N}}_d\right)\times \left(T_{\overline{N}}+\left(1-I_{\overline{N}}\right)+\left(1-F_{\overline{N}}\right)\right).$$

The de-neutrosophicated unit transportation costs of TP1 are displayed in Table 1. The NTP has been drawn as a bipartite neutrosophic graph, shown in Fig. 1, to apply the proposed algorithm.

Table 1 Transportation table for the LPP with de-neutrosophicated number.

	$\mathrm{F}1$	$\mathrm{F}2$	$\mathrm{F}3$	$\mathrm{F}4$	Supply
$\mathrm{O}1$	$2$	3	7	10	26
$\mathrm{O}2$	1	3	6	4	24
$\mathrm{O}3$	5	2	3	3	30
Demand	17	23	28	12	80

Close

Fig. 1

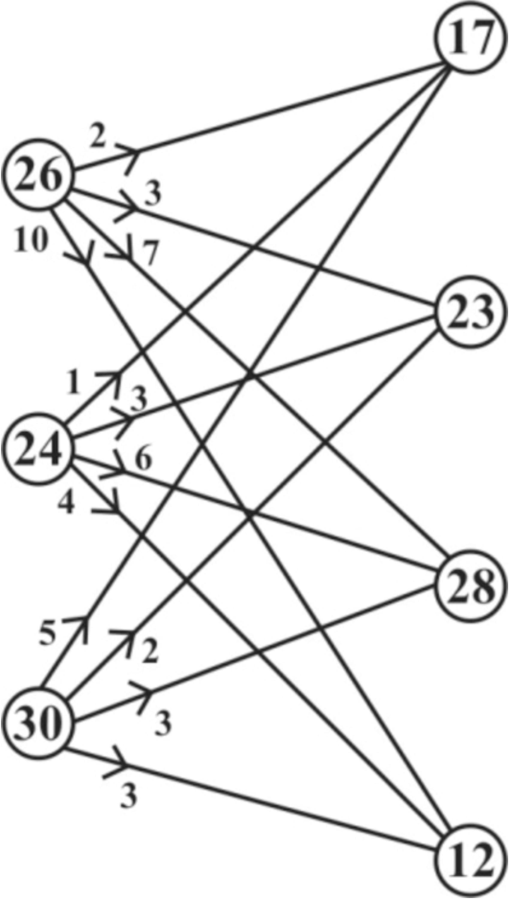
Bipartite neutrosophic graph with de-neutrosophicated edge weight.

Export to PPT

Figs. 2–4 illustrate the procedural steps of the proposed algorithm and the solution is obtained by BNGCA,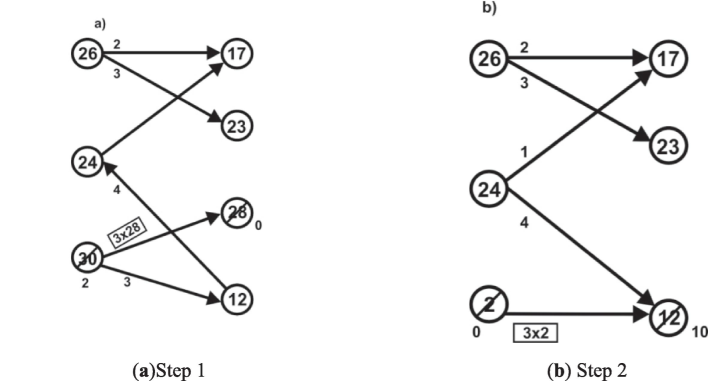

Close

Fig. 2

(a) Step 1, (b) Step 2.

Export to PPT

Close

Fig. 3

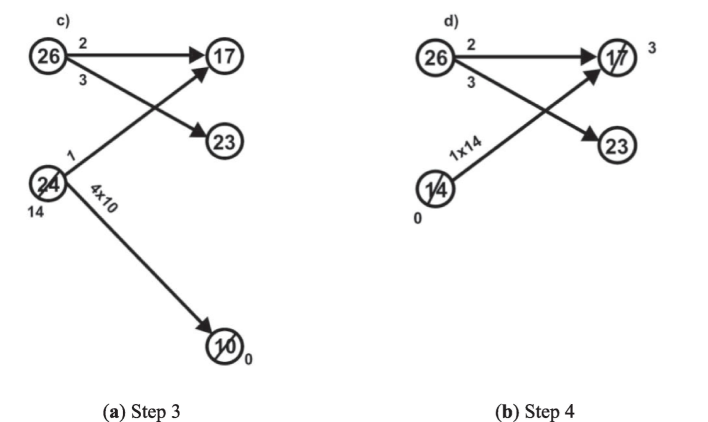
(a) Step 3, (b) Step 4.

Export to PPT

Close

Fig. 4

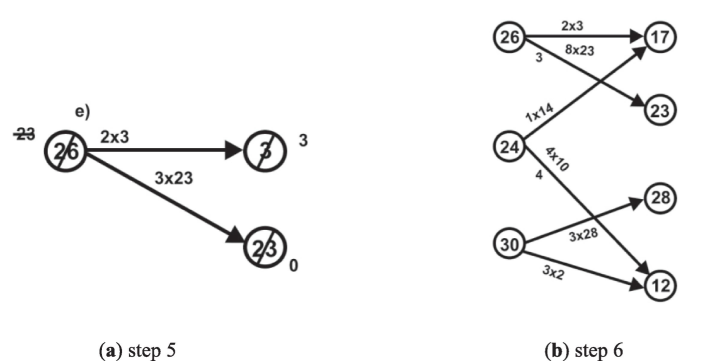
(a) step 5, (b) step 6.

Export to PPT

Step 6 forms a spanning tree with bipartite conditions, which provides the optimum result for the neutrosophic network, and leading to the final solutions, such as $x_{11}=3,x_{12}=23,x_{21}=14,x_{24}=10,x_{33}=28,x_{34}=2$ are the optimum solution being a minimum of $$\begin{array}{c}{\sum }_{i=1}^3{\sum }_{j=1}^4{\overline{c}}_{\mathit{ij}}^{\overline{X}}{x}_{\mathit{ij}}=23\left\{\langle \left(5,8,10,14\right);0.3,0.6,0.6\rangle \right\}+3\left\{\langle \left(3,5,6,8\right);0.6,0.4,0.5\rangle \right\}+14\left\{\langle \left(0,1,3,6\right);0.7,0.5,0.3\rangle \right\}\hfill \\ +10\left\{\langle \left(9,11,14,16\right);0.5,0.4,0.7\rangle \right\}+28\left\{\langle \left(5,7,8,10\right);0.5,0.4,0.7\rangle \right\}+2\left\{\langle \left(5,9,14,19\right);0.3,0.7,0.6\rangle \right\}\hfill \\ =\langle \left(364,537,682,908\right);0.3,0.7,0.7\rangle .\hfill \end{array}$$

3.3

3.3 Comparative study between proposed BGNCA and existing methods

Based on these computations, the cost values are expected to range from 364 to 908, corresponding to the maximum unit transportation costs outlined in Table 1. Tables 2 and 3 outlines the maximum allowable increase in unit transportation costs.The presented algorithm successfully addresses the linear programming problem associated with TSVNTP, sourced from Thamaraiselvi and Santhi (2016) and Souhail Dhouib (Dhouib, 2021). A comparison was made between the outcomes generated by BGNCA and the conventional zero-point allocation technique (Thamaraiselvi and Santhi, 2016), as well as Dhouib-Matrix-TP1 (Dhouib, 2021). The BGNCA proves to be highly advantageous, providing solutions within a limited iterations for TP1. Moreover, it is both easily comprehensible and straightforward to implement.

Comparison between the existing methods and proposed BNGCA:

a

• The neutrosophic basic feasible solution method – $\langle \left(370,543,694,938\right);0.3,0.7,0.7\rangle$

• Zero-point allocation by VAM – $\langle \left(364,537,694,908\right);0.3,0.7,0.7\rangle$

• Dhouib-Matrix-Tp1 – $\langle \left(370,537,683,908\right);0.3,0.8,0.8\rangle$

• Proposed BNGCA for TP1 – $\langle \left(364,537,694,908\right);0.3,0.7,0.7\rangle$

Fig. 5 depicts the visual representation of membership functions for truth, indeterminacy, and falsity in the context of TSVNTP. The illustration suggests that, by appropriately managing budget constraints, DM can achieve optimal cost ranges spanning from 364 to 908, based on the membership degrees of truth, indeterminacy, and falsity.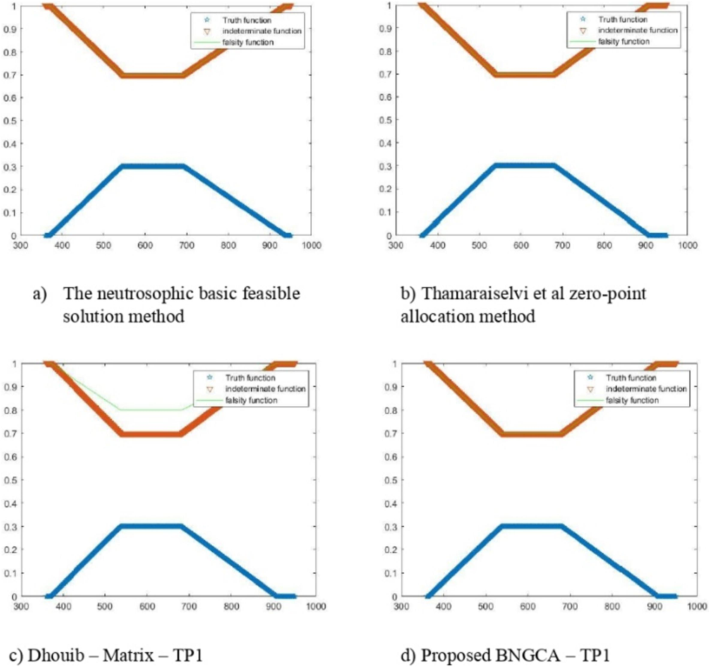

Close

Fig. 5

Graphical representation of membership functions of TSVNTP.

Export to PPT

4 Results and discussion

The proposed BNGCA for obtaining the optimal solution in LPP is both distinctive and effective. Its simplicity makes it easily comprehensible, while the computational process efficiently determines the indeterminacy transportation cost of the TSVNN. This method, BNGCA, is applicable to all indeterminacy transportation costs in SVNLPP that satisfy the conditions of a bipartite graph. Comparatively, the optimal neutrosophic solution $\langle \left(364,537,694,908\right);0.3,0.7,0.7\rangle$ outperforms the Dhouib-matrix-TP1 (Dhouib, 2021). The analysis indicates that the total minimum unit transportation cost falls between values greater than 364 and less than 908, and between values higher than 537 and less than 694.

The degrees of truth, indeterminacy, and falsity membership are as follows: $${\mu }_{\overline{X}}\left(a\right)=\left\{\begin{array}{c}0.3\left(\frac{a-364}{537-364}\right),for364\le a\le 537\\ 0.3,for537\le a\le 694\\ 0.3\left(\frac{908-a}{908-694}\right),for694\le a\le 908\\ 0,otherwise\end{array}\right.$$ $${\nu }_{\overline{X}}\left(a\right)=\left\{\begin{array}{c}\left(\frac{537-a+0.7(a-364)}{537-364}\right),for364\le a\le 537\\ 0.7,for537\le a\le 694\\ \left(\frac{a-636+0.7(908-a)}{908-694}\right),for694\le a\le 908\\ 1,otherwise\end{array}\right.$$ $${\lambda }_{\overline{X}}\left(a\right)=\left\{\begin{array}{c}\left(\frac{537-a+0.7(a-364)}{537-364}\right),for364\le a\le 537\\ 0.7,for537\le a\le 694\\ \left(\frac{a-694+0.7(908-a)}{908-694}\right),for694\le a\le 908\\ 1,otherwise\end{array}\right.$$ where ${\mu }_{\overline{X}}\left(a\right)\times 100$ is the degree of truthfulness, and a is the total cost,

In the referenced article (Thamaraiselvi and Santhi, 2016), the author employed the penalty and zero-point methods to determine the optimal cost. However, Souhail Dhouib challenged these assumptions and presented results using the DhouibMatrix-TP1 approach, which debunked the earlier findings (Dhouib, 2021). In contrast, the proposed BNGCA algorithm for NTP1 achieves the optimal value with minimal iterations, verified through sensitivity analysi. SA ensures that the allocated values in cells are accurate and the outcome is optimal.

The SA calculates the maximum cost range for all cells in TP1, revealing that the optimal cost remains unchanged within these limits. Additionally, the optimal values adhere to the critical conditions of trapezoidal neutrosophic numbers. According to the SA, the optimum value obtained by BNGCA is lower than that of DhouibMatrix-TP1. This difference becomes evident when conducting SA on the optimal cost transportation table in (Dhouib, 2021), where the unit transportation cost of cell (1, 1) in Table 1 fluctuates as $[4,\infty )$ from $[2,\infty )$ , contrary to the actual unit transportation cost.

5 Conclusion

The fundamental challenge in network problems is identifying the most economical and efficient path, known as the Shortest Path, from among various options. To address the need for minimizing both time complexity and cost, the bipartite neutrosophic graph contraction algorithm was proposed within the framework of the trapezoidal single-valued neutrosophic transportation problem network. This algorithm introduced a novel approach to the neutrosophic sets and demonstrated its effectiveness through practical network problem. Although, the score function used for de-neutrosophication was discussed for monotonicity and boundedness. Since it is not necessary that, the score and accuracy should be bounded between [0, 1]; because we use the costs, distance, time etc., as weights for NTP-1 as we were using score function for ranking. Eventhough, the monotonicity and boundedness were discussed for the purpose of neutrosophic arithmetic procedural problems.

A comparative analysis of BNGCA has highlighted its efficiency, showing that it produces high-quality results with minimal iterations. Specifically, BNGCA for TP1 has proven to be a simpler and more efficient solution compared to existing methodologies, offering significant improvements in both simplicity and performance also, the proposed method is applicable for type II NTP. To validate the optimal solution $\langle \left(364,537,694,908\right);0.3,0.7,0.7\rangle$ ’s robustness and effectiveness, sensitivity analysis was introduced as a novel approach to assessing results in neutrosophic set theory. By conducting SA without altering the optimal results, it improved the reliability and validity of the network problem analysis. This approach introduced a new dimension to result verification in the field of neutrosophic set theory, providing a more robust framework for evaluating the outcomes of network problems. The sensitivity report confirmed that the optimal solution remains unchanged within defined ranges, reinforcing the stability and reliability of the proposed method in solving network problems.

6 Future work

The proposed method will be applied to interval-valued neutrosophic set network problems also in type II neutrosophic transportation problem to identify the optimum solution. Additionally, future research will explore its application in Super Hyper Graphs and Neutrosophic Super Hyper Graphs.

CRediT authorship contribution statement

M. Kanchana: Writing – review & editing, Writing – original draft, Methodology, Formal analysis, Conceptualization. K. Kavitha: Supervision.