Quantum chemical calculations, spectroscopic properties and molecular docking studies of a novel piperazine derivative

2.1 Synthesis of (C₁₀H₁₆N₂)(NO₃)₂·H₂O

The mentioned molecule was prepared by dissolving 0.001 mol of the 1-phenylpiperazine compound in an ethanol–water solution (10 ml of ethanol in 20 ml of water). Thereafter, 0.002 mol of nitric acid was added. Brown monocrystals of (C₁₀H₁₆N₂)(NO₃)₂·H₂O of suitable size for a crystallographic study were formed after two days of slow evaporation (at room temperature). The synthesis reaction is as follows: C₁₀H₁₄N₂ + 2 HNO₃ + H₂O → (C₁₀H₁₆N₂)(NO₃)₂·H₂O

2.2 Spectroscopic and thermal measurements

The infrared measurements of 1PPNO₃ were determined by Perkin Elmer FT-IR Spectrophotometer in the scan region 4000–400 cm⁻¹. It was synthesized by using pellets enclosing the sample in question and KBr as a dispersant with 1.0 cm⁻¹ resolution.

The thermal analyses (DTA/TG and DSC) of 1PPNO3 were performed by means of a multimodule 92 Setaram analyzer with an average heating rate of 5 K/min under an argon atmosphere on a sample of mass m = 11.90 mg for DTA/TG and m = 4.90 mg for DSC

4.1 Geometrical structure

The geometric structure of 1-phenylpiperazin-1,4-diium nitrate monohydrate has been optimized with the Density functional theory (DFT) method using B3LYP-D and WB97XD levels of theory with 6-311++G** basis set (Fig. 1). Dispersion parameter is added to account for long range interactions (VDW). It provides energy corrections. The absence of imaginary frequencies confirms that the optimized structure corresponds to the minimum area of potential energy. Results reveal that the global minimum energy obtained by WB97XD is equal to −30945 eV (as seen in Table S1), whereas the value calculated by B3LYP-D was found to be −30955 eV (in the gas phase). In water, the lowest energy value is found also with B3LYP-D (E = −30957 eV). From the obtained energy values, it can be seen that with the functional B3LYP-D, 1PPNO₃ is slightly more stable. Otherwise, the dipole moment is in the order of 10.222 D and 10.257 D using B3LYP-D and WB97XD, respectively in the gas. Whereas, when we take into account the solvation (water), we found that the dipole moment value increases (32.112 and 23.140 Debye). This augmentation of the dipole moment promotes the formation of the hydrogen bond interactions. Furthermore, the dipole moment can impact the interaction between the receptor and the ligand.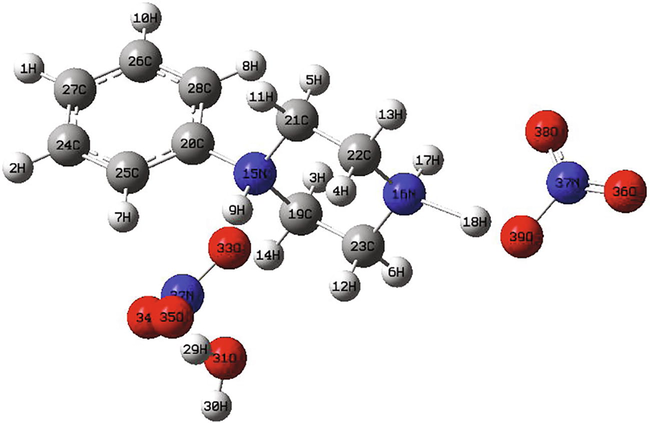

Close

Fig. 1

The optimized structure of (C₁₀H₁₆N₂)(NO₃)₂·H₂O molecule obtained from WB97XD/6-311++G** in gas phase.

Export to PPT

The geometric parameters of 1PPNO3 optimized by the methods B3LYP-D/6-311++G** WB97XD/6-311++G**, compared with the experimental values are listed in Table 1 and S2. These results are discussed in terms of RMSD (Root Mean Square Deviation). The RMSD value is equal to 0.1606 Å using WB97XD and 0.1645 Å using B3LYP-D functional (in the gas phase). As clearly seen, the low RMSD values are noticed by using WB97XD/6-311++G** basis sets. We notice that the value of RMSD decreases in water (RMSD_WB97XD = 0.1054 Å; RMSD_B3LYP-D = 0.1351 Å). The inspection of this table shows that the calculated distances have provided an excellent agreement with the experimental value based on the value of RMSD. So, from these results we can conclude that WB97XD functional is more reliable than B3LYP-D. We can therefore admit that this method has well optimized the geometry of the determined structural model. Thereby, we continue our calculation by WB97XD functional at 6-311++G** level of theory.

Indeed, a phenylpiperazine molecule consists of an aromatic ring which is phenyl (–C₆H₅) linked to one of the nitrogen atoms of piperazine ring (C₄H₁₀N₂) which is perpendicular to phenyl group. This compound has been utilized as a ligand in several complexes (Gatfaoui et al., 2020, 2014). The calculated bond lengths of the phenyl ring (C–C) vary between 1.3857 Å and 1.3908 Å (Table 1). Also, two independent nitrates (NO₃ groups exist in our molecule. This group consists of one nitrogen and three oxygen atoms, which form a plane; the average deviation from its mean plane is ±0.000000 Å. These two nitrate groups are attached to each other via the water molecule through hydrogen bonds (as shown in Fig. S1). By examining the interatomic distances between the different entities, we can determine the geometric characteristics of the hydrogen bonds. Results reveal several types of interactions: the O – H… O interaction which establish the links between the water molecules and the nitrate ions. From the determined values of the bond distance O–H and the bond angles O–H…O, we can see that our compound has medium strong hydrogen bonds. Also, N–H… O bond ranging from 2743 to 3180 Å which ensure the anchoring of organic molecules to the group [(NO₃)₂·H₂O]. C–H… O interaction with the donor–acceptor distances varying between 3.198 and 3.415 Å relatively long in comparison with those of type O (N)… O.

4.2 Topological analysis

This work reviews the most essential contributions to the study of the localization of electrons performed by using the Atoms In Molecules theory and the Electron Localization Function. We will discuss the most pertinent applications of the AIM and ELF examining to the study of the chemical bond and electronic structure.

4.2.2

4.2.2 Analysis of the electron localization function

The electron localization function (ELF) was introduced by Becke and Edgecombe (Becke and Edgecombe, 1990) to describe the chemical bond for approximately all classes of compounds. The topological analysis of the ELF function allows a partition of the molecular space not in atomic basin as in Bader's theory, or in regions of charge concentration, but in basins of electronic localization within which the excess of kinetic energy due to Pauli repulsion is minimum. This approach is capable of generating easily understandable images. Its graphed language earns it to determine the nature chemical bond. ELF gives very meaningful, easily comprehensible, and visually informative patterns of the chemical bonds. The 2D representation of the ELF isosurface for 1PPNO₃ compound has been carried out using Multiwfn program. This function can be projected on to a very precise plane of the crystal structure considered. Fig. 2 shows the evolution of ELF along the molecular axis for N₁₅, N₁₆, N₃₇ atoms. Another ELF surface map, on the plane of O₃₁, N₁₆, O₃₆ atoms, is plotted as shown in supplementary Fig. S3-a. The dashed lines show the regions that have decrease in electron density, while Fig. S3-b represents a colored ELF map. The blue color circle and particularly dark blue circle represent a depletion region between inner shell and valence shell. As it is shown, the carbon and the hydrogen regions have the minimum values of the localized orbital locator. A strong electronic localization is seen around the oxygen atoms (red and orange color) (Fig. S4).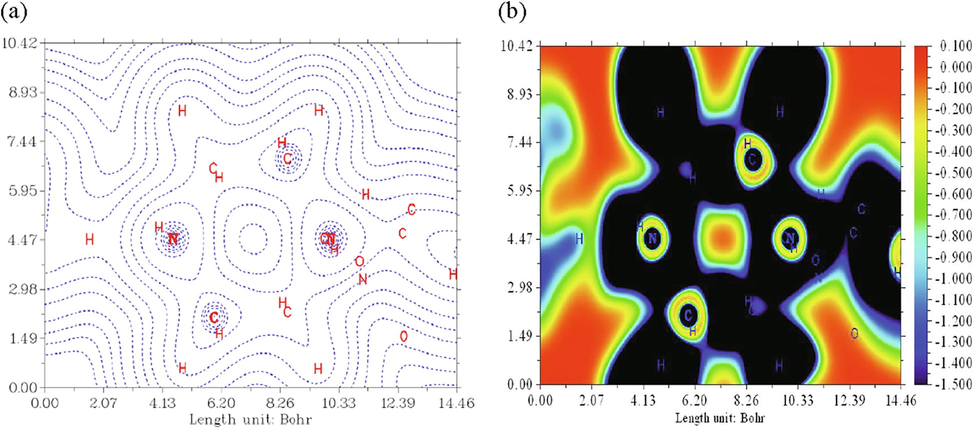

Close

Fig. 2

Electron localization function (ELF) maps of 1PPNO₃ along the molecular axis for N₁₅, N₁₆, N₃₇ atoms compound.

Export to PPT

4.2.3

4.2.3 NCI-RDG analysis

Reduced density gradient (RDG) is an approach to determine the nature of interactions, in particular non-covalent interactions (NCI). Owing to their important properties, NCI have attracted growing attention. Intermolecular interactions make it possible to understand how the molecules interacted and constitute biological organisms. It allows a description of H-bond, steric effect and van der Waals interactions. In Fig. 3, we present the classification of the different interactions of 1PPNO₃ compound, by giving a simple color code to distinguish between the different regions. The results were carried out and plotted by using Multiwfn and VMD programs. Fig. 3a illustrates the evolution of the RDG (a.u) as a function of the product sign of λ₂ time’s density (ρ). λ₂ represent the greatest eigenvalue of Hessian matrix. It characterizes the fluctuation of the electron density near the critical point. With the signλ_{2 *} ρ, we can discriminate between the three regions. So, we have tried to understand the nature of strength of the different interactions presenting in our compound. The strength and type of bond are related to the values of electron density and the Laplacian sign of electron density at critical points. Blue, red and green color codes are utilized to describe stabilizing H-bond, destabilizing steric and VDW interactions, respectively. As shown, the regions corresponding to the hydrogen bond (weak interaction) and the steric effect have a high density, while the van der Waals interaction zones have a low density. As clearly seen, these interactions appear as regions marked respectively by blue, red and green colors (Fig. 3b). A clear blue spot is checked between the hydrogen–oxygen- and the hydrogen–nitrogen atoms, which indicate the strong attractive interactions O…H–N and N…H–O (Table 2). The elliptic red plate situated at the center of the two rings is attributed to describe destabilizing steric interaction. The green plates indicate the weak interaction region situated between the hydrogen atoms, which is associated to VDW interactions. The graphical visualization of the NCI between two organic cations involved in a CH/π bond is given in Fig. 4. The benzene cycle of the phenylpiperazine cation is perfectly planar, since its average deviation from its mean plane is ±0.000311 Å. The two anti-parallel benzene rings are separated by a distance equal to 5.552 Å, which is fairly long to generate π-π interactions. But, between the two organic groups we notice the existence of CH/π interaction. If we compare this distance with the distances found in my previous work, where we studied two other phenylpiperazine derivatives “1-phenylpiperazine-1,4-diium bis(hydrogen sulfate)” (Noureddine et al., 2020a) and “4-phenylpiperazine-1-ium dihydrogen phosphate” (Noureddine et al., 2020b), we find that d_1PPNO3 = 5.552 Å> d_4PPHP = 4.870 Å> d_1PPHS = 3.985 Å.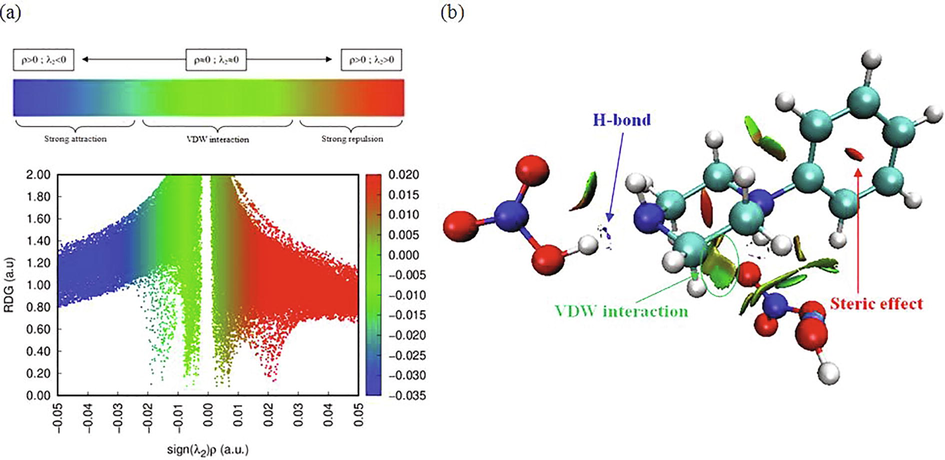

Close

Fig. 3

Classification of the different interactions of 1PPNO₃.

Export to PPT

Close

Fig. 4

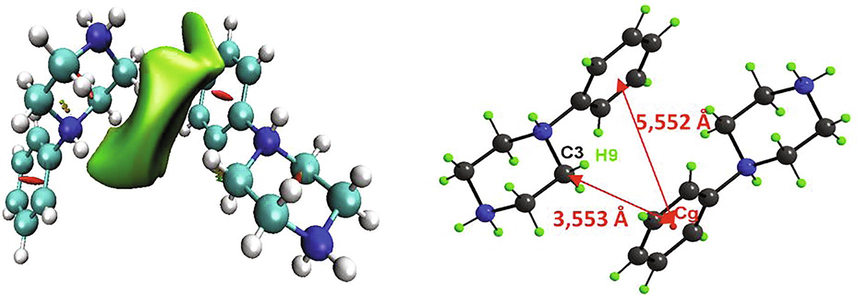
Different interactions between two organic cations involved in a CH/π bond.

Export to PPT

4.3 NBO and Mulliken charges analysis

Natural Bond Orbital (NBO) analysis is deemed as one of the most prevalent methods for examining the electronic transitions and the mutual interactions in molecular systems, especially for studying intra and intermolecular hydrogen bonding. Therefore, the interacting stabilization energy E⁽²⁾ is the most essential parameter to study the interactions between electron donors and acceptors. $$E^{\left(2\right)}=\mathrm{\Delta }{E}_{\mathit{ij}}=\frac{q_{i}F(i,j)}{{\epsilon }_i-{\epsilon }_j}$$

q_i: represents the occupation of the donor orbital; F (i, j): represents the operator of Fock and ε_i, ε_j: represent the energies of the NBO orbitals.

NBO analysis has been performed by using WB97XD/6-311++G** level of theory to better understand the interaction within 1PPNO₃ molecule. It gives much information about the nature and strength of interactions. Table 3 groups the energy values for the significant donor acceptor interactions. The increase in stabilization energy E⁽²⁾ generates the increase in electron donor–acceptor interactions (Tahenti et al., 2020). Results reveals that the bonding orbital σ → the anti- bonding orbital σ* interaction has a smaller E(2) than that of π → π* and the lone pairs LP → σ*. It is varied between 0.72 kcal/mol and 6.44 kcal/mol. The intra molecular interactions of σ(C₂₀-C₂₅) to σ*(H₇-C₂₅; σ(C₂₄-C₂₅) to σ*(H₇-C₂₅) and of σ(C₂₆-C₂₈) to σ*(N₁₅-C₂₀) leads to large stabilization of 6.38, 6.23 and 6.44 KJ/mol, respectively. The strong interaction of the LP to the anti-bonding orbital of the ring conducts to stabilization of some part of the ring as shown in Table 3. The stabilization energy between LP*(O)-σ*(N-O) roughly equal to 17.29 kcal/mol. Also, it can be seen the existence of strong H-bond interaction between oxygen lone electron pairs LP(2)-O₃₉ and the empty antibonding orbitals σ*(N₁₆-H₁₈). The interacting energy value is obtained as 12.35 kcal/mol.

Mulliken charges investigation has been developed to describe atomic charges distribution of molecular wave functions. They are principally based on first-order density functions within a LCAO MO approach (Pople and Beveridge, 1970). The atomic charge of the title compound, calculated by B3LYP-D/6-311++G** and WB97XD/6-311++G** level of theory, is tabulated in Table S3. As results, we found that all hydrogen atoms are positively charged. The charges on carbon atoms C₁₉, C₂₁, C₂₂, C₂₃, C₂₄, C₂₆, and C₂₄ are negative_, whereas C₂₀ and C₂₅ are positive. Hydrogen H₁₈ has the maximum of positive Mulliken charges. The Highest values of negative charges are located on O₃₁. The existence of substantial negative charges on oxygen atoms indicates that these atoms may have H-bond acceptors.

4.4 Hirshfeld surface investigations

Hirshfeld surfaces analysis (HS) has turn a precious tool for crystallographers, since it identifies each type of intermolecular interaction in the crystal structure. This surface outcome from the partition of the space separating one atom to the rest of the crystal. Hirshfeld surface of the title compound was determined by means of Crystal Explorer 3.1. This study allows a much detailed scrutiny by viewing intermolecular interactions and quantifying them in 2D fingerprint plot (Spackman and McKinnon, 2002). Fig. 5 illustrate the three-dimensional Hirshfeld d_norm (a) surface, Shape Index (a) and Curvedness (c) of (C₁₀H₁₆N₂)(NO₃)₂·H₂O molecule. Normalized distance d_norm (varies between −0.5429 and 1.1528) is one way of representing Hirshfeld surfaces. It makes it possible to generate a representation which implies standardized contact distances taking into account the van der Waals radius of the atoms involved in the analysis. Shape index (ranges −1.000 to 1.000) and curvedness (varies between −4.000 and 0.4000) maps can also be used to identify characteristic conditioning patterns existing in the crystal. Each point on the Hirshfeld surfaces can be defined by two distances d_i (is the distance to the nearest nucleus internal to the surface) and d_e (is the distance from the point to the nearest nucleus external to the surface). These two distances give a 2D fingerprint plot of inter-molecular interactions in crystals. We estimate in Fig. 6, the percentages of different intermolecular contacts existing in the structure of 1PPNO₃ molecule and the 2D fingerprints plots of important contacts. The examination of these figures shows that the principal contributions are from O…H /H…O (59.6%; Fig. 6a) with a maximum d_e + d_i ∼ 2.22 Å less than the sum of the van der Waals radii of involved atoms (H: 1.09 Å O: 1.52 Å), H…H (21.6%; Fig. 6b), these inter contacts centered around a sum d_i + d_e ∼ 2.4 Å greater than the sum of the van der Waals radii of the hydrogen atoms, H…C/C…H (Fig. 6c) comprise 12.2% of the entire Hirshfeld surface, these contacts represented in the form of two wings located around a sum d_e + d_i ∼ 2.8 Å greater than the sum of the van der Waals radii of considered atoms (C: 1.70 Å, H : 1.09 Å). According to this comparison concludes that only the H … O / O … H contacts considered close together they are attributed to the hydrogen bonds N–H … O, O–H … O and C–H … O. The very high percentage of C … H / H … C contacts confirms the presence of C–H … π interactions in the 1PPNO₃ material.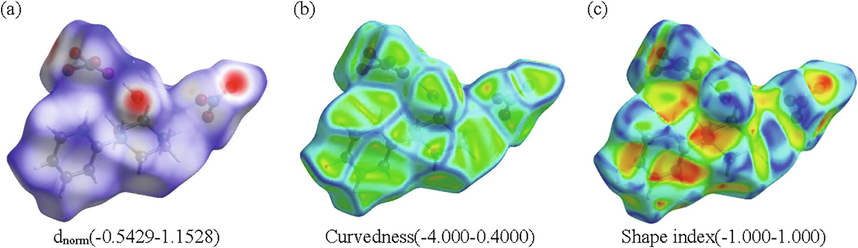

Close

Fig. 5

Hirshfeld surfaces plotted with (a) d_norm; (b) curvedness) and (c) shape-index for the title compound.

Export to PPT

Close

Fig. 6

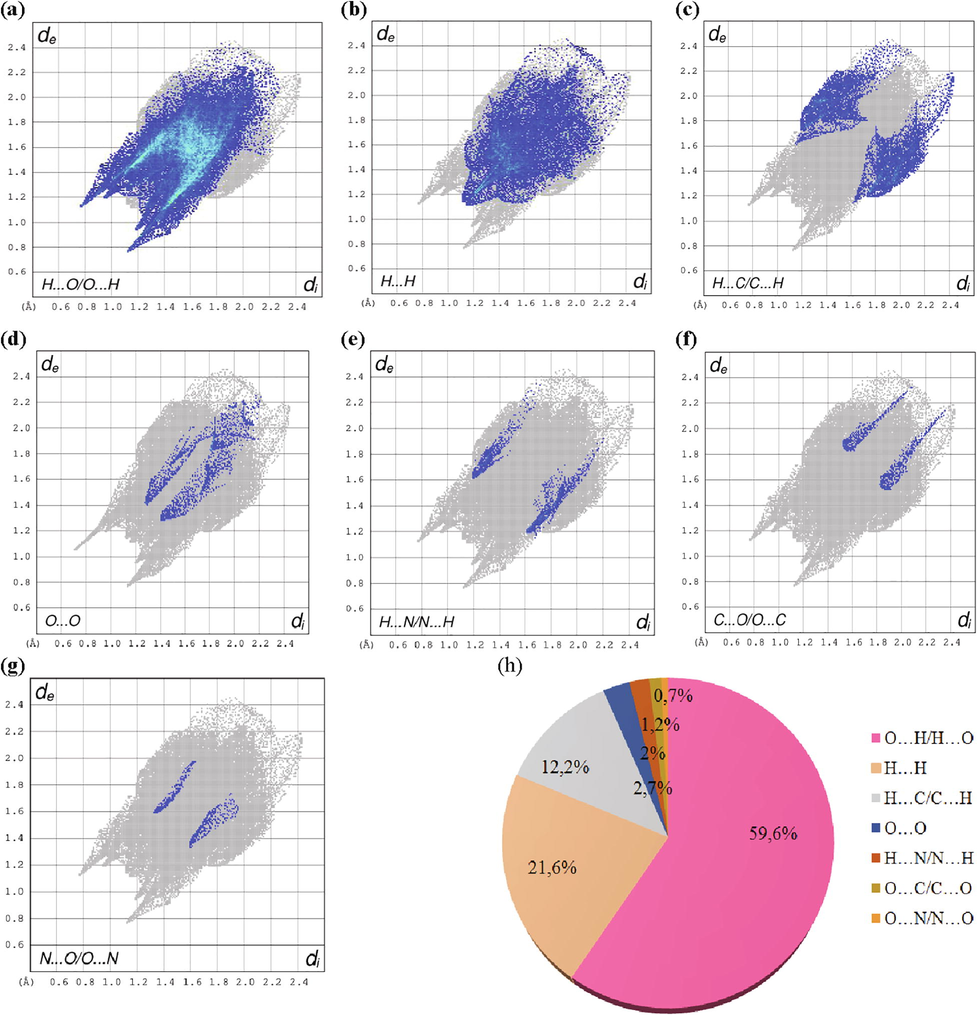
Fingerprint plots of the various intermolecular contacts existing in the Hirshfeld surface of (C₁₀H₁₆N₂)(NO₃)₂·H₂O compound.

Export to PPT

4.5 MEP analysis

To investigate the chemical reactivity; the nucleophilic and electrophilic sites within molecule, molecular electrostatic potential (MEP) maps were determined using WB97XD/6-311++G** process (Fig. S5). It confirms the positive and the negative potential regions with the total electron density surface. The nucleophilic and electrophilic regions promote the formation of hydrogen bonds. MEP surface was obtained by mapping electrostatic potential to the total electron density in simple color code, where the potential decrease in the order of blue > green > yellow > orange > red. As seen in Fig. S5, the color code is between −6.890.10⁻² (red color: corresponds to the potential negative values) and 6.890.10⁻² (blue color: corresponds to the potential positive value). The blue color indicates the strong attraction (electrophilic sites) while the red color shows a region of strong repulsion (nucleophilic sites) and the green indicates the neutral zone. It is clear that the oxygen atoms (especially O₃₅ and O₃₄) mainly exhibit a negative charge (red color region). Also, the nitrogen atom N₃₂ is localized in the negative region. Whereas all the hydrogen atoms represent a positive potential value (blue color). Results obtained may justify the presence of hydrogen-bond interactions in the 1PPNO₃ molecule.

4.6 HOMO-LUMO molecular orbital study

The electrons transition from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) happen liberally when the energy gap is small. LUMO and HOMO are named frontier molecular orbitals (FMOs). The HOMOs are able to denote an electron, while the LUMO is able to accept an electron. These orbitals participate in large part in the chemical stability of the molecule and play an important role in determining its electronic properties (Fukui, 1975). The molecular reactions are permitted if the FMOs are placed in such a way that the lobes of the same sign overlap. The difference between the energy of the HOMO and LUMO orbitals is defined as the gap energy ΔE. This latter reflect the polarizability and chemical activity within a molecule. It promotes the transfer of charges in the molecule. This energy quantity allows characterizing the chemical reactivity and the kinetic stability of the molecule. When the HOMO-LUMO energy gap is high, the flow of electrons at the higher energy state is difficult, making the molecule hard and less reactive. On the other hand, the lower HOMO-LUMO energy gap results in an easy flow of electrons, which makes the molecule soft.

The chemical reactivity behaviors of 1PPNO₃ have been carried out via TD-DFT approach. This method display its effectiveness compared to semi-empirical approaches and traditional ab-initio computations. We present, in Fig. 7, the frontier molecular orbitals LUMO and HOMO of the mentioned molecule as well as their calculated gap energies in gas phase and taking into account solvation. The green color corresponds to the negative phase and the red color indicates the positive phase. Results reveal that the HOMO-LUMO energies gap (E_HOMO-E_LUMO) in gas, water and in methanol is equal to −5.180 eV, −5.190 eV and −5.135 eV, respectively. We can notice that these energies take negative values. This indicates the stability of our compound, although band gap validate the eventual charge transfer interactions. We can conclude that 1PPNO₃ is more reactive in ethanol due to its lower value of gap energy $\left|\mathrm{\Delta }\mathrm{E}\right|=5.135\mathrm{e}\mathrm{V}$ . The Orbital Density Spectrum (DOS) is represented in Fig. S6 using GaussSum software (O'Boyle et al., 2008). These spectra describe the energy levels per unit energy increment and its composition in energy between −15 and 5 eV. Analysis of these figures show that the green and red lines in the DOS spectrum represent the HOMO (EHOMO) and the LUMO (ELUMO) levels, respectively. As predicted, the energies gaps determined by the DOS spectra are compatible with the calculated values. Starting from the energy orbitals, chemical parameters like the chemical potential, the global hardness, the softness and the electrophilicity maximum charge transfer index between the frontier molecular orbital of 1-Phenylpiperazin-1, 4-Diium Nitrate Monohydrate are calculated in different solvents using the TD-B3LYP method (Table 4). These parameters are often determined through Koopmans' theorem (Geerlings et al., 2003). The chemical potential is donated as; μ ≈ 1/2(E_LUMO + E_HOMO) ≈ 1/2 (I + A), where I and A represent the ionization potential and the electron affinity (I = −E_HOMO; A = −E_LUMO), respectively. These parameters are found to be −4.889; −3.836 and −3.836 eV in gas; water and methanol, respectively. Similarly, the electro negativity χ can be defined as χ = 1/2(I + A). The global hardness (η) calculated based on the LUMO and HOMO energies: η ≈ (E_LUMO − E_HOMO) ≈ (I − A). Indeed, we found that the hardness in water (2,595 eV) greater than those obtained in gas and in methanol. Additionally, 1PPNO₃ has a softness S_water = 0.192 eV⁻¹ < S_gas = 0.193 eV⁻¹ < S_methanol = 0.194 eV⁻¹.

Close

Fig. 7

HOMO and LUMO frontier molecular orbitals of (C₁₀H₁₆N₂)(NO₃)₂·H₂O compound by using TD-DFT calculations in methanol (a), in gas phase (b) and in water (c).

Export to PPT

4.7 Docking calculations

In this paper, we have used docking calculations of GDP (5O33), JGA (5QQD), PPHS, 4PPHP, 1PPNO₃ ligands with “Kalirin-7” protein and of 1PPNO₃, 1-PPHS, 4PPHP, Farnesol (2BK3) and Isatin (2BK5) ligands with “monoamine oxidase B” protein to specify the zone of interactions. Only the ligand is mobile and the flexibility of the protein is not taken into account. It is a technique for describing the molecular docking binding sites available in discovery studio visualizer. This calculation has been used to exhibit how these proteins interact with small molecules (ligand) (Noureddine et al., 2021) for the purpose of prognosticate the most possible of interaction for the efficacy of the drugs. Treatments are determined predicated on the individual’s symptoms and how they react to different medicinal drug. Molecular docking algorithms engender a vast number of incorrect docking poses; we chose the position that has the lowest energy called “the best pose”. To explore how these inhibitors interact with the active sites of two enzymes, we have illustrated in Table 5, the energetic related results of the docking calculations. IGEMDOCK program makes it possible to determine the Van der Waals interactions and the hydrogen bonds which are the most important among the weak bonds. The hydrogen interaction can be constituted by the atom-pair types: donor–acceptor, acceptor–both, donor-both and both–both. If there are other combinations of pairs of atoms, then in this case they must form the steric state. Subsequently, the corresponding docked poses are given in Fig. 8 and different types of interaction between protein-ligands and their available interactions in 2D diagrams are represented in Fig. S7 and S8. As it is shown, the ligand is attached to the receptor by different types of interactions like pi-cation, pi-alkyl, alkyl, pi-sigma, pi-anion, amide pi-stacked, pi-sulfur, attractive charge, salt bridge, acceptor–acceptor, conventional hydrogen bonding, carbon-hydrogen bond, etc…

Close

Fig. 8

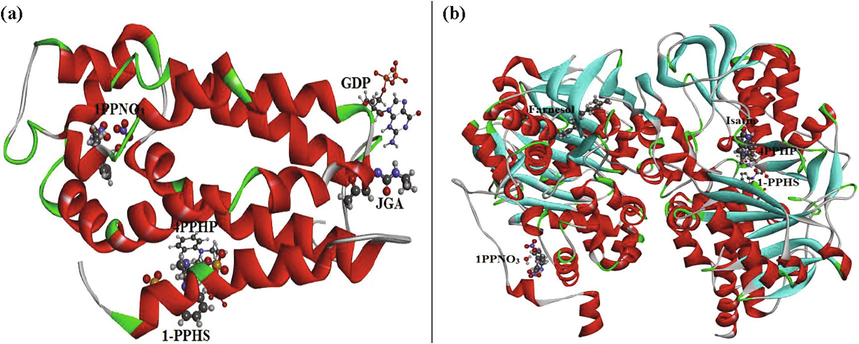
Best docked poses of GDP, 1PPNO₃, JGA. 1-PPHS. 4PPHP ligands inside Kalirin-7 protein (A); and of 1PPNO₃, 1-PPHS, Farnesol, 4PPHP, Isatin ligands inside the MAOB protein (B) in 3D views.

Export to PPT

Starting with Kalirin receptor (well-known as Huntingtin-associated protein-interacting protein (HAPIP)), which is a protein determined in 1997, interacting with huntingtin-associated protein 1. It helps in nerve growth and axonal development. Kalirin-7 is one of their isoforms; it has been informed that this protein is closely correlated with the development of Schizophrenia and Alzheimer's diseases. The examination of Table 5 revealed that the GDP ligand possessed agreeable total energy score (−92.939 kcal/mol) with the target protein Kalirin-7. This high total energy demonstrates that the ligand interacted powerfully with the receptor. Also, it has the highest VDW interaction with a value of −62.251 kcal/mol. Visual inspection of the 2D representations of GDP ligand reveals that the following atoms: N₂, O₂, N₄ and O₁₁ are linked to A:GLU14, A:GLU83, A:GLU84 and A:LYS12 binding residues respectively via conventional hydrogen bond interactions, with a range of distances varies between 2.40 and 2.96 Å (as clearly seen in Table S4). A:LYS13 form a pi-cation interaction with the pyrimidine ring and a pi-alkyl interaction with the imidazoline group indicating bond lengths 3.19 and 4.36 Å, respectively. In addition, the oxygen atoms O₆, O₉, O₁₀ also exhibit a pi-cation interaction with A:LYS13 residues with distances 3.04, 1.96 and 2.16 Å. Thereafter, we find our present compound 1PPNO₃ with such an important energy of the order of −90.762 kcal/mol and a VDW interaction equal to −40.910 kcal/mol. The docking pose of this complex showed that the benzene ring of 1PPNO3 molecule is oriented with two pi-alkyl interactions surrounded by the chains of A:ILE117 and A:ILE138 residues with bond lengths values 4.50 and 4.91 Å. The amino residues A:GLY122 and A:THR123 form 2 carbon-bond interactions with C₁₉ and C₂₃, having distances 3.63 and 3.21 Å. Subsequently, two conventional hydrogen bonds were being formed with the following amino acids: A:THR123 and A:GLN129. The JGA molecule has a lower energy than the two ligands mentioned (-75.021 kcal/mol) and the last two ligands (1-PPHS, 4PPHP) have weaker energies than the other complexes but as even remain important. In order to improve the recognition of the interactions which exist between proteins and ligands, we determined the affinities of these complexes by using AutoDockTools (ADT) (Morris et al., 2008). This affinity makes it possible to describe the strength of a non-covalent interaction between the protein and the ligand which binds to a site on its surface. It is based on the number and nature of the physicochemical interactions between the ligand and its target. From Table 5, it is observed that the affinities values (in ultimate value) are in the order of 7.0 > 5.0 > 3.6 > 3.5 > 1.5 kcal/mol for GDP, JGA, 1-PPHS, 4PPHP and 1PPNO3, respectively.

After the analysis of the best docking positions presented in Fig. 8, we can be concluded that the studied compounds are bound mainly by the many non-covalent interactions at the active site of the receptor. Recall that, most of the molecular docking methods are paying attention on effective prediction of the binding mode of non-covalent inhibitors in so-called reversible inhibition. Covalent inhibition is a strategy that is used to achieve irreversible inhibition. Covalent inhibitors possess some significant advantages over non-covalent inhibitors such as stronger binding affinity with the receptors because of the covalent linkage formed between the ligand (electrophilic) and the target (nucleophilic), stronger potency and prolonged duration of the biological effect of a ligand. The distribution of negative charges along the 1PPNO3 ligand indicates that it has a nucleophilic character. Therefore, the explanation for the non-covalent bond of this compound lies in their charge distribution and the methodology applied.

Now going to the second MAO-B protein, it represents a group of oxidoreductases involved in thrombocytes and chromaffin cells. It is found in neurons and astrocytes. The dysfunction of this protein is responsible for several neurological disorders, because of its vital role in the inactivation of neurotransmitters. Parkinson's and Alzheimer's diseases are both linked with high levels of MAO-B in the brain. Adding a MAO-B inhibitor slows the breakdown of dopamine in the brain. Among the five inhibitors tested, our compound 1PPNO₃ displayed better inhibition when compared with others. It is found to form the most stable protein–ligand complex since it has the best inhibitory effect with a total energy equal to −106.944 kcal/mol. It has a significant VDW interaction of value equal to −60.141 kcal/mol; moreover it has the strongest hydrogen bond of the order of −46.812 kcal/mol. Calculations show that for MAOB-1PPNO₃ complexes, B:THR195 and B:THR196 residues formed conventional H-bond interactions with O₅ and O₆ atoms having distances 2.65 and 2.54 Å. The oxygen atom O3 exhibit an attractive charge with B:ASP124 amino acids residues (4.28 Å) and a salt bridge with B:ARG127 (2.86 Å) (as illustrated in Table S3). Likewise 1-PPHS and Farnesol ligands have a good binding interaction with MAOB protein and it exhibited the total energy scores of −97.845 and −92.493 kcal/mol, respectively. Their VDW interactions are found to be −93.000 and −86.535 kcal/mol. As seen, several types of interactions appear in the 1-PPHS/MAOB complex as attractive charge, pi-alkyl, pi-sigma, pi-anion, pi-sulfur…, whose distances vary between 3.06 and 5.42 Å. We find also that the 4PPHP molecule interact well than Isatin with the receptor, indicating total energy score of −83.580 kcal/mol, E_VDW = −76.580 kcal/mol and E_H-bond = −7.000 kcal/mol. All those complexes present weaker affinities −1.9 kcal/mol (for 1PPNO3), −3.3 kcal/mol (1-PPHS), −4.4 kcal/mol (Farnesol), −3.7 kcal/mol (4PPHP) and −6.7 kcal/mol (for Isatin ligand).

The results obtained during our study reveal that the phenylpiperazine derivatives (1PPNO₃, 1-PPHS and 4PPHP) penetrates well into the active site of the two enzymes, so we can consider it as potent inhibitors of Parkinson, Schizophrenia and Alzheimer's disorders.

4.8 Thermal analysis

Thermal analysis methods (DTA, TGA and DSC) aim to study the transformations that affect the structure of solid materials when the temperature is varied. These methods are complementary to X thermal diffraction. Differential thermal analysis (DTA) is a very simple technique for monitoring the endothermic and exothermic phenomena that take place during a reaction. Thermogravimetric analysis (TGA) allows studying variations in the mass of samples, when they are subjected to a variation in temperature under a monitored atmosphere. Whereas, Differential Scanning Calorimetry (DSC) is a technique for measuring the differences in heat exchange between the sample and the reference (thermally inert material). The differential and thermogravimetric thermal analysis of 1PPNO₃ (Fig. 9a) is carried in temperature range (ambient temperature to 723 K) on a mass sample is equal to 11.90 mg with a heating rate of 5 K. min⁻¹ and under an argon atmosphere. DTA curve presents a fine and very intense exothermic peak at 396 K accompanied by a small loss of mass on the TG curve, this thermal transformation corresponds to the first stage of decomposition and elimination of a water molecule. A second endothermic peak appears around 438 K without loss of mass is attributed to a phenomenon of fusion during which our material loses its crystalline state and passes to the liquid state, this phenomenon is further confirmed by heating our compound on a Kofler bench which allows us to estimate the melting temperature of a material, this temperature (440 K) is close to that observed on DTA curve. Finally a series of peaks located respectively at 552, 554 and 560 K accompanied by a very large loss of mass relative to the rest of decomposition mechanism. During this decomposition stage, a transfer of protons between the cationic part and anionic part at high temperatures which leads to an internal redox reaction between the amine and nitric acid, and various other reactions can suppose, which leads to the ignition of the material (Gatfaoui et al., 2019). The transfer of protons to the NO₃⁻ anions is due to the weakening of the N–H bonds at high temperatures in the condensed phase.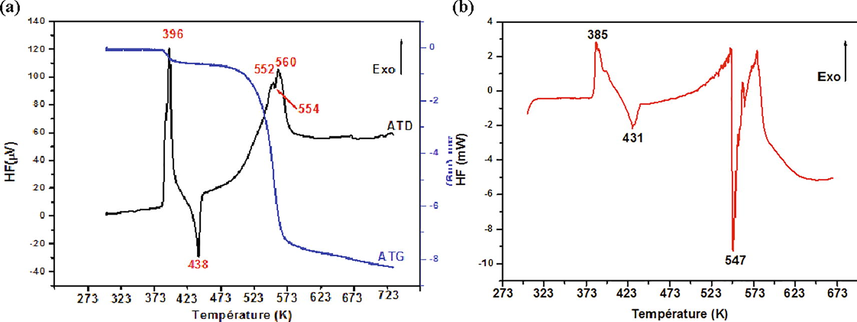

Close

Fig. 9

DTA, TGA (A) and DSC (B) thermograms of 1PPNO₃ molecule.

Export to PPT

The differential enthalpy analysis (DSC) of 1PPNO₃, is carried out in the temperature range from 303 to 673 K with a speed equal 5 K. min⁻¹, on a sample of mass m = 4.90 mg, under an atmosphere of argon. The curve obtained (Fig. 9b) shows the presence of an exothermic peak at 385 K indicating dehydration and decomposition and an endothermic peak at 392 K corresponding to the fusion of the remaining compound, observed in thermal and thermogravimetric analyzes differential in the same temperature range with ΔH_fusion = 11.51 kJ.mol⁻¹. A second very fine endothermic peak at 547 K is observed on the DSC curve. The same peak is observed on the DTA curve but with a very low intensity, the accuracy of the DSC compared to the DTA is may be due to the small mass of the sample used since the two analyzes are performed with the same speed.

4.9 Thermodynamic properties

The thermodynamic functions provide a diversity of formula that reveals many properties of the compounds. Among the most important properties, we can mention: the entropy S; the heat capacity Cp and the enthalpy H. All these thermodynamic properties strongly depend on the temperature and they are determined from the theoretical frequencies by using a Perl script “thermo.pl” (NIST) on various ranges of temperature (100–1000 K) and at atmospheric pressure are illustrated in Table S5. Note that generally these thermodynamic calculations can only be done in the gas phase and not in solution. The variations of the parameters as a function of the temperature are illustrated in Fig. S9. As clearly seen, the thermodynamic properties are increasing with temperature, since the vibrational intensities increase when the temperature increases. The correlation between these parameters with temperatures is an integrated quadratic formula. The corresponding fitting factors R² are equal to 0.9990, 0.9900 and 0.9990, respectively and adjusted by the following quadratic formulas:

The thermodynamic data gives important information for the study of the title compound. We can calculate other thermodynamic energies as a function of these thermodynamic relationships.

4.10 IR absorption spectroscopy study

To obtain more information on the crystal structure, we have undertaken a vibrational analysis by determining infrared spectroscopy and Raman scattering (Leela et al., 2015; Gunasekaran et al., 2009). IR spectroscopy can be used to distinguish molecular groups and to find microscopic information on their conformations. It is a very important technique to find the actual binding sites. The IR absorption spectrum was recorded with a spectral resolution in the region 4000–400 cm⁻¹. Both experimental and theoretical IR spectrum are compared in Fig. 10 (a and b), respectively. Also the Raman spectrum (4000–500 cm⁻¹) is determined in gas phase by using the WB97XD/6-311++G** method (Fig. S10). Table 6 shows the IR and Raman intensity, experimental and calculated frequencies (scaled and unscaled) and also vibrational assignments for 1PPNO₃ on the gaseous phase assigned by VEDA program (based on the percentage total energy). Using Gauss View program, these assignments are confirmed by molecular visualization effects. For vibrational frequency, we adopt uniform correlation coefficients: frequencies below 1700 are multiplied by 0.983, so that greater than 1700 are multiplied by 0.958. This correction is made to find a good agreement with the experimental frequencies. Theoretically, the calculated scaled values correlate greatly with observed values. (C₁₀H₁₆N₂)(NO₃)₂·H₂O molecule crystallizes in a monoclinic mesh with the space group P2₁/c (C_2h). Nitrate (NO₃) groups have C₁ symmetry. As a result, our molecule consists of 39 atoms, it has 3 N-6 (=3x39-6) = 111 fundamental normal modes of IR vibrations. All these modes are guessed using the PED calculations. The vibrational modes of 1PPNO₃ are classified in many group vibrations. Of the 111 modes, only 7 bands of vibration are observed on the IR absorption spectrum. This can be explained by the interaction between the different nitrate groups, which produces modes to which fairly wide bands correspond and which can correspond to several lines. For the organic cation, the attribution of the normal modes of vibrations is rather complex since these modes overlap with that of the nitrate group. In the configuration below, they exist many kinds of hydrogen bonds like C–H…O, O–H…O, N–H…O and O–H…N. Intra-molecular and inter-molecular hydrogen bonding arise when H atoms and O, N atoms exist within a molecule or between two molecules. The chosen compound contains aromatic and hetero-aromatic rings: the aromatic structure of the molecule of benzene is very sensitive by the nature of the substituent. Nowadays, in the spectroscopic field, much paper is dedicated to investigate the vibrational spectra of benzene derivatives (Rastogi et al., 2002).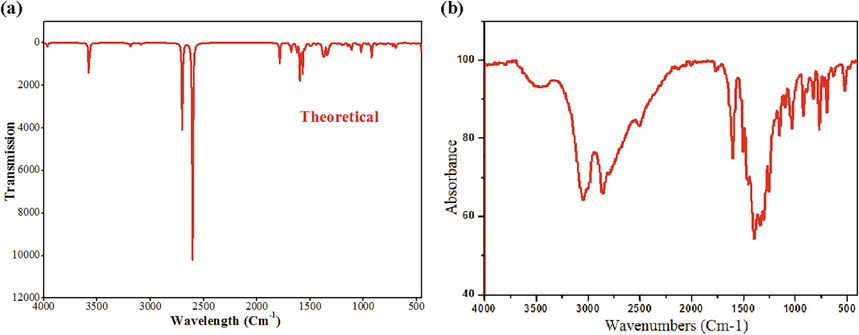

Close

Fig. 10

Theoretical (a) and experimental (b) IR spectra.

Export to PPT