Projectile motion revisited: Does the distance between the launcher and the object always increase?

1 Introduction

When we look at baseballs and tennis balls flying through the air, in a home run hit or a field goal kick, the balls follow a particular curved path through the air, exhibiting what we call projectile motion. Parabolic motion has been extensively studied over the years (Bajc, 1990; Bose, 1985; Lucie, 1979; Medina, 1978; Siegel, 2017; Tan and Giere, 1987). We believed that everything about its characteristics was known, but we have found a new and surprising occurrence.

When we launch a projectile, the particle appears to be constantly moving away from the launcher, both when we look at it from the perspective of the launcher and when we look at it from a position external to the launcher. In this work, we will show that this is not always the case as strange as it may sound. In fact, there are intervals in which the projectile approximates the launch point.

Our findings seem to go against students’ and teachers’ intuitions. We think that the projectile is always moving away, but there is an interval of angles in which there is a shortening of distance between the projectile and the launching point, in certain moments of the trajectory. There is a critical launch angle, above which there is an approximation. Below that critical angle, the projectile always moves away from the launcher. We will also calculate the length of the time interval in which the approximation occurs, an approximation which depends on the angle at which the projectile has been launched.

2 Parabolic motion in dimensionless coordinates

Projectile motion is two-dimensional free-fall motion under the influence of only gravity. We will neglect the influence of air resistance, leading to results that are a good approximation of reality for relatively heavy objects moving relatively slowly over relatively short distances.

Projectile motion follows a parabolic trajectory with two independent motions: uniform motion at constant velocity in the horizontal direction x, and constant acceleration, the gravity, in the vertical direction y (Freedman and Young, 2020; Halliday et al., 2014; Knight, 2016; Serway and Vuille, 2017; Tipler and Mosca, 2008; Wolfson and Pasachoff, 2017). Considering the particle is launched with speed v₀ at angle θ from the origin of the Cartesian coordinate system, mathematically the motion is described by

In this paper, we want to analyze in detail the distance from an object in parabolic motion to the launching point. We are specifically interested in the behaviour of this magnitude, so launching speed is irrelevant, as we will see later. The only variable that will appear is the initial launch angle. Based on this, we will carry out the following variable change in the preceding equations

In vectorial terms, the position of the projectile each moment is given by the dimensionless position vector

We can find the dimensionless time of flight, $\overline{T}$ , from Eq. (7) by setting $\overline{y}=0$

3 Distance from projectile to launch point

The distance at any point between the launcher and the position of the object is the magnitude of position vector, Eq. (8), which is the square root of a fourth-degree polynomial in the new dimensionless time variable

Let us analyse this function more closely, studying its critical points. For this, we find the first derivative and we calculate its roots.

The trivial solution $\overline{t}=0$ will not be taken into account since it coincides with the beginning of the launch. The other two solutions correspond to the points in which Eq. (10) will have a relative maximum, t_M, and minimum, t_m, given by

To find out which of them correspond to a relative maximum and minimum of the $r\left(\overline{t}\right)$ function, we have carried out a second derivative, and we have calculated the signs that result from the noughts of the first derivative, that is, the noughts of Eqs. (12) and (13), resulting in

Therefore, it is correct to say that t_M corresponds to a relative maximum and t_m to a relative minimum. Also, t_m > t_M.

Eqs. (12) and (13) only have a real solution when the radicand that appears in them is higher or equal to 0.

Taking into account the double-angle formulae

With everything we have analysed up to this point, when we carry out a launch with an angle greater than the critical angle ${\theta }_c=70.{53}^{°}$ , that is, when $\theta >{\theta }_c$ , the distance to the launching point presents a similar behaviour to the one shown in Fig. 1.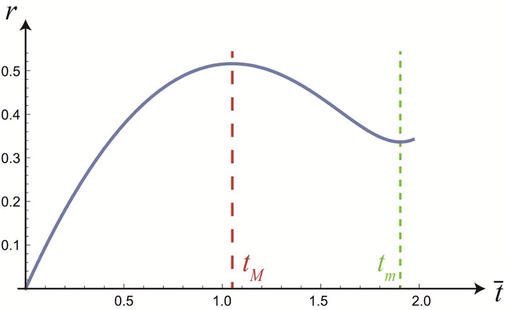

Close

Fig. 1

Distance from the projectile to the launch point at any moment for a launch angle of $\theta ={80}^{\mathrm{o}}$ , which is greater than the critical angle. ${\theta }_c.$

Export to PPT

This behaviour indicates that in the time interval between t_M and t_m, the distance between the projectile and the launching point decreases, which means that the object is approaching the launcher. This is a very curious and surprising result since intuitively we would mistakenly think that the projectile always moves away from the launch point, if we looked only at the horizontal direction x of the movement. It is necessary to carry out an exhaustive analysis of the position vector to conclude that there is an interval of launch angles in which, at a certain time interval, the projectile approximates the launcher.

3.1

3.1 Evolution of critical points with launch angle

Fig. 2 shows the evolution of critical points resulting from the analysis of the magnitude of position vector, $r\left(\overline{t}\right)$ , that determines the distance from the projectile to the launching point, depending on the launching angle, and always taking into account that we are in higher angles to the critical angle calculated in the previous section, Eq. (17). The inflection point, t_ip, indicates the time for which variable $r\left(\overline{t}\right)$ changes its curvature. In this particular case, in Fig. 1 we can see that it goes from a concave downwards curvature with a maximum in t_M, given by Eq. (12), to an upwards concave curvature with a minimum in t_m, given by Eq. (13).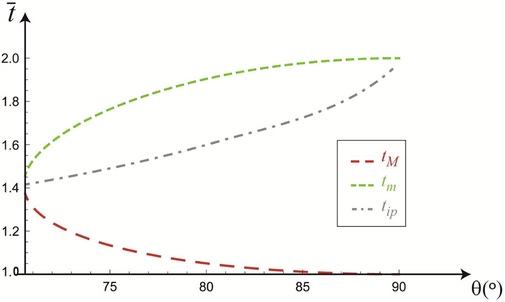

Close

Fig. 2

Evolution of the maximum t_M, minimum t_m and inflection point t_ip in the function that determines the distance from the projectile to the launching point with the different possible lunching angles, always greater than ${\theta }_c$ .

Export to PPT

As can be seen in Fig. 2, as the launch angle θ increases, the maximum t_M decreases, asymptotically tending to 1. In other words, for larger launch angles, the point at which the projectile starts approaching the launching point occurs sooner. On the other hand, the minimum time t_m increases as θ increases, asymptotically tending to 2. That is, the time at which the projectile starts to move away from the launcher gets longer. From these results, we can state that the time interval in which the object is approaching its original point increases as the launch angle also increases, as can be seen in Fig. 3.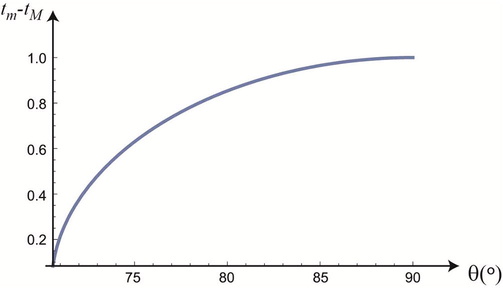

Close

Fig. 3

Time interval of the approximation of the projectile to the launching point depending on the launch angle, it being always bigger than. ${\theta }_c$

Export to PPT

Note that the time interval of approximation asymptotically tends to 1. Bearing in mind that for $\theta ={90}^{°}$ (linear motion along the y-axis), the flight time is 2, Eq. (9), it is easy to understand that, for this particular angle, the interval of approximation is half of the time of flight. In a completely vertical launch, for half of the time, the particle is going up and, therefore, moving away from the launcher. And the other half of the time, the particle goes down approximating the launch point.

Regarding the inflection point, it is always closer to the minimum of the function, that is, closer to the value of t_m, see Fig. 2. In addition, it has an almost linear shift towards the right in the timeline in the first part of the graph, until the launch angle is just over 80°.

To show all these results in a more visual way, in Fig. 4 we represented the distance from the projectile to the launch point, $r\left(\overline{t}\right)$ , indicating the times at which the maximum, the minimum and the inflection point take place. We also represented the vertical coordinate $\overline{y}\left(\overline{t}\right)$ and the time at which it reaches its maximum value, ${\overline{T}}_{1/2}$ , the point from which the projectile starts to descent vertically. This time corresponds half of the time of flight, ${\overline{T}}_{1/2}=\overline{T}/2$ .

Close

Fig. 4

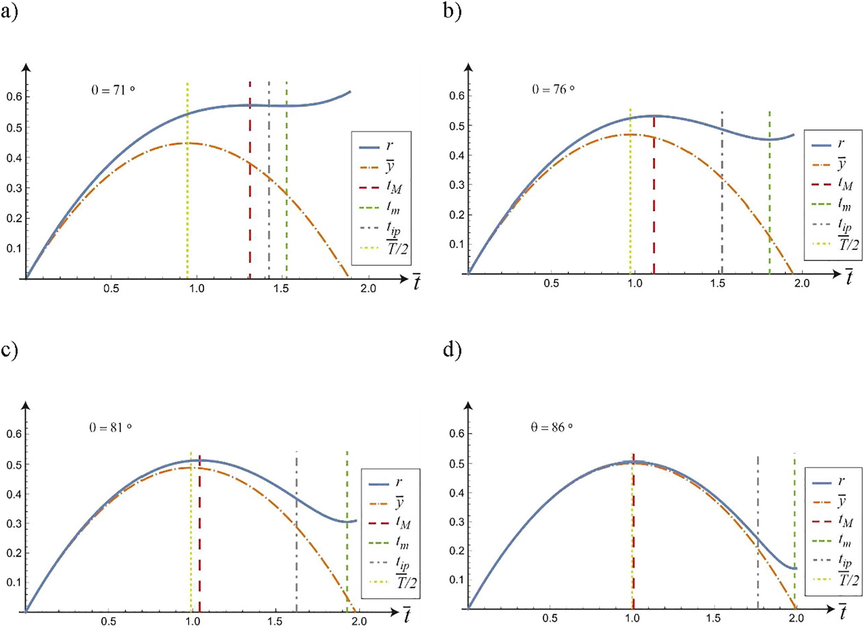
Vertical position of the projectile at each moment, $\overline{y}\left(\overline{t}\right)$ , the time at which the projectile reaches its maximum height ${\overline{T}}_{1/2}$ , the distance from the projectile to the launch point at each moment, $r\left(\overline{t}\right)$ with its corresponding critical points t_M, t_m and t_ip for launch angles: a) $\theta ={71}^{°}$ ; b) $\theta ={76}^{°}$ ; c) $\theta ={81}^{°}$ and d) $\theta ={86}^{°}$

Export to PPT

As we can see, the time interval in which the projectile is approaching the launch point always takes place when the projectile is descending, and it increases as the verticality of the launch increases. This increase is more pronounced in the angles closer to the critical angle. Note that the maximum time t_M, over which the projectile stops moving away from the launcher, is closer to the time in which the projectile reaches its maximum height ${\overline{T}}_{1/2}$ , until it coincides with the said point for a launch angle of $\theta ={90}^{°}$ .

3.2

3.2 Growth rate of the approximation interval

Analyzing in detail the time interval of approximation to the launch point, in Fig. 5 we have represented the rate, $v_{\theta }$ , at which the interval increases depending on the launch angle

(18)

$$v_{\theta }=\frac{d}{d\theta }\left(t_m-t_M\right)$$

Close

Fig. 5

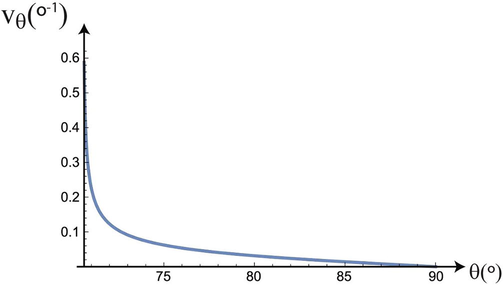
Growth rate of interval t_m-t_M depending on launch angle.

Export to PPT

As we can see, the speed of separation between the critical points t_M and t_m decreases drastically in the interval close to the critical angle, from 70.6° to 71°. In the last part, for $\theta >{80}^{°}$ , the decrease of the growth rate of the interval t_m-t_M is practically linear, with a slope of 0.003.

4 Polar coordinates

Let us analyze the problem in terms of radial and angular coordinates in order to see the situation from another point of view.

In Fig. 6 we have represented any point of the parabolic trajectory corresponding to a parabolic motion in polar coordinates. Note that we are still working with the dimensionless variables defined in the last section, so that the radial coordinate is also non-dimensional. It is evident that this radial coordinate is the magnitude of the position vector, Eq. (10), but expressed as a function of other variables.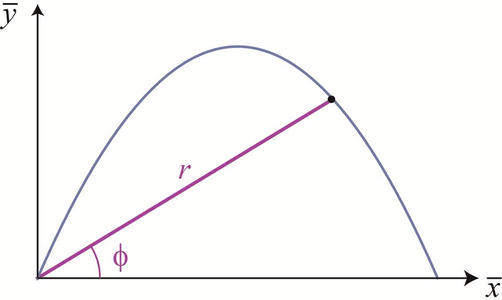

Close

Fig. 6

Parabolic trajectory corresponding to the parabolic motion and representation of any point in the trajectory with its polar coordinates.

Export to PPT

The dimensionless trajectory equation is given by

Substituting this change of variables, Eqs. (19) and (20), in the trajectory equation, we find

And eliminating the trivial solution $r=0$ which corresponds to the initial position, we obtain

Close

Fig. 7

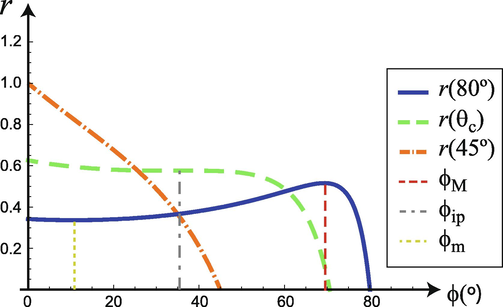
Distance as a function of the angular variable for three initial shot angles. The blue curve (──) corresponds to $\theta ={80}^{°}$ , which is above the critical initial angle and, hence it has a maximum, ${\varphi }_M$ , and a minimum ${\varphi }_m$ , between which the projectile is approaching. The green curve ( ) corresponds to the critical initial angle, ${\theta }_c$ , which has an inflection point ${\varphi }_{\mathit{ip}}={\theta }_c/2$ . And the curve in orange ( ) corresponds to an angle $\theta ={45}^{°}$ , which is below the critical initial angle and hence the projectile is always moving away from the launcher.

Export to PPT

Using the equality of the tangent of the sum, we obtain

And using Eq. (24),

Which will have real solutions when the discriminant that appears in them is higher or equal to 0, obtaining the same result as in Eq. (17), $\theta \ge 70.{53}^{°}$ .

The blue curve in Fig. 7 corresponds to $\theta ={80}^{°}$ , which is above the critical initial angle and, hence it has a maximum, ${\varphi }_M$ , and a minimum ${\varphi }_m$ , between which the projectile is approaching. The curve in orange corresponds to an angle $\theta ={45}^{°}$ , which is below the critical initial angle and hence the projectile is always moving away from the launcher. The green curve corresponds to the critical initial angle, ${\theta }_c$ , which has an inflection point $\varphi ={\theta }_c/2$ because

Which is the tangent of ${\theta }_c/2$ , a fact that can be seen using the half-angle tangent formula

5 Conclusions

We have obtained a particularity of projectile motion when launched from the ground and without air friction. The distance between the launched object and the launcher does not always increase. Depending on the launch angle, there is a time interval in which the distance decreases and the object approximates the launcher only to move away once again, if it is possible. This happens when the angle is greater than the critical angle whose value is approximately 70.53°. The critical angle does not depend on speed. Below this angle, this effect does not occur. We can say that this is an effect that only takes place for big angles.