Translate this page into:
Prediction of thermal conductivities of polyacrylonitrile electrospun nanocomposite fibers using artificial neural network and prey predator algorithm
⁎Corresponding author. nwwaf977@gmail.com (Nawaf N. Hamadneh)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this study, artificial neural networks were employed to predict thermal conductivity of polyacrylonitrile (PAN) electrospun nanocomposite fibers embedded with multiwalled carbon nanotubes (MWCNTs) and Nickel Zinc ferrites [(Ni0.6Zn0.4) Fe2O4]. The prey predator algorithm was used to train the neural networks to find the best models. This is the first paper on the application of multilayer perception neural network (MLPNN) with the prey predator algorithm for the prediction of thermal conductivity of PAN Electrospun nanocomposites. The method of nonlinear regression was used to minimize the error distribution between the experimental data and the predicted results. Both MWCNTs and Nickel Zinc ferrites were used in different weight proportions. The predicted ANN responses were analyzed statistically using z-test and error functions for both nanoinclusions. The predicted ANN responses for PAN Electrospun nanocomposite fibers were compared with the experimental data and were found in good agreement.
Keywords
Thermal conductivity
PAN Electrospun fibers
Artificial neural network
Prey predator algorithm
Carbon nanotubes
1 Introduction
In the field of nanotechnology, nanocomposites having at least one dimension in nanometer range have been extensively investigated for their wide range of applications, low-cost, ease in processability, good adhesion to substrate and excellent physicochemical properties (Zhang et al., 2009; Khan et al., 2016). Polyacrylonitrile (PAN) is the widely used polymer in different industries such as tissue engineering, wound dressing, protected clothing, filtration and biomedical applications (Kirecci et al., 2012). PAN fibers are widely used in weaving carpet, blankets and are also used in housing instead of asbestos (Farsani et al., 2009). PAN is the main precursor for carbon fibers; therefore, it is studied extensively due to its commercial importance in the production of high-performance carbon fibers. PAN fibers possess several advantages such as high melting temperature (317–330 °C), large yield of carbon fibers and high degree of molecular orientation (Saufi and Ismail, 2002). The glass transition temperature of PAN is between 85 and 95 °C. PAN is around 34% crystalline thermoplastic non-soluble polymer. Generally, crystalline polymers have higher thermal conductivities than non-crystalline (amorphous) polymers since the thermal energy can be easily transmitted along the chains of polymers than between the molecules (Ajayan et al., 1994). The thermal conductivity of polymer is found to increase with the square root of molecular weight (O’connell, 2006). Due to outstanding properties, carbon nanotubes can be used as ideal filler materials in polymer nanocomposites (Ajayan et al., 1994; O’connell, 2006; Harris, 2004; Moniruzzaman and Winey, 2006).
The micro filler materials deteriorate the properties of nanocomposites and result in phase separation due to micro-sized dimensions of filler materials. The phase separation creates interface deficiency and results in establishing most critical place, where void is formed. Therefore, it is indispensable to minimize interface deficiency by replacing micro-fillers with nano-fillers. Ajayan et al. (1994) first incorporated multiwalled carbon nanotubes in polymer matrix to fabricate nanocomposites. Afterwards, numerous projects and reports have appeared on the use of multiwalled carbon nanotubes as filler material in the fabrication of nanocomposites (O’connell, 2006; Harris, 2004; Moniruzzaman and Winey, 2006).
Nickel zinc ferrites are important ferrites from technological point of view. They have high electrical resistivity, good magnetic permeability, high chemical stability and high mechanical strength. They have wide applications in data storage devices, actuators, sensors and targeted drug delivery. Nickel zinc ferrites have spinal structure and they are semi-conductor materials. These ferrites have much lower thermal conductivity than multiwalled carbon nanotubes. Nearly all polymers are non-conducting due to their low values of thermal conductivities; however, polymers can be made conductive by embedding nanofillers such as graphene, carbon blacks, CNTs, and other metallic and ceramic structured nanoinclusions into the polymeric matrices (Norkhairunnisa et al., 2012). Ni-Zn ferrites possess high thermal conductivity due to the nature and structure of these nanoparticles. Due to higher heat conduction, these nanoparticles possess higher vibrational modes and the ferrite nanoparticles form conductive path (percolation network) way at 4 wt% loading of ferrite nanoparticles, which are commonly referred to as “percolation threshold” (Flaifel et al., 2013). This percolation encourages the phonon conduction inside the nanocomposite and increases the thermal conductivity (Gojny et al., 2006). Thermal energy causes atoms to be displaced from their equilibrium site by a small amount, this results in lattice vibrations, which is associated to the heat conduction mechanism in polymeric materials (Hansen and Ho, 1965). In non-metallic materials, the main heat carriers are phonons. The phonons vibration and thermal properties are widely pretentious by the diminution in dimension. The dimensionality of nanomaterials determines their phonon density of states thereby affecting their thermal properties. It has been shown experimentally that the reduction in dimensions may either stimulate or dampen thermal transport mechanism depending on the system and configuration used in measurements (Balandin et al., 2008; Donadio, 2016). The significance of reduction in dimensions is the higher surface-to-volume ratio which helps in transport mechanism (Donadio, 2016).
The thermal conductivity is very sensitive to linear extent of polymeric molecules thus linear polymer have higher thermal conductivity due to lesser interface between the molecules of the polymer chain (Hansen and Ho, 1965; Slade and Jenkins, 1970). In MWCNTs based nanocomposites, phonons have to travel through the matrix phase, which is insulating. Thermal conductivity of insulators is due to the dispersive lattice vibrations or phonon interactions. This lattice vibrations influence the thermal conductivity in nanomaterials. However, lattice vibration causes higher interfacial thermal resistance between nanotubes. The phonon-phonon coupling transfer energy from high-frequency mode to low-frequency mode within the nanotubes (O’connell, 2006).
ANNs offer the advantage of demonstrating complex input-output relationships and is wonderful when used for presenting data classification, signal processing and functional approximation (Hamadneh et al., 2012). Hassoun (1995) defined concepts for majority of ANNs analysis. Hassan et al. (2009) employed ANNs concepts in calculating porosity, density and hardness of composite materials. Some studies have indicated that by applying ANNs concepts, the research in material science and technology has invigorated (Sumpter and Noid, 1996; Giri Dev et al., 2009). Khan et al. (2017) employed ANNs in Prediction of thermal conductivity of polyvinylpyrrolidone (PVP) electrospun nanocomposite fibers.
The above literature reveals that no researcher studied ANN modeling and statistical analysis of thermal conductivity of PAN Electrospun nanocomposite fibers. The main objective of this study was to investigate the effects of nanoinclusions such as Ni-Zn ferrite and MWCNTs on thermal conductivity of PAN Electrospun nanocomposite fibers using ANN modeling and statistical analysis. For this purpose, a neural network approach was used to predict the thermal conductivity of PAN Electrospun nanocomposite fibers as function of weight% of MWCNTs and Ni-Zn ferrites. Experiments were performed on PAN nanocomposite fibers. In developing the ANN model, several configurations were considered. Optimal neural network was selected with two input neurons, several hidden neurons in one hidden layer, and two output neurons for each nanoinclusion. Prey predator algorithm (PPA) is a new algorithm developed for handling a complex optimization applications in engineering, transportation, management, economics, artificial intelligence, and decision science, etc (Hamadneh et al., 2013; Tilahun et al., 2016). It is inspired by the interaction between a predator and prey of animals in the ecosystem (Tilahun and Ong, 2015). The neural networks were trained using PPA to evaluate several neural networks parameters. Predicted thermal conductivity values obtained from neural networks models were examined statistically and compared with actual values obtained from experiments. Several error functions were also used to check the goodness of fit of the models.
2 Experimental
2.1 Materials
Following materials were selected for the experiment:
-
Polyacrylonitrile polymer (molecular weight = 150,000 g/mole)
-
Dimethylformamide (DMF) and
-
Multiwalled carbon nanotubes ( nm and µm)
-
Ni-Zn ferrite (0.6/0.4 ratio).
In the laboratory, Ni-Zn ferrite nanoparticles (21.5 nm) were prepared by means of co-precipitation technique (Khan et al., 2010). In this process, Ni-, Zn-, and Fe-sulfates (NiSO4, ZnSO4, and Fe2 (SO4)3) were first dissolved in deionized (DI) water, and heated to 80 °C for 2–3 h. Sodium Hydroxide was then included drop by drop in the solution to initiate chemical reaction to form ferrites. After around 2 h of agitation under magnetic stirrer, the nickel zinc ferrites (Ni0.6Zn0.4Fe2O4) were slowly formed and began to precipitate. After washing with DI water several times to remove all residual sulfates, fine ferrite (nanosize) particles were produced. The ferrite sample was then dried at room temperature. Crystallinity of a polymers influence the properties of polymers, especially their thermal properties. That is why crystalline ferrite nanoparticles were embedded in PAN polymer and their results were compared with MWCNTs. The atomic force micrograph showed the particle size of approximately 21.5 nm.
2.2 Method
Different wt% of MWCNTs (0%, 0.5%, 1%, 2% and 4%) and Ni0.6Zn0.4Fe2O4 (0%, 1%, 2%, 4%, 8% and 16%) were separately dispersed in DMF solvent and sonicated for 30 min, and then calculated amount of PAN powder was added to the solution. The solution was then stirred on a hot plate at 60 °C at approximately 700 rpm for around 12 h to make a homogeneous blend of PAN polymeric solution. The well-dispersed solution was electrospun to generate nanocomposite fibers.
The polymeric solutions containing different wt% of MWCNTs and ferrite particles (Ni0.6Zn0.4Fe2O4) were shifted to a 10 ml plastic syringe which is connected to a capillary tube having an inside diameter of 0.5 mm and fitted with syringe pump. A platinum electrode having 0.25 mm diameter was connected between syringe and high DC supply. The applied voltage (spinning voltage), pump speed and the distance between capillary tube and collector screen were maintained at 25 kV, 1 ml/hr. and 25 cm, respectively. The collector screen was grounded. After the electrospinning process continued for several hours, the electrospun fibers were collected on a grounded screen and dried in an oven at 60 °C for 6 to 8 h to remove all residual solvents. Conventional fiber forming techniques produces fibers with the diameter within the range of 2–10 microns, while electrospinning produces fibers in nano range. Electrospinning has gained tremendous attention in the last decade due to colossal interest in the new emerging field of nanotechnology. With the help of electrostatic field, fine nanosized continuous polymeric fibers are generated without the help of mechanical or shearing forces, which are necessary in conventional fiber forming processes. Electrospinning utilizes high electrical field that is applied to the polymeric solution to provide an electrostatic force that stretch the fiber jet to nanosize on a collector screen, placed at some distance from the syringe pump (Khan et al., 2010). When the electrostatic field is applied and its magnitude increases to an extent where the electrostatic forces surpasses the surface tension of the polymeric solution, a jet emerges, which travels linearly for 1–2 cm distance and then experiences a looping or chaotic pattern, which is commonly referred to as “bending Instability” of the electrified jet (Khanlou et al., 2014). This bending instability stretches the jet thousands of time (plastic deformation) resulting in very thin fibers. Fig. 1 shows the experimental setup of an electrospinning process. The experimental procedure and data, in detail, has been reported elsewhere (Khan et al., 2013). The experimental arrangement for thermal conductivity testing is depicted in Fig. 2.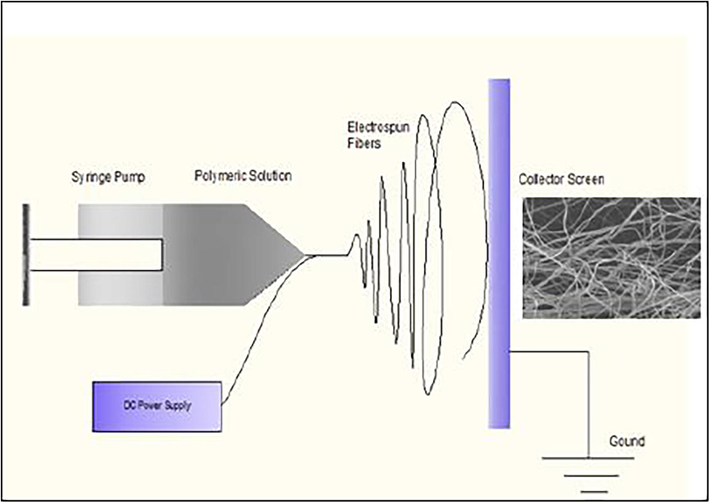
Experimental setup of an electrospinning process.
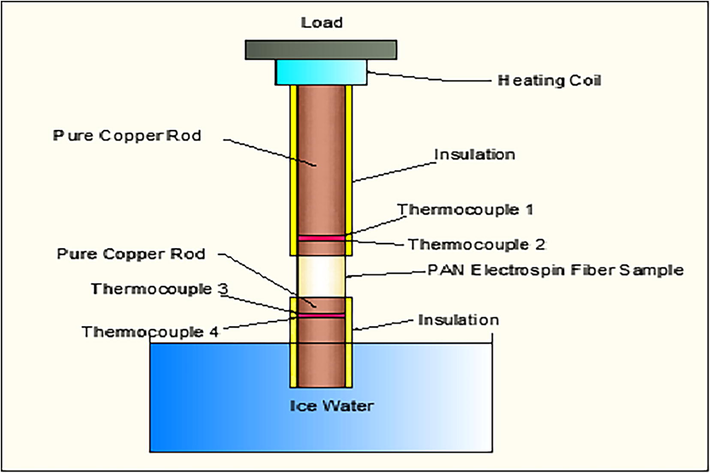
Experimental arrangement of thermal conductivity measurement.
2.3 Artificial neural networks
ANNs are computational models which are constructed to employ inspiration from the functional aspects of biological neural network (Hamadneh et al., 2013; Rakhshandehroo et al., 2012). ANNs are composed of countless neurons known as processing units, which are generally categorized in a series of input, hidden and output layers. Multilayer perception (MLP) is termed as architecture of ANNs (Yeung et al., 2016; Mefoued, 2013). Several algorithms are available to train ANNs. Prey predator algorithm was found to be the most effective algorithm to be used in this study. Each neuron possesses three unique characteristics in the network. These include: a non-linear output, more layers of hidden neurons and high connectivity of network. A structure of the MLPNN is shown in Fig. 3 (Yeung et al., 2016; Mefoued, 2013).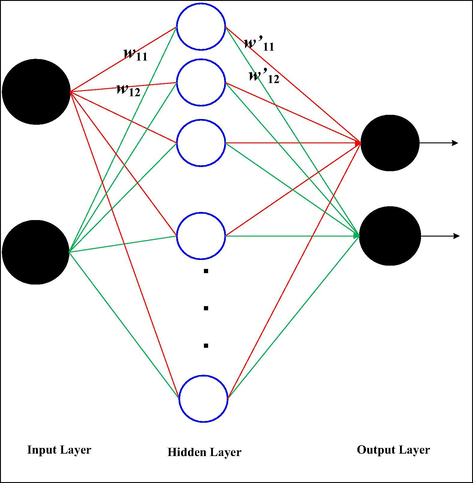
A structure of multilayer neural network.
The activation function in the hidden layer is assumed to be the sigmoid function, which can be given by Eq. (1):
Optimization and validation are two important areas in artificial neural network in order to build networks that are efficient and fast with a suitable function. Training methods are useful for the neural networks to improve their performance. We have used the sum of squared error (SSE) as an objective function to test the performance of the neural networks (Mefoued, 2013). It is given by
We have used prey predator algorithm as neural learning algorithm to estimate the parameters which are the input and the output weights in the neural models.
n: Number of hidden nouns
m: Number of input data
s: Number of input neurons
k: Number of output neurons
: Input weight which is between the input neuron j and hidden neuron k
: Output weight which is between the hidden neuron k and output neuron i
The optimum values of input and output weights are displayed in Table 1.
Model parameters
PAN with MWCNTs
PAN with Ni-Zn Ferrites
Model parameters
PAN with MWCNTs
PAN with Ni-Zn Ferrites
0.6419
0.6369
0.5580
0.0558
0.2370
0.0734
0.4261
0.0463
1.0189
0.0704
−0.0842
0.0793
0.6528
0.9491
−0.0185
0.0199
−0.1338
−0.0413
1.5041
0.7546
0.8800
0.1471
0.0437
0.0971
2.4 Prey predator algorithm
Prey predator algorithm is one of the new swarm based metaheuristic algorithm (Tilahun and Ong, 2015). The algorithm has been found to be effective while applied to different problems, including neural networks, weight minimization of a speed reducer, bi-level problem model of electric market, parameter setting of grinding process, and single frequency bus timetabling (Tilahun and Ong, 2015). It has also been modified to suit combinatorial optimization problems like travel salesman problem, and exam timetabling problem (Tilahun et al., 2016). Comparative study shows that its performance is well and also it is a generalized swarm based algorithm where firefly algorithms, particle swarm optimization algorithm, gravitational search algorithm and random search are the special cases of this algorithm (Tilahun and Ong, 2014; Tilahun et al., 2017; Hamadneh et al., 2013). In PPA, a randomly generated solution sets will be categorized into three categories, the predator, with worst performance of all, the best prey, with the best performance of all, and the rest as ordinary prey (Tilahun and Ong, 2015). The best prey in the other hand does only a local search for exploitation purpose. The main steps of the prey predictor algorithm for training experimental data are explained in Hamadneh et al. (2013), Tilahun and Ong (2015).
3 Statistical analysis
To examine experimental and predicted responses, several statistical tests and error functions are available. The most common statistical tests include z-test (for large samples to test means), F-test (to test variances) and Chi-square test, whereas error functions include Nonlinear Chi-square test (χ2), the sum of the squares of the errors (SSE), the average relative error (ARE), the sum of the absolute errors (EABS), the hybrid fractional error function (HYBRID) (Kumar et al., 2008; Triola, 2006).
3.1 Hypothesis testing
The experimental data for each nanoinclusion was assessed statistically by z-test, which can be employed to test large samples
(Triola, 2006). Appropriate standard errors enable us to judge whether the difference happens to be substantial or not at certain confidence levels. To examine our experimental results statistically, we define a null hypothesis
by assuming that the addition of nanoinclusions (MWCNTs or Ni-Zn Ferrites) in PAN polymers has no effect on thermal conductivity k which is comparable to test
. An alternative hypothesis will show that the addition of nanoinclusions (MWCNTs or Ni-Zn Ferrites) is effective and has significant effects on thermal conductivity k. The level of significance is assumed to be 0.05. For
,
The results of z-test for both nanoinclusions are reported in Section 4 Table 2). The comparison of statistical results demonstrate that
in both cases, therefore, we reject our null hypothesis and conclude that the addition of MWCNTs and Ni-Zn ferrites has significant effect on thermal conductivity.
wt%. MWCNTs
Experimental K
wt%. Ni-Zn Ferrites
Experimental k
Mean
6.322
0.181
7.912134
0.043785
Variance
30.809
3.52E−03
25.01985
2.98E−05
Observations
54
54
58
58
Hypothesized Mean Difference
0
0
Z-value
8.130
11.980
P(Z<=z) one-tail
0.000
0.000
Z Critical one-tail
1.645
1.645
P(Z<=z) two-tail
0.000
0.000
Z Critical two-tail
1.960
3.2 Error functions
In addition to the sum of squared error function which is mentioned above, the following error functions are used in this study to determine the best fit between experimental and ANN predicted results.
3.2.1 The average relative error (ARE)
This error function minimizes the fractional error distribution across the entire concentration range (Kumar et al., 2008). It is given by: where is the experimentally measured thermal conductivity and is the thermal conductivity predicted by ANN.
3.2.2 The sum of the absolute errors (EABS)
This approach is similar to the “ERRSQ” function and it gives a better fit as the magnitude of the errors increase. It is given by Kumar et al. (2008):
3.2.3 Nonlinear chi-square test
This statistical tool is necessary for the best fit of experimental data. The value of chi-square is given by Triola (2006):
3.2.4 The hybrid fractional error function (HYBRID)
This function is used to improve ERRSQ fit at low wt% nanoinclusion concentrations. It considers both the number of data points and the number of parameters. The expression of this error function is given by Kumar et al. (2008):
The results of these error functions are reported in Table 3 for each nanoinclusion. The comparison of error function reveals that ANN predictions are much better for Ni-Zn Ferrites than MWCNTs.
Error Functions
PAN Polymers
MWCNTs
Ni-Zn Ferrites
RMSD
0.0293
0.000684
SSE
0.0455
2.67E−05
ARE
1.65E+01
1.24E+00
EABS
1.3098
0.03042
Chi-square
2.85E−01
6.40E−04
HYBRID
5.39E−01
1.12E−03
4 Results and discussion
This study is divided into three steps. The first step is to find thermal conductivity of PAN Electrospun nanocomposite fibers values for different values of weight% of MWCNTs and Ni-Zn ferrites. Multilayer perceptron neural network is trained using prey predator algorithm in order to build neural network models (NNM), as shown in Fig. 4. In NNM, the inputs are weight% of MWCNTs and Ni-Zn ferrites. The output of NNM is the corresponding value of thermal conductivity of PAN Electrospun nanocomposite fibers. Accordingly, no need once again to go back to step one; because in step two, the NNs are trained based on step one. As a result, the NNMs can be used to find the corresponding values of thermal conductivity of PAN Electrospun nanocomposite fibers for different values of weight% of MWCNTs and Ni-Zn ferrites.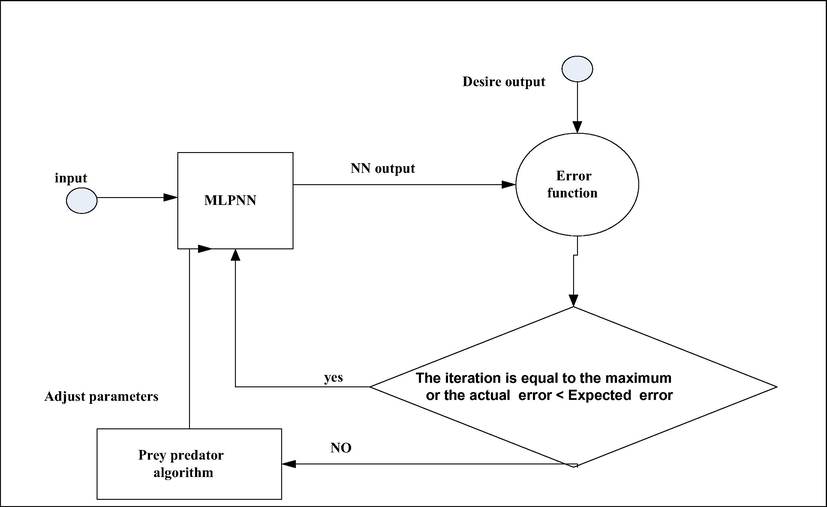
Structure of training MLPNN using prey predator algorithm.
The architecture of the neural networks which we used is two input neurons- one hidden layer with several neurons, and two output neurons. The trial and error method was employed to select the best number of the hidden neurons. We used PPA in the training process to determine the input weights and output weights to minimize the error of the neural networks. The considered PPA applied in this study has 100 local search directions, with 120 solutions and 9 predators. The MATLAB software has been used to implement the PPA and ANNs.
To train the neural network, we used 50% data as training data. PPA is executed 50 times with 100 iterations in order to find best model that has minimum error Fig. 5). As mentioned above, the error is the difference between the actual values and the predicted values in training data. In the first experiment, we trained the neural network with PAN data (wt% of MWCNTs was used as input data and thermal conductivity as output data). In the next step, we test the untrained data and confirm the predicted values Fig. 6).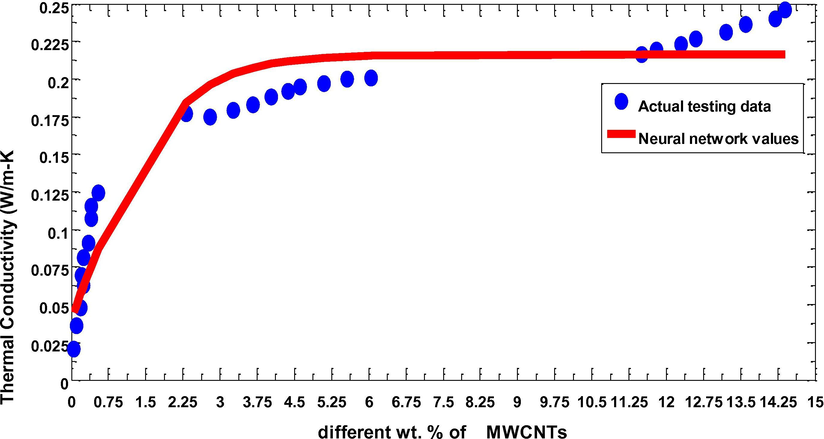
Training actual data for PAN with different wt% of MWCNTs.
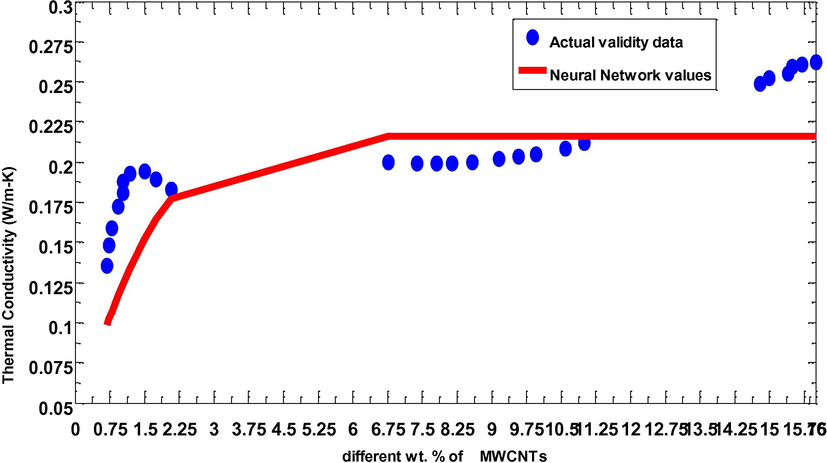
Validity of actual data with ANN data for PAN with different wt% of MWCNTs.
The best convergence speed of PPA in terms of SSE in MLPNN is depicted in Fig. 7 with SSE = 0.00149. The corresponding parameters, that represent the best model, are listed in Table 1. Fig. 8 presents the final comparison between simulated and experimental values of thermal conductivities for the PAN fibers incorporated with MWCNTs. It shows smallest dispersion between the two results. In fact, the correlation has a standard error of 0.013 and a coefficient of determination of 0.978 which is considered as a good value for the correlation. It demonstrates that the neural network system gives predictions with a least standard error. For instance, with 0, 2, 4, 8 and 16 wt% of MWCNTs in PAN fibers, the thermal conductivity values increase to 0.02, 0.18, 0.20 and 0.26 W/m-K, respectively. It was presumed initially that the thermal conductivity of PAN nanocomposite fibers would enhance significantly with the addition of MWCNTs. However, the test results failed to display any drastic improvement in thermal conductivity of PAN nanocomposite fibers even at higher concentration of MWCNTs, i.e. 16 wt%. The reason for this small-scale improvement is the presence of air pockets in fiber texture and interfacial resistance between MWCNTs and polymer matrix. The other reasons could be the alignment of nanotubes, dispersion techniques and size of nanotubes.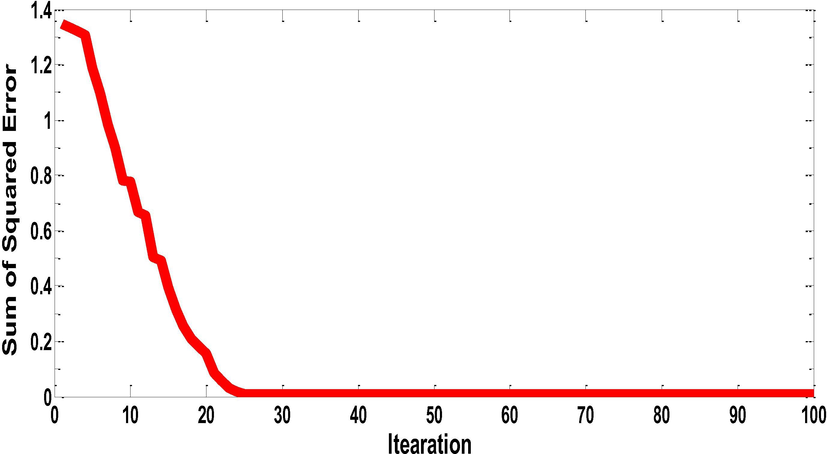
Best performance of prey predator algorithm in terms of sum of squared error for PAN nanocomposites with different wt% of MWCNTs.
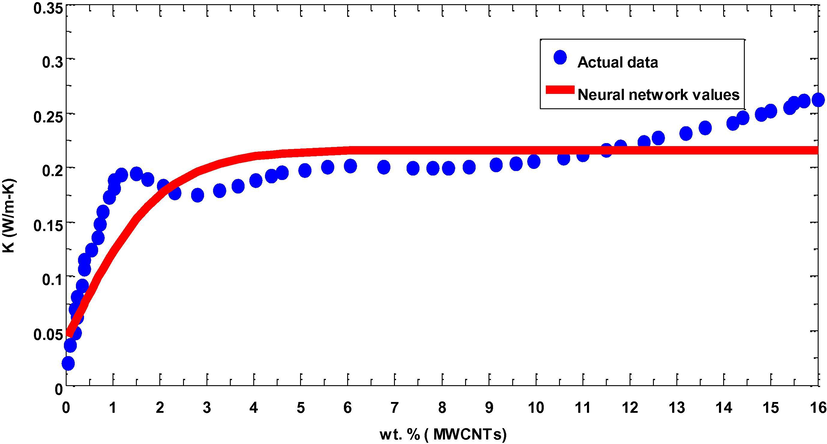
Comparison of actual data with ANN data for PAN with different wt% of MWCNTs.
We repeated the same experiment with PAN data having different wt% of Ni-Zn ferrites as input data and the thermal conductivity as output data and found the best model with minimum error Fig. 9). We found that the best model has 2 input neurons-6 hidden neurons- 2output neurons; because of the minimal SSE is equal 0.00014. The comparison between simulated and experimental results for the PAN fibers incorporated with Ni-Zn ferrites is displayed in Fig. 10. The results show that the addition of Ni-Zn ferrites to PAN polymer matrix increases the thermal conductivity of PAN nanocomposite fibers, which is also supported by the statistical analysis Table 2. The experimental data shows that the thermal conductivity values increase up to 4% Ni-Zn ferrite nanoparticles, and after this concentration, the thermal conductivity did not show any marked improvement. This may be due to lower thermal conductivity of Ni-Zn ferrites than MWCNTs. The other reasons may be nanoparticle size and shape, volume fraction of nanoinclusions as well as dispersion techniques. Predicted results are plotted against experimental results in Fig. 11 for MWCNTs and in Fig. 12 for Ni-Zn ferrites respectively. The correlation coefficient between the experimental data and predicted data is found to be greater than 0.90 for both cases which is greater than 0.811 (Triola, 2006).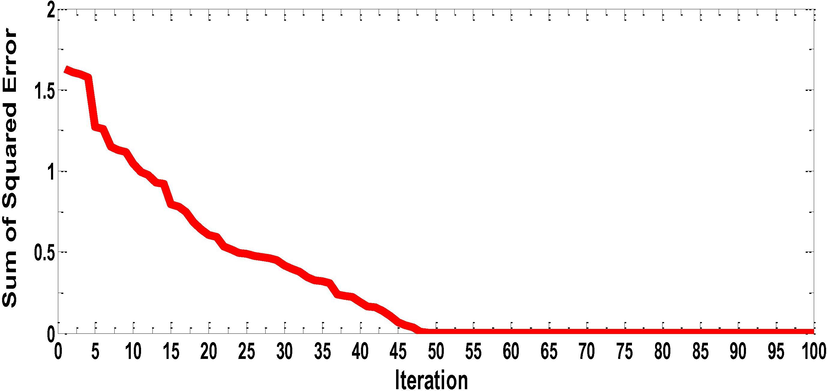
The best performance of prey predator algorithm in terms of sum of squared error for PAN with different wt% of Ni-Zn Ferrites.
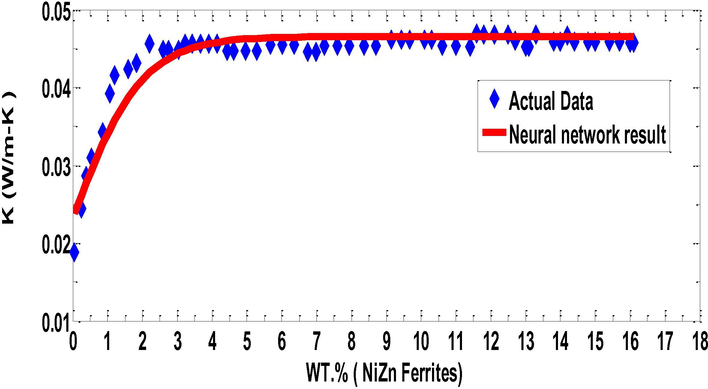
Comparison of actual data with expected data for PAN with different wt% of Ni-Zn ferrites.
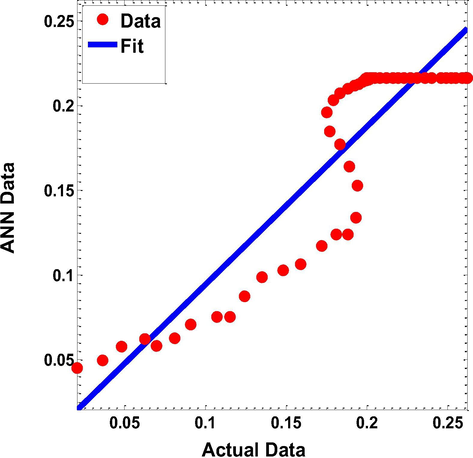
Linear correlation of actual data versus neural network values of Thermal Conductivity (PAN POLYMER with wt% of MWCNTS) (R = 0.9).
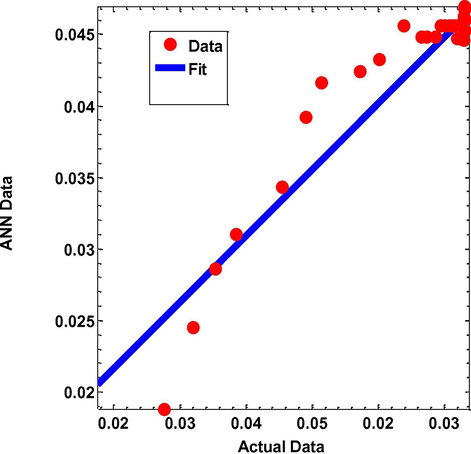
Linear correlation of actual data versus neural network values of Thermal Conductivity (PAN POLYMER with wt% of Ni-Zn ferrites (R = 0.95).
5 Conclusions
Multilayer perception neural network (MLPNN) and prey predator algorithm were employed successfully to predict the thermal conductivity of PAN nanocomposite fibers embedded with MWCNTs and Ni-Zn ferrites and the predictions have been validated statistically using z-test and error functions. Nonlinear regression analysis was used to minimize the error distribution between the experimental data and predicted results. The increase in the thermal conductivity of PAN fibers incorporated with MWCNTs or Ni-Zn ferrites was not found as per our expectations. The predicted ANN responses for PAN electrospun nanocomposite fibers were compared with the experimental data and were found in good agreement.
References
- Aligned carbon nanotube arrays formed by cutting a polymer resin-nanotube composite. Sci.-AAAS-Weekly Paper Ed.. 1994;265(5176):1212-1214.
- [Google Scholar]
- Superior thermal conductivity of single-layer graphene. Nano Lett.. 2008;8(3):902-907.
- [Google Scholar]
- Simulation of Dimensionality Effects in Thermal Transport. Thermal Transport in Low Dimensions. Springer; 2016. pp. 275–304
- FT-IR study of stabilized PAN fibers for fabrication of carbon fibers. World Acad. Sci., Eng. Technol.. 2009;50:430-433.
- [Google Scholar]
- Thermalconductivity and dynamic mechanical analysis of NiZn ferrite nanoparticles filled thermoplastic natural rubber nanocomposite. Compos. B Eng.. 2013;52:334-339.
- [Google Scholar]
- Prediction of water retention capacity of hydrolysed electrospun polyacrylonitrile fibers using statistical model and artificial neural network. J. Appl. Polym. Sci.. 2009;113(5):3397-3404.
- [Google Scholar]
- Evaluation and identification of electrical and thermal conduction mechanisms in carbon nanotube/epoxy composites. Polymer. 2006;47(6):2036-2045.
- [Google Scholar]
- Learning logic programming in radial basis function network via genetic algorithm. J. App. Sci.. 2012;12(9):840.
- [Google Scholar]
- Design optimization of pin fin geometry using particle swarm optimization algorithm. PloS one.. 2013;8(5):e66080.
- [Google Scholar]
- Prey-predator algorithm as a new optimization technique using in radial basis function neural networks. Res. J. Appl. Sci.. 2013;8(7):383-387.
- [Google Scholar]
- Thermal conductivity of high polymers. J. Polym. Sci. Part A: Gen. Papers. 1965;3(2):659-670.
- [Google Scholar]
- Carbon Nanotubes and Related Structures: New Materials for the Twenty-First Century. AAPT; 2004.
- Prediction of density, porosity and hardness in aluminum–copper-based composite materials using artificial neural network. J. Mater. Process. Technol.. 2009;209(2):894-899.
- [Google Scholar]
- Fundamentals of Artificial Neural Networks. MIT press; 1995.
- Dielectric properties of electrospun PVP and PAN nanocomposite fibers at various temperatures. J. Nanotechnol. Eng. Med.. 2010;1(4):041017.
- [Google Scholar]
- Thermal conductivities of electrospun PAN and PVP nanocomposite fibers incorporated with MWCNTs and NiZn ferrite nanoparticles. Int. J. Therm. Sci.. 2013;71:74-79.
- [Google Scholar]
- Polymer Nanocomposites – Synthesis Techniques, Classification and Properties. SCIENCE and Applications of Tailored Nanostructures. One Central Press (OCP); 2016.
- Prediction of thermal conductivity of polyvinylpyrrolidone (PVP) electrospun nanocomposite fibers using artificial neural network and prey-predator algorithm. PloS One. 2017;12(9):e0183920.
- [Google Scholar]
- Prediction and optimization of electrospinning parameters for polymethyl methacrylate nanofiber fabrication using response surface methodology and artificial neural networks. Neural Comput. Appl.. 2014;25(3–4):767-777.
- [Google Scholar]
- Determination of optimal production parameters for polyacrylonitrile nanofibers. J. Appl. Polym. Sci.. 2012;124(6):4961-4968.
- [Google Scholar]
- Isotherms and thermodynamics by linear and non-linear regression analysis for the sorption of methylene blue onto activated carbon: comparison of various error functions. J. Hazard. Mater.. 2008;151(2):794-804.
- [Google Scholar]
- Mefoued S., ed. Assistance of knee movements using an actuated orthosis through subject's intention based on MLPNN approximators. Neural Networks (IJCNN), The 2013 International Joint Conference on. IEEE; 2013.
- Polymer nanocomposites containing carbon nanotubes. Macromolecules. 2006;39(16):5194-5205.
- [Google Scholar]
- Thermal stability and electrical behavior of polydimethylsiloxane nanocomposites with carbon nanotubes and carbon black fillers. J. Compos. Mater.. 2012;46(8):903-910.
- [Google Scholar]
- Carbon Nanotubes: Properties and Applications. CRC press; 2006.
- Forecasting groundwater level in Shiraz plain using artificial neural networks. Arabian J. Sci. Eng.. 2012;1–13
- [Google Scholar]
- Development and characterization of polyacrylonitrile (PAN) based carbon hollow fiber membrane. Songklanakarin J. Sci. Technol.. 2002;24:843-854.
- [Google Scholar]
- Thermal characterization techniques. Marcel Dekker; 1970.
- On the design, analysis, and characterization of materials using computational neural networks. Annu. Rev. Mater. Sci.. 1996;26(1):223-277.
- [Google Scholar]
- Prey Predator Algorithm for Travelling Salesman Problem: Application on the Ethiopian Tourism Sites. Handbook of Research on Holistic Optimization Techniques in the Hospitality. Tourism, and Travel Industry; 2016. p. :400.
- Comparison between genetic algorithm and prey-predator algorithm. Malaysian J. Fundam. Appl. Sci.. 2014;9(4)
- [Google Scholar]
- Prey-predator algorithm: a new metaheuristic algorithm for optimization problems. Int. J. Inf. Technol. Dec. Making. 2015;14(06):1331-1352.
- [Google Scholar]
- Elementary Statistics. MA: Pearson/Addison-Wesley Reading; 2006.
- MLPNN training via a multiobjective optimization of training error and stochastic sensitivity. IEEE Trans. Neural Netw. Learn. Syst.. 2016;27(5):978-992.
- [Google Scholar]
- Electrospun polyacrylonitrile nanocomposite fibers reinforced with Fe3O4 nanoparticles: fabrication and property analysis. Polymer. 2009;50(17):4189-4198.
- [Google Scholar]







