Optimal perturbation iteration method for Bratu-type problems

Sinan Deniz; Necdet Bildik

doi:10.1016/j.jksus.2016.09.001

View/Download PDF

Buy Reprints

PDF

Translate this page into:

30 (

); 91-99

doi:

10.1016/j.jksus.2016.09.001

Optimal perturbation iteration method for Bratu-type problems

Sinan Deniz, Necdet Bildik^⁎

Celal Bayar University, Faculty of Arts and Science, Department of Mathematics, 45047 Manisa, Turkey

⁎Corresponding author. n.bildik@cbu.edu.tr (Necdet Bildik)

Received: 2016-5-4, Accepted: 2016-9-5, Published: 2016-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this paper, we introduce the new optimal perturbation iteration method based on the perturbation iteration algorithms for the approximate solutions of nonlinear differential equations of many types. The proposed method is illustrated by studying Bratu-type equations. Our results show that only a few terms are required to obtain an approximate solution which is more accurate and efficient than many other methods in the literature.

Keywords

Optimal perturbation iteration method

Perturbation methods

Bratu-type equations

Show Related Articles from PubMed

1 Introduction

Many nonlinear differential equations are used in many scientific studies and most of them cannot be solved analytically using traditional methods. Therefore these problems are often handled by a broad class of analytical and numerical methods such as Adomian decomposition method (Adomian, 1988; Deniz and Bildik, 2014), Taylor collocation method (Bildik and Deniz, 2015), differential transform method (Bildik and Konuralp, 2006), homotopy perturbation method (Öziş and Ağırseven, 2008), variational iteration method (He, 2003). These methods can give accurate solutions to nonlinear problems but they have also some problems about the convergence region of their series solution. These regions are generally small according to the desired solution. In order to cope with this task, researchers have recently proposed some new methods (Marinca and Herişanu, 2008; Liao, 2012; Idrees et al., 2010 ). Perturbation iteration method is one of them and has been recently developed by Pakdemirli et.al. It has proven that this method is very effective for solving many nonlinear equations arising in the scientific world (Aksoy and Pakdemirli, 2010; Aksoy et al., 2012; Şenol et al., 2013; Dolapçı et al., 2013; Khalid et al., 2015 ). In the presented study, we construct a new optimal perturbation iteration method which is applicable to a wide range of equations and does not require special transformations. In order to show the efficiency of the proposed method, we try to solve Bratu initial and boundary value problems which are used in a large variety of applications, such as the fuel ignition model of the theory of thermal combustion, the thermal reaction process model, radioactive heat transfer, nanotechnology and theory of chemical reaction (Doha et al., 2013; He et al., 2014; Raja, 2014 ).

2 Perturbation iteration method

Pakdemirli and his co-workers have modified the well-known perturbation method to construct perturbation iteration method (PIM). PIM has been efficiently applied to some strongly nonlinear systems and yields very approximate results (Aksoy et al., 2012; Şenol et al., 2013). In this section; we give basic information about perturbation iteration algorithms. They are classified with respect to the number of correction terms (n) and with respect to the degrees of derivatives in the Taylor expansions (m). Briefly, this process is represented as PIA ( $n, m$ ).

2.1

2.1 PIA (1,1)

In order to illustrate the algorithm, consider a second-order differential equation in closed form:

(2.1)

F (y^{″}, y^{'}, y, ε) = 0

where

y = y (x)

and

ε

is the perturbation parameter. For PIA (1,1), we take one correction term from the perturbation expansion:

(2.2)

y_{n + 1} = y_{n} + ε {(y_{c})}_{n}

Substituting (2.2) into (2.1) and then expanding in a Taylor series gives

(2.3)

F ({y_{n}}^{″}, y_{n}^{'}, y_{n}, 0) + F_{y} {(y_{c})}_{n} ε + F_{y^{'}} {({y_{c}}^{'})}_{n} ε + F_{y^{″}} {({y_{c}}^{″})}_{n} ε + F_{ε} ε = 0

Rearranging Eq. (2.3) yields a linear second order differential equation:

(2.4)

{({y_{c}}^{″})}_{n} + \frac{F_{y^{'}}}{F_{y^{″}}} {({y_{c}}^{'})}_{n} + \frac{F_{y}}{F_{y^{″}}} {(y_{c})}_{n} = - \frac{\frac{F}{ε} + F_{ε}}{F_{y^{″}}}

We can easily obtain ${(y_{c})}_{0}$ from Eq. (2.4) by using an initial guess $y_{0}$ . Then first approximation $y_{1}$ is determined by using this information.

2.2

2.2 PIA (1,2)

As distinct from PIA (1,1), we need to take $n = 1, m = 2$ to obtain PIA (1,2). In other words, second order derivatives must be taken into consideration:

(2.5)

F (y_{n}^{″}, y_{n}^{'}, y_{n}, 0) + F_{y} {(y_{c})}_{n} ε + F_{y^{'}} {(y_{c}^{'})}_{n} ε + F_{y}^{″} {(y_{c}^{″})}_{n} ε + F_{ε} ε + \frac{1}{2} ε^{2} F_{y^{″} y^{″}} {(y_{c}^{″})}_{n}^{2} + \frac{1}{2} ε^{2} F_{y^{'} y^{'}} {(y_{c}^{'})}_{n}^{2} + \frac{1}{2} ε^{2} F_{yy} {(y_{c})}_{n}^{2} + ε^{2} F_{y^{″} y^{'}} {(y_{c}^{″})}_{n} {(y_{c}^{'})}_{n} + ε^{2} F_{y^{'} y} {(y_{c}^{'})}_{n} {(y_{c})}_{n} + ε^{2} F_{y^{″} y} {(y_{c}^{″})}_{n} {(y_{c})}_{n} + F_{ε y^{″}} {(y_{c}^{″})}_{n} ε^{2} + F_{ε y^{'}} {(y_{c}^{'})}_{n} ε^{2} + F_{ε y} {(y_{c})}_{n} ε^{2} + \frac{1}{2} ε^{2} F_{ε ε} = 0

or by rearranging

(2.6)

{(y_{c}^{″})}_{n} (ε F_{y^{″}} + ε^{2} F_{ε y^{″}}) + {(y_{c}^{'})}_{n} (ε F_{y^{'}} + ε^{2} F_{ε y^{'}}) + {(y_{c})}_{n} (ε F_{y} + ε^{2} F_{ε y}) + {(y_{c}^{″})}_{n}^{2} (\frac{ε^{2}}{2} F_{y^{″} y^{″}}) + {(y_{c}^{'})}_{n}^{2} (\frac{ε^{2}}{2} F_{y^{'} y^{'}}) + {(y_{c})}_{n}^{2} (\frac{ε^{2}}{2} F_{yy}) + {(y_{c})}_{n} {(y_{c}^{'})}_{n} (ε^{2} F_{y^{'} y}) + {(y_{c}^{″})}_{n} {(y_{c}^{'})}_{n} (ε^{2} F_{y^{'} y^{″}}) + {(y_{c}^{″})}_{n} {(y_{c})}_{n} (ε^{2} F_{{yy}^{″}}) = - F - F_{ε} ε - \frac{ε^{2} F_{ε ε}}{2} .

Note that all derivatives and functions are calculated at $ε = 0$ . By means of (2.2) and (2.6), iterative scheme is developed for the equation under consideration.

3 Optimal perturbation iteration method

To illustrate the basic concept of the optimal perturbation iteration method (OPIM), we first reconsider Eq. (2.1) as:

(3.1)

F (y^{″}, y^{'}, y, ε) = Ly + N (y^{″}, y^{'}, y, ε), B (y, y^{'}) = 0

where L is a linear operator, N denotes the nonlinear terms and B is a boundary operator respectively. We then expand only nonlinear terms in a Taylor series to decrease the volume of calculations. Because, it is useless and unnecessary to expand the whole equation for each problem. This is the first step of OPIM to decrease the time needed for computations.

After Eqs. (2.4) and (2.6) in the solution processes for PIAs (1,m), we offer to use the formula

(3.2)

y_{n + 1} = y_{n} + S_{n} (ε) {(y_{c})}_{n}

to increase the accuracy of the results and effectiveness of the method. Here

S_{n} (ε)

is an auxiliary function which provides us to adjust and control the convergence. This is the crucial point of OPIM. The choices of functions

S_{n} (ε)

could be exponential, polynomial, etc. In this study, we select auxiliary function in the form

(3.3)

S_{n} (ε) = C_{0} + ε C_{1} + ε^{2} C_{2} + ε^{3} C_{3} + \dots = \sum_{i = 0}^{n} ε^{i} C_{i}

where

C_{0}, C_{1}, \dots

are constants which are to be determined later.

The following algorithm can be used for OPIM:

a) Take the governing differential equation as:

(3.4)

Ly + N (y^{″}, y^{'}, y, ε) = 0, y = y (x), a ⩽ x ⩽ b

b) Substitute (2.2) into the nonlinear part of (3.4) and expand it in a Taylor series:

(3.5)

N ({y_{n}}^{″}, y_{n}^{'}, y_{n}, 0) + N_{y} {(y_{c})}_{n} ε + N_{y^{'}} {({y_{c}}^{'})}_{n} ε + N_{y^{″}} {({y_{c}}^{″})}_{n} ε + N_{ε} ε = 0

and

(3.6)

\begin{matrix} N + N_{y} {(y_{c})}_{n} ε + N_{y^{'}} {(y_{c}^{'})}_{n} ε + N_{ε} ε + N_{ε y} {(y_{c})}_{n} ε^{2} + N_{ε y^{'}} {(y_{c}^{'})}_{n} ε^{2} + \frac{N_{ε ε} ε^{2}}{2} + \frac{N_{yy} ε^{2} {(y_{c})}_{n}^{2}}{2} + \frac{N_{y^{'} y^{'}} ε^{2} {(y_{c}^{'})}_{n}^{2}}{2} = 0 \end{matrix}

c) After finding ${(y_{c})}_{0}$ for each algorithm as in PIAs (1,m), substitute it into Eq. (3.2) to find the first approximate result:

(3.7)

y_{1} = y_{0} + S_{0} (ε) {(y_{c})}_{0} = y_{0} + C_{0} {(y_{c})}_{0}

By using initial condition and setting $ε = 1$ yields

(3.8)

y_{1} = y (x, C_{0})

Using Eq. (3.8) and repeating the similar steps, we have:

(3.9)

\begin{matrix} y_{2} (x, C_{0}, C_{1}) = y_{1} + S_{1} (ε) {(y_{c})}_{0} = y_{1} + (C_{0} + C_{1}) {(y_{c})}_{1} \\ y_{3} (x, C_{0}, C_{1}, C_{2}) = y_{2} + (C_{0} + C_{1} + C_{2}) {(y_{c})}_{2} \\ ⋮ \\ y_{m} (x, C_{0}, \dots, C_{m - 1}) = y_{m - 1} + (C_{0} + \dots + C_{m - 1}) {(y_{c})}_{m - 1} \end{matrix}

d) Substitute the approximate solution $y_{m}$ into Eq. (3.4) and the general problem results in the following residual:

(3.10)

R (x, C_{0}, \dots, C_{m - 1}) = L (y_{m} (x, C_{0}, \dots, C_{m - 1})) + N (y_{m} (x, C_{0}, \dots, C_{m - 1}))

Obviously, when $R (x, C_{0}, \dots, C_{m - 1}) = 0$ then the approximation $y_{m} (x, C_{0}, \dots, C_{m - 1}) = y^{(m)} (x, C_{i})$ will be the exact solution. Generally it doesn’t happen, especially in nonlinear equations. To determine the optimum values of $C_{0}, C_{1}, \dots$ ; we here use the equations

(3.11)

R (x_{1}, C_{i}) = R (x_{2}, C_{i}) = \dots = R (x_{m}, C_{i}) = 0, i = 0, 1, \dots, m - 1

where

x_{i} \in (a, b)

. Generally it is quite impossible to solve the system of Eq. (3.11) other than numerically. Therefore, one needs to use a computer program such that Mathematica, Maple etc. Note that the solution of the system (3.11) is not unique, but all obtained constants would yield the same approximate solutions.

The constants $C_{0}, C_{1}, \dots$ can also be defined from the method of least squares:

(3.12)

J (C_{0}, \dots, C_{m - 1}) = \int_{a}^{b} R^{2} (x, C_{0}, \dots, C_{m - 1}) dx

where a and b are selected from the domain of the problem. Putting these constants into the last one of Eq. (3.9), the approximate solution of order m is well-determined. It should be also emphasized that, Eq. (3.12) is not always useful to find the constants

C_{0}, C_{1}, \dots

especially for strongly nonlinear equations. So,we use Eq. (3.11) to get those constants in this work. For much more information and different usage about this process, please see Herisanu et al. (2015) and Marinca and Herişanu (2012)

4 Applications

Example 1. Consider the following nonlinear differential equation (Wazwaz, 2005):

(4.1)

y^{″} - 2 e^{y} = 0, y (0) = y^{'} (0) = 0, 0 ⩽ x ⩽ 1 .

which has the exact solution

y = - 2 \ln (\cos x)

4.1

4.1 OPIA (1,1)

Consider Eq. (4.1) as:

(4.2)

F (y^{″}, y, ε) = y^{″} - 2 e^{ε y} = y^{″} + N (y, ε) .

OPIA (1,1) requires to compute:

(4.3)

N (y_{n}, 0) + N_{y} (y_{n}, 0) {(y_{c})}_{n} ε + N_{ε} ε = 0

which is approximately half of the volume of calculations that in PIA (1,1). Using Eqs. (2.2), (4.3) and setting

ε = 1

yields

(4.4)

{({y_{c}}^{″})}_{n} = - y_{n}^{″} + 2 y_{n} + 2

One may start the iteration by taking a trivial solution which satisfies the given initial conditions:

(4.5)

y_{0} = 0 .

Substituting (4.5) into Eq. (4.4), we have

(4.6)

{(y_{c})}_{0} = x^{2} + c

Now, Eq. (4.6) is inserted into Eq. (3.2) and applying the initial conditions we get

(4.7)

y_{1} = y_{0} + S_{n} (ε) {(y_{c})}_{0} = C_{0} x^{2}

It is worth mentioning that $y_{1}$ does not represent the first correction term; rather it is the approximate solution after the first iteration. Following the same procedure, we obtain new and more approximate results:

(4.8)

y_{2} = C_{0} x^{2} + (C_{0} + C_{1}) (x^{2} - C_{0} x^{2} + \frac{C_{0} x^{4}}{6})

(4.9)

y_{3} = [2 C_{0} + C_{1} - C_{0} (C_{0} + C_{1}) + (- 1 + C_{0}) (- 1 + C_{0} + C_{1}) (C_{0} + C_{1} + C_{2})] x^{2} + [\frac{1}{6} C_{0} (C_{0} + C_{1}) + \frac{1}{15} (- 5 C_{0}^{2} - 5 C_{0} (- 1 + C_{1}) + \frac{5 C_{1}}{2}) (C_{0} + C_{1} + C_{2})] x^{4} + [\frac{1}{90} C_{0} (C_{0} + C_{1}) (C_{0} + C_{1} + C_{2})] x^{6}

To determine the constants, we proceed as in Section 3. First, the residual

(4.10)

R (x, C_{0}, C_{1}, C_{2}) = L (y_{3} (x, C_{0}, C_{1}, C_{2})) + N (y_{3} (x, C_{0}, C_{1}, C_{2})) = 2 C_{0} + (C_{0} + C_{1}) (2 - 2 C_{0} + 2 C_{0} x^{2}) + \frac{(C_{0} + C_{1} + C_{2})}{15} \times [30 (- 1 + C_{0}) (- 1 + C_{0} + C_{1}) + 12 (- 5 C_{0}^{2} - 5 C_{0} (- 1 + C_{1}) + \frac{5 C_{1}}{2}) x^{2} + 5 C_{0} (C_{0} + C_{1}) x^{4}] - 2 Exp [\begin{matrix} C_{0} x^{2} + (C_{0} + C_{1}) (x^{2} - C_{0} x^{2} + \frac{C_{0} x^{4}}{6}) + \frac{1}{6} C_{0} (C_{0} + C_{1}) x^{6} \\ \frac{(C_{0} + C_{1} + C_{2})}{15} (15 (- 1 + C_{0}) (- 1 + C_{0} + C_{1}) x^{2} + (- 5 C_{0}^{2} - 5 C_{0} (- 1 + C_{1}) + \frac{5 C_{1}}{2}) x^{4}) \end{matrix}]

is constructed for the third order approximation. Using Eq. (3.11) with

x = 0.3, 0.6, 0.9

, we get

(4.11)

C_{0} = 1.00096007239, C_{1} = 0.034138423506, C_{2} = - 0.049127633506

Inserting the constants into Eq. (4.9), we obtain the approximate solution of the third order:

(4.12)

y_{3} (x) = 1.00112456947 x^{2} + 0.152984774463 x^{4} + 0.076778117636 x^{6}

Note that some complex numbers arise from solving Eq. (4.10). They can also be used instead of $C_{0}, C_{1}, C_{2}$ to get the same result. We here give only real solutions for simplicity.

4.2

4.2 OPIA (1,2)

One can construct the OPIA (1,2) by taking one correction term in the perturbation expansion and two derivatives in the Taylor series. Note that one needs to enter the data in Eq. (2.4) into the computer for PIA (1,2). But, it is sufficient to use

(4.13)

N + N_{y} {(y_{c})}_{n} ε + N_{ε} ε + N_{ε y} {(y_{c})}_{n} ε^{2} + \frac{N_{ε ε} ε^{2}}{2} + \frac{N_{yy} ε^{2} {(y_{c})}_{n}^{2}}{2} = 0

for OPIA (1,2). After making the relevant calculations, the algorithm takes the simplified form:

(4.14)

{({y_{c}}^{″})}_{n} - 2 {(y_{c})}_{n} = - y_{n}^{″} + 2 y_{n} + y_{n}^{2} + 2

Using the trivial solution $y_{0} = 0$ , we have second order problem

(4.15)

{({y_{c}}^{″})}_{0} - 2 {(y_{c})}_{0} = 2

Using Eqs. (3.2), (4.15) and the initial conditions, we obtain

(4.16)

y_{1} = C_{0} (\cosh (\sqrt{2} x) - 1)

Following the same procedure using (4.16), the second iteration is obtained as

(4.17)

y_{2} = \frac{1}{3} (\begin{matrix} - 3 C_{0} + 3 C_{0} \cosh [\sqrt{2} x] - \frac{3 {C_{0}}^{2} (C_{0} + C_{1}) x \sinh [\sqrt{2} x]}{\sqrt{2}} \\ + ((C_{0} + C_{1}) (6 + C_{0} (- 6 + 5 C_{1}) + C_{0}^{2} \cosh [\sqrt{2} x])) \sinh {[\frac{x}{\sqrt{2}}]}^{2} \end{matrix})

One can easily realize that, we have functional expansion for OPIA (1,2) instead of a polynomial expansion.

Following the same procedure, from the residual

(4.18)

R (x, C_{0}, C_{1}) = L (y_{2}) + N (y_{2}) = \frac{1}{3} [\begin{matrix} - 2 (- 3 C_{1} + C_{0} (3 (- 2 + C_{1}) + C_{0} (3 + C_{0} + C_{1}))) \cosh [\sqrt{2} x] \\ + C_{0}^{2} (C_{0} + C_{1}) (2 \cosh [2 \sqrt{2} x] - 3 \sqrt{2} x \sinh [\sqrt{2} x]) \end{matrix}] - 2 Exp [\frac{1}{3} (\begin{matrix} (C_{0} + C_{1}) (6 + C_{0} (- 6 + 5 C_{0}) + C_{0}^{2} \cosh [\sqrt{2} x]) \sinh {[\frac{x}{\sqrt{2}}]}^{2} \\ - \frac{3 {C_{0}}^{2} (C_{0} + C_{1}) x \sinh [\sqrt{2} x]}{\sqrt{2}} - 3 C_{0} + 3 C_{0} \cosh [\sqrt{2} x] \end{matrix})]

the constants

C_{0}

and

C_{1}

can be determined as

(4.19)

C_{0} = 1.000861120478, C_{1} = 0.0266135748038

Thus, we have the second-order approximate solution:

(4.20)

y_{2} (x) = - 1.1784311655118591 x \sinh (\sqrt{2} x) + 2.1406095945289634 \cosh (\sqrt{2} x) + 0.13215241067298802 \cosh (2 \sqrt{2} x) - 2.2728821098149927

One can also compute more approximate results by following the same procedure with a computer program. We do not give higher iterations due to huge amount of calculations. Fig. 1 and Table 1 shows a comparison of OPIAs and exact solution. It is clear that the results obtained by OPIM are more accurate than those of PIM in Aksoy and Pakdemirli (2010).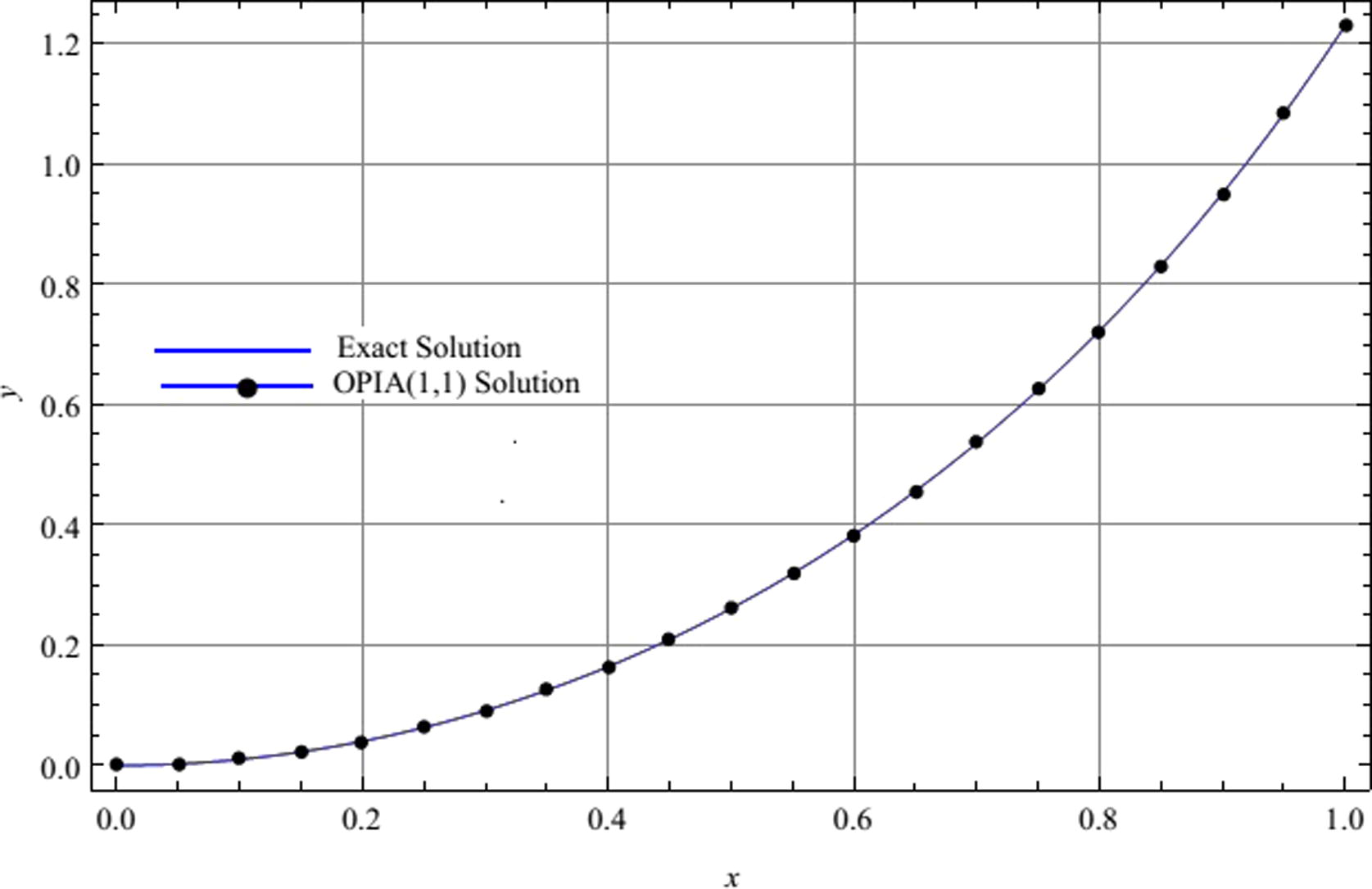

Comparison between the three-term OPIA (1,1) approximate solution and the exact solution for Example 1.

Table 1 Comparison of absolute errors of Example 1 at different orders of approximations.

x	Absolute errors for OPIA (1,1) solutions			Absolute errors for OPIA (1,2) solutions		Exact solution
x	$\|y - y_{1}\|$	$\|y - y_{2}\|$	$\|y - y_{3}\|$	$\|y - y_{1}\|$	$\|y - y_{2}\|$	$y = - 2 \ln (\cos x)$
0.1	0.000449452	0.000169553	$9.9097 \times$ $10^{- 6}$	$2.402 \times$ $10^{- 6}$	$9.4728 \times$ $10^{- 6}$	0.010016711
0.2	0.001595127	0.000583911	$2.5126 \times 10^{- 5}$	$9.453 \times 10^{- 6}$	$3.3152 \times 10^{- 5}$	0.040269546
0.3	0.002812140	0.000976872	$1.3047 \times 10^{- 5}$	$1.9420 \times 10^{- 5}$	$2.7254 \times 10^{- 5}$	0.091383311
0.4	0.003000543	0.000963454	$4.7213 \times 10^{- 5}$	$2.4899 \times 10^{- 6}$	$4.4563 \times 10^{- 6}$	0.164458038
0.5	0.000485555	0.000139394	0.000126132	$4.916 \times 10^{- 6}$	$5.55112 \times 10^{- 8}$	0.261168480
0.6	0.007148548	0.001752633	0.000116507	$8.8755 \times 10^{- 5}$	$7.2047 \times 10^{- 5}$	0.383930338
0.7	0.023329621	0.004551758	0.000144037	0.000354849	$7.0044 \times 10^{- 5}$	0.536171515
0.8	0.052947212	0.007229526	0.000727717	0.000982654	0.000128213	0.722781493
0.9	0.103126097	0.007116353	0.001202366	0.002323371	0.000452361	0.950884887
1	0.184637089	0.001509956	0.000365479	0.005024005	$4.44089 \times 10^{- 8}$	1.231252940

Example 2. Bratu’s first boundary value problem is given as (Wazwaz, 2005):

(4.21)

y^{″} + λ e^{y} = 0, 0 ⩽ x ⩽ 1, y (0) = y (1) = 0

with the exact solution

y (x) = - 2 \ln [\frac{\cosh ((x - \frac{1}{2}) \frac{θ}{2})}{\cosh (\frac{θ}{4})}]

where

θ

satisfies

θ = \sqrt{2 λ} \cosh (\frac{θ}{4}) .

4.3

4.3 OPIA (1,1)

An artificial perturbation parameter is inserted for Eq. (4.21) as follows

(4.22)

F (y^{″}, y, ε) = y^{″} + λ e^{ε y} = Ly + N (y, ε) = 0 .

By making necessary computations using Eqs. (2.2), (4.3) and setting $ε = 1$ , we easily get

(4.23)

{(y_{c}^{″})}_{n} = - λ y_{n} - (y_{n}^{″} + λ) .

One may start with the trivial solution

(4.24)

y_{0} = 0

and using Eq. (3.2) the iterations are reached as follows:

(4.25)

y_{1} = - \frac{λ C_{0}}{2} (x^{2} - x)

(4.26)

y_{2} = - \frac{λ C_{0}}{2} (x^{2} - x) + \frac{(C_{0} + C_{1})}{24} (- 1 + x) x λ [- 12 + (12 + (- 1 - x + x^{2}) λ) C_{0}]

(4.27)

\begin{matrix} y_{3} = \frac{λ x}{720} \times [\begin{matrix} 30 (C_{0} + C_{1}) x (- 12 + C_{0} (12 + λ (- 2 + x) x)) - 360 C_{0} (- 1 + x) - \\ (C_{0} + C_{1} + C_{2}) x \{\begin{matrix} 360 (- 1 + C_{0}) (- 1 + C_{0} + C_{1}) - 60 C_{0} (- 1 + C_{0} + C_{1}) λ x \\ + 30 (- C_{1} + 2 C_{0} (- 1 + C_{0} + C_{1})) λ x^{2} - 3 C_{0} (C_{0} + C_{1}) λ^{2} x^{3} \\ + C_{0} (C_{0} + C_{1}) λ^{2} x^{4} \end{matrix}\} \end{matrix}] \end{matrix}

For the constants $C_{0}, C_{1}$ and $C_{2}$ , the method given in Section 3.(d) is used, and we obtain the following values for $λ = 1$ :

(4.28)

C_{0} = 0.00896621251, C_{1} = 0.086955412771, C_{2} = - 0.000213669444

for the

x_{i} = 0.3, 0.6, 0.9

. Thus, the approximate solution of the third order is:

(4.29)

\begin{matrix} y_{3} (x) = & 0.549359811237294 x - 0.5001682773565349 x^{2} - 0.09044598683883211 x^{3} \\ + 0.025373292932254158 x^{4} + 0.023828818721721115 x^{5} - 0.00794805048551452 x^{6} \end{matrix}

4.4

4.4 OPIA (1,2):

One just needs to construct

(4.30)

N + N_{y} {(y_{c})}_{n} ε + N_{ε} ε + N_{ε y} {(y_{c})}_{n} ε^{2} + \frac{N_{ε ε} ε^{2}}{2} + \frac{N_{yy} ε^{2} {(y_{c})}_{n}^{2}}{2} = 0

where

(4.31)

N (y, ε) = λ e^{ε y} .

After making the relevant calculations, the algorithm takes the simplified form:

(4.32)

{(y_{c}^{″})}_{n} + λ {(y_{c})}_{n} = - λ y_{n} - y_{n}^{″} - λ - \frac{λ}{2} y_{n}^{2} .

Using Eqs. (3.2), (4.24), (4.32) and the initial conditions, we obtain

(4.33)

y_{1} = C_{0} (- 1 + \cos [x \sqrt{λ}] + \sin [x \sqrt{λ}] \tan [\frac{\sqrt{λ}}{2}])

(4.34)

\begin{matrix} y_{2} = C_{0} (- 1 + \cos [x \sqrt{λ}] + \sin [x \sqrt{λ}] \tan [\frac{\sqrt{λ}}{2}]) + \frac{(C_{0} + C_{1})}{48} (\sec {[\frac{\sqrt{λ}}{2}]}^{2} (- 24 (1 - C_{0} + C_{0}^{2}) \cos {[x \sqrt{λ}]}^{2}) \\ + (C_{0} + C_{1}) (\begin{matrix} (12 - 12 C_{0} + C_{0}^{2}) \cos [\sqrt{λ}] - C_{0}^{2} \cos [(1 - 3 x) \sqrt{λ}] + 3 (4 - 4 C_{0} + 3 C_{0}^{2} \\ + C_{0}^{2} \cos [(1 - 2 x) \sqrt{λ}] + 2 (- 1 + C_{0}) \cos [(- 1 + x) \sqrt{λ}] + C_{0}^{2} \cos [2 x \sqrt{λ}] \\ - 2 \cos [(1 + x) \sqrt{λ}] + 2 C_{0} \cos [(1 + x) \sqrt{λ}] - C_{0}^{2} \cos [(1 + x) \sqrt{λ}] \\ - 2 C_{0}^{2} x \sqrt{λ} \sin [\sqrt{λ}]) \end{matrix}) \\ + 2 (C_{0} + C_{1}) \cos [x \sqrt{λ}] + (C_{0} + C_{1}) \sec [\frac{\sqrt{λ}}{2}] \sin [x \sqrt{λ}] \times \\ [\begin{matrix} 6 C_{0}^{2} (- 2 + 3 x) \sqrt{λ} \cos [\frac{\sqrt{λ}}{2}] + 6 C_{0}^{2} x \sqrt{λ} \cos [\frac{3 \sqrt{λ}}{2}] + 12 \sin [\frac{\sqrt{λ}}{2}] - 12 C_{0} \sin [\frac{\sqrt{λ}}{2}] + 17 C_{0}^{2} \sin [\frac{\sqrt{λ}}{2}] \\ + 12 \sin [\frac{3 \sqrt{λ}}{2}] - 12 C_{0} \sin [\frac{3 \sqrt{λ}}{2}] + C_{0}^{2} \sin [\frac{3 \sqrt{λ}}{2}] + C_{0}^{2} Sin [\frac{1}{2} (1 - 6 x) \sqrt{λ}] - 6 C_{0}^{2} \sin [\frac{1}{2} (1 - 4 x) \sqrt{λ}] \\ - 3 C_{0}^{2} \sin [\frac{1}{2} (3 - 4 x) \sqrt{λ}] + 18 \sin [\frac{1}{2} (1 - 2 x) \sqrt{λ}] - 18 C_{0} \sin [\frac{1}{2} (1 - 2 x) \sqrt{λ}] + 18 C_{0}^{2} \sin [\frac{1}{2} (1 - 2 x) \sqrt{λ}] \\ + C_{0}^{2} \sin [\frac{3}{2} (1 - 2 x) \sqrt{λ}] + 6 \sin [\frac{1}{2} (3 - 2 x) \sqrt{λ}] - 6 C_{0} \sin [\frac{1}{2} (3 - 2 x) \sqrt{λ}] + 6 C_{0}^{2} \sin [\frac{1}{2} (3 - 2 x) \sqrt{λ}] - \\ 18 \sin [\frac{1}{2} (1 + 2 x) \sqrt{λ}] + 18 C_{0} \sin [\frac{1}{2} (1 + 2 x) \sqrt{λ}] - 15 C_{0}^{2} \sin [\frac{1}{2} (1 + 2 x) \sqrt{λ}] \\ - 6 \sin [\frac{1}{2} (3 + 2 x) \sqrt{λ}] + 6 C_{0} \sin [\frac{1}{2} (3 + 2 x) \sqrt{λ}] - 3 A^{2} \sin [\frac{1}{2} (3 + 2 x) \sqrt{λ}] + 3 C_{0}^{2} \sin [\frac{1}{2} (1 + 4 x) \sqrt{λ}] \end{matrix}] \end{matrix}

For the constants $C_{0}$ and $C_{1}$ in Eq. (4.34), we proceed as earlier and get

(4.35)

C_{0} = - 1.0002036577189, C_{1} = 0.099502786321

for

λ = 1

. Thus, we have the second-order approximate solution:

(4.36)

\begin{matrix} y_{2} (x) = & - 1.078485122090 - 0.004293531433 x + 1.105765327206 \cos [x] - 0.0279349653844 \cos [2 x] \\ + 0.00065493410502 \cos [3 x] + 0.6114581430450 \sin [x] - 0.091877388999 \cos [x] \sin [x] + 0.011352766729676 \sin [3 x] \end{matrix}

for OPIA (1,2). It can be readily seen from Fig. 2 and Table 2 that approximate solutions obtained by the OPIAs are identical with that given by the analytical methods (Wazwaz, 2005). Note that more components in the solution series can be computed to enhance the approximation.

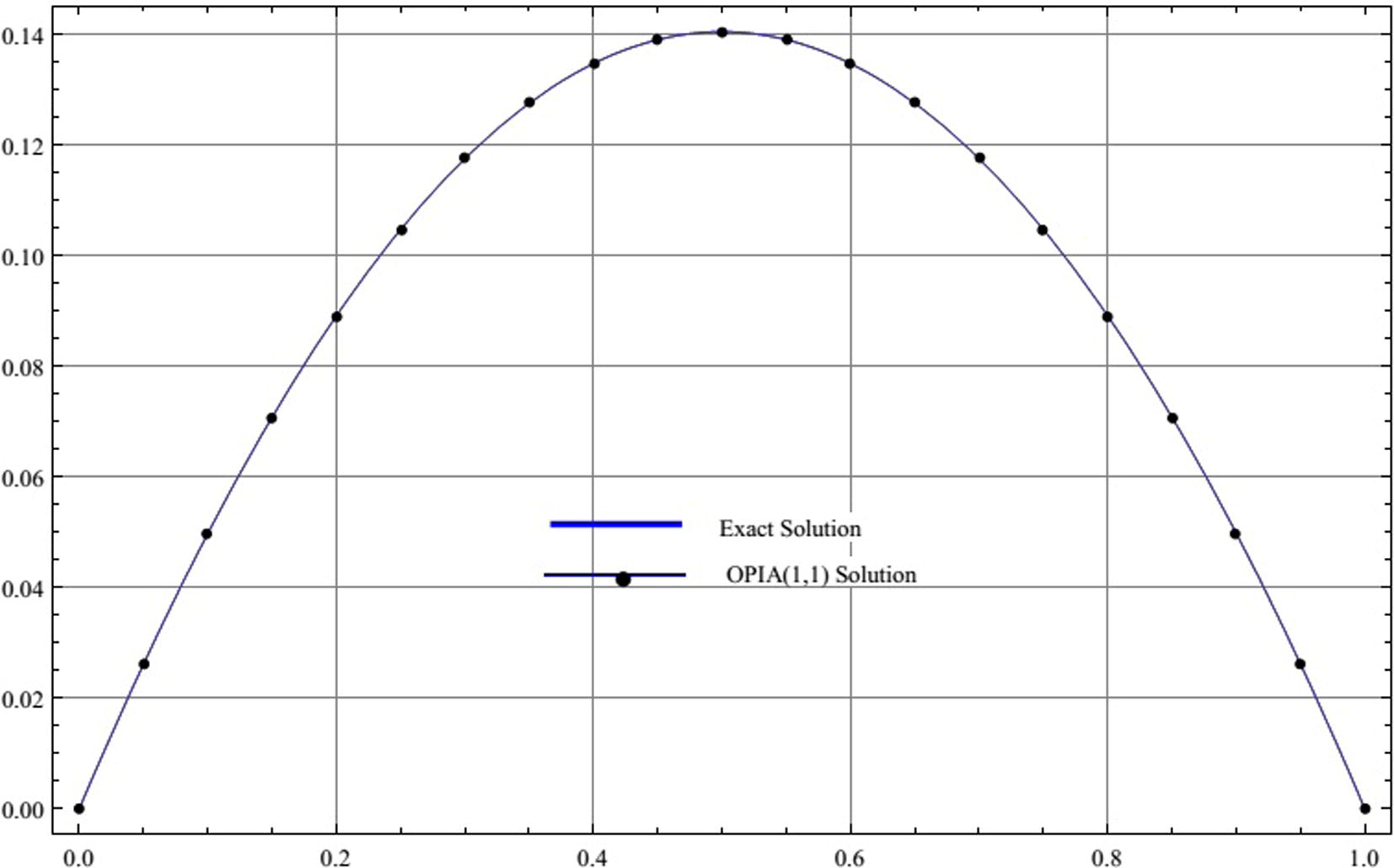
Comparison between the three-term OPIA (1,1) approximate solution and the exact solution for Example 2.

Table 2 Comparison of absolute errors of Example 2 at different orders of approximations.

x	Absolute errors for OPIA (1,1) solutions			Absolute errors for OPIA (1,2) solutions		Exact solution
x	$\|y - y_{1}\|$	$\|y - y_{2}\|$	$\|y - y_{3}\|$	$\|y - y_{1}\|$	$\|y - y_{2}\|$	for $λ = 1$
0.1	$1.05236 \times 10^{- 6}$	$8.05698 \times 10^{- 7}$	$1.19748 \times 10^{- 7}$	$5.22201 \times 10^{- 10}$	$1.23154 \times 10^{- 16}$	0.0498465
0.2	$1.08547 \times 10^{- 5}$	7.5067 $\times$ $10^{- 7}$	$3.35942 \times 10^{- 8}$	$7.90215 \times 10^{- 9}$	$2.36014 \times 10^{- 15}$	0.0891894
0.3	$4.96318 \times 10^{- 5}$	$1.00521 \times 10^{- 6}$	$1.12813 \times 10^{- 8}$	$5.20476 \times 10^{- 9}$	$5.10365 \times 10^{- 13}$	0.1176084
0.4	$9.55681 \times 10^{- 5}$	$5.96014 \times 10^{- 8}$	$9.08115 \times 10^{- 9}$	$2.63391 \times 10^{- 11}$	$5.30158 \times 10^{- 15}$	0.1347894
0.5	$7.56419 \times 10^{- 6}$	$7.22085 \times 10^{- 8}$	$7.33394 \times 10^{- 10}$	$9.89661 \times 10^{- 10}$	$5.60972 \times 10^{- 15}$	0.1405383
0.6	0.000121368	$5.00123 \times 10^{- 7}$	$1.13418 \times 10^{- 9}$	$2.00569 \times 10^{- 11}$	$9.12054 \times 10^{- 13}$	0.1347894
0.7	0.000802364	$4.20161 \times 10^{- 6}$	$6.13948 \times 10^{- 9}$	$4.11057 \times 10^{- 11}$	$2.03606 \times 10^{- 13}$	0.1176084
0.8	0.000110879	$1.00907 \times 10^{- 5}$	$1.00907 \times 10^{- 8}$	$8.05698 \times 10^{- 10}$	$7.45236 \times 10^{- 12}$	0.0891894
0.9	0.000569203	$2.10102 \times 10^{- 5}$	$7.75262 \times 10^{- 8}$	$2.05471 \times 10^{- 9}$	$1.00612 \times 10^{- 12}$	0.0498465

Example 3. Consider Bratu’s second boundary value problem (Wazwaz, 2005)

(4.37)

y^{″} + π^{2} e^{- y} = 0, 0 ⩽ x ⩽ 1, y (0) = y (1) = 0 .

Exact solution of this problem is mistakenly given as

(4.38)

y (x) = \ln [1 + \sin (1 + π x)]

in Wazwaz (2005) and Batiha (2010), whereas the correct exact solution is

(4.39)

y (x) = \ln [1 + \sin (π x)] .

4.5

4.5 OPIA (1,1)

By rearranging Eq. (4.37) as

(4.40)

F (y^{″}, y, ε) = y^{″} + π^{2} e^{- ε y} = Ly + N (y, ε)

and using Eqs. (2.2) and (4.3) with

ε = 1

, we have

(4.41)

{(y_{c}^{″})}_{n} = π^{2} y_{n} - (y_{n}^{″} + π^{2}) .

Without going into details here, we just give the successive iterations:

(4.42)

y_{0} = 0

(4.43)

y_{1} = \frac{π^{2} C_{0}}{2} (x - x^{2})

(4.44)

y_{2} = \frac{π^{2} C_{0}}{2} (x - x^{2}) - \frac{(C_{0} + C_{1})}{24} (- x + x^{2}) π^{2} [- 12 + (12 + (- 1 - x + x^{2}) π^{2}) C_{0}]

(4.45)

y_{3} = - \frac{π^{2} C_{0}}{2} (- x + x^{2}) - \frac{x π^{2}}{24} (C_{0} + C_{1}) (- 1 + x) (12 + C_{0} (- 12 + (- 1 + (- 1 + x) x) π^{2})) + \frac{(C_{0} + C_{1} + C_{2}) π^{2}}{720} [\begin{matrix} - 360 (- 1 + C_{0}) (- 1 + C_{0} + C_{1}) (- 1 + x) x \\ + 30 (- C_{1} + 2 C_{0} (- 1 + C_{0} + C_{1})) (x - 2 x^{3} + x^{4}) π^{2} \\ - C_{0} (C_{0} + C_{1}) x (- 3 + 5 x^{2} - 3 x^{4} + x^{5}) π^{4} \end{matrix}]

Proceeding as earlier we find constants $C_{0}, C_{1}$ and $C_{2}$ :

(4.46)

C_{0} = 0.00839960142, C_{1} = 0.08178563321, C_{2} = - 0.000193602314

Inserting the constants into Eq. (4.45), we obtain the approximate solution of the third order:

(4.47)

\begin{matrix} y_{3} (x) = & 3.134717936805843 x - 4.811906503098512 x^{2} + 4.266200757140372 x^{3} \\ - 4.407364172185969 x^{4} + 2.7222682887263185 x^{5} - 0.9036537597026911 x^{6} \end{matrix}

4.6

4.6 OPIA (1,2)

After making the relevant calculations, the algorithm

(4.48)

N + N_{y} {(y_{c})}_{n} ε + N_{ε} ε + N_{ε y} {(y_{c})}_{n} ε^{2} + \frac{N_{ε ε} ε^{2}}{2} + \frac{N_{yy} ε^{2} {(y_{c})}_{n}^{2}}{2} = 0

reduces to

(4.49)

{(y_{c}^{″})}_{n} - π^{2} {(y_{c})}_{n} = π^{2} y_{n} - \frac{π^{2}}{2} y_{n}^{2} - y_{n}^{″} - π^{2} .

Using Eqs. (3.2), (4.49) and the initial conditions, we get

(4.50)

y_{0} = 0

(4.51)

y_{1} = C_{0} (- 1 + \cosh [π x] + \sinh [π x] \tanh [\frac{π}{2}])

(4.52)

y_{2} (x) = C_{0} (- 1 + \cosh [π x] + \sinh [π x] \tanh [\frac{π}{2}]) + \frac{e^{- 2 π x} (- 1 + e^{π})}{12 {(1 + e^{π})}^{2}} (C_{0} + C_{1}) (- 1 + \coth [π]) \times [\begin{matrix} - 6 e^{π x} {(1 + e^{π})}^{2} (- 1 + e^{π x}) (- e^{π} + e^{π x}) + 6 A e^{π x} {(1 + e^{π})}^{2} (- 1 + e^{π x}) (- e^{π} + e^{π x}) \\ - C_{0}^{2} \{\begin{matrix} e^{2 π} + e^{3 π} - 3 e^{2 π x} + e^{4 π x} - 15 e^{2 π (1 + x)} - 3 e^{π (3 + 2 x)} - 15 e^{π + 2 π x} + e^{π + 4 π x} \\ + e^{π + π x} (2 + 3 π (- 1 + x)) + e^{3 π x} (2 - 3 π x) + 3 e^{π + 3 π x} (4 + π - 2 π x) + \\ e^{π (3 + x)} (2 + 3 π x) + 3 e^{π (2 + x)} (4 + π (- 1 + 2 x)) + e^{π (2 + 3 x)} (2 - 3 π (- 1 + x)) \end{matrix}\} \end{matrix}]

for OPIA (1,2). Using Eq. (3.11), the following values of

C_{0}

and

C_{1}

are obtained:

(4.53)

C_{0} = - 1.0286083214317654, C_{1} = 2.029583070812236

By using the above values, the approximate solution of the second order is:

(4.54)

\begin{matrix} y_{2} (x) = & 1.56204116701300 + (- 1.4080552742209 - 1.4777172978873 x) \cosh [π x] \\ + 0.15341644132458 \sinh [2 π x] - 0.15399004069623 \cosh [2 π x] \\ + (1.163463843313 + 1.6111742346200355 x) \sinh [π x] . \end{matrix}

One can easily observe from Table 3 and Fig. 3 that the results agree very well with the exact solution.

Table 3 Comparison of absolute errors of Example 3 at different orders of approximations.

x	Absolute errors for OPIA (1,1) solutions			Absolute errors for OPIA (1,2) solutions		Exact solution
x	$\|y - y_{1}\|$	$\|y - y_{2}\|$	$\|y - y_{3}\|$	$\|y - y_{1}\|$	$\|y - y_{2}\|$	Exact solution
0.1	0.0000752784	0.0000608251	0.0000719575	$9.05621 \times 10^{- 7}$	$8.8864 \times 10^{- 7}$	0.269276469
0.2	0.0004108547	0.0001009657	0.0000183205	$4.03657 \times 10^{- 7}$	$1.88504 \times 10^{- 7}$	0.462340122
0.3	0.0000296314	0.0000723684	$4.31405 \times 10^{- 6}$	$3.99521 \times 10^{- 7}$	$1.23351 \times 10^{- 7}$	0.592783600
0.4	0.0000955682	0.0000135841	$5.90773 \times 10^{- 6}$	$2.60399 \times 10^{- 6}$	$1.18017 \times 10^{- 7}$	0.668371029
0.5	0.0002856413	$2.90365 \times 10^{- 5}$	$1.28998 \times 10^{- 6}$	$3.05668 \times 10^{- 6}$	$2.73484 \times 10^{- 7}$	0.693147180
0.6	0.0000213685	$8.10269 \times 10^{- 6}$	$1.07103 \times 10^{- 6}$	$8.70569 \times 10^{- 7}$	$2.68334 \times 10^{- 7}$	0.668371029
0.7	0.0000723646	$9.30855 \times 10^{- 6}$	$1.1606 \times 10^{- 6}$	$5.19005 \times 10^{- 7}$	$9.46642 \times 10^{- 8}$	0.592783600
0.8	0.0000108799	$9.99237 \times 10^{- 6}$	$2.05027 \times 10^{- 6}$	$8.05111 \times 10^{- 7}$	$4.36073 \times 10^{- 7}$	0.462340122
0.9	0.0005692033	0.000111947	0.0000523313	$1.22014 \times 10^{- 6}$	$5.3818 \times 10^{- 7}$	0.269276469

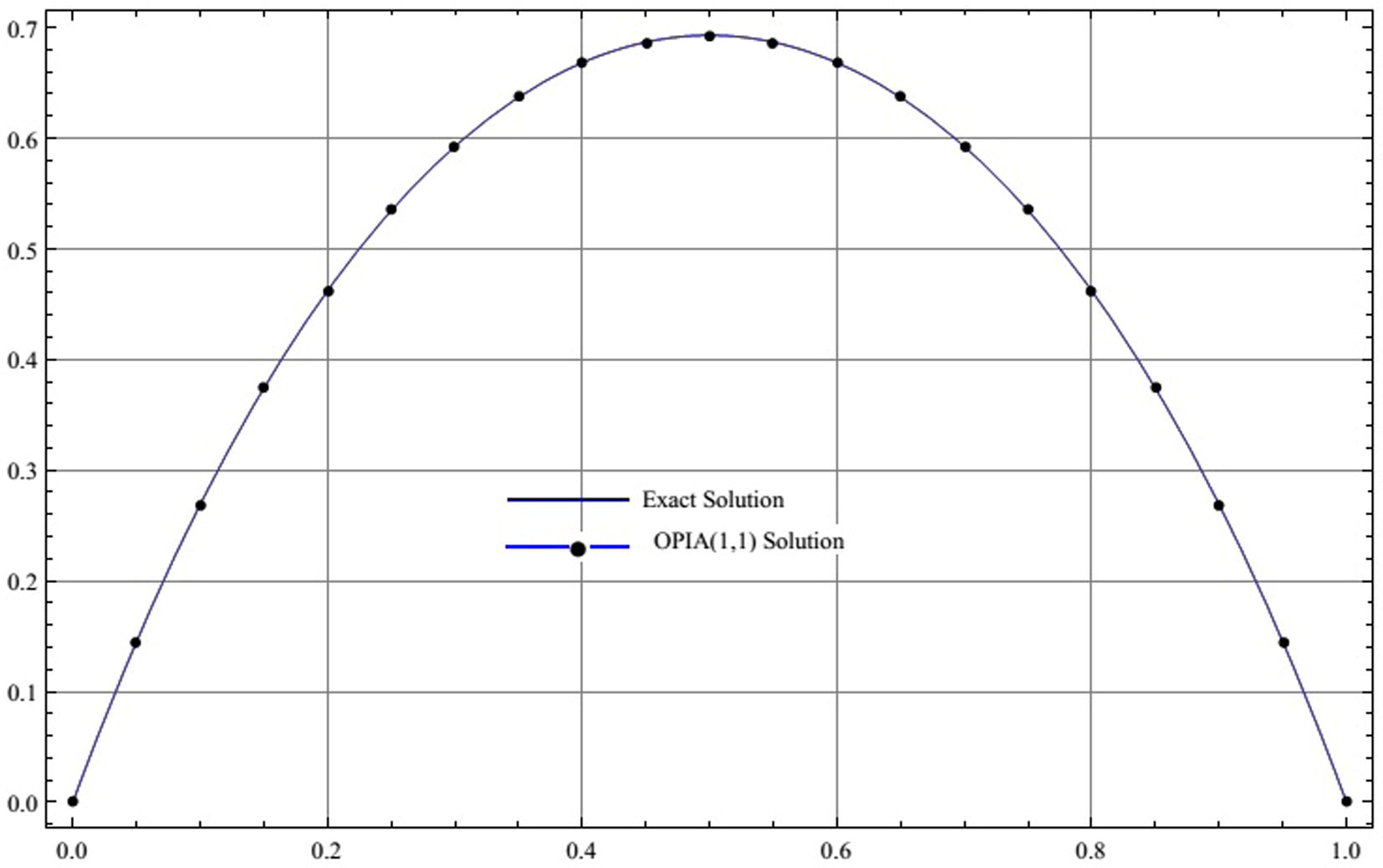
Comparison between the three-term OPIA (1,1) approximate solution and the exact solution for Example 3.

5 Conclusions

In this paper, a new technique OPIM is employed for the first time to obtain a new analytic approximate solution of Bratu-type differential equations. This new method provides us with an easy way to optimally control and adjust the convergence solution series. OPIM gives a very good approximation even in a few terms which converges to the exact solution. This fact is obvious from the use of the auxiliary function $S_{n} (ε)$ which depends on n coefficients $C_{0}, C_{1}, \dots, C_{n}$ . The results obtained in this paper confirm that the OPIM is a powerful and efficient technique for finding nearly exact solutions for differential equations which have great significance in many different fields of science and engineering.

References

Adomian G., . A review of the decomposition method in applied mathematics. J. Math. Anal. Appl.. 1988;135(2):501-544.
[Google Scholar]
Aksoy Y., Pakdemirli M., . New perturbation–iteration solutions for Bratu-type equations. Comput. Math. Appl.. 2010;59(8):2802-2808.
[Google Scholar]
Aksoy Y., Pakdemirli M., Abbasbandy S., Boyaci H., . New perturbation–iteration solutions for nonlinear heat transfer equations. Int. J. Numer. Methods Heat Fluid Flow. 2012;22(7):814-828.
[Google Scholar]
Batiha B., . Numerical solution of Bratu-type equations by the variational iteration method. Hacettepe J. Math. Stat.. 2010;39(1)
[Google Scholar]
Bildik N., Deniz S., . Comparison of solutions of systems of delay differential equations using taylor collocation method, Lambert W function and variational iteration method. Sci. Iran. Trans. D, Comput. Sci. Eng. Electr.. 2015;22(3):1052.
[Google Scholar]
Bildik N., Konuralp A., . The use of variational iteration method, differential transform method and Adomian decomposition method for solving different types of nonlinear partial differential equations. Int. J. Nonlinear Sci. Numer. Simul.. 2006;7(1):65-70.
[Google Scholar]
Deniz S., Bildik N., . Comparison of Adomian decomposition method and Taylor matrix method in solving different kinds of partial differential equations. Int. J. Model. Optim.. 2014;4(4):292.
[Google Scholar]
Doha E., Bhrawy A., Baleanu D., Hafez R., . Efficient Jacobi-gauss collocation method for solving initial value problems of Bratu type. Comput. Math. Math. Phys.. 2013;53(9):1292-1302.
[Google Scholar]
He J.-H., . Variational approach to the Lane–Emden equation. Appl. Math. Comput.. 2003;143(2):539-541.
[Google Scholar]
He J.-H., Kong H.-Y., Chen R.-X., Hu M.-S., Chen Q.-L., . Variational iteration method for Bratu-like equation arising in electrospinning. Carbohydrate Polym.. 2014;105:229-230.
[Google Scholar]
Herisanu N., Marinca V., Madescu G., . An analytical approach to non-linear dynamical model of a permanent magnet synchronous generator. Wind Energy. 2015;18(9):1657-1670.
[Google Scholar]
Idrees M., Islam S., Haq S., Islam S., . Application of the optimal homotopy asymptotic method to squeezing flow. Comput. Math. Appl.. 2010;59(12):3858-3866.
[Google Scholar]
Khalid M., Sultana M., Zaidi F., Khan F.S., . Solving polluted lakes system by using perturbation-iteration method. Int. J. Comput. Appl.. 2015;114(4)
[Google Scholar]
Liao S., . Optimal homotopy analysis method. In: Homotopy Anal. Method Nonlinear Differ. Equ.. Springer; 2012. p. :95-129.
[Google Scholar]
Marinca V., Herişanu N., . Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transfer. 2008;35(6):710-715.
[Google Scholar]
Marinca V., Herişanu N., . Optimal parametric iteration method for solving multispecies Lotka-Volterra equations. Discr. Dyn. Nat. Soc. 2012
[Google Scholar]
Öziş T., Ağrseven D., . He’s homotopy perturbation method for solving heat-like and wave-like equations with variable coefficients. Phys. Lett. A. 2008;372(38):5944-5950.
[Google Scholar]
Raja M.A.Z., . Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ann optimised with PSO and SQP. Connection Sci.. 2014;26(3):195-214.
[Google Scholar]
Senol M., Timuçin Dolapç I., Aksoy Y., Pakdemirli M., . Perturbation–iteration method for first-order differential equations and systems. In: Abstract and Applied Analysis. Vol vol. 2013. Hindawi Publishing Corporation; 2013.
[Google Scholar]
Timuçin Dolapç I., Senol M., Pakdemirli M., . New perturbation iteration solutions for Fredholm and Volterra integral equations. J. Appl. Math. 2013
[Google Scholar]
Wazwaz A.-M., . Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput.. 2005;166(3):652-663.
[Google Scholar]