Translate this page into:
On the Perturbation-Iteration Algorithm for fractional differential equations
?Corresponding author. msenol@nevsehir.edu.tr (Mehmet Senol),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this study, Perturbation-Iteration Algorithm, namely PIA, is applied to solve some types of fractional differential equations (FDEs) for the first time. To illustrate the efficiency of the method, numerical solutions are compared with the results published in the literature by considering some FDEs. The results confirm that the PIA is a powerful, efficient and accurate method for solving nonlinear fractional differential equations.
Keywords
Caputo fractional derivative
Fractional differential equations
Initial value problems
Perturbation-Iteration method
1 Introduction
As an important mathematical branch investigating the properties of derivatives and integrals, the history of fractional calculus goes back to the beginning of the ordinary calculus. Even though there is a long period of time since the beginning of fractional calculus, various applications of fractional calculus over real engineering problems just emerged in the last decades. The evolution of the symbolic computation programs such as Mathematica, also helped this development. There is a large cycle of works as applications of fractional calculus in various branches of engineering. Especially interdisciplinary problems in applied sciences can be expressed by the fractional integrals and derivatives. In control theory (Senol et al., 2014), viscoelasticity (Yu and Lin, 1998), electrochemistry (Oldham, 2010), electromagnetic (Heaviside, 2008), fractional differential equations are used for modeling some different types of engineering problems. For example, in Hamamci (2007). Some basic definitions and applications of fractional derivatives are also given in Mainardi (1997) and Podlubny (1998).
As parallel to the studies in engineering and science, much attention is given to FDEs in applied mathematics. Especially, solution of FDE (analytically or/and numerically) methods is studied by many author in the last decades.
Existence and uniqueness of the solutions are also studied by some mathematicians, (see Yakar and Koksal (2012) and the references therein).
There are a number of differential equations whose solution can not be found analytically. Those situations appear in FDEs more than other types of differential equations. In this case, as the study of algorithms using numerical approximation for the problems of mathematical analysis, the field of numerical analysis is used for approximate solutions of FDEs.
Various numerical methods have been studied for approximate solutions of FDEs. These methods include, fractional variational iteration method (Wu and Lee, 2010; Guo and Mei, 2011; Wu and Baleanu, 2013), homotopy perturbation method (Abdulaziz et al., 2008; He, 2012, Momani and Odibat, 2007; Zhang et al., 2014), Adomian decomposition method (Duan et al., 2012) and fractional differential transform method (Momani et al., 2007; Arikoglu and Ozkol, 2009; El-Sayed et al., 2014).
In this paper, the previously developed method (PIA), suitable for a broad class of equations which do not require special assumptions and transformations , is studied to give approximate solutions of some fractional differential equations.
Two major definitions of fractional derivative of an arbitrary order are the Riemann-Liouville and Caputo fractional derivatives. The two definitions have different orders of evaluation of derivation.
Riemann-Liouville fractional integration of order
is defined by:
The following two equations are defined as Riemann-Liouville and Caputo fractional derivatives of order
, respectively.
Due to the appropriateness of the initial conditions, fractional definition of Caputo is often used in recent years.
The fractional derivative of
in the Caputo sense is defined as
Also, we need here two of its basic properties.
If
and
then
After this introductory section, Section 2 is reserved for a brief review of the Perturbation-Iteration Algorithm PIA(1,1), in Section 3 some examples are presented to show the efficiency and simplicity of the algorithm. Finally the paper ends with a conclusion in Section 4.
2 Overview of the Perturbation-Iteration Algorithm PIA(1,1)
As one of the most practical subjects of physics and mathematics, differential equations create models for a number of problems in science and engineering to give an explanation for a better understanding of the events. Perturbation methods have been used for this purpose for over a century (Nayfeh, 2008; Jordan and Smith, 1987; Skorokhod et al., 2002). These methods could be used to search approximate solutions of integral equations, difference equations, integro-differential equations and partial differential equations.
But the main difficulty in the application of perturbation methods is the requirement of a small parameter or to install a small artificial parameter in the equation. For this reason, the obtained solutions are restricted by a validity range of physical parameters. Therefore, to overcome the disadvantages come with the perturbation techniques, some methods have been suggested by several authors (He, 2001; Mickens, 1987, 2005, 2006; Cooper and Mickens, 2002; Hu and Xiong, 2003; He, 2012; Wang and He, 2008; Iqbal and Javed, 2011; Iqbal et al., 2010).
Parallel to these studies, recently a new Perturbation-Iteration Algorithm has been proposed by Aksoy, Pakdemirli and their co-workers (Aksoy and Pakdemirli, 2010; Pakdemirli et al., 2011; Aksoy et al., 2012). A previous attempt of constructing root finding algorithms systematically (Pakdemirli and Boyac, 2007; Pakdemirli et al., 2007, 2008) finally guided to generalization of the method to differential equations also (Aksoy and Pakdemirli, 2010; Pakdemirli et al., 2011; Aksoy et al., 2012). In the new technique, an iterative algorithm is established on the perturbation expansion. The method has been applied to first order equations (Pakdemirli et al., 2011) and Bratu type second order equations (Aksoy and Pakdemirli, 2010) to obtain approximate solutions. Then the algorithms were tested on some nonlinear heat equations also (Aksoy et al., 2012). Finally, the solutions of the Volterra and Fredholm type integral equations (Dolapci et al., 2013) and ordinary differential equation and systems (şenol et al., 2013) are given by the present method.
In this study, the previously developed new technique is applied to some types of nonlinear fractional differential equations for the first time. To obtain the approximate solutions of equations, the most basic Perturbation-Iteration Algorithm PIA(1,1) is employed by taking one correction term in the perturbation expansion and correction terms of only first derivatives in the Taylor series expansion, i.e. .
Consider the following initial value problem.
In this method as
is the artificially introduced perturbation parameter we use only one correction term in the perturbation expansion.
Replacing (10) into (7) and writing in the Taylor Series expansion for only first order derivatives gives
Beginning with an initial function , first has been determined by the help of (12). Then substituting into (10) gives . Iteration process is repeated using (12) and (10) until achieving an acceptable result.
3 Application
Consider the following fractional nonlinear Riccati equation (Odibat and Momani, 2008):
Eq. (12) can be rearranged in the following form:
When employing the iteration formula (10), we start with an initial function compatible to the boundary condition and we determine coefficients from the boundary condition at each step. Beginning with the initial function
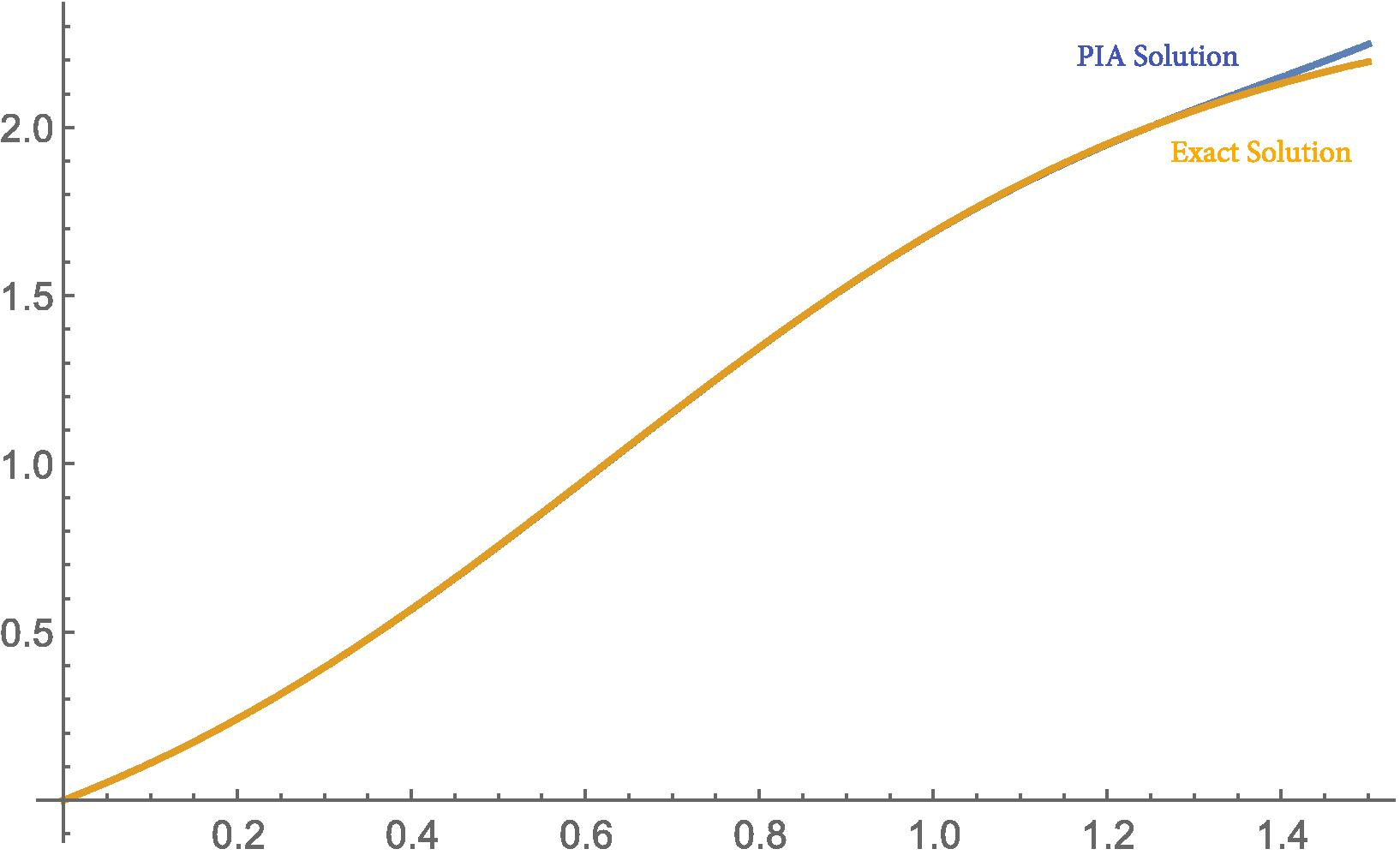
Due to brevity reasons, higher iterations are not given here. It is easy to calculate other iterations up to any order by the help of a software such as Mathematica . In Fig. 1 we compare our solution with the exact solution graphically and in Table 1 some of our iterations are compared with the exact solutions, the modified homotopy perturbation method (Odibat and Momani, 2008) and the fractional variational iteration method (Merdan, 2012) solutions. The results show that the proposed method can give much better approximations. We also defined residual functions to check validness of our approximate solutions for each iteration results and named them , ,. and so on. In Figs. 2-5, and are shown for and 0.95. As seen, for higher order iterations and bigger values of alpha we obtain more approximate solutions.
For the second example consider another Riccati equation (Odibat and Momani, 2008):
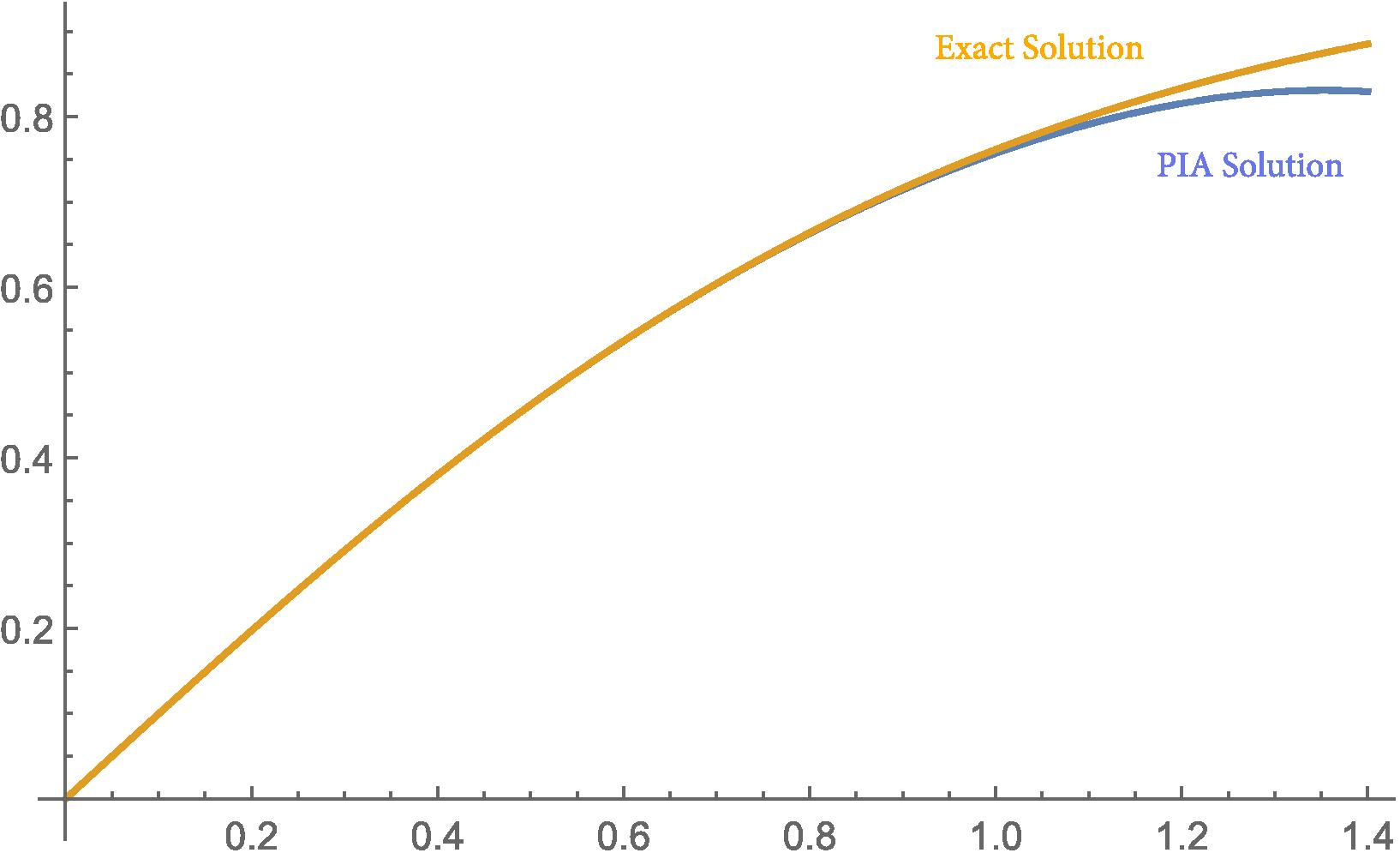
- Comparison of the exact solution and the PIA solution (
) of Example 3.1 for
.
| x | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ours | MHPM | FVIM | Ours | MHPM | FVIM | Ours | MHPM | FVIM | Exact solution | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.1 | 0.273239 | 0.273875 | 0.086513 | 0.184607 | 0.184795 | 0.190102 | 0.099667 | 0.099668 | 0.099667 | 0.099668 |
| 0.2 | 0.450722 | 0.454125 | 0.161584 | 0.312989 | 0.313795 | 0.310033 | 0.197375 | 0.197375 | 0.197375 | 0.197375 |
| 0.3 | 0.566159 | 0.573932 | 0.238256 | 0.413024 | 0.414562 | 0.405062 | 0.291312 | 0.291312 | 0.291320 | 0.291313 |
| 0.4 | 0.632329 | 0.644422 | 0.321523 | 0.490946 | 0.492889 | 0.483479 | 0.379946 | 0.379944 | 0.380005 | 0.379949 |
| 0.5 | 0.659574 | 0.674137 | 0.413682 | 0.550818 | 0.462117 | 0.550470 | 0.462103 | 0.462078 | 0.462375 | 0.462117 |
| 0.6 | 0.657975 | 0.671987 | 0.515445 | 0.596448 | 0.597393 | 0.610344 | 0.536983 | 0.536857 | 0.537923 | 0.537050 |
| 0.7 | 0.637491 | 0.648003 | 0.626403 | 0.631701 | 0.631772 | 0.666961 | 0.604124 | 0.603631 | 0.606768 | 0.604368 |
| 0.8 | 0.607570 | 0.613306 | 0.745278 | 0.660394 | 0.660412 | 0.723760 | 0.663300 | 0.661706 | 0.669695 | 0.664037 |
| 0.9 | 0.576669 | 0.579641 | 0.870074 | 0.686074 | 0.687960 | 0.783638 | 0.714382 | 0.709919 | 0.728139 | 0.716298 |
| 1.0 | 0.551855 | 0.558557 | 0.998176 | 0.711773 | 0.718260 | 0.848783 | 0.757166 | 0.746032 | 0.784126 | 0.761594 |
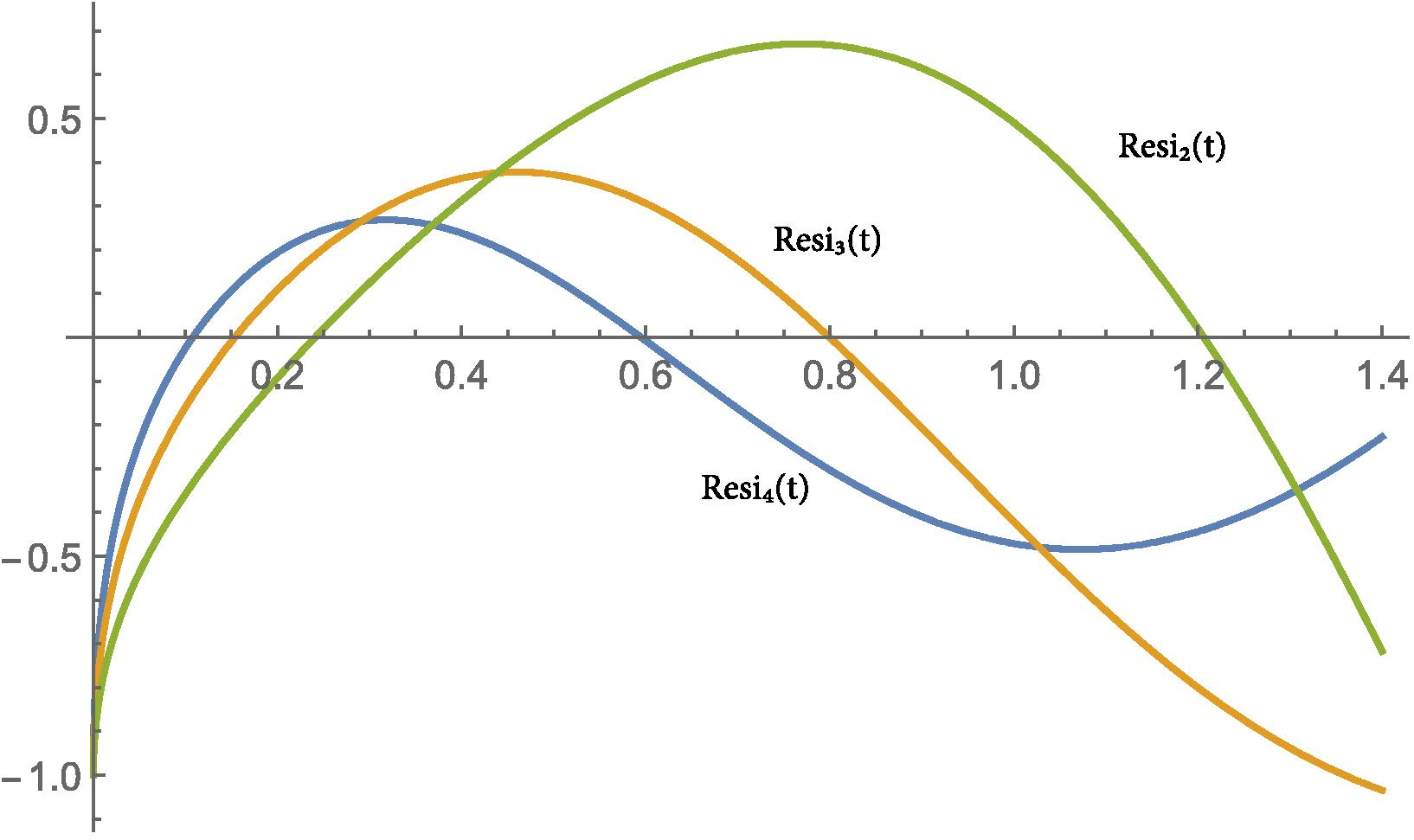
-
and
values for
of Example 3.1.
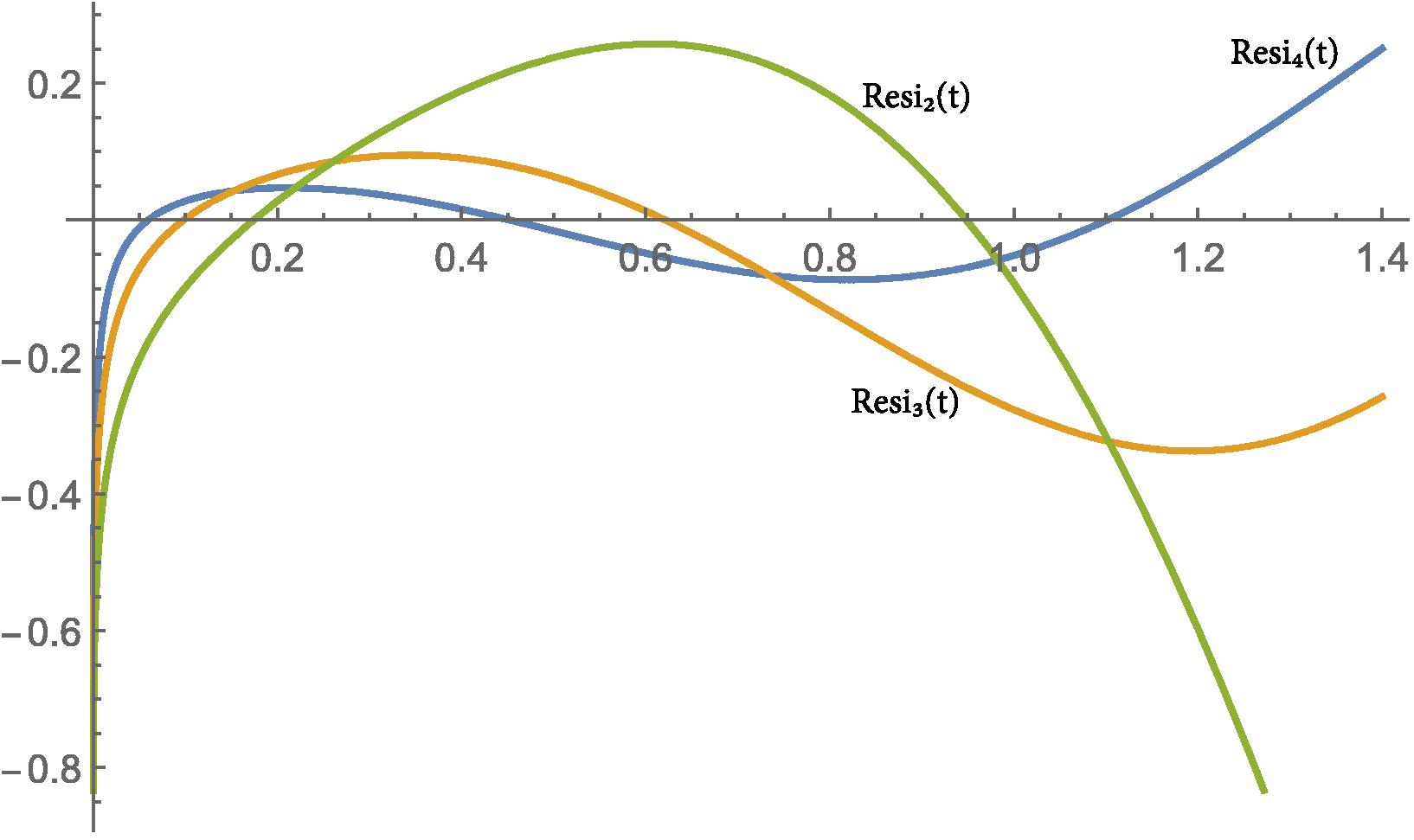
-
and
values for
of Example 3.1.
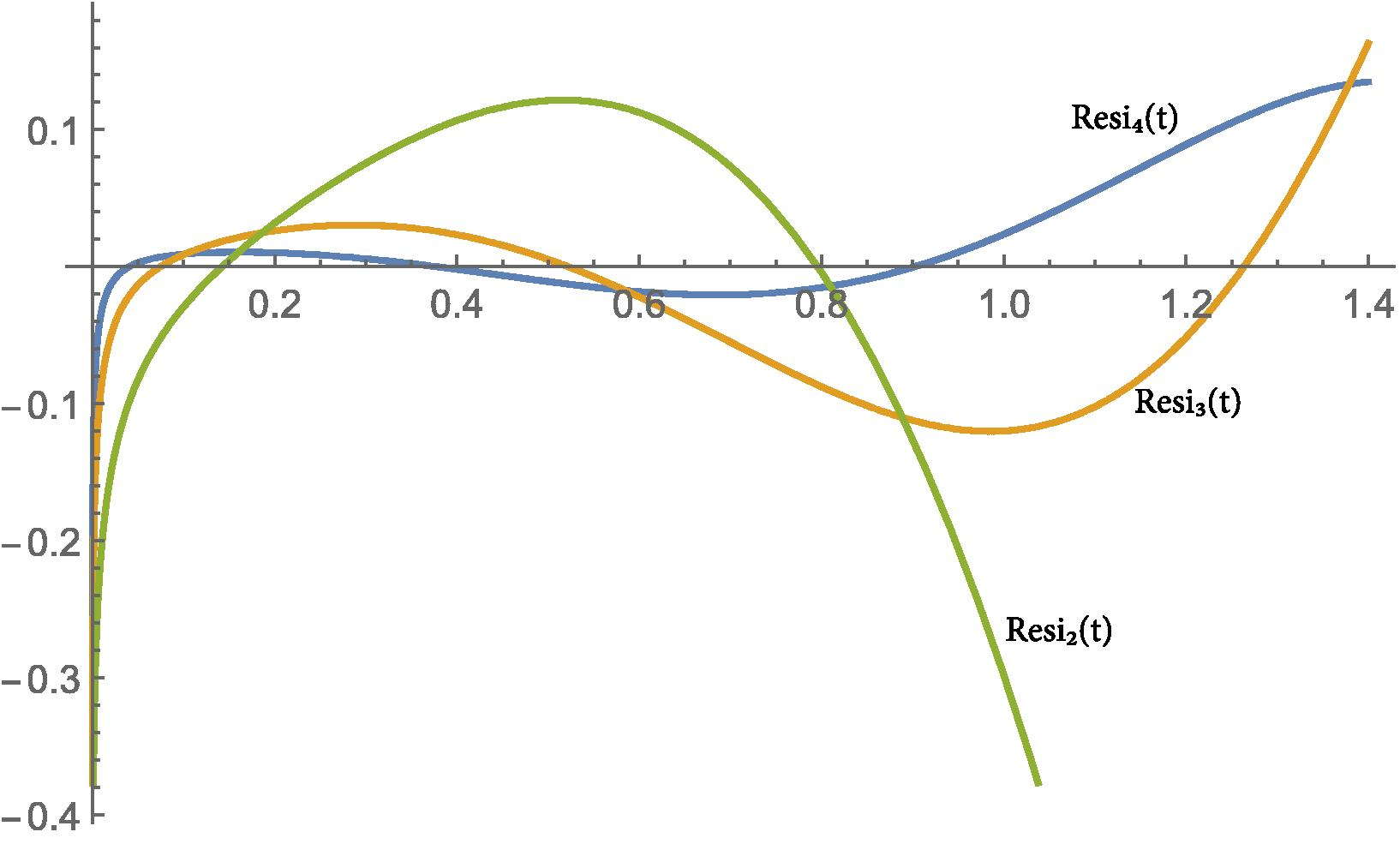
-
and
values for
of Example 3.1.
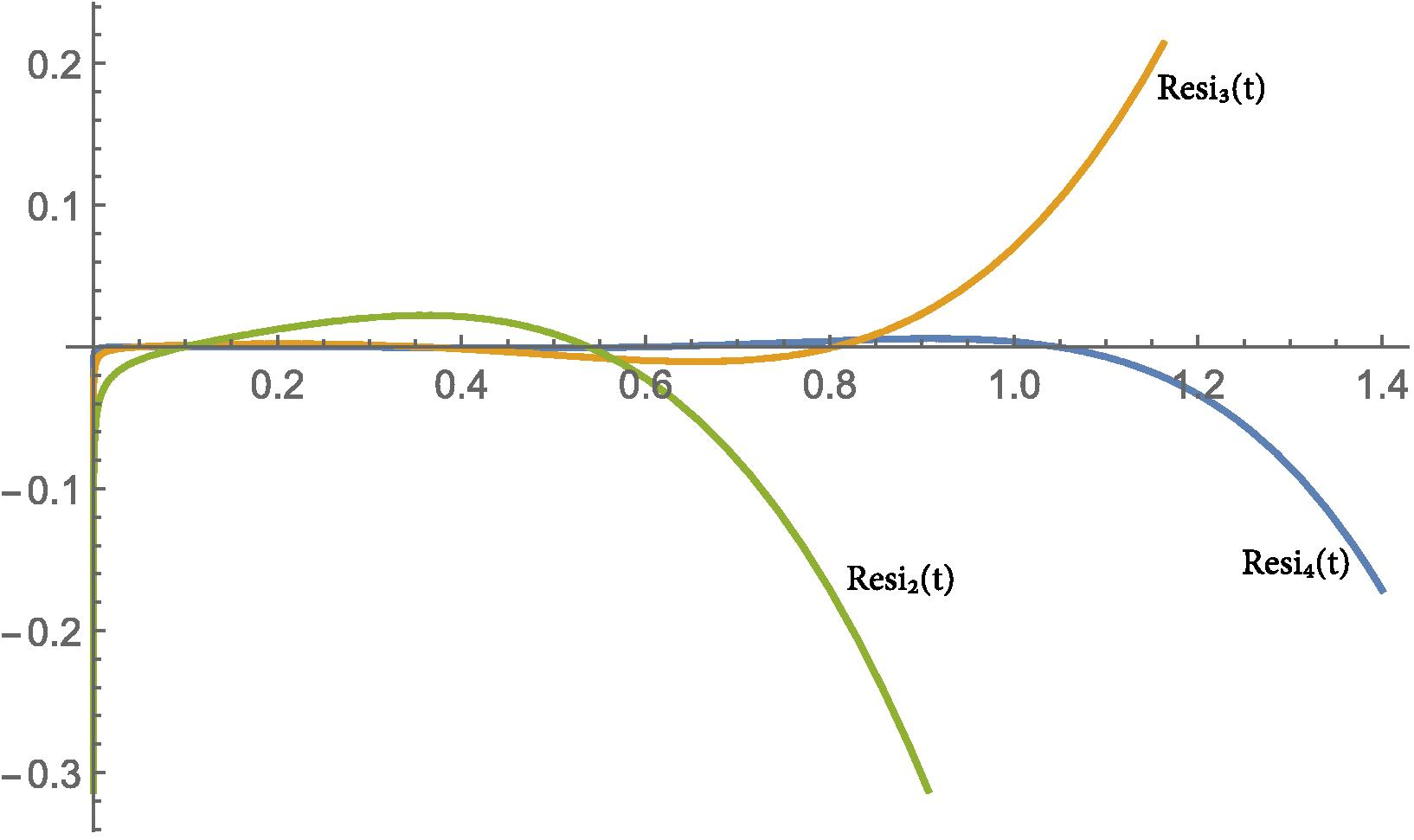
-
and
values for
of Example 3.1.
Eq. (19) can be rewritten in the following form:
Beginning with the initial function
In Fig. 6 and in Table 2 our solution and some of our iterations are compared with the exact solutions, the modified homotopy perturbation method and the fractional variational iteration method solutions.
Next, we consider the fractional differential equation (Jafari et al., 2011):
- Comprasion of the exact solution and the PIA solution (
) of Example 3.2 for
.
| x | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ours | MHPM | FVIM | Ours | MHPM | FVIM | Ours | MHPM | FVIM | Exact solution | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.1 | 0.320883 | 0.321730 | 0.577431 | 0.216584 | 0.216866 | 0.244460 | 0.110294 | 0.110294 | 0.110266 | 0.110295 |
| 0.2 | 0.623380 | 0.629666 | 0.912654 | 0.426883 | 0.428892 | 0.469709 | 0.241949 | 0.241965 | 0.241585 | 0.241977 |
| 0.3 | 0.920289 | 0.940941 | 1.166253 | 0.647833 | 0.654614 | 0.698718 | 0.394957 | 0.395106 | 0.393515 | 0.395105 |
| 0.4 | 1.202508 | 1.250737 | 1.353549 | 0.874795 | 0.891404 | 0.924319 | 0.567397 | 0.568115 | 0.564013 | 0.567812 |
| 0.5 | 1.456864 | 1.549439 | 1.482633 | 1.099158 | 1.132763 | 1.137952 | 0.755256 | 0.757564 | 0.749528 | 0.756014 |
| 0.6 | 1.669872 | 1.825456 | 1.559656 | 1.310787 | 1.370240 | 1.331462 | 0.952588 | 0.958259 | 0.945155 | 0.953566 |
| 0.7 | 1.829997 | 2.066523 | 1.589984 | 1.499559 | 1.594278 | 1.497600 | 1.152054 | 1.163459 | 1.144826 | 1.152949 |
| 0.8 | 1.929388 | 2.260633 | 1.578559 | 1.656755 | 1.794879 | 1.630234 | 1.345789 | 1.365240 | 1.341552 | 1.346364 |
| 0.9 | 1.965134 | 2.396839 | 1.530028 | 1.776325 | 1.962239 | 1.724439 | 1.526505 | 1.554960 | 1.527690 | 1.526911 |
| 1.0 | 1.939933 | 2.466004 | 1.448805 | 1.855903 | 2.087384 | 1.776542 | 1.688651 | 1.723810 | 1.695238 | 1.689498 |
4 Conclusion
In this paper we have applied previously developed a numerical method so-called Perturbation-Iteration Algorithm (PIA) to find approximate solutions of some nonlinear fractional differential equations for the first time. the numerical results obtained in this study show that method PIA is a remarkably successful numerical technique for solving FDEs. We expect that the present method could used to calculate the approximate solutions of other types of fractional differential equations such as fractional integro-differential equations and fractional partial differential equations. Our next study will be about these types of equations.
References
- Solving systems of fractional differential equations by homotopy-perturbation method. Phys. Lett. A. 2008;372(4):451-459.
- [Google Scholar]
- New perturbation-iteration solutions for Bratu-type equations. Comput. Math. Appl.. 2010;59(8):2802-2808.
- [Google Scholar]
- New perturbation-iteration solutions for nonlinear heat transfer equations. Int. J. Numer. Methods H. 2012;22(7):814-828.
- [Google Scholar]
- Solution of fractional integro-differential equations by using fractional differential transform method. Chaos Soliton Fract.. 2009;40(2):521-529.
- [Google Scholar]
- Generalized harmonic balance numerical method for determining analytical approximations to the periodic solutions of the x4/3 potential. J. Sound Vib.. 2002;250(5):951-954.
- [Google Scholar]
- New perturbation iteration solutions for Fredholm and Volterra integral equations. J. Appl. Math. 2013Article ID 682537 5 pages
- [Google Scholar]
- A review of the Adomian decomposition method and its applications to fractional differential equations. Commun. Frac. Calc.. 2012;3(2):73-99.
- [Google Scholar]
- A study of projectile motion in a quadratic resistant medium via fractional differential transform method. Appl. Math. Model. 2014;39(10):2829-2835.
- [Google Scholar]
- The fractional variational iteration method using He's polynomials. Phys. Lett. A. 2011;375(3):309-313.
- [Google Scholar]
- An algorithm for stabilization of fractional-order time delay systems using fractional-order PID controllers. IEEE Trans.. 2007;52(10):1964-1969.
- [Google Scholar]
- Iteration perturbation method for strongly nonlinear oscillators. J. Sound Vib.. 2001;7:631-642.
- [Google Scholar]
- Homotopy perturbation method with an auxiliary term. Abstr. Appl. Anal. 2012Article ID 857612 7 pages
- [Google Scholar]
- Electromagnetic Theory. Vol vol. 3. Cosimo Inc; 2008.
- Application of optimal homotopy asymptotic method for the analytic solution of singular Lane-Emden type equation. Appl. Math. Comput.. 2011;217(19):7753-7761.
- [Google Scholar]
- Some solutions of the linear and nonlinear Klein-Gordon equations using the optimal homotopy asymptotic method. Appl. Math. Comput.. 2010;216(10):2898-2909.
- [Google Scholar]
- Application of Legendre wavelets for solving fractional differential equations. Comput. Math. Appl.. 2011;62(3):1038-1045.
- [Google Scholar]
- Nonlinear Ordinary Differential Equations. Oxford Press; 1987.
- Fractals and Fractional Calculus in Continuum Mechanics. Springer Verlag; 1997.
- On the solutions fractional Riccati differential equation with modified Riemann-Liouville derivative. Int. J. Differ. Equ. 2012Article ID 346089 17 pages
- [Google Scholar]
- Iteration procedure for determining approximate solutions to non-linear oscillator equations. J. Sound Vib.. 1987;116(1):185-187.
- [Google Scholar]
- A generalized iteration procedure for calculating approximations to periodic solutions of truly nonlinear oscillators. J. Sound Vib.. 2005;287(4):1045-1051.
- [Google Scholar]
- Iteration method solutions for conservative and limit-cycle x1/3 force oscillators. J. Sound Vib.. 2006;292(3):964-968.
- [Google Scholar]
- Homotopy perturbation method for nonlinear partial differential equations of fractional order. Phys. Lett. A. 2007;365(5):345-350.
- [Google Scholar]
- Generalized differential transform method for solving a space-and time-fractional diffusion-wave equation. Phys. Lett. A. 2007;370(5):379-387.
- [Google Scholar]
- Perturbation Methods. John Wiley & Sons; 2008.
- Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. Chaos Soliton Fract.. 2008;36(1):167-174.
- [Google Scholar]
- Fractional differential equations in electrochemistry. Adv. Eng. Softw.. 2010;41(1):9-12.
- [Google Scholar]
- Generation of root finding algorithms via perturbation theory and some formulas. Appl. Math. Comput.. 2007;184(2):783-788.
- [Google Scholar]
- Perturbative derivation and comparisons of root-finding algorithms with fourth order derivatives. Math. Comput. Appl.. 2007;12(2):117.
- [Google Scholar]
- A root-finding algorithm with fifth order derivatives. Math. Comput. Appl.. 2008;13(2):123.
- [Google Scholar]
- A new perturbation-iteration approach for first order differential equations. Math. Comput. Appl.. 2011;16(4):890-899.
- [Google Scholar]
- Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications. Vol vol. 198. Academic press; 1998.
- Perturbation-iteration method for first-order differential equations and systems. Abstr. Appl. Anal. 2013Article ID 704137 6 pages
- [Google Scholar]
- A numerical investigation for robust stability of fractional-order uncertain systems. ISA Trans.. 2014;53(2):189-198.
- [Google Scholar]
- Random Perturbation Methods with Applications in Science and Engineering. Vol vol. 150. Springer Science & Business Media; 2002.
- Nonlinear oscillator with discontinuity by parameter-expansion method. Chaos Soliton Fract.. 2008;35(4):688-691.
- [Google Scholar]
- Variational iteration method for the Burgers' flow with fractional derivatives-new Lagrange multipliers. Appl. Math. Model.. 2013;37(9):6183-6190.
- [Google Scholar]
- Fractional variational iteration method and its application. Phys. Lett. A. 2010;374(25):2506-2509.
- [Google Scholar]
- Existence results for solutions of nonlinear fractional differential equations. Abstr. Appl. Anal. 2012Article ID 267108 12 pages
- [Google Scholar]
- Numerical research on the coherent structure in the viscoelastic second-order mixing layers. Appl. Math. Mech.-Engl.. 1998;19(8):717-723.
- [Google Scholar]
- Homotopy perturbation method for two dimensional time-fractional wave equation. Appl. Math. Model.. 2014;38(23):5545-5552.
- [Google Scholar]







