Numerical solution of two-parameter singularly perturbed boundary value problems via exponential spline

1 Introduction

It is well known that in various fields of science and engineering many reaction–diffusion as well as convection–diffusion problems naturally occur. Heat transfer with large Péclet numbers, nuclear engineering, combustion, control theory, elasticity, fluid mechanics, aerodynamics, quantum mechanics, optimal control, chemical-reactor theory, convection–diffusion process and geophysics are some examples of these fields. However, reaction–diffusion problem when ε_d = 0 and convection–diffusion problem when ε_d = 1 are enclosed in the two-parameter singularly perturbed boundary value problem (Gracia et al., 2006; Kadalbajoo and Gupta, 2009; Kadalbajoo and Yadaw, 2008; Lin et al., 2009; Linß and Roos, 2004; Rao and Chakravarthy, 2012; Rao and Kumar, 2008; Rao et al., 2010; Reddy and Pramod, 2003; Roos and Uzelac, 2003; Stynes and Kopteva, 2011; Valanarasu and Ramanujam, 2003; Valarmathi and Ramanujam, 2003). This two-parameter singularly perturbed semi-linear boundary value problem has the following form:

Different numerical methods were proposed to solve singularly perturbed problem with ε_c = 1 and ε_c = 0 such as Reddy and Pramod (2003), Kadalbajoo and Gupta (2009), Lin et al. (2009), Rao and Kumar (2008), Rao and Chakravarthy (2012), Rao et al. (2010) and Stynes and Kopteva (2011). On the other hand, the solution of the two-parameter singular perturbation problem was made in limited researches such as Gracia et al. (2006), Valanarasu and Ramanujam (2003) and Valarmathi and Ramanujam (2003). Linß and Roos (2004) considered linear two-parameter singularly perturbed convection–diffusion problem and used the simple upwind-difference scheme on Shishkin mesh to establish almost first-order convergence, independently of the parameters ε_c and ε_d. Roos and Uzelac (2003) also considered linear two-parameter singularly perturbed boundary value problem. They used stream-line diffusion finite element method on properly chosen Shishkin mesh. As a result they proved almost second-order pointwise convergence uniformly with respect to the parameters ε_c andε_d. B-spline collocation method for solving linear two-parameter singularly perturbed boundary value problems on piecewise-uniform Shishkin mesh was investigated by Kadalbajoo and Yadaw (2008), they conclude the uniform convergence of the second order.

Herein, the exponential spline difference scheme method is used to solve the two-parameter singularly perturbed boundary value problems given by Eqs. (1) and (2) by utilizing a properly chosen piecewise-uniform Shishkin mesh proving that the method is uniformly convergent independently of parameters ε_c and ε_d.

This paper is organized as follows: Section 2 provides a priori estimates of the continuous problem. In Section 3, the Shishkin mesh technique is introduced. The design of exponential spline difference scheme method is presented in Section 4 followed by the uniform convergence of the method in Section 5. In Section 6, numerical results and the comparison of approximate solutions are presented to demonstrate the uniformity of the convergence. Finally, Section 7 is devoted for the conclusions.

2 Properties of the continuous problem

The construction of a layer-adapted mesh as well as the analysis of the method requires information about the behavior of derivatives of the exact solution, where we substitute f(x, y) = r(x)y − g(x) into Eq. (1). To describe the layers at x = 0 and x = 1, the characteristic equation is used as given in Linß and Roos (2004), as follows:

3 Mesh selection strategy

In this section, for the selection of the mesh for the previously discussed three subintervals; the solution regions are provided. It is known that on an equidistant mesh no scheme can attain convergence at all mesh points uniformly in ε_c and ε_d, unless its coefficients have an exponential property. Therefore, unless a specially chosen mesh is used, we cannot obtain a parameter-uniform convergence at all the mesh points. The simple possible non-uniform mesh, namely a piecewise-uniform mesh discussed by Linß and Roos (2004), is sufficient for the construction of a parameter-uniform method. It is fine near layers but coarser otherwise. We do not claim that these piecewise-uniform meshes are optimal in any sense. It is attractive because of its simplicity and adequacy for handling a wide variety of singularly perturbed problems. The Shishkin mesh one should have a priori knowledge about the location and nature of the layers which, applicable only by using. To obtain the discrete counterpart of the two-parameter singularly perturbed boundary value problems Eqs. (1) and (2), firstly the considered mesh discretized the domain $\overline{\mathrm{\Omega }}=[0\text{,}1]$ into three subintervals: $${\Lambda }_0=[0\text{,}{\gamma }_1]\text{,}{\Lambda }_c=[{\gamma }_1\text{,}1-{\gamma }_2]\text{and}{\Lambda }_1=[1-{\gamma }_2\text{,}1]\text{,}$$ where transition parameters are given by $${\gamma }_1=\min \left(\frac{1}{4}\text{,}\frac{2}{{\psi }_1}\ln n\right)\text{,}{\gamma }_2=\min \left(\frac{1}{4}\text{,}\frac{2}{{\psi }_2}\ln n\right)\text{,}$$ with n to be the number of subdivision points of the interval [0, 1] and we place n/4, n/2 and n/4 mesh points, respectively, in [0, γ₁], [γ₁, 1 − γ₂] and [1 − γ₂, 1]. Denote the step sizes in each subinterval by $h_1=\frac{4{\gamma }_1}{n}\text{,}{h}_2=\frac{2(1-{\gamma }_1-{\gamma }_2)}{n}$ and $h_3=\frac{4{\gamma }_2}{n}$ , respectively. Accordingly the resulting piecewise-uniform Shishkin mesh may be represented by: $$\tilde{h}=\left\{\begin{array}{cc}{h}_1=\frac{4{\gamma }_1}{n}\text{,}\hfill & x_i=x_{i-1}+h_1\text{,}\text{for}i=1\text{,}2\text{,}\dots \text{,}n/4\text{,}\hfill \\ h_2=\frac{2(1-{\gamma }_1-{\gamma }_2)}{n}\text{,}\hfill & x_i=x_{i-1}+h_2\text{,}\text{for}i=n/4+1\text{,}\dots \text{,}3n/4\text{,}\hfill \\ h_3=\frac{4{\gamma }_2}{n}\text{,}\hfill & x_i=x_{i-1}+h_3\text{,}\text{for}i=3n/4+1\text{,}\dots \text{,}n\text{.}\hfill \end{array}\right.$$

4 Description of the current method

Consider a uniform mesh Δ with nodal point x_i on the interval [0, 1] such that Δ: 0 = x₁ < x₂ < ⋯ < x_n−1  < x_n = 1 where

To obtain the necessary conditions for the coefficients introduced in Eq. (7), the segment values of $Q_i(x_i)\text{,}{Q}_i(x_{i+1})\text{,}{Q}_i^{(1)}(x_i)$ and $Q_i^{(1)}(x_{i+1})$ should be considered at the common node. Expressions for the four coefficients of (7) can be developed in terms of S_i, S_i+1, M_i, and M_i+1, by defining:

Using the continuity of the first derivative at the point (x_i, S_i), where $Q_{i-1}^{\prime }(x)$ and $Q_i^{\prime }(x)$ the following relation for i = 1,2, … .,n − 1 is obtained;

5 Convergence analysis

In this section, the convergence analysis of the current method is investigated. The exponential spline solution of Eqs. (1) and (2) is based on the nonlinear equation given by Eq. (13). It can easily be seen that the system given by Eq. (13) gives n − 1 nonlinear algebraic equations in the n − 1 unknowns S_i,i = 1, 2, …, n − 1. This can be written in the standard matrix equation as:

6 Numerical examples

In this section, we apply our method to the following example and verify experimentally uniform convergence.

The exact solution is given by

The exact solution is given by

The exact solution is given by:

The exact solution is given by

The estimated maximum pointwise error using exponential spline method applied to example1 is shown in Table 6. To compute the experimental rates of convergence Ordⁿ for every fixed ε_c and ε_d, we use the rate of convergence from: $${\mathit{Ord}}^n=\frac{\ln E^n-\ln E^{2n}}{\ln 2}$$ The numerical results presented in Tables 1–4 clearly indicate that the proposed scheme with uniform mesh is not uniformly convergent for sufficiently small value of ε_c and ε_d and the maximal nodal error increases as the number of mesh points increases as in Table 4. To overcome this drawback, we have used a special piecewise uniform mesh known as Shishkin mesh. The numerical results displayed in Tables 5 and 6 clearly indicate that the proposed method based on exponential spline with Shishkin mesh is ε-uniformly convergent. Fig. 1 shows the exact and the approximate solution for various values of ε_d = 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵ and for fix ε_c = 10⁻⁶. Also, we note as ε_ddecreases for fixed ε_c the width of boundary layer decreases and becomes more and more stiff at x = 0 and x = 1, this shows clearly the effect of ε_d and ε_con the boundary layer (see Table 6). Fig. 2 shows the exact and approximate solutions which are taking the same shape and behavior. Also, numerical results generated by the proposed scheme indicate that the maximal nodal errors are smaller than those obtained by Lin et al. (2009), Rao and Kumar (2008), Rao et al. (2010), Kadalbajoo and Yadaw (2008) and Roos and Uzelac (2003).

Close

Figure 1

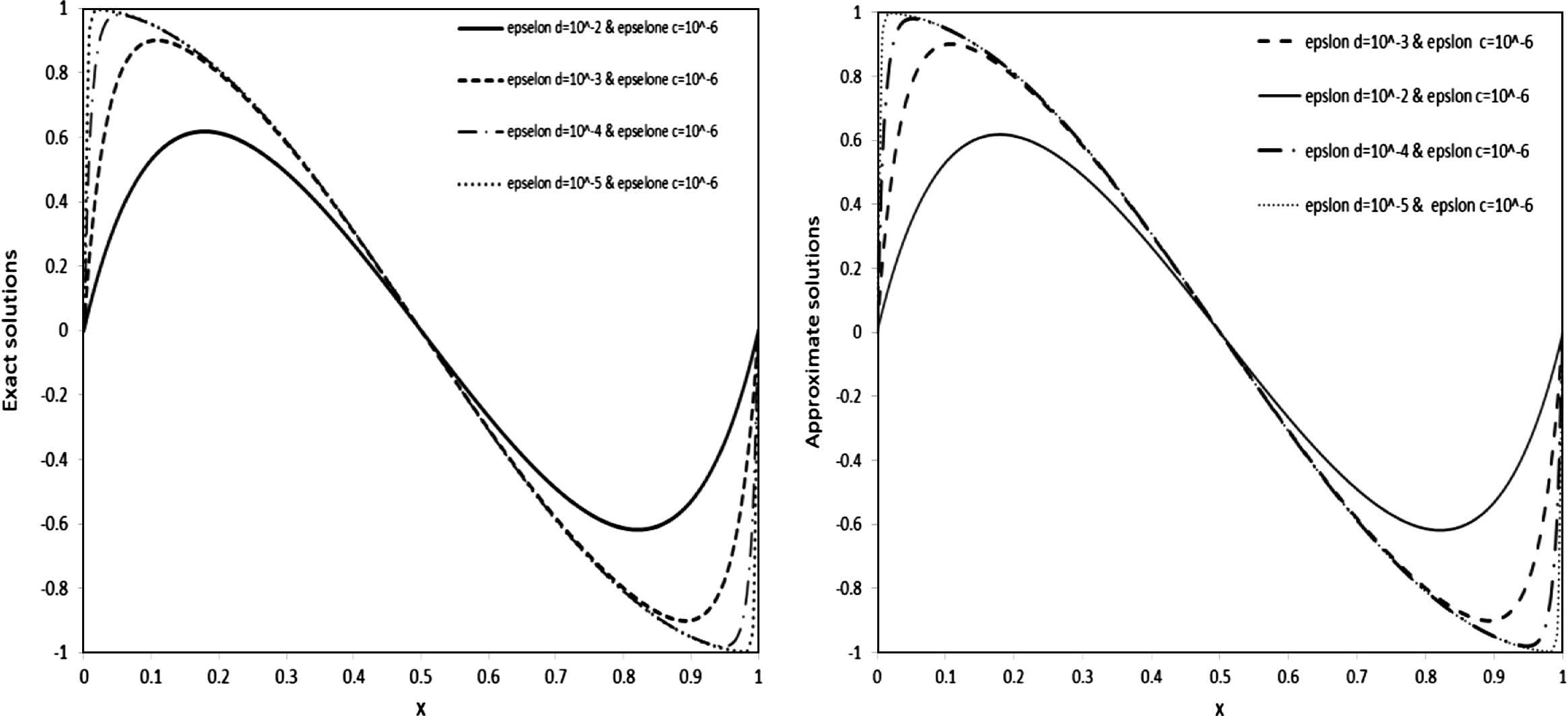
Exact and approximate solutions for example1 at different values of ε_d = 10⁻², 10⁻⁴, 10⁻³, 10⁻⁵ and for fix ε_c = 10⁻⁶.

Export to PPT

Close

Figure 2

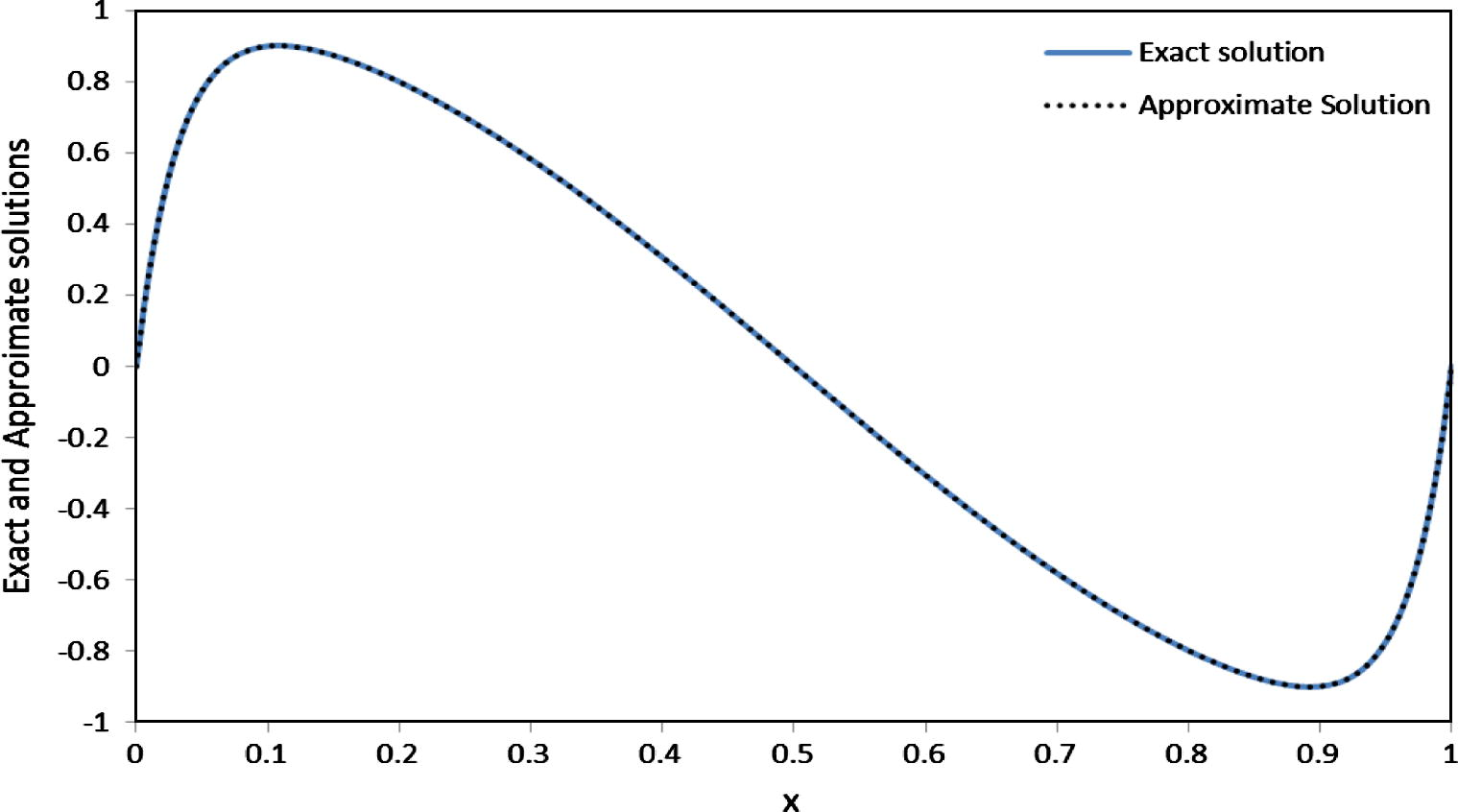
Exact and Approximate solutions for example1 at ε_d = 10⁻³ and ε_c = 10⁻⁶.

Export to PPT

7 Conclusion

A numerical method is developed to solve two-parameter singularly perturbed semi-Linear boundary value problems given by Eqs. (1) and (2). This method is based on exponential spline with a piecewise uniform Shishkin mesh. The method is shown to be uniformly convergent independent of mesh parameters and perturbation parameters ε_c and ε_d. It has been found that the proposed algorithm gives highly accurate numerical results and higher order of convergence than other existing methods.