Mittag-Leffler function for discrete fractional modelling

Guo-Cheng Wu; Dumitru Baleanu; Sheng-Da Zeng; Wei-Hua Luo

doi:10.1016/j.jksus.2015.06.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

28 (

); 99-102

doi:

10.1016/j.jksus.2015.06.004

Mittag-Leffler function for discrete fractional modelling

Guo-Cheng Wu^{^a,^b}, Dumitru Baleanu^{^c,^d,⁎}, Sheng-Da Zeng^{^a,^b}, Wei-Hua Luo^{^a,^b}

a Data Recovery Key Laboratory of Sichuan Province, College of Information Science and Mathematics, Neijiang Normal University, Neijiang 641100, Sichuan, China

b Institute of Applied Nonlinear Science, College of Mathematics and Information Science, Neijiang Normal University, Neijiang 641100, Sichuan, China

c Department of Mathematics and Computer Sciences, Cankaya University, 06530 Balgat, Ankara, Turkey

d Institute of Space Sciences, Magurele-Bucharest, Romania

⁎Corresponding author. dumitru@cankaya.edu.tr (Dumitru Baleanu),

Received: 2015-4-1, Accepted: 2015-6-15, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

From the difference equations on discrete time scales, this paper numerically investigates one discrete fractional difference equation in the Caputo delta’s sense which has an explicit solution in form of the discrete Mittag-Leffler function. The exact numerical values of the solutions are given in comparison with the truncated Mittag-Leffler function.

Keywords

Discrete fractional calculus

Discrete Mittag Leffler function

Show Related Articles from PubMed

1 Introduction

The fractional calculus has become as an efficient tool in various applied areas. For example, due to the beautiful memory effects, it often appears in diffusion in the porous media (Benson et al., 2000; Berkowitz et al., 2002; Bhrawya and Zaky, 2015; Liu et al., 2004; Sun et al., 2009; Yang et al., 2013 ), the material’s properties (Bagley and Torvik, 1983; Carpinteri and Cornetti, 2002; Mainardi, 2010; Rossikhin and Shitikova, 1997 ), biological population (Atangana, 2014) and control systems (Baleanu et al., 2011; Li and Chen, 2004; Machado, 1997 ) et al.

In the applications of the mentioned topic, one frequently comes across the discrete Mittag-Leffler function (DMLF) (Abdeljawad, 2011; Acar and Atici, 2013; Atici and Eloe, 2007; Pillai and Jayakumar, 1995; Nagai, 2003; Liu et al., 2014 ). Due to the functions’ infinity series’ expression, the truncated form is often approximately used. However, the function leads to truncated errors in fractional modelling and explicit analytical calculus for real-world applications. As a result, much effort has been dedicated to numerical approximations of the Mittag-Leffler functions (Garrappa and Popolizio, 2013; Moret and Novati, 2011; Podlubny, 2005; Valerio and Machado, 2014 ).

Very recently, the discrete fractional calculus is developed as a discrete fractional modelling tool (Abdeljawad, 2011; Atici and Eloe, 2009, 2011; Chen et al., 2011 ). In this paper, we consider exact numerical values of the DMLF (Abdeljawad, 2011; Abdeljawad et al., 2012; Acar and Atici, 2013 ) which was given in a limit

(1)

E_{ν} (λ, t) = \lim_{k \to \infty} \sum_{i = 0}^{k} λ^{i} \frac{{(t + i (ν - 1))}^{(i ν)}}{Γ (1 + i ν)},

where

t^{(ν)}

is the falling factorial function as

t^{(ν)} = \frac{Γ (t + 1)}{Γ (t + 1 - ν)} .

The numerical formula of one fractional difference equation is given by the discrete fractional difference in this paper. It is organised as follows. In Section 2, some preliminaries of the fractional calculus are introduced and the numerical formula is given by the DFC. In Section 3, the DMLF is illustrated through the solution of the discrete fractional difference equation. In Section 4, we conclude our work.

2 Preliminaries

Let’s revisit basics of the fractional sum and difference in the following.

Definition 2.1

Definition 2.1 See Atici and Eloe, 2009, 2011

Let $ϕ (t) : N_{a} = {a, a + 1, a + 2, \dots,} \to R$ and $0 < ν$ . Then, the fractional $ν$ order sum is defined by

(2)

_{a} Δ_{t}^{- ν} ϕ (t) = \frac{1}{Γ (ν)} \sum_{s = a}^{t - ν} {(t - s - 1)}^{(ν - 1)} ϕ (s), t \in {(N)}_{a + ν},

where a

\in R

Definition 2.2

Definition 2.2 See Abdeljawad, 2011

For $m - 1 < ν ⩽ m$ , and $ϕ (t)$ defined on $N_{a}$ , the left Caputo-like delta difference is defined by

(3)

{_{a}}^{C} Δ_{t}^{ν} ϕ (t) = \frac{1}{Γ (m - ν)} \sum_{s = a}^{t - (m - ν)} {(t - s - 1)}^{(m - 1 - ν)} Δ^{m} ϕ (s), t \in N_{a + (m - ν)} .

Within this definition, existence results of fractional difference equation are investigated in Chen et al. (2011)

(4)

{}_{a}^{C}Δ_{t}^{ν} u (t) = f (u (t + ν - 1), t + ν - 1), t \in N_{a + 1 - ν}, u (a) = Ω, 0 < ν \leq 1,

among which a discrete equivalent form was given as

(5)

u (t) = Ω + \frac{1}{Γ (ν)} \sum_{s = a + 1 - ν}^{t - ν} {(t - s - 1)}^{(ν - 1)} f (u (s + ν - 1), s + ν - 1), t \in N_{a + 1} .

We can have a numerical formula as

(6)

u (a + n) = u (a) + \frac{1}{Γ (ν)} \sum_{j = 1}^{n} \frac{Γ (n - j + ν)}{Γ (n - j + 1)} f (u (a + j - 1), a + j - 1), u (a) = Ω .

Different from fractional differential equations or differential ones, the iteration solution from (6) is an exact one of the difference equation. In this way, the discrete fractional maps have been proposed as well as the chaotic behaviours and diffusion discussed (Wu and Baleanu, 2014a,b; Wu et al., 2015 ).

3 Discrete fractional difference equation

Let us consider one example about the DMLF. The following fractional difference equation

(7)

{}_{a}^{C}Δ_{t}^{ν} y (t) = λ y (t + ν - 1), y (a) = y_{0}, t \in N_{a + 1 - ν}, a = 0, 0 < ν ⩽ 1

has an exact solution,

(8)

y (t) = y_{0} E_{α} (λ, t), t \in N_{0} .

Considering the existence results (Chen et al., 2011), one can have the sufficient condition

(9)

- \frac{1}{1 + ν} < λ < \frac{1}{1 + ν} .

From the fractional sum (6), we can have

(10)

y (n) = y_{0} + \frac{λ}{Γ (ν)} \sum_{j = 1}^{n} \frac{Γ (n - j + ν)}{Γ (n - j + 1)} y (j - 1), y_{0} = 1

with which we plot a numerical solution for

ν = 0.8

in Fig. 1.

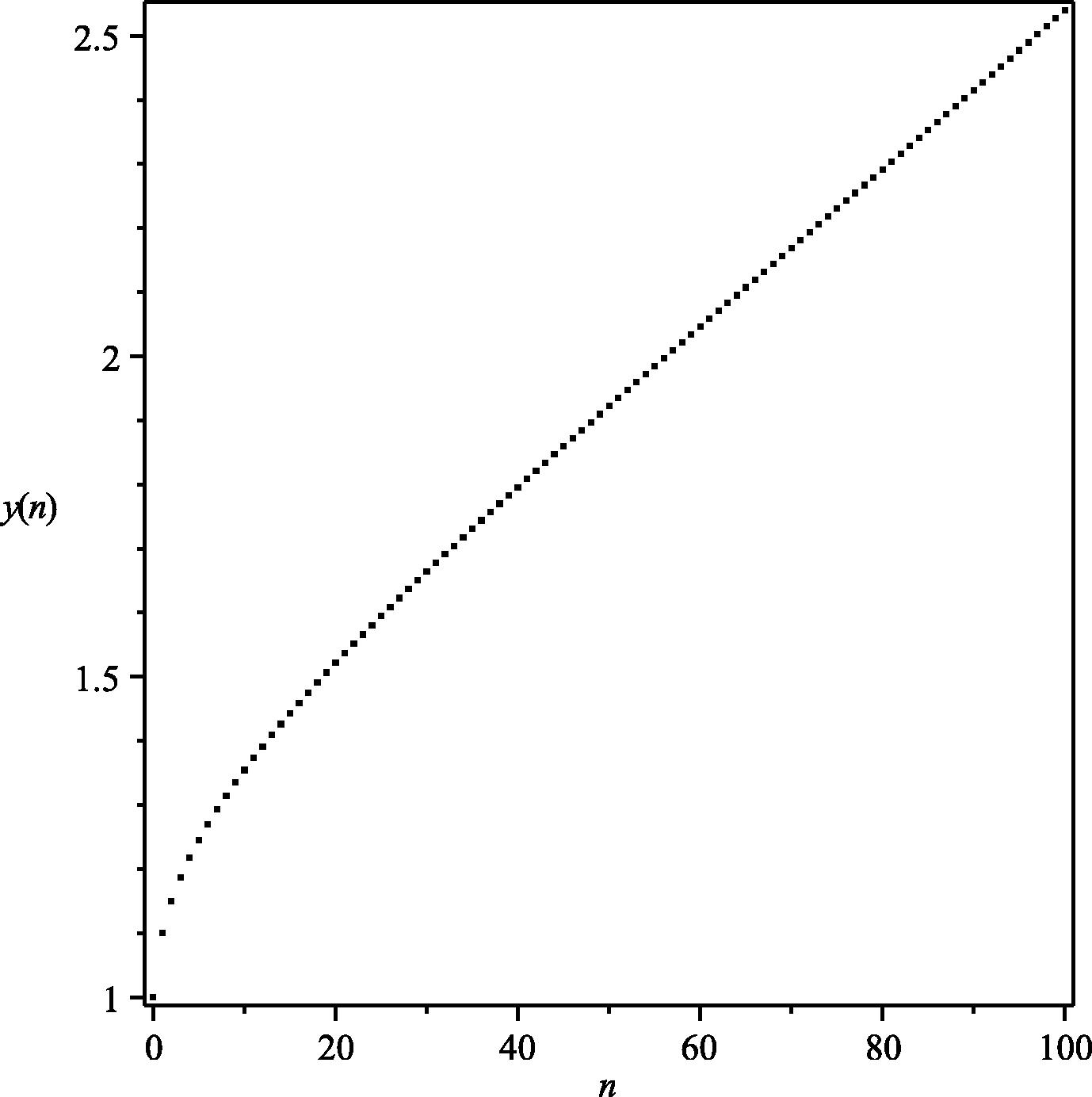
Exact numerical solution for λ = 0.1 , ν = 0.8 and y 0 = 1 .

In Fig. 2, we compare the exact numerical solution with the truncated DMLFs

(11)

y_{3} = \sum_{i = 0}^{3} λ^{i} \frac{{(t + i (ν - 1))}^{(i ν)}}{Γ (1 + i ν)}

and

(12)

y_{4} = \sum_{i = 0}^{4} λ^{i} \frac{{(t + i (ν - 1))}^{(i ν)}}{Γ (1 + i ν)}, t \in N_{0} .

We can conclude that for

i \to \infty, y_{i}

tends to

E_{a} (λ, t)

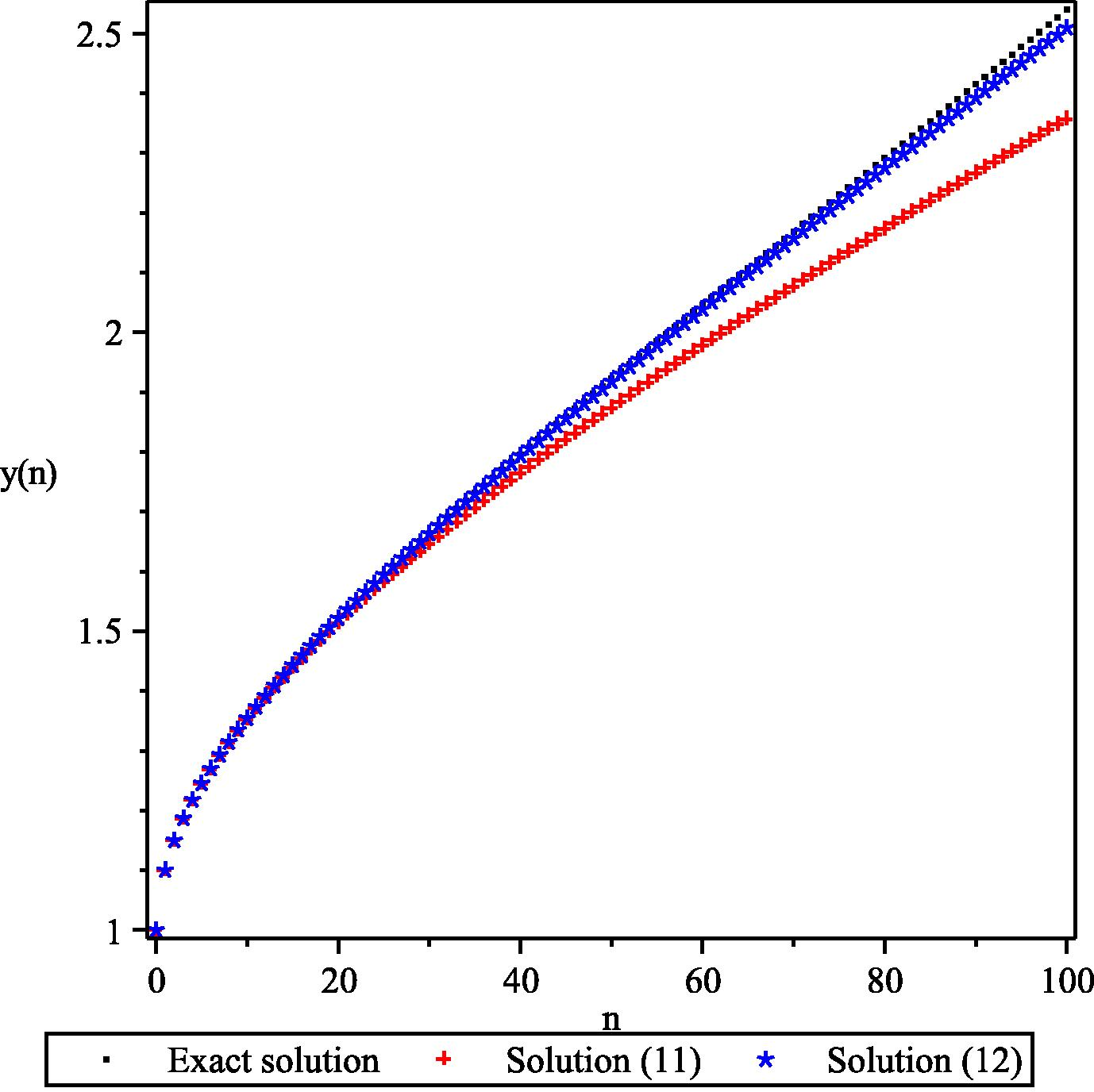
Exact numerical solution versus truncated DMLF solutions for λ = 0.1 , ν = 0.8 and y 0 = 1 .

From the above comparison, we suggest that we can directly use the fractional difference equation in fitting experimental data or other data. One can directly substitute the experimental data into the iteration equation to generate a system with respect to $ν$ . We can use the least square method to determine the fractional order. Considering the continuous MLF (Podlubny, 2005) for fractional differential equation, there is no tedious numerical calculation.

Besides, we also can consider a direct fractional finite difference method for the DFC equation as

(13)

{_{a}}^{C} Δ_{t}^{ν} y (t + 1 - ν) = λ y (t), y (a) = y_{0}, t \in N_{a}, a = 0, 0 < ν ⩽ 1,

with which we can obtain the same solution.

4 Conclusions

In this paper, we revisit the explicit expression of the DMLF. With the existence condition of solutions, the corresponding fractional difference equation on time scales is considered to investigate the function. From the equivalent fractional sum, we derive a numerical formula which leads to the exact numerical solution. We suggest the application to the discrete fractional modelling and experimental fitting. This also shows that the fractional difference equation or map provides a promising tool for discrete systems.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (Grant No. 11301257) and the Fund of Sichuan Provincial Education Department (13ZB0006).

References

Abdeljawad T., . On Riemann and Caputo fractional differences. Comput. Math. Appl.. 2011;62(3):1602-1611.
[Google Scholar]
Abdeljawad T., Jarad F., Baleanu D., . A semigroup-like property for discrete Mittag-Leffler functions. Adv. Differ. Equ.. 2012;2012(1):1-7.
[Google Scholar]
Acar N., Atici F.M., . Exponential functions of discrete fractional calculus. Appl. Anal. Discrete Math.. 2013;7(2):343-353.
[Google Scholar]
Atangana A., . Convergence and stability analysis of a novel iteration method for fractional biological population equation. Neural Comput. Appl.. 2014;25(5):1021-1030.
[Google Scholar]
Atici F.M., Eloe P.W., . A transform method in discrete fractional calculus. Int. J. Differ. Equ.. 2007;2(2):165-176.
[Google Scholar]
Atici F.M., Eloe P.W., . Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theor. Differ. Equ.. 2009;2009(3):1-12.
[Google Scholar]
Atici F.M., Eloe P.W., . Two-point boundary value problems for finite fractional difference equations. J. Differ. Equ. Appl.. 2011;17(4):445-456.
[Google Scholar]
Bagley R.L., Torvik P., . A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol.. 1983;27(3):201-210.
[Google Scholar]
Baleanu D., Machado J.A.T., Luo A.C., . Fractional Dynamics and Control. Springer; 2011.
Benson D.A., Wheatcraft S.W., Meerschaert M.M., . The fractional-order governing equation of Levy motion. Water Resour. Res.. 2000;36(6):1413-1423.
[Google Scholar]
Berkowitz B., Klafter J., Metzler R., Scher H., . Physical pictures of transport in heterogeneous media: advection–dispersion, random-walk, and fractional derivative formulations. Water Resour. Res.. 2002;38(10):1191.
[Google Scholar]
Bhrawya A.H., Zaky M.A., . method based on the Jacobi tau approximation for solving multi-term time–space fractional partial differential equations. J. Comput. Phys.. 2015;281(15):876-895.
[Google Scholar]
Carpinteri A., Cornetti P., . A fractional calculus approach to the description of stress and strain localization in fractal media. Chaos Soliton Fract.. 2002;13(1):85-94.
[Google Scholar]
Chen F., Luo X., Zhou Y., . Existence results for nonlinear fractional difference equation. Adv. Differ. Equ.. 2011;2011:713201.
[Google Scholar]
Garrappa R., Popolizio M., . Evaluation of generalized Mittag-Leffler functions on the real line. Adv. Comput. Math.. 2013;39(1):205-225.
[Google Scholar]
Li C., Chen G., . Chaos in the fractional order Chen system and its control. Chaos Solitons Fract.. 2004;22(3):549-554.
[Google Scholar]
Liu F., Anh V., Turner I., . Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math.. 2004;166(1):209-219.
[Google Scholar]
Liu K., Hu R.J., Cattani C., Xie G.N., Yang X.J., Zhao Y., . Local fractional Z transforms with applications to signals on Cantor sets. Abstr. Appl. Anal.. 2014;2014 (Article ID 638648)
[Google Scholar]
Machado J.A.T., . Analysis and design of fractional-order digital control systems. Syst. Anal. Model. Sim.. 1997;27(2–3):107-122.
[Google Scholar]
Mainardi F., . Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. Singapore: World Scientific; 2010.
Moret I., Novati P., . On the convergence of Keylov subspace methods for matrix Mittag-Leffler functions. SIAM J. Numer. Anal.. 2011;49(5):2144-2164.
[Google Scholar]
Nagai, A., 2003. Discrete Mittag-Leffler function and its applications. RIMS K $\hat{o}$ ky $\hat{u} r$ oku, 1302, pp. 1–20.
Pillai R., Jayakumar K., . Discrete Mittag-Leffler distributions. Stat. Probab. Lett.. 1995;23(3):271-274.
[Google Scholar]
Podlubny, I., 2005. <http://www.mathworks.com/matlabcentral/fileexchange/8738-mittag-leffler-function>.
Rossikhin Y.A., Shitikova M.V., . Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev.. 1997;50(1):15-67.
[Google Scholar]
Sun H., Chen W., Chen Y., . Variable-order fractional differential operators in anomalous diffusion modeling. Physica A. 2009;388(21):4586-4592.
[Google Scholar]
Valerio D., Machado J.A.T., . On the numerical computation of the Mittag-Leffler function. Commun. Nonlinear Sci. Numer. Simul.. 2014;19(10):3419-3424.
[Google Scholar]
Wu G.C., Baleanu D., . Discrete fractional logistic map and its chaos. Nonlinear Dyn.. 2014;75:283-287.
[Google Scholar]
Wu G.C., Baleanu D., . Chaos synchronization of the discrete fractional logistic map. Signal Process.. 2014;102:96-99.
[Google Scholar]
Wu G.C., Baleanu D., Zeng S.D., Deng Z.G., . Discrete fractional diffusion equation. Nonlinear Dyn.. 2015;80(1–2):281-286.
[Google Scholar]
Yang A.M., Yang X.J., Li Z.B., . Local fractional series expansion method for solving wave and diffusion equations on Cantor sets. Abstr. Appl. Anal.. 2013;2013 (Article ID 351057)
[Google Scholar]

Introduction

Preliminaries

Discrete fractional difference equation

Conclusions

Fulltext Views
2

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abdeljawad T., . On Riemann and Caputo fractional differences. Comput. Math. Appl.. 2011;62(3):1602-1611.
[Google Scholar]

[2] Abdeljawad T., Jarad F., Baleanu D., . A semigroup-like property for discrete Mittag-Leffler functions. Adv. Differ. Equ.. 2012;2012(1):1-7.
[Google Scholar]

[3] Acar N., Atici F.M., . Exponential functions of discrete fractional calculus. Appl. Anal. Discrete Math.. 2013;7(2):343-353.
[Google Scholar]

[4] Atangana A., . Convergence and stability analysis of a novel iteration method for fractional biological population equation. Neural Comput. Appl.. 2014;25(5):1021-1030.
[Google Scholar]

[5] Atici F.M., Eloe P.W., . A transform method in discrete fractional calculus. Int. J. Differ. Equ.. 2007;2(2):165-176.
[Google Scholar]

[6] Atici F.M., Eloe P.W., . Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theor. Differ. Equ.. 2009;2009(3):1-12.
[Google Scholar]

[7] Atici F.M., Eloe P.W., . Two-point boundary value problems for finite fractional difference equations. J. Differ. Equ. Appl.. 2011;17(4):445-456.
[Google Scholar]

[8] Bagley R.L., Torvik P., . A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol.. 1983;27(3):201-210.
[Google Scholar]

[9] Baleanu D., Machado J.A.T., Luo A.C., . Fractional Dynamics and Control. Springer; 2011.

[10] Benson D.A., Wheatcraft S.W., Meerschaert M.M., . The fractional-order governing equation of Levy motion. Water Resour. Res.. 2000;36(6):1413-1423.
[Google Scholar]

[11] Berkowitz B., Klafter J., Metzler R., Scher H., . Physical pictures of transport in heterogeneous media: advection–dispersion, random-walk, and fractional derivative formulations. Water Resour. Res.. 2002;38(10):1191.
[Google Scholar]

[12] Bhrawya A.H., Zaky M.A., . method based on the Jacobi tau approximation for solving multi-term time–space fractional partial differential equations. J. Comput. Phys.. 2015;281(15):876-895.
[Google Scholar]

[13] Carpinteri A., Cornetti P., . A fractional calculus approach to the description of stress and strain localization in fractal media. Chaos Soliton Fract.. 2002;13(1):85-94.
[Google Scholar]

[14] Chen F., Luo X., Zhou Y., . Existence results for nonlinear fractional difference equation. Adv. Differ. Equ.. 2011;2011:713201.
[Google Scholar]

[15] Garrappa R., Popolizio M., . Evaluation of generalized Mittag-Leffler functions on the real line. Adv. Comput. Math.. 2013;39(1):205-225.
[Google Scholar]

[16] Li C., Chen G., . Chaos in the fractional order Chen system and its control. Chaos Solitons Fract.. 2004;22(3):549-554.
[Google Scholar]

[17] Liu F., Anh V., Turner I., . Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math.. 2004;166(1):209-219.
[Google Scholar]

[18] Liu K., Hu R.J., Cattani C., Xie G.N., Yang X.J., Zhao Y., . Local fractional Z transforms with applications to signals on Cantor sets. Abstr. Appl. Anal.. 2014;2014 (Article ID 638648)
[Google Scholar]

[19] Machado J.A.T., . Analysis and design of fractional-order digital control systems. Syst. Anal. Model. Sim.. 1997;27(2–3):107-122.
[Google Scholar]

[20] Mainardi F., . Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. Singapore: World Scientific; 2010.

[21] Moret I., Novati P., . On the convergence of Keylov subspace methods for matrix Mittag-Leffler functions. SIAM J. Numer. Anal.. 2011;49(5):2144-2164.
[Google Scholar]

[22] Nagai, A., 2003. Discrete Mittag-Leffler function and its applications. RIMS K $\hat{o}$ ky $\hat{u} r$ oku, 1302, pp. 1–20.

[23] Pillai R., Jayakumar K., . Discrete Mittag-Leffler distributions. Stat. Probab. Lett.. 1995;23(3):271-274.
[Google Scholar]

[24] Podlubny, I., 2005. <http://www.mathworks.com/matlabcentral/fileexchange/8738-mittag-leffler-function>.

[25] Rossikhin Y.A., Shitikova M.V., . Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev.. 1997;50(1):15-67.
[Google Scholar]

[26] Sun H., Chen W., Chen Y., . Variable-order fractional differential operators in anomalous diffusion modeling. Physica A. 2009;388(21):4586-4592.
[Google Scholar]

[27] Valerio D., Machado J.A.T., . On the numerical computation of the Mittag-Leffler function. Commun. Nonlinear Sci. Numer. Simul.. 2014;19(10):3419-3424.
[Google Scholar]

[28] Wu G.C., Baleanu D., . Discrete fractional logistic map and its chaos. Nonlinear Dyn.. 2014;75:283-287.
[Google Scholar]

[29] Wu G.C., Baleanu D., . Chaos synchronization of the discrete fractional logistic map. Signal Process.. 2014;102:96-99.
[Google Scholar]

[30] Wu G.C., Baleanu D., Zeng S.D., Deng Z.G., . Discrete fractional diffusion equation. Nonlinear Dyn.. 2015;80(1–2):281-286.
[Google Scholar]

[31] Yang A.M., Yang X.J., Li Z.B., . Local fractional series expansion method for solving wave and diffusion equations on Cantor sets. Abstr. Appl. Anal.. 2013;2013 (Article ID 351057)
[Google Scholar]