Translate this page into:
Lie group analysis of thermophoresis on a vertical surface in a porous medium
⁎Corresponding author at: Department of Mathematics, Prince Sattam bin Abdulaziz University, College of Science and Humanity Studies, Al-Kharj, Saudi Arabia. eng_hossam21@yahoo.com (Hossam A. Nabwey)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The magnetohydrodynamic and thermophoretic effects on a vertical surface in a porous medium are investigated. The fascinating aspects of thermo diffusion and diffusion-thermo impacts are given. Mathematical modelling via Lie group method was applied. Thereafter, the infinitesimal generators of governing equations are computed. Using suitable similarity variables the existing system which was non-linear is converted into expressions having no dimensions. The resulting expressions were solved numerically using shooting method and the characteristics of embedded parameters such as temperature, velocity, concentration profiles have been displayed graphically. We have compared our findings with those of previous ones to assure the affirmity of our analysis. The change in Sherwood number for progressive Dufour solutal values are also analyzed.
Keywords
Lie group method
Hydromagnetic flow
Porous medium
Heat transfer
Nomenclature
- x,y
-
Coordinates along and normal to the surface (m)
-
Velocity components in x and y directions (m/s)
- Ts
-
Temperature at the surface (k)
- Cs
-
Concentration at the surface (kg/m2)
-
Temperature (k)
-
Concentration (kg/m2)
- Tam
-
Ambient temperature (k)
- Cam
-
Ambient concentration (kg/m2)
- K
-
Permeability of the porous medium (m2)
- ρ
-
Fluid density (kg/m3)
- μ
-
Viscosity of the base fluid (kg m−1 s−1)
- H0
-
Magnetic field (T)
- g
-
Gravitational acceleration (m/s2)
- v
-
Kinematic viscosity (m2 s−1)
- βT
-
Volumetric thermal coefficient of the base fluid (1/k)
- βc
-
Solutal expansion coefficient of the base fluid (m2/kg)
- Cp
-
Specific heat due to constant pressure (J·kg−1·K−1)
- α
-
Thermal diffusivity (m2 s−1)
- VT
-
Thermophoretic velocity (m/s)
- Κv
-
The thermophoretic diffusivity (m−2 s−1)
- λgλp
-
Thermal conductivity of gas and diffused particles, respectively (W m−1 k−1)
- kn
-
Knudsen number
- Z1,Z2,Z3,Z4,Z5,Z6
-
Constants
- Z7,Z8,Z9,Z10,k1,k2,k3,k4
-
Arbitrary constants
- Ra
-
Rayleigh number
- L
-
Characteristic length of the plate (m)
- Pr
-
Prandtl number
- Le
-
Lewis number
- V(x)
-
Transpiration velocity (m/s)
- Df
-
Dufour number
- Sr
-
Soret number
- B
-
The parameter of buoyancy
- CT
-
The parameter for thermophoresis
- D
-
Chemical molecular diffusivity
- θ
-
Dimensionless temperature function
- ϕ
-
Dimensionless species concentration function
- ψ
-
Stream function (m2·s−1)
- η
-
Non-dimensional pseudo-similarity variable
- F
-
Dimensionless stream function
- ε
-
Lie group parameter
- F, Θ, Φ
-
Arbitrary functions
1 Introduction
Since last few decades’ fluid flow in porous media has been intensively investigated by various mathematicians. In many of these investigations, emphasis has been given to insulation systems - both granular as well as fibrous, which are used to contain the movement of radio nuclides from nuclear waste material deposits. Since then many papers were published on boundary-layer flow past surfaces of diverse flow configuration models. For some applications which require further theoretical and experimental developments, see Nield and Bejan (2013), Vafai (2000), Pop and Ingham (2001), and Ingham and Pop (1998).
Magnetohydrodynamic (MHD) is a momentous and riveting region of science which delineates with the movement of electrically conducting fluid. The paramount factuality on the backside of MHD is to beget current due to applying magnetic field; the impact of this process induces Lorentz force which significantly impacts the fluid motion. The multifarious MHD fluids exist in nature as salt water, plasmas and electrolysis; see Ingham and Pop (1998), Pai (1962). Lately, MHD is a content of intensive era of study because of its numerous industrial applications like glass manufacturing, MHD electrical generation process and procedure for magnetic materials. Additionally, it has alluring characteristics in the field of geophysics and astrophysics i.e. it is habituated in energy extraction and radio propagation. Engineering products like MHD fluid flow meters and MHD pumps which exploited the MHD phenomenon. However, in view of such motivation, authors have investigations in MHD flow for several geometries (see refs. Liuta and Larachi, 2003; Chamkha et al., 2013; Rashad, 2008; EL-Kabeir et al., 2010; Hayat et al., 2013).
Heat and mass transfer flows with Dufour and Soret impacts are of substantial attraction among numerous authors owing to several grown engineering applications like manufacture for rubber and plastic sheets, Catalytic process, chemical production engineering, geophysical procedures, compact heat insulation exchangers and layout of nuclear reactor. A considerable amount of investigation has been performed to demonstrate the significance of these two impacts for various aspects – For instance, Dursunkaya and Worek (1992) and Anghel et al. (2000) investigated for fluids, the effect on convection flow of fluid over a stretchable surface porous medium by Hayat et al. (2010), Makinde and Olanrewaju (2011) analyzed the combined convective with Dufour and Soret impacts over a permeable surface roving through a mixture of fluid. And for more details see Beg et al. (2009), Aziz (2008) and Chamkha and Rashad (2014; Rashad and Chamkha, 2014).
Many mathematicians were illustrated and explained in their research papers the importance of applying the group theory in the field of fluid mechanics. See (Bakier et al., 2009; Nabwey et al., 2017, 2015; EL-Kabeir et al., 2008)
The prime purpose of the current investigation is to analyse the influence of Soret and Dufour effects on heat and mass transfer by MHD flow through a vertical surface in a porous medium with thermophoresis. The mathematical model which represent the case study is transformed to couple non-linear ODEs by impose the Lie group method. The system is solved numerically by shooting method. Finally, the effect of the associated physical fluid dynamical parameters on the flow is exhibited and analyzed using the graphical aid and tabular forms.
2 Analysis
Here we consider the flow of electrically conducting fluid over a heated vertical surface passing through a porous medium. The surface is maintained at constant temperature
and the concentration
, while their ambient values are denoted by
and
respectively. From the above basic assumptions and following Chiou (1998) and Chamkha, and Pop (2004) the governing equations for an unsteady flow are:
In this work, the boundary conditions were taken as:
where V (x) is the permeability of the porous surface (negative sign refer to suction and a positive sign indicates injection). Since the temperature gradient is higher along y-axis, the thermophoretic velocity VT is considered along y-axis and is given by:
The next step is to define the dimensionless variables as:
represent the characteristic velocity
represent the Rayleigh number,
is a characteristic length of the plate.
From the above Eqs. (1)-(5) becomes:
Then the new boundary conditions are:
And the boundary conditions (5) become:
3 Determination of the symmetry groups
3.1 Lie-point symmetries equations
For symmetry of a differential equations and some methods of its calculations we refer to (Ovsiannikov, 1982; Olver, 1986; Bluman and Kumei, 1989; Ibragimov, 1999; EL-Kabeir et al., 2007, 2008; Nabwey et al., 2015, 2017); consider the one-parameter Lie group of infinitesimal transformations in
given by:
The action of ℵ is extended to all derivatives appearing in (16)-(18) through the second prolongation
,
,
Proper algebraic calculations gives the following infinitesimals:
when ,
when ,
when
,
From the above we get:
Thus the boundary conditions complying with symmetries (19) are given by
3.2 Proposition
The BVP given in Eqs. (16)-(18) and (19), have the following multi-parameter group of symmetries:
But Eq. (29) is the admissible form of data on the boundaries. From (27), we can find the symmetry corresponding to those problems studied in (Nabwey et al., 2015, 2017). By neglecting the parameters and , the scaling group is parameterized by .
4 Group-Invariant solutions
Here, we examine the group-invariant solutions of the symmetry group gained in the last sections. For details on group-invariant solutions see (Ovsiannikov, 1982; Olver, 1986). Suppose is solution of the problem (16)-(18). This solution will remain the same under the transformation group in Eq. (33) if the following hold:
, , and ,
Or
The following system can be solved with the method of characteristics.
The group-invariant solution of the system is given by Eqs. (35.1)-(35.4). It can be observed that the IBVP have been transformed into BVP of non-similar transient equations, which are easily solvable and it is noted that our solution make a reduction to the number of independent variables
5 Scaling symmetry
We restrict our study with regard to Scaling Symmetry and accordingly we have chosen
and
. We revisit the problem presented in (Cheng and Mynkowycz, 1977; Bejan and Khair, 1985) without considering the Dufour and Soret effects with thermophoresis impact, whose transformation equations are given by:
With above parameters, the similarity solutions (35.1)-(35.4) become:
By Putting the value of (37) in Eqs. (16)-(18), we notice that the number of independent variables get reduced by one and accordingly, the transformed mathematical model is:
The new boundary conditions are:
Here the parameter denotes the suction/injection, such that the permeability of the porous surface V(X) varies inversely to square root of x, in order to make Fw independent of x. Four new arbitary constants i.e., have been introduced; so the coefficients in the above equations do not reflect the fluid properties explicitly.
For κ = 0 (absence of thermophoresis) and B = 0, we notice that the Eqs. (38)-(39) reduce to the system represented by Cheng and Minkowycz (Pai, 1962) while at the system reduce to the one given by Bejan and Khair (EL-Kabeir et al., 2007) respectively.
6 Results and discussion
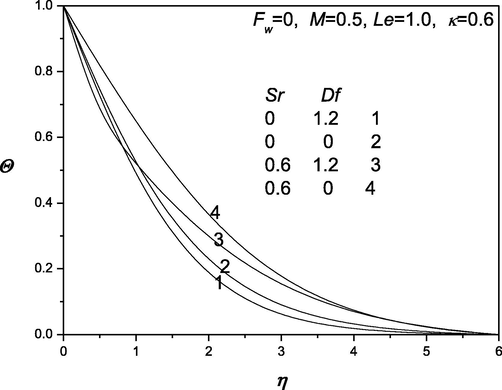
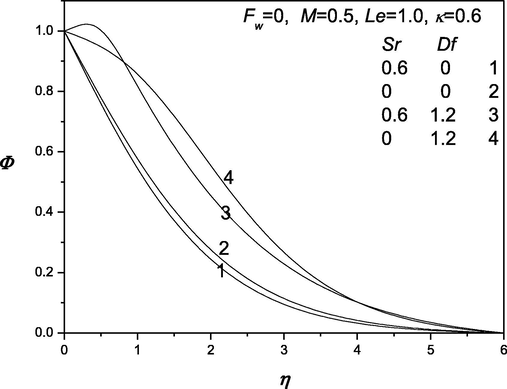
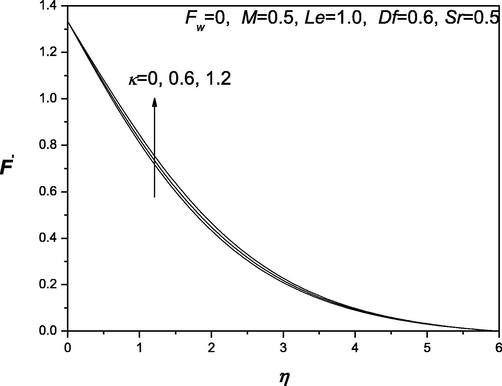
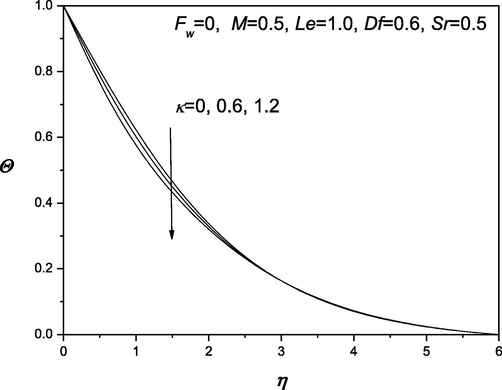
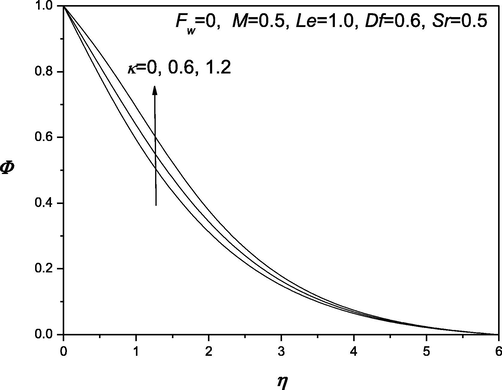
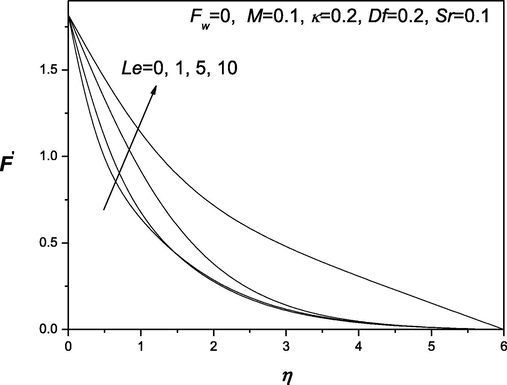
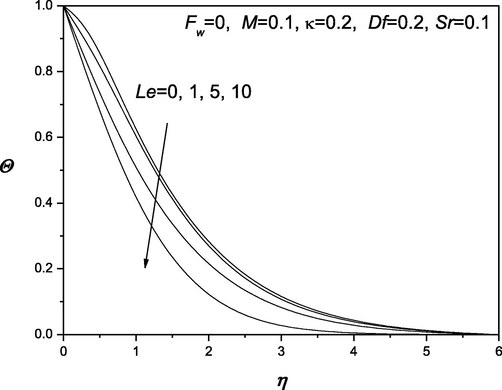
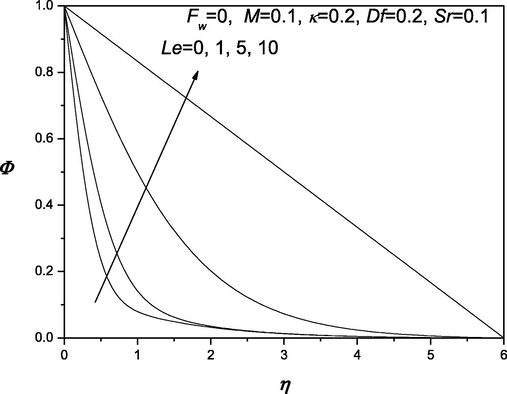
The convenient similarity transformations in (37) are applied to gain identical ordinary differential equations from the flow, heat and transfer arising governing equations (38) which are highly nonlinear in nature. Shooting technique is accustomed along with Runge-Kutta method to find the solution of these equations. The impacts of various dimensionless quantities on velocity, temperature and concentration distributions are exhibited and analyzed using the graphical aid (see Fig. 1–12]. Shooting technique is one of the techniques that are used to solve the initial value problems. The behavior of suction/injection parameter, Fw and magnetic parameter M on velocity is exposed in Fig. 1. It is manifested that velocity regime appears to be reduced with the decrease of the suction/injection parameter Fw and the magnetic parameter M. Figs. 2 and 3 portray the effect of suction/injection parameter, Fw on the temperature and concentration distributions. It is illustrated that for decreasing values of Fw temperature and concentration distribution become more uniform and the thermal boundary layer thickness increases. Figs. 4–6 is exhibited to visualize the behavior of involved sundry such as Dufour and Soret numbers (Df and Sr) on the of profiles velocity, temperature and concentration. It is perceived that the velocity of the fluid declines as Df and Sr grow but the temperature reduces (or concentration enhances) with the incerment in Df and increase in Sr. Figs. 7–12 demonstrate the effects of thermophroesis parameter and Schmidt number on velocity, temperature, and concentration profiles. These graphs clarify that the temperature declines as the thermophroesis parameter and Schmidt number decrease, while the velocity and concentration decrease as the thermophroesis parameter and Schmidt number increase. The behaviors of magnetic parameter M, Dufour and Soret numbers (Df and Sr) and thermophroesis parameter κ on the rate of heat transfer
and the rate of mass transfer
are exposed in Tables 1–2. It is manifested that local Nusselt numbers Nu and Sherwood number Sh reduce as M increases. Furhertmore, From Table 2, It is engrossed that by increasing the the thermophroesis parameter κ increases, the rate of heat transfer
increases whereas rate of mass transfer
decreases.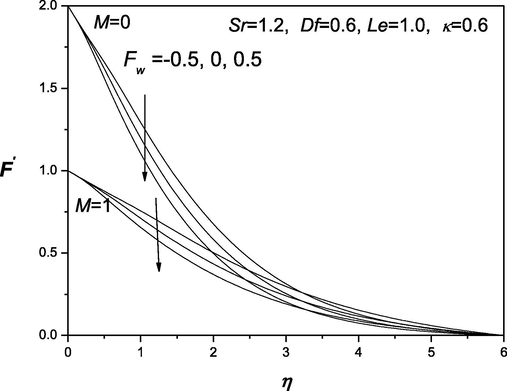
Distribution of velocity.
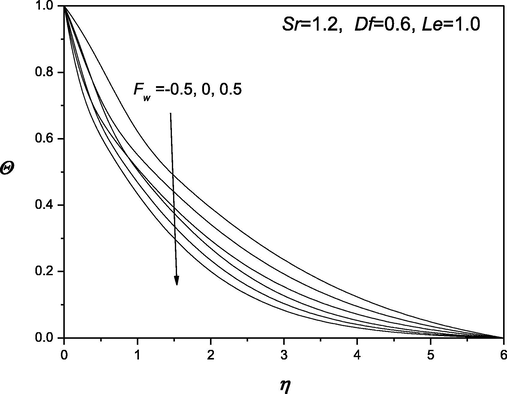
Distribution of temperature.
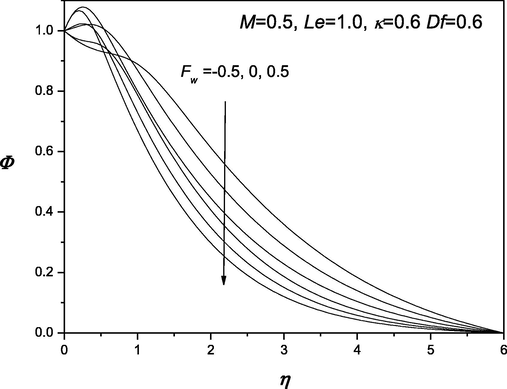
Distribution of concentration.
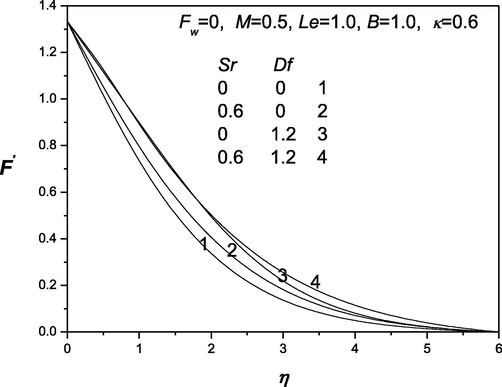
Distribution of velocity.
Distribution of temperature.
Distribution of concentration.
Distribution of velocity.
Distribution of temperature.
Distribution of concentration.
Distribution of velocity.
Distribution of temperature.
Distribution of concentration.
M
Df
Sr
−θ’(0)
−ϕ’(0)
0
0.05
0.2
0.6374
0.4991
1
0.05
0.2
0.4673
0.3765
2
0.05
0.2
0.3999
0.3301
0
0.075
0.8
0.6665
0.2896
1
0.075
0.8
0.4839
0.2447
2
0.075
0.8
0.4107
0.2351
0
0.6
0.1
0.4698
0.5831
1
0.6
0.1
0.3688
0.4253
2
0.6
0.1
0.3331
0.3631
κ
Df
Sr
−θ’(0)
−ϕ’(0)
0.05
0.05
0.2
0.4620
0.4217
0.5
0.05
0.2
0.4673
0.3765
0.8
0.05
0.2
0.4709
0.3471
1.2
0.05
0.2
0.4756
0.3089
0.05
0.075
0.8
0.4773
0.2907
0.5
0.075
0.8
0.4839
0.2447
0.8
0.075
0.8
0.4883
0.2148
1.2
0.075
0.8
0.4941
0.1763
0.05
0.6
0.1
0.3461
0.4632
0.5
0.6
0.1
0.3688
0.4253
0.8
0.6
0.1
0.3856
0.3973
1.2
0.6
0.1
0.4100
0.3562
7 Conclusion
In this study we analyze phenomenon of thermophoresis on a vertical surface in a porous medium. The fascinating aspects of thermo diffusion and diffusion-thermo impacts are accounted with magnetic field and thermophoresis influence. In this communication, it can be seen that after incorporating these impacts and utilizing Lie group method, the mathematical model has been designed using PDE which are non-linear and subsequently transforming into the system of ODE by using suitable similarity transformations. The numerical solutions of the system have been arrived and the following results are arrived:
-
Velocity profiles are growing due to acceleration in the value of suction/injection parameter and magnetic parameter but declination happens by increasing the Dufour and Soret numbers.
-
Increase in the value of thermophroesis parameter results in reduction of both velocity and concentration profiles and enhancement of temperature profiles.
-
Considerable reduction in local Nusselt and Sherwood numbers is exhibited by promoting the values of magnetic parameter.
-
Massive in reduction in local Nusselt number and declination in Sherwood number for elevating the values of thermophroesis parameter.
-
Both Local Nusselt Number and Sherwood number varies inversely with Soret Number but with Dufour number it is vice-versa.
References
- Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and soret and dufour effects. Can. J. Chem. Eng.. 2014;92(4):758-767.
- [CrossRef] [Google Scholar]
- Influence of radiation on MHD free convection from a vertical flat plate embedded in porous media with thermophoretic deposition of particles. Commun. Nonlinear Sci. Numer. Simulat.. 2008;13:2213-2222.
- [CrossRef] [Google Scholar]
- Heat and mass transfer by natural convection flow about a truncated cone in porous media with Soret and Dufour Effects. Int. J. Numer. Meth. Heat Fluid Flow. 2014;24(3):595-612.
- [CrossRef] [Google Scholar]
- Group method analysis of melting effect on MHD mixed convection flow from radiate vertical plate embedded in a saturated porous media. Commun. Nonlinear Sci. Numer. Simul.. 2009;14:2160-2170.
- [CrossRef] [Google Scholar]
- Coupled heat and mass transfer by MHD free convection flow along a vertical plate with streamwise temperature and species concentration variations. Heat Transfer-Asian Res.. 2013;42(2):100-110.
- [CrossRef] [Google Scholar]
- Anghel, M., Takhar, H.S., Pop, I., 2000. Dufour and Soret effects on free convection boundary-layer over a vertical surface embedded in a porous medium. Studia Univ Babes-Bolyai Math .11–22. XLV.
- Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer by hydromagnetic three-dimensional free convection over a permeable stretching surface with radiation. Phys. Lett. A. 2008;372(3):263-272.
- [Google Scholar]
- Numerical study of free convection magnetohydro-dynamic heat and mass transfer from a stretching surface to a saturated porous medium with Soret and Dufour effects. Comput. Mater. Sci.. 2009;46(1):57-65.
- [Google Scholar]
- Int. J. Heat Mass Transfer. 1985;28:900.
- Symmetries and Differential Equations. New York: Springer-Verlag; 1989.
- Convection in Porous Media (4th edition). New York: Springer; 2013.
- Ingham, D.B., Pop, I., 1998. Transport Phenomena in Porous Media, Pergamon, Oxford, vol. II.
- Diffusion-thermo and thermal-diffusion effects in transient and steady natural convection from vertical surface. Int J Heat Mass Transfer.. 1992;35(8):2060.
- [Google Scholar]
- Thermophoretic deposition of particles in gas flowing over cold surfaces. J. Colloid interface Sci.. 1985;107:21-37.
- [Google Scholar]
- Heat and mass transfer for Soret and Dufour’s effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Commun. Nonlinear Sci. Numer Simul.. 2010;15(5):1183-1196.
- [Google Scholar]
- Convective Heat Transfer: mathematical and computational modelling of viscous fluids and porous media. Oxford: Pergamon; 2001.
- Effect of thermophoresis particle deposition in free convection boundary layer from a vertical flat plate embedded in a porous medium. Inter. Comm. Heat mass transfer.. 2004;31:421-430.
- [Google Scholar]
- Handbook of Porous Media. Marcel: Marcel Dekker; 2000.
- Thermophoresis of particles in a heated boundary layer. J. Fluid Mech.. 1980;101:737-758.
- [Google Scholar]
- Group analysis of differential equations. New York: Academic Press; 1982.
- Magnetohydrodynamics of trickle bed reactors: mechanistic model, experimental validation and simulations. Chem. Eng. Sci.. 2003;58:297-307.
- [Google Scholar]
- Effect of thermophoresis on sub-micron particle deposition from a forced laminar boundary layer flow on to an isothermal moving plate. Acta Mech.. 1998;129:219-229.
- [Google Scholar]
- Unsteady mixed convection with Soret and Dufour effects past a porous plate moving through a binary mixture of chemically reacting fluid. Chem. Eng. Commun.. 2011;198:920-938.
- [Google Scholar]
- Elementary Lie group analysis and ordinary differential equations. New York: John Wiley & Sons; 1999.
- Group method analysis of mixed convection stagnation-point flow of non-Newtonian nanofluid over a vertical stretching surface. Indian J. Phys.. 2017;91:731.
- [CrossRef] [Google Scholar]
- Lie Group analysis of effects of radiation and chemical reaction on heat and mass transfer by unsteady slip flow from a non-isothermal stretching sheet immersed in porous medium. J. Comput. Theor. Nanosci.. 2015;12(11):4056-4062.
- [CrossRef] [Google Scholar]
- J. Geophys. Res.. 1977;82:2040.
- Application of Lie groups to differential equations. Berlin: Springer; 1986.
- Magnetogasdynamics and plasma dynamics. Berlin: Springer; 1962.
- Heat and mass transfer by MHD stagnation-point flow of a power-law fluid towards a stretching surface with radiation. chemical reaction and Soret and Dufour effects. Int. J. Chem. Reactor Eng.. 2010;8:1-18.
- [Google Scholar]
- Unsteady MHD combined convection over a moving vertical sheet in a fluid saturated porous medium with uniform surface heat flux. Math. Comput. Modell.. 2007;46:384-397.
- [Google Scholar]
- Group method analysis of combined heat and mass transfer by MHD non-Darcy non-Newtonian natural convection adjacent to horizontal cylinder in a saturated porous medium. Appl. Math. Model.. 2008;32:2378-2395.
- [CrossRef] [Google Scholar]
- Lie group analysis of unsteady MHD three dimensional by natural convection from an inclined stretching surface saturated porous medium. J. Comput. Appl. Math.. 2008;213:582-603.
- [Google Scholar]
- MHD axisymmetric flow of third grade fluid between stretching sheets with heat transfer. Comput. Fluids. 2013;86:103-108.
- [Google Scholar]







