Fractional derivative of the Hurwitz ?-function and chaotic decay to zero

1 Introduction

In recent years, fractional calculus has more and more become one of the most suitable tools for research both in theory and in applications, spreading over almost all fields of science and technology. For instance, fundamental problems of fracture mechanics, electromagnetism, speech signals, sound wave propagation in rigid porous materials, fluid mechanics, viscoelasticity, and edge detection, were easily solved and correctly explained using fractional calculus (Dalir and Bashour, 2010; Tarasov, 2008, 2006). In particular, because of the local definition of differential operators, the local approach of fractional calculus has opened new perspectives in scientific investigation with many interesting results (Bhrawy and Abdelkawy, 2015; Liu et al., 2014; Yang et al., 2013a,b; Zhao et al., 2013).

A very interesting topic is the geometrical interpretation of fractional operators. In fact, like the integer order derivative that gives the linear approximation of smooth (differentiable) functions, it should be expected that fractional derivative might give the non-linear approximation of the local behavior of non-differentiable functions (see e.g. Wang, 2012), thus opening new perspectives in research, by the investigation of fractional derivatives on non-differentiable sets, like the Cantor sets (Liu et al., 2014; Yang et al., 2013a,b; Zhao et al., 2013) or by investigating the non-differentiability of some special functions.

Almost all special functions are functions of complex variables (Abramowitz and Stegun, 1964). For this reason, the Ortiguera definition of fractional derivative of complex functions (Li et al., 2009; Ortigueira, 2006) seems to be the most suitable tool for studying complex functions. Using the Ortiguera fractional derivative we will give, in the following, the explicit form of the fractional derivative of the Hurwitz and Riemann ?-function together with some properties thereof. The famous Riemann ?-function is a special case of the more general Hurwitz ?-function which is a Dirichlet series. So, we will compute first the Ortiguera fractional derivative of the Hurwitz ?-function to obtain the fractional derivative of the Riemann ?-function as a special case (for preliminary results see also Guariglia, 2015). There are several applications of the analysis of Riemann ?-function in physics, such as in the scattering inverse methods where quantum potentials correspond to zeroes of the Riemann zeta (Schumayer et al., 0562; Sierra, 2010), or in the chaotic behavior of quantum energy levels related to these zeroes (Pozdnyakov, 2012). To this goal we will show in Section 4.1 that the fractional derivative of the Riemann ?-function also decays chaotically to zero. In particular, as application to a dynamical system we will show that zero is an attractor for this fractional derivative. Our aim is to compute the Caputo-Ortiguera fractional derivative of the Hurwitz zeta function and show its main properties.

2 Preliminary remarks on Riemann and Hurwitz zeta function

3 Remarks on fractional calculus

Let us start with the Cauchy formula of repeated integration: $$J^{n}f(x){\displaystyle \stackrel{\mathrm{def}}{=}}{f}^{(-n)}(x)=\frac{1}{(n-1)!}{?}_a^x{(x-t)}^{(n-1)}f(t)\mathit{dt}$$ where f is a continuous function on the interval $[a\text{,}b]$ with $a?x?b$ (Lazarevic, 2014). This formula suggests us a suitable generalization to a repeated integral of any real order $?$ . By replacing the factorials with Gamma function, being $\mathrm{?}(n-1)=n!\text{,}n?{\mathbb{Z}}^{+}$ , and the integer order n of the above with some real value $??{\mathbb{R}}^{+}$ we have the following:

The fractional derivative in the Caputo sense (Caputo, 1967) is defined through a fractional integral, as follows:

This definition holds true for all real powers (Boyadjiev et al., 2005), including negative or null values. In fact, for $?<0$ , it is $D^{?}=f(t)=J^{-?}f(t)$ while for $?=0$ it is $D^{0}f(t)=f(t)$ . Thus, in the fractional calculus, the two operators integration and differentiation are unified as one single operator, sometime called differintegral (Lazarevic, 2014; de Oliveira and Tenreiro, 2014).

As a consequence of its definition we have:

For other properties about the differintegral defined from the Riemann-Liouville and Caputo approaches, see also (Kamata and Nakamula, 2002; Lazarevic, 2014; Bagley, 2010).

Based on the Caputo derivatives we give now a suitable generalization of fractional derivative of complex functions (Guariglia, 2015; Li et al., 2009; Ortigueira, 2006).

Using this definition, we can obtain the fractional $?$ -derivative of a complex function along the $?$ -direction of the complex plane. This is a natural generalization of the Caputo derivative, because for a real function, i.e. $?=?$ , we re-obtain (3.1) (Li et al., 2009).

4 Fractional derivatives of the Dirichlet Series and of the Hurwitz zeta function

In this section, the fractional derivative of a function defined by a Dirichlet series (Apostol, 2010, chp. 11), is given. As a consequence we can easily define both the fractional derivative of the Hurwitz zeta function and as a special case of the Riemann zeta function.

Proof

Let us start with the general form of a Dirichlet series given by (2.3). Using (3.2), we have (Apostol, 2010, chp. 11): $${}_c{\mathrm{D}}^{?}F(s)=\frac{e^{j(?-?)(?-m)}}{\mathrm{?}(m-?)}\times {?}_0^{?}\frac{d^m}{{\mathit{ds}}^m}{\displaystyle \underset{n=1}{\overset{?}{?}}}\left(f(n)n^{-{\mathit{xe}}^{j?}-s}{x}^{m-?-1}\right)\mathit{dx}=\frac{e^{j(?-?)(?-m)}}{\mathrm{?}(m-?)}\frac{d^m}{{\mathit{ds}}^m}{\displaystyle \underset{n=1}{\overset{?}{?}}}f(n)n^{-s}\times {?}_0^{?}\left(n^{-{\mathit{xe}}^{j?}}{x}^{m-?-1}\right)\mathit{dx}$$ The last integral on the RHS of this equality has been already given in Guariglia (2015), as $${?}_0^{?}\left(n^{-{\mathit{xe}}^{j?}}{x}^{m-?-1}\right)\mathit{dx}=e^{j?(m-?)}{(\log n)}^{?-m}\mathrm{?}(m-?)$$ where, $m-?>0$ . There follows that: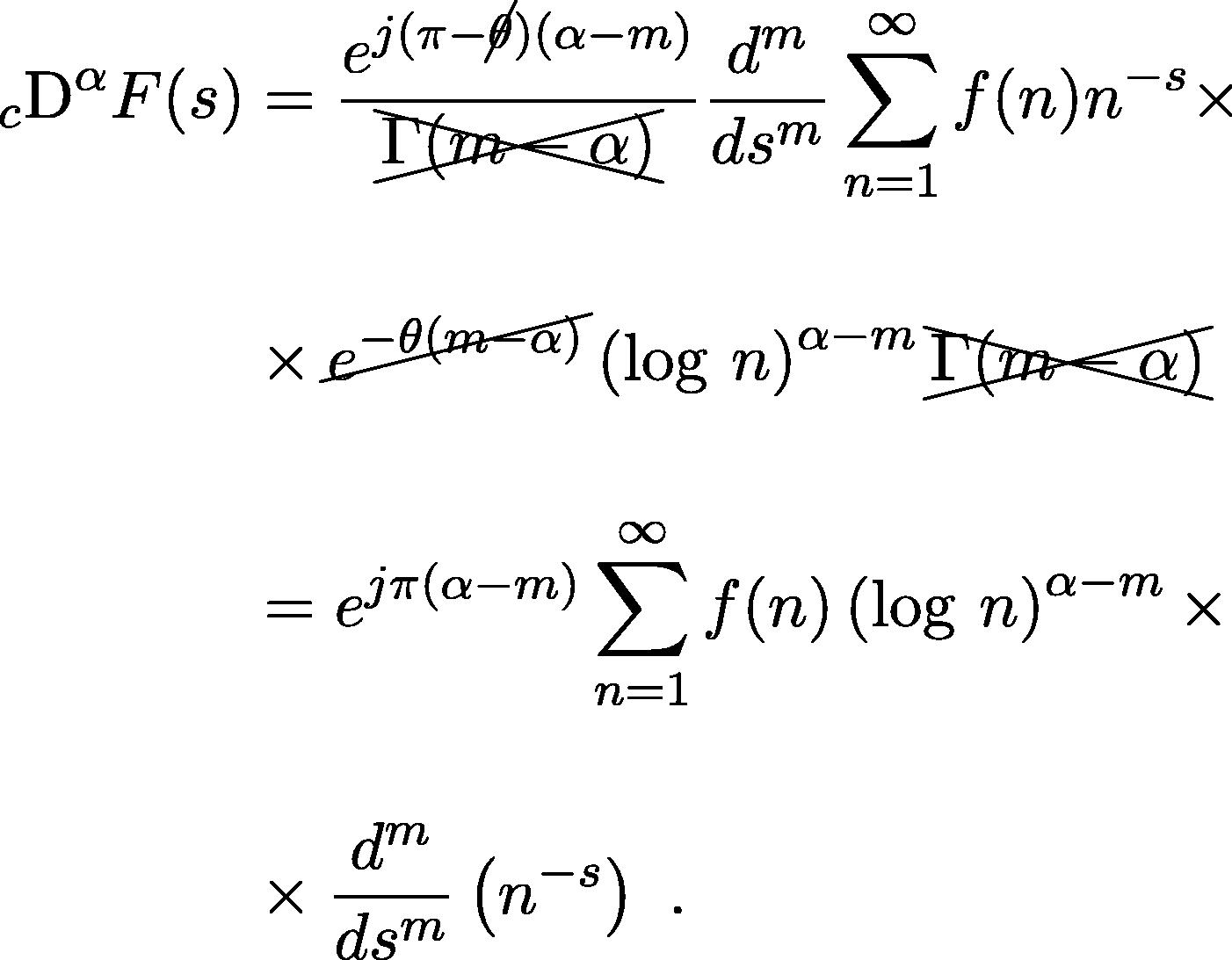

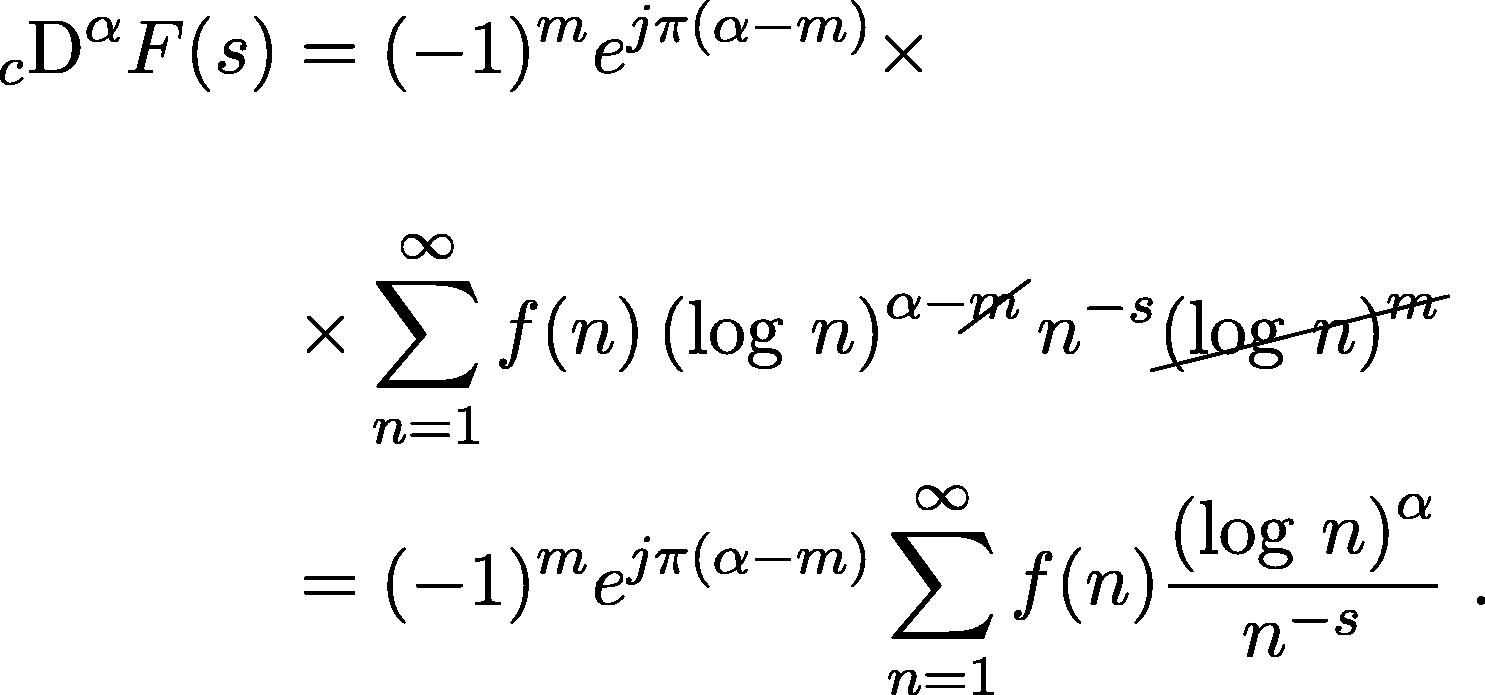
Close

Export to PPT

Since it is (Guariglia, 2015) $$\frac{d^m}{{\mathit{ds}}^m}\left(n^{-s}\right)={(-1)}^m{n}^{-s}{\left(\log n\right)}^m$$ then

Close

Export to PPT

The computation of the fractional derivative of the Dirichlet series enables us to easily compute also the corresponding derivative of the Hurwitz zeta function. In fact, in the previous equation, by writing $f(s)=?(s\text{,}a)$ , we get: $${}_c{\mathrm{D}}^{?}?(s\text{,}a)=\frac{e^{j(?-?)(?-m)}}{\mathrm{?}(m-?)}\times {?}_0^{?}\frac{d^m}{{\mathit{ds}}^m}{\displaystyle \underset{n=1}{\overset{?}{?}}}\left({(n+a)}^{-{\mathit{xe}}^{j?}-s}\times x^{m-?-1}\right)\mathit{dx}=\frac{e^{j(?-?)(?-m)}}{\mathrm{?}(m-?)}\frac{d^m}{{\mathit{ds}}^m}\times {\displaystyle \underset{n=1}{\overset{?}{?}}}{(n+a)}^{-s}{?}_0^{?}{(n+a)}^{-{\mathit{xe}}^{j?}}\times x^{m-?-1}\mathit{dx}\text{.}$$ If we call I the last integral of the RHS, we have that: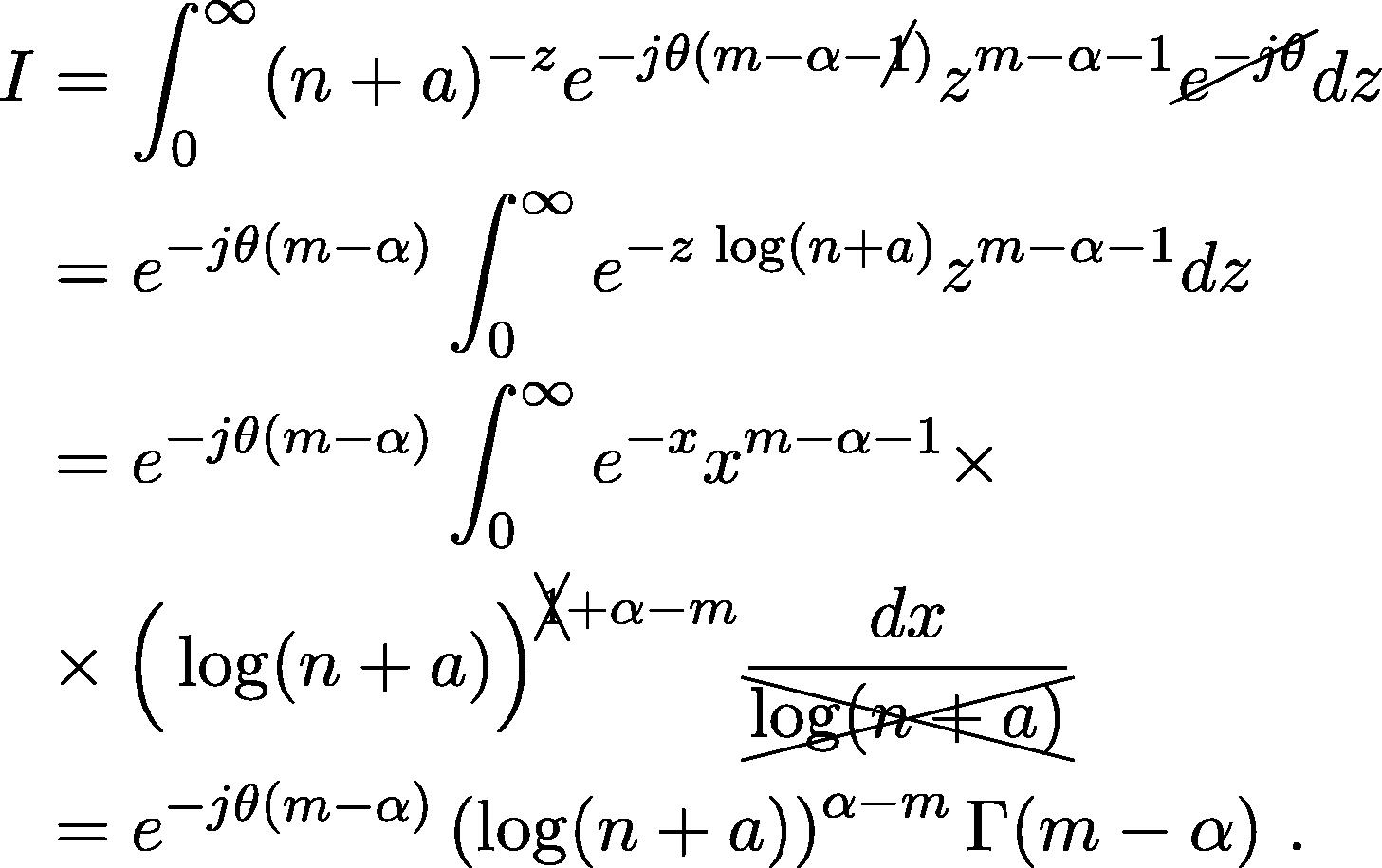

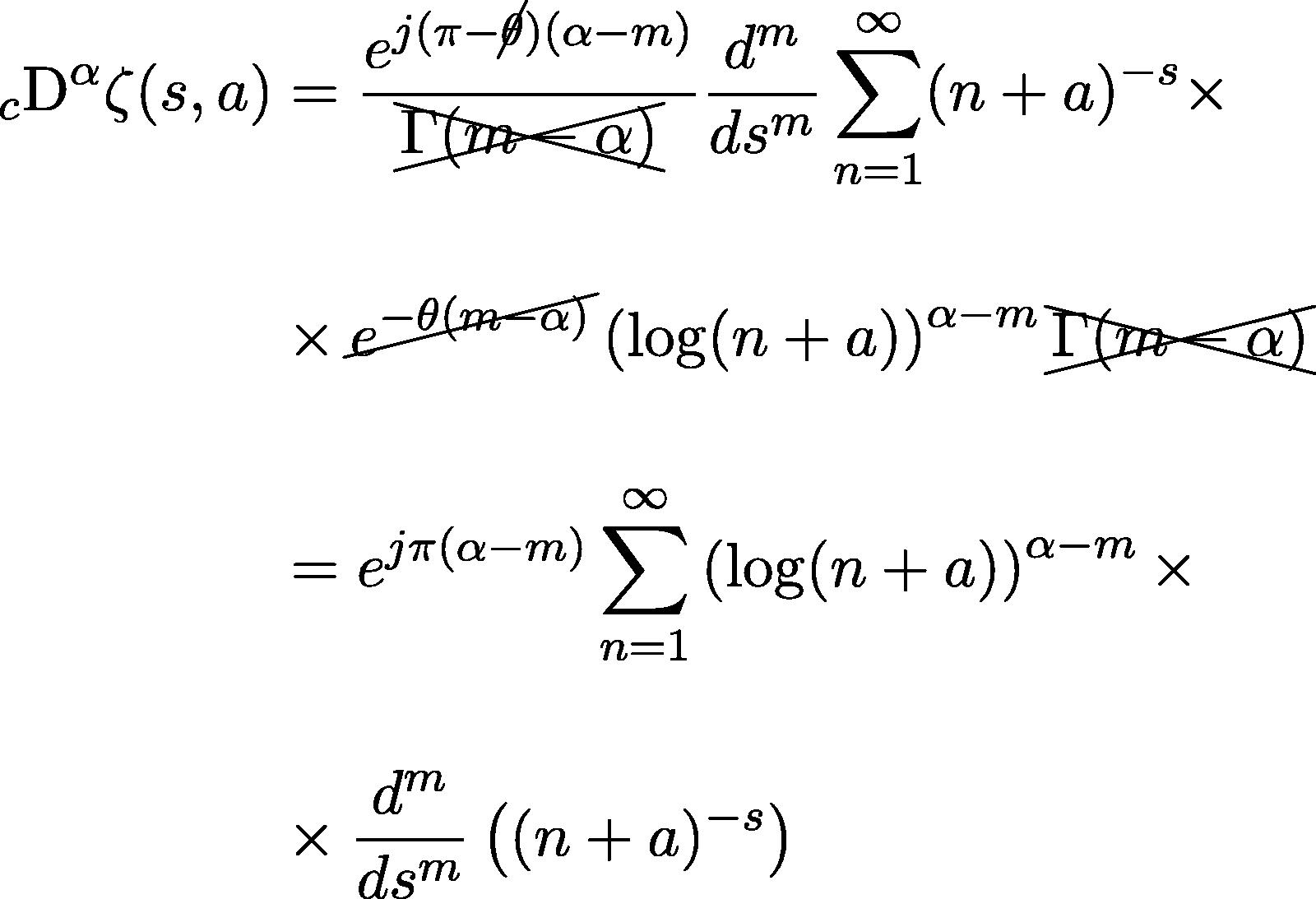
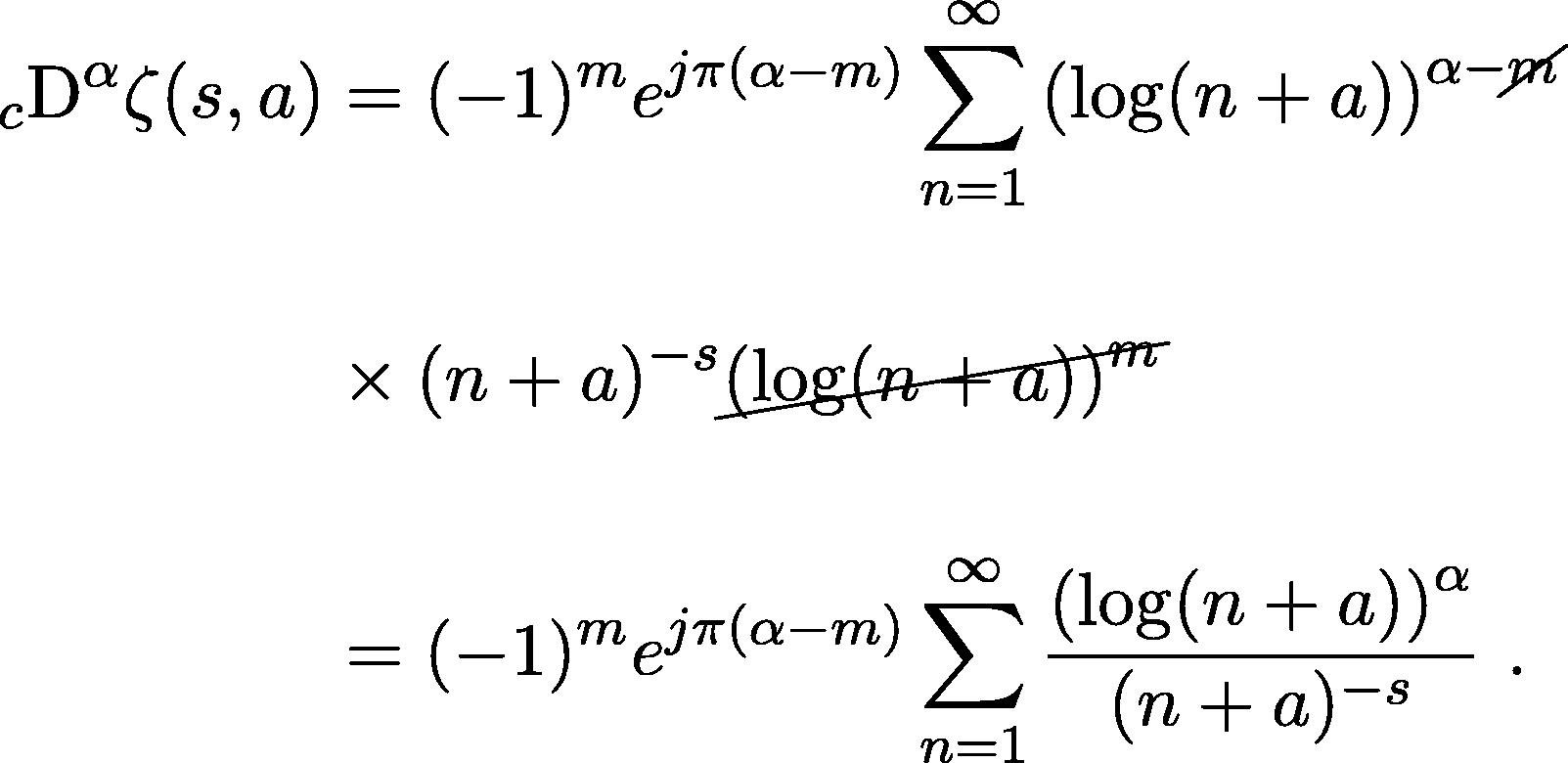
Close

Export to PPT

The last equation was obtained by changing variables twice: first $x^{j?}=z$ , and second $z\log (n+a)=x$ , so that:

Close

Export to PPT

and, since $$\begin{array}{cc}\hfill & \frac{d}{\mathit{ds}}\left({(n+a)}^{-s}\right)=-{(n+a)}^{-s}\log (n+a)\hfill \\ \hfill & \frac{d^2}{{\mathit{ds}}^2}\left({(n+a)}^{-s}\right)={(-1)}^2{(n+a)}^{-s}{\left(\log (n+a)\right)}^2\hfill \\ \hfill & ?\hfill \\ \hfill & \frac{d^m}{{\mathit{ds}}^m}\left({(n+a)}^{-s}\right)={(-1)}^m{(n+a)}^{-s}{\left(\log (n+a)\right)}^m\hfill \end{array}$$ we finally get

Close

Export to PPT

 ?

These two results (4.1) generalize, in a coherent way, what has been already considered in Guariglia (2015) for the fractional derivative of Riemann zeta function, so that the fractional derivative of the Riemann zeta function can be seen in a more general scheme. In fact, if in ${}_c{D}^{?}F(s)$ we put $f(n)=1$ , we have ${}_c{D}^{?}?(s)$ , which is coherent because $?(s)$ is a Dirichlet series with $f(n)=1$ . Analogously for the Hurwitz zeta function: with $a=1$ in ${}_c{\mathrm{D}}^{?}?(s\text{,}a)$ , we obtain ${}_c{\mathrm{D}}^{?}?(s)$ , which is coherent because $?(s\text{,}1)=?(s)$ .

It should be noticed that the Ortigueira fractional derivative gives a natural generalization of the already known (integer order) derivative of the Riemann zeta function. In fact, a known result is that the derivative of integer order $k?{\mathbb{Z}}_0^{+}$ of the Riemann zeta function is (Apostol, 2010, chp. 12) $${?}^{(k)}(s)={(-1)}^k{\displaystyle \underset{n=1}{\overset{?}{?}}}\frac{{(\log n)}^k}{n^s}$$ which coincides with the Eqs. (4.1), by putting an integer order factor, $?(s)=?(s\text{,}1)=$ and $?(s)=F(s\text{;}f(n)=1)$ .

4.1

4.1 Some properties of the fractional derivatives (4.1)

Let us consider Eq. (4.1)₁ with $f(n)=1$ , i.e. $${}_c{D}^{?}\{F(s)\}(f(n)=1)={(-1)}^m{e}^{j?(?-m)}\times {\displaystyle \underset{n=1}{\overset{?}{?}}}\frac{{(\log n)}^{?}}{n^s}={}_c{D}^{?}\{?(s)\}$$

Moreover, without restricts, we set $m=1$ and the constant factor $e^{j?(?-m)}$ equal to 1: thus, we obtain the following function

(4.2)

$$?(s\text{,}?){\displaystyle \stackrel{\mathrm{def}}{=}}{}_c{D}^{?}\{?(s)\}(m=1)e^{j?(m-?)}=(-1){\displaystyle \underset{n=1}{\overset{?}{?}}}\frac{{(\log n)}^{?}}{n^s}=(-1){\displaystyle \underset{n=1}{\overset{?}{?}}}{[(\log n)n^{-s/?}]}^{?}\text{.}$$

In the case when the variable s is a pure real number $s=-x$ , the partial sum (for a fixed n) is a function with rapid decay to zero. For a pure complex number, i.e. $s=-\mathit{jy}$ then we have a complex function whose real part (4.2) $\mathfrak{R}[?(s\text{,}?)]$ (see Fig. 1) is a slow decay even function while the complex part $\mathfrak{I}[?(s\text{,}?)]$ it is a slow decay odd function (Fig. 2).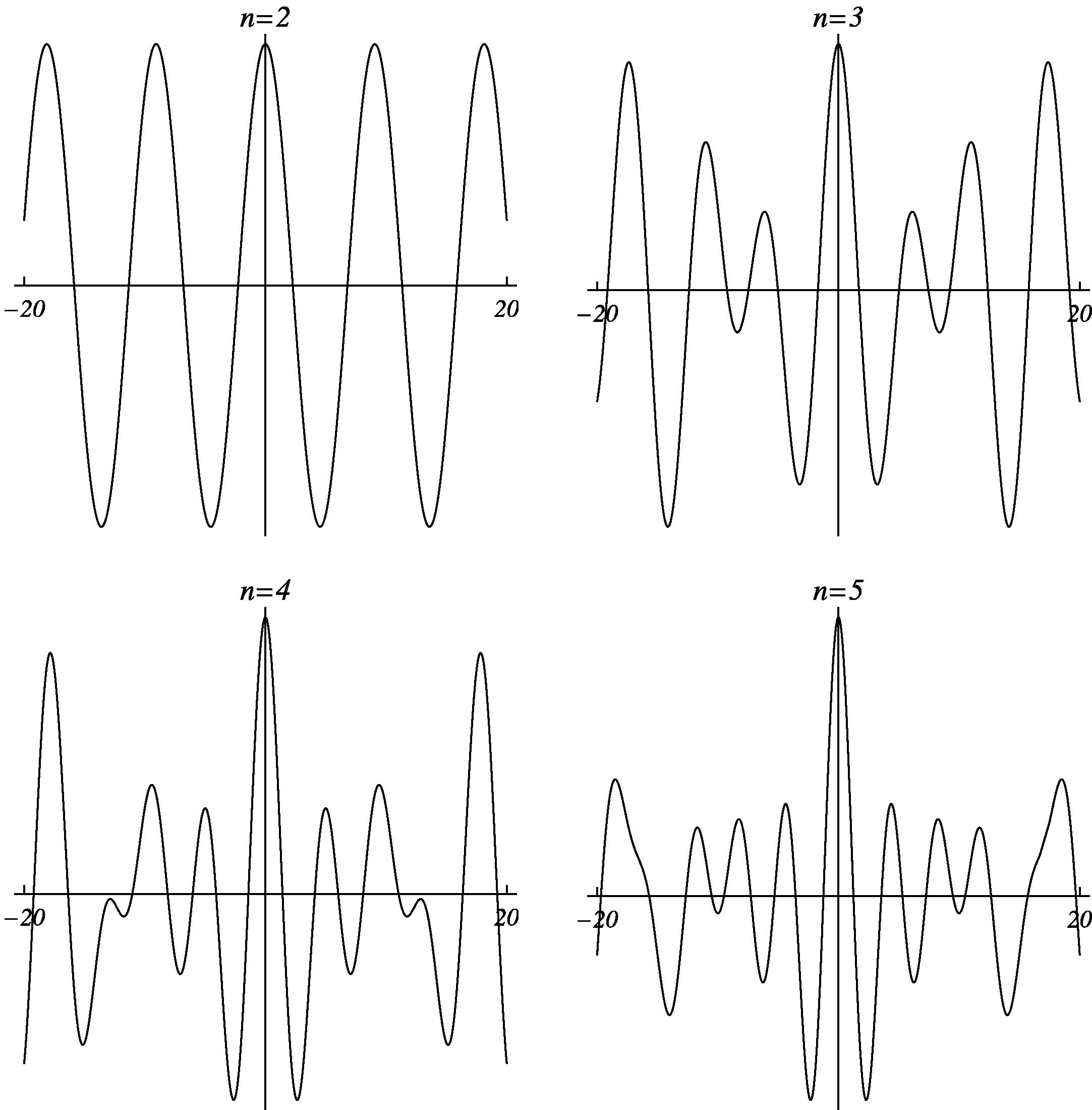

Close

Figure 1

The real part of the complex function (4.2) with $x=0$ and $?=0.6$ .

Export to PPT

Close

Figure 2

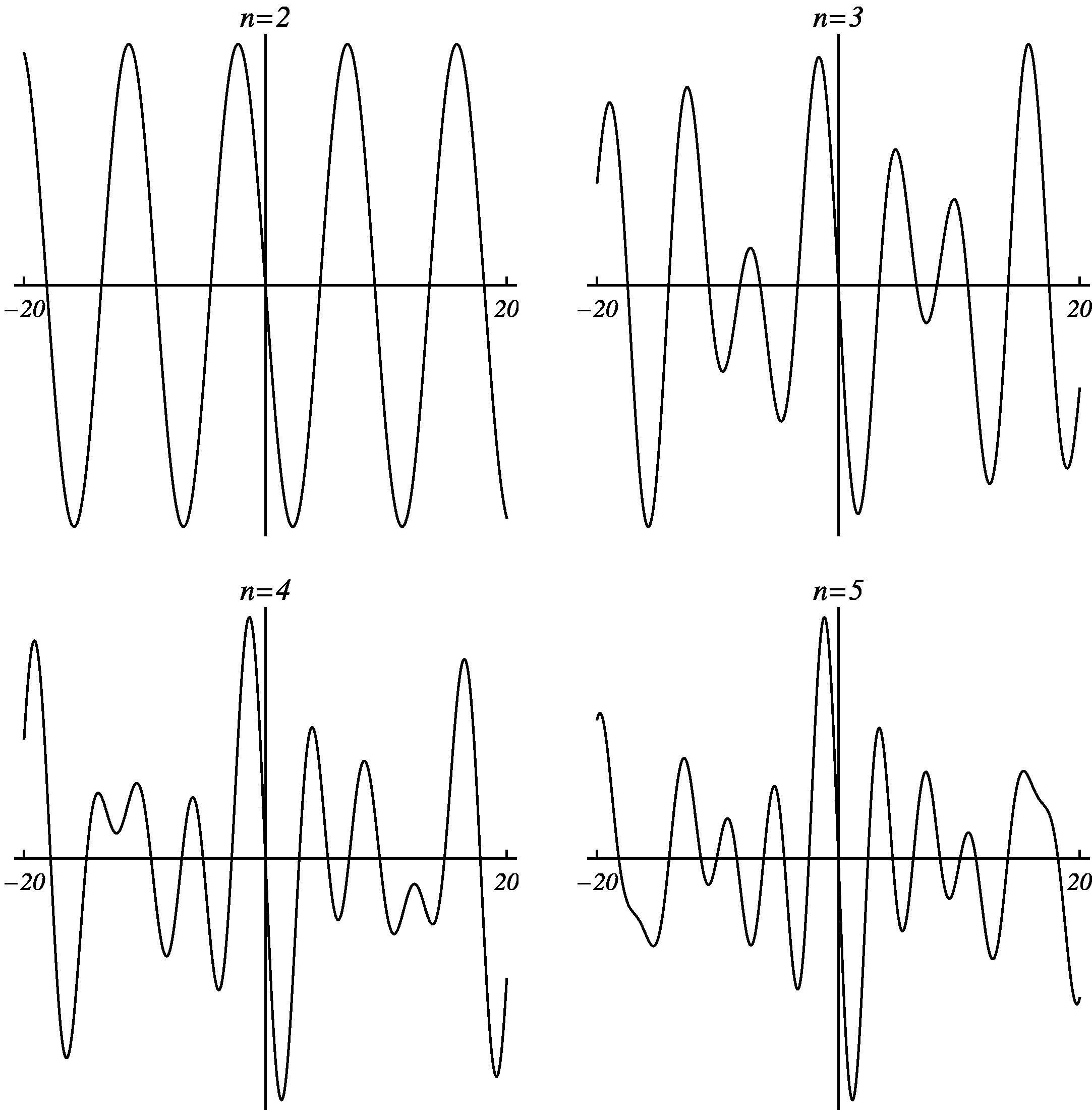
The imaginary part of the complex function (4.2) with $x=0$ and $?=0.6$ .

Export to PPT

If we plot the real and imaginary part of the function (4.2) in the same plane, then we have the parametric plot of the complex (4.2) with $x=0$ of Fig. 3.

Close

Figure 3

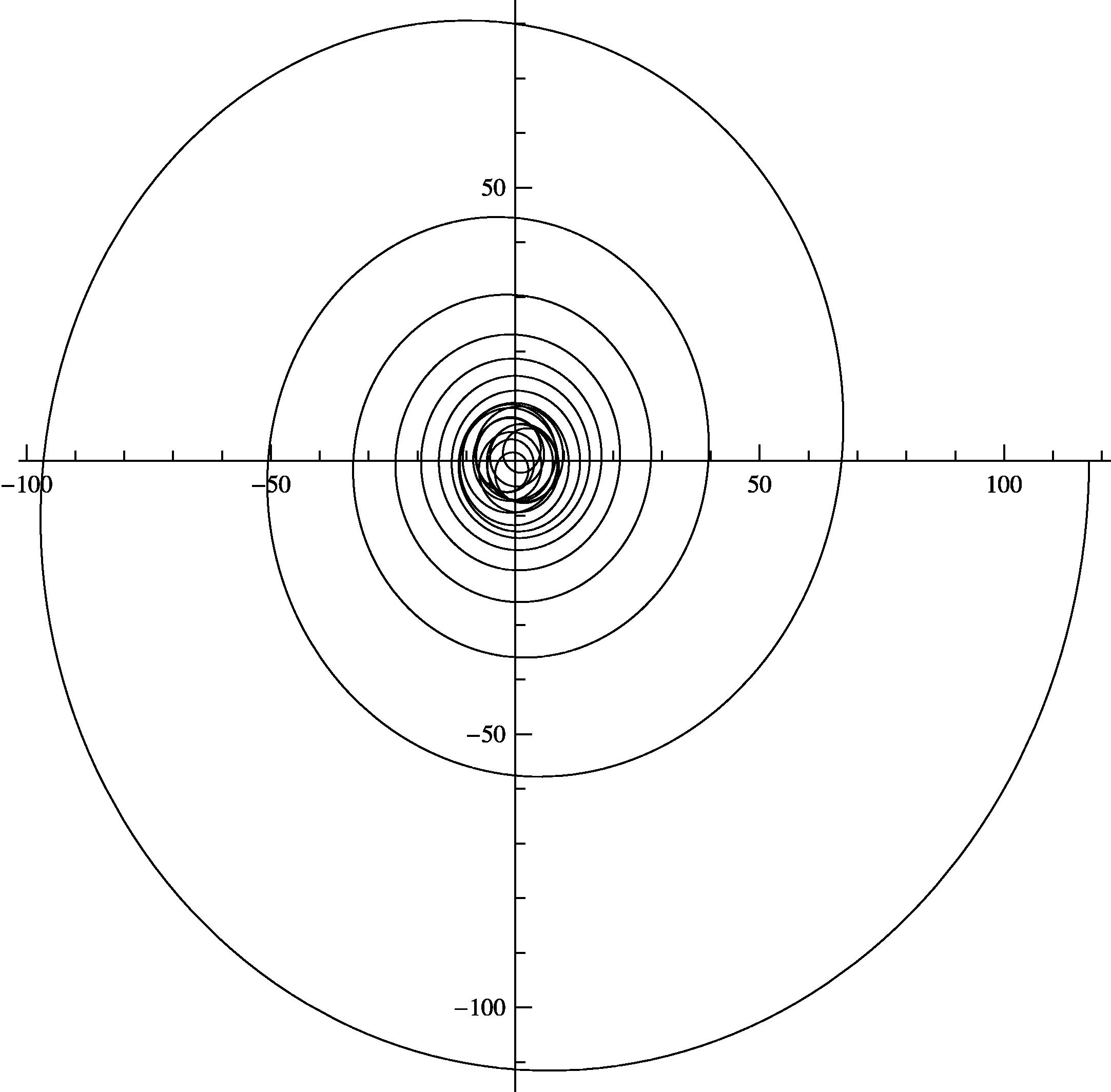
Parametric plot of the complex function (4.2) with $x=0\text{,}?=0.6$ , the upper limit of the sum $n=60$ and the upper bound of $y=30$ .

Export to PPT

We can say that the parametric plot of the fractional derivatives (4.2) of the Riemann zeta function is a spiral having the origin as an asymptotic attractor. However, if we zoom in around the origin we can see that the spiral becomes a self-intersecting non-differentiable function.

Moreover, from (4.2) by the series expansions we have $$\begin{array}{c}\log (n+1)={\displaystyle \underset{k=0}{\overset{?}{?}}}{(-1)}^k\frac{n^{k+1}}{k+1}\hfill \\ n^{s/?}={\displaystyle \underset{k=0}{\overset{?}{?}}}\frac{1}{k!{?}^k}{n}^k{[s]}^{k/-?}\hfill \end{array}$$ being $${[s]}^{k/-?}\stackrel{\mathrm{def}}{=}s(s-?)(s-2?).(s-(k-1)?)$$ the so-called generalized Pochammer symbol.

Since it is $${\displaystyle \underset{n=1}{\overset{?}{?}}}\log n={\displaystyle \underset{n=0}{\overset{?}{?}}}\log (n+1)$$ and, for every $s?0$ , being $${\displaystyle \underset{n=1}{\overset{?}{?}}}{n}^{s/?}=\left({\displaystyle \underset{n=0}{\overset{?}{?}}}{n}^{s/?}\right)-0^{s/?}={\displaystyle \underset{n=0}{\overset{?}{?}}}{n}^{s/?}$$ we get from (4.2) $$?(s\text{,}?)=(-1){\displaystyle \underset{n=1}{\overset{?}{?}}}{[(\log n)n^{-s/?}]}^{?}=(-1){\displaystyle \underset{n=0}{\overset{?}{?}}}{[(\log (n+1))n^{-s/?}]}^{?}=(-1){\displaystyle \underset{n=0}{\overset{?}{?}}}{\left[\left({\displaystyle \underset{k=0}{\overset{?}{?}}}{(-1)}^k\frac{n^{k+1}}{k+1}\right)\times {\displaystyle \underset{h=0}{\overset{?}{?}}}\frac{1}{h!{?}^h}{n}^h{[s]}^{h/-?}\right]}^{?}\text{,}s?0$$ Thus, for every complex number $s?0$ , it is: $$?(s\text{,}?)=(-1){\displaystyle \underset{n=0}{\overset{?}{?}}}{\left[{\displaystyle \underset{h\text{,}k=0}{\overset{?}{?}}}{(-1)}^k\frac{n^{k+h+1}}{(k+1)h!{?}^h}{[s]}^{h/-?}\right]}^{?}$$ There follows that, apart a constant factor, the Ortigueira fractional derivative of the Riemann zeta function can be also expressed as a complex power series (by the Pochammer symbol).

5 Conclusion

In this paper the integer order derivative of the Riemann zeta function has been generalized to fractional order derivative. This generalization has been obtained using the Ortigueira definition of fractional derivative of complex function which has been applied to the Hurwitz zeta function and to a Dirichlet series. The fractional derivative of the Riemann zeta function has been studied to show some interesting properties, such as a chaotic decay to zero (in the Gaussian plane) and a promising expression as a complex power series. The chaotic decay might suggest that the fractional derivative of the Riemann zeta function is non-differentiable function around zero. Thus opening new perspectives in the applications to the theory of dynamical systems.