Flat-ended circular cylindrical punch for initially stressed Neo-Hookean solids

Parul Tiwari; Yasir Khan

doi:10.1016/j.jksus.2010.07.014

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original Article

23 (

); 229-234

doi:

10.1016/j.jksus.2010.07.014

Flat-ended circular cylindrical punch for initially stressed Neo-Hookean solids

Parul Tiwari^a, Yasir Khan^b,⁎

a Department of Mathematics, Ideal Institute of Technology, Ghaziabad 201 003, UP, India

b Modern Textile Institute, Donghua University, 1882 Yan’an Xilu Road, Shanghai 200051, China

⁎Corresponding author. Tel.: +86 2162374513. yasirmath@yahoo.com (Yasir Khan)

Received: 2010-6-22, Accepted: 2010-7-10, Published: 2010-04-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 15 July 2010

Peer-review under responsibility of King Saud University.

Abstract

The present paper reports the indentation of integral transform technique for a semi-infinite initially stressed elastic medium under the action of an axi-symmetric flat-ended circular cylindrical punch pressing the medium normally. The incremental deformation theory is used to solve the problems for Neo-Hookean solid. The distribution of incremental stress and strain is obtained by using the Hankel’s transformation. The effects of the punch have been studied numerically and presented in various forms of curves. The plane punch indentation has its broad applications in the field of Engineering Mechanics. There are so many firing and launching pads, which use the Neo-Hookean solid as buffer and bear the punch during the action of machines. Thus the present problem has a lot of applications to find the effect of punch on machines.

Keywords

Flat-ended circular cylindrical punch

Incremental deformation theory

Integral transform technique

Bessel function

Stresses

Neo-Hookean solids

Show Related Articles from PubMed

Nomenclature

$x_{i}$: cartesian coordinates
$S_{ij}$: initial stress, corresponding to initial finite deformation, referred to $x_{i}$
$n_{i}$: components of unit normal to boundary surface
$ρ$: density in a finite deformation
$u_{i}$: incremental displacement (infinitesimal)
$W$: elastic potential per unit volume
$e_{ii}$: incremental strain
$λ_{i}$: extension ratio
$ϕ$: displacement function
$w_{ii}$: incremental rotation
$μ_{0}$: shear modulus in an unstrained state
$E$: incremental volume expansion
$P$: initial all-around compressive stress
$p_{0}$: pressure in a punch
$a$: radius of a punch in initially deformed body
$s_{ij}$: incremental stress referred to axes which are incrementally displaced with the medium
$Δ f_{i}$: incremental boundary force per unit initial area
$C_{1} (ξ), C_{2} (ξ)$: integral constants

1 Introduction

The incremental deformation theory of elasticity concerns a deformation when the state of strain and stress at any time differ only slightly from that of a known finite deformation. Various elastic bodies possess initial stress by the action of body forces. If such a body is further subjected to deforming forces then apart from the initial finite deformation, it will have incremental deformation. The basic equations of this theory have been given by Green et al. (1952), Green and Zerna (1954), Biot (1938, 1940), Neuber (1943), Mushkhelishvili (1953) and Trefftz (1933).

Biot has discussed some interesting problems with the help of this theory like surface buckling, internal buckling, etc. He used the Cartesian concepts and Elementary Mathematical Model in place of tensor calculus. Therefore, Biot’s concepts are not only easy to understand the physical meaning of incremental stress and strain but also useful in mathematical analysis.

Later on, Kurashige (1969, 1971) discussed a circular crack problem and the two dimensional crack problems for initially stressed Neo-Hookean solids. Hara et al. (1989) has studied an axi-symmetric contact problem of a transversely isotropic layer indented by an annular rigid punch. Some contact problems have been discussed by Inove et al. (1990), Sokamoto et al. (1990), Babich et al. (2004), Yang (2005) and Nadler and Tang (2008). In linear elastic fracture mechanics analysis, determination of the stresses is always a major consideration and has to be evaluated by using Hankel’s transformation. Kuo and Keer (1992) used the Hankel transform to solve numerically the contact problem of a layered transversely isotropic half space. Sneddon, (1975) has given an application of integral transform techniques. Recently various powerful techniques such as decomposition method (Khan, 2009; Khan and Faraz, 2010, 2011a,b ), homotopy perturbation method (Yildirim, 2010a,b) and variational methods (Faraz et al., 2011) have been proposed for obtaining exact and approximate solutions. Many results obtained in the literature regarding punch such as a sequential punch of flat-ended and wedge-shaped profile with crack initiating at one end of the contact region in Hasebe et al. (1989, 1990), who used a rational mapping function and complex stress function.

Fan and Chyanbin (1996) have solved punch problems by combining Stork’s formalism and the method of analytic continuation. Vibration of an elliptic plate with variable thickness is discussed in Singh and Tyagi (1985) and Singh and Goel (1985). Recently, an analysis, based on finite element approach is given in Anifantis (2001) and initiation and propagation of surface cracks in Dag and Erdogan (2002). The present problem has been solved with the help of the theory of Bessel’s function.

The present work is directed towards obtaining stresses for flat-ended circular cylindrical punch for initially stressed Neo-Hookean solids. The purpose of this paper is to obtain analytic expressions for stresses and displacements. These expressions of stresses and displacement containing infinite integrals and involving Bessel’s function are solved numerically. After that the characteristics of such numerical modeling are discussed graphically. A semi-infinite initially stressed elastic medium is used, which is pressed normally by an axi-symmetric rigid punch. The medium is supposed to be isotropic, homogenous and incompressible.

2 Formulation of the problem

The equation of motion for incremental deformation theory in rectangular cartesian co-ordinates $x_{i}$ and $t$ is

(1)

\frac{\partial s_{ij}}{\partial x_{j}} + S_{jk} \frac{\partial w_{ik}}{\partial x_{j}} + S_{ik} \frac{\partial w_{jk}}{\partial x_{j}} - e_{jk} \frac{\partial S_{ik}}{\partial x_{j}} = ρ \frac{\partial^{2} u_{i}}{\partial t^{2}}

The expression for incremental boundary force per unit area is

(2)

Δ f_{i} = (s_{ij} + S_{jk} w_{ik} + S_{ij} e - S_{ik} e_{jk}) n_{j},

where the usual convention for summation over repeated indices is applied.

The elastic potential per unit volume for the material (so called Neo-Hookean solid) is expressed in the form given below according to Trefftz (1933)

(3)

W = \frac{1}{2} μ_{0} (λ_{1}^{2} + λ_{2}^{2} + λ_{3}^{2} - 3),

with

(4)

λ_{1} λ_{2} λ_{3} = 1 .

With the help of Eqs. (3) and (4), the stress–strain relations are

(5)

S_{11} - S_{22} = μ_{0} (λ_{1}^{2} - λ_{2}^{2})

(6)

S_{22} - S_{33} = μ_{0} (λ_{2}^{2} - λ_{3}^{2})

(7)

S_{33} - S_{11} = μ_{0} (λ_{3}^{2} - λ_{1}^{2})

The equation of motion is reduced in cylindrical polar co-ordinates $(r, θ, z)$ from rectangular cartesian co-ordinates $(x_{i}, t)$ that are connected as

(8)

r = \sqrt{x_{1}^{2} + x_{2}^{2}}, θ = \tan^{- 1} (x_{2} / x_{1}), z = x_{3}

The components $S_{rr}, S_{θ θ}$ and $S_{zz}$ of initial stress are assumed to be non-zero and are uniform throughout the body and the body is assumed in the state of symmetrical incremental strain with respect to the z-axis. Therefore, the Eq. (1) reduces in cylindrical polar co-ordinates to

(9)

\frac{\partial s_{rr}}{\partial r} + \frac{s_{rr} - s_{θ θ}}{r} + \frac{\partial s_{rz}}{\partial z} - (S_{rr} - S_{zz}) \frac{\partial w_{rz}}{\partial z} = ρ \frac{\partial^{2} u_{r}}{\partial t^{2}},

(10)

\frac{\partial s_{zz}}{\partial z} + \frac{1}{r} \frac{\partial}{\partial r} ({rs}_{zr}) - (S_{rr} - S_{zz}) \frac{1}{r} \frac{\partial}{\partial r} ({rw}_{rz}) = ρ \frac{\partial^{2} u_{z}}{\partial t^{2}} .

The expressions for incremental displacement $u_{r}$ and $u_{z}$ in terms of scalar function $Φ (r, z)$ are given by

(11)

u_{r} = - \frac{\partial^{2} Φ}{\partial r \partial z},

(12)

u_{z} = \frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial Φ}{\partial r}) .

The function $Φ$ is given by the simple partial differential equation as follows

(13)

\{\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial}{\partial r}) + \frac{\partial^{2}}{\partial z^{2}}\} \{k^{2} \frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial Φ}{\partial r}) + \frac{\partial^{2} Φ}{\partial z^{2}} - \frac{ρ}{μ_{0}} \frac{\partial^{2} Φ}{\partial t^{2}}\} = 0,

and the expression for stress ‘s’ is as follows

(14)

s = μ_{0} λ_{z}^{2} \frac{\partial^{3} Φ}{\partial z^{3}} - ρ \frac{\partial^{3} Φ}{\partial z \partial t^{2}},

(15)

where k = \frac{λ_{r}}{λ_{z}}

Using the Hankel transform and inversion transform of order zero, the function $Φ$ and $\bar{Φ}$ (Hankel transform of $Φ$ ) are defined by

(16)

\bar{Φ} = \int_{0}^{\infty} Φ (r, z) {rJ}_{0} (r ξ) dr,

(17)

Φ = \int_{0}^{\infty} \bar{Φ} (r, z) ξ J_{0} (r ξ) d ξ

From which the following formulae for differentiated function are obtained

(18)

\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial Φ}{\partial r}) = - \int_{0}^{\infty} \bar{Φ} ξ^{3} J_{0} (r ξ) d ξ,

(19)

\frac{\partial}{\partial r} Φ = - \int_{0}^{\infty} \int_{0}^{\infty} \bar{Φ} ξ^{2} J_{1} (r ξ) d ξ,

where

J_{0}

and

J_{1}

are the Bessel’s function of order 0 and 1, respectively.

Using these formulae, the expressions for incremental displacement $u_{r}$ and $u_{z}$ with the help of Eqs. (11) and (12) in Hankel inversion are expressed as follows

(20)

u_{r} = \int_{0}^{\infty} \frac{\partial \bar{Φ}}{\partial z} ξ^{2} J_{1} (r ξ) d ξ

(21)

u_{z} = - \int_{0}^{\infty} \bar{Φ} ξ^{3} J_{0} (r ξ) d ξ .

Similarly, the components of incremental stress $s_{zz}, s_{zr}$ and $s_{rr}$ are as follows

(22)

s_{zz} = s - μ_{0} λ_{z}^{2} (2 + k^{2}) \int_{0}^{\infty} ξ^{3} \frac{\partial \bar{Φ}}{\partial z} J_{0} (r ξ) d ξ,

(23)

s_{zr} = \frac{1}{2} μ_{0} λ_{z}^{2} (1 + k^{2}) \int_{0}^{\infty} (ξ^{4} \bar{Φ} + ξ^{2} \frac{\partial^{2} \bar{Φ}}{\partial z^{2}}) J_{1} (r ξ) d ξ,

(24)

s_{rr} = μ_{0} λ_{z}^{2} \{\int_{0}^{\infty} (k^{2} ξ^{3} \frac{\partial Φ}{\partial z} + ξ \frac{\partial^{3} \bar{Φ}}{\partial z^{3}}) J_{0} (r ξ) d ξ - \frac{2 k^{2}}{r} \int_{0}^{\infty} ξ^{2} \frac{\partial \bar{Φ}}{\partial z} J_{1} (r ξ) d ξ\}

where

(25)

s = \frac{1}{2} (s_{rr} + s_{θ θ}) = μ_{0} λ_{z}^{2} \int_{0}^{\infty} ξ \frac{\partial^{3} \bar{Φ}}{\partial z^{3}} J_{0} (r ξ) d ξ .

Considering the steady state condition of $Φ (r, z), \frac{\partial^{2} Φ}{\partial t^{2}} = 0$ in Eq. (13) and using Hankel transform, the equation reduces to the ordinary differential equation

(26)

(D^{2} - ξ^{2}) (D^{2} \bar{Φ} - k^{2} ξ^{2} \bar{Φ}) = 0,

where

D = \frac{d}{dz}

2.1

2.1 Boundary conditions

The semi-infinite elastic medium is deformed by the normal indentation of the boundary by a flat-ended circular cylinder of radius $a$ . Assuming that the semi-infinite medium $z ⩾ 0$ is initially deformed and the components $s_{zz}$ and $s_{θ θ}$ are zero so that

(27)

S_{rr} = μ_{0} (λ_{r}^{2} - λ_{z}^{2}) = - P .

For no initial stress, $P = 0,$ from Eqs. (15) and (27) we get $k = 1 .$

The equation of the punch is $z = f (r)$ , which is in the form of a solid of revolution (Fig. 1). Referring the tip of the punch as origin, if the pressure $p (r)$ is assumed to be applied in the plane $z = 0$ and the contact is frictionless, the boundary conditions are

(28)

\begin{matrix} u_{r} (r, 0) = p (r) & (0 ⩽ r ⩽ \infty) \\ s_{rz} = 0 & (0 ⩽ r ⩽ \infty) \end{matrix}\}

(29)

\begin{matrix} u_{z} = D_{1} - f (r) & (0 ⩽ r ⩽ a) \\ s_{zz} = 0 & (r > a) \end{matrix}\}

where the physical significance of parameter

D_{1}

is that it is the depth to which the punch penetrates the elastic half space and

f (0) = 0 .

In case of flat-ended circular cylindrical punch, the profile of the punch is not smooth at

r = a,

f (r) = 0 .

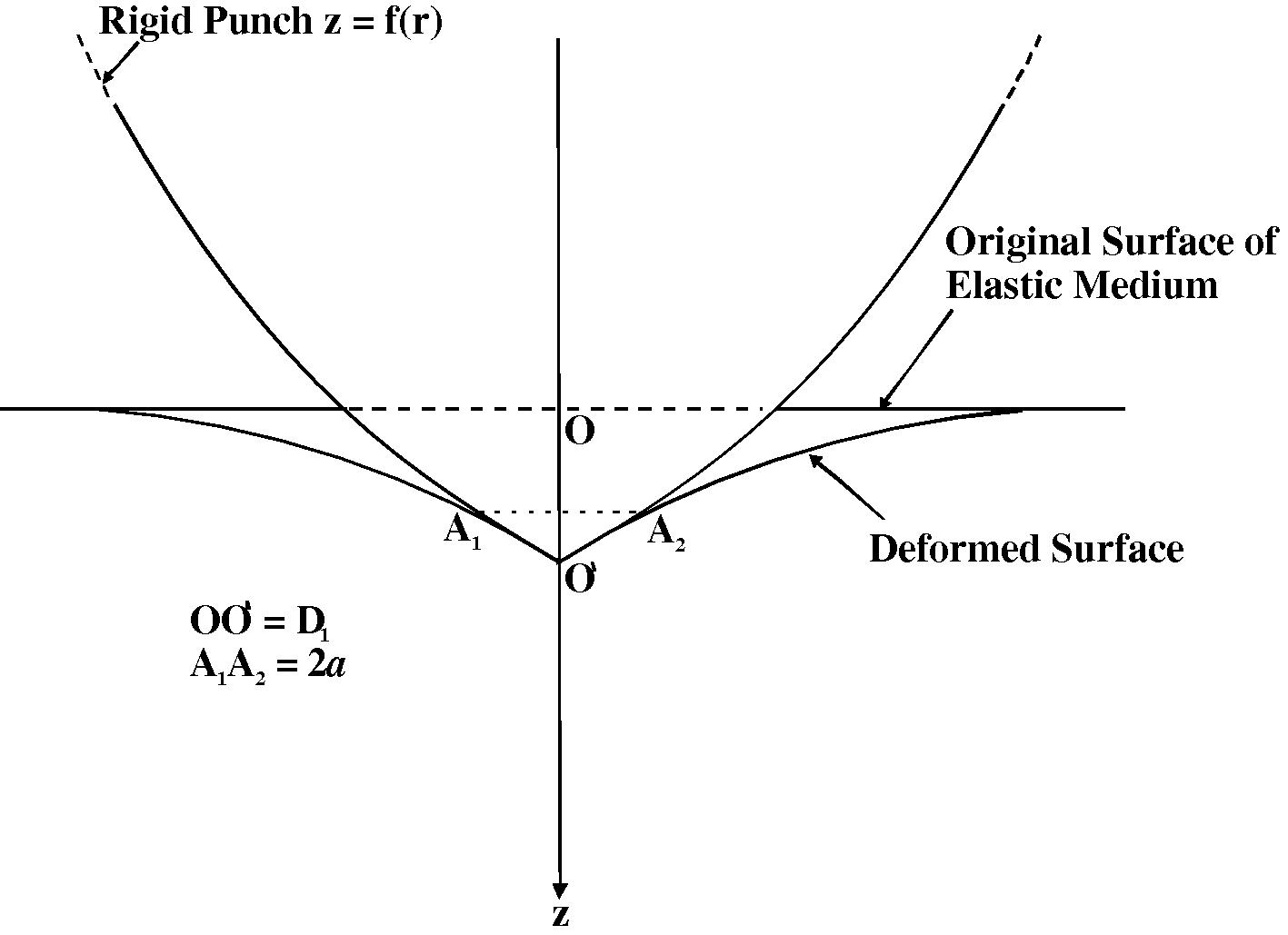
Indentation of a semi-infinite solid by an axi-symmetrical rigid punch.

3 Solution of the problem

The solution of the ordinary differential Eq. (26) for a half space z ⩾ 0 is given by

(30)

\bar{Φ} = C_{1} (ξ) e^{- ξ z} + C_{2} (ξ) e^{- k ξ z}

where

C_{1} (ξ)

and

C_{2} (ξ)

are the integral constants.

Now applying the boundary conditions (28) to the Eq. (30), we have

(31)

\frac{- \bar{p} (ξ)}{ξ^{2}} = C_{1} (ξ) + C_{2} (ξ),

and

(32)

0 = 2 C_{1} (ξ) + (1 + k^{2}) C_{2} (ξ) .

Solving the Eqs. (31) and (32), we get

(33)

\begin{matrix} C_{1} (ξ) = \frac{1 + k^{2}}{1 - k^{2}} \frac{\bar{p} (ξ)}{ξ^{2}}, \\ C_{2} (ξ) = \frac{- 2}{1 - k^{2}} \frac{\bar{p} (ξ)}{ξ^{2}} . \end{matrix}\}

The first boundary condition in Eq. (29) does not correspond accurately to the normal pressure in the punch in all cases. In this case, the punch is assumed to be of very small depth so that the surface of the punch may be taken to be coincident with the plane $z = 0,$ applying the boundary condition (29) to Eq. (30), we obtain the following dual integral equations

(34)

\int_{0}^{\infty} ξ \bar{p} (ξ) J_{0} (r ξ) d ξ = D_{1} - f (r), 0 ⩽ r ⩽ a)

(35)

\int_{0}^{\infty} ξ^{2} \bar{p} (r ξ) J_{0} (r ξ) d ξ = 0 . (r > a)

Making the substitutions $a ξ = η, r = ax, D^{'} = {aD}_{1}$ , the Eqs. (34) and (35) reduce to that of solving the dual integral equations

(36)

\int_{0}^{\infty} ψ (η) J_{0} (x η) d η = D^{'} - f_{1} (x), (0 ⩽ x ⩽ 1)

(37)

\int_{0}^{\infty} η ψ (η) J_{0} (x η) d η = 0 . (x > 1)

Eq. (36) is equivalent to the Abel’s integral equation

(38)

\sqrt{\frac{2}{π}} \int_{0}^{r} \frac{g (t) dt}{\sqrt{r^{2} - t^{2}}} = D^{'} - f_{1} (x), (r > 0)

where the unknown function g(t) is given by

(39)

g (t) = \sqrt{\frac{2}{π}} \{D^{'} - t \int_{0}^{t} \frac{f_{1}^{'} (x)}{\sqrt{t^{2} - x^{2}}} dx\},

(40)

and D^{'} = \int_{0}^{1} \frac{f_{1}^{'} (x)}{\sqrt{1 - x^{2}}} dx,

(41)

or D_{1} = \int_{0}^{a} \frac{{af}^{'} (r)}{\sqrt{a^{2} - r^{2}}} dr .

The solution of Eq. (37) is given by Sneddon (1975) as follows

(42)

ψ (n) = \sqrt{\frac{2}{π}} \int_{0}^{1} g (t) \cos (η t) dt .

For a flat-ended circular cylindrical punch the profile of the punch is not smooth at $r = a,$ so $f_{1} (x) = 0$ and from Eq. (39), we get

(43)

g (t) = \sqrt{\frac{2}{π}} {aD}^{'}

and from Eq. (42)

ψ (n) = \sqrt{\frac{2}{π}} \int_{0}^{1} \sqrt{\frac{2}{π}} {aD}^{'} \cos η t dt = \frac{2 {aD}^{'}}{π} \frac{\sin η}{η},

ψ (a ξ) = \frac{2 D^{'}}{π ξ} \sin a ξ .

Therefore, we have

(44)

\bar{p} (ξ) = \frac{2 D_{1}}{π} \frac{\sin a ξ}{ξ^{2}} .

Now putting the values of $C_{1} (ξ), C_{2} (ξ), \bar{p} (ξ)$ in Eq. (30), we get

(45)

Φ = \frac{2 D_{1}}{π (1 - k^{2})} \{(1 + k^{2}) e^{- ξ z} - 2 e^{- k ξ z}\} \frac{\sin a ξ}{ξ^{4}}

Thus the non-vanishing components of stresses and displacements in terms of Hankel inversion are as follows

(46)

s_{zz} = \frac{2 D_{1} μ_{0} λ_{z}^{2}}{π (1 - k^{2})} \int_{0}^{\infty} \{{(1 + k^{2})}^{2} e^{- ξ z} - 4 {ke}^{- k ξ z}\} \sin a ξ J_{0} (r ξ) d ξ,

(47)

s_{zr} = \frac{2 D_{1} μ_{0} λ_{z}^{2}}{π (1 - k^{2})} \int_{0}^{\infty} {(1 + k^{2})}^{2} (e^{- ξ z} - e^{- k ξ z}) \sin a ξ J_{1} (r ξ) d ξ,

(48)

\begin{matrix} s_{rr} = \frac{- 2 D_{1} μ_{0} λ_{z}^{2}}{π (1 - k^{2})} [\int_{0}^{\infty} \{{(1 + k^{2})}^{2} e^{- ξ z} - 4 k^{3} e^{- k ξ z}\} \sin a ξ J_{0} (r ξ) d ξ \\ \frac{- 2 k^{2}}{r} \int_{0}^{\infty} \{{(1 + k^{2})}^{2} e^{- ξ z} - 2 {ke}^{- k ξ z}\} . \frac{\sin a ξ}{ξ} J_{1} (r ξ) d ξ], \end{matrix}

(49)

u_{z} = \frac{- 2 D_{1}}{π (1 - k^{2})} \int_{0}^{\infty} \{(1 + k^{2}) e^{- ξ z} - 2 e^{- k ξ z}\} \frac{\sin a ξ}{ξ} J_{0} (r ξ) d ξ,

and

(50)

u_{r} = \frac{- 2 D_{1}}{π (1 - k^{2})} \int_{0}^{\infty} \{(1 + k^{2}) e^{- ξ z} - 2 {ke}^{- k ξ z}\} \frac{\sin a ξ}{ξ} J_{1} (r ξ) d ξ .

3.1

3.1 Limiting case

The case of non-initial stresses and displacements will be obtained by making k → 1. The results agree with those already obtained by Sneddon (1975) for materials which obey Hook’s law. From the expressions of stresses and displacements, it appears that as k → 1, all components of stresses and displacements tend to infinity which means that the situation becomes unstable.

4 Numerical results and discussion

For a flat-ended circular cylindrical punch, variations of incremental stress and displacement component $s_{zz}, s_{rr}$ and $u_{r}$ with various parameters are plotted in Figs. 2–5 . For a non-initially stressed body, $P = 0$ which is given by $k = 1 .$ If the initial stress is high, $P / μ_{0}$ tends to unity. For different values of $P / μ_{0}$ between 0.1 and 0.4, variations of stresses and displacement have been shown. Attention has been paid to investigate the influences of the initial stress.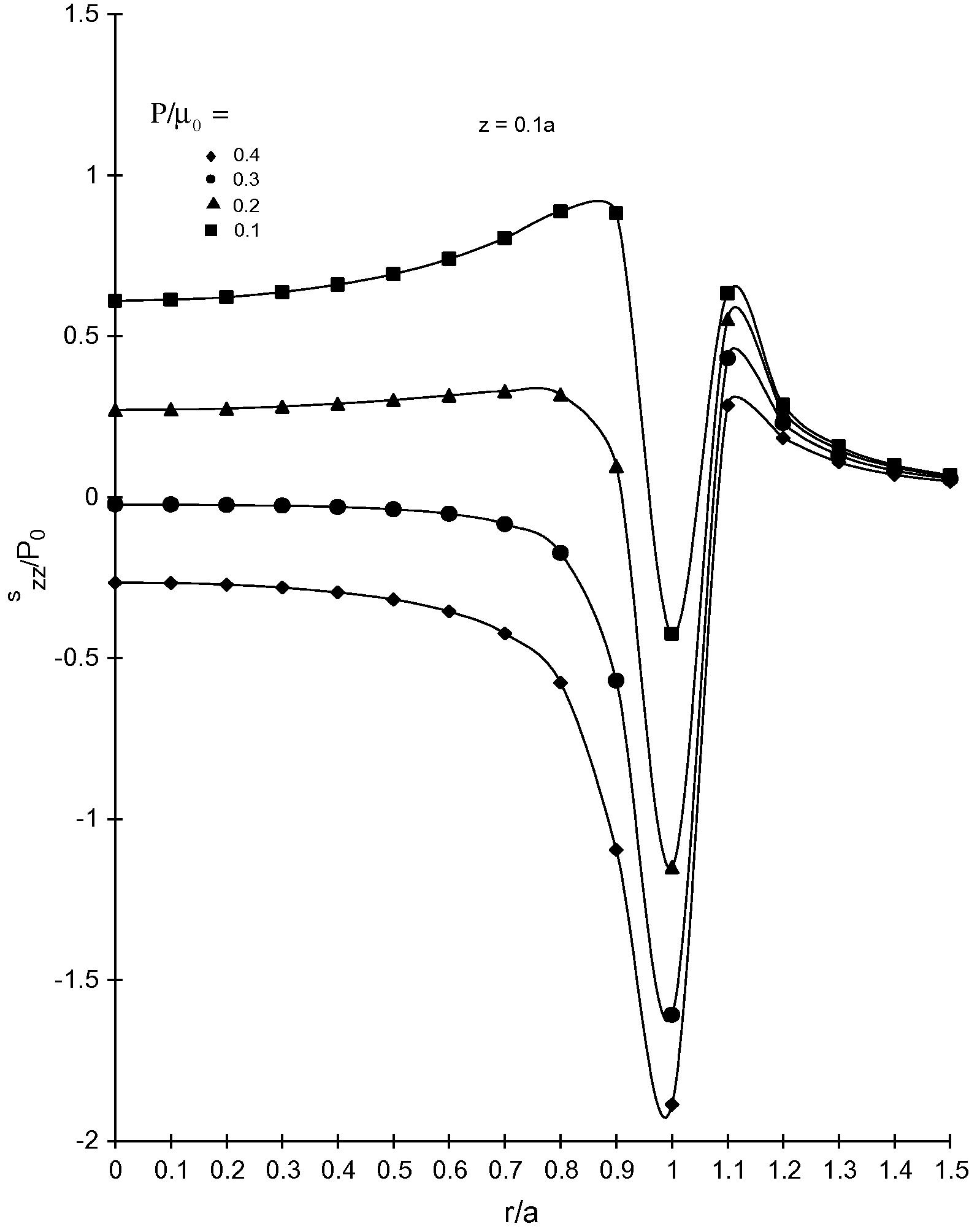

Variation of normal component of incremental stress szz with r.

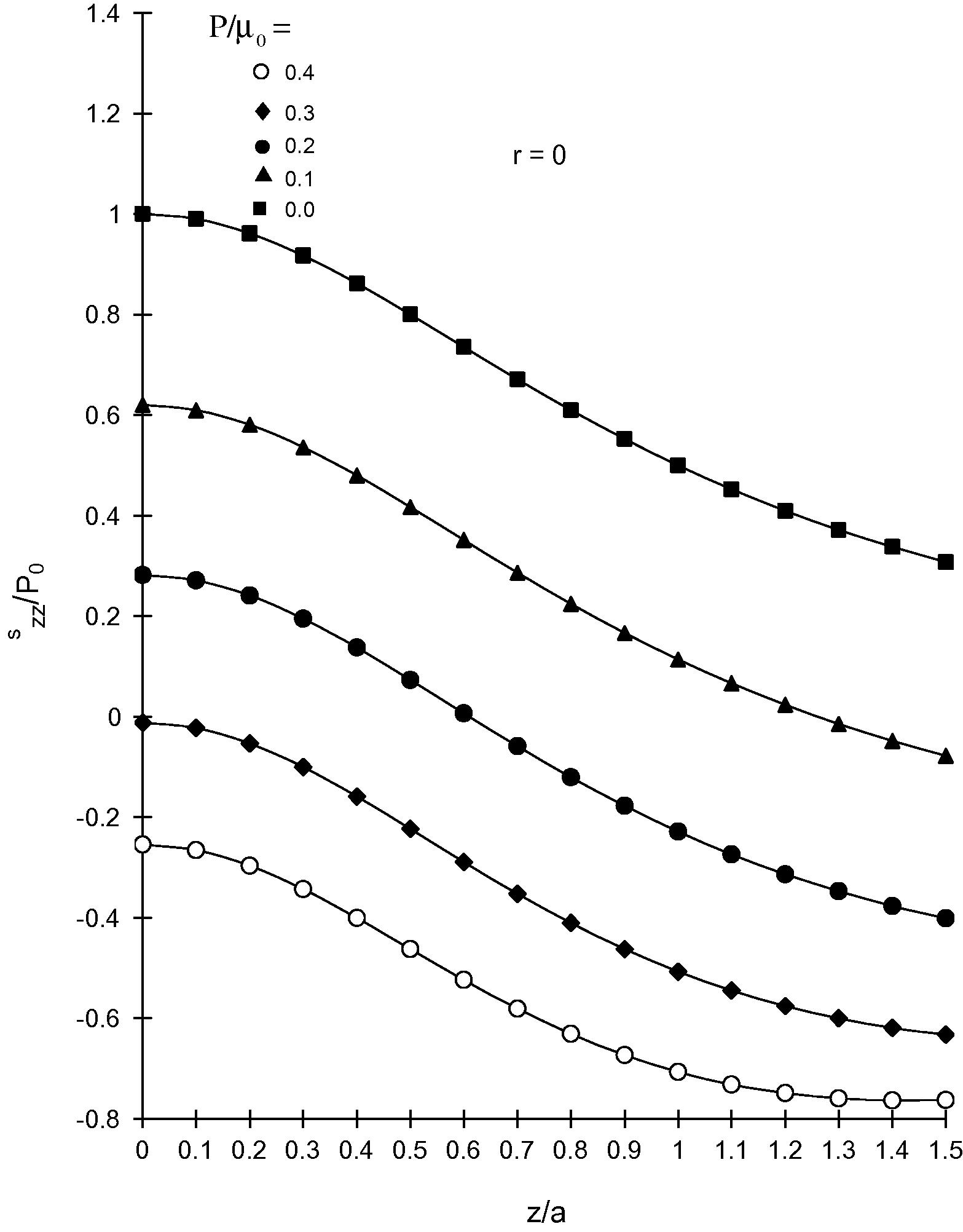
Variation of radial component of incremental stress szz with z.

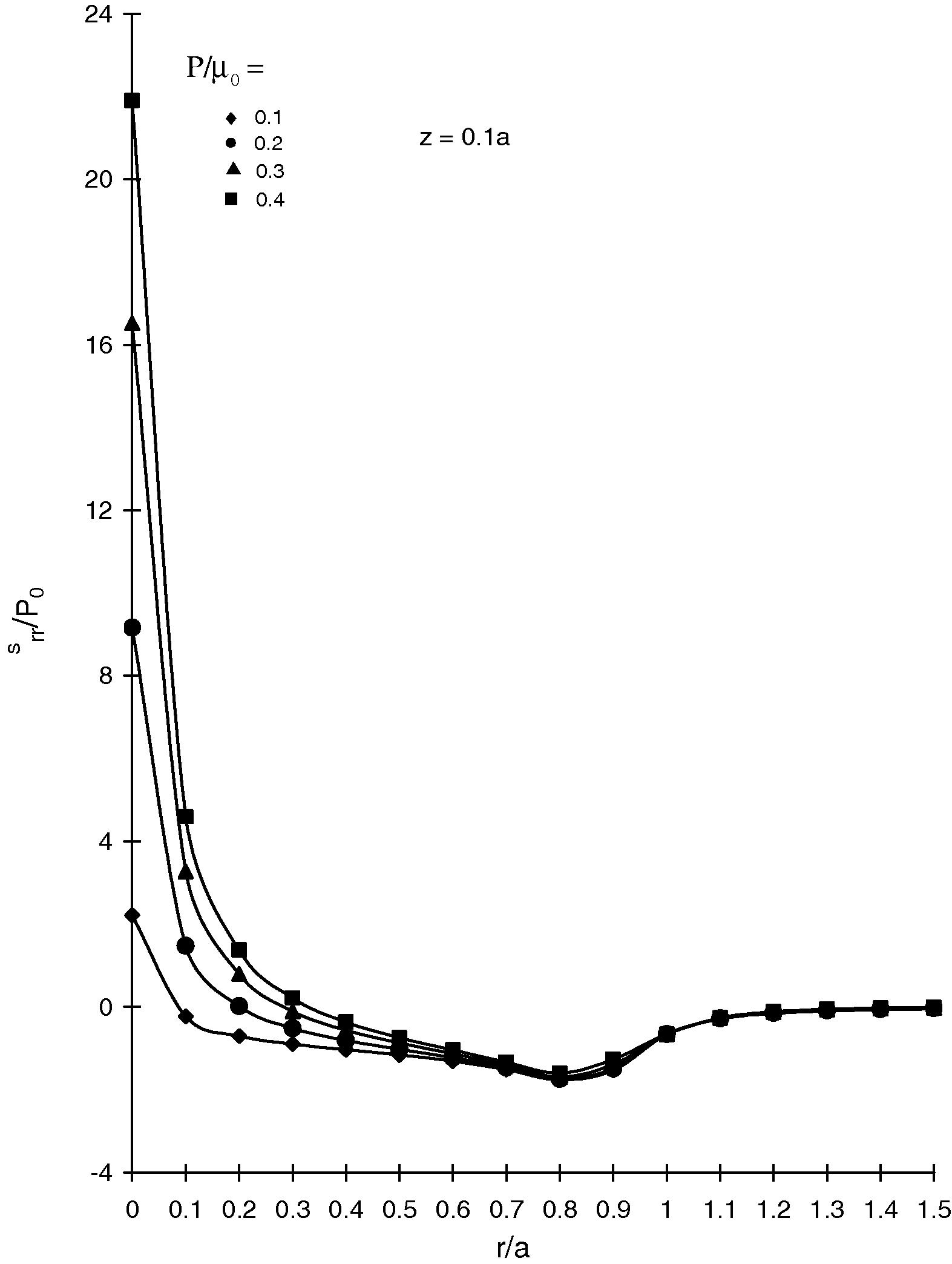
Variation of radial component of incremental stress srr with r.

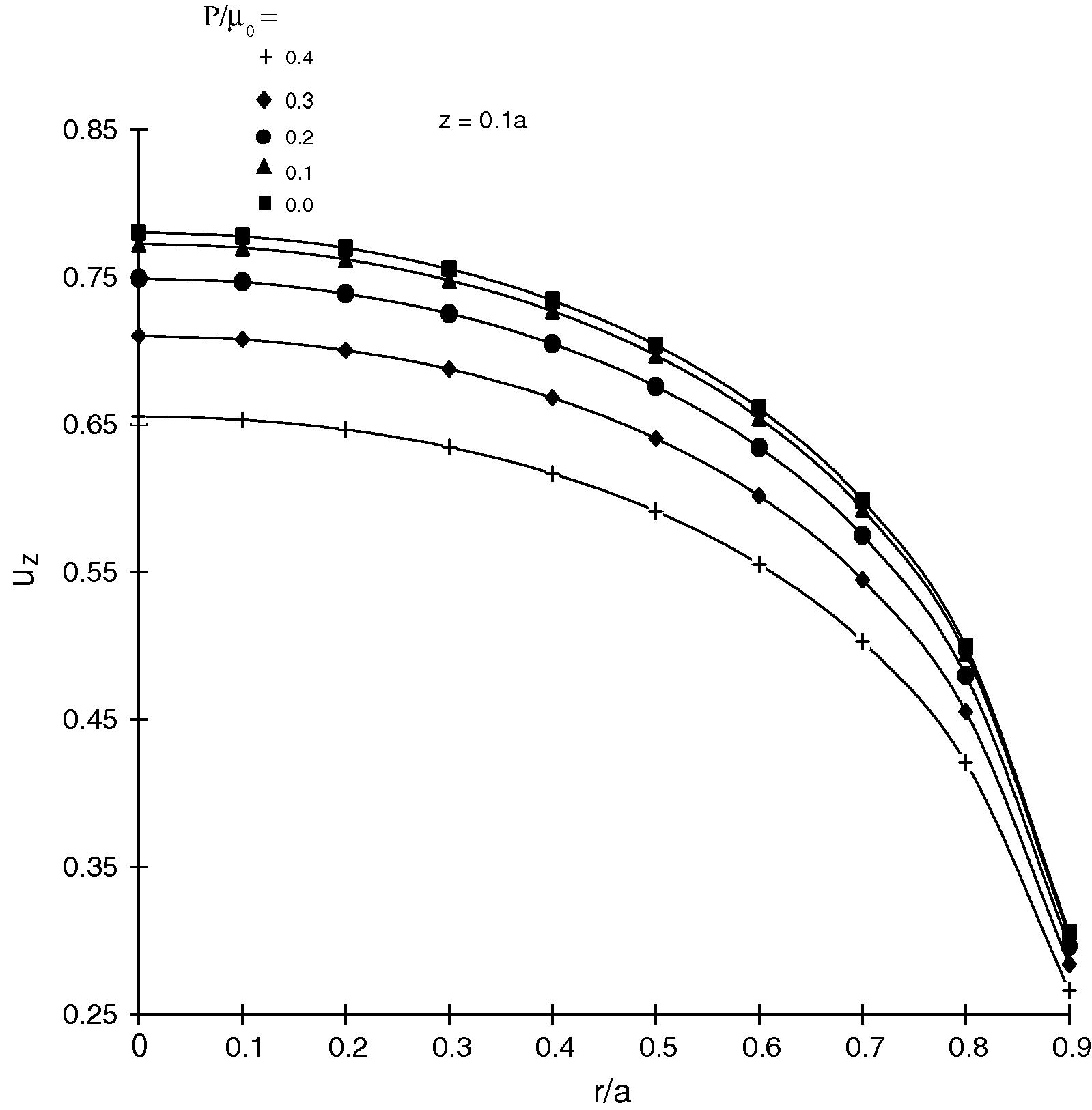
Variation of normal component of incremental displacement uz with r.

Fig. 2 shows the variation of normal component of incremental stress $s_{zz}$ along $z / a = 0.1$ . There is a sharp rise and fall in the neighbourhood of the edge of punch. It shows that as the punch comes in contact with elastic body, it produces larger stresses and explains the discontinuity of stress near $r = a .$

Fig. 3 shows the distribution of normal component of incremental stress $s_{zz}$ along z-axis. The normal component of the incremental stress has a peak at a point from the surface of the punch and it decreases monotonically as the value of $z$ increases for high initial stress. For no initial stress the peak is higher.

Fig. 4 shows the variation of radial component of incremental stress $s_{rr}$ with $r$ . It shows that there is a little influence on the variation of incremental stress in the neighbourhood of the edge of the punch.

Fig. 5 shows the distribution of normal component of incremental displacement $u_{z}$ with $r$ along $z / a = 0.1 .$ As the initial stress decreases, incremental stress has a high peak. The incremental stress decreases near the edge of the punch.

References

Anifantis N.K., . Crack surface interference. a finite element analysis. Eng. Fracture Mech.. 2001;68:1403-1415.
[Google Scholar]
Babich S.Yu., Guz A.N., Rudnitskii V.B., . Contact problems for pre-stressed elastic bodies and rigid and elastic punches. Int. Appl. Mech.. 2004;40(7):744-765.
[Google Scholar]
Biot M.A., . Non-linear theory of elasticity and the linearized case for body under initial stresses. Phil. Mag.. 1938;27(7):486-489.
[Google Scholar]
Biot M.A., . Elastizitatstheoric Zweiter Ordnung Mit Anwendungen. ZAMM. 1940;20:88-89.
[Google Scholar]
Dag E., Erdogan F., . A surface crack in a graded medium under general loading condition. ASME J. Appl. Mech.. 2002;69:580-588.
[Google Scholar]
Fan C.W., Chyanbin H.W., . Punch problems for an-isotropic elastic half-plane. ASME J. Appl. Mech.. 1996;63:69-76.
[Google Scholar]
Faraz N., Khan Y., Yildirim A., . Analytical approach to two-dimensional viscous flow with a shrinking sheet via variational iteration algorithm-II. J. King Saud Univ. Sci.. 2011;23(1):77-81.
[Google Scholar]
Green A.E., Zerna W., . Theoretical Elasticity. Oxford Clarendon Press; 1954. pp. 114–148
Green A.E., Rivlin R.S., Shield R.T., . Small deformation superposed on finite deformation. Proc. Roy. Soc. A. 1952;211:123-135.
[Google Scholar]
Hara T., Sakamoto H., Shibuya T., Koizumi T., . An axisymmetric contact problem of a transversely isotropic layer indented by an annular rigid punch. JSME Int. J. Ser. 1. 1989;32(1):94-100.
[Google Scholar]
Hasebe N., Okumura M., Nakamura T., . Frictional punch and crack in linear elasticity. ASCE J. Eng. Mech.. 1989;115:1137-1149.
[Google Scholar]
Hasebe N., Okumura M., Nakamura T., . Crack due to wedge shaped punch with friction. ASCE J. Eng. Mech.. 1990;116:2173-2185.
[Google Scholar]
Inove H., Shibuya T., Koizumi T., . The contact problem between an elliptical punch and an elastic half-space with friction. JSME Int. J. Ser. 1. 1990;32(2):160-166.
[Google Scholar]
Khan Yasir, . An effective modification of the Laplace decomposition method for nonlinear equations. Int. J. Nonlinear Sci. Num. Simul.. 2009;10(11–12):1373-1376.
[Google Scholar]
Khan Y., Faraz N., . Application of modified Laplace decomposition method for solving boundary layer equation. J. King Saud Univ. Sci.. 2011;23(1):115-119.
[Google Scholar]
Khan Yasir, Faraz Naeem, . A new approach to differential difference equations. J. Adv. Res. Differ. Equ.. 2010;2(2):1-12.
[Google Scholar]
Khan Y., Faraz N., . Modified fractional decomposition method having integral ${(d ξ)}^{α}$ . J. King Saud Univ. Sci.. 2011;23(2):157-161.
[Google Scholar]
Kuo C.H., Keer L.M., . Contact stress analysis of a layered transversely isotropic half-space. ASME J. Appl. Mech.. 1992;114:253-262.
[Google Scholar]
Kurashige M., . Circular crack problem for initially stressed Neo-Hookean solid. ZAMM. 1969;49:671-678.
[Google Scholar]
Kurashige M., . Two-dimensional crack problem for initially stressed Neo-Hookean solid. ZAMM. 1971;51:145-147.
[Google Scholar]
Mushkhelishvili N.I., . Some Basic Problems of the Mathematical Theory of Elasticity. Holland: P. Noordhoff Groningen Ltd.; 1953. pp. 427–450
Nadler B., Tang T., . Decohesion of a rigid punch from non-linear membrane undergoing finite axisymmetric deformation. Int. J. Non-linear Mech.. 2008;43:716-721.
[Google Scholar]
Neuber H., . Die Grundgleiehungen Der Elastisehen Stabilital in Allgemeinen Koordinaten and Ihreintegration. ZAMM. 1943;23:321-330.
[Google Scholar]
Singh, B., Goel, R., 1985. Transverse vibration of an elliptic plate with variable thickness. In: Proceedings, Workshop on Solid Mechanics, March 13–16, University of Roorkee, India. pp. 19–27.
Singh B., Tyagi D.K., . Transverse vibration of an elliptic plate with variable thickness. J. Sound Vib.. 1985;99(3):379-391.
[Google Scholar]
Sneddon I.N., . Applications of Integral Transform in the Theory of Elasticity. New York: Pringer-Verlag Inc.; 1975.
Sokamoto M., Hara T., Shibuya T., Koizumi T., . Indentation of a penny-shaped crack by a disc shaped rigid inclusion in an elastic layer. JSME Int. J. Ser. 1. 1990;33(4):425-430.
[Google Scholar]
Trefftz E., . Zur Theoric Der Stabilitat Des Elastichen Gleichgewichts. ZAMM. 1933;13:160-165.
[Google Scholar]
Yang F., . Adhesive contact between an elliptical rigid flat-ended punch, an elastic half space. J. Phys. D: Appl. Phys.. 2005;38(8):1211-1214.
[Google Scholar]
Yildirim A., . Analytical approach to Fokker-Planck equation with space- and time-fractional derivatives by means of the homotopy perturbation method. J. King Saud Univ. Sci.. 2010;22(4):257-264.
[Google Scholar]
Yıldırım A., . Analytical approach to fractional partial differential equations in fluid mechanics by means of the homotopy perturbation method. Int. J. Numer. Meth. Heat Fluid Flow. 2010;20(2):186-200.
[Google Scholar]