Translate this page into:
Exp-function method for some nonlinear PDE’s and a nonlinear ODE’s
*Corresponding author. Tel.: +98 21 22431653; fax: +98 21 22431650 k_parand@sbu.ac.ir (Kourosh Parand),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 11 August 2010
Abstract
In this paper, we apply the Exp-function method to find some exact solutions for two nonlinear partial differential equations (NPDE) and a nonlinear ordinary differential equation (NODE), namely, Cahn-Hilliard equation, Allen-Cahn equation and Steady-State equation, respectively. It has been shown that the Exp-function method, with the help of symbolic computation, provides a very effective and powerful mathematical tool for solving NPDE’s and NODE’s. Mainly we try to present an application of Exp-function method taking to consideration rectifying a commonly occurring errors during some of recent works. The results of the other methods clearly indicate the reliability and efficiency of the used method.
Keywords
The Cahn-Hilliard equation
Allen-Cahn equation
Steady-State equation
Exp-function method
NPDE
NODE
1 Introduction
The study of exact solutions of nonlinear partial differential equations (NPDE) plays an important role in mathematical physics, engineering and the other sciences. In the past several decades, various methods for obtaining solutions of NPDEs and ODE’s have been presented, such as, tanh-function method (Wazwaz, 2005, 2006a,b), Adomian decomposition method (Hashim et al., 2006; Tatari et al., 2007), Homotopy perturbation method (Rashidi et al., 2009; Biazar et al., 2009; Berberler and Yildirim, 2009), variational iteration method (Shakeri and Dehghan, 2008; Soliman and Abdou, 2007; Yusufoglu and Bekir, 2007), spectral method (Parand and Taghavi, 2009; Parand et al., 2009, 2010), sine–cosine method (Tascan and Bekir, 2009; Wazwaz, 2007), radial basis method (Tatari and Dehghan, 2010; Dehghan and Shokri, 2009) and so on. Recently, He and Wu (2006) proposed a novel method, so called Exp-function method, which is easy, succinct and powerful to implement to nonlinear partial differential equations arising in mathematical physics. The Exp-function method has been successfully applied to many kinds of NPDEs, such as, KdV equation with variable coefficients (Zhang, 2007), Maccari’s system (Zhang, 2007), Boussinesq equations (Abdou et al., 2007), Burger’s equations (Ebaid, 2007; Biazar and Ayati, 2009; Ebaid, 2009), Double Sine-Gordon equation (Domairry et al., 2010; He and Abdou, 2007), Fisher equation (Ozis and Koroglu, 2008), Jaulent–Miodek equations (He and Zhang, 2008) and the other important nonlinear partial differential equations (Koroglu and zis, 2009; Shin et al., 2009; Zhang, 2008). Recently, in some of papers applying the Exp-function method (He and Wu, 2006) have been occurred with common errors. Seven common errors are formulated and classified by (Kudryashov, 2009). In this paper we try to apply this method taking to rectifying these common errors to look exact solutions of three nonlinear differential equations, namely, Cahn-Hilliard equation, Allen-Cahn equation and Steady-State equation given by respectively, which and are the constants.
The Cahn–Hilliard equation was proposed to describe phase separation phenomena in binary systems (Cahn et al., 1958). This equation is related with a number of interesting physical phenomena like the spinodal decomposition, phase separation and phase ordering dynamics. It is also very crucial in material sciences (Chan, 1961; Choo et al., 2004; Gurtin, 1996). On the other hand, this equation is very hard and difficult to solve. The Cahn-Hilliard equation has been extensively studied by Wang and Shi (1993), Jabbari and Peppas (1995), Puri and Binder (1991) for the study of interfaces. Global existence and uniqueness of the solution have been shown by Elliott and Zheng (1986). Jingxue (1992) has shown the existence of continuous solution for the problem with degenerate mobility. Recently, Dehghan and Mirzaei (2009) applied a numerical method based on the boundary integral equation and dual reciprocity methods for one-dimensional Cahn-Hilliard equation. Ugurlu and Kaya (2008) solved Cahn-Hilliard equation by tanh-function method. Furihata (2001) applied finite difference for Cahn-Hilliard equation. Many articles have investigated this equation mathematically and numerically this equation (Mello et al., 2005; Kim, 2007; Wells et al., 2006). Also, Allen-Cahn equation arise in many scientific applications such as mathematical biology, quantum mechanics and plasma physics. It is well known that wave phenomena of plasma media and fluid dynamics are modelled by kink shaped and tanh solution or bell shaped sech solutions (Wazwaz, 2007; Tascana and Bekir, 2009).
The rest of the paper is organized as follows: Section 2 describes Exp-function method for finding exact solutions to the NPDEs. The applications of the proposed analytical scheme presented in Section 3. The conclusions are discussed in the Section 4. exp-function calculations are provided in the end.
2 Basic idea of Exp-function method
We consider a general nonlinear PDE in the following form
3 Applications of the Exp-function method
Let us consider the Cahn-Hilliard equation (Ugurlu and Kaya, 2008; Dahmani and Benbachir, 2009) in the form
Case 1.
Case 2.
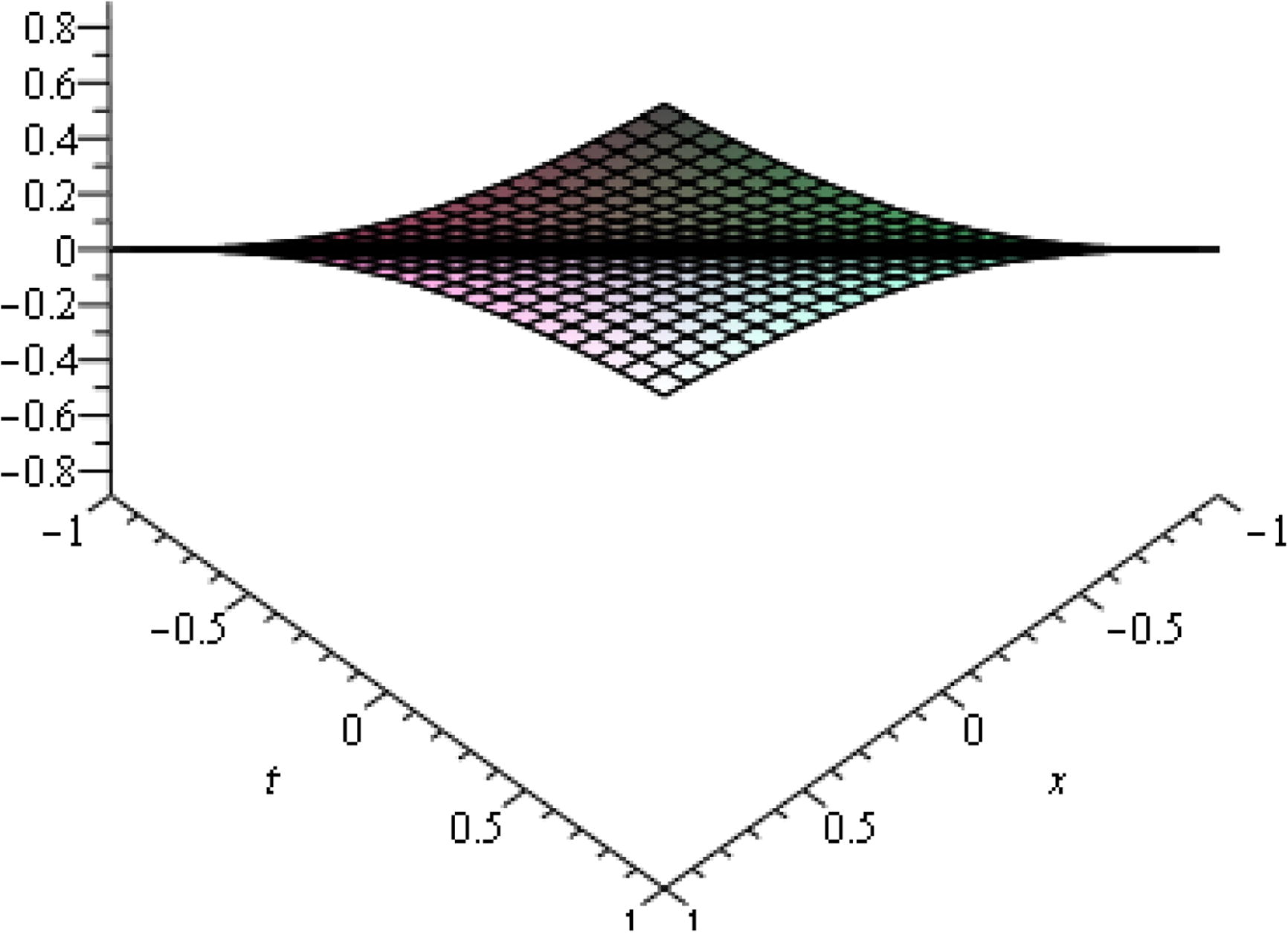
The solutions of Eq. (24).
Case 3.
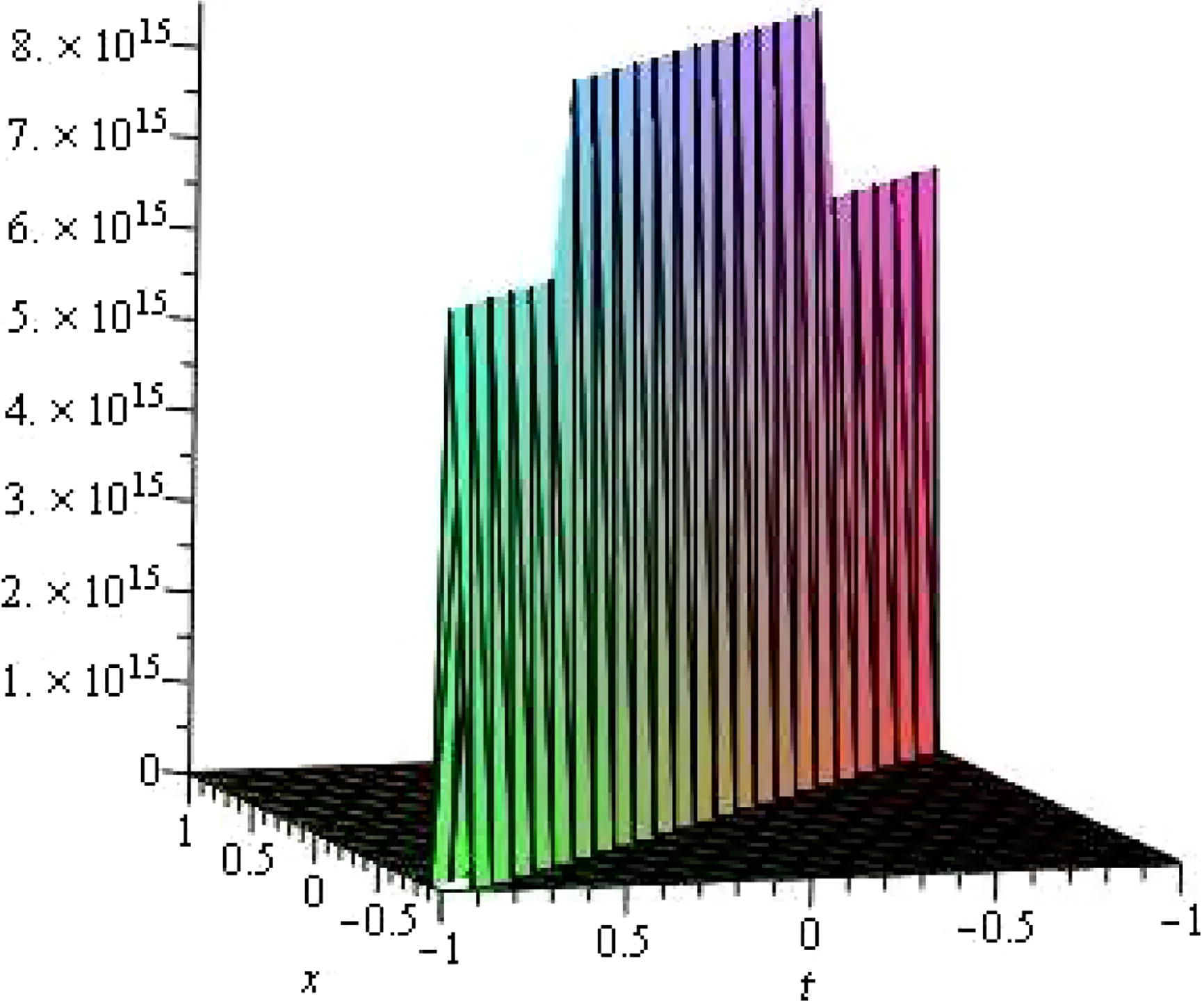
The solutions of Eq. (32).
Case 4.
Case 5.
Now we consider the Allen-Cahn equation (Wazwaz, 2007; Tascana and Bekir, 2009)
Case 1.
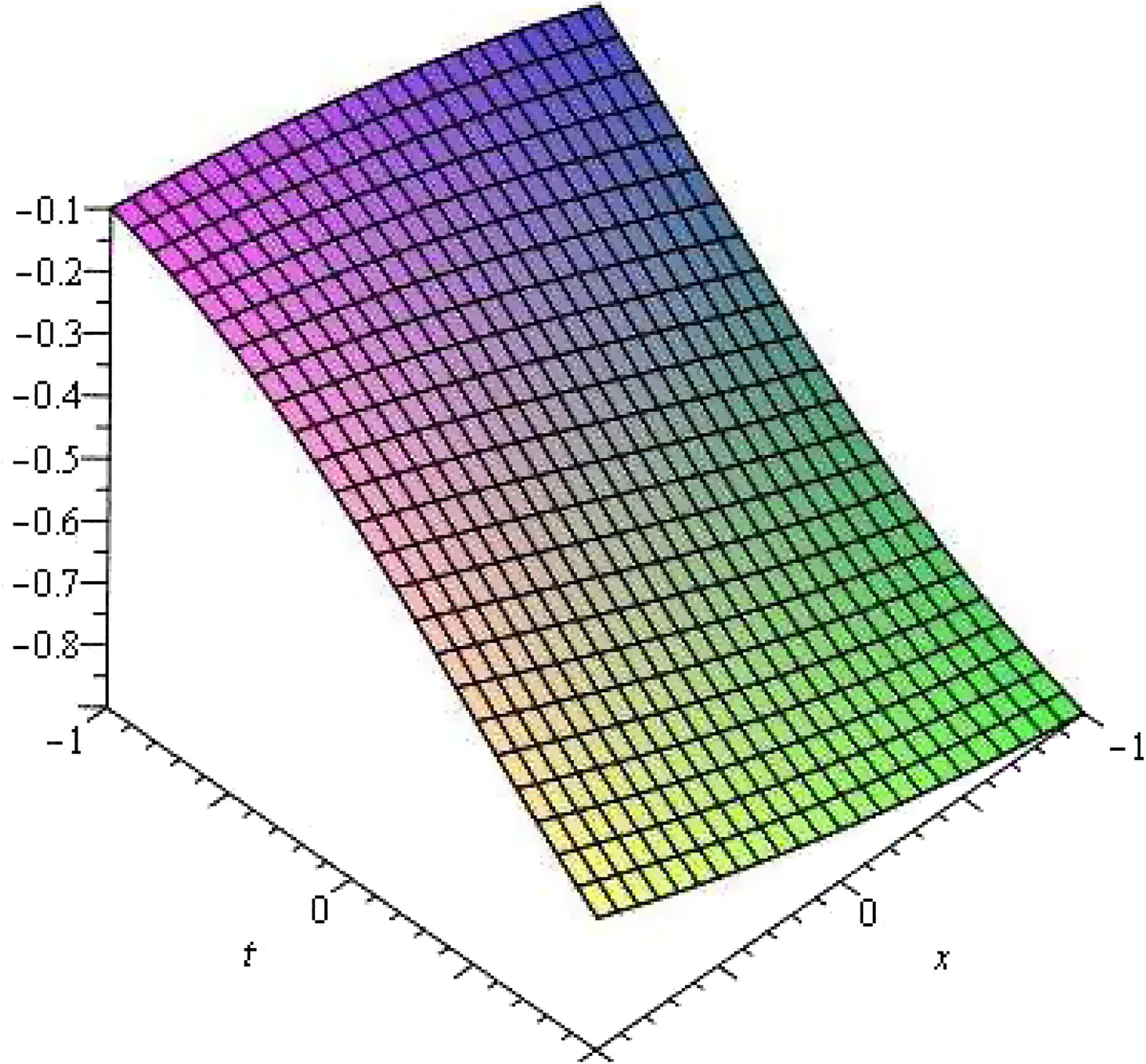
The solutions of Eq. (44) for the parameter value
.
Case 2.
Finally, we consider the solution of steady-state equation that is presented by a ordinary differential equation in the following form (Elliott and French, 1987):
Case 1.
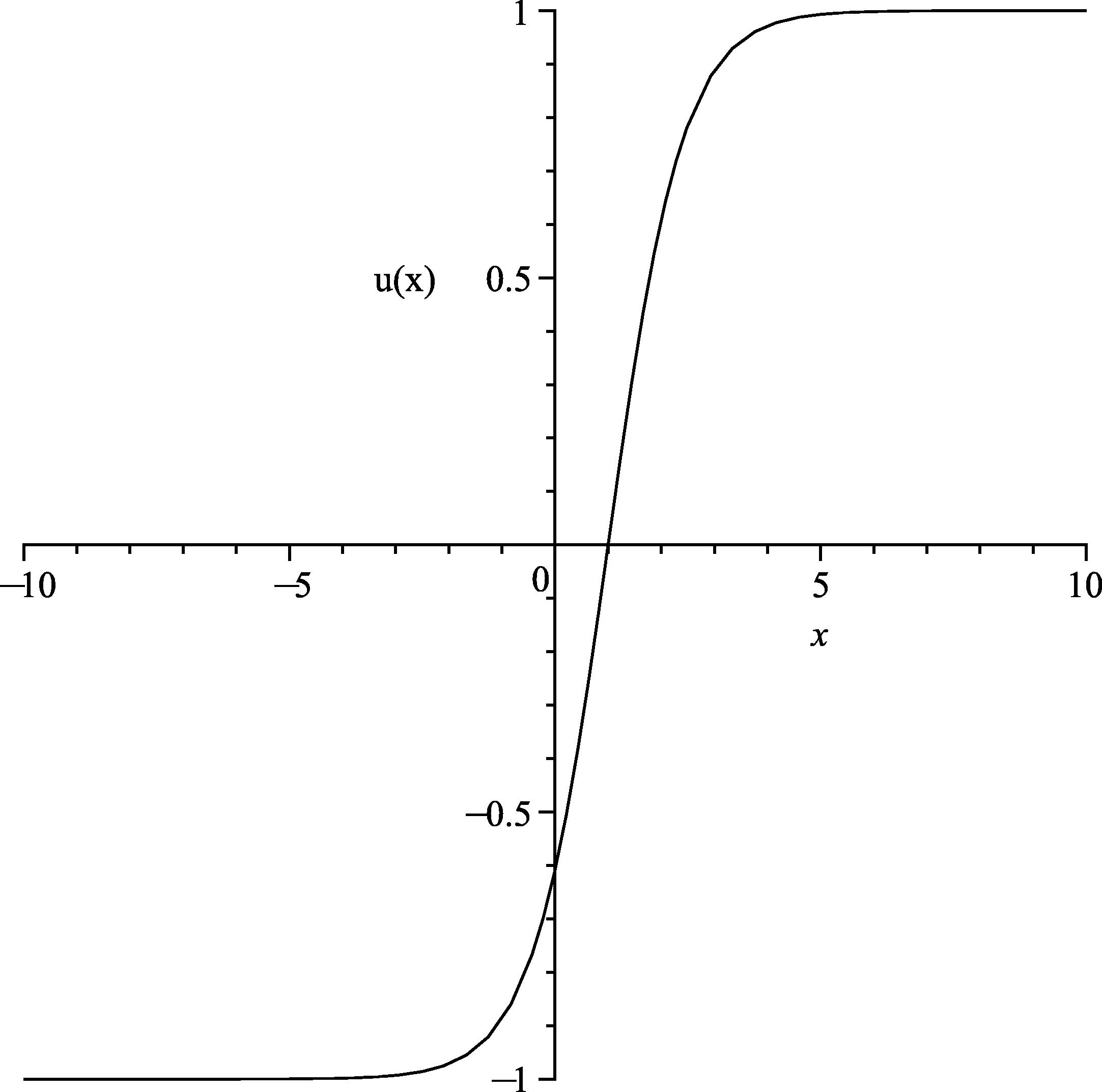
The solutions of Eq. (53) for the parameter value
.
Case 2.
4 Conclusion
In this paper, the Exp-function method has been tested by applying it successfully to the Cahn–Hilliard equations, Allen–Cahn equation and Steady-State equation. In the Exp-function method, the free parameters may imply some physical meaningful results for the problem considered. The free parameters, of course, might be related to initial conditions as well. The performance of the Exp-function method is reliable and effective. Many methods (such as Adomian decomposition method (ADM), Homotopy analysis method (HAM) or variational iteration method (VIM)) can only obtain a special equation with special boundary (initial) conditions; some obtained solutions are physically meaningless. This paper obtains solutions with free parameters that can be determined via boundary (initial) conditions. In applications of Exp-function method in past decade common errors in finding exact solutions of nonlinear problems have been omitted (53). In this paper we present an application of this method with tackling these common errors. The solving procedure reveals that the exp-function method is a straightforward, succinct and promising tool for solving nonlinear partial differential equation and nonlinear ordinary differential equation.
References
- New application of exp-function method for improved Boussinesq equation. Physics Letters, Section A: General, Atomic and Solid State Physics. 2007;369:469-475.
- [Google Scholar]
- He’s homotopy perturbation method for solving the shock wave equation. Applicable Analysis. 2009;88:997-1004.
- [Google Scholar]
- Extension of the exp-function method for systems of two-dimensional Burger’s equations. Computers and Mathematics with Applications. 2009;58:2103-2106.
- [Google Scholar]
- Application of the homotopy perturbation method to Zakharov–Kuznetsov equations. Computers and Mathematics with Applications. 2009;58:2391-2394.
- [Google Scholar]
- Free energy of a nonuniform system. I: Interfacial free energy. The Journal of Chemical Physics. 1958;28:258-267.
- [Google Scholar]
- A conservative difference scheme for the viscous Cahn–Hilliard with a nonconstant gradient energy coefficient. Applied Numerical Mathematics. 2004;51:207-219.
- [Google Scholar]
- Solutions of the Cahn–Hilliard equation with time-and space-fractional derivatives. International Journal of Nonlinear Science. 2009;8:19-26.
- [Google Scholar]
- A numerical method based on the boundary integral equation and dual reciprocity methods for one-dimensional Cahn–Hilliard equation. Engineering Analysis with Boundary Elements. 2009;33:522-528.
- [Google Scholar]
- Numerical solution of the nonlinear Klein–Gordon equation using radial basis functions. Journal of Computational and Applied Mathematics. 2009;230:400-410.
- [Google Scholar]
- Solutions for the double sine-Gordon equation by exp-function, tanh, and extended tanh methods. Numerical Methods for Partial Differential Equations. 2010;26:384-398.
- [Google Scholar]
- Exact solitary wave solutions for some nonlinear evolution equations via exp-function method. Physics Letters, Section A: General, Atomic and Solid State Physics. 2007;365:213-219.
- [Google Scholar]
- Generalization of He’s exp-function method and new exact solutions for Burgers equation. Zeitschrift fur Naturforschung Section A: Journal of Physical Sciences. 2009;64:604-608.
- [Google Scholar]
- Numerical studies of the Cahn–Hilliard equation for phase separation. IMA Journal of Applied Mathematics. 1987;38:97-128.
- [Google Scholar]
- On the Cahn–Hilliard equation. Archive for Rational Mechanics and Analysis. 1986;96:339-357.
- [Google Scholar]
- A stable and conservative finite difference scheme for the Cahn–Hilliard equation. Numerische Mathematik. 2001;87:675-699.
- [Google Scholar]
- Generalised Ginzburg–Landau and Cahn–Hilliard equations based on a microforce balance. Physica D. 1996;92:178-192.
- [Google Scholar]
- Solving the generalized Burgers–Huxley equation using the Adomian decomposition method. Mathematical and Computer Modelling. 2006;43:1404-1411.
- [Google Scholar]
- New periodic solutions for nonlinear evolution equations using exp-function method. Chaos, Solitons and Fractals. 2007;34:1421-1429.
- [Google Scholar]
- Exp-function method for nonlinear wave equations. Chaos, Solitons and Fractals. 2006;30:700-708.
- [Google Scholar]
- Generalized solitary solution and compacton-like solution of the Jaulent–Miodek equations using the exp-function method. Physics Letters, Section A: General, Atomic and Solid State Physics. 2008;372:1044-1047.
- [Google Scholar]
- A model for interdiffusion at interfaces of polymers with dissimilar physical properties. Polymer. 1995;36:575-586.
- [Google Scholar]
- On the existence of nonnegative continuous solutions of the Cahn–Hilliard equation. Journal of Differential Equations. 1992;97:310-327.
- [Google Scholar]
- A numerical method for the Cahn–Hilliard equation with a variable mobility. Communications in Nonlinear Science and Numerical Simulation. 2007;12:1560-1571.
- [Google Scholar]
- A novel traveling wave solution for Ostrovsky equation using exp-function method. Computers and Mathematics with Applications. 2009;58:2142-2146.
- [Google Scholar]
- Seven common errors in finding exact solutions of nonlinear differential equations. Communications in Nonlinear Science and Numerical Simulation. 2009;14:3507-3529.
- [Google Scholar]
- Numerical study of the Cahn–Hilliard equation in one, two and three dimensions. Physica A: Statistical Mechanics and its Applications. 2005;347:429-443.
- [Google Scholar]
- A novel approach for solving the Fisher equation using exp-function method. Physics Letters, Section A: General, Atomic and Solid State Physics. 2008;372:3836-3840.
- [Google Scholar]
- Rational scaled generalized Laguerre function collocation method for solving the Blasius equation. Journal of Computational and Applied Mathematics. 2009;233:980-989.
- [Google Scholar]
- Sinc-collocation method for solving the Blasius equation. Physics Letters, Section A: General, Atomic and Solid State Physics. 2009;373:4060-4065.
- [Google Scholar]
- Parand, K., Dehghan, M., Rezaei, A.R., Ghaderi, S.M., An approximation algorithm for the solution of the nonlinear Lane–Emden type equations arising in astrophysics using hermite functions collocation method, Computer Physics Communications. doi:10.1016/j.cpc.2010.02.018.
- Phenomenological theory for the formation of interfaces via the interdiffusion of layers. Physical Review B. 1991;44:9735-9738.
- [Google Scholar]
- Explicit analytical solutions of the generalized Burger and Burger–Fisher equations by homotopy perturbation method. Numerical Methods for Partial Differential Equations. 2009;25:409-417.
- [Google Scholar]
- Numerical solution of the Klein–Gordon equation via he’s variational iteration method. Nonlinear Dynamics. 2008;51:89-97.
- [Google Scholar]
- Some exact and new solutions of the Nizhnik–Novikov–Vesselov equation using the exp-function method. Computers and Mathematics with Applications. 2009;58:2147-2151.
- [Google Scholar]
- Numerical solutions of nonlinear evolution equations using variational iteration method. Journal of Computational and Applied Mathematics. 2007;207:111-120.
- [Google Scholar]
- Travelling wave solutions of the Cahn–Allen equation by using first integral method. Applied Mathematics and Computation. 2009;207:279-282.
- [Google Scholar]
- Analytic solutions of the (2 + 1)-dimensional nonlinear evolution equations using the sine–cosine method. Applied Mathematics and Computation. 2009;215:3134-3139.
- [Google Scholar]
- A method for solving partial differential equations via radial basis functions: application to the heat equation. Engineering Analysis with Boundary Elements. 2010;34:206-212.
- [Google Scholar]
- Application of the Adomian decomposition method for the Fokker–Planck equation. Mathematical and Computer Modelling. 2007;45:639-650.
- [Google Scholar]
- Solutions of the Cahn–Hilliard equation. Computers and Mathematics with Applications. 2008;56:3038-3045.
- [Google Scholar]
- The tanh method: exact solutions of the sine-Gordon and the sinh-Gordon equations. Applied Mathematics and Computation. 2005;167:1196-1210.
- [Google Scholar]
- The variable separated ode and the tanh methods for solving the combined and the double combined sinh–cosh-Gordon equations. Applied Mathematics and Computation. 2006;177:745-754.
- [Google Scholar]
- Exact solutions for the generalized sine-Gordon and the generalized sinh-Gordon equations. Chaos, Solitons and Fractals. 2006;28:127-135.
- [Google Scholar]
- New solitary wave solutions to the modified Kawahara equation. Physics Letters, Section A: General, Atomic and Solid State Physics. 2007;360:588-592.
- [Google Scholar]
- The tanh–coth method for solitons and kink solutions for nonlinear parabolic equations. Applied Mathematics and Computation. 2007;188:1467-1475.
- [Google Scholar]
- A discontinuous Galerkin method for the Cahn–Hilliard equation. Journal of Computational Physics. 2006;218:860-877.
- [Google Scholar]
- The variational iteration method for solitary patterns solutions of gbbm equation. Physics Letters A. 2007;367:461-464.
- [Google Scholar]
- Application of exp-function method to a KdV equation with variable coefficients. Physics Letters, Section A: General, Atomic and Solid State Physics. 2007;365:448-453.
- [Google Scholar]
- Exp-function method for solving Maccari’s system. Physics Letters, Section A: General, Atomic and Solid State Physics. 2007;371:65-71.
- [Google Scholar]
- Application of exp-function method to high-dimensional nonlinear evolution equation. Chaos, Solitons and Fractals. 2008;38:270-276.
- [Google Scholar]
Appendix A
Appendix B
Appendix C







