Efficient removal of Pb(II) from water using silica gel functionalized with thiosalicylic acid: Response surface methodology for optimization

2.1 Materials

Silica gel (Merck, India), 3-aminopropyltrimethoxysilane (Sigma Aldrich) and thiosalicylic acid (HiMedia Laboratories, India) were used to prepare the adsorbent. Lead (II) nitrate, sodium hydroxide pellets and HCl were procured from Merck, India.

2.2 Instrumentation

Atomic absorption spectrometer (AAS) (GBC Scientific, Australia) and digital pH meter (Eutech instruments, Singapore) were employed to measure the Pb(II) concentration and solution pH, respectively. Water bath shaker with variable speed and temperature control was used to agitate the solution mixture.

2.3 Synthesis of TSA@ amine modified SiO₂

The synthesis of TSA@ amine modified SiO₂ was carried out according to the method reported in the literature (Rahman and Nasir, 2020).

2.4 Experimental design for optimization

RSM via BBD was employed to optimize the influencing operating parameters for the removal of Pb(II). Design Expert (trial version 11.1.0.1) Software was used to generate BBD matrix, regression analysis and 3D response surface plots for the optimization of variables of adsorption process. In BBD, the number of experimental runs required is less than those for central composite design and thus, reducing the consumption of chemicals in the optimization process. In the present study, three independent factors namely, pH (X), adsorbent dose (Y) and initial concentration (Z) of Pb(II) were selected and each factor was investigated at three levels (high (+1), central point (0) and low (−1)) which are given in Table S1 (Supplementary information). BBD matrix suggested a total 17 sets of preliminary experiments involving different combinations of independent variables to achieve the best response (percent removal). BBD matrix is presented in Table 1.

RSM was applied to optimize influencing factors by using the data obtained from the experimental design for the removal efficiency of Pb(II) as a response (% R) and the empirical relation between the response and the independent factors were evaluated by the second order polynomial equation.

2.5 Adsorption isotherms

In order to study the adsorption isotherms, experiments were conducted under the optimal conditions (pH: 6; adsorbent dose: 0.20 g) using different concentrations of Pb(II) and temperatures. In this study, 20 mL solutions of different concentration of Pb(II) (10–100 mg/L) maintained at pH 6 were transferred to a series of 50 mL conical flasks. To each flask, TSA@ amine modified SiO₂ (0.20 g) was added and the mixture was agitated (125 rpm) at a desired temperature (300–315 K) in a shaker for 50 min. The adsorbent was removed by filtration and the Pb(II) content in the filtrate was determined by AAS. For AAS determination, calibration curve was constructed using standard solution of Pb(II) in the range of 1–20 mg/L. The detection limit of the AAS instrument was 0.01 mg/L. The adsorbed amount at equilibrium, q_e (mg/g) and removal efficiency, R (%) were computed using Eqs. (1) and (2):

where C₀ and C_e are initial and equilibrium Pb(II) concentration (mg/L) in the solution, respectively. M and V represent mass of the adsorbent (g) and solution volume (L), respectively.

2.6 Adsorption kinetics

The kinetic experiments were performed in batch mode. In general, 0.20 g of TSA@amine modified SiO₂ was mixed with 20 mL of Pb(II) solution (50 mg/L; pH 6.0) in a series of Erlenmeyer flasks. The resulting solutions were agitated (125 rpm) in temperature-controlled shaker at the desired temperature (300–315 K). Conical flasks were withdrawn from the water bath at different time intervals and then solutions were separated from the adsorbent. Finally, the residual Pb(II) content was estimated by AAS and then adsorbed amount (q_t, mg/g) of Pb(II) onto TSA@amine modified SiO₂ at predetermined time intervals was computed.

2.7 Evaluation of error functions

The values of correlation coefficient (R²) are not sufficient to judge the best fitted model. Therefore, different statistical error functions were calculated to validate the adequacy of the isotherm and kinetic models. The equations of the chosen error functions are mentioned in Table 2.

3.1 Model validation

The experiments were conducted according to the BBD matrix and percent removal of Pb(II) was determined (Table 1). The results were examined by different regression models (Linear, interactive and quadratic models) and statistical parameters are presented in Table S2 (Supplementary Information). Quadratic model was selected based on lower p-value, high F-value, minimum predicted residual sum of square value and highest R² value. The second degree polynomial quadratic model that correlates the response to the selected variables can be given by Eqs. (3) and (4) in terms of coded and actual factors, respectively.

In coded factors

In actual factors

The results of analysis of variance (ANOVA) were used to examine the significance of the model terms (Table 3). Model terms are considered as significant when p-value < 0.05 and F-value greater than the value of standard distribution table for a given degree of freedom at 95% confidence level. In the present study the high F-value (16504.65) and p-value < 0.0001 of the quadratic model illustrated its suitability and adequacy. The reliability of the quadratic model for prediction of response was judged by the adequate precision which is the signal to noise ratio and its high value (308.3165) pointed towards the adequate signal and confirming the goodness of the model (Chowdury, et al., 2016). The p-value for lack-of-fit was not given by the software but it was suggested that the lack-of-fit is insignificant. Further, the low value of coefficient of variance (0.8039%) and high correlation coefficient value (R² = 0.9999) suggested the accuracy and precision of the developed model. It was found that if the difference between the values of correlation coefficient (R²) for the adjusted and predicted response is<0.20, then it would be a reasonable agreement between them. Herein, the difference between adjusted R² (0.9999) and predicted R² (0.9992) is < 0.20 which indicated closeness between predicted and experimental values (Fig. S1, Supplementary information). Moreover, the model term XY is not significant because its p-value is 0.4642. Therefore, the contribution of model term XY can be ignored and modified second order polynomial quadratic model in coded and actual factors are represented by Eqs. (5) and (6), respectively.

3.2 Response surface analysis

The regression equation is graphically represented by 3-D response surface plots (Fig. 1). Fig. 1a shows the interactive effect of pH (X) and initial concentration (Z) on the removal (% R) when adsorbent dose (Y) was fixed at center point (Y = 20 mg and contact time 50 min). It was observed that the removal (%) at any fixed pH, increases with increasing the initial concentration upto 50 mg/L and maximum removal efficiency (98.78%) was achieved at contact time of 50 min. Further increase in Pb(II) ion concentration showed a decreasing trend in removal efficiency due to unavailability of binding sites on the surface of TSA@amine modified SiO₂. The interaction effect of adsorbent dose (Y) and initial concentration (Z) while keeping the pH (X) at the center point on the removal efficiency revealed that the removal efficiency increases from 51.77% to 98.78% with increasing the amount of TSA@amine modified SiO₂ from 0.10 g to 0.20 g. Further increase in the amount of adsorbent did not improve the removal efficiency. Hence the maximum removal was achieved with 0.20 g of TSA@amine modified SiO₂. This resulted due to the increase in the surface area and number of active sites to bind with Pb(II) ions (Fig. 1b).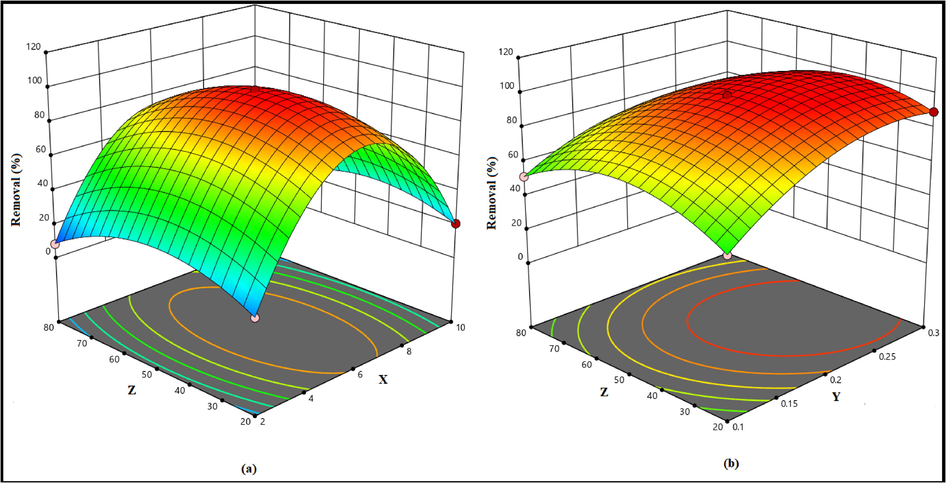

Close

Fig. 1

Response surface plots to show the effects of (a) pH and initial concentration and (b) adsorbent dose and initial concentration on the percentage removal of Pb(II).

Export to PPT

3.3 Adsorption isotherms

The equilibrium data for the uptake of Pb(II) onto TSA@)amine modified SiO₂ were applied to Langmuir, Freundlich, and Temkin isotherm models for proper description of the nature of interaction between Pb(II) and the adsorbent. Table 4 shows the nonlinear equations of the studied isotherm models. Error functions such as ARED, SSE, SAE and χ² were calculated to validate the best fit isotherm model (Table 4). The nonlinear isotherm parameters were computed by using Microsoft Excel SOLVER function spread sheet method (Rahman and Nasir, 2018) and results are presented in Table 4. The nonlinear fit(q_e (mg/g) predicted versus C_e (mg/L)) of Langmuir, Freundlich and Temkin, models are presented in Fig. 2(a)–(c), respectively.

Close

Fig. 2

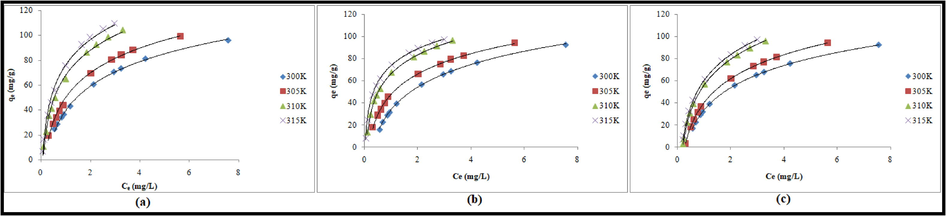
Nonlinear (a) Langmuir, (b) Freundlich and (c) Temkin isotherm plots for the adsorption of Pb (II) onto TSA@amine modified SiO_2.

Export to PPT

The maximum capacities calculated from Langmuir isotherm were 96.131, 99.156, 104.217 and 109.478 mg/g at 300, 305, 310 and 315 K, respectively. The affinity between TSA@)amine modified SiO₂ and Pb(II) was evaluated from the Langmuir isotherm constant ( ${\mathrm{K}}_{\mathrm{L}})$ using dimensionless separation factor, $R_L$ which is defined by Eq. (7) (Rahman and Haseen, 2015):

Where ${\mathrm{C}}_{\mathrm{o}}$ is the initial concentration of Pb(II). For adsorption to occur favourably, it is required that 0<   $R_L$  < 1.In this study, the values of $R_L$ were in the range of 0.022–0.184, 0.017–0.148, 0.012–0.107 and 0.008–0.071 at 300, 305, 310 and 315 K, respectively which suggested the favorable uptake of Pb(II).

Freundlich isotherm model deals with the multilayer adsorption of solute onto the adsorbent surface. In this model, the parameter 1/n is related to the degree of surface heterogeneity. The small value of 1/n denotes the more heterogeneous surface while a value near unity suggested that the adsorbent has more homogeneous surface (Chen et al., 2007). The values of 1/n obtained for adsorption of Pb(II) onto TSA@)amine modified SiO₂ were 0.521, 0.501, 0.499 and 0.468 at 300, 305, 310 and 315 K, respectively which indicated that the involvement of heterogeneous surface of adsorbent.

Temkin isotherm model assumes that the free energy of adsorption is a function of surface coverage and indicates the adsorbate/adsorbent interaction. The values of $A_T$ were in the range of 3.158–6.299 at the studied temperatures. The values of b_T,heat of adsorption, were 84.493, 81.321, 77.974 and 76.114 J/mol at 300,305, 310 and 315 K, respectively. The positive values of b_T demonstrated the endothermic nature of adsorption process.

All studied isotherm models exhibit high correlation coefficient (R² > 0.990) but the best fitting model cannot be judged accurately based on R² values only. The maximum adsorption capacities evaluated from Langmuir isotherm model were not closely related to the experimental adsorption capacities. The adsorption capacities obtained from Freundlich and Temkin models were near to the experimental values at all the studied temperatures. Additionally, the values of error functions such as ARED, SSE, SAE and χ² were found to be lowest for Freundlich model in comparison to those obtained for Temkin and Langmuir models at 300, 305, 310 and 315 K. Therefore, it was suggested that both Freundlich and Temkin isotherm models are capable to interpret the uptake of Pb(II) ions onto TSA@amine modified SiO₂. Further, the applicability of Freundlich isotherm model suggested that multilayer adsorption of Pb(II) ions occurred on heterogeneous surface of TSA@amine modified SiO₂ and Temkin model revealed the interaction between Pb(II) ion and active surface sites of the adsorbent.

3.4 Adsorption kinetics

Kinetic models such as the pseudo-first order, pseudo-second order, Elovich, and double exponential models were used to study the adsorption kinetic data. The nonlinear equations of pseudo-first order and pseudo-second order kinetic models are presented in Table 5. Nonlinear regression analysis (Rahman and Nasir, 2017, 2020) was performed to determine the kinetic parameters of pseudo-first and pseudo-second order models (Table 5). Fig. 3(a) and (b) show nonlinear fit of pseudo-first and pseudo-second order models using the predicted q_t values, respectively. The values of pseudo first order rate constant ( $k_1$ ) were found to be 0.046, 0.062, 0.107 and 0.201 min⁻¹ at 300 , 305, 310 and 315 K, respectively which indicated that the uptake of Pb(II) increased with increasing temperature. On the other hand, the values of pseudo second order rate constant ( $k_2$ ) varied over the range 0.002–0.006 g/mg/min as the temperature increased from 300 to 315 K.

Close

Fig. 3

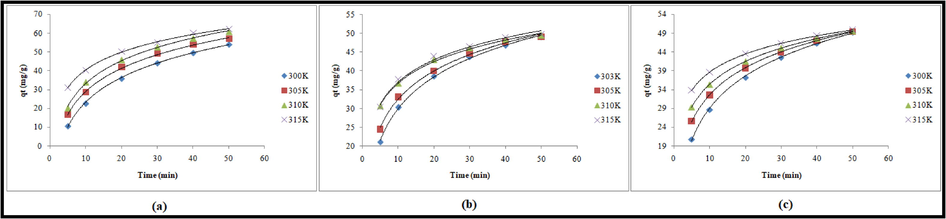
Nonlinear (a) pseudo-first order, (b) pseudo-second order and (c) Elovich kinetic plots for the adsorption of Pb (II) onto TSA@amine modified SiO_2.

Export to PPT

It was observed that the values of R² were >0.990 for both pseudo-first order and pseudo second order kinetic models over the temperature range 300–315 K. The suitability of kinetic model cannot be decided on the basis of R²values only. The capacities obtained from pseudo-first order model were 54.09, 56.94, 60.81 and 62.12 mg/g corresponding to 300, 305, 310 and 315 K, respectively and these values deviated from the experimentally determined adsorption capacities (49.01, 49.24, 49.51 and 49.73 mg/g corresponding to temperatures 300, 305, 310 and 315 K). On the other hand, the values of adsorption capacity computed from pseudo second order kinetic model were comparable at studied temperatures. Moreover, the values of error functions were very low for pseudo-second order model as compared to pseudo-first order model. Therefore, it is concluded that the uptake of Pb(II) on the heterogeneous surface of TSA@amine modified SiO₂ was accurately demonstrated by pseudo-second order model. Further, it is suggested that chemisorption is also involved in the uptake of Pb(II) ions.

To validate the uptake of Pb(II) onto heterogeneous surface of TSA@amine modified SiO₂ as a chemisorption process kinetic data were fitted to Elovich model (R² > 0.99). The nonlinear regression analysis of Elovich equation yielded the kinetic parameters and results are presented in Table 5. The nonlinear fitting of Elovich model is shown in Fig. 3c. Nonlinear regression of Elovich equation showed high values of R²with low values of ARED, SSE, SAE and χ²over the temperature range 300–315 K which demonstrated the chemical nature of adsorption process.

3.5 Double-exponential model

Wilczak and Keinath (1993) have applied the double exponential model to explain the uptake of Cu(II) and Pb(II) onto activated carbon. This model suggested the involvement of two steps namely rapid and slow stages in the adsorption process. Rapid phase of the model is due to the external mass transfer of solute from bulk solution to the adsorbent surface where it interacts with the binding sites whereas slow stage is due to the intraparticle diffusion. Similarly, Rahman and Nasir (2020) have suggested that the upatake of acetaminophen by the adsorbent occurred in two stages which was validated by double exponential model. Double exponential model is expressed by Eq. (8):

where D₁ and K_D1 are the rapidly adsorbed fraction of the solute (mg/L) and the rate constant of rapid step (min⁻¹), respectively. D₂ and K_D2 are slowly adsorbed fraction of solute and rate constant of slow step of adsorption. M denotes the mass of adsorbent (g/L). The fraction of solute adsorbed in rapid and slow steps and their corresponding rate constants can be determined by the following assumption.

When K_D1≫ K_D2 then slow step contributes to overall kinetics and Eq. (8) is reduced to:

Eq. (9) can be linearized as:

The values of D₂ and KD₂were computed from ln (q_e- q_t) versus t plot. The values of D₁ and KD₁ can be calculated using Eq. (11):

The values of KD₁ and KD₂are not able to illustrate the exact quantification of the rapid and slow steps of the sorption. Therefore, the fraction of solute adsorbed in rapid (RF) and slow (SF) stages can be computed using Eqs. (12) and (13):

The kinetic parameters for both slow and rapid steps were determined from the plots of ln{q_e-q_t-(D₂/M)exp(-k_D2 t)} vs t (Fig. 4) and presented in the Table 6. It was found that the D₁ increases whereas D₂ decreases with increasing temperature. The difference between the KD₂ (0.104–0.100) and KD₁ (0.110–0.121) is not high, indicating the importance of both slow and rapid steps at all temperatures. The values SF (37.120–30.432) and RF (62.026–69.568) confirmed that major fraction of Pb(II) was absorbed in the rapid step due to the interaction with the active sites available on the adsorbent surface. In the slow step, the intraparticle diffusion is involved in the adsorption process. From these observations, it was concluded that both chemical and physical interactions were responsible for adsorption of Pb(II) ontoTSA@amine modified SiO₂. Similar results were reported for the adsorption of Th(IV) onto amino group functionalized titanosilicate (Milani and Karimi, 2017).

C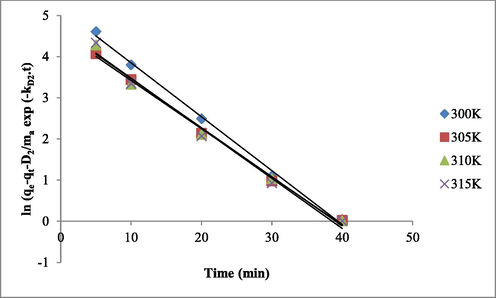lose

Fig. 4

Double exponential plots of ln{q_e-q_t-(D₂/M)exp(-k_D2 t)} vs t.

Export to PPT

3.6 Thermodynamics of adsorption

Thermodynamic parameters for the uptake of Pb(II) onto TSA@amine modified SiO₂ were calculated using the values of thermodynamic equilibrium constant ( $k_c$ ) at different temperatures. The values of ΔG°, ΔH° and ΔS° were evaluated using Eqs. (14), (15) and (16) (Rahman and Varshney, 2020).

where R and T are the universal gas constant (8.314 J/mol/K) and temperature (Kelvin), respectively. The value of $k_c$ can be calculated to become dimensionless by multiplying it by 1000 assuming the solution density $\approx$ 1 g/mL (Milonjic, 2007). The values of free energy change (ΔG⁰) were found to vary from −9.388 to −13.089 kJ/mol over the temperature range 300–315 K. The values of ΔH° and ΔS° were computed from linear plot of $\mathit{ln}{k}_C$ versus $\frac{1}{T}$ (Fig S2; Supplementary information). The positive values of enthalpy change (ΔH° = 65.381 kJ/mol) and entropy change (ΔS° = 0.249 kJ/mol) indicated the endothermic nature of adsorption of Pb(II) onto TSA@amine modified SiO₂ and enhanced randomness at adsorbent/liquid interface.