Effects of internal heat generation and Soret/Dufour on natural convection of non-Newtonian fluids over a vertical permeable cone in a porous medium

Chuo-Jeng Huang

doi:10.1016/j.jksus.2016.09.009

View/Download PDF

Buy Reprints

PDF

Translate this page into:

30 (

); 106-111

doi:

10.1016/j.jksus.2016.09.009

Effects of internal heat generation and Soret/Dufour on natural convection of non-Newtonian fluids over a vertical permeable cone in a porous medium

Chuo-Jeng Huang

Department of Aircraft Engineering, Air Force Institute of Technology, Taiwan, ROC

Received: 2016-8-1, Accepted: 2016-9-28, Published: 2016-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

This investigation examines numerically the combined heat and mass transfer of a uniform blowing/suction, non-Newtonian power-law fluid, and the effects of internal heat generation on natural convection adjacent to a vertical cone in a porous medium in the presence of Soret/Dufour effects. The surface of the vertical cone has a uniform wall temperature and a uniform wall concentration (UWT/UWC). A non-similarity analysis is carried out, and the transformed governing equations are solved using the Keller box method. The effects of the Dufour parameter, the Soret parameter, the Lewis number, the buoyancy ratio, the power-law index of the non-Newtonian fluid, the blowing/suction parameter and the internal heat generation coefficient on the heat and mass transfer characteristics were elucidated. In general, for the case of blowing, both the local Nusselt number and the local Sherwood number decrease. This trend reversed for suction of fluid. The local Nusselt (Sherwood) number decreases (increases) as the internal heat generation coefficient A^∗ is increased. Increasing the non-Newtonian fluid n reduces both the local Nusselt number and the local Sherwood number. The physical aspects of the problem are discussed in detail.

Keywords

Non-Newtonian fluid

Soret/Dufour effects

Internal heat generation

Natural convection

Vertical permeable cone

Porous medium

Show Related Articles from PubMed

1 Introduction

Convective heat transfer in porous media has various applications such as geothermal reservoirs, geophysical engineering, nuclear waste disposal, chemical reactor engineering and the storage of heat-generating materials grain and coal. Nield and Bejan (2006) recently provided a comprehensive account of available information in this field.

With respect to pure heat transfer with a lateral mass flux, Yih (1998) presented the effect of a uniform lateral mass flux on the natural convection of non-Newtonian fluids over a cone in a porous medium. Chamkha and Quadri (2002) studied the combined heat and mass transfer by hydromagnetic natural convection over a cone embedded in a non-Darcian porous medium with heat generation/absorption effects. Kechil and Hashim (2008) presented the series of solutions for boundary-layer flows in porous media with a lateral mass flux. Turkyilmazoglu and Pop (2012) examined the Soret and heat source effects on the unsteady radiative MHD free convection flow from an impulsively started infinite vertical plate. Chamkha et al. (2014) investigated the effect of suction/injection on free convection along a vertical plate in a nanofluid-saturated non-Darcy porous medium with internal heat generation.

A well-known phenomenon that involves coupled heat and mass transfer is the thermal energy flux that is generated by concentration gradients is called the Dufour (diffusion-thermal) effect. The Soret (thermo-diffusion) effect is the effect of the temperature gradient on mass flux. Partha et al. (2006) elucidated the Soret and Dufour effects in a non-Darcy porous medium. Lakshmi Narayana and Murthy (2008) investigated the Soret and Dufour effects on free convective heat and mass transfer from a horizontal flat plate in a Darcy porous medium. Cheng (2009) studied the Soret and Dufour effects on natural convective heat and mass transfer from a vertical cone in a porous medium. Turkyilmazoglu (2011) investigated the multiple solutions of hydromagnetic permeable flow and heat for viscoelastic fluid.

Internal heat generation arises in many important contexts, including reactor safety analyses, metal waste that is produced by spent nuclear fuel, fire and combustion studies, and the storage of radioactive materials. Grosan et al. (2004) presented the free convective boundary layer over a vertical cone in a non-Newtonian fluid-saturated porous medium with internal heat generation. Mahmoud (2012) examined the effect of radiation on free convection in a non-Newtonian fluid over a vertical cone in a porous medium with heat generation. Turkyilmazoglu (2012) studied the dual and triple solutions for MHD slip flow of non-newtonian fluid over a shrinking surface. Yih and Huang (2015) elucidated the effect of internal heat generation on free convective flow in non-Newtonian fluids over a vertical truncated cone in porous media VWT/VWC.

This work extends the works of Yih (1998), Cheng (2009) and Grosan et al. (2004) by investigating the heat and mass transfer on natural convection in non-Newtonian fluids over a vertical cone with a uniform wall temperature and a uniform wall concentration (UWT/UWC) in a porous medium, considering both Soret and Dufour effects with internal heat generation and uniform blowing/suction.

2 Analysis

The problem concerns the effect of uniform blowing/suction on the natural convection of non-Newtonian fluids over a vertical cone in a porous medium with internal heat generation and Soret/Dufour effects, where the boundary conditions are a uniform wall temperature T_w and a uniform wall concentration C_w (UWT/UWC). Fig. 1 displays the flow model and the physical coordinate system. The origin of the coordinate system is the vertex of the vertical cone, where x and y are Cartesian coordinates along and normal to, respectively, the vertical cone surface.

Flow model and physical coordinate system.

All of the properties of the fluid are assumed to be constant, except for the density, whose variation is in the buoyancy term. Using the boundary layer and Boussinesq approximations, the governing equations and the boundary conditions that are based on the Darcy law can be written as follows.

Continuity equation:

(1)

\frac{\partial (ru)}{\partial x} + \frac{\partial (rv)}{\partial y} = 0

Momentum (Darcy) equation:

(2)

u^{n} = \frac{ρ_{\infty} \cdot g \cos γ \cdot K (n)}{μ} [β_{T} (T - T_{\infty}) + β_{C} (C - C_{\infty})]

Energy equation:

(3)

u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = α_{m} \frac{\partial^{2} T}{\partial y^{2}} + \frac{D_{m}}{C_{s}} \cdot \frac{k_{T}}{C_{p}} \cdot \frac{\partial^{2} C}{\partial y^{2}} + \frac{q^{‴}}{ρ \cdot C_{p}}

Concentration equation:

(4)

u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y} = D_{m} \frac{\partial^{2} C}{\partial y^{2}} + \frac{D_{m} \cdot k_{T}}{T_{m}} \cdot \frac{\partial^{2} T}{\partial y^{2}}

Boundary conditions:

(5)

y = 0 : v = V_{w}, T = T_{w}, C = C_{w}

(6)

y \to \infty : u = 0, T = T_{\infty}, C = C_{\infty}

Here, u and v are the Darcian velocities in the x- and y-directions, respectively; n is the power-law index of the non-Newtonian fluid; r is the local radius of the cone; K(n) is the permeability of the porous medium; γ is the half-angle of the cone; g is the acceleration due to gravity; ρ and μ are the density and absolute viscosity of liquid, respectively; T and C are the volume-averaged temperature and concentration of liquid in boundary layer, respectively; α_m and D_m are the equivalent thermal diffusivity and mass diffusivity, respectively;

q^{‴}

is the internal heat generation rate per unit volume; C_p and C_s are the specific heat at constant pressure and concentration susceptibility, respectively; T_m is the mean fluid temperature; β_T and β_C are the thermal and concentration expansion coefficients of the fluid, respectively; and V_w is the uniform blowing/suction velocity.

The second and third terms on the right-hand side of the energy equation, Eq. (3), represent the Dufour effect and the heat absorbed per unit volume, and the last term of the concentration equation, Eq. (4), denotes the Soret effect.

The power-law fluid index n for various fluids: (i) n < 1 for pseudo-plastic fluids. (ii) n = 1 for Newtonian fluids. (iii) n > 1 for dilatant fluids. The power law model of Ostwald-de-Waele is according to Christopher and Middleman (1965) and Dharmadhirkari and Kale (1985).

The stream function ψ is defined by

(7)

ru = \partial ψ / \partial y and rv = - \partial ψ / \partial x

Therefore, the continuity equation is automatically satisfied.

The following dimensionless variables are used.

(8.1)

ξ = \frac{2 V_{w} x}{α_{m} \cdot {Ra}_{x}^{1 / 2 n}}

(8.2)

η = \frac{y}{x} {Ra}_{x}^{1 / 2 n}

(8.3)

f (ξ, η) = \frac{ψ}{α_{m} \cdot r \cdot {Ra}_{x}^{1 / 2 n}}

(8.4)

θ (ξ, η) = \frac{T - T_{\infty}}{T_{w} - T_{\infty}}

(8.5)

ϕ (ξ, η) = \frac{C - C_{\infty}}{C_{w} - C_{\infty}}

(8.6)

{Ra}_{x} = \frac{ρ_{\infty} \cdot g \cos γ \cdot β_{T} [T_{w} - T_{\infty}] \cdot K (n)}{μ} {(\frac{x}{α})}^{n}

where Ra_x is the local Rayleigh number.

The internal heat generation rate per unit volume $q^{‴}$ is modeled by the following equation;

(9)

q^{‴} = A^{*} \cdot \frac{k (T_{w} - T_{\infty})}{x^{2}} \cdot {Ra}_{x}^{1 / n} \cdot e^{- η}

where k is the equivalent thermal conductivity of the porous medium, and A^∗ is the internal heat generation coefficient. Notably, A^∗ = 0 corresponds to case 1 without internal heat generation (designated as NIHG), and A^∗ > 0 corresponds to case 2 with internal heat generation (WIHG).

Substituting Eqs. (8) and (9) into Eqs. (2)–(6) yields

(10)

{(f^{'})}^{n} = θ + N ϕ

(11)

θ^{'} + \frac{3}{2} f θ^{'} + D ϕ^{'} + A^{*} \cdot e^{- η} = \frac{1}{2} ξ (f^{'} \frac{\partial θ}{\partial ξ} - θ^{'} \frac{\partial f}{\partial ξ})

(12)

\frac{1}{Le} ϕ^{'} + \frac{3}{2} f ϕ^{'} + S θ^{'} = \frac{1}{2} ξ (f^{'} \frac{\partial ϕ}{\partial ξ} - ϕ^{'} \frac{\partial f}{\partial ξ})

The boundary conditions are defined as follows.

(13)

η = 0 : f = - \frac{ξ}{4}, θ = 1, ϕ = 1

(14)

η \to \infty : θ = 0, ϕ = 0

where primes denote differentiation with respect to η. ξ, defined in Eq. (8.1), is the surface blowing/suction parameter. For blowing, V_w > 0 so ξ > 0. For suction, V_w < 0 so ξ < 0. The buoyancy ratio N, the Lewis number Le, the Dufour parameter D and the Soret parameter S are respectively defined as follows.

(15)

N = \frac{β_{C} [C_{w} - C_{\infty}]}{β_{T} [T_{w} - T_{\infty}]}, Le = \frac{α_{m}}{D_{m}}

(16)

D = \frac{D_{m} \cdot k_{T} \cdot [C_{w} - C_{\infty}]}{C_{s} \cdot C_{P} \cdot α_{m} \cdot [T_{w} - T_{\infty}]}, S = \frac{D_{m} \cdot k_{T} \cdot [T_{w} - T_{\infty}]}{T_{m} \cdot [C_{w} - C_{\infty}]}

The resulting heat and mass transfer rates are practically useful. They are expressed in terms of the local Nusselt number Nu_x and the local Sherwood number Sh_x, which are respectively defined as follows.

(17)

{Nu}_{x} = \frac{h_{x} x}{k} = \frac{q_{w} x}{[T_{w} - T_{\infty}] k} = \frac{- {(\frac{\partial T}{\partial y})|}_{y = 0} x}{[T_{w} - T_{\infty}] k}

(18)

{Sh}_{x} = \frac{h_{m, x} x}{D_{m}} = \frac{m_{w} x}{[C_{w} - C_{\infty}] D_{m}} = \frac{- {(\frac{\partial C}{\partial y})|}_{y = 0} x}{[C_{w} - C_{\infty}] D_{m}}

Eq. (8) yields the local Nusselt number Nu_x and the local Sherwood number Sh_x in terms of ${Ra}_{x}^{1 / 2 n}$ as,

(19)

\frac{{Nu}_{x}}{{Ra}_{x}^{1 / 2 n}} = - θ^{'} (ξ, 0)

(20)

\frac{{Sh}_{x}}{{Ra}_{x}^{1 / 2 n}} = - ϕ^{'} (ξ, 0)

For the case of A^∗ = 0 (NIHG), n = 1 (Newtonian fluid), ξ = 0 (without blowing/suction), Eqs. (10)–(14) are reduced to those of Cheng (2009) who obtained the previously mentioned similarity solution.

3 Results and discussion

This analysis integrates the system of equations, Eqs. (10)–(14), using the implicit finite difference approximation and the modified Keller box method of Cebeci and Bradshaw (1984). The details of the solution method are omitted here to conserve space.

The accuracy of the proposed method was confirmed by comparing the results obtained herein with those of Yih (1998) and Yih and Huang (2015). Table 1 compares −θ′(ξ, 0) for various values of n and ξ with N = D = S = A^∗ = 0. Table 2 compares –θ′(ξ, 0) and –ϕ′(ξ, 0) for various values of n and A^∗ with D = S = ξ = 0, N = 4 and Le = 10. All values in Tables 1 and 2 agreed very closely with the numerical data in previous works.

Table 1 −θ′(ξ, 0) for various values of n and ξ with N = D = S = A^∗ = 0.

ξ	−θ′(ξ, 0)
	n = 0.5		n = 2.0
	Yih (1998)	Present results	Yih (1998)	Present results
−4	2.1650	2.1649	2.3163	2.3148
−2	1.3008	1.3008	1.5055	1.5054
0	0.6522	0.6521	0.8552	0.8552
2	0.2791	0.2791	0.4109	0.4103
4	0.1011	0.0983	0.1609	0.1594

Table 2 −θ′(ξ, 0) and –ϕ′(ξ, 0) for various values of n and A^∗ with D = S = ξ = 0, N = 4, Le = 10.

A^∗	n	−θ′(ξ, 0)		−ϕ′(ξ, 0)
A^∗	n	Yih and Huang (2015)	Present results	Yih and Huang (2015)	Present results
0 (NIHG)	0.5	1.7511	1.7512	11.0144	11.0149
	1.0	1.1797	1.1797	5.6954	5.6957
	2.0	1.0443	1.0443	4.1600	4.1602

1 (WIHG)	0.5	0.9984	0.9984	11.0893	11.0898
	1.0	0.5429	0.5429	5.7367	5.7370
	2.0	0.4437	0.4437	4.1820	4.1822

Numerical results are presented for buoyancy ratio N = 1, Lewis number Le = 2, Dufour parameter D = 0.3, the Soret parameter S = 0.5, internal heat generation A^∗ from zero to unity, non-Newtonian fluid n from 0.5 to 2.0, and blowing/suction parameter ξ from −3 to 3.

Fig. 2 presents the dimensionless temperature and concentration profiles for three values of the blowing/suction parameter ξ (ξ = −3, 0 and 3) with N = 1, Le = 2, D = 0.3, S = 0.5, n = 2.0 and A^∗ = 1. Fig. 2(a) demonstrates blowing (ξ > 0) reduces the dimensionless wall temperature gradient −θ′(ξ, 0). The phenomenon of overshoot in the dimensionless temperature profile occurs at ξ = 3, where heat is transferred from the porous medium to the vertical cone. Fig. 2(b) indicates suction (ξ < 0) tends to increase the dimensionless wall concentration gradient –ϕ′(ξ, 0). Blowing (ξ > 0) increases both the thermal boundary layer thickness δ_T and the concentration boundary layer thickness δ_C. However, suction (ξ < 0) has the opposite effects.

Figure 2

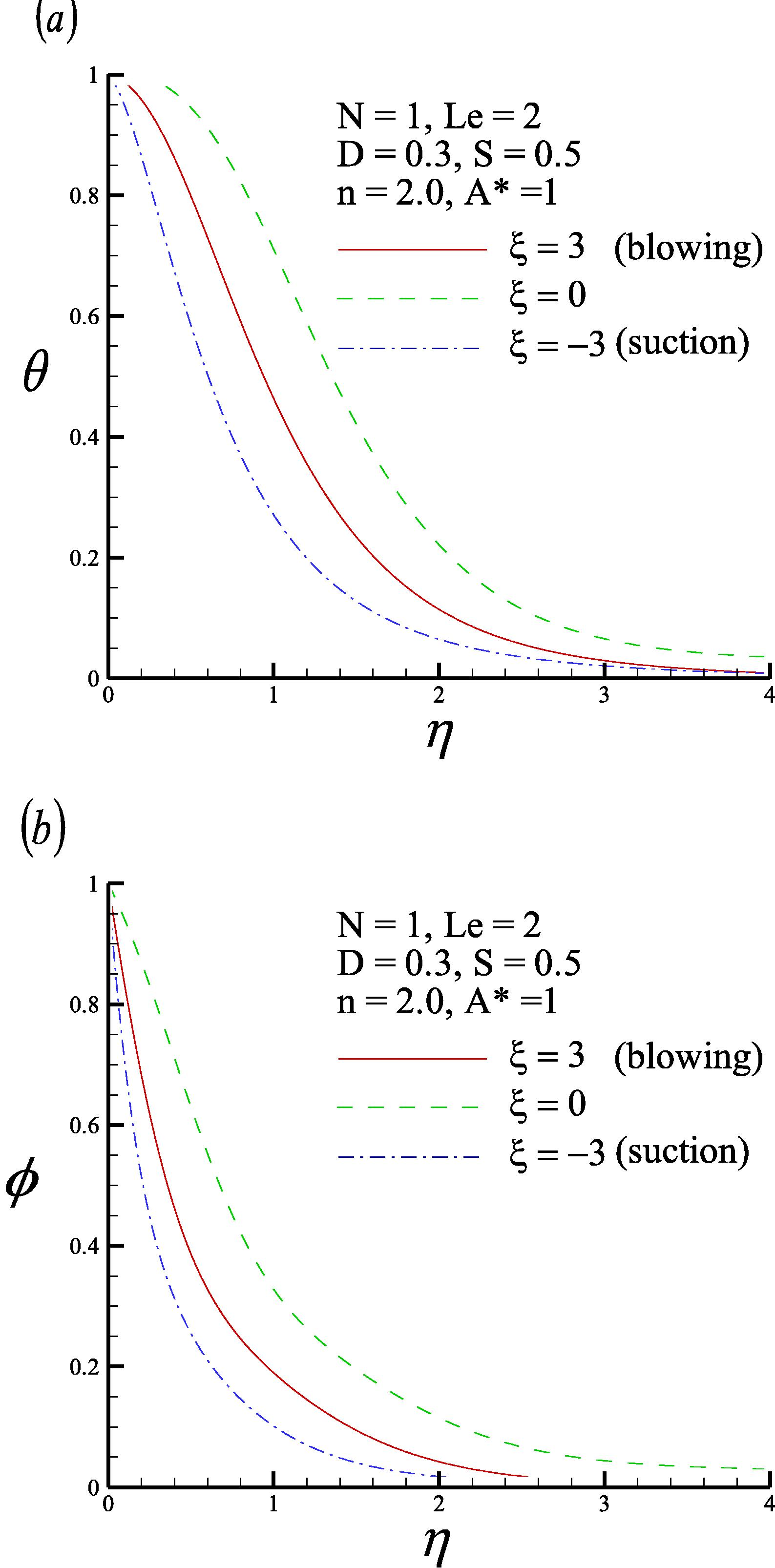
(a) Dimensionless temperature profile and (b) dimensionless concentration profile for three values of blowing/suction parameter ξ.

Table 3 presents the values of local Nusselt number ${Nu}_{x} / {Ra}_{x}^{1 / 2 n}$ and the local Sherwood number ${Sh}_{x} / {Ra}_{x}^{1 / 2 n}$ for various values of ξ with N = 1, Le = 2, D = 0.3, S = 0.5, n = 2.0 and A^∗ = 1. Suction, ξ < 0, generally increases both the local Nusselt number and the local Sherwood number because suction increases both the dimensionless surface temperature and the concentration gradients, as displayed in Fig. 2. Equations (19) and (20) indicate that a larger dimensionless surface temperature and larger concentration gradients are associated with larger local Nusselt and Sherwood numbers.

Table 3 Values of

{Nu}_{x} / {Ra}_{x}^{1 / 2 n}

and

{Sh}_{x} / {Ra}_{x}^{1 / 2 n}

for various values of ξ with N = 1, Le = 2, D = 0.3, S = 0.5, n = 2.0, A^∗ = 1.

ξ	${Nu}_{x} / {Ra}_{x}^{1 / 2 n}$	${Sh}_{x} / {Ra}_{x}^{1 / 2 n}$
−3	0.2955	3.6968
−2	0.1890	3.0191
−1	0.1122	2.3721
0	0.0593	1.7770
1	0.0200	1.2639
2	−0.0161	0.8529
3	−0.0531	0.5528

Fig. 3 plots the effects of the internal heat generation coefficient A^∗ (A^∗ = 0.0, 0.5 and 1.0) on the dimensionless temperature profile and the dimensionless concentration profile with N = 1, Le = 2, D = 0.3, S = 0.5, n = 2 and ξ = - 1.5. Increasing the internal heat generation coefficient A^∗ tends to reduce the dimensionless wall temperature gradient −θ′(ξ, 0) but to increase the dimensionless wall concentration gradient −ϕ′(ξ, 0).

Figure 3

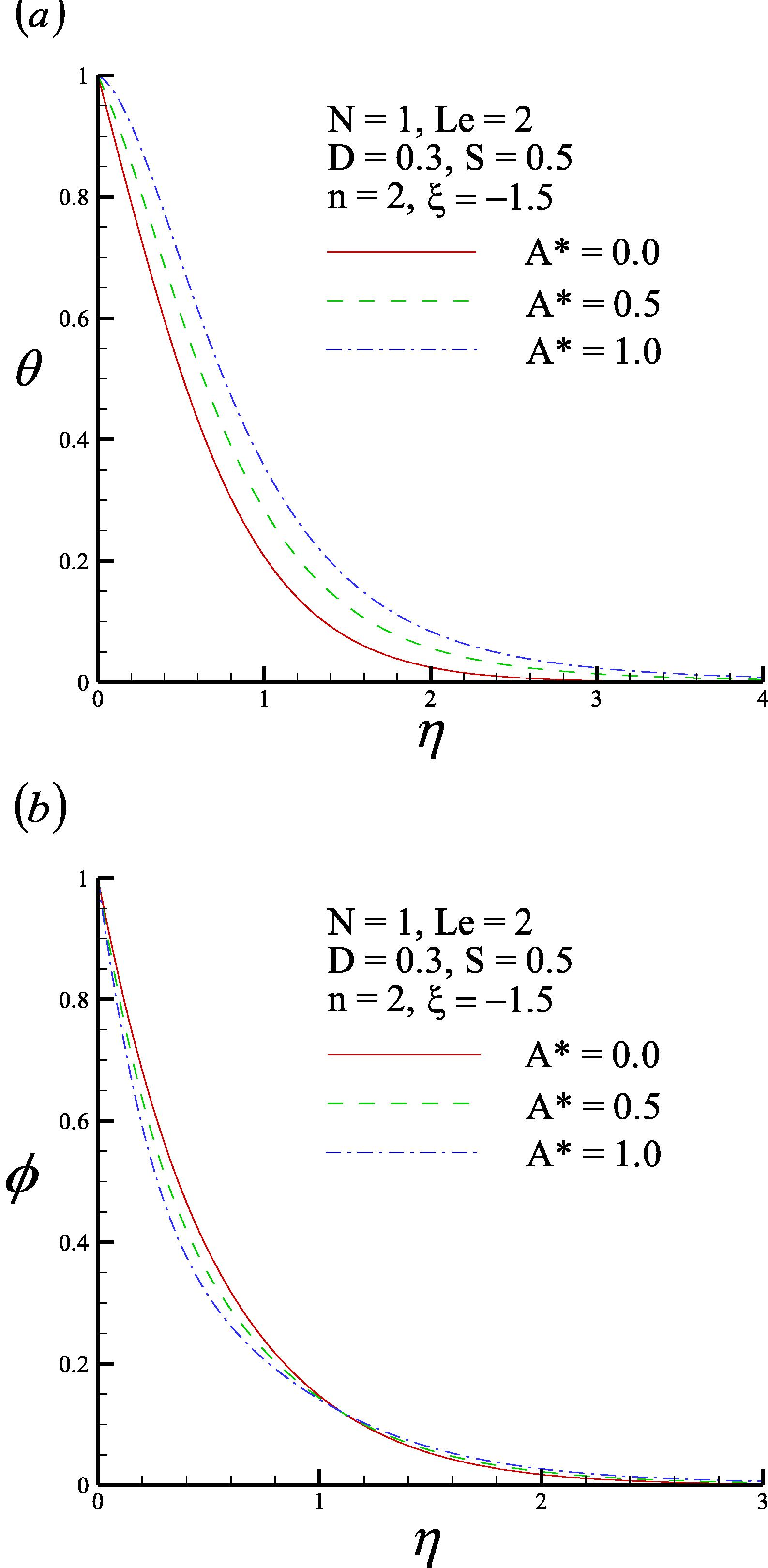
(a) Dimensionless temperature profile and (b) dimensionless concentration profile for three values of internal heat generation coefficient A^∗.

Table 4 presents the values of the local Nusselt number ${Nu}_{x} / {Ra}_{x}^{1 / 2 n}$ and the local Sherwood number ${Sh}_{x} / {Ra}_{x}^{1 / 2 n}$ for various values of the internal heat generation coefficient A^∗ with N = 1, Le = 2, D = 0.3, S = 0.5, n = 2 and ξ = - 1.5. Increasing the internal heat generation coefficient A^∗ generally reduces the local Nusselt number and slightly increases the local Sherwood number because increasing the internal heat generation coefficient A^∗ reduces the dimensionless surface temperature gradient −θ′(ξ, 0) and increases the dimensionless surface concentration gradient −ϕ′(ξ, 0), as displayed in Fig. 3.

Table 4 Values of

{Nu}_{x} / {Ra}_{x}^{1 / 2 n}

and

{Sh}_{x} / {Ra}_{x}^{1 / 2 n}

for various values of A^∗ with N = 1, Le = 2, D = 0.3, S = 0.5, n = 2 and ξ = −1.5.

A^∗	${Nu}_{x} / {Ra}_{x}^{1 / 2 n}$	${Sh}_{x} / {Ra}_{x}^{1 / 2 n}$
0.0	1.0515	1.8673
0.25	0.8209	2.0780
0.50	0.5938	2.2852
0.75	0.3693	2.4896
1.0	0.1471	2.6915

Fig. 4 shows the dimensionless temperature and concentration profiles for three values of the non-Newtonian fluid n (n = 0.5, 1.0 and 1.5) with N = 1, Le = 2, D = 0.3, S = 0.5, ξ = 1.5, and A^∗ = 1. The dimensionless temperature profiles θ(ξ, η) and the dimensionless concentration profiles ϕ(ξ, η) clearly decrease as the non-Newtonian fluid n decreases, enhancing the dimensionless surface temperature and concentration gradients, because reducing the non-Newtonian fluid n tends to increase the buoyancy force and the flow velocity.

Figure 4

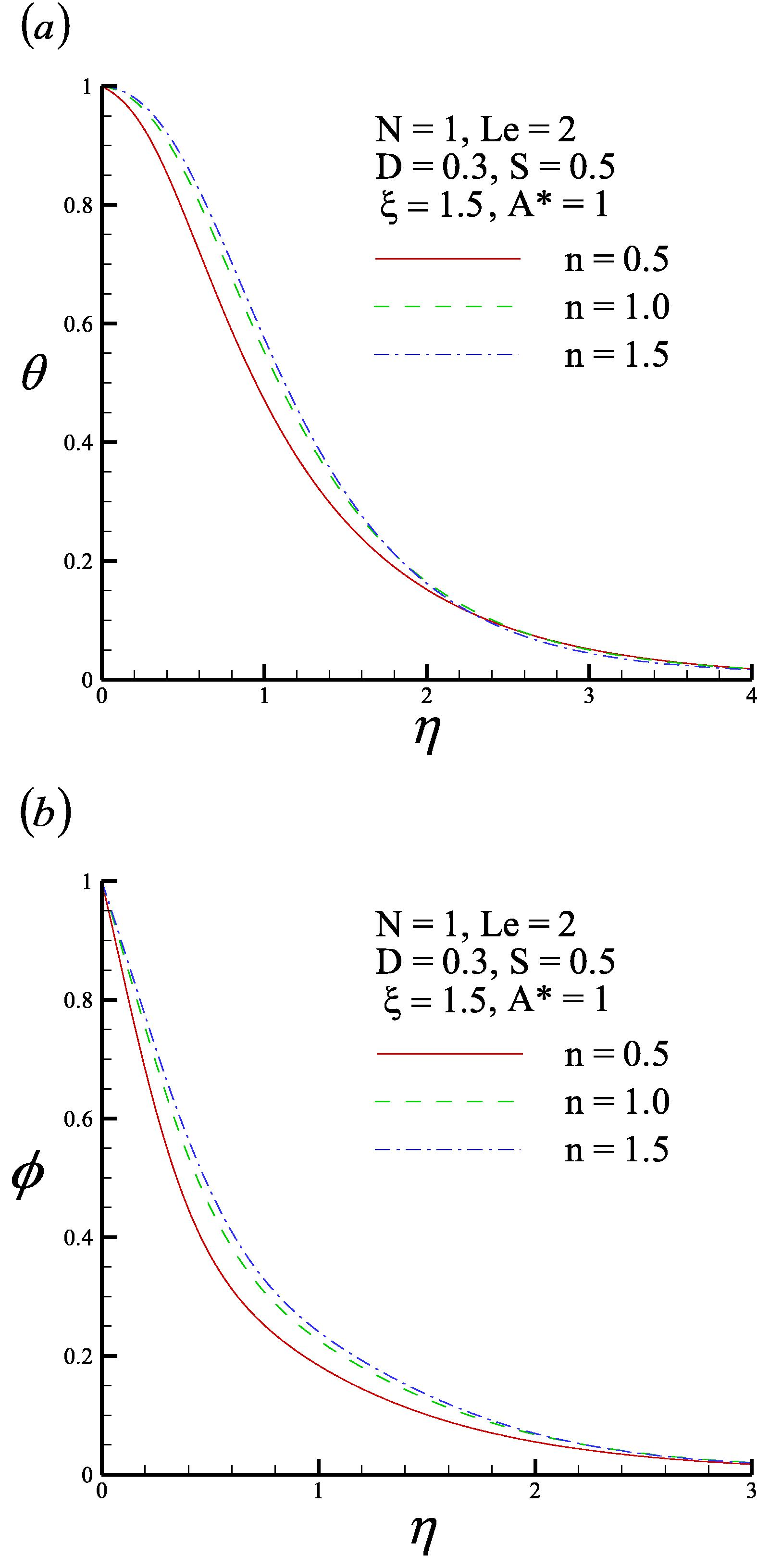
(a) Dimensionless temperature profile and (b) dimensionless concentration profile for three values of the non-Newtonian fluid n.

Table 5 presents the values of local Nusselt number ${Nu}_{x} / {Ra}_{x}^{1 / 2 n}$ and the local Sherwood number ${Sh}_{x} / {Ra}_{x}^{1 / 2 n}$ for various values of the non-Newtonian fluid n (n = 0.5–1.5) with N = 1, Le = 2, D = 0.3, S = 0.5, ξ = 1.5 and A^∗ = 1. Increasing the non-Newtonian fluid n reduces both the local Nusselt number and the local Sherwood number because increasing n tends to reduce the velocity of the flow and the dimensionless surface temperature and concentration gradients, as displayed in Fig. 4. Therefore pseudoplastic fluids (n = 0.5) are superior to dilatant fluids (n = 1.5) with respect to the transfer rates of heat and mass by natural convection from a vertical cone in a porous medium that is saturated with non-Newtonian power-law fluids.

Table 5 Values of

{Nu}_{x} / {Ra}_{x}^{1 / 2 n}

and

{Sh}_{x} / {Ra}_{x}^{1 / 2 n}

for various values of n with N = 1, Le = 2, D = 0.3, S = 0.5, ξ = 1.5 and A^∗ = 1.

n	${Nu}_{x} / {Ra}_{x}^{1 / 2 n}$	${Sh}_{x} / {Ra}_{x}^{1 / 2 n}$
0.5	0.1437	1.5675
0.8	0.0606	1.2706
1.0	0.0382	1.1879
1.5	0.0128	1.0894
2.0	0.0019	1.0447

4 Conclusions

A two-dimensional laminar boundary layer analysis is carried out to elucidate the effect of uniform blowing/suction on the natural convection of non-Newtonian fluids over a vertical cone in a porous medium with internal heat generation and Soret/Dufour effects. After the coordinate transformation, the transformed governing equations are solved using the Keller box method (KBM). Comparisons show excellent agreement between results obtained herein and those published previously. Numerical solutions are obtained various values of the internal heat generation coefficient A^∗, the power-law index of the non-Newtonian fluid n and the blowing/suction parameter ξ. The analytical results indicate that increasing the internal heat generation coefficient A^∗ reduces the local Nusselt number and increases the local Sherwood number. As the power-law index of the non-Newtonian fluid n increases, both the local Nusselt number and the local Sherwood number decrease. In the case of suction, both the local Nusselt number and the local Sherwood number increase. Blowing has the opposite effect.

References

Cebeci T., Bradshaw P., . Physical and Computational Aspects of Convective Heat Transfer. New York: Springer-Verlag; 1984.
Chamkha A.J., Quadri M.M.A., . Combined heat and mass transfer by hydromagnetic natural convection over a cone embedded in a non-Darcian porous medium with heat generation/absorption effects. Heat Mass Transfer. 2002;38:487-495.
[Google Scholar]
Chamkha A.J., Rashad A.M., Reddy C.R., . Effect of suction/injection on free convection along a vertical plate in a nanofluid saturated non-Darcy porous medium with internal heat generation. Indian J. Pure Appl. Math.. 2014;45:321-342.
[Google Scholar]
Cheng C.Y., . Soret and Dufour effects on natural convection heat and mass transfer from a vertical cone in a porous medium. Int. Commun. Heat Mass Transfer. 2009;36:1020-1024.
[Google Scholar]
Christopher R.V., Middleman S., . Power-law flow through a packed tube. Ind. Eng. Chem. Fundam.. 1965;4(4):424-426.
[Google Scholar]
Dharmadhirkari R.V., Kale D.D., . Flow of non-Newtonian fluids through porous media. Chem. Eng. Sci.. 1985;40(3):527-529.
[Google Scholar]
Grosan T., Postelnicu A., Pop I., . Free convection boundary layer over a vertical cone in a non-Newtonian fluid saturated porous medium with internal heat generation. Tech. Mech.. 2004;24:91-104.
[Google Scholar]
Kechil S.A., Hashim I., . Series solutions of boundary-layer flows in porous media with lateral mass flux. Heat Mass Transfer. 2008;44:1179-1186.
[Google Scholar]
Lakshmi Narayana P.A., Murthy P.V.S.N., . Soret and Dufour effects on free convection heat and mass transfer from a horizontal flat plate in a Darcy porous medium. J. Heat Transfer. 2008;130:104504-1-104504-5.
[Google Scholar]
Mahmoud M.A.A., . Radiation effect on free convection of a non-Newtonian fluid over a vertical cone embedded in a porous medium with heat generation. J. Appl. Mech. Tech. Phys.. 2012;53:743-750.
[Google Scholar]
Nield D.A., Bejan A., . Convection in Porous Media. New York: Springer-Verlag; 2006.
Partha M.K., Murthy P.V.S.N., Raja Sekhar G.P., . Soret and Dufour effects in a non-Darcy porous medium. J. Heat Transfer. 2006;128:605-610.
[Google Scholar]
Turkyilmazoglu M., . Dual and triple solutions for MHD slip flow of non-newtonian fluid over a shrinking surface. Comput. Fluids. 2012;70:53-58.
[Google Scholar]
Turkyilmazoglu M., . Multiple solutions of hydromagnetic permeable flow and heat for viscoelastic fluid. J. Thermophys. Heat Transfer. 2011;25:595-605.
[Google Scholar]
Turkyilmazoglu M., Pop I., . Soret and heat source effects on the unsteady radiative MHD free convection flow from an impulsively started infinite vertical plate. Int. J. Heat Mass Transfer. 2012;55:7635-7644.
[Google Scholar]
Yih K.A., . Uniform lateral mass flux effect on natural convection of non-Newtonian fluids over a cone in porous media. Int. Commun. Heat Mass Transfer. 1998;25:959-968.
[Google Scholar]
Yih K.A., Huang C.J., . Effect of internal heat generation on free convection flow of non-Newtonian fluids over a vertical truncated cone in porous media: VWT/VWC. J. Air Force Instit. Technol.. 2015;14(1):1-18.
[Google Scholar]

Introduction

Analysis

Results and discussion

Conclusions

Fulltext Views
6

PDF downloads
6

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Cebeci T., Bradshaw P., . Physical and Computational Aspects of Convective Heat Transfer. New York: Springer-Verlag; 1984.

[2] Chamkha A.J., Quadri M.M.A., . Combined heat and mass transfer by hydromagnetic natural convection over a cone embedded in a non-Darcian porous medium with heat generation/absorption effects. Heat Mass Transfer. 2002;38:487-495.
[Google Scholar]

[3] Chamkha A.J., Rashad A.M., Reddy C.R., . Effect of suction/injection on free convection along a vertical plate in a nanofluid saturated non-Darcy porous medium with internal heat generation. Indian J. Pure Appl. Math.. 2014;45:321-342.
[Google Scholar]

[4] Cheng C.Y., . Soret and Dufour effects on natural convection heat and mass transfer from a vertical cone in a porous medium. Int. Commun. Heat Mass Transfer. 2009;36:1020-1024.
[Google Scholar]

[5] Christopher R.V., Middleman S., . Power-law flow through a packed tube. Ind. Eng. Chem. Fundam.. 1965;4(4):424-426.
[Google Scholar]

[6] Dharmadhirkari R.V., Kale D.D., . Flow of non-Newtonian fluids through porous media. Chem. Eng. Sci.. 1985;40(3):527-529.
[Google Scholar]

[7] Grosan T., Postelnicu A., Pop I., . Free convection boundary layer over a vertical cone in a non-Newtonian fluid saturated porous medium with internal heat generation. Tech. Mech.. 2004;24:91-104.
[Google Scholar]

[8] Kechil S.A., Hashim I., . Series solutions of boundary-layer flows in porous media with lateral mass flux. Heat Mass Transfer. 2008;44:1179-1186.
[Google Scholar]

[9] Lakshmi Narayana P.A., Murthy P.V.S.N., . Soret and Dufour effects on free convection heat and mass transfer from a horizontal flat plate in a Darcy porous medium. J. Heat Transfer. 2008;130:104504-1-104504-5.
[Google Scholar]

[10] Mahmoud M.A.A., . Radiation effect on free convection of a non-Newtonian fluid over a vertical cone embedded in a porous medium with heat generation. J. Appl. Mech. Tech. Phys.. 2012;53:743-750.
[Google Scholar]

[11] Nield D.A., Bejan A., . Convection in Porous Media. New York: Springer-Verlag; 2006.

[12] Partha M.K., Murthy P.V.S.N., Raja Sekhar G.P., . Soret and Dufour effects in a non-Darcy porous medium. J. Heat Transfer. 2006;128:605-610.
[Google Scholar]

[13] Turkyilmazoglu M., . Dual and triple solutions for MHD slip flow of non-newtonian fluid over a shrinking surface. Comput. Fluids. 2012;70:53-58.
[Google Scholar]

[14] Turkyilmazoglu M., . Multiple solutions of hydromagnetic permeable flow and heat for viscoelastic fluid. J. Thermophys. Heat Transfer. 2011;25:595-605.
[Google Scholar]

[15] Turkyilmazoglu M., Pop I., . Soret and heat source effects on the unsteady radiative MHD free convection flow from an impulsively started infinite vertical plate. Int. J. Heat Mass Transfer. 2012;55:7635-7644.
[Google Scholar]

[16] Yih K.A., . Uniform lateral mass flux effect on natural convection of non-Newtonian fluids over a cone in porous media. Int. Commun. Heat Mass Transfer. 1998;25:959-968.
[Google Scholar]

[17] Yih K.A., Huang C.J., . Effect of internal heat generation on free convection flow of non-Newtonian fluids over a vertical truncated cone in porous media: VWT/VWC. J. Air Force Instit. Technol.. 2015;14(1):1-18.
[Google Scholar]