Translate this page into:
Consideration of transient stream/aquifer interaction with the nonlinear Boussinesq equation using HPM
⁎Corresponding author. Tel.: +45 99408457. amin78404@yahoo.com (A. Barari) ab@civil.aau.dk (A. Barari)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 15 July 2010
Peer-review under responsibility of King Saud University.
Abstract
The phenomenon of stream–aquifer interaction was investigated via mathematical modeling using the Boussinesq equation. A new approximate solution of the one-dimensional Boussinesq equation is presented for a semi-infinite aquifer when the hydraulic head at the source is an arbitrary function of time. The differential equations were solved using the method of Homotopy Perturbation. The simplicity and accuracy of the approximation are compared with “exact” solution and illustrated numerically and graphically. The results reveal that the HPM is very effective and simple and provides highly accurate solutions for nonlinear differential equations.
Keywords
Transient stream/aquifer interaction
Mathematical model
Boussinesq equation
Approximate analytical solution
Homotopy Perturbation Method (HPM)
1 Introduction
The study of stream–aquifer hydraulics is of great interest as several flow and contaminant problems can be modeled, understood and quantified. It is an important problem in studying of alluvial aquifer. Alluvial valley aquifers are hydraulically connected to their adjacent channels and exchange flow through the streambed (Perkins and Koussis, 1996). The connection causes ground water levels in these systems to fluctuate with respect to the other. Small changes in the stream elevation can cause a large variation in the groundwater elevation in the aquifer. If the stream stage increases over a short period of time, a flow reversal between the channel and aquifer will occur as a result of a change in the hydraulic gradient (Workman et al., 1997). A flood wave is then propagated into the aquifer and increases bank storage. While the stream is returning to normal flows, the bank storage is released. The quantification of the hydraulics of the stream–aquifer in an alluvial valley require a good knowledge of the controlling input hydro-geological parameters, such as hydraulic conductivity, specific yield, recharge, as well as boundary conditions (Srivastava et al., 2006). Alluvial valley aquifers pose some interesting boundary conditions. One side of the flow domain is the river source/sink, which is fluctuating. As a result of the alluvial valley formation, the other side of the flow domain is the valley wall, which is a no flow boundary condition. The spread of contaminants in stream–aquifer systems from the river to the aquifer or from the aquifer to the river is also of concern (Serrano et al., 2007).
The hydraulics of the stream–aquifer system could be studied via the solution of the Laplace equation subject to a nonlinear free-surface boundary condition, and time-dependent river boundary conditions. In this way, the groundwater flow in an unconfined aquifer may be approximately modeled by the nonlinear Boussinesq equation, assuming Dupuit’s hypothesis of zero resistance to vertical flow is valid, to be a viable alternative to the use of Laplace’s equation. With the Boussinesq equation, the vertical coordinate does not exist, and the free-surface boundary condition is not needed (Serrano and Workman, 1998). The result is a simplified model where the effect of time-dependent river boundary conditions can easily be incorporated into the analysis. Solutions of the Boussinesq equation are applied in catchment hydrology and base flow studies as well as agricultural drainage problems and constructed, subsurface wetlands (Lockington et al., 2000).
The governing equation for one-dimensional, lateral, unconfined groundwater flow similar to the Fig. 1 with Dupuit assumptions is the Boussinesq equation (Bear, 1979):
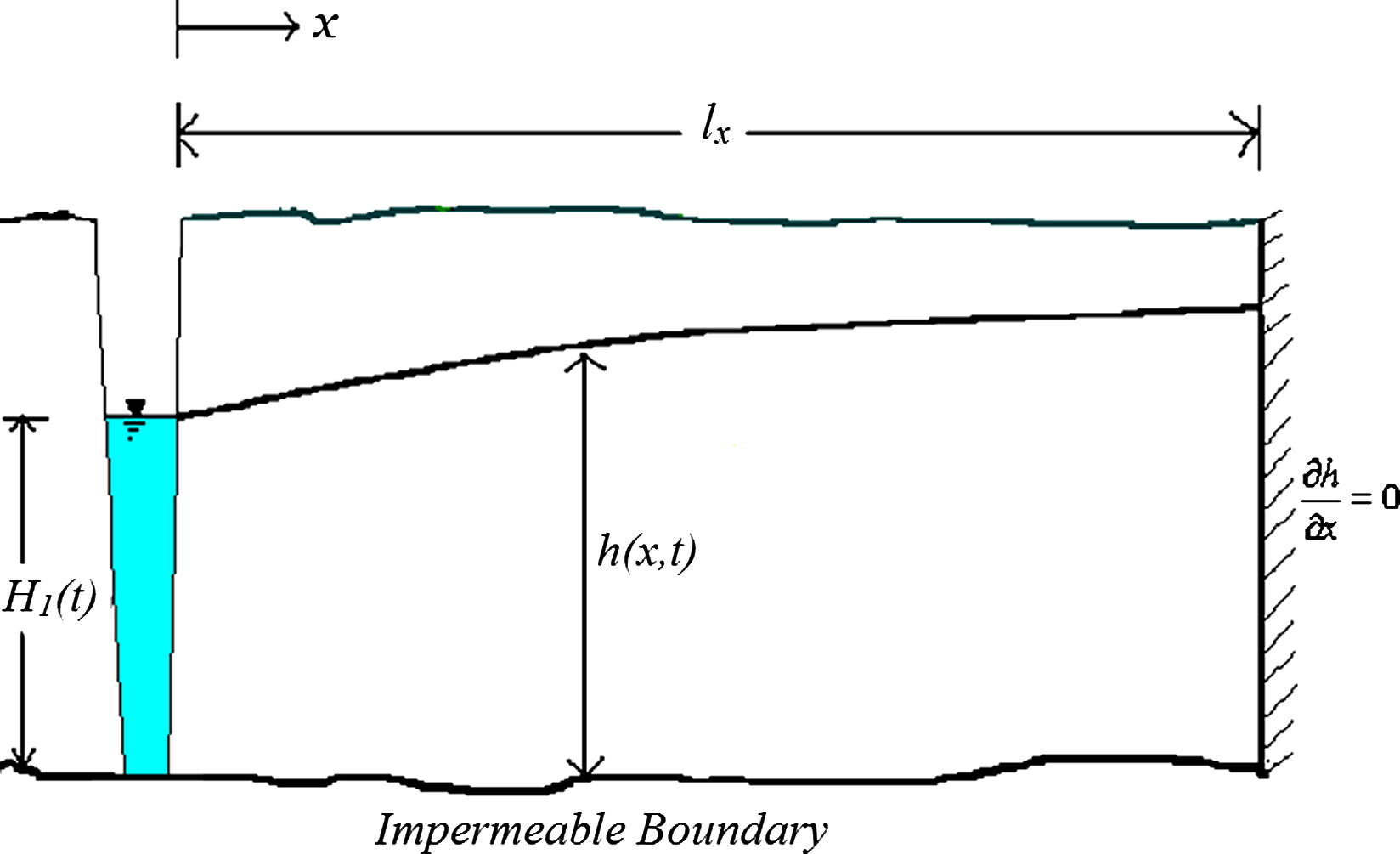
Idealized cross section for the mathematical modeling of transient stream–aquifer interaction.
Until recently, analytical solutions of nonlinear partial differential equations were rare, due to the lack of systematic solution methods. Next section is a very brief review on some analytical methods for this class of equations. One of the most beneficent of these methods is the Homotopy Perturbation Method (HPM). In this paper, we solve the Boussinesq equation by means of HPM and then compare the obtained results with exact solution.
2 Analysis of the Homotopy Perturbation Method
Nonlinear phenomena play a crucial role in applied mathematics and physics. Although it is very easy for us now to find the solutions of some problems by means of computers, it is still rather difficult to solve nonlinear problems either numerically or theoretically or obtaining an exact solution for these problems. So, it is often more useful to have an approximate closed form solution to describe a nonlinear problem. In recent decades, numerical analysis and the approximate methods have been developed considerably for nonlinear partial equations. More recently, some promising analytical techniques have been proposed, such as Lindstedt–Poincaré (He, 2002b,c), Parameter-Expanding (Shou and He, 2007; Ganji et al., 2009a), Parameterized Perturbation (He, 1999), Harmonic Balance (Telli and Kopmaz, 2006; Gottlieb, 2006), Linearized Perturbation (He, 2003), Energy Balance (He, 2002a; Momeni et al., 2010; Ganji et al., 2009), Variational Approach (Xu, 2008; He, 2004; Ganji et al., 2008), Max–Min (Babazadeh et al., 2010; Ibsen et al., 2010), Exp-Function (Ganji et al., 2009b; Mohyud-Din et al., 2010), Amplitude–Frequency Formulation (Ganji et al., 2010b), Adomian Decomposition (Mirgolbabaei et al., 2010; Wazwaz, 2005), Variational Iteration (Faraz et al., 2011; Babaelahi et al., 2009; Barari et al., 2008a,b; Fouladi et al., 2010), and the Homotopy Perturbation Method (He, 2000, 2005; Ghotbi et al., 2008; Omidvar et al., 2010; Miansari et al., 2010; Ganji et al., 2009c, 2010a).
The Homotopy Perturbation Method is a combination of the classical perturbation and Homotopy technique. To explain this, we consider the following nonlinear differential equation:
Subject to boundary condition:
In case that the nonlinear Eq. (2) has no “small parameter”, we can construct the following Homotopy:
Where,
In Eq. (6),
is an embedding parameter and u0 is the first approximation that satisfies the boundary condition. We can assume that the solution of Eq. (5) can be written as a power series in p, as follows:
Then the best approximation for the solution is:
3 Analytical solution to the nonlinear transient groundwater flow
Assume that the aquifer is in contact with a drainage canal at x = 0 and it is bounded by a condition of zero flux at the impervious surface at x = 3 so, the horizontal dimension of the aquifer is lx = 3 (use a dimensionless length scale for convenience). Initial water table in the aquifer is express by:
So, the water level at x = 3 is H2 (t) = 3/2. Note that the initial depth at x = 0 is taken as zero. The depth of the canal located at x = 0 varies with time by
We aim to solve the dimensionless Boussinesq equation (Parlange et al., 2000):
Note that we take K/S = 1. With the initial condition Eq. (9), the boundary condition Eq. (10) at x = 0 and the condition of zero flux at the impervious surface x = 3 together (Parlange et al., 2000):
The exact solution of Eq. (9)–(12) is Parlange et al., 2000,:
Using HPM for solving Eq. (11), we have:
We consider
as follows:
Assuming
and some simplification and rearranging based on powers of p-terms, we have:
Solving Eq. (16)–(19) (n = 30), we have:
The solution of Eq. (11) when
will be as follows:
To assess the efficiency of the HPM, the results together with the exact solution are given in Tables 1 and 2. From Fig. 2, it can be seen that the two graphs are similar such that the error is negligible. The exact and HPM solutions whose results are given in Tables 1 and 2 are also compared by the consequent results of the two different methods as shown in Figs. 1 and 2.
xi
t = 0.25
HPM
Exact
|Error|
0.00
0.19247665008383366747
0.19247665008383366772
2.5 E-19
0.20
0.34714331675050033416
0.34714331675050033439
2.3 E-19
0.40
0.49114331675050033417
0.49114331675050033439
2.2 E-19
0.60
0.62447665008383366757
0.62447665008383366772
1.5 E-19
0.80
0.74714331675050033425
0.74714331675050033439
1.4 E-19
1.00
0.85914331675050033425
0.85914331675050033439
1.4 E-19
1.20
0.96047665008383366764
0.96047665008383366772
8.0 E-20
1.40
1.05114331675050033430
1.05114331675050033440
1.0 E-19
1.60
1.13114331675050033420
1.13114331675050033440
2.0 E-19
1.80
1.20047665008383366750
1.20047665008383366770
2.0 E-19
2.00
1.25914331675050033430
1.25914331675050033440
1.0 E-19
2.20
1.30714331675050033430
1.30714331675050033440
1.0 E-19
2.40
1.34447665008383366760
1.34447665008383366770
1.0 E-19
2.60
1.37114331675050033450
1.37114331675050033440
1.0 E-19
2.80
1.38714331675050033440
1.38714331675050033440
0.00000
3.00
1.39247665008383366770
1.39247665008383366770
0.00000
xi
t = 0.50
HPM
Exact
|Error|
0.00
0.31037069665646221117
0.31037069710444830360
4.4798609243 E-10
0.20
0.43925958560536966603
0.43925958599333719249
3.8796752647 E-10
0.40
0.55925958566124902048
0.55925958599333719249
3.3208817202 E-10
0.60
0.67037069682410027460
0.67037069710444830360
2.8034802900 E-10
0.80
0.77259291909392342844
0.77259291932667052583
2.3274709740 E-10
1.00
0.86592625247071848192
0.86592625266000385916
1.8928537726 E-10
1.20
0.95037069695448543506
0.95037069710444830360
1.4996286852 E-10
1.40
1.02592625254522428790
1.02592625266000385920
1.1477957130 E-10
1.60
1.09259291924293504030
1.09259291932667052590
8.3735485600 E-11
1.80
1.15037069704761769250
1.15037069710444830360
5.6830611100 E-11
2.00
1.19925958595927224440
1.19925958599333719250
3.4064948100 E-11
2.20
1.23925958597789869590
1.23925958599333719250
1.5438496700 E-11
2.40
1.27037069710349704700
1.27037069710444830360
9.5125640000 E-13
2.60
1.29259291933606729790
1.29259291932667052580
9.3967721000 E-12
2.80
1.30592625267560944830
1.30592625266000385920
1.5605589200 E-11
3.00
1.31037069712212349850
1.31037069710444830360
1.7675194800 E-11
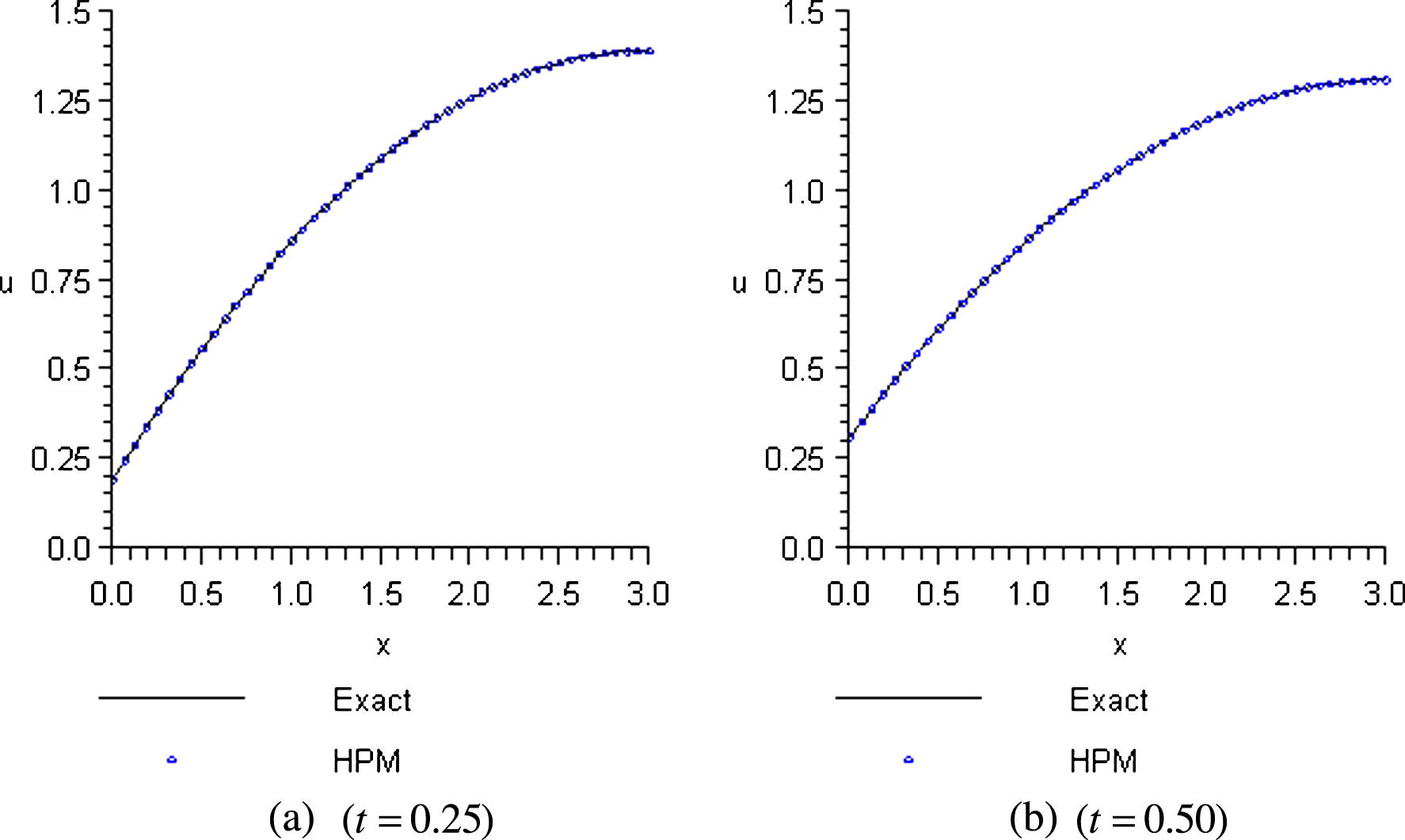
Comparison of the HPM and exact solutions for n = 30.
4 Conclusions
In this article the effect of highly fluctuating stream stage on the adjacent alluvial valley aquifer is studied with a new analytical solution to the nonlinear transient groundwater flow equation subject to stochastic conductivity and time varying boundary conditions (Fig. 3). The drainage system under consideration is modeled by nonlinear Boussinesq equation. An approximate closed form solution constrained by initial and boundary conditions of the system is presented which can be used for prediction of the transient water table via the Homotopy Perturbation Method (HPM). For illustration the HPM solution compared with the exact one numerically and graphically. It is apparently seen that HPM is a powerful and efficient technique for solving large class of linear and nonlinear, ordinary or partial, deterministic or stochastic differential equations arising in various fields of science and engineering and present a rapid convergence for the solutions.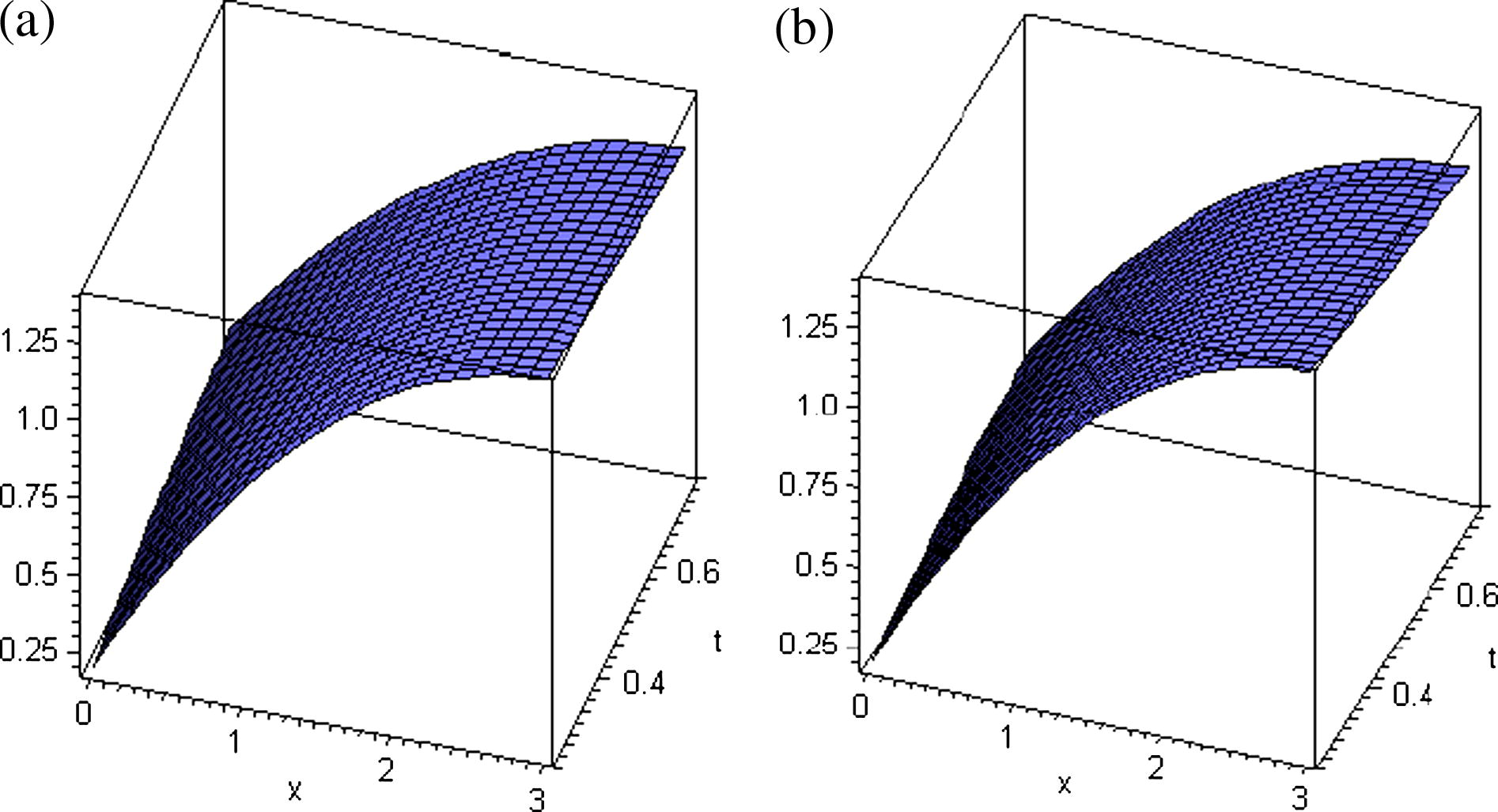
Three-dimensional plot for the exact and HPM solutions for n = 30. (a) Exact and (b) HPM.
References
- Babaelahi, M., Ganji, D.D., Joneidi, A.A., 2009. Analysis of velocity equation of steady flow of a viscous incompressible fluid in channel with porous walls. International Journal for Numerical Methods in Fluids. doi:10.1002/fld.2114.
- Babazadeh, H., Domairry, G., Barari, A., Azami, R., Davodi, A.G., 2010. Numerical analysis of strongly nonlinear oscillation systems using He’s max–min method, Frontiers of Mechanical Engineering in China. doi:10.1007/s11465-010-0029-6.
- Application of Homotopy Perturbation Method and variational iteration method to nonlinear oscillator differential equations. Acta Applicandae Mathematicae. 2008;104:161-171.
- [Google Scholar]
- An approximate solution for boundary value problems in structural engineering and fluid mechanics. Journal of Mathematical Problems in Engineering 2008:1-13. (Article ID 394103)
- [Google Scholar]
- Hydraulics of Groundwater. New York, NY: McGraw-Hill; 1979.
- Faraz, Naeem, Khan, Yasir, Yildirim, Ahmet, 2011. Analytical approach to two-dimensional viscous flow with a shrinking sheet via variational iteration algorithm-II, Journal of King Saud University – Science. 23 (1), 77–81.
- Highly nonlinear temperature dependent fin analysis by variational iteration method. Journal of Heat Transfer Research. 2010;41(2):155-165.
- [Google Scholar]
- Ganji, S.S., Karimpour, S., Ganji, D.D., Ganji, Z.Z., 2009. Periodic solution for strongly nonlinear vibration systems by energy balance method. Acta Applicandae Mathematicae. doi:10.1007/s10440-008-9283-6.
- Variational approach method for nonlinear oscillations of the motion of a rigid rod rocking back and cubic–quintic duffing oscillators. Progress in Electromagnetics Research M. 2008;4:23.
- [Google Scholar]
- Ganji, S.S., Sfahani, M.G., Modares Tonekaboni, S.M., Moosavi, A.K., Ganji, D.D., 2009. Higher-order solutions of coupled systems using the parameter expansion method. Mathematical Problems in Engineering 2009, p. 20 (Article ID 327462). doi:10.1155/2009/327462.
- Application of exp–function method to reduced Ostrovsky equation and Kuramoto–Sivashinsky equation. Asian–European Journal of Mathematics. 2009;2(4):567-578.
- [Google Scholar]
- Applications of He’s homotopy perturbation method to obtain second-order approximations of the coupled two-degree-of-freedom systems. International Journal of Nonlinear Sciences and Numerical Simulation. 2009;10(3):303.
- [Google Scholar]
- Ganji, D.D., Houman B., Rokni, Ganji, S.S., Sfahani, M.G., 2010. Approximate traveling wave solutions for coupled Whitham–Broer–Kaup shallow water. Advances in Engineering Software. doi:10.1016/j.advengsoft.2010.05.008.
- Ganji, S.S., Ganji, D.D., Sfahani, M.G., Karimpour, S., 2010. Application of AFF and HPM to the systems of strongly nonlinear oscillation. Current Applied Physics. doi:10.1016/j.cap.2010.03.015.
- Solving ratio-dependent predator–prey system with constant effort harvesting using Homotopy Perturbation Method. Journal of Mathematical Problems in Engineering 2008:1-8. (Article ID 945420)
- [Google Scholar]
- Harmonic balance approach to limit cycles for nonlinear jerk equations. Journal of Sound and Vibration. 2006;297:243.
- [Google Scholar]
- Some new approaches to duffing equation with strongly and high order nonlinearity (II) parameterized perturbation technique. Communications in Nonlinear Science and Numerical Simulation. 1999;4:81.
- [Google Scholar]
- Homotopy perturbation method for bifurcation of nonlinear problems. International Journal of Non-Linear Mechanics. 2000;35(1):37.
- [Google Scholar]
- Preliminary report on the energy balance for nonlinear oscillations. Mechanics Research Communications. 2002;29:107.
- [Google Scholar]
- Modified Lindstedt–Poincare methods for some strongly nonlinear oscillations, Part I: a new transformation. International Journal of Non-linear Mechanics. 2002;37:315.
- [Google Scholar]
- Modified Lindstedt–Poincare methods for some strongly nonlinear oscillations, Part II: expansion of a constant. International Journal of Non–linear Mechanics. 2002;37:309.
- [Google Scholar]
- Linearized perturbation technique and its applications to strongly nonlinear oscillators. Computers and Mathematics with Applications. 2003;45:1.
- [Google Scholar]
- Variational principles for some nonlinear partial differential equations with variable coefficients. Chaos, Solitons and Fractals. 2004;19(4):847.
- [Google Scholar]
- Homotopy perturbation method for bifurcation on nonlinear problems. International Journal of Non-Linear Sciences and Numerical Simulation. 2005;6:207.
- [Google Scholar]
- Analysis of highly nonlinear oscillation systems using He’s max–min method and comparison with homotopy analysis and energy balance methods. Sadhana. 2010;35(4):1-16.
- [Google Scholar]
- Similarity solution of the Boussinesq equation. Advances in Water Resources. 2000;23:725-729.
- [Google Scholar]
- Analysis of Blasius equation for flat-plate flow with infinite boundary value. International Journal for Computational Methods in Engineering Science and Mechanics. 2010;11(2):79-84.
- [Google Scholar]
- Numerical solution of boundary layer flow and convection heat transfer over a flat plate. Archives of Civil and Mechanical Engineering. 2010;10(2):41-51.
- [Google Scholar]
- Mohyud-Din, Syed Tauseef, Noor, Muhammad Aslam, Noor, Khalida Inayat, 2010. Exp-function method for traveling wave solutions of modified Zakharov–Kuznetsov equation. Journal of King Saud University – Science. 22 (4), 213–216.
- Momeni, M., Jamshidi, N., Barari, A., Ganji, D.D., 2010, Application of He’s Energy Balance Method to Duffing Harmonic Oscillators, International Journal of Computer Mathematics. doi:10.1080/00207160903337239.
- New class of solutions for water infiltration problems in unsaturated soils. Geomechanics and Geoengineering: An International Journal. 2010;5(2):127-135.
- [Google Scholar]
- On an exact analytical solution of the Boussinesq equation. Transport in Porous Media. 2000;39:339-345.
- [Google Scholar]
- Stream–aquifer interaction model with diffusive wave routing. ASCE Journal of Hydraulic Engineering. 1996;122(4):210-217.
- [Google Scholar]
- Modeling transient stream/aquifer interaction with the non-linear Boussinesq equation and its analytical solution. Journal of Hydrology. 1998;206:245-255.
- [Google Scholar]
- Models of nonlinear stream aquifer transients. Journal of Hydrology. 2007;336:199-205.
- [Google Scholar]
- Application of parameter-expanding method to strongly nonlinear oscillators. International Journal of Non-Linear Science and Numerical Simulation. 2007;8(1):121.
- [Google Scholar]
- Stochastic modeling of transient stream–aquifer interaction with the nonlinear Boussinesq equation. Journal of Hydrology. 2006;328:538-547.
- [Google Scholar]
- Free vibrations of a mass grounded by linear and nonlinear springs in series. Journal of Sound and Vibration. 2006;289:689-710.
- [Google Scholar]
- Wazwaz, A.M., 2005. Adomian decomposition method for a reliable treatment of the Bratu-type equations. Journal of Applied Mathematics and Computing 166, 652.
- Development and application of an analytical model of stream/aquifer interaction. Journal of Hydrology. 1997;200:149-163.
- [Google Scholar]
- Variational approach to Solitons of nonlinear dispersive K(m,n) equations. Chaos, Solitons and Fractals. 2008;37:137.
- [Google Scholar]







