Approximations for higher order boundary value problems using non-polynomial quadratic spline based on off-step points

Shahna; Arshad Khan

doi:10.1016/j.jksus.2018.06.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

31 (

); 737-745

doi:

10.1016/j.jksus.2018.06.004

Approximations for higher order boundary value problems using non-polynomial quadratic spline based on off-step points

Shahna, Arshad Khan^⁎

Department of Mathematics, Jamia Millia Islamia, New Delhi 110025, India

⁎Corresponding author. akhan2@jmi.ac.in (Arshad Khan)

Received: 2017-12-28, Accepted: 2018-6-14, Published: 2018-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Non-polynomial quadratic spline method based on off-step points is used to develop a numerical algorithm for obtaining an approximate solution of higher even order boundary value problems. For the employment of the method, decomposition procedure is used. Higher order boundary value problems are reduced into the corresponding system of second order boundary value problems. Convergence analysis of the method is also discussed. Seven numerical examples are given to illustrate the applicability and efficiency of new method. It is also shown that the new method gives approximations, which are better than those produced by other existing fourth order methods except higher degree splines.

Keywords

Higher order

Singular

Non-linear

Second order

Non-polynomial quadratic spline

Off-step points

Convergence analysis

Show Related Articles from PubMed

1 Introduction

The higher order boundary value problems have been studied as their mathematical applications are in diversified applied sciences. Conditions for the existence and uniqueness of solutions of the higher-order boundary-value problems was discussed in Agarwal (1986, pp. 89–93). Several numerical algorithms have been developed to determine the approximate solution of higher-order boundary-value problems. In this paper, we consider the higher order boundary value problems of the form

(1)

y^{(2 N)} = f (x, y, y^{(1)}, y^{(2)}, y^{(3)} \dots, y^{(2 N - 1)}), a ⩽ x ⩽ b, where N = 2, 3, 4

subject to the boundary conditions

(2)

y (a) = λ_{1}, y^{(2)} (a) = λ_{2}, \dots, y^{(2 N - 2)} (a) = λ_{N}, y (b) = δ_{1}, y^{(2)} (b) = δ_{2}, \dots, y^{(2 N - 2)} (b) = δ_{N} .

We rewrite the Eq. (1) and (2) as system of second order boundary value problems:

(3)

y_{i}^{(2)} (x) = F_{i} (x, y_{1}, y_{2}, \dots, y_{i}, \dots, y_{N}, y_{1}^{(1)}, y_{2}^{(1)}, \dots, y_{i}^{(1)}, \dots, y_{N}^{(1)}), i = 1, 2, \dots, N

subject to the modified boundary conditions;

(4)

y_{i} (a) = λ_{i}, y_{i} (b) = δ_{i}, i = 1, 2, \dots, N .

We assume that, for

a < x < b

, for

m = 1, 2, \dots, N, i = 1, 2, \dots, N

and

- \infty < y_{m} < y_{m}^{(1)} < \infty

$F_{i}$ is continous,
$\frac{\partial F_{i}}{\partial y_{m}}$ and $\frac{\partial F_{i}}{\partial y_{m}^{(1)}}$ exist and are continous,
$\frac{\partial F_{i}}{\partial y_{m}} > 0$ and $| \frac{\partial F_{i}}{\partial y_{m}} | ⩽ C$ , for some constant C.

These conditions from Keller (1968, (pp. 6–8 and 15–16)) ensure the existence and uniqueness of the solution of the above boundary value problem (3) and (4).

Here, our aim is to solve the boundary value problems of fourth, sixth and eighth orders of the form (1) and (2) with $N = 2, 3$ and 4. There are various methods available in literature for solving these boundary value problems. For example, non-polynomial spline technique was used by Siddiqi and Akram (2007) to determine the solution of eighth-order and Akram and Siddiqi (2006) to determine the solution of sixth order boundary value problems. Meŝtroviĉ (2007) used modified decomposition method for the solution of eighth-order boundary value problems. Islam et al. (2008) used non-polynomial splines approach to the solution of sixth-order non-linear boundary value problems of the form (1) and (2). Solution of special sixth order boundary-value problems was given by Boutayeb and Twizell (1992). Khan and Khandelwal (2012) used parametric septic splines and Jalilian and Rashidinia (2010) used nonic-spline for the solution of non-linear sixth-order two point boundary value problems.

The above system involves the second order boundary value problems. Polynomial and non-polynomial spline approach (Ramadan et al., 2007), quintic non-polynomial spline method (Srivastava et al., 2011), cubic spline method (Al-Said, 2001), non-polynomial spline (Jha and Mohanty, 2011; Mohanty et al., 2017), spline in tension (Mohanty et al., 2005), spline in compression (Mohanty et al., 2004) were used in previous papers to solve second order boundary value problems. Here, we use lower degree non-polynomial quadratic spline for solving system of second order boundary value problems. This non-polynomial quadratic spline is based on off-step points.

When linear BVPs are implemented over the method, we get a linear system of equations which are solved by using LU decomposition method and when non-linear BVPs are implemented we get a non-linear system which is solved by Block Newton Raphson method. The outline of this paper is organised into five sections. In Section 2, consistency relation and in Section 2.1 truncation error and end equations are discussed. In Section 3, application of the method to solve the sixth order BVPs is given. Section 4 gives the convergence analysis of the method. In Section 5, seven examples are considered to illustrate the accuracy and performance of the method presented in the paper.

2 Non-polynomial quadratic spline function

To develop the new method based on off-step points, we divide the interval $[a, b]$ into $n + 1$ subintervals, s.t. $a = x_{0} < x_{1 / 2} < x_{3 / 2} < \dots < x_{n - 1 / 2} < x_{n} = b .$ We introduce a finite set of grid points $x_{i}$ as $x_{i} = a + (i - 1 / 2) h, i = 0, 1, \dots, n and h = (b - a) / n .$

Let

(5)

P_{i} (x) = a_{i} \cos k (x - x_{i}) + b_{i} e^{k (x - x_{i})} + c_{i}

be a non-polynomial quadratic spline

P_{i}

is defined on [a, b] which interpolates the uniform mesh points

x_{i}

depends on a parameter k, reduces to an ordinary quadratic spline in [a,b] as

k ⟶ 0

and

k > 0

To determine the coefficients $a_{i}, b_{i}$ and $c_{i}$ , we define the following interpolatory conditions as

(6)

P_{i} (x_{i + 1 / 2}) = y_{i + 1 / 2}, P_{i}^{(1)} (x_{i}) = Q_{i}, P_{i}^{(2)} (x_{i + 1 / 2}) = R_{i + 1 / 2}, i = 0, 1, \dots, n

By using the conditions (6) we calculated the coefficients as

\begin{matrix} a_{i} = & - \frac{1}{k^{2}} R_{i + 1 / 2} \sec (\frac{θ}{2}) + \frac{1}{k} Q_{i} e^{\frac{θ}{2}} \sec (\frac{θ}{2}) \\ b_{i} = & \frac{1}{k} Q_{i} \\ c_{i} = & y_{i + 1 / 2} + \frac{1}{k^{2}} R_{i + 1 / 2} - \frac{2}{k} Q_{i} e^{\frac{θ}{2}} \end{matrix}

where,

θ = kh .

Using the continuity of first derivative, $P_{i - 1}^{(m)} (x_{i}) = P_{i}^{(m)} (x_{i}), m = 0, 1$ the following consistency relation is derived

(7)

\begin{matrix} α_{1} y_{i - 3 / 2} + β_{1} y_{i - 1 / 2} + γ_{1} y_{i + 1 / 2} \\ = h^{2} (α_{2} R_{i - 3 / 2} + β_{2} R_{i - 1 / 2} + γ_{2} R_{i + 1 / 2}), & i = 2, 3, \dots, n - 1 \end{matrix}

where,

\begin{matrix} α_{2} = & \frac{1}{θ^{2}} [e^{2 θ} + [(e^{\frac{θ}{2}} - e^{θ}) \sin θ \sec \frac{θ}{2} + e^{\frac{3 θ}{2}} (1 + \cos θ \csc θ) - e^{θ} \cos θ \sec \frac{θ}{2}] e^{\frac{θ}{2}} \sin θ \sec \frac{θ}{2}] \\ β_{2} = & \frac{1}{θ^{2}} [- 1 + e^{θ} + e^{2 θ} + [e^{θ} \sec \frac{θ}{2} - e^{\frac{3 θ}{2}} \csc θ - e^{\frac{θ}{2}} \sin θ \sec \frac{θ}{2} + \cos θ \sec \frac{θ}{2} \\ + \sin θ \sec \frac{θ}{2} - e^{\frac{θ}{2}} - e^{\frac{θ}{2}} \cos θ \csc θ] e^{\frac{θ}{2}} \sin θ \sec \frac{θ}{2}] \\ γ_{2} = & \frac{1}{θ^{2}} [- e^{θ} - e^{\frac{θ}{2}} \sin θ \sec^{2} \frac{θ}{2} + e^{\frac{θ}{2}} \sin θ \sec \frac{θ}{2} + e^{θ} \sec \frac{θ}{2}] \\ γ_{1} = & - e^{θ} + e^{\frac{θ}{2}} \sin θ \sec \frac{θ}{2} \\ α_{1} = & {[γ_{1}]}^{2} \\ β_{1} = & γ_{1} - {[γ_{1}]}^{2} . \end{matrix}

Remark 1

Our method reduces to Ramadan et al. (2007) based on quadratic spline when

(8)

(α_{1}, β_{1}, γ_{1}, α_{2}, β_{2}, γ_{2},) = (1, - 2, 1, \frac{1}{8}, \frac{6}{8}, \frac{1}{8}) .

2.1

2.1 Truncation error

Expanding the scheme (7) by using Taylor series, we obtained the following truncation error

(9)

\begin{matrix} t_{i} = & [α_{1} + β_{1} + γ_{1}] y_{i} + [\frac{- 3 α_{1} - β_{1} + γ_{1}}{2}] {hy}_{i}^{(1)} + h^{2} [\frac{9 α_{1} + β_{1} + γ_{1}}{2^{2} 2!} - (α_{2} + β_{2} + γ_{2})] y_{i}^{(2)} \\ + h^{3} [\frac{- 27 α_{1} - β_{1} + γ_{1}}{2^{3} 3!} - (\frac{- 3 α_{2} - β_{2} + γ_{2}}{2})] y_{i}^{(3)} + h^{4} [\frac{81 α_{1} + β_{1} + γ_{1}}{2^{4} 4!} - (\frac{9 α_{2} + β_{2} + γ_{2}}{2^{2} 2!})] y_{i}^{(4)} \\ + h^{5} [\frac{- 243 α_{1} - β_{1} + γ_{1}}{2^{5} 5!} - (\frac{- 27 α_{2} - β_{2} + γ_{2}}{2^{3} 3!})] y_{i}^{(5)} + h^{6} [\frac{729 α_{1} + β_{1} + γ_{1}}{2^{6} 6!} - (\frac{81 α_{2} + β_{2} + γ_{2}}{2^{4} 4!})] y_{i}^{(6)} \\ + O (h^{7}), i = 2, 3, \dots, n - 1 . \end{matrix}

For different values of parameters, we get the second as well as fourth order method. For $α_{2} + β_{2} + γ_{2} = 1$ and $α_{2} = γ_{2}$ we get the second order method. For the choice of parameters $(α_{1}, β_{1}, γ_{1}, α_{2}, β_{2}, γ_{2}) = (1, - 2, 1, 1 / 12, 10 / 12, 1 / 12)$ we get the fourth order method.

Eq. (7) forms a system of $(n - 2)$ linear equations in n unknowns $y_{i - 1 / 2}, i = 1, 2, \dots, n$ . Thus, we need two more equations, one at each end of range of integration. These boundary conditions are obtained by using method of undetermined coefficients.

The equations for second order method are given by Islam et al. (2006) as

(10)

2 y_{0} - 3 y_{1 / 2} + y_{3 / 2} = \frac{h^{2}}{24} [15 R_{1 / 2} + 3 R_{3 / 2}] + O (h^{4}), i = 1

(11)

2 y_{n} - 3 y_{n - 1 / 2} + y_{n - 3 / 2} = \frac{h^{2}}{24} [15 R_{n - 1 / 2} + 3 R_{n - 3 / 2}] + O (h^{4}), i = n

The truncation error for second order method for $(α_{1}, β_{1}, γ_{1}, α_{2}, β_{2}, γ_{2}) = (1, - 2, 1, 1 / 8, 6 / 8, 1 / 8)$ is given as follows: $t_{i} = \{\begin{matrix} - \frac{1}{64} h^{4} y_{0}^{(4)} + O (h^{5}), & i = 1 \\ - \frac{1}{24} h^{4} y_{i}^{(4)} + O (h^{5}), & i = 2, 3, \dots, n - 1 \\ - \frac{1}{64} h^{4} y_{n}^{(4)} + O (h^{5}), & i = n \end{matrix}$ and for fourth order method are obtained as

(12)

2 y_{0} - 3 y_{1 / 2} + y_{3 / 2} = \frac{h^{2}}{384} [233 R_{1 / 2} + 63 R_{3 / 2} - 9 R_{5 / 2} + R_{7 / 2}] + O (h^{6}), i = 1

(13)

2 y_{n} - 3 y_{n - 1 / 2} + y_{n - 3 / 2} = \frac{h^{2}}{384} [233 R_{n - 1 / 2} + 63 R_{n - 3 / 2} - 9 R_{n - 5 / 2} + R_{n - 7 / 2}] + O (h^{6}), i = n .

The truncation error for the fourth order method is given as follows: $t_{i} = \{\begin{matrix} \frac{11}{7680} h^{6} y_{0}^{(6)} + O (h^{7}), & i = 1 \\ - \frac{1}{240} h^{6} y_{i}^{(6)} + O (h^{7}), & i = 2, 3, \dots, n - 1 \\ \frac{11}{7680} h^{6} y_{n}^{(6)} + O (h^{7}), & i = n . \end{matrix}$

3 Application of the algorithm to the higher order boundary value problems for $N = 3$

We consider a sixth order boundary value problem i.e N = 3 in (1–2) of the form

(14)

y^{(6)} (x) = a (x) y^{(5)} (x) + b (x) y^{(4)} (x) + c (x) y^{(3)} (x) + d (x) y^{(2)} (x) + e (x) y^{(1)} (x) + f (x) y (x) + g (x)

subject to boundary conditions

\begin{matrix} y (a) = & λ_{1}, y^{(2)} (a) = λ_{2}, y^{(4)} (a) = λ_{3} \\ y (b) = & δ_{1}, y^{(2)} (b) = δ_{2}, y^{(4)} (b) = δ_{3} \end{matrix}

where

λ_{i}

and

δ_{i} (i = 1, 2, 3)

are finite real constants and the functions

a (x), b (x), c (x), d (x), e (x), f (x)

and

g (x)

are continuous on

[a, b]

. We decompose the above problem into the system of second order boundary value problems as follows:

(15)

y^{(2)} (x) = u (x),

(16)

u^{(2)} (x) = v (x),

(17)

v^{(2)} (x) = a (x) v^{(1)} (x) + b (x) v (x) + c (x) u^{(1)} (x) + d (x) u (x) + e (x) y^{(1)} (x) + f (x) y (x) + g (x) . \equiv F (x, y, u, v, y^{(1)}, u^{(1)}, v^{(1)})

subject to modified boundary conditions

(18)

y (a) = λ_{1}, y (b) = δ_{1},

(19)

u (a) = λ_{2}, u (b) = δ_{2},

(20)

v (a) = λ_{3}, v (b) = δ_{3} .

Therefore by implementing the scheme (7) on the boundary value problems (15)–(17), we get the following system of equations

(21)

α_{1} y_{i - 3 / 2} + β_{1} y_{i - 1 / 2} + γ_{1} y_{i + 1 / 2} = h^{2} (α_{2} u_{i - 3 / 2} + β_{2} u_{i - 1 / 2} + γ_{2} u_{i + 1 / 2}), i = 2, 3, \dots, n - 1

(22)

α_{1} u_{i - 3 / 2} + β_{1} u_{i - 1 / 2} + γ_{1} u_{i + 1 / 2} = h^{2} (α_{2} v_{i - 3 / 2} + β_{2} v_{i - 1 / 2} + γ_{2} v_{i + 1 / 2}), i = 2, 3, \dots, n - 1

(23)

α_{1} v_{i - 3 / 2} + β_{1} v_{i - 1 / 2} + γ_{1} v_{i + 1 / 2} = h^{2} (α_{2} F_{i - 3 / 2} + β_{2} F_{i - 1 / 2} + γ_{2} F_{i + 1 / 2}), i = 2, 3, \dots, n - 1

The fourth order method is obtained by using the parameters $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$ in the scheme (21)–(23) and replacing (23) by the following as: $α_{1} v_{i - 3 / 2} + β_{1} v_{i - 1 / 2} + γ_{1} v_{i + 1 / 2} = h^{2} (\frac{1}{12} F_{i - 3 / 2} + \frac{10}{12} {\tilde{F}}_{i - 1 / 2} + \frac{1}{12} F_{i + 1 / 2}), i = 2, 3, \dots, n - 1$ where, $\begin{matrix} F_{i - 3 / 2} = & F (x, y_{i - 3 / 2}, u_{i - 3 / 2}, v_{i - 3 / 2}, y_{i - 3 / 2}^{'}, u_{i - 3 / 2}^{'}, v_{i - 3 / 2}^{'}), \\ F_{i - 1 / 2} = & F (x, y_{i - 1 / 2}, u_{i - 1 / 2}, v_{i - 1 / 2}, y_{i - 1 / 2}^{'}, u_{i - 1 / 2}^{'}, v_{i - 1 / 2}^{'}), \\ F_{i + 1 / 2} = & F (x, y_{i + 1 / 2}, u_{i + 1 / 2}, v_{i + 1 / 2}, y_{i + 1 / 2}^{'}, u_{i + 1 / 2}^{'}, v_{i + 1 / 2}^{'}), \\ {\tilde{F}}_{i - 1 / 2} = & F (x, y_{i - 1 / 2}, u_{i - 1 / 2}, v_{i - 1 / 2}, {\tilde{y}}_{i - 1 / 2}^{'}, {\tilde{u}}_{i - 1 / 2}^{'}, {\tilde{v}}_{i - 1 / 2}^{'}), \end{matrix}$ and the finite difference approximations to derivatives are $\begin{matrix} y_{i - 1 / 2}^{'} = & \frac{y_{i + 1 / 2} - y_{i - 3 / 2}}{2 h}, \\ y_{i - 3 / 2}^{'} = & \frac{- 3 y_{i - 3 / 2} + 4 y_{i - 1 / 2} - y_{i + 1 / 2}}{2 h}, \\ y_{i + 1 / 2}^{'} = & \frac{y_{i - 3 / 2} - 4 y_{i - 1 / 2} + 3 y_{i + 1 / 2}}{2 h}, \\ {\tilde{y}}_{i - 1 / 2}^{'} = & \frac{y_{i + 1 / 2} - y_{i - 3 / 2}}{2 h} - \frac{h}{20} (R_{i + 1 / 2} - R_{i - 3 / 2}) . \end{matrix}$ The fourth order approximations of derivatives involved in the end Eqs. (12) and (13) are as follows: $\begin{matrix} {hy}_{1 / 2}^{(1)} = & - \frac{32}{35} y_{0} + \frac{1}{6} y_{1 / 2} + y_{3 / 2} - \frac{3}{10} y_{5 / 2} + \frac{1}{21} y_{7 / 2} \\ {hy}_{3 / 2}^{(1)} = & \frac{32}{105} y_{0} - y_{1 / 2} + \frac{1}{6} y_{3 / 2} + \frac{3}{5} y_{5 / 2} - \frac{1}{14} y_{7 / 2} \\ {hy}_{5 / 2}^{(1)} = & - \frac{32}{105} y_{0} + \frac{5}{6} y_{1 / 2} - \frac{5}{3} y_{3 / 2} + \frac{9}{10} y_{5 / 2} + \frac{5}{21} y_{7 / 2} \\ {hy}_{7 / 2}^{(1)} = & \frac{32}{35} y_{0} - \frac{7}{3} y_{1 / 2} + \frac{7}{2} y_{3 / 2} - \frac{21}{5} y_{5 / 2} + \frac{89}{42} y_{7 / 2} . \end{matrix}$ Here, we derive only the second order method. On combining (21)–(23), we obtain the vector difference equation for the boundary value problem (15)–(17) as

(24)

A_{i} W_{i - 3 / 2} + B_{i} W_{i - 1 / 2} + C_{i} W_{i + 1 / 2} = H_{i}

which are as follows:

[\begin{matrix} {ai}_{11} & {ai}_{12} & {ai}_{13} \\ {ai}_{21} & {ai}_{22} & {ai}_{23} \\ {ai}_{31} & {ai}_{32} & {ai}_{33} \end{matrix}] [\begin{matrix} y_{i - 3 / 2} \\ u_{i - 3 / 2} \\ v_{i - 3 / 2} \end{matrix}] + [\begin{matrix} {bi}_{11} & {bi}_{12} & {bi}_{13} \\ {bi}_{21} & {bi}_{22} & {bi}_{23} \\ {bi}_{31} & {bi}_{32} & {bi}_{33} \end{matrix}] [\begin{matrix} y_{i - 1 / 2} \\ u_{i - 1 / 2} \\ v_{i - 1 / 2} \end{matrix}] + [\begin{matrix} {ci}_{11} & {ci}_{12} & {ci}_{13} \\ {ci}_{21} & {ci}_{22} & {ci}_{23} \\ {ci}_{31} & {ci}_{32} & {ci}_{33} \end{matrix}] [\begin{matrix} y_{i + 1 / 2} \\ u_{i + 1 / 2} \\ v_{i + 1 / 2} \end{matrix}] = [\begin{matrix} h_{i 1} \\ h_{i 2} \\ h_{i 3} \end{matrix}], i = 2, 3, \dots, n - 1

where,

\begin{matrix} {ai}_{11} = & - α_{1}, {ai}_{12} = h^{2} α_{2}, {ai}_{13} = 0, {ai}_{21} = 0, \\ {ai}_{22} = & - α_{1}, {ai}_{23} = h^{2} α_{2}, \\ {ai}_{31} = & - \frac{3 h}{2} α_{2} e_{i - 3 / 2} + h^{2} α_{2} f_{i - 3 / 2} - \frac{h}{2} β_{2} e_{i - 1 / 2} \\ + \frac{h}{2} γ_{2} e_{i + 1 / 2}, \\ {ai}_{32} = & - \frac{3 h}{2} α_{2} c_{i - 3 / 2} + h^{2} α_{2} d_{i - 3 / 2} - \frac{h}{2} β_{2} c_{i - 1 / 2} \\ + \frac{h}{2} γ_{2} c_{i + 1 / 2}, \\ {ai}_{33} = & - α_{1} - \frac{3 h}{2} α_{2} a_{i - 3 / 2} + h^{2} α_{2} b_{i - 3 / 2} - \frac{h}{2} β_{2} a_{i - 1 / 2} \\ + \frac{h}{2} γ_{2} a_{i + 1 / 2}, \\ {bi}_{11} = & - β_{1}, {bi}_{12} = h^{2} β_{2}, {bi}_{13} = 0, {bi}_{21} = 0, \\ {bi}_{22} = & - β_{1}, {bi}_{23} = h^{2} β_{2}, \\ {bi}_{31} = & 2 h α_{2} e_{i - 3 / 2} + h^{2} β_{2} f_{i - 1 / 2} - 2 h γ_{2} e_{i + 1 / 2}, \\ {bi}_{32} = & 2 h α_{2} c_{i - 3 / 2} + h^{2} β_{2} d_{i - 1 / 2} - 2 h γ_{2} c_{i + 1 / 2}, \\ {bi}_{33} = & - β_{1} + 2 h α_{2} a_{i - 3 / 2} + h^{2} β_{2} b_{i - 1 / 2} - 2 h γ_{2} a_{i + 1 / 2}, \\ {ci}_{11} = & - γ_{1}, {ci}_{12} = h^{2} γ_{2}, {ci}_{13} = 0, {ci}_{21} = 0, \\ {ci}_{22} = & - γ_{1}, {ci}_{23} = h^{2} γ_{2}, \\ {ci}_{31} = & - \frac{1}{2} h α_{2} e_{i - 3 / 2} + \frac{1}{2} h β_{2} e_{i - 1 / 2} + \frac{3}{2} h γ_{2} e_{i + 1 / 2} \\ + h^{2} γ_{2} f_{i + 1 / 2}, \\ {ci}_{32} = & - \frac{1}{2} h α_{2} c_{i - 3 / 2} + \frac{1}{2} h β_{2} c_{i - 1 / 2} + \frac{3}{2} h γ_{2} c_{i + 1 / 2} \\ + h^{2} γ_{2} d_{i + 1 / 2}, \\ {ci}_{33} = & - γ_{1} - \frac{1}{2} h α_{2} a_{i - 3 / 2} + \frac{1}{2} h β_{2} a_{i - 1 / 2} + \frac{3}{2} h γ_{2} a_{i + 1 / 2} \\ + h^{2} γ_{2} b_{i + 1 / 2}, \\ h_{i 1} = & 0, \\ h_{i 2} = & 0, \\ h_{i 3} = & - h^{2} (α_{2} g_{i - 3 / 2} + β_{2} g_{i - 1 / 2} + γ_{2} g_{i + 1 / 2}), \\ i = 2, 3, \dots, n - 1 . \end{matrix}

Now for i = 1, we have

(25)

B_{1} W_{1 / 2} + C_{1} W_{3 / 2} = H_{1}

which can be written as

[\begin{matrix} b 1_{11} & b 1_{12} & b 1_{13} \\ b 1_{21} & b 1_{22} & b 1_{23} \\ b 1_{31} & b 1_{32} & b 1_{33} \end{matrix}] [\begin{matrix} y_{1 / 2} \\ u_{1 / 2} \\ v_{1 / 2} \end{matrix}] + [\begin{matrix} c 1_{11} & c 1_{12} & c 1_{13} \\ c 1_{21} & c 1_{22} & c 1_{23} \\ c 1_{31} & c 1_{32} & c 1_{33} \end{matrix}] [\begin{matrix} y_{3 / 2} \\ u_{3 / 2} \\ v_{3 / 2} \end{matrix}] = [\begin{matrix} h_{11} \\ h_{12} \\ h_{13} \end{matrix}]

where,

\begin{matrix} b 1_{11} = & 3, b 1_{12} = \frac{15 h^{2}}{24}, b 1_{13} = 0, b 1_{21} = 0, b 1_{22} = 3, b 1_{23} = \frac{15 h^{2}}{24}, \\ b 1_{31} = & - \frac{15}{24} {he}_{1 / 2} + \frac{15}{24} h^{2} f_{1 / 2} - \frac{3}{24} {he}_{3 / 2}, \\ b 1_{32} = & - \frac{15}{24} {hc}_{1 / 2} + \frac{15}{24} h^{2} d_{1 / 2} - \frac{3}{24} {hc}_{3 / 2}, \\ b 1_{33} = & 3 - \frac{15}{24} {ha}_{1 / 2} + \frac{15}{24} h^{2} b_{1 / 2} - \frac{3}{24} {ha}_{3 / 2}, \\ c 1_{11} = & - 1, c 1_{12} = \frac{3 h^{2}}{24}, c 1_{13} = 0, c 1_{21} = 0, c 1_{22} = - 1, c 1_{23} = \frac{3 h^{2}}{24}, \end{matrix}

\begin{matrix} c 1_{31} = & \frac{15}{24} {he}_{1 / 2} + \frac{3}{24} {he}_{3 / 2} + \frac{3}{24} h^{2} f_{3 / 2}, \\ c 1_{32} = & \frac{15}{24} {hc}_{1 / 2} + \frac{3}{24} {hc}_{3 / 2} + \frac{3}{24} h^{2} d_{3 / 2}, \\ c 1_{33} = & - 1 + \frac{15}{24} {ha}_{1 / 2} + \frac{3}{24} {ha}_{3 / 2} + \frac{3}{24} h^{2} b_{3 / 2}, \\ h_{11} = & 2 y_{0}, h_{12} = 2 u_{0}, h_{13} = 2 v_{0} - \frac{h^{2}}{24} (15 g_{1 / 2} + 3 g_{3 / 2}) . \end{matrix}

Now for i = n, we have

(26)

A_{n} W_{n - 3 / 2} + B_{n} W_{n - 1 / 2} = H_{n}

which can be written as

[\begin{matrix} {an}_{11} & {an}_{12} & {an}_{13} \\ {an}_{21} & {an}_{22} & {an}_{23} \\ {an}_{31} & {an}_{32} & {an}_{33} \end{matrix}] [\begin{matrix} y_{n - 3 / 2} \\ u_{n - 3 / 2} \\ v_{n - 3 / 2} \end{matrix}] + [\begin{matrix} {bn}_{11} & {bn}_{12} & {bn}_{13} \\ {bn}_{21} & {bn}_{22} & {bn}_{23} \\ {bn}_{31} & {bn}_{32} & {bn}_{33} \end{matrix}] [\begin{matrix} y_{n - 1 / 2} \\ u_{n - 1 / 2} \\ v_{n - 1 / 2} \end{matrix}] = [\begin{matrix} h_{n 1} \\ h_{n 2} \\ h_{n 3} \end{matrix}]

where,

\begin{matrix} {an}_{11} = & 3, {an}_{12} = \frac{15 h^{2}}{24}, \\ {an}_{13} = & 0, {an}_{21} = 0, \\ {an}_{22} = & 3, {an}_{23} = \frac{15 h^{2}}{24}, \\ {an}_{31} = & - \frac{15}{24} {he}_{n - 1 / 2} + \frac{15}{24} h^{2} f_{n - 1 / 2} - \frac{3}{24} {he}_{n - 3 / 2}, \\ {an}_{32} = & - \frac{15}{24} {hc}_{n - 1 / 2} + \frac{15}{24} h^{2} d_{n - 1 / 2} - \frac{3}{24} {hc}_{n - 3 / 2}, \\ {an}_{33} = & 3 - \frac{15}{24} {ha}_{n - 1 / 2} + \frac{15}{24} h^{2} b_{n - 1 / 2} - \frac{3}{24} {ha}_{n - 3 / 2} \\ {bn}_{11} = & - 1, {bn}_{12} = \frac{3 h^{2}}{24}, \\ {bn}_{13} = & 0, {bn}_{21} = 0, \\ {bn}_{22} = & - 1, {bn}_{23} = \frac{3 h^{2}}{24}, \\ {bn}_{31} = & \frac{15}{24} {he}_{n - 1 / 2} + \frac{3}{24} {he}_{n - 3 / 2} + \frac{3}{24} h^{2} f_{n - 3 / 2}, \\ {bn}_{32} = & \frac{15}{24} {hc}_{n - 1 / 2} + \frac{3}{24} {hc}_{n - 3 / 2} + \frac{3}{24} h^{2} d_{n - 3 / 2}, \\ {bn}_{33} = & - 1 + \frac{15}{24} {ha}_{n - 1 / 2} + \frac{3}{24} {ha}_{n - 3 / 2} + \frac{3}{24} h^{2} b_{n - 3 / 2}, \\ h_{n 1} = & 2 y_{n}, \\ h_{n 2} = & 2 u_{n}, \\ h_{n 3} = & 2 v_{n} - \frac{h^{2}}{24} (15 g_{n - 1 / 2} + 3 g_{n - 3 / 2}) . \end{matrix}

4 Convergence analysis

In this section, we study the convergence analysis of the second order method developed in Section 2 where $(α_{1}, β_{1}, γ_{1}, α_{2}, β_{2}, γ_{2}) = (1, - 2, 1, 1 / 8, 6 / 8, 1 / 8)$ . The method has the following form

(27)

AW = M

where,

(28)

A = [\begin{matrix} B_{1} & C_{1} \\ A_{2} & B_{2} & C_{2} \\ ⋱ & ⋱ & ⋱ \\ ⋱ & ⋱ & ⋱ \\ ⋱ & ⋱ & ⋱ \\ A_{n - 1} & B_{n - 1} & C_{n - 1} \\ A_{n} & B_{n} \end{matrix}]

where, A is a triblockdiagonal matrix in which

A_{i} (i = 2, 3, \dots, n), B_{i} (i = 1, 2, \dots, n)

and

C_{i} (i = 2, 3, \dots, n - 1)

are matrices of order

2 \times 2

W = {[w_{1 / 2}, w_{3 / 2}, \dots, w_{n - 1 / 2}]}^{T}

where,

w_{i - 1 / 2} = {[y_{i - 1 / 2}, u_{i - 1 / 2}, v_{i - 1 / 2}]}^{T}, i = 1, 2, \dots, n

and the right hand side vector

M = {[m_{1}, m_{2}, \dots, m_{n}]}^{T}

, where

m_{i} = {[m_{i 1}, m_{i 2}]}^{T}, i = 1, 2, \dots, n

We also have,

(29)

A \tilde{W} = M + T

where

\tilde{W} = {[{\tilde{w}}_{1 / 2}, {\tilde{w}}_{3 / 2}, \dots, {\tilde{w}}_{n - 1 / 2}]}^{T}

where,

{\tilde{w}}_{i - 1 / 2} = {[{\tilde{y}}_{i - 1 / 2}, {\tilde{u}}_{i - 1 / 2}, {\tilde{v}}_{i - 1 / 2}]}^{T}, i = 1, 2, \dots, n

be the exact solution and

T = {[t_{1}, t_{2}, \dots, t_{n}]}^{T}

where,

t_{i} = {[{\tilde{y}}_{i - 1 / 2} - y_{i - 1 / 2}, {\tilde{u}}_{i - 1 / 2} - u_{i - 1 / 2}, {\tilde{v}}_{i - 1 / 2} - v_{i - 1 / 2}]}^{T}, i = 1, 2, \dots, n

be the local truncation error. From (27) and (29) we have,

\begin{matrix} A (\tilde{W} - W) = T, \\ AE = T, \\ E = \tilde{W} - W = {[{\tilde{e}}_{1}, {\tilde{e}}_{2}, \dots, {\tilde{e}}_{n - 1}]}^{T} \end{matrix}

Let

0 < R \in Z^{+}

is the minimum of

| a_{i} |, | b_{i} |, | c_{i} |, | d_{i} |, | e_{i} |

and

| f_{i} |

Then $‖ C_{i} ‖ ⩽ \max_{1 ⩽ i ⩽ n - 1} \{\begin{matrix} 1 + γ_{1} + h^{2} (γ_{2} + \frac{3}{24}), & j = 1 \\ 1 + γ_{1} + h^{2} (γ_{2} + \frac{3}{24}), & j = 2 \\ 1 + γ_{1} + \frac{1}{2} h (α_{2} + β_{2} + 3 γ_{2}) R + h^{2} γ_{2} R + \frac{18}{24} hR + \frac{3}{24} h^{2} R, & j = 3 \end{matrix}$ $‖ A_{i} ‖ ⩽ \max_{2 ⩽ i ⩽ n} \{\begin{matrix} 3 + α_{1} + h^{2} (α_{2} + \frac{15}{24}), & j = 1 \\ 3 + α_{1} + h^{2} (α_{2} + \frac{15}{24}), & j = 2 \\ 3 + α_{1} + \frac{1}{2} h (3 α_{2} + β_{2} + γ_{2}) R + h^{2} α_{2} R + \frac{18}{24} hR + \frac{15}{24} h^{2} R, & j = 3 \end{matrix}$ Further, $\begin{matrix} ‖ C_{i} ‖_{\infty} ⩽ \max_{1 ⩽ i ⩽ n - 1} \{\begin{matrix} 2 + \frac{1}{4} h^{2}, & j = 1 \\ 2 + \frac{1}{4} h^{2}, & j = 2 \\ 2 + \frac{11}{8} hR + \frac{1}{4} h^{2} R, & j = 3 \end{matrix} \\ ‖ A_{i} ‖_{\infty} ⩽ \max_{2 ⩽ i ⩽ n} \{\begin{matrix} 4 + \frac{1}{2} h^{2}, & j = 1 \\ 4 + \frac{1}{2} h^{2}, & j = 2 \\ 4 + \frac{11}{8} hR + \frac{1}{2} h^{2} R, & j = 3 \end{matrix} \end{matrix}$ This shows that $‖ C_{i} ‖_{\infty} \leq 2$ and $‖ A_{i} ‖_{\infty} \leq 4$ for sufficiently small h. Hence, A is irreducible. Now we have to show that A is monotone.

To show matrix A is monotone first we calculate the sum of each row of the matrix A. $S_{1 j} = \{\begin{matrix} \sum_{k = 1}^{3} a 1_{1 k} + b 1_{1 k}, & j = 1 \\ \sum_{k = 1}^{3} a 1_{2 k} + b 1_{2 k}, & j = 2 \\ \sum_{k = 1}^{3} a 1_{3 k} + b 1_{3 k}, & j = 3 \end{matrix}$ $S_{ij} = \{\begin{matrix} \sum_{k = 1}^{3} {ai}_{1 k} + {bi}_{1 k} + {ci}_{1 k}, & j = 1, i = 1, 4, 7, \dots, n - 3 \\ \sum_{k = 1}^{3} {ai}_{2 k} + {bi}_{2 k} + {ci}_{2 k}, & j = 2, i = 2, 5, 8, \dots, n - 2 \\ \sum_{k = 1}^{3} {ai}_{3 k} + {bi}_{3 k} + {ci}_{3 k}, & j = 3, i = 3, 6, 9, \dots, n - 1 \end{matrix}$ $S_{n j} = \{\begin{matrix} \sum_{k = 1}^{3} {an}_{1 k} + {bn}_{1 k}, & j = 1 \\ \sum_{k = 1}^{3} {an}_{2 k} + {bn}_{2 k}, & j = 2 \\ \sum_{k = 1}^{3} {an}_{3 k} + {bn}_{3 k}, & j = 3 \end{matrix}$ We have $S_{1 j} = \{\begin{matrix} 2 + \frac{18}{24} h^{2}, & j = 1 \\ 2 + \frac{18}{24} h^{2}, & j = 2 \\ 2 + \frac{15}{24} h^{2} (f_{1 / 2} + d_{1 / 2} + b_{1 / 2}) - \frac{3}{24} h^{2} (f_{3 / 2} + d_{3 / 2} + b_{3 / 2}), & j = 3 \end{matrix}$ $\begin{matrix} S_{ij} = \{\begin{matrix} - (α_{1} + β_{1} + γ_{1}) + 2 h^{2} (α_{2} + β_{2} + γ_{2}), & i = 1, 4, 7, \dots, n - 3, & j = 1 \\ - (α_{1} + β_{1} + γ_{1}) + 2 h^{2} (α_{2} + β_{2} + γ_{2}), & i = 2, 5, 8, \dots, n - 2, & j = 2 \\ - (α_{1} + β_{1} + γ_{1}) + h^{2} α_{2} (f_{i - 3 / 2} + d_{i - 3 / 2} + b_{i - 3 / 2}) + h^{2} β_{2} (f_{i - 1 / 2} + d_{i - 1 / 2} + b_{i - 1 / 2}) + h^{2} γ_{2} (f_{i + 1 / 2} + d_{i + 1 / 2} + b_{i + 1 / 2}), & i = 3, 6, 9, \dots, n - 1, & j = 3 \end{matrix} \\ = \{\begin{matrix} 2 h^{2}, i = 1, 4, 7, \dots, n - 3, & j = 1 \\ 2 h^{2}, i = 2, 5, 8, \dots, n - 2, & j = 2 \\ \frac{1}{8} h^{2} (f_{i - 3 / 2} + d_{i - 3 / 2} + b_{i - 3 / 2}) + \frac{6}{8} h^{2} (f_{i - 1 / 2} \\ + d_{i - 1 / 2} + b_{i - 1 / 2}) + \frac{1}{8} h^{2} (f_{i + 1 / 2} + d_{i + 1 / 2} + b_{i + 1 / 2}), i = 3, 6, 9, \dots, n - 1, & j = 3 \end{matrix} \\ S_{n j} = \{\begin{matrix} 2 + \frac{18}{24} h^{2}, & j = 1 \\ 2 + \frac{18}{24} h^{2}, & j = 2 \\ 2 + \frac{15}{24} h^{2} (f_{n - 1 / 2} + d_{n - 1 / 2} + b_{n - 1 / 2}) - \frac{3}{24} h^{2} (f_{n - 3 / 2} + d_{n - 3 / 2} + b_{n - 3 / 2}), & j = 3 \end{matrix} \end{matrix}$ For sufficiently small h, we can easily show that the matrix A is irreducible and monotone. Therefore, $A^{- 1}$ exist and $A^{- 1} \geq 0$ .

Hence, $‖ E ‖ = ‖ A^{- 1} ‖ ‖ T ‖ .$ Now for sufficiently small h, we have $\begin{matrix} S_{1 j} ⩾ \{\begin{matrix} \frac{18}{24} h^{2}, & j = 1 \\ \frac{18}{24} h^{2}, & j = 2 \\ \frac{18}{24} h^{2} R, & j = 3 \end{matrix} \\ S_{ij} ⩾ \{\begin{matrix} h^{2}, i = 1, 4, \dots, n - 3, & j = 1 \\ h^{2}, i = 2, 5, \dots, n - 2, & j = 2 \\ h^{2} R, i = 3, 6, \dots, n - 1, & j = 3 \end{matrix} \\ S_{n j} ⩾ \{\begin{matrix} \frac{18}{24} h^{2}, & j = 1 \\ \frac{18}{24} h^{2}, & j = 2 \\ \frac{18}{24} h^{2} R, & j = 3 \end{matrix} \end{matrix}$ $S_{1} ⩾ \max [\frac{18}{24} h^{2}, \frac{18}{24} h^{2}, \frac{18}{24} {Rh}^{2}] = \frac{18}{24} {Rh}^{2}, i = 1$ $S_{i} ⩾ \max [h^{2}, h^{2}, {Rh}^{2}] = {Rh}^{2}, i = 2, \dots, n - 1$ $S_{n} ⩾ \max [\frac{18}{24} h^{2}, \frac{18}{24} h^{2}, \frac{18}{24} {Rh}^{2}] = \frac{18}{24} {Rh}^{2}, i = n$ Therefore, we get $\begin{matrix} \frac{1}{S_{1}} ⩽ \{\begin{matrix} \frac{24}{18 {Rh}^{2}}, & i = 1 \end{matrix} \\ \frac{1}{S_{i}} ⩽ \{\begin{matrix} \frac{1}{{Rh}^{2}}, & i = 2, 3, \dots, n - 1 \end{matrix} \\ \frac{1}{S_{n}} ⩽ \{\begin{matrix} \frac{24}{18 {Rh}^{2}}, & i = n \end{matrix} \end{matrix}$ Further, $\frac{1}{S_{i}} ⩽ \{\begin{matrix} \frac{24}{18 h^{2} R}, & i = 1 \\ \frac{1}{h^{2} R}, & i = 2, 3, \dots, n - 1 \\ \frac{24}{18 h^{2} R}, & i = n \end{matrix}$ Let $A^{- 1} = (a_{i, j}^{*})$ , then by theory of matrices (Varga, 1962), we get

$\sum_{i = 1}^{n} a_{i, j}^{*} S_{i} = 1, j = 1, \dots, n$ .

Therefore, $\begin{matrix} a_{i, j}^{*} ⩽ & \frac{1}{S_{i}} \\ ‖ A^{- 1} ‖ = & \max_{1 ⩽ i ⩽ n} \sum_{j = 1}^{n} | a_{i, j}^{*} | ⩽ \sum_{i = 1}^{n} \frac{1}{S_{i}} = \frac{1}{h^{2} R} (\frac{24}{9} + 1), \\ i = 1, \dots, n and \\ ‖ T_{i} ‖ = & \max_{1 ⩽ i ⩽ n} \sum_{i = 1}^{n} | T_{i} | \end{matrix}$ The error is given by $‖ E ‖ = ‖ A^{- 1} ‖ ‖ T ‖ ⩽ \frac{1}{h^{2} R} (\frac{33}{9}) ‖ T ‖ .$ Therefore, using (9) we get $‖ T ‖ = O (h^{4})$ for second order method. $‖ E ‖ ⩽ \frac{1}{h^{2} R} (\frac{33}{9}) O (h^{4}) = O (h^{2}) .$ Hence, our method is second order convergent. By repeating the same procedure we can find the bound for error of fourth order method which is as follows: $‖ E ‖ = ‖ A^{- 1} ‖ ‖ T ‖ ⩽ \frac{1}{h^{2} R} (\frac{33}{9}) ‖ T ‖ .$ Therefore, using (9) we get $‖ T ‖ = O (h^{6})$ for fourth order method. $‖ E ‖ ⩽ \frac{1}{h^{2} R} (\frac{33}{9}) O (h^{6}) = O (h^{4}) .$ Hence, our method is also fourth order convergent.

Theorem

The method given by Eq. (7) for solving the boundary value problem (1), (2) for sufficiently small h has a second as well as fourth order convergence depending upon the parameters.

5 Numerical Illustrations

We now consider seven numerical examples involving higher order non-linear and linear boundary value problems along with two singular problems involving first and third derivatives illustrating the efficiency of the presented method. We compared the results with the existing methods of fourth order. We have also provided the numerical rate of convergence $(ρ^{n})$ for the non-linear singular fourth order BVPs. The numerical rate of convergence is computed using $ρ^{_{n}} = \ln_{2} (E^{n} / E^{2 n})$ The maximum absolute errors for h = 1/8, 1/16 and 1/32 are tabulated in the Tables 1–7 .

Example 5.1

Consider the following fourth order non-linear boundary value problem for $0 \leq x \leq 4 - e$ as

(30)

y^{(4)} (x) = - 6 \exp (- 4 y (x)),

where,

\begin{matrix} y (0) = & 1, y (4 - e) = \ln (4), \\ y^{(2)} (0) = & - \frac{1}{e^{2}}, y^{(2)} (4 - e) = - \frac{1}{16} . \end{matrix}

The exact solution of the problem is

y (x) = \ln (e + x)

. The maximum absolute errors of the problem (30) are given in Table 1 and results are compared with (Wazwaz, 2002). Graph between the exact and the approximate solutions of Example 5.1 for N = 16 is shown in Fig. 1.

Example 5.2

Consider the following sixth order non-linear boundary value problem as

(31)

y^{(6)} (x) = 20 \exp [- 36 y (x)] - 40 {(1 + x)}^{- 6}, x \in [0, 1]

where,

\begin{matrix} y (0) = & 0, y (1) = \frac{1}{6} \log 2, \\ y^{(2)} (0) = & - \frac{1}{6}, y^{(2)} (1) = - \frac{1}{24}, \\ y^{(4)} (0) = & - 1, y^{(4)} (1) = - \frac{1}{16} . \end{matrix}

The exact solution of the problem is

y (x) = \frac{1}{6} \log (1 + x)

. The maximum absolute errors of the problem (31) are given in Table 2 and results are compared with (Khan and Khandelwal, 2012; Islam et al., 2008). Graph between the exact and the approximate solutions of Example 5.2 for N = 32 is shown in Fig. 2.

Example 5.3

For $0 \leq x \leq 1$ , the sixth order non-linear boundary value problem is considered as,

(32)

y^{(6)} (x) = \exp [- x] y^{2} (x),

where,

\begin{matrix} y (0) = & 1, y (1) = \exp (1), \\ y^{(2)} (0) = & 1, y^{(2)} (1) = \exp (1), \\ y^{(4)} (0) = & 1, y^{(4)} (1) = \exp (1) . \end{matrix}

The analytical solution of the above problem is

y (x) = \exp (x)

. The maximum absolute errors of the problem (32) are given in Table 3 and results are compared with (Khan and Khandelwal, 2012). Graph between the exact and the approximate solutions of Example 5.3 for N = 16 is shown in Fig. 3.

Example 5.4

For $0 \leq x \leq 1$ , the eighth order non-linear boundary value problem is considered as,

(33)

y^{(8)} (x) = \exp [- x] y^{2} (x),

where,

\begin{matrix} y (0) = & 1, y (1) = \exp (1), \\ y^{(2)} (0) = & 1, y^{(2)} (1) = \exp (1), \\ y^{(4)} (0) = & 1, y^{(4)} (1) = \exp (1), \\ y^{(6)} (0) = & 1, y^{(6)} (1) = \exp (1) . \end{matrix}

The analytical solution of the above problem is

y (x) = \exp (x)

. The maximum absolute errors of the problem (33) are given in Table 4 and results are compared with (Meŝtroviĉ, 2007). Graph between the exact and the approximate solutions of Example 5.4 for N = 32 is shown in Fig. 4.

Example 5.5

Consider the following sixth order linear boundary value problem as

(34)

y^{(6)} (x) + y (x) = 6 [2 x \cos (x) + 5 \sin (x)], x \in [- 1, 1]

where,

\begin{matrix} y (- 1) = & 0, y (1) = 0, \\ y^{(2)} (- 1) = & - 4 \cos (- 1) + 2 \sin (- 1), \\ y^{(2)} (1) = & 4 \cos (1) + 2 \sin (1), \\ y^{(4)} (- 1) = & 8 \cos (- 1) - 12 \sin (- 1), \\ y^{(4)} (1) = & - 8 \cos (1) - 12 \sin (1) . \end{matrix}

The exact solution of the problem is

y (x) = (x^{2} - 1) \sin (x)

. The maximum absolute errors of the problem (34) are given in Table 5 and results are compared with (Islam et al., 2008). Graph between the exact and the approximate solutions of Example 5.5 for N = 32 is shown in Fig. 5.

Example 5.6

Consider the following non-linear singular fourth order boundary value problem as

(35)

y^{(4)} (x) + \frac{4}{x} y^{(3)} (x) = y^{3} + \frac{\cos (x)}{x} [x \frac{\sin (2 x)}{2} - 4], x \in [0, 1]

where,

\begin{matrix} y (0) = & 0, y (1) = \sin (1), \\ y^{(2)} (0) = & 0, y^{(2)} (1) = - \sin (1) . \end{matrix}

The exact solution of the problem is

y (x) = \sin (x)

. The results of the problem (35) are given in Table 6 and compared with (Mohanty et al., 2017). Graph between the exact and the approximate solutions of Example 5.6 for N = 32 is shown in Fig. 6.

Example 5.7

Consider the following non-linear singular fourth order boundary value problem as

(36)

y^{(4)} (x) + \frac{4}{x} y^{(3)} (x) + \frac{5}{x} y^{(1)} (x) = y^{3} + \frac{\cos (x)}{x} + \sin x \cos^{2} (x), x \in [0, 1]

where,

\begin{matrix} y (0) = & 0, y (1) = \sin (1), \\ y^{(2)} (0) = & 0, y^{(2)} (1) = - \sin (1) . \end{matrix}

The exact solution of the problem is

y (x) = \sin (x)

. The results of the problem (36) are given in Table 7. Graph between the exact and approximate solutions of Example 5.7 for N = 32 is shown in Fig. 7.

Table 1 Maximum absolute errors for Example 5.1.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$1.8041 \times 10^{- 8}$	$1.2112 \times 10^{- 9}$	$7.7281 \times 10^{- 11}$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$7.4684 \times 10^{- 6}$	$1.9008 \times 10^{- 6}$	$4.7705 \times 10^{- 7}$
Wazwaz (2002)	$9.14 \times 10^{- 5}$	–	–

Table 2 Maximum absolute errors for Example 5.2.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$2.6956 \times 10^{- 6}$	$2.3833 \times 10^{- 7}$	$1.6610 \times 10^{- 8}$
Khan and Khandelwal (2012)	$3.06 \times 10^{- 6}$	$4.34 \times 10^{- 7}$	$3.53 \times 10^{- 8}$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$5.8363 \times 10^{- 5}$	$1.5815 \times 10^{- 5}$	$4.0262 \times 10^{- 6}$
Islam et al. (2008)	$2.3 \times 10^{- 3}$	$3.4 \times 10^{- 4}$	$1.54 \times 10^{- 4}$

Table 3 Maximum absolute errors for Example 5.3.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$1.8014 \times 10^{- 7}$	$1.1957 \times 10^{- 8}$	$7.5853 \times 10^{- 10}$
Khan and Khandelwal (2012)	$7.02 \times 10^{- 6}$	$4.35 \times 10^{- 6}$	$7.87 \times 10^{- 7}$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$1.1216 \times 10^{- 4}$	$3.1010 \times 10^{- 5}$	$7.7930 \times 10^{- 6}$
Khan and Khandelwal (2012)	$2.19 \times 10^{- 4}$	$3.88 \times 10^{- 5}$	–

Table 4 Maximum absolute errors for Example 5.4.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$1.8034 \times 10^{- 7}$	$1.1971 \times 10^{- 8}$	$7.5941 \times 10^{- 10}$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$1.2179 \times 10^{- 4}$	$3.1046 \times 10^{- 5}$	$7.8021 \times 10^{- 6}$
Meŝtroviĉ (2007)	$1.43 \times 10^{- 4}$	–	–

Table 5 Maximum absolute errors for Example 5.5.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$3.0468 \times 10^{- 5}$	$2.7373 \times 10^{- 6}$	$1.8321 \times 10^{- 7}$
Islam et al. (2008)	$6.97 \times 10^{- 4}$	$3.60 \times 10^{- 5}$	$7.44 \times 10^{- 7}$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$3.30 \times 10^{- 3}$	$9.2908 \times 10^{- 4}$	$2.3651 \times 10^{- 4}$
Islam et al. (2008)	$1.23 \times 10^{- 2}$	$2.80 \times 10^{- 3}$	$1.60 \times 10^{- 3}$

Table 6 Maximum absolute errors for Example 5.6.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$8.7479 \times 10^{- 6}$	$5.2045 \times 10^{- 7}$	$3.0265 \times 10^{- 8}$
$ρ^{n}$	$4.0711$	$4.1040$	$-$
Mohanty et al. (2017)	$3.0756 \times 10^{- 5}$	$1.8795 \times 10^{- 6}$	$1.1320 \times 10^{- 7}$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$4.1197 \times 10^{- 3}$	$9.1777 \times 10^{- 4}$	$2.1645 \times 10^{- 4}$

Table 7 Maximum absolute errors for Example 5.7.

Our Method	$h = 1 / 8$	$h = 1 / 16$	$h = 1 / 32$
Fourth order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{12}, \frac{10}{12}, \frac{1}{12})$	$2.3953 \times 10^{- 6}$	$1.4326 \times 10^{- 7}$	$8.4006 \times 10^{- 9}$
$ρ^{n}$	$4.0635$	$4.0920$	$-$
Second order method for $(α_{2}, β_{2}, γ_{2}) = (\frac{1}{8}, \frac{6}{8}, \frac{1}{8})$	$1.005 \times 10^{- 3}$	$2.2503 \times 10^{- 4}$	$5.3021 \times 10^{- 5}$

Graph of the exact solution versus the approximate solution for N = 16 for Example 5.1.

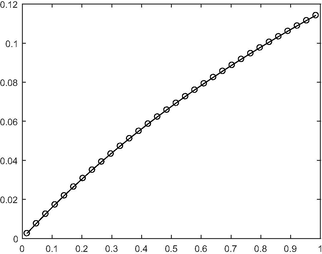
Graph of the exact solution versus the approximate solution for N = 32 for Example 5.2.

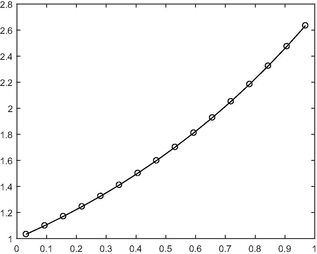
Graph of the exact solution versus the approximate solution for N = 16 for Example 5.3.

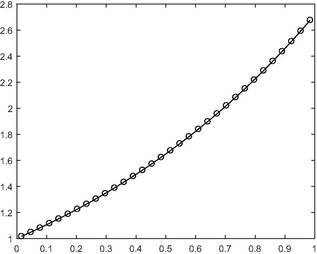
Graph of the exact solution versus the approximate solution for N = 32 for Example 5.4.

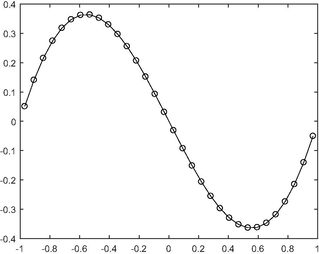
Graph of the exact solution versus the approximate solution for N = 32 for Example 5.5.

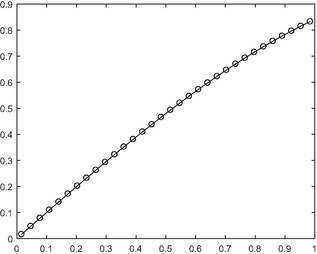
Graph of the exact solution versus the approximate solution for N = 32 for Example 5.6.

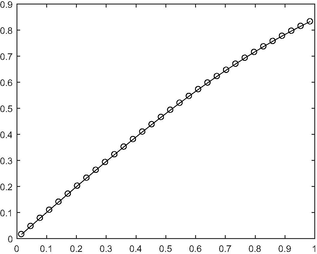
Graph of the exact solution versus the approximate solution for N = 32 for Example 5.7.

6 Conclusion

In this paper, we developed a non-polynomial quadratic spline method based on off-step points for solving higher even order boundary value problems. Advantage of the off-step points is to solve the higher order singular boundary value problems. We reduced the given problem into system of second order boundary value problems. The developed scheme (7) is second as well as fourth order accurate depending upon the parameters. Comparison of our method with the existing methods are shown in Tables 1–6 and graphs between exact and approximate solutions of the Examples 5.1–5.7 are shown in Figs. 1–7 respectively. These results shows that our fourth order method is far better than the existing fourth order methods except higher degree splines.

Acknowledgements

First author is thankful to UGC for providing MANJRF. The authors are also thankful to the referees for their useful suggestions which greatly improved the quality of the paper.

References

Agarwal R.P., . Boundary Value Problems for Higher-Order Differential Equations. Singapore: World Scientific; 1986.
Akram G., Siddiqi S.S., . Solution of sixth-order boundary value problems using non-polynomial spline technique. Appl. Math. Comput.. 2006;181:708-720.
[Google Scholar]
Al-Said E.A., . The use of cubic splines in the numerical solution of a system of second-order boundary value problems. Comput. Math. Appl.. 2001;42:861-869.
[Google Scholar]
Boutayeb A., Twizell E.H., . Numerical methods for the solution of special sixth order boundary-value problems. Int. J. Comput. Math.. 1992;45:207-223.
[Google Scholar]
Islam S., Noor M.A., Tirmizi I.A., Khan M.A., . Quadratic non-polynomial spline approach to the solution of a system of second-order boundary-value problems. Appl. Math. Comput.. 2006;179:153-160.
[Google Scholar]
Islam S., Tirmizi I.A., Haq F., Khan M.A., . Non-polynomial splines approach to the solution of sixth-order boundary value problems. Appl. Math. Comput.. 2008;195:270-284.
[Google Scholar]
Jalilian R., Rashidinia J., . Convergence analysis of nonic-spline solutions for special nonlinear sixth-order boundary value problems. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:3805-3813.
[Google Scholar]
Jha N., Mohanty R.K., . TAGE iterative algorithm and non-polynomial spline basis for the solution of non-linear singular second order ordinary differential equations. Appl. Math. Comput.. 2011;218:3289-3296.
[Google Scholar]
Keller H.B., . Numerical Methods for Two Point Boundary Value Problems. New York: Blaisdell Publications Co; 1968.
Khan A., Khandelwal P., . Solution of non-linear sixth-order two point boundary-value problems using parametric septic splines. Int. J. Nonlin. Sci.. 2012;2:184-195.
[Google Scholar]
Meŝtroviĉ M., . The modified decomposition method for eighth-order boundary value problems. Appl. Math. Comput.. 2007;188:1437-1444.
[Google Scholar]
Mohanty R.K., Jha N., Evans D.J., . Spline in compression method for the numerical solution of singularly perturbed two point singular boundary value problems. Int. J. Comput. Math.. 2004;81:615-627.
[Google Scholar]
Mohanty R.K., Evans D.J., Arora U., . Convergent spline in tension methods for singularly perturbed two point singular boundary value problems. Int. J. Compu. Math.. 2005;82:55-66.
[Google Scholar]
Mohanty R.K., Nayak S., Khan A., . Non-polynomial cubic spline discretization for system of non-linear singular boundary value problems using variable mesh. Adv. Diff. Eqs.. 2017;327
[Google Scholar]
Ramadan M.A., Lashien I.F., Zahra W.K., . Polynomial and non-polynomial spline approaches to the numerical solution of second order boundary value problems. Appl. Math. Comput.. 2007;184:476-484.
[Google Scholar]
Siddiqi S.S., Akram G., . Solution of eighth-order boundary value problems using the non-polynomial spline technique. Int. J. Comput. Math.. 2007;84:347-368.
[Google Scholar]
Srivastava P.K., Kumar M., Mohapatra R.N., . Quintic non-polynomial spline method for the solution of a second-order boundary-value problem with engineering applications. Comput. Math. Appl.. 2011;62:1707-1714.
[Google Scholar]
Varga R.S., . Matrix Iterative Analysis. Englewood Cliffs, NJ: Prentice-Hall; 1962.
Wazwaz A.M., . The numerical solution of special fourth order boundary value problems by modified decomposition method. Int. J. Comput. Math.. 2002;79:345-356.
[Google Scholar]