Approximate solution of integro-differential equation of fractional (arbitrary) order

Asma A. Elbeleze; Adem Kılıçman; Bachok M. Taib

doi:10.1016/j.jksus.2015.04.006

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

28 (

); 61-68

doi:

10.1016/j.jksus.2015.04.006

Approximate solution of integro-differential equation of fractional (arbitrary) order

Asma A. Elbeleze^{^a}, Adem Kılıçman^{^b,⁎}, Bachok M. Taib^{^a}

a Faculty of Science and Technology, Universiti Sains Islam Malaysia (USIM), 71800 Nilai, Malaysia

b Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia

⁎Corresponding author. akilic@upm.edu.my (Adem Kılıçman),

Received: 2015-3-6, Accepted: 2015-4-27, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In the present paper, we study the integro-differential equations which are combination of differential and Fredholm–Volterra equations that have the fractional order with constant coefficients by the homotopy perturbation and the variational iteration. The fractional derivatives are described in Caputo sense. Some illustrative examples are presented.

Keywords

Fractional calculus

Homotopy perturbation method

The variational iteration method

Fractional integro-differential equations

Show Related Articles from PubMed

1 Introduction

During the past decades, the topic of fractional calculus has attracted many scientists and researchers due to its applications in many areas, see Podlubny (1999), Gaul et al. (1991), Glockle and Nonnenmacher (1995); Hilfert (2000). Thus several researchers have investigated existence results for solutions to fractional differential equations due to the fact that many mathematical formulations of physical phenomena lead to integro-differential equations, for instance, mostly these types of equations arise in continuum and statistical mechanics and chemical kinetics, fluid dynamics, and biological models, for more details see Baleanu et al. (2012), Kythe and Puri (2002), Mainardi (1997).

Integro-differential equations are usually difficult to solve analytically, so it is required to obtain an efficient approximate solution. The homotopy perturbation method and variational iteration method which are proposed by He (1999a,b) are of the methods which have received much concern. These methods have been successfully applied by many authors such as Abbasbandy (2007), Abdulaziz et al. (2008); Yıldırım (2008). In this work, we study the Integro-differential equations which are combination of differential and Fredholm–Volterra equations that have the fractional order. In particular, we applied the HPM and VIM for fractional Fredholm Integro-differential equations with constant coefficients of the form

(1.1)

\sum_{k = 0}^{\infty} P_{k} D_{*}^{α} u (t) = g (t) + λ \int_{0}^{a} H (x, t) u (t) dt, a \leq x, t \leq b

under the initial-boundary conditions

(1.2)

\begin{matrix} D_{*}^{α} u (a) = u (0) \\ D_{*}^{α} u (0) = u^{'} (a) \end{matrix}

where a is constant and

1 < α \leq 2

and

D_{*}^{α}

is the fractional derivative in the Caputo sense.

2 Preliminaries

In this section, we give some basic definitions and properties of fractional calculus theory which are used in this paper.

Definition 2.1

A real function $f (x), x > 0$ is said to be in space $C μ, μ \in R$ if there exists a real number $p > μ$ , such that $f (x) = x^{p} f_{1} (x)$ where $f_{1} (x) \in C (0, \infty)$ , and it is said to be in the space $C_{μ}^{n}$ if $f^{n} \in R_{μ}, n \in N$ .

Definition 2.2

The Riemann–Liouville fractional integral operator of order $α \geq 0$ of a function $f \in C μ, μ \geq - 1$ is defined as:

(2.1)

J^{α} f (x) = \frac{1}{(Γ (α))} \int_{0}^{x} {(x - t)}^{α - 1} f (t) dt, α > 0, t > 0

in particular

J^{0} f (x) = f (x)

For $β ⩾ 0$ and $γ ⩾ - 1$ , some properties of the operator $J^{α}$

$J^{α} J^{β} f (x) = J^{α + β} f (x)$
$J^{α} J^{β} f (x) = J^{β} J^{α} f (x)$
$J^{α} x^{γ} = \frac{Γ (γ + 1)}{Γ (α + γ + 1)} x^{α + γ}$

Definition 2.3

The Caputo fractional derivative of $f \in C_{- 1}^{m}, m \in N$ is defined as:

(2.2)

D^{α} f (x) = \frac{1}{Γ (m - α)} \int_{0}^{x} {(x - t)}^{m - α - 1} f^{m} (t) dt, m - 1 < α \leq m

Lemma 2.4

if $m - 1 < α \leq m$ , $m \in N, f \in C_{μ}^{m}, μ > - 1$ then the following two properties hold

$D^{α} [J^{α} f (x)] = f (x)$
$J^{α} [D^{α} f (x)] = f (x) - \sum_{k = 1}^{m - 1} f^{k} (0) \frac{x^{k}}{k!}$

3 Homotopy perturbation method

The homotopy perturbation method first proposed by He (2005, 2006) is applied to various problems (He, 2005,, 2006, 2000, 2003 ).

To illustrate the basic idea of this method, we consider the following nonlinear differential equation

(3.1)

A (u) - f (r) = 0, r \in Ω

with boundary conditions

(3.2)

B (u, \frac{\partial u}{\partial n}) = 0, r \in Γ

where A is a general differential operator, B is a boundary operator,

f (r)

is a known analytic function, Γ is the boundary of the domain Ω.

In general, the operator A can be divided into two parts L and N, where L is linear, while N is nonlinear. Eq. (3.1) therefore can be rewritten as follows

(3.3)

L (u) + N (u) - f (r) = 0

By the homotopy technique (Liao, 1995, 1997). We construct a homotopy

v (r, p) : Ω \times [0, 1] \to R

which satisfies

(3.4)

H (v, p) = (1 - p) [L (v) - L (u_{0})] + p [A (v) - f (r)] = 0 p \in [0, 1], r \in Ω

(3.5)

H (v, p) = L (v) - L (u_{0}) + pL (u_{0}) + p [N (v) - f (r)] = 0

where

p \in [0, 1]

is an embedding parameter,

u_{0}

is an initial approximation of Eq. (3.1) which satisfies the boundary conditions.

From Eqs. (3.4), (3.5) we have

(3.6)

H (v, 0) = L (v) - L (u_{0}) = 0,

(3.7)

H (v, 1) = A (v) - f (r) = 0 .

The changing in the process of p from zero to unity is just that of

v (r, p)

from

u_{0} (r)

u (r)

. In topology this is called deformation and

L (v) - L (u_{0})

, and

A (v) - f (r)

are called homotopic.

Now, assume that the solution of Eqs. (3.4), (3.5) can be expressed as

(3.8)

v = v_{0} + {pv}_{1} + p^{2} v_{2} + \dots

The approximate solution of Eq. (3.1) can be obtained by Setting

p = 1

(3.9)

u = \underset{p \to 1}{\lim v} = v_{0} + v_{1} + v_{2} + \dots

4 The variational iteration method

To illustrate the basic concepts of VIM, we consider the following differential equation

(4.1)

L (u) + N (u) = g (x)

where L is a linear operator, N nonlinear operator, and

g (x)

is an non-homogeneous term.

According to VIM, one constructs a correction functional as follows

(4.2)

y_{n + 1} = y_{n} + \int_{0}^{x} λ [{Ly}_{n} (s) - N \tilde{y_{n}} (s)] ds

where λ is a general Lagrange multiplier, and

\tilde{y_{n}}

denotes restricted variation i.e

δ \tilde{y_{n}}

=0.

Remark

For the analysis of HPM and VIM we refer the reader to Kadem and Kilicman (2012); Elbeleze et al. (2012).

5 Numerical examples

In this section, we have applied the homotopy perturbation method and variational iteration method to linear and nonlinear Fredholm Integro-differential equations of fractional order with known exact solution

Example 5.1

Consider the following linear Fredholm integro-differential equation:

(5.1)

D^{α} u (x) = 2 e^{x} - 1 - \int_{0}^{x} u (t) dt 0 \leq x \leq 1, 1 < α \leq 2 .

with initial boundary conditions

(5.2)

u (0) = 1, u^{'} (1) = e

the exact is

u (x) = e^{x}

HPM According to HPM, we construct the following homotopy:
(5.3)
$D^{α} u (x) = p (2 e^{x} - 1 - \int_{0}^{x} u (t) dt)$ Substitution of (3.8) in (5.3) and then equating the terms with same powers of p we get the series
(5.4)
$\begin{matrix} p^{0} : D^{α} u_{0} (x) = 0 \\ p^{1} : D^{α} u_{1} (x) = 2 e^{x} - 1 - \int_{0}^{x} u_{0} (t) dt \end{matrix}$ $\begin{matrix} ⋮ \\ p^{n} : D^{α} u_{n} (x) = - \int_{0}^{x} e^{t} u_{n - 1} (t) dt \end{matrix}$ Now applying the operator $J_{α}$ to Eqs. (5.4). In order to satisfy the boundary conditions and convenient calculation, we will choose $u_{0} (x), u_{1} (x) and u_{n} (x) (n = 2, 3, 4, \dots)$ as follows:
(5.5)
$\begin{matrix} u_{0} (x) = 1 \\ u_{1} (x) = Ax + J^{α} (2 e^{2 x} - 1 - \int_{0}^{x} u_{0} dt) \end{matrix}$ $\begin{matrix} ⋮ \\ u_{n} (x) = J^{α} (- \int_{0}^{x} u_{n - 1} (t) dt) \end{matrix}$ Then by solving Eqs. (5.5), we obtain $u_{1}, u_{2}, \dots$ as $\begin{matrix} u_{1} (x) = Ax + \frac{x^{α}}{Γ (α + 1)} + \frac{x^{α + 1}}{Γ (α + 2)} + \frac{2 x^{α + 2}}{Γ (α + 3)} + \frac{2 x^{α + 3}}{Γ (α + 4)} \\ u_{2} (x) = \frac{- \frac{A}{2} x^{α + 2}}{Γ (α + 3)} - \frac{x^{2 α + 1}}{Γ (2 α + 2)} - \frac{x^{2 α + 2}}{Γ (2 α + 3)} - \frac{2 x^{2 α + 3}}{Γ (2 α + 4)} - \frac{2 x^{2 α + 4}}{Γ (2 α + 5)} \end{matrix}$ Now, we can form the 2-term approximation
(5.6)
$ϕ_{2} (x) = 1 + Ax + \frac{x^{α}}{Γ (α + 1)} + \frac{x^{α + 1}}{Γ (α + 2)} + \frac{2 x^{α + 2}}{Γ (α + 3)} + \frac{2 x^{α + 3}}{Γ (α + 4)} \frac{- \frac{A}{2} x^{α + 2}}{Γ (α + 3)} - \frac{x^{2 α + 1}}{Γ (2 α + 2)} - \frac{x^{2 α + 2}}{Γ (2 α + 3)} - \frac{2 x^{2 α + 3}}{Γ (2 α + 4)} - \frac{2 x^{2 α + 4}}{Γ (2 α + 5)} + \dots$ where A can be determined by imposing initial-boundary conditions (5.2) on $ϕ_{2}$ . Table 1 shows the value of A for different values of α.
VIM According to the variational iteration method, Eq. (5.1) can be expressed in the following form:
(5.7)
$u_{k + 1} (x) = u_{k} (x) - \frac{(α - 1)}{2} J^{α} [D^{α} u (x) - 2 e^{x} - 1 - \int_{0}^{x} u_{k} (t) dt]$ Then, in order to avoid the complex and difficult fractional integration, we can take the truncated Taylor expansions for exponential term in (5.7) for example, $e^{x} \sim 1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6}$ and further, suppose that an initial approximation has the following form which satisfies the initial-boundary conditions
(5.8)
$u_{0} (x) = 1 + Ax$ Now by iteration formula (5.7), the first approximation takes the following form
(5.9)
$u_{1} (x) = u_{0} (x) - \frac{(α - 1)}{2} J^{α} [D^{α} u_{0} (x) - 2 e^{x} - 1 - \int_{0}^{x} u_{0} (t) dt] = 1 + Ax + \frac{(α - 1)}{2} x^{α} [\frac{1}{Γ (α + 1)} + \frac{x}{Γ (α + 2)} + \frac{(2 - A) x^{2}}{Γ (α + 3)} + \frac{2 x^{3}}{3 Γ (α + 4)}]$ By imposing initial-boundary conditions (5.2) on $u_{1}$ .

Example 5.2

Consider the following nonlinear Fredholm integro-differential equation:

(5.10)

D^{α} u (x) = x \cos x - 2 \sin x + \int_{0}^{x} tu (t) dt 0 \leq x \leq π / 2, 1 < α \leq 2 .

with initial boundary conditions

(5.11)

u (0) = 0, u^{'} (π / 2) = 0

the exact is

u (x) = \sin x

HPM We follow the same procedure in Example (5.1) by HPM, so the approximate solution is
(5.12)
$ϕ_{2} (x) = Ax - \frac{x^{α + 1}}{Γ (α + 2)} + \frac{x^{α + 3}}{Γ (α + 4)} - \frac{3 x^{α + 5}}{Γ (α + 6)} + \frac{5 x^{α + 7}}{Γ (α + 8)} + \dots$
VIM we follow the same procedure in Example (5.1) by VIM, so the approximate solution is
(5.13)
$u_{1} (x) = u_{0} (x) - \frac{(α - 1)}{2} J^{α} [D^{α} u_{0} (x) x \cos x - 2 \sin x + \int_{0}^{x} {tu}_{0} (t) dt] = Ax - \frac{(α - 1)}{2} x^{α} [\frac{2 x}{Γ (α + 2)} - \frac{(2 A - 1) x^{3}}{Γ (α + 4)} - \frac{3 x^{5}}{Γ (α + 6)} + \frac{5 x^{7}}{Γ (α + 8)}]$

Example 5.3

Consider the following linear Fredholm integro-differential equation:

(5.14)

D^{α} u (x) = (\frac{1}{2} + \frac{1}{2} e^{2 x}) + \int_{0}^{x} (1 - e^{t}) u (t) dt 0 \leq x \leq 1, 1 < α \leq 2 .

with initial boundary conditions

(5.15)

u (0) = 1, u^{'} (1) = e

the exact is

u (x) = e^{x}

HPM We follow the same procedure in Example (5.1) by HPM, so the approximate solution is
(5.16)
$ϕ_{2} (x) = 1 + Ax + \frac{x^{α}}{Γ (α + 1)} + \frac{x^{α + 1}}{Γ (α + 2)} + \frac{x^{α + 2}}{Γ (α + 3)} + \frac{3 x^{α + 3}}{2 Γ (α + 4)} + \dots$
VIM we follow the same procedure in Example (5.1) by VIM, so the approximate solution is
(5.17)
$u_{1} (x) = 1 + Ax + \frac{(α - 1)}{2} x^{α} [\frac{1}{Γ (α + 1)} + \frac{x}{Γ (α + 2)} + \frac{(A - 1) x^{2}}{2 Γ (α + 3)} + \frac{(\frac{3 + 2 A}{12}) x^{3}}{Γ (α + 4)} - \frac{{Ax}^{4}}{2 Γ (α + 5)}]$

Example 5.4

Consider the following nonlinear Fredholm integro-differential equation:

(5.18)

D^{α} u (x) + \int_{0}^{x} u^{2} (t) dt + (\frac{x}{2} - \sinh x - \frac{1}{4} \sinh 2 x) 0 \leq x \leq 1, 1 < α \leq 2 .

with initial boundary conditions

(5.19)

u (0) = 0, u^{'} (1) = \cosh 1

the exact is

u (x) = \sinh x

HPM We follow the same procedure in Example (5.1) by HPM, so the approximate solution is
(5.20)
$ϕ_{2} (x) = Ax + \frac{x^{α + 1}}{Γ (α + 2)} + \frac{3 x^{α + 3}}{Γ (α + 4)} + \frac{9 x^{α + 5}}{Γ (α + 6)} + \frac{33 x^{α + 7}}{Γ (α + 8)} + \dots$
VIM we follow the same procedure in Example (5.1) by VIM, so the approximate solution is
(5.21)
$u_{1} (x) = Ax + \frac{(α - 1)}{2} x^{α} [\frac{x}{Γ (α + 2)} + \frac{(3 - 2 A^{2}) x^{3}}{Γ (α + 4)} + \frac{9 x^{5}}{Γ (α + 6)} + \frac{33 x^{7}}{Γ (α + 8)}]$

Table 1 Value of A for different values of α using (5.6) and (5.9).

	$α = 1.25$	$α = 1.5$	$α = 1.75$	$α = 2$
$A (HPM)$	0.1452034490	0.4549747740	0.7244709330	0.9516151533
$A (VIM)$	1.432940029	1.241066017	1.138179159	1.108032497

6 Results and discussion

The FIDEs with initial-boundary conditions have been solved by using HPM and VIM. Based on preliminary calculations, we decided to use 2-term in HPM and first-order in VIM solutions. We note that increasing the number of terms improves the accuracy of HPM solutions.

Table (1) shows the values of A for different values of α using (5.6) and (5.9). In Fig. (1) absolute error functions $E_{1} (x), E_{2} (x)$ , and $E_{3} (x)$ by HPM, $E_{4} (x), E_{5} (x)$ , and $E_{6} (x)$ by VIM for different values of α, where $E (x) = |u_{exact} - u_{approximate}|$ have been drawn. From this figure we can see that the absolute error for $α = 1.75$ is smaller than the absolute errors for $α = 1.25, 1.5$ in both methods. In addition, the absolute errors for all α slightly increased from 0 till reaching a maximum value then slightly decreased till reaching zero at $x = 1$ . It can be observed from this figure that increasing the accuracy of the HPM and VIM solution by increasing the fractional derivative. While, Fig. (2) displays the approximate solution when $α = 2$ for HPM and VIM with exact solution.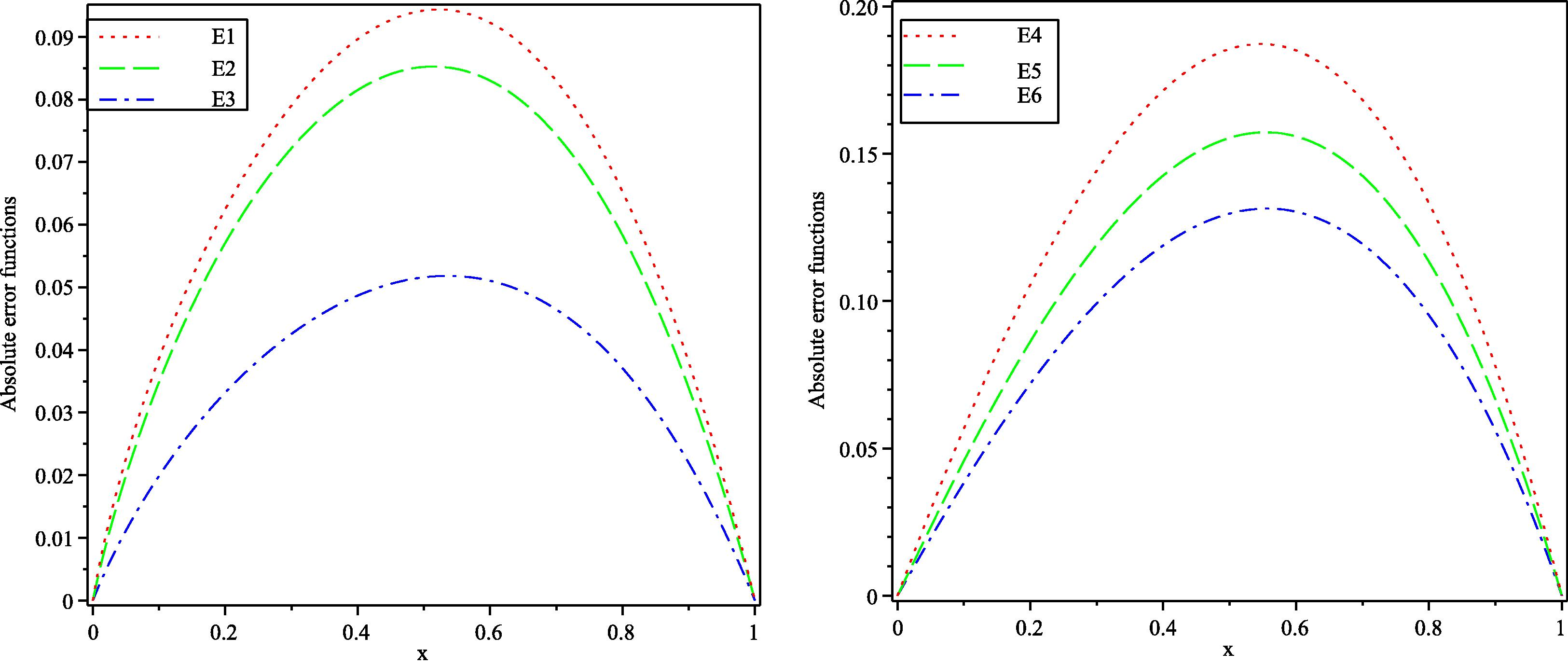

Absolute error of functions E 1 ( x ) , E 2 ( x ) and E 3 ( x ) obtained by 2-term HPM and E 4 ( x ) , E 5 ( x ) and E 6 ( x ) obtained by VIM with α = 1.25 , α = 1.5 , α = 1.75 for Example (5.1).

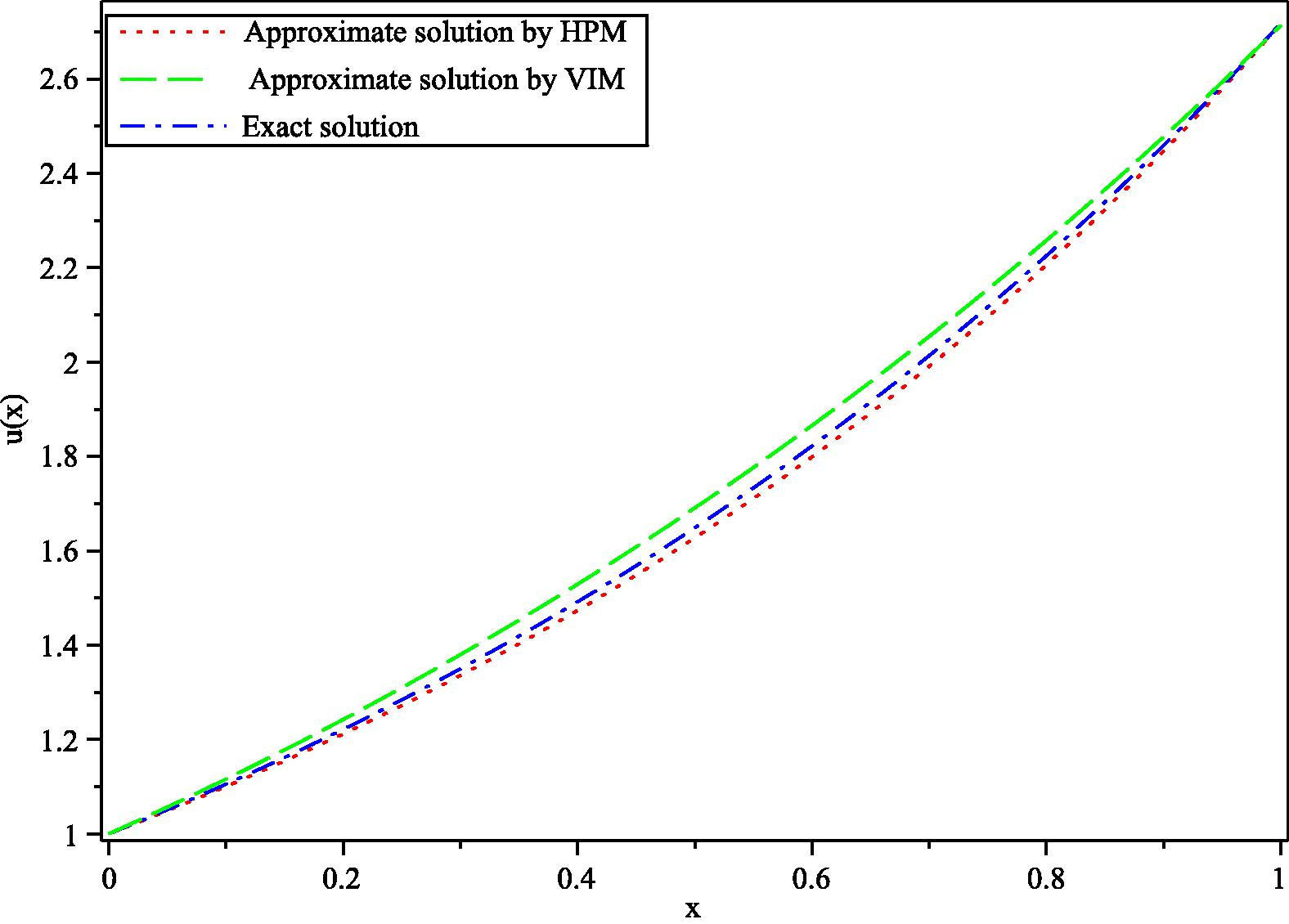
Comparison of approximate solutions obtained by 3-term HPM and with exact solution at α = 2 for Example (5.1).

Table (2) shows the values of A for different values of α using (5.12) and (5.13). The absolute error functions $E_{7} (x)$ , $E_{8} (x)$ , $E_{9} (x)$ by HPM and $E_{10} (x), E_{11} (x)$ and $E_{12} (x)$ by VIM of Example (5.2) for different values of α, where have been drawn in Fig. (3). From this figure we can see that the absolute error for all α by HPM smaller than the absolute errors for all α by VIM. In addition also it can be observed from this figure that increasing the accuracy of the HPM and VIM solution by increasing the fractional derivative. While, Fig. (4) displays the approximate solution $α = 2$ for HPM and VIM with exact solution.

Table 2 Value of A for different values of α using (5.12) and (5.13).

	$α = 1.25$	$α = 1.5$	$α = 1.75$	$α = 2$
$A (HPM)$	1.229102855	1.154176102	1.078262573	1.005549222
$A (VIM)$	0.7967121064	0.9093326779	0.9808215282	1.017387171

Absolute error of functions E 7 ( x ) , E 8 ( x ) and E 9 ( x ) obtained by 1-term HPM and E 10 ( x ) , E 11 ( x ) and E 12 ( x ) obtained by VIM with α = 1.25 , α = 1.5 , α = 1.75 for Example (5.2).

Comparison of approximate solutions obtained by 2-term HPM with exact solution at α = 2 for Example 5.2.

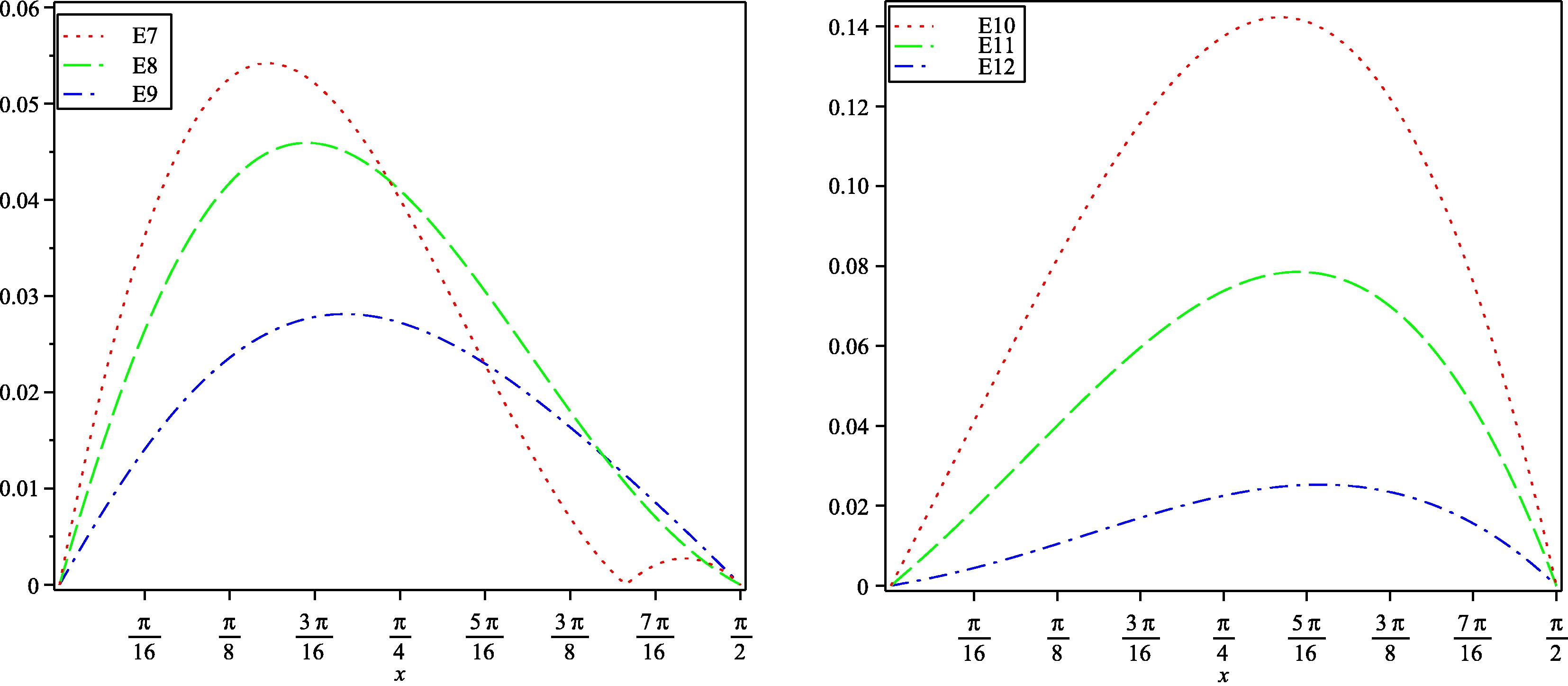
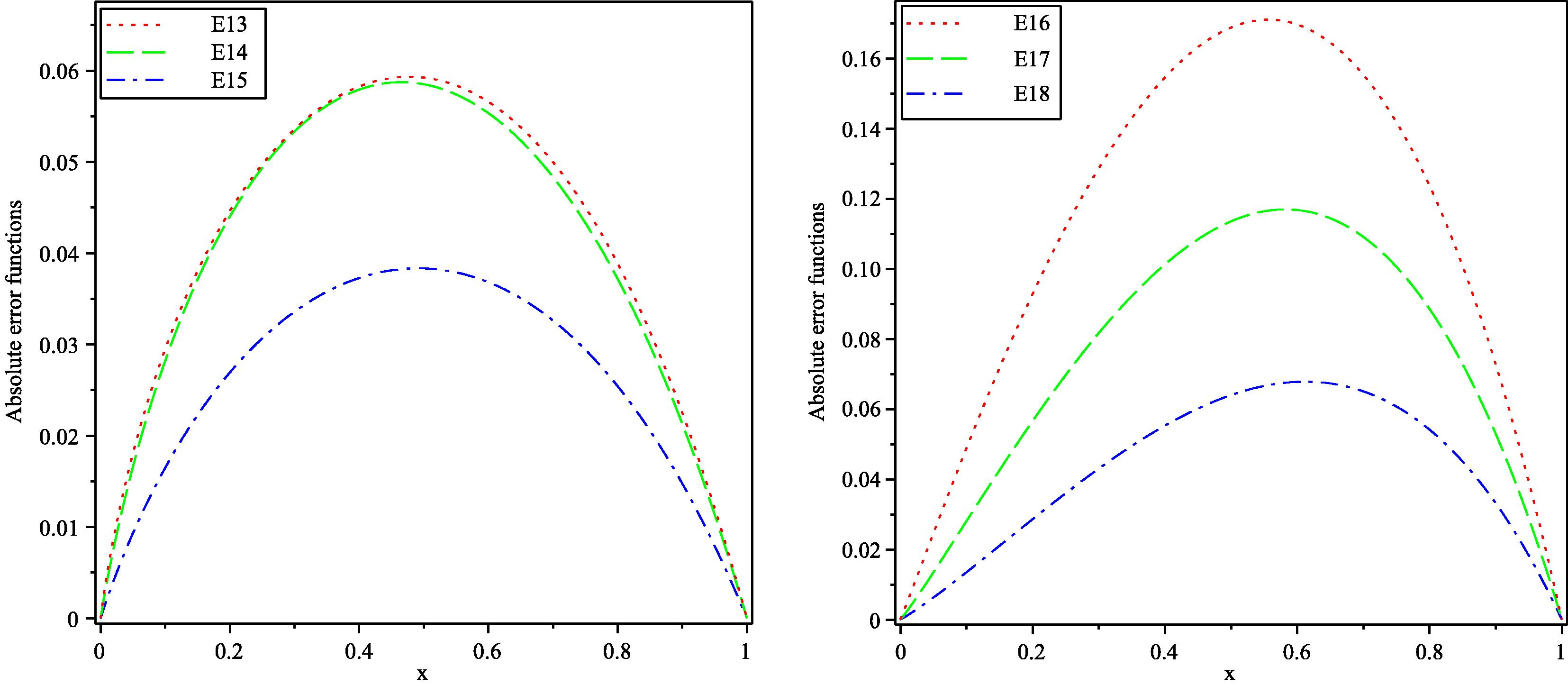
Table (3) shows the values of A for different values of α using (5.16) and (5.17). The absolute error functions $E_{13} (x)$ , $E_{14} (x)$ , $E_{15} (x)$ by HPM and $E_{16} (x), E_{17} (x)$ and $E_{18} (x)$ by VIM of Example (5.3) for different values of α, have been drawn in Fig. (5). From this figure we can see that the absolute error for $α = 1.75$ is smaller than the absolute errors for $α = 1.25, 1.5$ in both methods. In addition, the absolute errors for all α slightly increase from 0 till reaching a maximum value then slightly decreased till reaching zero at $x = 1$ . Also, we can see that the absolute error for all α by HPM is smaller than the absolute errors for all α by VIM. It can be observed from this figure that increasing the accuracy of the HPM and VIM solution by increasing the fractional derivative. While, Fig. 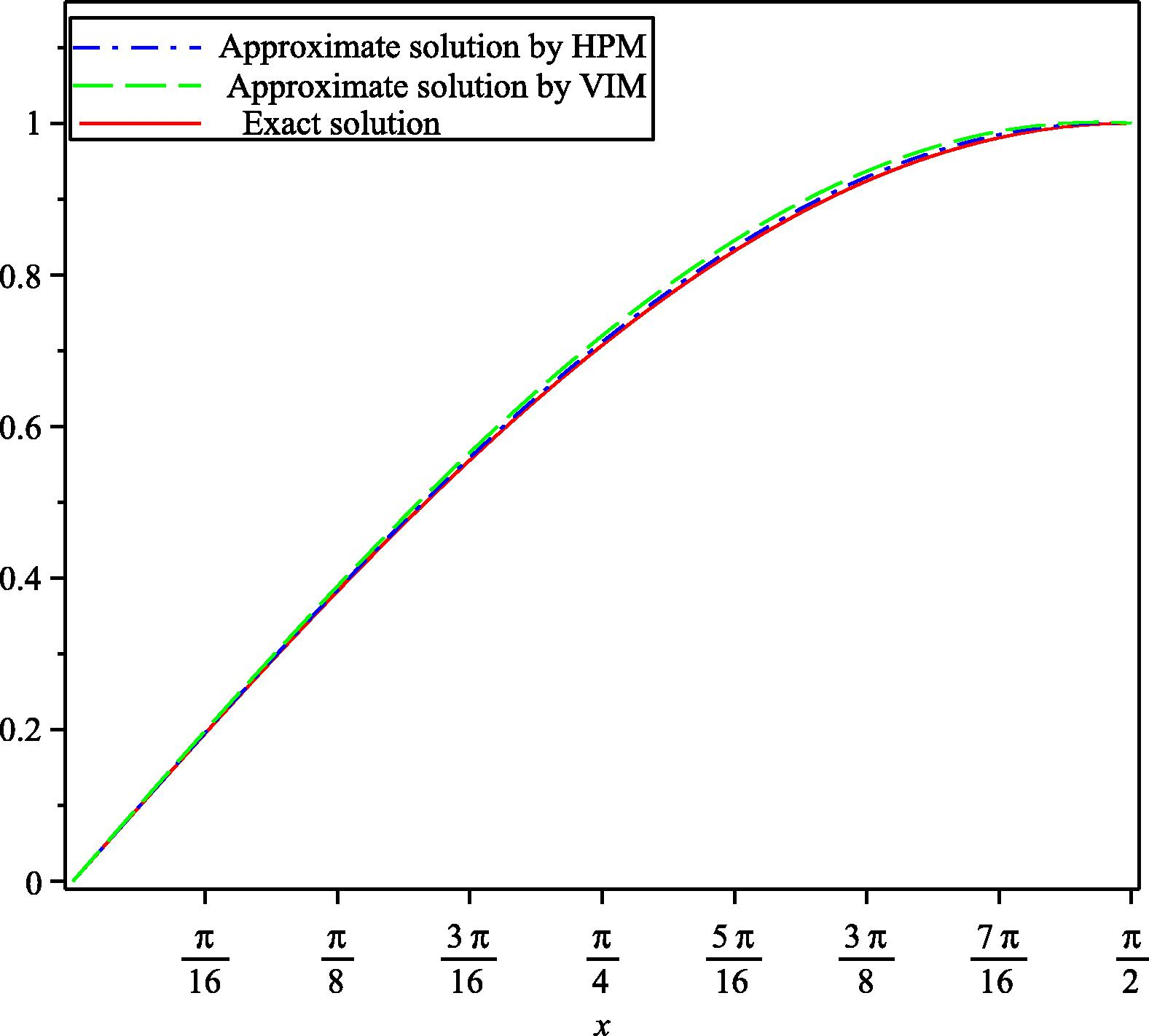(6) displays the approximate solution $α = 2$ for HPM and VIM with exact solution.

Table 3 Value of A for different values of α using (5.16) and (5.17).

	$α = 1.25$	$α = 1.5$	$α = 1.75$	$α = 2$
$A (HPM)$	0.2375025470	0.5218416880	0.7720691390	0.9849484867
$A (VIM)$	1.411203960	1.208885080	1.100882101	1.068880597

Absolute error of functions E 13 ( x ) , E 14 ( x ) and E 15 ( x ) obtained by 1-term HPM and E 16 ( x ) , E 17 ( x ) and E 18 ( x ) obtained by VIM with α = 1.25 , α = 1.5 , α = 1.75 for Example (5.3).

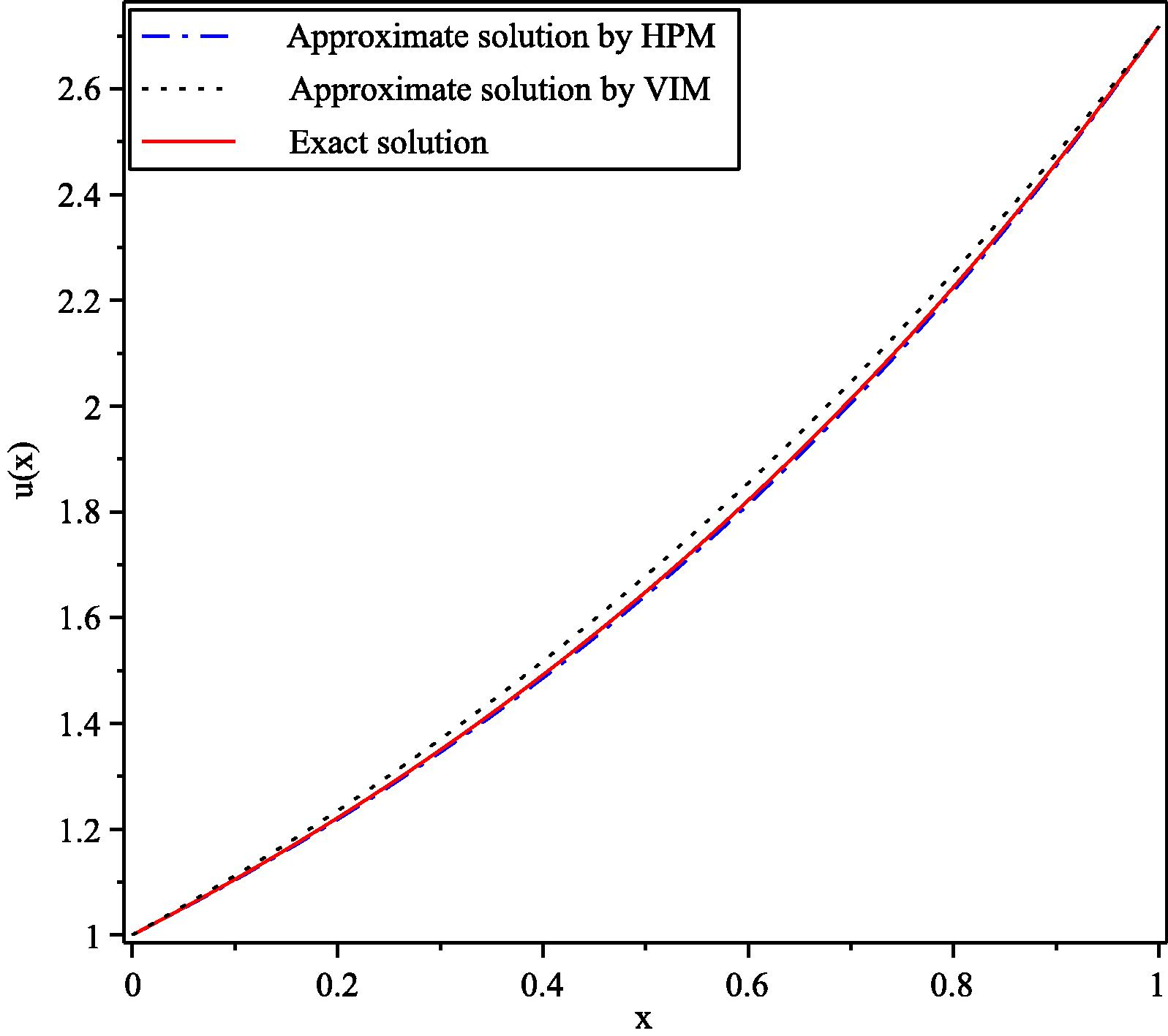
Comparison of approximate solutions obtained by 2-term HPM with exact solution at α = 2 for Example (5.3).

Table (4) shows the values of A for different values of α using (5.20) and (5.21). The absolute error functions $E_{19} (x)$ , $E_{20} (x)$ , $E_{21} (x)$ by HPM and $E_{22} (x), E_{23} (x)$ and $E_{24} (x)$ by VIM of Example (5.4) for different values of α, have been drawn in Fig. (7). From this figure we can see that the maximum absolute error for $α = 1.75$ by HPM is smaller than the absolute errors for $α = 1.75$ by VIM, while the maximum absolute error for $α = 1.25, 1.5$ by HPM is greater than the maximum absolute error for $α = 1.25, 1.5$ by VIM. Fig. (8) displays the approximate solution $α = 2$ for HPM and VIM with exact solution.

Table 4 Value of A for different values of α using (5.20) and (5.21).

	$α = 1.25$	$α = 1.5$	$α = 1.75$	$α = 2$
$A (HPM)$	0.6894636978	0.8118993456	0.9079287321	0.9816578735
$A (VIM)$	0.8410301049	0.8387819527	0.8648448808	0.9053789914

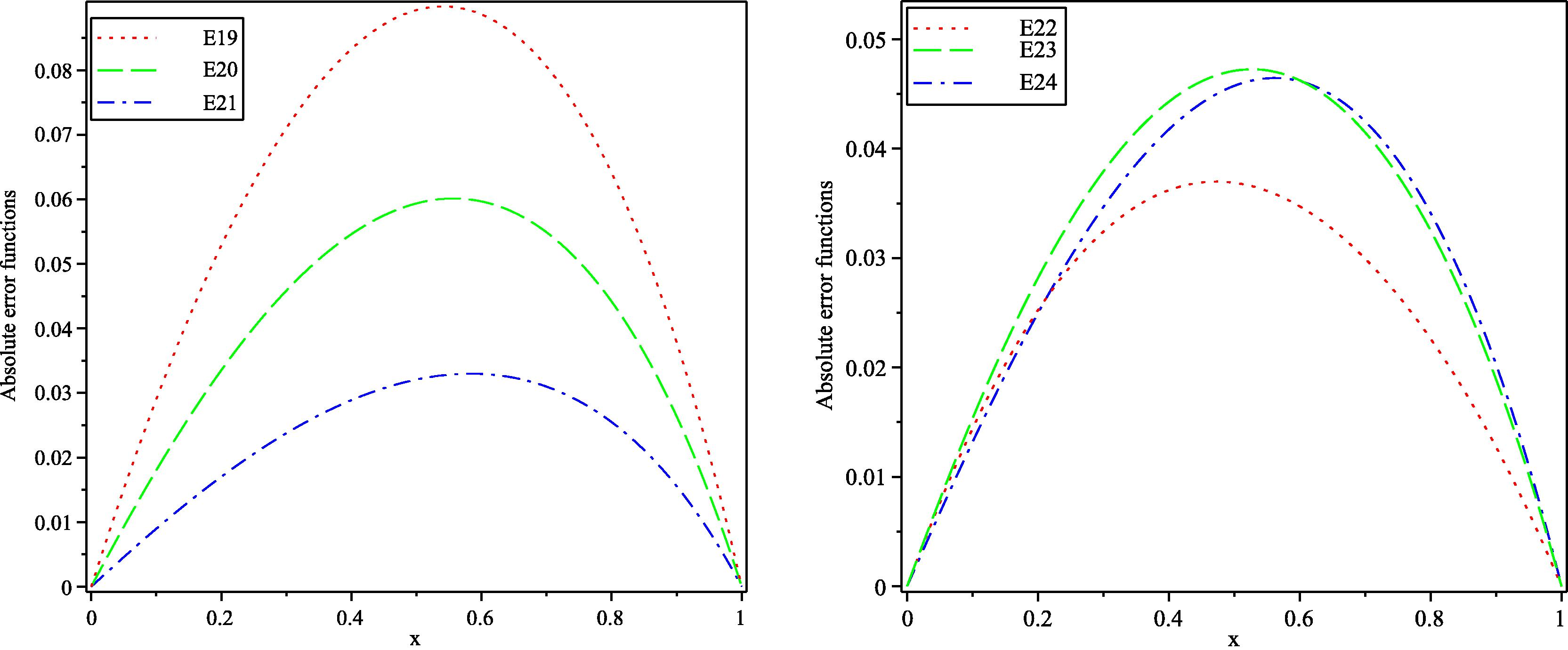
Absolute error of functions E 19 ( x ) , E 20 ( x ) and E 21 ( x ) obtained by 1-term HPM and E 22 ( x ) , E 23 ( x ) and E 24 ( x ) obtained by VIM with α = 1.25 , α = 1.5 , α = 1.75 for Example (5.4).

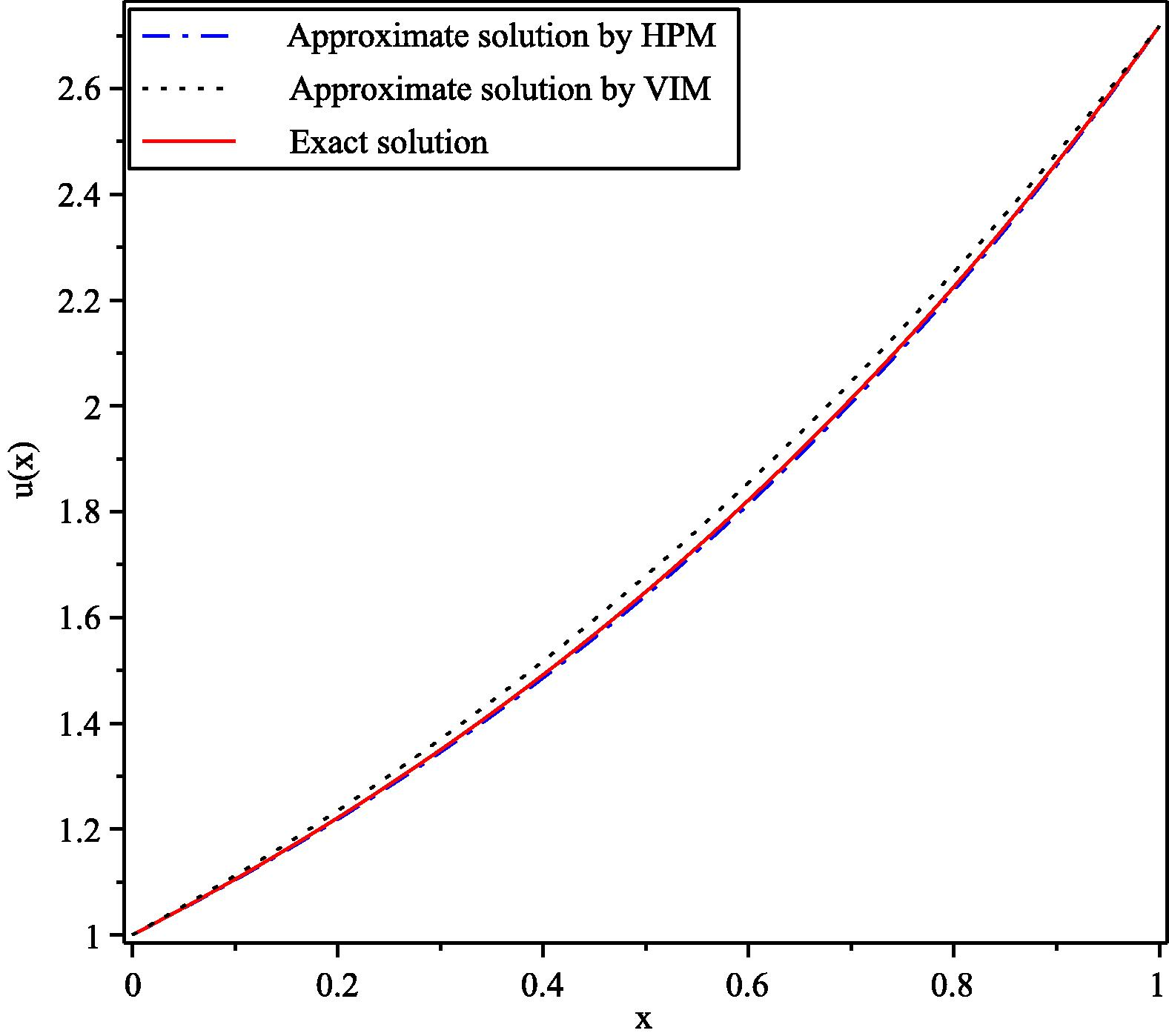
Comparison of approximate solutions obtained by 2-term HPM with exact solution at α = 2 for Example 5.4.

Overall, it can be seen that the approximate solution is in excellent agreement with exact solution. Also, it is to be noted that the accuracy can be improved by computing more terms of approximated solution and/or by taking more terms in the Taylor expansion of the exponential term.

References

Abbasbandy S., . An approximation solution of a nonlinear equation with Riemann–Liouville’s fractional derivatives by He’s variational iteration method. J. Comput. Appl. Math.. 2007;207(1):53-58.
[Google Scholar]
Abdulaziz O., Hashim I., Momani S., . Application of homotopy–perturbation method to fractional IVPs. J. Comput. Appl. Math.. 2008;216(2):574-584.
[Google Scholar]
Baleanu D., Diethelm K., Scalas E., Trujillo J.J., . Fractional Calculus, of Series on Complexity, Nonlinearity and Chaos. Vol vol. 3. Hackensack, NJ, USA: World Scientific; 2012.
Elbeleze A., Kilicman A., Taib M.B., . Application of homotopy perturbation and variational iteration methods for Fredholm integro-differential equation of fractional order. Abstr. Appl. Anal.. 2012;2012 14 p.
[Google Scholar]
Gaul L., Klein P., Kemple S., . Damping description involving fractional operators. Mech. Syst. Signal Process.. 1991;5(2):81-88.
[Google Scholar]
Glockle W.G., Nonnenmacher T.F.A., . A fractional calculus approach of self-similar protein dynamics. Biophys. J.. 1995;68:46-53.
[Google Scholar]
He J.-H., . Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng.. 1999;178(3–4):257-262.
[Google Scholar]
He J.-H., . Variational iteration method-a kind of non-linear analytical technique: some examples. Int. J. Non-Linear Mech.. 1999;34(4):699-708.
[Google Scholar]
He J.-H., . A Coupling Method of Homotopy Technique and Perturbation Technique for Nonlinear Problems. Int. J. Non-Linear Mech.. 2000;35:37-43.
[Google Scholar]
He J.-H., . Homotopy perturbation method for solving boundary value problems. Phys. Lett. A. 2006;350(1–2):87-88.
[Google Scholar]
He J.-H., . Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fract.. 2005;26(3):695-700.
[Google Scholar]
He J.-H., . Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul.. 2005;6(2):87-88.
[Google Scholar]
He J.-H., . Homotopy perturbation method: a new nonlinear analytic technique. Appl. Math. Comput.. 2003;135:73-79.
[Google Scholar]
Hilfert R., . Applications of fractional calculus in physics. River Edge, NJ, USA: World Scientific; 2000.
Kadem A., Kilicman A., . The approximate solution of fractional Fredholm integrodifferential equations by variational iteration and homotopy perturbation methods. Abstr. Appl. Anal.. 2012;2012:10. Article ID 486193, 10 p.
[Google Scholar]
Kythe P.K., Puri P., . Computational methodsfor linear integralequations. Boston, Mass, USA: Birkhauser; 2002.
Liao S.J., . An approximate solution technique not depending on small parameters: a special example. Int. J. Non-Linear Mech.. 1995;30(3):371-380.
[Google Scholar]
Liao S.-J., . Boundary element method for general nonlinear differential operators. Eng. Anal. Boundary Elem.. 1997;20(2):91-99.
[Google Scholar]
Mainardi F., . Fractional calculus: some basic problems in continuum and statistical mechanics. In: Fractals and Fractional Calculus in Continuum Mechanics. In: CISM Courses and Lectures. Vol vol. 378. Vienna, Austria: Springer; 1997. p. :291-348.
[Google Scholar]
Podlubny I., . Fractional differential equations. In: Mathematics in Science and Engineering. Vol vol. 198. San Diego, Calif, USA: Academic Press; 1999.
[Google Scholar]
Yıldırım A., . Solution of BVPs for fourth-order integro-differential equations by using homotopy perturbation method. Comput. Math. Appl.. 2008;56(12):3175-3180.
[Google Scholar]