A reliable algorithm for solving nonlinear Jaulent–Miodek equation

Jafar Biazar; Mostafa Eslami

doi:10.1016/j.jksus.2010.06.021

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original Article

23 (

); 133-137

doi:

10.1016/j.jksus.2010.06.021

A reliable algorithm for solving nonlinear Jaulent–Miodek equation

Jafar Biazar, Mostafa Eslami^⁎

Department of Mathematics, Faculty of Sciences, University of Guilan, P.O. Box 413351914, P.C. 4193833697, Rasht, Iran

⁎Corresponding author. mostafa.eslami@hotmail.com (Mostafa Eslami)

Received: 2010-5-29, Accepted: 2010-6-29, Published: 2010-04-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 1 July 2010

Peer-review under responsibility of King Saud University.

Abstract

Homotopy perturbation method has been applied to solve many functional equations so far. In this work, we propose this method (HPM), for solving Jaulent–Miodek (JM) equation (Kaya and El-Sayed, 2003; Fan, 2003). Numerical solutions obtained by the homotopy perturbation method are compared with the exact solutions. The results for some values of the variables are shown in tables and the solutions are presented as plots as well, showing the ability of the method.

Keywords

A reliable algorithm

Jaulent–Miodek equation

Show Related Articles from PubMed

1 Introduction

Large varieties of physical, chemical, and biological phenomena are governed by nonlinear evolution equations. Except a limited number of these problems, most of them do not have precise analytical solutions, so they have to be solved by other methods which lead to closed approximate solutions or numerical solutions. Homotopy perturbation method has been used by many mathematicians and engineers to solve various functional equations. This method continuously deforms the difficult problems under study into a simple problem (He, 2000, 1999). In recent years the application of homotopy perturbation theory has appeared in many researches (He, 2003, 2004, 2005a, b, 2006; Biazar et al., 2007; Ariel et al., 2006; Siddiqui et al., 2006; Odibat and Momani, 2008; Cveticanin, 2006; Ozis and Yildirim, 2007 ).

2 Solution of system of partial differential equations by homotopy perturbation method

We first consider the system of partial differential equations written in an operator form

(1)

\begin{matrix} \frac{\partial u_{1}}{\partial t} + \frac{\partial u_{2}}{\partial x_{1}} + \dots + \frac{\partial u_{n}}{\partial x_{n - 1}} + N_{1} = g_{1}, \\ \frac{\partial u_{2}}{\partial t} + \frac{\partial u_{1}}{\partial x_{1}} + \dots + \frac{\partial u_{n}}{\partial x_{n - 1}} + N_{2} = g_{2}, \\ ⋮ \\ \frac{\partial u_{n}}{\partial t} + \frac{\partial u_{2}}{\partial x_{1}} + \dots + \frac{\partial u_{1}}{\partial x_{n - 1}} + N_{n} = g_{n} . \end{matrix}

with initial conditions

(2)

\begin{matrix} u_{1} (x_{1}, x_{2}, \dots x_{n - 1}, 0) = f_{1} (x_{1}, x_{2}, \dots x_{n - 1}), \\ u_{2} (x_{1}, x_{2}, \dots x_{n - 1}, 0) = f_{2} (x_{1}, x_{2}, \dots x_{n - 1}), \\ ⋮ \\ u_{n} (x_{1}, x_{2}, \dots x_{n - 1}, 0) = f_{n} (x_{1}, x_{2}, \dots x_{n - 1}) . \end{matrix}

Where

N_{1}, N_{2}, \dots N_{n}

are nonlinear operators, and

g_{1}, g_{2}, \dots g_{n}

are inhomogeneous terms.

To solve system (1) by homotopy perturbation method, we construct the following homotopies:

(3)

\begin{matrix} (1 - p) (\frac{\partial U_{1}}{\partial t} - \frac{\partial u_{10}}{\partial t}) \\ + p (\frac{\partial U_{1}}{\partial t} + \frac{\partial U_{2}}{\partial x_{1}} + \dots + \frac{\partial U_{n}}{\partial x_{n - 1}} + N_{1} - g_{1}) = 0, \\ (1 - p) (\frac{\partial U_{2}}{\partial t} - \frac{\partial u_{20}}{\partial t}) \\ + p (\frac{\partial U_{2}}{\partial t} + \frac{\partial U_{1}}{\partial x_{1}} + \dots + \frac{\partial U_{n}}{\partial x_{n - 1}} + N_{2} - g_{2}) = 0, \\ ⋮ \\ (1 - p) (\frac{\partial U_{n}}{\partial t} - \frac{\partial u_{n 0}}{\partial t}) \\ + p (\frac{\partial U_{n}}{\partial t} + \frac{\partial U_{2}}{\partial x_{1}} + \dots + \frac{\partial U_{1}}{\partial x_{n - 1}} + N_{n} - g_{n}) = 0 . \end{matrix}

consider the solution of the system (3) as the following

(4)

\begin{matrix} U_{1} = U_{10} + {pU}_{11} + p^{2} U_{12} + \dots, \\ U_{2} = U_{20} + {pU}_{21} + p^{2} U_{22} + \dots, \\ U_{3} = U_{30} + {pU}_{31} + p^{2} U_{32} + \dots, \\ ⋮ \\ U_{n} = U_{n 0} + {pU}_{n 1} + p^{2} U_{n 2} + \dots . \end{matrix}

Equating the coefficients of the terms with the identical powers of

p

leads to

p^{0} : \{\begin{matrix} \frac{\partial U_{10}}{\partial t} - \frac{\partial u_{10}}{\partial t} = 0, \\ \frac{\partial U_{20}}{\partial t} - \frac{\partial u_{20}}{\partial t} = 0, \\ ⋮ \\ \frac{\partial U_{n 0}}{\partial t} - \frac{\partial u_{n 0}}{\partial t} = 0, \end{matrix}

p^{1} : \{\begin{matrix} \frac{\partial U_{11}}{\partial t} + \frac{\partial u_{10}}{\partial t} + \frac{\partial U_{20}}{\partial x_{1}} + \dots + \frac{\partial U_{n 0}}{\partial x_{n - 1}} + M_{10} - g_{1} = 0, \\ \frac{\partial U_{22}}{\partial t} + \frac{\partial u_{20}}{\partial t} + \frac{\partial U_{10}}{\partial x_{1}} + \dots + \frac{\partial U_{n 0}}{\partial x_{n - 1}} + M_{20} - g_{2} = 0, \\ ⋮ \\ \frac{\partial U_{n 1}}{\partial t} + \frac{\partial u_{10}}{\partial t} + \frac{\partial U_{20}}{\partial x_{1}} + \dots + \frac{\partial U_{n 0}}{\partial x_{n - 1}} + M_{n 0} - g_{n} = 0, \end{matrix}

\begin{matrix} p^{2} : \{\begin{matrix} \frac{\partial U_{12}}{\partial t} + \frac{\partial U_{21}}{\partial x_{1}} + \dots + \frac{\partial U_{n 1}}{\partial x_{n - 1}} + M_{11} = 0, \\ \frac{\partial U_{22}}{\partial t} + \frac{\partial U_{11}}{\partial x_{1}} + \dots + \frac{\partial U_{n 1}}{\partial x_{n - 1}} + M_{21} = 0, \\ ⋮ \\ \frac{\partial U_{n 2}}{\partial t} + \frac{\partial U_{21}}{\partial x_{1}} + \dots + \frac{\partial U_{11}}{\partial x_{n - 1}} + M_{n 1} = 0, \end{matrix} \\ ⋮ \end{matrix}

\begin{matrix} p^{j} : \{\begin{matrix} \frac{\partial U_{1 j}}{\partial t} + \frac{\partial U_{2 j - 1}}{\partial x_{1}} + \dots + \frac{\partial U_{nj - 1}}{\partial x_{n - 1}} + M_{1 j - 1} = 0, \\ \frac{\partial U_{2 j}}{\partial t} + \frac{\partial U_{1 j - 1}}{\partial x_{1}} + \dots + \frac{\partial U_{nj - 1}}{\partial x_{n - 1}} + M_{2 j - 1} = 0, \\ ⋮ \\ \frac{\partial U_{nj}}{\partial t} + \frac{\partial U_{2 j - 1}}{\partial x_{1}} + \dots + \frac{\partial U_{1 j - 1}}{\partial x_{n - 1}} + M_{nj - 1} = 0 . \end{matrix} \\ ⋮ \end{matrix}

Where

M_{ij}, i = 1, 2, \dots n, j = 0, 1, 2, \dots n - 1

, are terms that are obtained with equating the coefficients of the nonlinear operators

N_{ij}

i = 1, 2, \dots n, j = 0, 1, 2, \dots n - 1

, with the identical powers of

p

For simplicity we take

(5)

\begin{matrix} U_{10} = u_{10} = f_{1} (x_{1}, x_{1}, \dots, x_{n - 1}), \\ U_{20} = u_{20} = f_{2} (x_{1}, x_{1}, \dots, x_{n - 1}), \\ ⋮ \\ U_{n 0} = u_{n 0} = f_{n} (x_{1}, x_{1}, \dots, x_{n - 1}) . \end{matrix}

So we have

\begin{matrix} U_{11} (x, t) = - \int_{0}^{t} (\frac{\partial U_{20}}{\partial x_{1}} + \dots + \frac{\partial U_{n 0}}{\partial x_{n - 1}} + M_{10} - g_{1}) dt, \\ U_{21} (x, t) = - \int_{0}^{t} (\frac{\partial U_{10}}{\partial x_{1}} + \dots + \frac{\partial U_{n 0}}{\partial x_{n - 1}} + M_{20} - g_{2}) dt, \\ ⋮ \\ U_{n 1} (x, t) = - \int_{0}^{t} (\frac{\partial U_{20}}{\partial x_{1}} + \dots + \frac{\partial U_{10}}{\partial x_{n - 1}} + M_{n 0} - g_{n}) dt . \end{matrix}

For j > 1, we derive the following recurrent relation

U_{1 j} (x, t) = - \int_{0}^{t} (\frac{\partial U_{2 j - 1}}{\partial x_{1}} + \dots + \frac{\partial U_{n 0}}{\partial x_{n - 1}} + M_{1 j - 1}) dt, j = 2, 3, \dots,

U_{2 j} (x, t) = - \int_{0}^{t} (\frac{\partial U_{1 j - 1}}{\partial x_{1}} + \dots + \frac{\partial U_{nj - 1}}{\partial x_{n - 1}} + M_{2 j - 1}) dt, j = 2, 3, \dots,

⋮

U_{nj} (x, t) = - \int_{0}^{t} (\frac{\partial U_{2 j - 1}}{\partial x_{1}} + \dots + \frac{\partial U_{1 j - 1}}{\partial x_{n - 1}} + M_{nj - 1}) dt, j = 2, 3, \dots .

The approximate solutions of (1) can be obtained by letting

p

tend to one

(6)

\begin{matrix} u_{1} = \lim_{p \to 1} U_{1} = U_{10} + U_{11} + U_{12} + \dots, \\ u_{2} = \lim_{p \to 1} U_{2} = U_{20} + U_{21} + U_{22} + \dots, \\ u_{3} = \lim_{p \to 1} U_{3} = U_{30} + U_{31} + U_{32} + \dots, \\ ⋮ \\ u_{n} = \lim_{p \to 1} U_{n} = U_{n 0} + U_{n 1} + U_{n 2} + \dots . \end{matrix}

3 Applications

Consider the following Jaulent–Miodek equation

(7)

\begin{matrix} \frac{\partial u}{\partial t} + \frac{\partial^{3} u}{\partial x^{3}} + \frac{3}{2} v \frac{\partial^{3} v}{\partial x^{3}} + \frac{9}{2} \frac{\partial v}{\partial x} \frac{\partial^{2} v}{\partial x^{2}} - 6 u \frac{\partial u}{\partial x} - 6 uv \frac{\partial v}{\partial x} - \frac{3}{2} \frac{\partial u}{\partial x} v^{2} = 0, \\ \frac{\partial v}{\partial t} + \frac{\partial^{3} v}{\partial x^{3}} - 6 \frac{\partial u}{\partial x} v - 6 u \frac{\partial v}{\partial x} - \frac{15}{2} \frac{\partial v}{\partial x} v^{2} = 0 . \end{matrix}

Subject to initial conditions

(8)

\begin{matrix} u (x, 0) = \frac{1}{4} c_{2} - \frac{1}{4} b_{0}^{2} - \frac{1}{2} b_{0} \sqrt{c_{2}} \sec h (\sqrt{c_{2}} x) - \frac{3}{4} c_{2} \sec h^{2} (\sqrt{c_{2}} x), \\ v (x, 0) = b_{0} + \sqrt{c_{2}} \sec h (\sqrt{c_{2}} x) . \end{matrix}

With the exact solutions

u = \frac{1}{4} (c_{2} - b_{0}^{2}) - \frac{1}{2} b_{0} \sqrt{c_{2}} \sec h (\sqrt{c_{2}} (x + \frac{1}{2} (6 b_{0}^{2} + c_{2}) t)) - \frac{3}{4} c_{2} \sec h^{2} (\sqrt{c_{2}} (x + \frac{1}{2} (6 b_{0}^{2} + c_{2}) t)),

v = b_{0} + \sqrt{c_{2}} \sec h (\sqrt{c_{2}} (x + \frac{1}{2} (6 b_{0}^{2} + c_{2}) t)) .

Where

b_{0}, c_{2}

are arbitrary constants.

For solving Eq. (7) with initial conditions (8) according to the homotopy perturbation method the following homotopy can be constructed $(1 - p) (\frac{\partial U}{\partial t} - \frac{\partial u_{0}}{\partial t}) + p (\frac{\partial U}{\partial t} + \frac{\partial^{3} U}{\partial x^{3}} + \frac{3}{2} V \frac{\partial^{3} V}{\partial x^{3}} + \frac{9}{2} \frac{\partial V}{\partial x} \frac{\partial^{2} V}{\partial x^{2}} - 6 U \frac{\partial U}{\partial x} - 6 UV \frac{\partial V}{\partial x} - \frac{3}{2} \frac{\partial U}{\partial x} V^{2}) = 0,$ $(1 - p) (\frac{\partial V}{\partial t} - \frac{\partial v_{0}}{\partial t}) + p (\frac{\partial V}{\partial t} + \frac{\partial^{3} V}{\partial x^{3}} - 6 \frac{\partial U}{\partial x} V - 6 U \frac{\partial V}{\partial x} - \frac{15}{2} \frac{\partial V}{\partial x} V^{2}) = 0,$ or $\frac{\partial U}{\partial t} - \frac{\partial u_{0}}{\partial t} + p (\frac{\partial u_{0}}{\partial t} + \frac{\partial^{3} U}{\partial x^{3}} + \frac{3}{2} V \frac{\partial^{3} V}{\partial x^{3}} + \frac{9}{2} \frac{\partial V}{\partial x} \frac{\partial^{2} V}{\partial x^{2}} - 6 U \frac{\partial U}{\partial x} - 6 UV \frac{\partial V}{\partial x} - \frac{3}{2} \frac{\partial U}{\partial x} V^{2}) = 0,$

(9)

\frac{\partial V}{\partial t} - \frac{\partial v_{0}}{\partial t} + p (\frac{\partial v_{0}}{\partial t} + \frac{\partial^{3} V}{\partial x^{3}} - 6 \frac{\partial U}{\partial x} V - 6 U \frac{\partial V}{\partial x} - \frac{15}{2} \frac{\partial V}{\partial x} V^{2}) = 0 .

Suppose the solutions of Eq. (9) has the following form

(10)

\begin{matrix} U = U_{0} + {pU}_{1} + p^{2} U_{2} + \dots \\ V = V_{0} + {pV}_{1} + p^{2} V_{2} + \dots . \end{matrix}

Substituting (10) into (9) and equating the coefficients of the terms with the identical powers of

p

leads to

P^{0} : \{\begin{matrix} \frac{\partial U_{0}}{\partial t} - \frac{\partial u_{0}}{\partial t} = 0, \\ \frac{\partial V_{0}}{\partial t} - \frac{\partial v_{0}}{\partial t} = 0, \end{matrix}

P^{1} : \{\begin{matrix} \frac{\partial U_{1}}{\partial t} + \frac{\partial u_{0}}{\partial t} + \frac{\partial^{3} U_{0}}{\partial x^{3}} + \frac{3}{2} V_{0} \frac{\partial^{3} V_{0}}{\partial x^{3}} + \frac{9}{2} \frac{\partial V_{0}}{\partial x} \frac{\partial^{2} V_{0}}{\partial x^{2}} - 6 U_{0} \frac{\partial U_{0}}{\partial x} \\ - 6 U_{0} V_{0} \frac{\partial V_{0}}{\partial x} - \frac{3}{2} \frac{\partial U_{0}}{\partial x} V_{0}^{2} = 0, \\ \frac{\partial V_{1}}{\partial t} + \frac{\partial v_{0}}{\partial t} + \frac{\partial^{3} V_{0}}{\partial x^{3}} - 6 \frac{\partial U_{0}}{\partial x} V_{0} - 6 U_{0} \frac{\partial V_{0}}{\partial x} - \frac{15}{2} \frac{\partial V_{0}}{\partial x} V_{0}^{2} = 0, \end{matrix}

\begin{matrix} P^{2} : \{\begin{matrix} \frac{\partial U_{2}}{\partial t} + \frac{\partial^{3} U_{1}}{\partial x^{3}} + \frac{3}{2} V_{0} \frac{\partial^{3} V_{1}}{\partial x^{3}} + \frac{3}{2} V_{1} \frac{\partial^{3} V_{0}}{\partial x^{3}} + \frac{9}{2} \frac{\partial V_{0}}{\partial x} \frac{\partial^{2} V_{1}}{\partial x^{2}} + \frac{9}{2} \frac{\partial V_{1}}{\partial x} \frac{\partial^{2} V_{0}}{\partial x^{2}} \\ - 6 U_{1} \frac{\partial U_{0}}{\partial x} - 6 U_{0} \frac{\partial U_{1}}{\partial x} - 6 U_{1} V_{0} \frac{\partial V_{0}}{\partial x} - 6 U_{0} V_{1} \frac{\partial V_{0}}{\partial x} \\ - 6 U_{0} V_{0} \frac{\partial V_{1}}{\partial x} - \frac{3}{2} \frac{\partial U_{1}}{\partial x} V_{0}^{2} - 3 \frac{\partial U_{0}}{\partial x} V_{1} V_{0} = 0, \\ \frac{\partial V_{2}}{\partial t} + \frac{\partial^{3} V_{1}}{\partial x^{3}} - 6 \frac{\partial U_{1}}{\partial x} V_{0} - 6 \frac{\partial U_{0}}{\partial x} V_{1} - 6 U_{1} \frac{\partial V_{0}}{\partial x} \\ - 6 U_{0} \frac{\partial V_{1}}{\partial x} - \frac{15}{2} \frac{\partial V_{1}}{\partial x} V_{0}^{2} - 15 \frac{\partial V_{0}}{\partial x} V_{1} V_{0} = 0, \end{matrix} \\ ⋮ \end{matrix}

\begin{matrix} P^{j} : \{\begin{matrix} \frac{\partial U_{j}}{\partial t} + \frac{\partial^{3} U_{j - 1}}{\partial x^{3}} + \frac{3}{2} \sum_{0}^{j - 1} V_{k} \frac{\partial^{3} V_{j - 1 - k}}{\partial x^{3}} + \frac{9}{2} \sum_{k = 0}^{j - 1} \frac{\partial V_{k}}{\partial x} \frac{\partial^{2} V_{j - 1 - k}}{\partial x^{2}} - 6 \sum_{k = 0}^{j - 1} U_{k} \frac{\partial U_{j - 1 - k}}{\partial x} \\ - 6 \sum_{i = 0}^{j - 1} \sum_{k = 0}^{j - i - 1} U_{i} V_{k} \frac{\partial V_{j - k - i - 1}}{\partial x} - \frac{3}{2} \sum_{i = 0}^{j - 1} \sum_{k = 0}^{j - i - 1} \frac{\partial U_{i}}{\partial x} V_{k} V_{j - k - i - 1} = 0, \\ \frac{\partial V_{j}}{\partial t} + \frac{\partial^{3} V_{j - 1}}{\partial x^{3}} - 6 \sum_{k = 0}^{j - 1} \frac{\partial U_{k}}{\partial x} V_{j - 1 - k} - 6 \sum_{k = 0}^{j - 1} U_{k} \frac{\partial V_{j - 1 - k}}{\partial x} \\ - \frac{15}{2} \sum_{i = 0}^{j - 1} \sum_{k = 0}^{j - i - 1} \frac{\partial V_{i}}{\partial x} V_{k} V_{j - k - i - 1} = 0, \end{matrix} \\ ⋮ \end{matrix}

Let us start with initial approximations

u (x, 0)

and

v (x, 0)

given by Eq. (8)

(11)

\begin{matrix} U_{0} = u_{0} = \frac{1}{4} c_{2} - \frac{1}{4} b_{0}^{2} - \frac{1}{2} b_{0} \sqrt{c_{2}} \sec h (\sqrt{c_{2}} x) - \frac{3}{4} c_{2} \sec h^{2} (\sqrt{c_{2}} x), \\ V_{0} = v_{0} = b_{0} + \sqrt{c_{2}} \sec h (\sqrt{c_{2}} x) . \end{matrix}

And we have the following recurrent equations for

j = 1, 2, 3, \dots

(12)

\begin{matrix} U_{j} = - \int_{0}^{t} (\begin{matrix} \frac{\partial^{3} U_{j - 1}}{\partial x^{3}} + \frac{3}{2} \sum_{k = 0}^{j - 1} V_{k} \frac{\partial^{3} V_{j - 1 - k}}{\partial x^{3}} + \frac{9}{2} \sum_{k = 0}^{j - 1} \frac{\partial V_{k}}{\partial x} \frac{\partial^{2} V_{j - 1 - k}}{\partial x^{2}} \\ - 6 \sum_{k = 0}^{j - 1} U_{k} \frac{\partial U_{j - 1 - k}}{\partial x} - 6 \sum_{i = 0}^{j - 1} \sum_{k = 0}^{j - i - 1} U_{i} V_{k} \frac{\partial V_{j - k - i - 1}}{\partial x} \\ - \frac{3}{2} \sum_{i = 0}^{j - 1} \sum_{k = 0}^{j - i - 1} \frac{\partial U_{i}}{\partial x} V_{k} V_{j - k - i - 1} \end{matrix}) dt, \\ V_{j} = - \int_{0}^{t} (\frac{\partial^{3} V_{j - 1}}{\partial x^{3}} - 6 \sum_{k = 0}^{j - 1} \frac{\partial U_{k}}{\partial x} V_{j - 1 - k} - 6 \sum_{k = 0}^{j - 1} U_{k} \frac{\partial V_{j - 1 - k}}{\partial x} \\ - \frac{15}{2} \sum_{i = 0}^{j - 1} \sum_{k = 0}^{j - i - 1} \frac{\partial V_{i}}{\partial x} V_{k} V_{j - k - i - 1}) dt . \end{matrix}

All terms of the expansions (10) can be obtained via iterative formula (12)

U_{1} = \frac{3}{4} \sqrt{c_{2}^{5}} \sec h^{2} (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x) t + 6 b_{0} c_{2}^{2} \sec h (\sqrt{c_{2}} x) \tanh^{3} (\sqrt{c_{2}} x) t - \frac{23}{4} b_{0} c_{2}^{2} \sec h (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}}) x) t + \frac{3}{2} {tb}_{0}^{3} c_{2} \sec h (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x) + \frac{9}{2} {tb}_{0}^{2} \sqrt{c_{2}^{3}} \sec h^{2} (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x) + 6 {tb}_{0} c_{2}^{2} \sec h^{3} (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x),

V_{1} = 6 c_{2}^{2} \sec h (\sqrt{c_{2}} x) \tanh^{3} (\sqrt{c_{2}} x) t - \frac{13}{2} c_{2}^{2} \sec h (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x) t - 3 {tb}_{0}^{2} c \sec h (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x) + 6 {tc}_{2}^{2} \sec h^{3} (\sqrt{c_{2}} x) \tanh (\sqrt{c_{2}} x),

⋮

An approximation to the solution of (7) can be obtained by letting

p

tend to one.

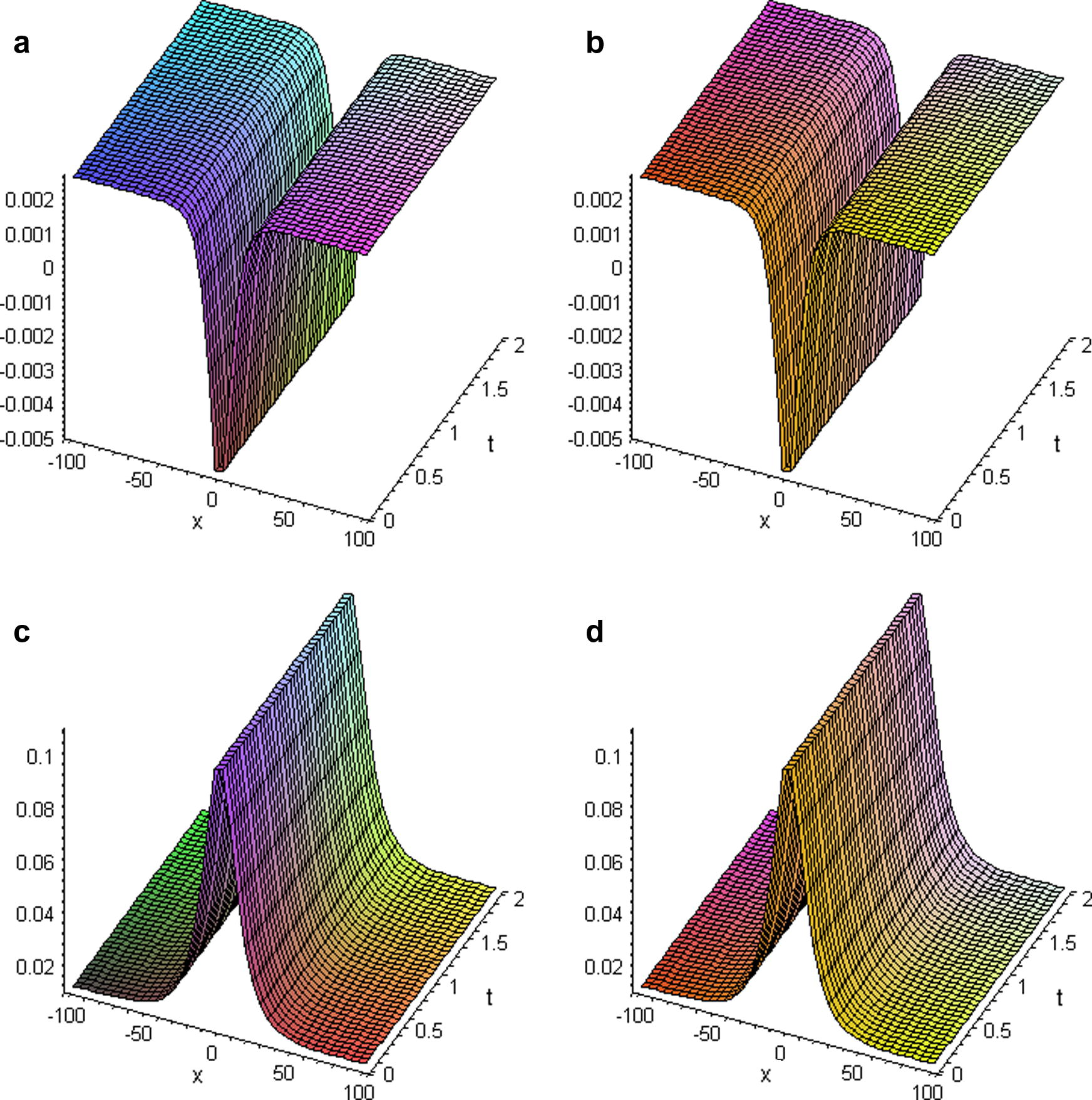
For numerical study four terms approximations have been considered. Suppose $u^{*} = \sum_{j = 0}^{3} U_{j},$ and $v^{*} = \sum_{j = 0}^{3} V_{j},$ the results are presented in Table 1 and Fig. 1

Table 1 The numerical results, when

b_{0} = c_{2} = 0.01

for solutions of Eq. (7) for initial conditions (8).

$x$	$t$	$u^{*} (x, t)$	$\| u^{*} - u \|$	$v^{*} (x, t)$	$\| v^{*} - v \|$
0.1	0.1	−0.00552421681535966474	$4 \times 10^{- 20}$	0.109994947072326492	$1.6 \times 10^{- 19}$
0.1	0.15	−0.00552421268119929705	$2.1 \times 10^{- 19}$	0.109994920399016371	$8.3 \times 10^{- 19}$
0.15	0.1	−0.00552324416776666749	$4 \times 10^{- 20}$	0.109988671429124380	$1.6 \times 10^{- 19}$
0.2	0.3	−0.00552185135682729130	$3.26 \times 10^{- 18}$	0.109979684175985571	$1.329 \times 10^{- 17}$
0.35	0.25	−0.00551544200337122719	$1.55 \times 10^{- 18}$	0.109938317095391529	$6.37 \times 10^{- 18}$
0.45	0.45	−0.00550916080832543826	$1.622 \times 10^{- 17}$	0.109897761088575401	$6.657 \times 10^{- 17}$
0.5	0.3	−0.00550553384209772092	$3.19 \times 10^{- 18}$	0.109874335473663468	$1.311 \times 10^{- 17}$
0.45	0.7	−0.00550906801481426520	$9.504 \times 10^{- 17}$	0.109897161826108341	$3.8981 \times 10^{- 16}$
0.4	0.8	−0.00551234934376313588	$1.6273 \times 10^{- 16}$	0.109918350605131830	$6.6674 \times 10^{- 16}$
0.8	0.8	−0.00547508560544371429	$1.5616 \times 10^{- 16}$	0.109677468293014595	$6.4730 \times 10^{- 16}$
0.85	0.95	−0.00546861261467419606	$3.0831 \times 10^{- 16}$	0.109635567784157087	$1.28058 \times 10^{- 15}$
0.9	0.9	−0.00546189829138478970	$2.4645 \times 10^{- 16}$	0.109592087075285587	$1.02594 \times 10^{- 15}$
0.95	0.9	−0.00545477408645114569	$2.4448 \times 10^{- 16}$	0.109545931955545074	$1.02005 \times 10^{- 15}$
1	1	−0.00544719469399408060	$3.6944 \times 10^{- 16}$	0.109496805097819525	$1.54524 \times 10^{- 15}$

The numerical results for u ∗ ( x , t ) , v ∗ ( x , t ) are, respectively, (a) and (c) in comparison with the analytical solutions u ( x , t ) and v ( x , t ) are, respectively, (b) and (d) with the initial conditions (8) of Eq. (7), when b 0 = 0.01 and c 2 = 0.01 .

4 Conclusions

In this article, we have applied homotopy perturbation method for solving the nonlinear Jaulent–Miodek (JM) equation (Kaya and El-Sayed, 2003; Fan, 2003). The approximate solutions obtained by the homotopy perturbation method are compared with the exact solutions. The results show that the homotopy perturbation method is a powerful mathematical tool for solving systems of nonlinear partial differential equations, which appears in mathematical modeling of different phenomena. This model has been solved by Adomian method, as well (Kaya and El-Sayed, 2003) Homotopy perturbation method in comparison with Adomian’s decomposition method has the advantage of overcoming the difficulty arising in calculating Adomain polynomial in ADM. In our work, we use the maple package to carry the computations.

References

Ariel P.D., Hayat T., Asghar S., . Homotopy perturbation method and axisymmetric flow over a stretching sheet. International Journal of Nonlinear Science and Numerical Simulation. 2006;7(4):399-406.
[Google Scholar]
Biazar J., Eslami M., Ghazvini H., . Homotopy perturbation method for systems of partial differential equations. International Journal of Nonlinear Science and Numerical Simulation. 2007;8(3):411-416.
[Google Scholar]
Cveticanin L., . Homotopy-perturbation method for pure nonlinear differential equation. Chaos, Solitons and Fractals. 2006;30:1221-1230.
[Google Scholar]
Fan Engui, . Uniformly constructing a series of explicit exact solutions to nonlinear equations in mathematical physics. Chaos, Solitons and Fractals. 2003;16:819-839.
[Google Scholar]
He J.H., . Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering. 1999;178:257-262.
[Google Scholar]
He J.H., . A coupling method of homotopy technique and perturbation technique for nonlinear problems. International Journal of Non-Linear Mechanics. 2000;35(1):37-43.
[Google Scholar]
He J.H., . Homotopy perturbation method: a new nonlinear analytical technique. Applied Mathematics and Computation. 2003;135:73-79.
[Google Scholar]
He J.H., . The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation. 2004;151:287-292.
[Google Scholar]
He J.H., . Application of homotopy perturbation method to nonlinear wave equations. Chaos, Solitons and Fractals. 2005;26:695-700.
[Google Scholar]
He J.H., . Limit cycle and bifurcation of nonlinear problems. Chaos, Solitons and Fractals. 2005;26(3):827-833.
[Google Scholar]
He J.H., . Homotopy perturbation method for solving boundary value problems. Physics Letters A. 2006;350:87-88.
[Google Scholar]
Kaya D., El-Sayed S.M., . A numerical method for solving Jaulent–Miodek equation. Physics Letters A. 2003;318:345-353.
[Google Scholar]
Odibat Z., Momani S., . Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. Chaos, Solitons and Fractals. 2008;36(1):167-174.
[Google Scholar]
Ozis T., Yildirim A., . A note on He’s homotopy perturbation method for van der Pol oscillator with very strong nonlinearity. Chaos, Solitons and Fractals. 2007;34(3):989-991.
[Google Scholar]
Siddiqui A.M., Zeb A., Ghori Q.K., . Homotopy perturbation method for thin film flow of a fourth grade fluid down a vertical cylinder. Physics Letters A. 2006;352:404-410.
[Google Scholar]