Translate this page into:
Theoretical analysis and of three dimensional free surface of electrospinning
⁎Corresponding authors. zhyliang@dhu.edu.cn (Zhiyong Liang), xhqin@dhu.edu.cn (Xiaohong Qin)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Electrospinning is a new type of free-end spinning built on the electric field. The electric force of PAN polymer solution overcomes the surface tension of the solution, and then it causes wave and forms jet flow. In the process of injection, the solution is evaporated or solidified, and eventually forming a fiber on the receiving device. Different from ordinary single needle head, in this study, a new type of three-dimension free surface nozzle is used to produce multiple jets at the same time, this will greatly improve production efficiency. In this paper the model of three-dimension free surface is analyzed by the theory of fluid mechanics, the relationship among the wave length and surface tension and the electric field is obtained. Through the experiment, the conclusion is verified, and the formula is correct.
Keywords
Electrospinning
Free surface
Surface tension
Wavelength
1 Introduction
Electrostatic spinning method is a kind of new method for preparation of polymer nanofibers. Because of its simple equipment, less cost and convenient operation, it is widely used in mass production of polymer nanofibers. Since 1970, Dupont Company developed nanofibers, a lot of breakthrough have been achieved in the development of electrostatic spinning. Reneker started the study of electrostatic spinning in 1995, they first proposed that nanofibers with axial orientation. In 2002, Hohman studied the electrostatic spinning’s stability, and the stability theorem is presented. Domestic research also presents a diversified trend. Donghua university uses the PAN and Cellulose Acetate to make porous nanofibers. Jiang Nan University uses nylon 6 (PA6) and polymerization of ethylene oxide (PEO) to make composite nanofiber felt. Zhejiang University of science and technology uses formic acid as solvent to make regenerated silk fibroin nanofibers by electrostatic spinning method. Although electrostatic nanofibers have many advantages, but the existing spinning method’s output is low, it is not conducive to industrialization production.
By applying high voltage to PAN solution, it creates a large electric field between the nozzle and the receiver. The electric field force exerted on the surface of the solution produces an electrical current. Since like charges repel each other, electric field force is contrast to the solution surface tension. When electric field force is equal to the solution surface tension, the charged droplet is hanging in balance at the end of the capillary. With the increase of electric field force, capillary at the ends of the droplet under the action of electric field force will be stretched into cone shape, and then a Taylor cone is formed. Finally, the solution overcomes the surface tension and forms the jet flow. After evaporation and curing, the solvent becomes nanofibers on receiving device.
As a result of the traditional single needle spinning method can only produce a single jet, the production efficiency is extremely low, this study adopts three-dimensional free liquid surface electrostatic spinning technology. This research adopts a kind of three layers of round free surface nozzle which is designed by Donghua University. Because at the edges of each layer of the nozzle have maximum electric field intensity, the electric charge accumulation produced by polymer solution surface will make larger electric field force imposed on the edge of the solution. So when the electric field force is large enough, the edge of the solution surface will produce tiny fluctuations. Each peak position is equivalent to a Taylor cone. In this way, the peak position will pull out fiber, this will greatly improving the production efficiency. The nozzle’s sketch map is shown in Fig. 1: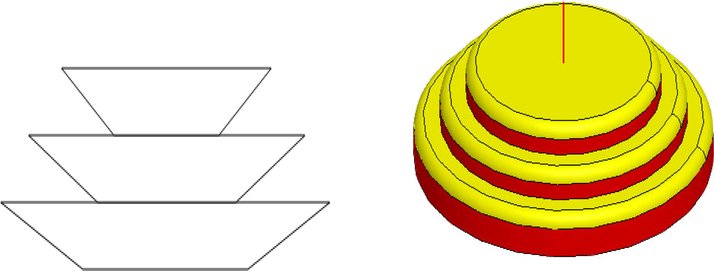
The three dimensional free surface nozzle’s sketch map.
2 Mechanism analysis of three dimensional free surface electrostatic spinning
2.1 Current physical theory analysis
Electro-fluid mechanics study involves the fluid mechanics, computational fluid mechanics, electromagnetism, physical chemistry and so on, it mainly analyzes the electric field force and fluid force interaction and its impact in the medium. Electro-fluid mechanics equation consists of electromagnetism equations and fluid mechanics equations.
Maxwell’s equations as follows:
Fluid equations of mass conservation equation and momentum conservation equation are as follows:
The leakage medium model of electric field to:
Equations on the right side respectively express Coulomb force, bound charge force and electrostrictive force.
2.2 The three-dimension model of the free surface electrostatic spinning method
The three-dimension free surface electrostatic spinning method of experimental model can generate multiple Taylor cone. Due to the small fluctuation occurs on the surface of the polymer solution and combined with the related knowledge of fluid mechanics we can establish a microwave on the surface of the polymer solution model to analyze it. Due to round nozzle is adopted in the experiment, each layer within the edge has the maximum electric field strength, electric field distribution is uniform, the electric field intensity is determined by the applied voltage. We only select a layer of solution to analyze. The circular symmetrical model is simplified to one-dimension linear model. As shown in Fig. 2, solution connects the anode voltage, receiving device is polarity negative ground. The high voltage static electric field between the two metal plate can make the solution surface charge polarization and produce electric field force. If the voltage is large enough, the solution surface will break through the steady state and continue to fluctuate, finally it will pull out nanofibers in the wave crest.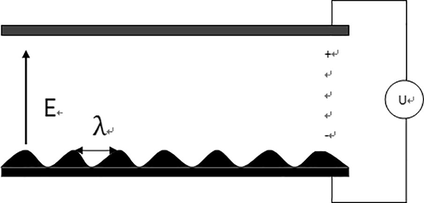
3-d model for the free surface electrostatic spinning.
2.3 Mechanics analysis of the electrostatic spinning jet
The surface tension of liquid surface is due to the gravitational pull of uneven between molecules. The existence of surface tension, by definition, is to shrink the surface of the polymer solution. Because of the stress uniform symmetry, the internal molecular of solution’s resultant force is zero. The surface molecule’s gravity is greater than the air molecule’s. Surface molecule has a tendency of inward movement. On the edge of the solution is in a horizontal steady state. In electrostatic spinning jet, tensile force is imposed by the difference of electric field force and surface tension. As a kind of leaky dielectric, charges only distribute on the surface of the polymer solution. After high pressure electric field applied, edge layer solution will be subject to an electric field force which is produced by charge polarization.
2.4 Layer of polymer solution under the effect of high-voltage electrostatic field mathematical model
In the free surface electrostatic spinning of study, this study uses PAN solution is a kind of incompressible Newtonian fluid. The density of the solution of different concentration and shear viscosity are constant. Due to the molecular thermodynamic instability, in the gas-liquid interface solution can produce capillary wave disturbance. We generally adopt sine wave equation to describe the disturbance. First we present the equation of motion of the disturbance wave:
By the Navier-Stokes equations of fluid mechanics:
In the above formula, ρ is fluid density, ν is fluid velocity, t is time, p is pressure, μ is coefficient of viscosity, λ is expansion viscous coefficient, is outside force.
In this study, the solution we adopt is a kind of incompressible fluid. By its definition we can know that fluid density is constant, that is . By the fluid continuity equation we can get: , for further reduction formula available:
Considering the solution of the viscous effects, the flow of the solution speed is very slow, almost can be thought of as the static flow, namely . External force in the form of volume force can be added to the pressure and then we can get:
Polymer free liquid on the surface of the internal pressure is equal to the external surface tension of liquid. By the continuity on the surface of the gas-liquid interaction can be obtained:
Because there is no pressure on the surface of the gas, that result in the gas phase on the interface of viscous force and the surface tension force is equal to zero, that is . Because the rate of non-zero entries in x direction so the above formula can be represented as:
After integral it can be represented as: and are constant, they can be obtained by the boundary conditions.
Analyze the motion of the solution we can get that solution layer and metal solid border have no slip boundary, at , the solution and gas phase interface is a free pressure liquid surface. Therefore we can analyze the following boundary conditions:
Considering these boundary conditions, we can obtain , . Then we can obtain the velocity distribution:
By the velocity distribution, the average velocity of solution can be obtained:
On the surface of , the flow can be obtained by the average speed:
Further, through the law of conservation of quality, we can get this experimental model of incompressible fluid flow conditions, namely:
And since , further we can obtain:
The above formula is free surface electrostatic spinning’s continuity equation of the one-dimensional model of polymer solution. From the above formula we can know that the change of the height of the solution in the vertical direction will cause the horizontal movement. Solution appears fluctuations, produces peaks and troughs and the movement of solution gradually moves forward. Through the above analysis, we can obtain the equation of motion of the polymer solution, namely:
The equation of motion can be concluded that the stress P and polymer solution at the gas-liquid interface of exercise has a direct relationship. From our research object and you can see, the pressure mainly includes electric field force and surface tension. The above analysis shows that the surface tension of the solution surface is to make the solution surface tend to shrink, the solution surface will therefore tend to be gentle and steady. On the contrary, the electric field force which is produced by high voltage electric field is opposite to surface tension, this will make the solution surface tends to be unstable. Through the analysis, the expression of pressure can be given as follows:
is the surface tension, or known as capillary pressure, is the electrostatic voltage which is produced by high voltage electric field, is gravity pressure. For capillary pressure, it can be obtained by the following formula:
R is the radius of curvature of the liquid layer of polymer solution, it can be obtained by the following formula:
Based on the analysis of all the above, we can obtain:
For the electrostatic voltage, it can be obtained by the following formula:
is the permittivity of vacuum and . is the dielectric constant of the polymer solution, it differs from different concentration of the polymer solution. is the electric field intensity of the surface solution. We can calculate the total capacitance by cascading the air capacitor and the solution capacitor.
For the electrostatic voltage , it can be obtained by the following formula:
By the wave theory of knowledge, the arbitrary tiny vibration wave equation can be approximately seen as a sine curve: ζ is the amplitude of the wave, q is the wave vector, is the rate of rise.
After derivation, the above formulas can be calculated:
After dividing out all the nonlinear term, we can get:
After calculating partial differential and dividing , the above formula can be written as:
We can know from the dispersion relation that the change of wave vector is closely related to the dispersion relation. Without outside pressure, the disturbance will gradually disappear because of the existence of surface tension, and it will finally reach a steady state. We need to require wavelength when the fluctuation grows the fastest. When the above formula’s derivation is zero, the growth of the fluctuation reaches peak, and then the growth will be subdued.
When , the fluctuation grows the fastest, then we can obtain the corresponding wavelength is:
Finally substituting the electric field intensity and electrostatic voltage formula into the above formula, we can get the relationship between the wavelength λ and surface tension γ and the voltage U:
Conclusion from the above two formulas: the wavelength λ is directly proportional to the surface tension , the wavelength λ is inversely proportional to the voltage U.
3 Conclusions
This paper involves a thorough theoretical deduction on the three dimensional free surface nozzle of the electrostatic spinning equipment’s working mechanism. Through the establishment of the fluid mechanics model and the basic formula, we get the relationship of the wavelength of the nanofibers and the surface tension of the PAN polymer solution and the voltage of high voltage electric field. In conclusion:
-
(1)
In the three-dimension free surface electrostatic spinning, the polymer solution surface is mainly subject to surface tension and electric field force. When the electric field force is big enough, the solution at the surface of edge will fluctuate and generate jet flow a peak position. After evaporation and curing, the solvent becomes nanofibers on receiving device.
-
(2)
For three-dimension free surface electrostatic spinning method, we establish a one-dimensional mathematical model. We analysis the surface boundary solution’s wave equation and Navier-Stokes equation. We also combine electromagnetism principle with the dispersion relations to study. Finally we obtain the related formula, from these formula we can get wavelength is directly proportional to half time the surface tension of solution, is inversely proportional to the voltage.
Acknowledgements
This work was partly supported by the Chang Jiang Youth Scholars Program of China and grants (51373033 and 11172064) from the National Natural Science Foundation of China to Prof. Xiaohong Qin. As well as “The Fundamental Research Funds for the Central Universities” and “DHU Distinguished Young Professor Program” to her. It also has the support of the Key grant Project of Chinese Ministry of Education (No 113027A). This work has also been supported by “Sailing Project” from Science and Technology Commission of Shanghai Municipality (14YF1405100) to Dr. Hongnan Zhang.







