Translate this page into:
Thermal radiation on unsteady electrical MHD flow of nanofluid over stretching sheet with chemical reaction
⁎Corresponding author at: UTM Centre for Industrial and Applied Mathematics, Ibnu Sina Institute for Scientific and Industrial Research, 81310 UTM Johor Bahru, Johor, Malaysia. zainalaz@utm.my (Zainal Abdul Aziz),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
Unsteady MHD natural convection flow of revised nanofluid is formulated. Thermal radiation, viscous dissipation, and Joule heating are used in the energy equation. Pertinent parameters with suction/injection and chemical reaction are examined. Computations are made through implicit finite difference scheme.
Abstract
This paper focuses on the effects of suction as well as thermal radiation, chemical reaction, viscous dissipation and Joule heating on a two-dimensional natural convective flow of unsteady electrical magnetohydrodynamics (MHD) nanofluid over a linearly permeable stretching sheet. One significant aspect of this study is that electric field employed in revised Buongiorno model has been introduced in view of enhancement of thermal conductivity and consequently better convective heat transfer. The constitute governing equations have been converted into strong non-linear ordinary differential equations by employing suitable transformations and these transformed equations are solved by the Implicit finite difference. From this study, it is found that the presence of magnetic field and suction slows down the fluid motion while it enhances for higher values of an electric field which tends to firmness sticky effect. It is also found that enhancing thermal radiation leads to an increase in nanofluid temperature. The Nusselt number increases with both Brownian motion and unsteadiness parameters.
Keywords
MHD nanofluid
Thermal radiation
Chemical reaction
Electric field
Suction
Nomenclature
-
magnetic field
-
applied magnetic field
-
skin friction coefficient
-
Brownian diffusion coefficient
-
thermophoresis diffusion coefficient
-
electric field factor
-
electrical field parameter
-
applied electric field
-
Eckert number
-
dimensionless velocity
-
Grashof number
-
mass Grashof number
-
Joule current
-
rate of chemical reaction
-
thermal conductivity
-
thermal conductivity of the base fluid and nanoparticle
-
magnetic field parameter
-
Brownian motion parameter
-
thermophoresis parameter
-
Nusselt number
-
Prandtl number
-
wall mass flux
-
radiative heat flux
-
wall heat flux
-
radiation parameter
-
local Reynolds number
-
temperature
-
reference temperature
-
surface temperature at the wall
-
ambient temperature
-
velocity component along and direction
-
stretching velocity
-
velocity fluid
-
wall mass transfer
-
Steffan-Boltzmann constant
-
electrical conductivity
-
unsteadiness parameter
-
dimensionless similarity variable
-
dynamic viscosity of the fluid
-
kinematic viscosity of the fluid
-
density
-
particle density
-
density of the fluid
-
heat capacity of the fluid
-
effective heat capacity of a nanoparticle
-
stream function
-
concentration of the fluid
-
reference concentration
-
nanoparticle volume fraction at the surface
-
ambient concentration
-
dimensionless temperature
-
dimensionless concentration
-
ratio between the effective heat transfer capacity and the heat capacity of the fluid
-
surface shear stress
-
chemical reaction parameter
Greek symbols
-
condition at the free stream
-
condition at the wall/surface
Subscripts
1 Introduction
In recent times, Magnetohydrodynamics (MHD) boundary layer flow and heat transfer of electrically conducting fluids have various science, engineering and industrial applications include petroleum industries, crystal growth, geothermal engineering, nuclear reactors, liquid metals, aerodynamics and metallurgical processes (Hsiao, 2016; Khan et al., 2016, 2017c; Ullah et al., 2017; Makinde et al., 2017, 2016; Makinde and Animasaun, 2016; Ibrahim and Makinde, 2016; Hayat et al., 2017e, 2016b; Daniel, 2015c). Considering the effects of natural convective heat transfer occurrences tangled usually in the fields of science and engineering with relevant applications to geothermal systems, solar energy collectors, space technology, cooling of electronic equipment, lubricants, cooling of nuclear reactors etc (Sheikholeslami et al., 2016; Sheremet et al., 2016; Hayat et al., 2016a, 2017d, 2017c; Daniel, 2015a,b). Natural convection against permeable media has been employed for chemical catalytic, insulation for buildings, grain storage, reactors etc. Advanced kinds of fluid were required to meet up with the demands and expectations for more efficient performance in devices. Nanofluid was proposed a new kind of fluid to improve the thermal conductivity and convective heat transfer. This is achieved through ultrafine composed of nanoparticles of size 1–100 nm dispersed in a convention fluid (Choi and Eastman, 1995; Sharma et al., 2019). This fascinating features of kind of fluid known as nanofluids play a remarkable role in convective heat transfer processes. A novel kind of fluid should be interchanged as a replacement for of common working fluid. The virtue of enhanced thermal conductivity, nanofluids can be regarded as the best for heat transfer agents to pure fluid due to unpredictable enhancement (Kasaeian et al., 2017; Tamoor et al., 2017; Hayat et al., 2016c,g). Consequently, this draws the attention of various researchers to the analysis of convective boundary layer flow and heat transfer in nanofluids highly (Sheikholeslami and Ganji, 2017; Nayak et al., 2017; Waqas et al., 2016; Ahmed et al., 2019; Daniel et al., 2017c,b,a; Daniel, 2016a). Buongiorno (2006) developed a unique analytical model for the convective transport phenomena in nanofluid by considering Brownian motion and thermophoresis effects. Several authors have studied the problem of MHD boundary layer flow, heat and mass transfer about different surface geometries in electrically conducting fluids. Influence of Lorentz forces on nanofluid flow motion and thermal radiation (Sheikholeslami, 2017; Biglarian et al., 2017; Sheikholeslami and Shamlooei, 2017; Pal and Mandal, 2017; Khan and Azam, 2017; Daniel et al., 2017d; Daniel and Daniel, 2015; Daniel, 2016b). Radiative heat transfer is crucial due to remarkable applications includes power generation, nuclear reactor cooling, and combustion (Nayak et al., 2017; Hayat et al., 2017b; Sheikholeslami and Shehzad, 2017; Hayat et al., 2017a, 2016e; Daniel et al., 2017e). Such influences largely happened when the dissimilarity between the surface and ambient temperature is enormous, mostly in space vehicle re-entry, astrophysical flows, fossil fuel, solar power technology etc. Good insight of the processes involved in solar radiation has vital roles in the design of innovative energy conversion systems achieved at the advanced temperature (Sheikholeslami and Rokni, 2017; Waqas et al., 2017).
The chemical reaction stimulus a great role in the investigation involving heat and mass transfer in areas of science and engineering technology as result of wide coverage of industrial applications (Hayat et al., 2016d). It is deliberated to be essential as results of its key role in the design of chemical processing equipment, polymer production, cooling towers, pollution, creation and distribution of fog, temperature and fibrous insulation, etc (Khan et al., 2017a,b; Hayat et al., 2017f,h). Raw materials are built to go through the chemical reaction in industrial chemical practices to transform economy raw materials into advanced standard produces such as oxidation and synthesis of constituents, destruction of crops as results of cold, processing of food, moisture dispersal on cultivated fields, etc. Such chemical transformations are performed in a reactor. A chemical reaction between the conventional liquid and nanoparticles are classified as a homogeneous reaction during a given phase or heterogeneous reaction that is surrounded by a boundary of the phase. Reaction rate in a first-order chemical reaction is straightly related to the concentration. In view of the pertinent applications, several authors have considered and produced their results on chemical reaction effects on the flow of heat and mass transfer with different geometries (Hayat et al., 2016f, 2017g; Pontes et al., 2019).
The main aim here is to investigate the unsteady hydromagnetic natural convective flow of a revised nanofluid bounded by a linearly stretching sheet with an electric field. Flow analysis is investigated through permeable linear sheet which is imperiled to a transverse magnetic field normal to the plate. Brownian motion and thermophoresis are developed in energy and concentration expressions with chemical reaction. The boundary condition is passively controlled rather than active (Kuznetsov and Nield, 2013) with base fluid water (Mabood et al., 2015). Natural convection flow phenomenon has been studied in view of thermal radiation, viscous dissipation, and Joule heating as well as chemical reaction with the effect of suction considering passively flow behavior; this variation has not been considered by previous investigators. Hence, the motivation of this paper is to bridge this knowledge gap. The governing mathematical systems are supplementary compound and linear in the frame of unsteady natural convection impacts. The arising mathematical modeling is scrutinized through the implementation of implicit finite difference scheme. The nonlinear ordinary differential systems of equations are computed with the sundry parameters. The nanofluid velocity, thermal and nanoparticle concentration fields are presented graphically and in tabular form in view of a number of governing parameters. Representation of skin friction coefficient and local Nusselt number are addressed through numerical values. It is hoped that the achieved results based on the computational scheme will not only provide valuable information for applications but also serve as a foundation for studying other related systems in engineering and industrial applications such as in polymer, food processing technology, and chemical manufacturing industries, numerous attempts have been made to analyze the effect of transverse magnetic field on boundary layer flow characteristics.
2 Mathematical formulation
Consider thermal radiation, chemical reaction, viscous dissipation and Joule heating on a two-dimensional unsteady natural convection flow of electrical magnetohydrodynamic (MHD) nanofluid due to a linearly stretching sheet with suction effect. The velocity of the stretching sheet is denoted as
, where
is the stretching rate and
represent the constant having dimension (time)-1 such as (
). The boundary layer equations of the fluid flow are consist of the continuity equation, the momentum equation, energy equation and concentration equation, the flow equation is formulated based on Maxwell’s equation, Ohm’s law in the presence of electrical Magnetohydrodynamics (MHD). The flow is due to stretching of the sheet from a slot through two equal and opposite force and thermally radiative. Magnetic and electric fields of strength
and
are applied normal to the flow field, such that the magnetic Reynolds number is selected small. The induced magnetic field is smaller to the applied magnetic field. Hence the induced magnetic field is absence for small magnetic Reynolds number. We choose the Cartesian coordinate system such that
is chosen along the stretching sheet and
-axis denotes the normal to the stretching sheet,
and
are the velocity components of the fluid in the
and
-direction see Fig. 1. The two-dimensional natural convection of electrical magnetohydrodynamic (MHD) boundary layer flow equations (Pal and Mondal, 2010; Hayat et al., 2014; Hsiao, 2017; INCLINED, 2003; Mukhopadhyay and Dandapat, 2004):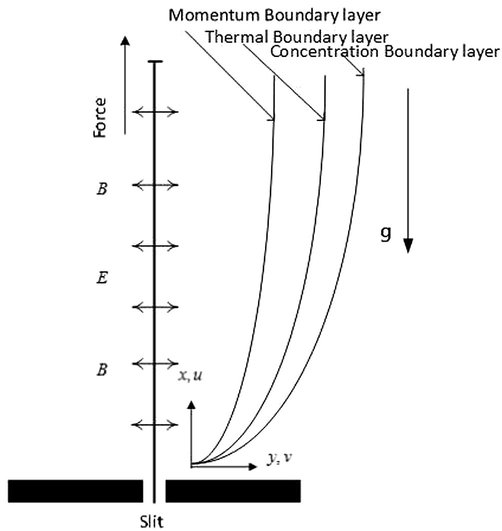
Physical configuration of the geometry.
Continuity equation
Energy equation
The boundary conditions at the sheet for the physical model are presented by
The radiative heat flux
via Rosseland approximation as discussed in (Daniel and Daniel, 2015) is applied to Eq. (4), such that.
Using Eq. (8) into Eq. (7), we get
Use Eq. (9) in Eq. (4), we obtain
Using the order of magnitude analysis for the y-direction momentum equation which is normal to the stretching sheet and boundary layer approximation (Ibrahim and Shankar, 2013), such as
After the analysis, the boundary layer Eqs. (1)–(5) are reduced to the following as:
The boundary conditions for the physical model are presented as:
Eqs. (12)–(16) are reduced into the dimensionless form by introducing the following suitable dimensionless quantities.
The stream function
can be defined as:
The equations of momentum, energy and nanoparticle concentration in dimensionless form, after using Eqs. (17) and (18) into Eqs. (12)–(16) become:
The boundary conditions are given by
The skin friction coefficient and the local Nusselt number are
Here
is the shear stress in the stretching surface,
is the surface heat flux,
is the Reynolds number and
is the thermal conductivity of the nanofluid. For the local skin-friction coefficient and local Nusselt number are presented in non-dimensional form as
3 Results and discussion
The system of nonlinear ordinary differential Eqs. (19)–(21) subjected to the boundary conditions (22) is solved numerically for the diverse values of physical emerging parameters such as magnetic field
, electric field
, suction parameter
, Grashof number
, mass Grashof number
, thermal radiation
, Eckert number
, unsteadiness parameter
, Brownian motion parameter
, thermophoresis parameter
, Schmidt number
, and chemical reaction parameter
. Numerical results were achieved through implicit finite difference scheme known as Keller box method detailed description of the method see (Cebeci & Bradshaw, 2012). For the validation of present numerical scheme, the results are presented and examined with (Ibrahim and Shankar, 2013) in some limiting case when
. The numerical values are in good agreement as displayed from Table 1 presents the effects of emerging parameters on the skin friction coefficient.
s
Ref (Ibrahim and Shankar, 2013)
Present results
0
0.5
0
0
1.2808
1.280777
0.5
1.5000
1.500000
1.0
1.6861
1.686141
1.5
1.8508
1.850781
2.0
2.0000
2.000000
1.0
0
1.4142
1.414214
0.2
1.5177
1.517745
0.7
1.8069
1.806880
1.0
2.0000
2.000000
0.2
0.1
–
1.335083
0.3
–
1.003660
0.5
–
0.698797
0.1
0.2
–
1.400699
0.7
–
1.547543
1.5
–
1.774626
Fig. 2 render the influence of electric field
and suction
parameters on the dimensionless velocity of nanofluid by keeping other physical parameters constant. Increasing in the suction, the dimensionless velocity reduces in the vicinity of the sheet for the lower values of electric field parameter. For remarkably boost up in the magnitude of the electric field, the resistance between fluid particles increases so that Lorentz force tends to accelerate the body forces and hence leads to increase in the flow of the nanofluid velocity and hence thicker momentum boundary layer. It also resolves sticky effect on the nanoparticles in the fluid. Inside momentum boundary layer, the dimensionless velocity decreases with an increase in the suction and increases with the electric field parameter. In the absence of both suction and magnetic field parameters, the dimensionless velocity in the hydrodynamic boundary layer is found to be larger and it decreases with an increase in the magnetic field and the variation in the suction parameters. The behavior of magnetic field and suction parameters on the nanofluid velocity within the hydrodynamic boundary layer are demonstrations in Fig. 3. In the absence of magnetic field M and suction s, the nanofluid velocity noticed to be higher and decreases with increasing magnetic field and suction parameters. Intense magnetic field influence contributes resistance to flow in the stretching direction. Physically, the outcome of the magnetic field is such that it offers rise to Lorentz force as result of interaction with the electrically conducting nanofluid in a direction which opposes the flow leading to decrease in the velocity. The profiles adhere to the boundary for strong magnetic field indicating that boundary layer thickness is a decreasing function of magnetic field. Fig. 4 elucidates the influence of thermal radiation without and with suction on nanofluid temperature profile. In this figure that the effect of thermal radiation enhances the nanofluid temperature and its associated thermal thickness of the boundary layer to the maximum in the absence of suction. For large values of radiation parameter, generates a significant amount of heating to the nanofluid which enhances the nanofluid temperature profile and thicker thermal boundary layer thickness. The impact of magnetic field M and suction s on the nanofluid temperature profile is a sketch in Fig. 5. It is worth notice that temperature of the nanofluid enhances significantly with increase in the magnetic field without suction. It is interesting to note that increasing magnetic field parameter resistance between fluid particles upsurges, so that heat is created and as a result, the thermal layer becomes thicker and leads to a rise in the temperature of the nanofluid. In Fig. 6 depicts the influence of electric field parameter E1 and suction s on the nanofluid temperature. It is evident that an increase in the electric field leads to the increment in the temperature profile. Because for higher values of the electric field, Lorentz force accelerated the body forces as results of interaction with the electrically conducting nanofluid yield increases in the temperature of the nanofluid and thicker thermal boundary layer. Fig. 7 reveals the effect of Schmidt number Sc and suction s on the nanoparticle concentration profile. The Schmidt number is the ratio of kinematic viscosity to molecular mass diffusivity for an increase in Schmidt number caused a reduction in mass diffusivity in the system which resulted in a decrease greatly with suction in nanoparticle concentration. The effects of the suction s and chemical reaction γ parameters on the nanoparticles concentration profiles are presented in Fig. 8. It is discerned from this Fig that the concentration profile diminishes with an increase in the chemical reaction and suction parameters. It is also noticed that nanoparticle concentration and layer thickness shrinkage with the destructive chemical reaction. Considerably, the presence of destructive sources the change of the species as a cause of chemical reaction and suction which drops the concentration profiles in the concentration boundary layer thickness.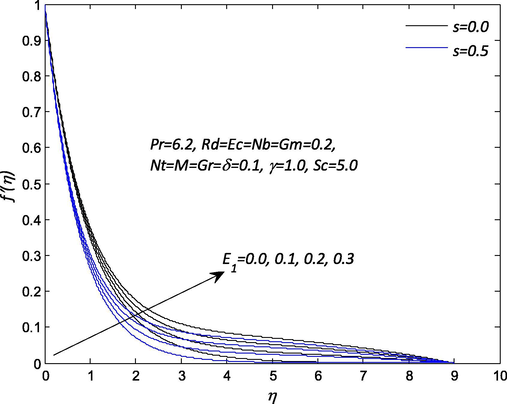
Influence of
on the velocity profile
.
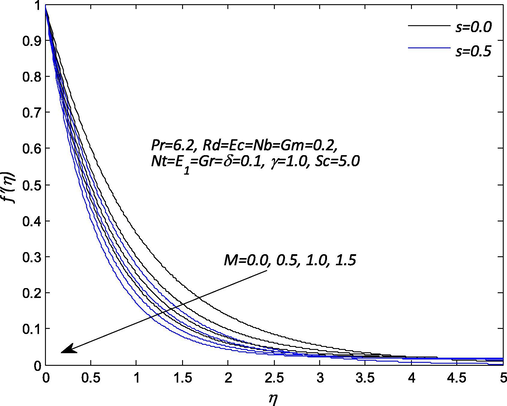
Influence of M on the velocity profile
.
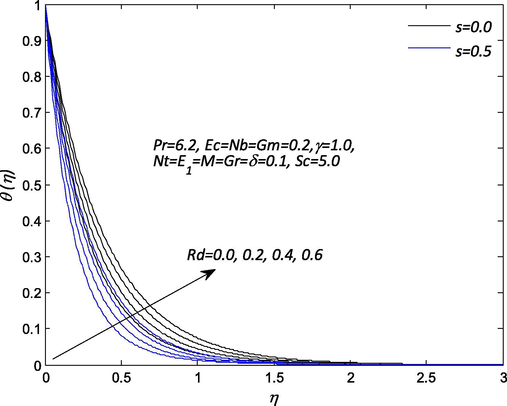
Influence of
on the temperature profile
.
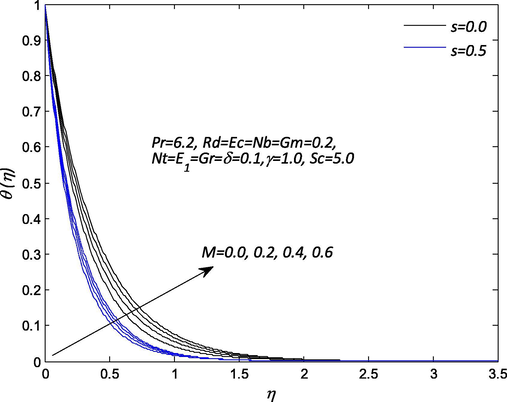
Influence of M on the temperature profile
.
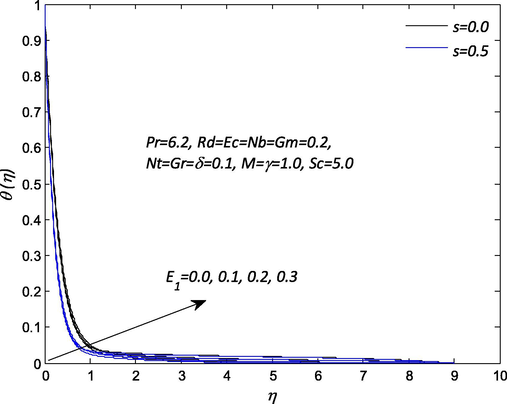
Influence of
on the temperature profile
.
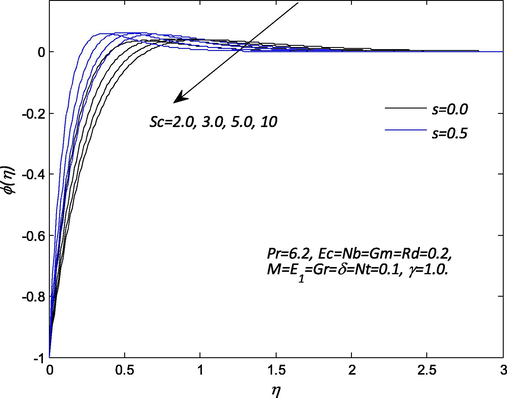
Influence of
on the concentration profile
.
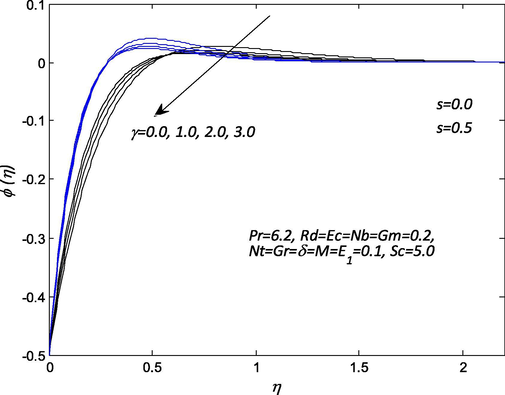
Influence of
on the concentration profile
.
Fig. 9 elucidates the effects of the suction parameter on the skin friction for different values of magnetic field. It is worthy of note that the suction parameter compliment the skin friction coefficient. Higher values of magnetic field parameter lead to an increment in the skin friction profiles. The reason is that the magnetic field retards the flow of the nanofluid over the stretching sheet surface due to a stronger hydromagnetic body force which leads to an increase in the skin friction coefficient. However, the injection parameter helps in decreasing the skin friction coefficient. The effects of the electric field and suction/injection parameters on the skin friction profile are portrayed in Fig. 10. It is important to note that both electric field and injection parameters tend to decrease the skin friction. It is interesting to note that increases in an electric field cause Lorenz force to intensify and leads to a substantial flow of the nanofluid due to convection over the sheet surface. Conversely rising in the values of suction parameter caused a rise in the skin friction profile. The influence of the nanofluid parameters via unsteadiness and Brownian motion parameters on the Nusselt number is painted in Fig. 11 for various values. It is imperative to observe that both Brownian motion and unsteadiness parameters yielded to an increase in the profile. So, the Nusselt number increases with augmenting of this parameter. Enhance in the unsteadiness which can be associated with reducing the nanofluid temperature and the thermal layer. In addition, the temperature enhances for the lower acceleration. As the random motion of nanoparticles intensifies, the collision of nanoparticles and kinetic energy rises. Hence, the heat transfer rate on the surface of the sheet increase with an effect of kinetic energy is transformed into heat energy with passively control conditions. Fig. 12 entails the effect of Eckert number and thermophoresis parameters on the Nusselt number for different values necessitates. In the presence of suction, the Nusselt number profile is lower with an increase in the Eckert number. As results of the viscosity of fluid gain energy from nanoparticle randomness motion and converts it into internal energy due to which nanofluid temperature is heated. Nonetheless, the thermophoresis parameter tends to increase the profile for higher values.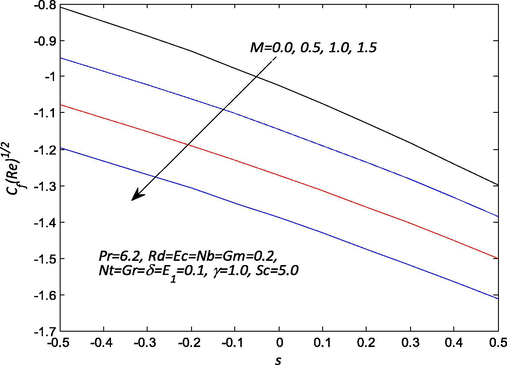
Influence of M and s on the skin friction
.
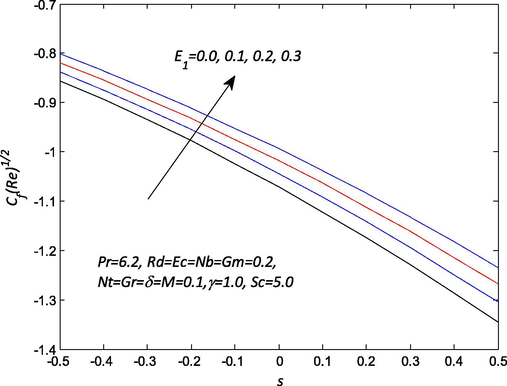
Influence of
and s on the skin friction
.
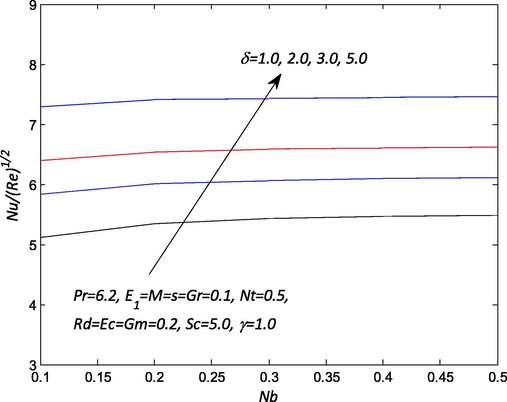
Influence of
and
on the Nusselt number
.
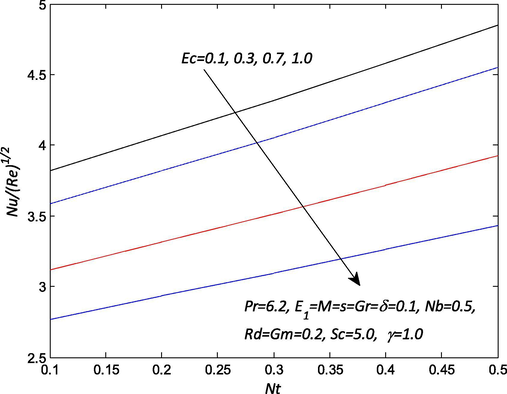
Influence of
and
on the Nusselt number
.
4 Conclusion
The combined effects of thermal radiation, chemical reaction, viscous dissipation and Joule Heating in a two-dimensional natural convection flow of an electrical MHD nanofluid due to the revised model were discussed in the presence of suction. Main findings of the present study are potted below:
-
Velocity and temperature profiles rise for increment in the values of electric field parameter.
-
It was seen that the Lorentz force due to the presence of magnetic field have a bearing on its resistance to fluid motion and enhances the thermal resistance.
-
Temperature profile shows increasing behavior for larger values of thermal radiation and viscous dissipation. An increase in chemical reaction parameter leads to lower nanoparticles concentration profile.
-
Larger values of suction cause decreasing in velocity, temperature, and nanoparticles concentration distributions.
-
Skin friction for larger values of electric and magnetic fields displayed opposite behavior in the presence of suction/injection.
-
Nusselt number profiles get higher with nanofluid parameter viz Brownian motion and thermophoresis in the presence of unsteadiness parameter.
-
The present results reduce to the steady force convection fluid flow case when .
Acknowledgments
The authors would like to acknowledge Ministry of Higher Education and Research Management Centre, UTM for the financial support through GUP with vote number 11H90, Flagship grants with vote numbers 03G50 and 03G53 for this research.
References
- Entropy generation due to mixed convection over vertical permeable cylinders using nanofluids. J. King Saud Univ.-Sci.. 2019;31:352-361.
- [CrossRef] [Google Scholar]
- H2O based different nanofluids with unsteady condition and an external magnetic field on permeable channel heat transfer. Int. J. Hydrogen Energy 2017
- [CrossRef] [Google Scholar]
- Physical and Computational Aspects of Convective Heat Transfer. Springer Science & Business Media; 2012.
- Choi, S., Eastman, J., 1995. Enhancing thermal conductivity of fluids with nanoparticles. ASME International menchanical engineering congress and exposition. American Society of Mechanical Engineers, San Francisco.
- Presence of heat generation/absorption on boundary layer slip flow of nanofluid over a porous stretching sheet. Am. J. Heat Mass Transfer. 2015;2:15-30.
- [Google Scholar]
- Presence of heat generation/absorption on boundary layer slip flow of nanofluid over a porous stretching sheet. Am. J. Heat Mass Transfer. 2015;2:15.
- [Google Scholar]
- Steady MHD laminar flows and heat transfer adjacent to porous stretching sheets using HAM. Am. J. Heat Mass Transfer. 2015;2:146-159.
- [Google Scholar]
- Laminar convective boundary layer slip flow over a flat plate using homotopy analysis method. J. Inst. Eng. (India): Ser. E. 2016;97:115-121.
- [Google Scholar]
- Steady MHD boundary-layer slip flow and heat transfer of nanofluid over a convectively heated of a non-linear permeable sheet. J. Adv. Mech. Eng.. 2016;3:1-14.
- [Google Scholar]
- Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alexandria Eng. J.. 2015;54:705-712.
- [Google Scholar]
- Effects of slip and convective conditions on MHD flow of nanofluid over a porous nonlinear stretching/shrinking sheet. Aust. J. Mech. Eng. 2017:1-17.
- [Google Scholar]
- Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys.. 2017;55:630-651.
- [Google Scholar]
- Entropy analysis in electrical magnetohydrodynamic (MHD) flow of nanofluid with effects of thermal radiation, viscous dissipation, and Chemical reaction. Theor. Appl. Mech. Lett. 2017
- [CrossRef] [Google Scholar]
- Impact of thermal radiation on electrical MHD flow of nanofluid over nonlinear stretching sheet with variable thickness. Alexandria Eng. J. 2017
- [CrossRef] [Google Scholar]
- Numerical study of Entropy analysis for electrical unsteady natural magnetohydrodynamic flow of nanofluid and heat transfer. Chin. J. Phys.. 2017;55:1821-1848.
- [Google Scholar]
- Effect of Joule heating and thermal radiation in flow of third grade fluid over radiative surface. PLoS ONE. 2014;9:e83153.
- [Google Scholar]
- MHD 2D flow of Williamson nanofluid over a nonlinear variable thicked surface with melting heat transfer. J. Mol. Liq.. 2016;223:836-844.
- [Google Scholar]
- MHD flow of Jeffrey liquid due to a nonlinear radially stretched sheet in presence of Newtonian heating. Res. Phys.. 2016;6:817-823.
- [Google Scholar]
- Analysis of thixotropic nanomaterial in a doubly stratified medium considering magnetic field effects. Int. J. Heat Mass Transfer. 2016;102:1123-1129.
- [Google Scholar]
- Chemically reactive flow of third grade fluid by an exponentially convected stretching sheet. J. Mol. Liq.. 2016;223:853-860.
- [Google Scholar]
- A model of solar radiation and Joule heating in magnetohydrodynamic (MHD) convective flow of thixotropic nanofluid. J. Mol. Liq.. 2016;215:704-710.
- [Google Scholar]
- On 2D stratified flow of an Oldroyd-B fluid with chemical reaction: an application of non-Fourier heat flux theory. J. Mol. Liq.. 2016;223:566-571.
- [Google Scholar]
- On model of Burgers fluid subject to magneto nanoparticles and convective conditions. J. Mol. Liq.. 2016;222:181-187.
- [Google Scholar]
- Numerical simulation for melting heat transfer and radiation effects in stagnation point flow of carbon–water nanofluid. Comput. Methods Appl. Mech. Eng.. 2017;315:1011-1024.
- [Google Scholar]
- MHD effects on a thermo-solutal stratified nanofluid flow on an exponentially radiating stretching sheet. J. Appl. Mech. Tech. Phys.. 2017;58:214-223.
- [Google Scholar]
- Magnetohydrodynamic (MHD) stretched flow of tangent hyperbolic nanoliquid with variable thickness. J. Mol. Liq.. 2017;229:178-184.
- [Google Scholar]
- Impacts of constructive and destructive chemical reactions in magnetohydrodynamic (MHD) flow of Jeffrey liquid due to nonlinear radially stretched surface. J. Mol. Liq.. 2017;225:302-310.
- [Google Scholar]
- Magnetohydrodynamic flow of burgers fluid with heat source and power law heat flux. Chin. J. Phys.. 2017;55:318-330.
- [Google Scholar]
- Impact of variable thermal conductivity in doubly stratified chemically reactive flow subject to non-Fourier heat flux theory. J. Mol. Liq.. 2017;234:444-451.
- [Google Scholar]
- Importance of chemical reactions in flow of Walter-B liquid subject to non-Fourier flux modeling. J. Mol. Liq.. 2017;238:229-235.
- [Google Scholar]
- On doubly stratified chemically reactive flow of Powell-Eyring liquid subject to non-Fourier heat flux theory. Res. Phys.. 2017;7:99-106.
- [Google Scholar]
- Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng.. 2016;98:850-861.
- [Google Scholar]
- Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng.. 2017;112:1281-1288.
- [Google Scholar]
- Magnetohydrodynamic stagnation point flow of a power-law nanofluid towards a convectively heated stretching sheet with slip. Proc. Inst. Mech. Eng. Part E. 2016;230:345-354.
- [Google Scholar]
- MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids. 2013;75:1-10.
- [Google Scholar]
- Finite amplitude long wave instability of a film of conducting fluid flowing down an inclined plane in presence of electromagnetic field. Int. J. Appl. Mech. Eng.. 2003;8:379-383.
- [Google Scholar]
- Nanofluid flow and heat transfer in porous media: a review of the latest developments. Int. J. Heat Mass Transfer. 2017;107:778-791.
- [Google Scholar]
- Unsteady heat and mass transfer mechanisms in MHD Carreau nanofluid flow. J. Mol. Liq.. 2017;225:554-562.
- [Google Scholar]
- Non-aligned MHD stagnation point flow of variable viscosity nanofluids past a stretching sheet with radiative heat. Int. J. Heat Mass Transfer. 2016;96:525-534.
- [Google Scholar]
- Chemically reactive flow of Maxwell liquid due to variable thicked surface. Int. Commun. Heat Mass Transfer. 2017;86:231-238.
- [Google Scholar]
- A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci.. 2017;498:85-90.
- [Google Scholar]
- Behavior of stratification phenomenon in flow of Maxwell nanomaterial with motile gyrotactic microorganisms in the presence of magnetic field. Int. J. Mech. Sci.. 2017;131:426-434.
- [Google Scholar]
- The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid: a revised model. Int. J. Heat Mass Transfer. 2013;65:682-685.
- [Google Scholar]
- MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: a numerical study. J. Magn. Magn. Mater.. 2015;374:569-576.
- [Google Scholar]
- Thermophoresis and Brownian motion effects on MHD bioconvection of nanofluid with nonlinear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. J. Mol. Liq.. 2016;221:733-743.
- [Google Scholar]
- MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq.. 2016;219:624-630.
- [Google Scholar]
- Stagnation point flow of MHD chemically reacting nanofluid over a stretching convective surface with slip and radiative heat. Proc. Inst. Mech. Eng. Part E. 2017;231:695-703.
- [Google Scholar]
- Nonlinear stability of conducting viscous film flowing down an inclined plane at moderate Reynolds number in the presence of a uniform normal electric field. J. Phys. D Appl. Phys.. 2004;38:138.
- [Google Scholar]
- 3D free convective MHD flow of nanofluid over permeable linear stretching sheet with thermal radiation. Powder Technol.. 2017;315:205-215.
- [Google Scholar]
- Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci.. 2017;126:308-318.
- [Google Scholar]
- Hydromagnetic non-Darcy flow and heat transfer over a stretching sheet in the presence of thermal radiation and Ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:1197-1209.
- [Google Scholar]
- Integral transform solution of micropolar magnetohydrodynamic oscillatory flow with heat and mass transfer over a plate in a porous medium subjected to chemical reactions. J. King Saud Univ.-Sci.. 2019;31:114-126.
- [CrossRef] [Google Scholar]
- Novel development of nanoparticles to bimetallic nanoparticles and their composites: a review. J. King Saud Univ.-Sci.. 2019;31:257-269.
- [CrossRef] [Google Scholar]
- Numerical investigation of MHD nanofluid free convective heat transfer in a porous tilted enclosure. Eng. Computations 2017
- [CrossRef] [Google Scholar]
- Transportation of MHD nanofluid free convection in a porous semi annulus using numerical approach. Chem. Phys. Lett.. 2017;669:202-210.
- [Google Scholar]
- Magnetic nanofluid natural convection in the presence of thermal radiation considering variable viscosity. Eur. Phys. J. Plus. 2017;132:238.
- [Google Scholar]
- Fe3O4–H2O nanofluid natural convection in presence of thermal radiation. Int. J. Hydrogen Energy. 2017;42:5708-5718.
- [Google Scholar]
- Thermal radiation of ferrofluid in existence of Lorentz forces considering variable viscosity. Int. J. Heat Mass Transfer. 2017;109:82-92.
- [Google Scholar]
- MHD free convection of Al2O3–water nanofluid considering thermal radiation: a numerical study. Int. J. Heat Mass Transfer. 2016;96:513-524.
- [Google Scholar]
- MHD natural convection in an inclined wavy cavity with corner heater filled with a nanofluid. J. Magn. Magn. Mater.. 2016;416:37-47.
- [Google Scholar]
- Magnetohydrodynamic flow of Casson fluid over a stretching cylinder. Res. Phys.. 2017;7:498-502.
- [Google Scholar]
- Unsteady MHD Falkner-Skan flow of Casson nanofluid with generative/destructive chemical reaction. Chem. Eng. Sci. 2017
- [CrossRef] [Google Scholar]
- Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transfer. 2016;102:766-772.
- [Google Scholar]
- Numerical simulation for magneto Carreau nanofluid model with thermal radiation: a revised model. Comput. Methods Appl. Mech. Eng.. 2017;324:640-653.
- [Google Scholar]







