How methoxy groups change nature of the thiophene based heterocyclic chalcones from p-channel to ambipolar transport semiconducting materials

Ahmad Irfan; Abdullah G. Al-Sehemi; Aijaz Rasool Chaudhry; Shabbir Muhammad

doi:10.1016/j.jksus.2017.03.010

View/Download PDF

Buy Reprints

PDF

Translate this page into:

30 (

); 458-465

doi:

10.1016/j.jksus.2017.03.010

How methoxy groups change nature of the thiophene based heterocyclic chalcones from p-channel to ambipolar transport semiconducting materials

Ahmad Irfan^{^a,^b,⁎}, Abdullah G. Al-Sehemi^{^a,^b}, Aijaz Rasool Chaudhry^{^b,^c}, Shabbir Muhammad^{^b,^c}

a Department of Chemistry, Faculty of Science, King Khalid University, Abha 61413, P.O. Box 9004, Saudi Arabia

b Research Center for Advanced Materials Science (RCAMS), King Khalid University, Abha 61413, P.O. Box 9004, Saudi Arabia

c Department of Physics, Faculty of Science, King Khalid University, Abha 61413, P.O. Box 9004, Saudi Arabia

⁎Corresponding author at: Department of Chemistry, Faculty of Science, King Khalid University, Abha 61413, P.O. Box 9004, Saudi Arabia. irfaahmad@gmail.com (Ahmad Irfan)

Received: 2017-1-8, Accepted: 2017-3-31, Published: 2017-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Charge transport nature (p-channel/ambipolar) in heterocyclic chalcones was lime lighted with the aim that how the methoxy groups change the characteristics from p- to ambipolar performance. Electro-optical and NLO properties were tuned by comprising di-/tri-methoxy at peripheral. Mono- and di-methoxy chalcone derivatives show the ambipolar performance. Balanced λ and better hole transfer integrals result in p-channel features (tri-methoxy).

Abstract

Chalcone derivatives gained significant consideration from scientific community due to their potential applications ranging from better biological activity to the efficient semiconducting properties. Present investigation deals with the in-depth study of three chalcone derivatives (2E)-1-(2,5-Dimethyl-3-thienyl)-3-(2-methoxyphenyl)prop-2-en-1-one (1), (2E)-3-(3,4-Dimethoxyphenyl)-1-(2,5-dimethylthiophen-3-yl)prop-2-en-1-one (2), and (E)-1-(2,5-Dimethyl-3-thienyl)-3-(2,4,5-trimethoxyphenyl)prop-2-en-1-one (3) highlighting their optoelectronic, charge transport (CT) and nonlinear optical (NLO) response. The ground and excited state geometries are optimized by applying density functional theory (DFT) and time dependent DFT, respectively. The effect of electron donating groups on the frontier molecular orbitals, absorption and emission wavelengths are investigated and discussed thoroughly using the quantum chemical calculations. The comprehensive intra-molecular charge transfer (ICT) is perceived from the occupied orbitals to the unoccupied molecular orbitals. A novel structure-property relationship is established on the basis of their calculated electronic structures, frontier orbitals and density of states. The electro-optical and nonlinear optical (NLO) properties are finely tuned in the chalcone derivatives comprising of di- and tri-methoxy groups at peripheral. The nature of the p-type and ambipolar charge transport behavior of the compounds 1–3 is limelighted on the basis of their ionization potentials, electron affinities, reorganization energies, transfer integrals and intrinsic mobility. The mono- and di-substituted methoxy chalcone derivatives show the ambipolar performance owing to the better transfer integral and intrinsic mobility values for hole and electron. Whilst tri-methoxy at peripheral would lead the p-channel characteristics due to the balanced reorganization energy (hole and electron) and superior hole transfer integrals leads to higher hole intrinsic mobility.

Keywords

Semiconductors

Density functional theory

Optoelectronic properties

Charge transport properties

Intrinsic mobility

Show Related Articles from PubMed

1 Introduction

Since their discovery, the organic semiconductor materials (OSMs) are immensely studied by experimental and theoretical approaches (Tsumura et al., 1986). The OSMs are cheap, light weight and also easy to fabricate. The OSMs also have larger area flexible displays via solution processing of active inks potentially a cheap production process. These prospective applications make them appropriate for optoelectronic devices (García de Arquer et al., 2017; Oehzelt et al., 2015).

The chalcones have distinctive properties which make them suitable for biological active compounds (Maydt et al., 2013), sensors (Niu et al., 2006) and semiconducting devices such as organic light-emitting diodes (OLEDs) (Makoto Satsuki et al., 2007), displays, thin film field effect transistors (TF-FET) (Itai, 2012), solar cells (Chambon et al., 2013) and photo-reaction agents, which can absorb energy in the form of light to initiate the reaction (Park, 2014). Moreover, thiophene based materials are auspicious because of the semiconducting nature, nonlinear optical response (Torruellas et al., 1990) and efficient electron transport properties (Venkataraman et al., 2006).

Previously, thiophene based heterocyclic chalcones showed improved electro-optical properties. (Ki-Jun, 2012). Therefore, in the present study, we have selected three chalcone derivatives comprising of thiophene moieties and methoxy groups. We aim to investigate the structural, frontier molecular orbitals, total/partial density of states (TDOS/PDOS)), optical (absorption (λ_abs) and fluorescence (λ_fl) spectra), nonlinear optical (NLO) and charge transport properties (ionization potentials (IPs), electron affinities (EAs), hole/electron reorganization energies (λ_h/λ_e.), hole/electron transfer integrals (t_h/t_e)) and intrinsic mobility (μ_h/μ_e) by density functional theory (DFT) and time dependent DFT. To the best of our knowledge, there is no such computational study for above selected chalcone derivatives. This is the first time that we are going to investigate in depth study of these chalcone derivatives, i.e., (2E)-1-(2,5-Dimethyl-3-thienyl)-3-(2-methoxyphenyl)prop-2-en-1-one (1) (Abdullah et al., 2010a), (2E)-3-(3,4-Dimethoxyphenyl)-1-(2,5-dimethylthiophen-3-yl)prop-2-en-1-one (2) (Abdullah et al., 2010b), and (E)-1-(2,5-Dimethyl-3-thienyl)-3-(2,4,5-trimethoxyphenyl)prop-2-en-1-one (3) (Abdullah et al., 2010c) (see Fig. 1).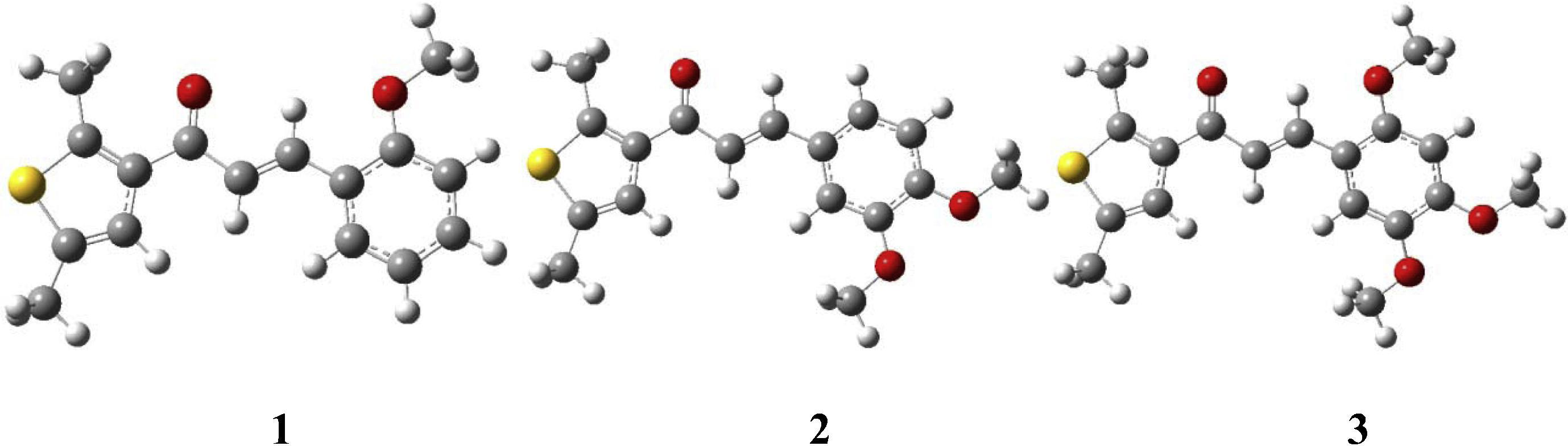

The optimized structures of the chalcone derivatives investigated in the presented study (yellow = S; red = O).

2 Computational details

In some earlier studies, it was found that among the standard DFT (Zhang et al., 2013) functionals, the B3LYP delivered the reasonable results for geometry optimizations of various size molecules (Sánchez-Carrera et al., 2006; Zhu et al., 2016; Cvejn et al., 2016; Irfan et al., 2017 ). Over the time, the B3LYP was used many times to calculate the optoelectronic and charge transfer properties, that provide good agreement with experimental evidences (Zhang et al., 2008). Earlier studies showed that the B3LYP/6-31G^∗∗ level of theory is good to reproduce the experimental data (Preat et al., 2010, 2009). Moreover, this level is rational to limelight on the electronic and charge transport properties (Huong et al., 2013). In the present study, B3LYP/6-31G^∗∗ level of theory was embraced to optimize the ground state (S₀) geometries, however the excited state (S₁) geometries, absorption and emission spectra were calculated at TD-DFT (Matthews et al., 1996) using the TD/B3LYP/6-31G^∗∗ level (Scalmani et al., 2006). The Marcus theory Eq. (1) was adopted to shed light on the charge transfer rate (Marcus and Sutin, 1985).

(1)

W = t^{2} / h {(π / λ k_{B})}^{1 / 2} \exp (- λ / 4 k_{B} T)

The transfer integrals (t) and reorganization energy (λ) are important parameters. For the superior mobility and charge transport t must be maximized while the λ should be smaller. We used the direct method to calculate the t values. In our previous studies, we successfully regenerate the experimentally reported mobilities using this approach. For instant, the hole mobility of α-α′-bis(dithieno[3,2-b:2′,3′-d]thiophene) (BDT) was experimentally reported as 0.05 cm² V⁻¹ s⁻¹ (Li et al., 1998) and it was successfully reproduced as 0.05 cm² V⁻¹ s⁻¹ (Irfan et al., 2011) by the direct method that has been explained in the computational details. In our recent studies (Chaudhry et al., 2014, 2015), the hole intrinsic mobilities of the parent crystals DPNDF and C8-DPNDF were reproduced as 1.1 and 4.69 cm² V⁻¹ s⁻¹ (Chaudhry et al., 2014, 2015), which are comparable to the experimentally reported hole mobilities, i.e. 1.3 and 3.6 cm² V⁻¹ s⁻¹ (Mitsui et al., 2012), respectively. Similarly, the electron mobility of mer-tris(8-hydroxyquinolinato)-aluminum(III) (mer-Alq3) has been reproduced (Lin et al., 2004) which is consistent with the experimental electron mobility 3 × 10⁻⁶ cm² V⁻¹ s⁻¹ (Naka et al., 2000). All above-mentioned results indicate that our adopted approach is very reliable to reproduce the comparable results and are in good agreement with the experimentally reported values of mobilities. In current investigation, we use the same direct method to compute the charge transport parameters. Computational details about the t and λ and intrinsic mobility can be found in Supporting information). All these quantum chemical calculations were performed by using Gaussian09 package (Frisch et al., 2009). The total/partial density of states (TDOS/PDOS) have been computed by GGA (generalized gradient approximation) at PW91 functional (Perdew et al., 1992) and DNP basis set (Nadykto, 2008) via DMol3 code (Delley, 2000) employed in Accelrys Materials Studio package (Materials Studio Modeling, 2004).

3 Results and discussion

3.1

3.1 Geometries

The S₀ and S₁ significant geometrical parameters, i.e., bond lengths (Å) and bond angles (degrees, °) of three chalcone derivatives 1–3 at B3LYP/6-31G^∗∗ and TD-B3LYP/6-31G^∗∗ levels of theory are tabulated in Table S1. The computed S₀ bond lengths and bond angles were found in reasonable agreement with the experimental crystal structural parameters The S₁-C₁₂ (S₁-C₁₄) bond lengths are being overestimated, i.e., 0.029 (0.024), 0.035 (0.033) and 0.036 (0.026) Å in 1–3, respectively. This overestimation in the bond lengths is due to the experimental geometrical data is in the solid phase whilst the computed parameters are in gas phase. No significant effect on the geometries was observed by varying the number of methoxy groups. Here, the lengthening or shortening in the bond lengths, as well as variation in the bond angles from S₀ to S₁ was also discussed. In compounds 1–3, the lengthening from the S₀ to S₁ was 0.027, 0.027 and 0.026 Å for S₁-C₁₂ bond length, respectively. For S₁-C₁₄ bond length, the shortening was discerned 0.016, 0.016 and 0.017 Å in 1–3 from S₀ to S₁, respectively. Whilst for C₉-O₂ bond length, the lengthening was noticed from S₀ to S₁, i.e., 0.042, 0.051 and 0.053 Å in compounds 1–3, respectively. The C₁₀-C₉-O₂ bond angle decreases 20.58°, 20.64° and 20.89° while C₁₀-C₉-C₈ increases 8.65°, 8.88° and 9.28° from S₀ to S₁ in 1–3, respectively.

3.2

3.2 Electro-optical properties

The frontier molecular orbitals (FMOs) including the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) distribution patterns of the thiophene based chalcone derivatives 1–3 have been illustrated in Figs. 2 and S1. Here, the charge density of the main FMOs participating in the absorption and emission spectral wavelengths has been clarified. The major transitions in the absorption spectra of all the studied derivatives 1–3 are H → L. The second peak in 1 and 3 is due to the H-1 → L whilst in 2 is because of H-3 → L transition. At ground state, the HOMO−1 is delocalized at thiophene moiety in 1 and 3. The HOMO of 1–3 is delocalized on the (phenyl)prop-2-en-1-one and oxygen of methoxy group/groups while LUMO is localized at entire compounds. Comprehensive intra-molecular charge transport (ICT) has been observed from HOMO−1 → LUMO, HOMO → LUMO as well as from HOMO−3 → LUMO. The major transitions in the emission spectra of 2 and 3 are from L → H while in 1 is from L → H-3. The second peak in 1, 2 and 3 is due to the L → H-1, L → H-2 and L → H-2 transitions, respectively. At excited state, in 1, the charge density of HOMO−3 and HOMO is distributed at (phenyl)prop-2-en-1-one and oxygen of methoxy group, HOMO−1 at thiophene moiety and LUMO at prop-2-en-1-one and phenyl unit. In 2 and 3, the HOMO−2 is distributed at the dimethyl-thiophene unit, HOMO−1 at keto group, HOMO at phenyl moiety and methoxy groups while LUMO at entire compounds. The major transitions in the emission spectra of 2 and 3 are L → H while in 1, L → H-3. The second peak in 1, 2 and 3 is due to the L → H-1, L → H-2 and L → H-2, respectively (see, Fig. S1).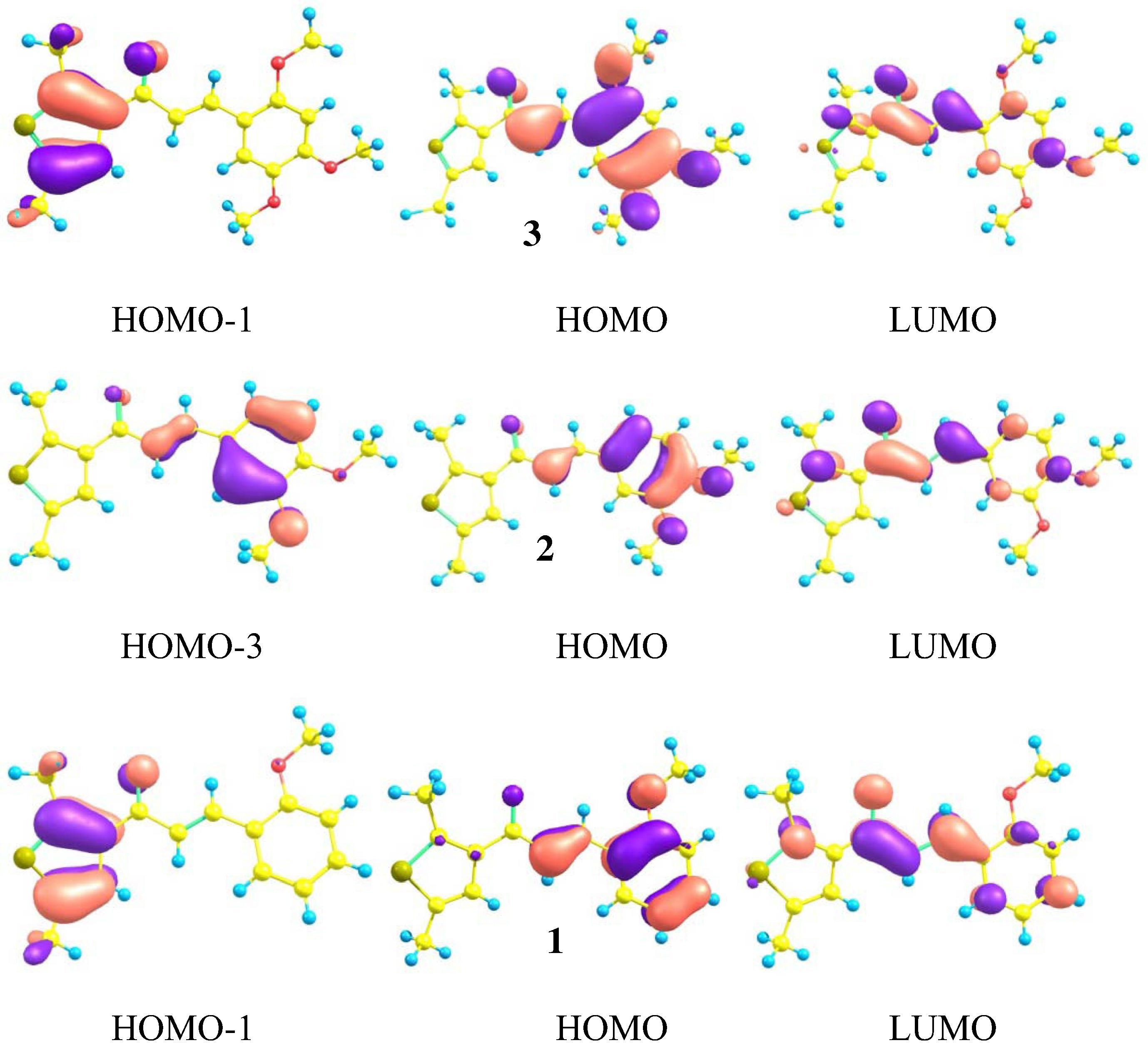

Distribution patterns of the HOMOs and LUMOs of chalcone derivatives at the ground states.

In Table 1, computed HOMO energies (E_HOMO), LUMO energies (E_LUMO) and HOMO-LUMO energy gaps (E_g) of chalcone derivatives 1–3 at B3LYP/6-31G^∗∗ (ground state) and TD-B3LYP/6-31G^∗∗ (excited state) levels of theory were tabulated, respectively. The trend in the E_HOMO and E_LUMO energy level is as: 3 > 2 > 1 for the ground and excited states. The tendency in the E_g has been observed as 1 > 2 > 3 at ground state while 3 > 2 > 1 at excited state. The hole and electron injection energies of 1–3 have been calculated and compared with each other. The electron injection energy can be estimated as (=−E_LUMO − (−work function of metal)). The work function of aluminum (Al) is −4.08 eV. The electron injection energy was found 2.26 eV (=−1.82 − (−4.08)), 2.33 eV (=−1.75 − (−4.08)), and 2.47 eV (=−1.61 − (−4.08)) from the 1–3 to Al electrode, respectively. The smaller E_LUMO would lead the injected electron stable. Here, the E_LUMO of 1 and 2 is low-lying than 3 revealing that prior derivatives would be thermodynamically more stable and charge transport can’t be quenched by losing the electrons. The hole injection energy of 1–3 has been predicted, i.e., 1.73 eV (=−4.08 − (−5.81)), 1.42 eV (=−4.08 − (−5.50)) and 1.07 eV (=−4.08 − (−5.15)) from 1–3 to the Al electrode, respectively. The –OCH₃ groups in compound 3 enhanced the donor strength leading to the better hole transport properties.

Table 1 The HOMO energies (E_HOMO), LUMO energies (E_LUMO), and HOMO-LUMO energy gaps (E_g) in eV for ground and first excited states computed at the B3LYP/6-31G^** and TD-B3LYP/6-31G^** level of theories, respectively.

Complexes	Ground states			First excited states
Complexes	E_HOMO	E_LUMO	E_g	E_HOMO	E_LUMO	E_g
1	−5.81	−1.82	3.99	−4.77	−2.54	2.23
2	−5.50	−1.75	3.75	−4.76	−2.43	2.33
3	−5.15	−1.61	3.54	−4.61	−2.27	2.34

In Table 2, the oscillator strengths (f), absorption and emission wavelengths (λ_a and λ_e), as well as major transitions particularized at TD-B3LYP/6-31G^∗∗ level of theory were organized. The maximum λ_a peak of compounds 1–3 was observed at 347, 354 and 382 nm with the major transition H → L. It can be seen that by improving the donor strength, the absorption wavelength shows red shift, i.e. 7 and 35 nm from 1 through 3, respectively. The second peak of the absorption wavelength was detected at 335, 300 and 331 nm with major transitions H-1 → L, H-3 → L and H-1 → L, respectively. The maximum λ_e peak of 1–3 was observed at 370, 364 and 394 nm with the major transitions from L → H-3, L → H-1 and L → H-1, respectively. By substituting three methoxy groups at methyl moiety in 3 lead to 24 nm red shift in λ_e as compared to the 1. The second peak of the emission wavelength was detected at 481, 463 and 456 nm with major transitions from L → H-1, L → H-2 and L → H-1, respectively. The Stokes shift from the absorption to the emission wavelengths was observed 23, 10 and 12 nm for 1–3, respectively.

Table 2 Computed absorption (λ_a) and emission wavelengths (λ_e) (nm), oscillator strengths (f) and major transitions of chalcone derivatives at TD-B3LYP/6-31G^** level of theory.

Complexes	f	λ_a	Transition	f	λ_e	Transition
1	0.397	347	H → L	0.005	481	L → H-1
1	0.164	335	H-1 → L	0.008	370	L → H-3
2	0.716	354	H → L	0.006	463	L → H-2
2	0.177	300	H-3 → L	0.634	364	L → H-1
3	0.462	382	H → L	0.010	456	L → H-2
3	0.033	331	H-1 → L	0.541	394	L → H-1

3.3

3.3 Charge transport parameters

3.3.1

3.3.1 Ionization potential, electron affinity and reorganization energies

The nature of the charge transfer and charge injection behavior in organic semiconductor materials can be understood by the IP and EA. It is well-known that the smaller IP shrink the hole injection barrier while higher EA values reduce the electron injection barrier resulting effective hole and electron injection ability, respectively. The adiabatic and vertical ionization potentials (IP_a, IP_v), adiabatic and vertical electron affinities (EA_a, EA_v), λ_h and λ_e of thiophene based heterocyclic chalcone derivatives 1–3 have been organized in Fig. 3 and Table S2 (Supporting information). The IP_a/IP_v of 2 and 3 decrease 0.29/0.26 and 0.68/0.60 eV as compared to 1, respectively. The tendency in EA of studied chalcone derivatives has been observed as 1 > 2 > 3 showing that electron injection ability of 1 and 2 might be superior to the compound 3. The trend in the λ_h of thiophene based heterocyclic chalcone derivatives has been observed as 1 < 2 < 3. However, here it must be clarified that reorganization energy is not a single appropriate parameter to properly understand the charge transport nature (p-type or ambipolar materials). Thus, to precisely apprehend the charge transfer behavior of the studied chalcone derivatives (1–3), we have calculated the transfer integrals and intrinsic carrier mobility in Section 3.3.2.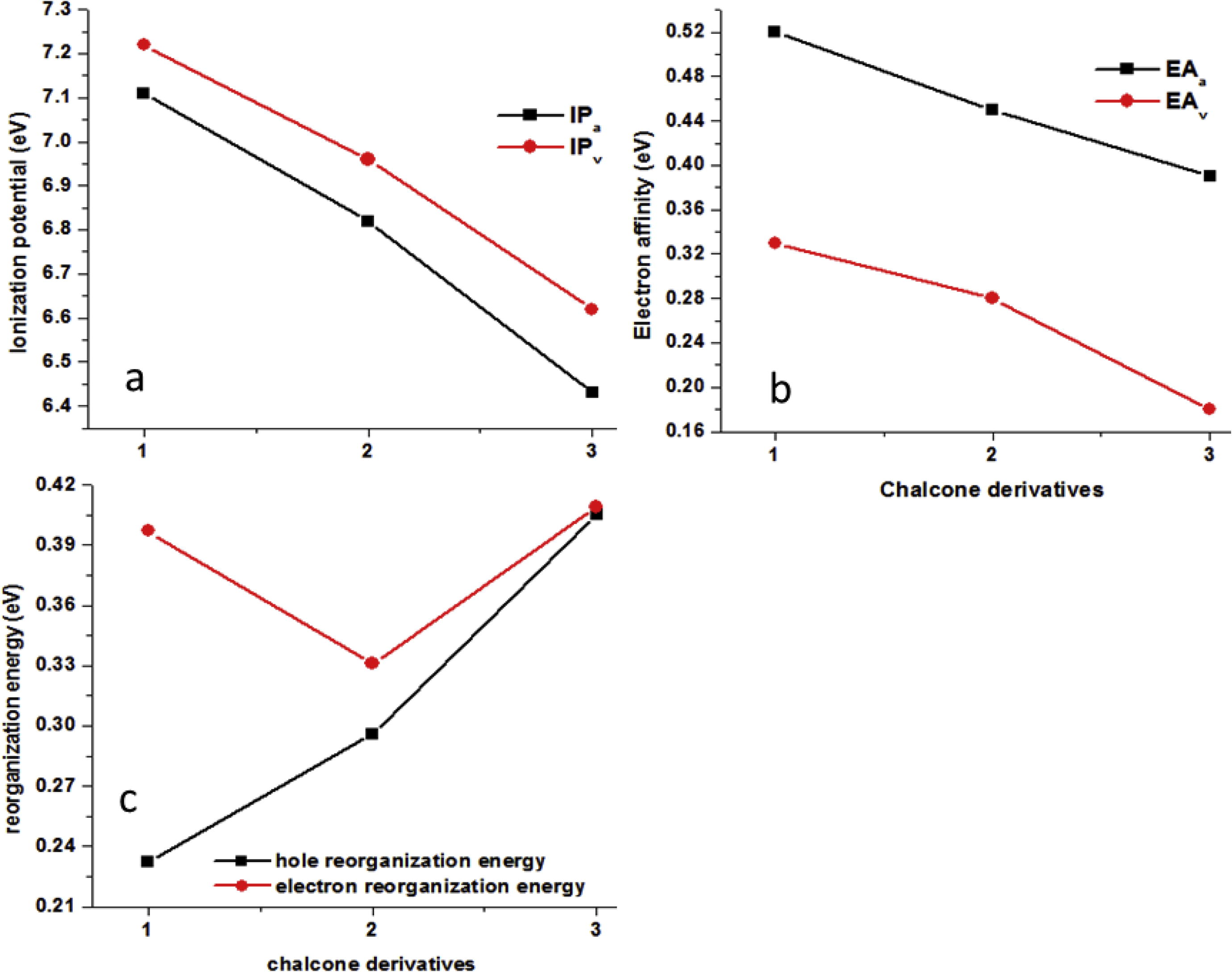

(a) Vertical and adiabatic ionization potentials (IPv/IPa), (b) vertical and adiabatic electronic affinities (EAv/EAa), (c) hole reorganization energies (λh) and electron reorganization energies (λe) of chalcone derivatives at the B3LYP/6-31G** level of theory.

3.3.2

3.3.2 Transfer integrals and intrinsic mobility

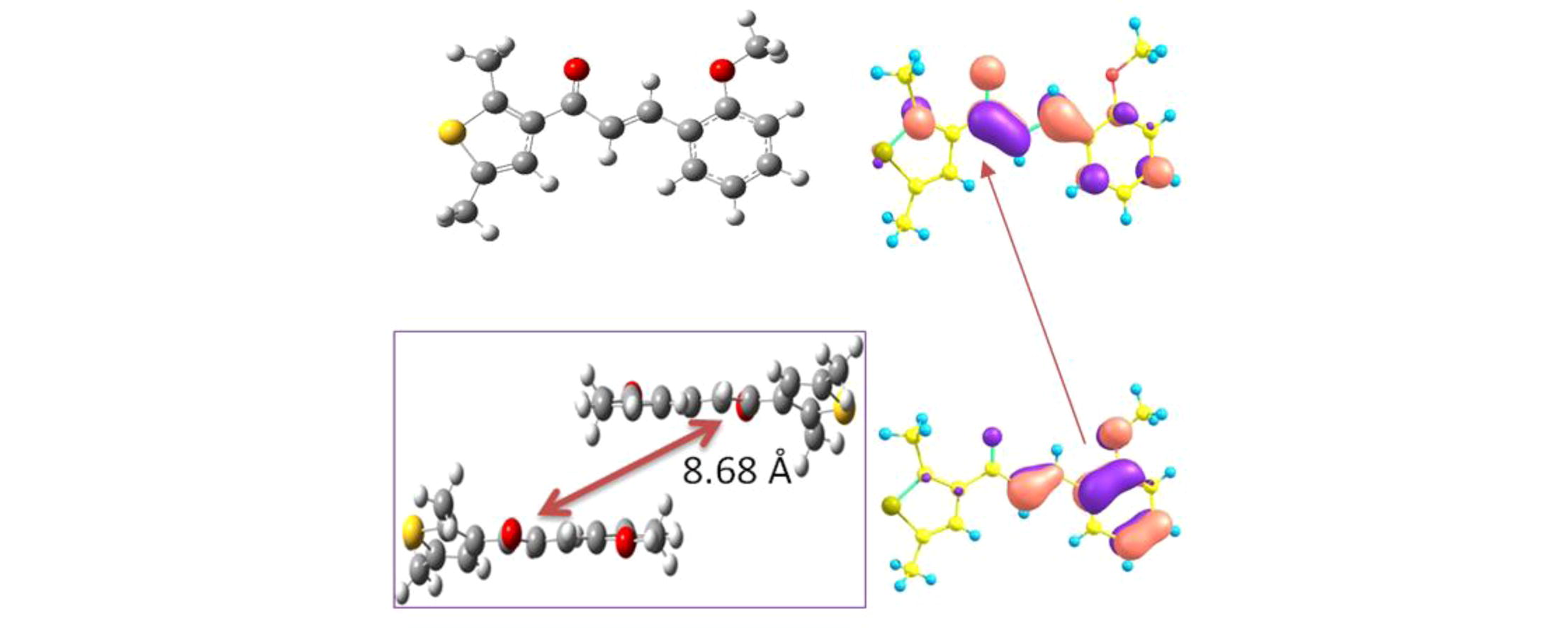
We defined five distinct neighboring hopping pathways to study the charge transport performance of chalcones derivatives (1–3) in detail. The Table 3 displays the t_h and t_e determined by the scheme expressed in Eq. (6) of computational details (see Supporting information). It was found that some pathways have negligible small values of t_h and t_e, hence not discussed in the text. The maximum values of t_h for 1 are 1.9 and 16.2 meV, whereas the values for t_e are −28.5 and 73.5 meV for two pathways of 1, respectively. Similarly, the two pathways for 2 display t_h as −35.5 and −37.8 meV, while the t_e was computed as 72.5 and 59.8 meV, respectively. The highest t_h for 3 are 61.6 and 4.93 × 10⁻⁴ meV, however the maximum values of t_e are −11.4 and −7.8 meV for two pathways, respectively. The Figs. 4 and S2 display all the dimers of compounds 1–3 with their packing for further clear understanding of the hopping pathways. The values of t_h and t_e for compounds 1 and 2 specify that these derivatives would be good ambipolar transport compounds while derivative 3 might be better as hole transport material.

Table 3 Calculated (hole/electron) transfer integrals, mass centers and (hole/electron) intrinsic mobilities of chalcone derivatives (1–3) for five pathways computed with DFT.

Molecules	Pathways	Transfer Integrals (meV)		Mass Centers (Å)	Mobility (cm²/V.s)
Molecules	Pathways	t_h	t_e	Mass Centers (Å)	μ_h	μ_e
1	i	1.9	−28.5	5.24	1.91 × 10⁻⁵	6.44 × 10⁻³
	ii	1.0	−1.6	2.31	2.84 × 10⁻⁷	1.24 × 10⁻⁸
	iii	9.26 × 10⁻⁵	73.5	8.68	2.96 × 10⁻¹⁰	0.78
	iv	16.2	−5.65 × 10⁻⁴	7.55	0.21	2.1 × 10⁻⁹
	v	4.67 × 10⁻⁴	−2.1	13.67	4.74 × 10⁻⁷	1.3 × 10⁻⁶

2	i	−35.5	72.5	3.0	3.03 × 10⁻²	0.13
	ii	−37.8	59.8	7.84	0.27	0.41
	iii	2.26 × 10⁻²	−1.3 × 10⁻³	4.28	1.01 × 10⁻²	2.72 × 10⁻⁸
	iv	2.1 × 10⁻³	−2.2 × 10⁻³	9.18	3.47 × 10⁻⁶	1.02 × 10⁻⁶
	v	−1.9	−1.6	4.91	6.66 × 10⁻⁷	8.19 × 10⁻⁸

3	i	6.0	−2.4	2.5	4.27 × 10⁻⁶	1.78 × 10⁻⁶
	ii	−1.6	4.0	3.51	4.32 × 10⁻⁸	2.74 × 10⁻⁵
	iii	−61.6	−11.4	6.65	0.34	6.42 × 10⁻³
	iv	1.44 × 10⁻⁴	3.6	10.95	2.70 × 10⁻¹¹	1.73 × 10⁻⁴
	v	4.93 × 10⁻⁴	−7.8	9.0	2.53 × 10⁻⁹	2.58 × 10⁻³

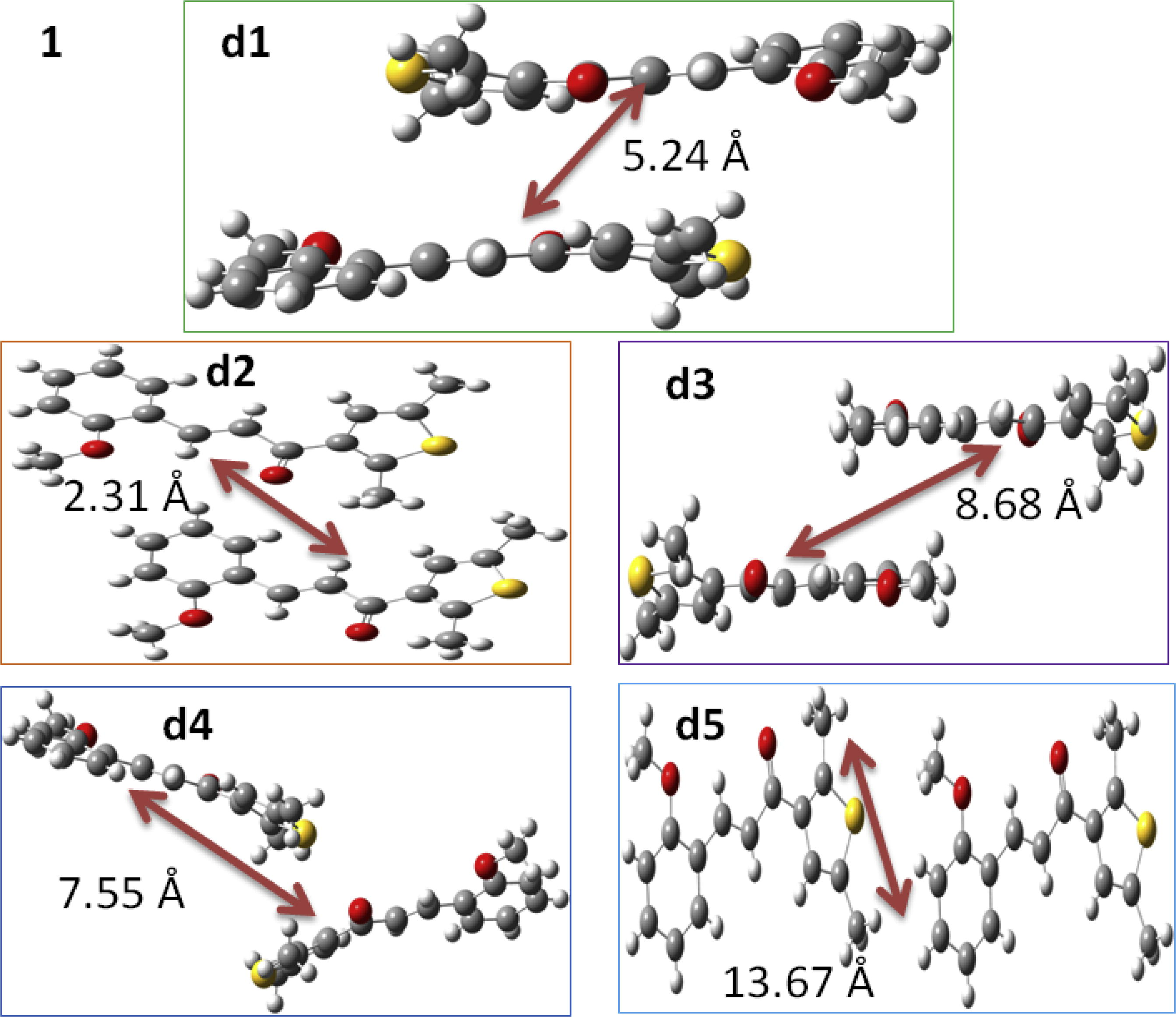
The dimers of chalcone derivative 1 studied in current investigation to calculate the transfer integrals and intrinsic mobilities.

The μ_h and μ_e of chalcones derivatives 1–3 were estimated as stated in Eq. (7) of computational details (see Supporting information) for five pathways and presented in Table 3. It was found that some pathways have negligible lower values of μ_h and μ_e, therefore those are not discussed in the text. The highest values of μ_h are 1.91 × 10⁻⁵ and 0.21 cm² V⁻¹ s⁻¹; along with the values of μ_e as 6.44 × 10⁻³ and 0.78 cm² V⁻¹ s⁻¹ for the two pathways of 1, respectively. The maximum values of μ_h for two pathways of 2 are 3.03 × 10⁻² and 0.27 cm² V⁻¹ s⁻¹ and the values of μ_e are 0.13 and 0.41 cm² V⁻¹ s⁻¹, respectively. Similarly, the two pathways of 3 display 0.34 and 2.53 × 10⁻⁹ cm² V⁻¹ s⁻¹ for μ_h, whereas, μ_e demonstrate as 6.42 × 10⁻³ and 2.58 × 10⁻³ cm² V⁻¹ s⁻¹, respectively.

Moreover, from the calculated intrinsic mobility values it can be predicted that the derivatives 1 and 2 might be used ambipolar materials as the computed μ_h and μ_e values are 0.21and 0.27 cm² V⁻¹ s⁻¹ for 1; 0.78 and 0.41 cm² V⁻¹ s⁻¹ for 2, respectively, while the derivative 3 would be hole transport material with μ_h of 0.34 cm² V⁻¹ s⁻¹.

3.4

3.4 Nonlinear optical properties (NLO)

In recent years, organic materials especially several chalcones are highlighted as a good candidate for NLO applications. The NLO materials have important utilization in numerous fields including optical data processing and frequency doubling etc. Over the past several years, our group has reported many compounds with efficient NLO response (Levine and Bethea, 1975). Due to their ease of fabrication, low economic cost and larger NLO responses, the organic compounds are presumed to be very promising (Zaitseva and Carman, 2001; Badan et al., 1993). In the present study, compounds 1–3 showed an ICT character as seen in their FMOs in the ground state, which highlights that these compounds are possibly good candidates as efficient NLO materials. Similar to our several previous studies (Muhammad et al., 2015), we have calculated the molecular electronic static second-order polarizability (β_tot) values for compounds 1–3 to check their possible NLO response. Using finite field (FF) approach, we have evaluated β_tot values at B3LYP/6-31G^∗∗ level of theory, for compounds 1–3 as given in Table S3. Computational details about NLO properties are provided in Supporting information.

The calculated values of second-order polarizability (β_tot) are 1358, 4657 and 4634 a. u. for compounds 1–3, respectively (see Table S3). These compounds are not only retaining nonzero β_tot values but also these are reasonably large in amplitudes. It is also interesting to compare the β_tot values to that of urea molecule (often used as reference NLO molecule in several investigations) at the same B3LYP/6-31G∗ level of theory. Comparing the these β_tot values illustrations that compounds 1–3 have ∼32, 108 and 107 times greater amplitudes as compared to that of urea molecules (43 a. u.) at the same level of theory, respectively (see Table S3). It is also important to highlight the reason behind the significant difference in the β_tot values of compound 1 and that of compounds 2 or 3. According to the widely used two-level model, (Oudar and Chemla, 1977) the transition energy and oscillator strengths play crucial role to tune the β_tot value as explained in several previous reports (Muhammad et al., 2016). A careful analysis of Table 2 in preceding Section 3.2, shows that both the compounds 2 and 3 possess relatively larger oscillator strengths and reasonably lower transition energies as compared to compound 1, which is perhaps the reason for their larger β_tot amplitudes at B3LYP/6-31G∗ level of theory. Thus, it is understandable from above discussion that our designed compounds possess the suitable nonlinear optical response and these are potential contenders as efficient NLO materials.

3.5

3.5 Fukui indices

The highly stable compounds are the demand of era. Fukui function is usually used to understand the reactive sites of the compounds. It is also expected that Fukui indices can shed some light on the stability of the compounds, i.e., less reactive sites might lead to more stability. The values of calculated Fukui functions ( $f_{j}^{+}$ , $f_{j}^{-}$ and $f_{j}^{0}$ ) and Δƒ(r) have been given in Table S4 along with computational details (Supporting information). It is expected that S (1) and O (2) positions in 2 might favor the nucleophilic attack (i.e., Δƒ > 0). It is also predicted from the Δƒ values that 1 and 3 might be more stable as these derivatives have no attractive sites for the electrophile or nucleophile attack. Position of reactive electrophilic sites and nucleophilic sites are accordance with the total electron density surface and chemical behavior.

3.6

3.6 Density of states

The partial and total DOS have been evaluated by implementing DMol3 software program available in Materials Studio within the framework of DFT at GGA/PW91/DNP level of theory to understand the electronic structure of chalcones derivatives 1–3. The PDOS and TDOS with contributions from s, p and d-orbital are shown in Fig. S3 for chalcone derivatives 1–3. For 1, the energy bands in the deep valence bands (VB) at energy regime −0.9 to −0.2 Ha are defined mostly by the s-orbitals of all atoms, while the major contribution from p-orbitals dominating from −0.4 to −0.1 Ha in upper VB. In lower conduction bands (CB), the peaks from 0.05 to 0.1 Ha have a major contribution from p-orbitals, while s-orbitals displaying minor contributions in the CB (see Fig. S3). Similarly the DOS profile of chalcones derivative 2 shows, the peaks between −0.8 to −0.2 Ha in the lower VB are contributions from the s-orbitals of all atoms, however, the p-orbitals are controlling the peaks from −0.4 to −0.1 Ha in upper VB. The peaks from 0 to 0.1 Ha in lower CB are defined equally by s and p-orbitals, while chalcones derivative 3 illustrates the peaks between −0.8 to −0.3 Ha in lower VB are contribution from the s-orbitals of all atoms, however, the p-orbitals are dominating the peaks from −0.5 to −0.1 Ha in higher VB. The peaks from 0 to 0.1 Ha in lower CB are defined equally by s and p-orbitals, (see Fig. S3). The DOS profiles of chalcones derivatives 1–3 revealed that the VB and CB are mostly of p-character, reflecting the major contribution of p-orbitals into the electronic properties of compounds 1–3.

4 Conclusions

The present investigation highlights several insights into structure-property relationship of above titled novel chalcone derivatives. The TD-DFT calculations show that the tri-methoxy substituted derivative is being 35 and 24 nm red shifted for the maximum absorption and emission wavelengths as compared to the mono-methoxy substituted compound, respectively. Furthermore, analysis of FMOs revealed a comprehensive ICT from the highest occupied to the lowest unoccupied molecular orbitals. The DOS profiles showed that the contribution of p-orbitals is significant in the electronic properties as well as in valence and conduction bands. The electron transfer integrals and intrinsic mobility of compounds 1 and 2 revealed that these compounds might be better ambipolar contestants. The smaller hole injection energy barrier, ionization potential, superior hole transfer integrals and intrinsic mobility of compound 3 as compared to the other counterparts showed that aforementioned derivative would be better as p-channel. Our investigation about NLO properties showed that the compounds 1–3 have ∼32, 108 and 107 times greater β_tot amplitudes than that of urea molecule indicating their significant potential for NLO applications. It is also anticipated that the compounds 1 and 3 might be more stable which have no effective electrophile or nucleophile attacking sites. Our quantum chemical exploration of the optoelectronic, charge transport and nonlinear optical properties displays that these materials possess worthy properties of interests and would be potential contestants for the organic optoelectronic device applications comprising of photovoltaic, light emitting diodes, field effect transistors and nonlinear optics.

Acknowledgements

The authors would like to express their gratitude to King Khalid University, Saudi Arabia for providing administrative and technical support. A. Irfan acknowledges the Prof. Zhang Jingping for her technical and computational support about MS/DMOL3 calculations.

References

Abdullah S.A.K., Asiri M., Nawaz Tahir M., . (2E)-1-(2,5-Dimethyl-3-thienyl)-3-(2-methoxyphenyl)prop-2-en-1-one. Acta Crystallogr. Sect. E Struct.. 2010;66:o2358.
[Google Scholar]
Abdullah S.A.K., Asiri M., Nawaz Tahir M., . (2E)-3-(3,4-Dimethoxyphenyl)-1-(2,5-dimethylthiophen-3-yl)prop-2-en-1-one. Acta Crystallogr. Sect. E. 2010;E66:o2133.
[Google Scholar]
Abdullah S.A.K., Asiri M., Nawaz Tahir M., . (E)-1-(2,5-Dimethyl-3-thienyl)-3-(2,4,5-trimethoxyphenyl)prop-2-en-1-one. Acta Crystallogr. Sect. E. 2010;E66:o2099.
[Google Scholar]
Badan, J., Hierle, R., Perigaud, A., Zyss, J., Williams, D., 1993. NLO properties of organic molecules and polymeric materials. In: American Chemical Society Symposium Series, American Chemical Society Washington, DC.
Chambon S., D'Aleo A., Baffert C., Wantz G., Fages F., . Solution-processed bulk heterojunction solar cells based on BF2-hydroxychalcone complexes. Chem. Commun.. 2013;49:3555-3557.
[Google Scholar]
Chaudhry A.R., Ahmed R., Irfan A., Shaari A., Al-Sehemi A.G., . Effects of electron withdrawing groups on transfer integrals, mobility, electronic and photo-physical properties of naphtho[2,1-b:6,5-b′]difuran derivatives: a theoretical study. Sci. Adv. Mater.. 2014;6:1727-1739.
[Google Scholar]
Chaudhry A.R., Ahmed R., Irfan A., Shaari A., Isa A.R., Muhammad S., Al-Sehemi A.G., . Effect of donor strength of extended alkyl auxiliary groups on optoelectronic and charge transport properties of novel naphtha[2,1-b:6,5-b′]difuran derivatives: simple yet effective strategy. J. Mol. Model.. 2015;21:1-16.
[Google Scholar]
Cvejn D., Achelle S., Pytela O., Malval J.-P., Spangenberg A., Cabon N., Bureš F., Robin-le Guen F., . Tripodal molecules with triphenylamine core, diazine peripheral groups and extended π-conjugated linkers. Dyes Pigm.. 2016;124:101-109.
[Google Scholar]
Delley B., . From molecules to solids with the DMol3 approach. J. Chem. Phys.. 2000;113:7756-7764.
[Google Scholar]
Frisch, M.J., Trucks, G.W., Schlegel, H.B., et al., 2009. In: Gaussian-09, Revision A.1, Gaussian Inc, Wallingford, CT.
García de Arquer F.P., Armin A., Meredith P., Sargent E.H., . Solution-processed semiconductors for next-generation photodetectors. Nat. Rev. Mater.. 2017;2:16100.
[Google Scholar]
Huong V.T.T., Nguyen H.T., Tai T.B., Nguyen M.T., . Π-Conjugated molecules containing naphtho[2,3-b]thiophene and their derivatives: theoretical design for organic semiconductors. J. Phys. Chem. C. 2013;117:10175-10184.
[Google Scholar]
Irfan A., Al-Sehemi A.G., Muhammad S., Zhang J., . Packing Effect on the Transfer Integrals and Mobility in α, α′-bis(dithieno[3,2-b:2′,3′-d]thiophene) (BDT) and its Heteroatom-Substituted Analogues. Aust. J. Chem.. 2011;64:1587-1592.
[Google Scholar]
Irfan A., Kalam A., Chaudhry A.R., Al-Sehemi A.G., Muhammad S., . Electro-optical, nonlinear and charge transfer properties of naphthalene based compounds: a dual approach study, Optik – Intern. J. Light Elect. Optics. 2017;132:101-110.
[Google Scholar]
Y. Itai, 2012. Thin film field effect transistor and display. US8188480 B2, in, 2012.
Ki-Jun H.-S.K., . Hwang, In-Cheol Han, Beom-Tae Kim, Synthesis of Heterocyclic Chalcone Derivatives and Their Radical Scavenging Ability Toward 2,2-Diphenyl-1-Picrylhydrazyl (DPPH) Free Radicals. Bull. Korean Chem. Soc.. 2012;33:2585-2591.
[Google Scholar]
Levine B.F., Bethea C.G., . Second and third order hyperpolarizabilities of organic molecules. J. Chem. Phys.. 1975;63:2666-2682.
[Google Scholar]
Li X.-C., Sirringhaus H., Garnier F., Holmes A.B., Moratti S.C., Feeder N., Clegg W., Teat S.J., Friend R.H., . A highly π-stacked organic semiconductor for thin film transistors based on fused thiophenes. J. Am. Chem. Soc.. 1998;120:2206-2207.
[Google Scholar]
Lin B.C., Cheng C.P., You Z.-Q., Hsu C.-P., . Charge transport properties of tris(8-hydroxyquinolinato)aluminum(III): why it is an electron transporter. J. Am. Chem. Soc.. 2004;127:66-67.
[Google Scholar]
N.I. Makoto Satsuki, Sadaharu Suga, Hisayoshi Fujikawa, Yasunori Taga, 2007. Organic light emitters using coumarin derivative as luminescent agents having efficiency and durability; display panels, in: US7252892 B2.
Marcus R.A., Sutin N., . Electron transfers in chemistry and biology. Biochim. Biophys. Acta Rev. Bioenerg.. 1985;811:265-322.
[Google Scholar]
R.A.I. Materials Studio Modeling, 2004. San Diego, Materials Studio Modeling, Release 3.0.1. (2004) Accelrys Inc., San Diego.
Matthews D., Infelta P., Grätzel M., . Calculation of the photocurrent-potential characteristic for regenerative, sensitized semiconductor electrodes. Sol. Energy Mater. Sol. Cells. 1996;44:119-155.
[Google Scholar]
Maydt D., De Spirt S., Muschelknautz C., Stahl W., Muller T.J., . Chemical reactivity and biological activity of chalcones and other alpha, beta-unsaturated carbonyl compounds. Xenobiotica. 2013;43:711-718.
[Google Scholar]
Mitsui C., Soeda J., Miwa K., Tsuji H., Takeya J., Nakamura E., . Naphtho[2,1-b:6,5-b′]difuran: a versatile motif available for solution-processed single-crystal organic field-effect transistors with high hole mobility. J. Am. Chem. Soc.. 2012;134:5448-5451.
[Google Scholar]
Muhammad S., Irfan A., Shkir M., Chaudhry A.R., Kalam A., AlFaify S., Al-Sehemi A.G., Al-Salami A.E., Yahia I.S., Xu H.L., . How does hybrid bridging core modification enhance the nonlinear optical properties in donor-π-acceptor configuration? A case study of dinitrophenol derivatives. J. Comput. Chem.. 2015;36:118-128.
[Google Scholar]
Muhammad S., Al-Sehemi A.G., Irfan A., Chaudhry A.R., Gharni H., AlFaify S., Shkir M., Asiri A.M., . The impact of position and number of methoxy group (s) to tune the nonlinear optical properties of chalcone derivatives: a dual substitution strategy. J. Mol. Model.. 2016;22:1-9.
[Google Scholar]
Nadykto A.B., Al Natsheh A., Yu F., Mikkelsen K.V., Herb J., . Chapter 21 computational quantum chemistry: a new approach to atmospheric nucleation. In: Michael E.G., Matthew S.J., eds. Adv Quantum Chem.. Academic Press; 2008. p. :449-478.
[Google Scholar]
Naka S., Okada H., Onnagawa H., Yamaguchi Y., Tsutsui T., . Carrier transport properties of organic materials for EL device operation. Synth. Met.. 2000;111:331-333.
[Google Scholar]
Niu C.G., Guan A.L., Zeng G.M., Liu Y.G., Li Z.W., . Fluorescence water sensor based on covalent immobilization of chalcone derivative. Anal. Chim. Acta. 2006;577:264-270.
[Google Scholar]
Oehzelt M., Akaike K., Koch N., Heimel G., . Energy-level alignment at organic heterointerfaces. Sci. Adv.. 2015;1
[Google Scholar]
Oudar J.L., Chemla D.S., . Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment. J. Chem. Phys.. 1977;66:2664-2668.
[Google Scholar]
S.-H. Park, 2014. Method of fabricating liquid crystal display device using a mixture of rubbing alignment material and UV alignment material. U.S.8654289, in, 2014.
Perdew J.P., Chevary J.A., Vosko S.H., Jackson K.A., Pederson M.R., Singh D.J., Fiolhais C., . Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B. 1992;46:6671-6687.
[Google Scholar]
Preat J., Michaux C., Jacquemin D., Perpète E.A., . Enhanced efficiency of organic dye-sensitized solar cells: triphenylamine derivatives. J. Phys. Chem. C. 2009;113:16821-16833.
[Google Scholar]
Preat J., Jacquemin D., Perpète E.A., . Design of new triphenylamine-sensitized solar cells: a theoretical approach. Environ. Sci. Technol.. 2010;44:5666-5671.
[Google Scholar]
Sánchez-Carrera R.S., Coropceanu V., da Silva Filho D.A., Friedlein R., Osikowicz W., Murdey R., Suess C., Salaneck W.R., Brédas J.-L., . Vibronic coupling in the ground and excited states of oligoacene cations†. J. Phys. Chem. B. 2006;110:18904-18911.
[Google Scholar]
Scalmani G., Frisch M.J., Mennucci B., Tomasi J., Cammi R., Barone V., . Geometries and properties of excited states in the gas phase and in solution: theory and application of a time-dependent density functional theory polarizable continuum model. J. Chem. Phys.. 2006;124:094107-094115.
[Google Scholar]
Torruellas W.E., Neher D., Zanoni R., Stegeman G.I., Kajzar F., Leclerc M., . Dispersion measurements of the third-order nonlinear susceptibility of polythiophene thin films. Chem. Phys. Lett.. 1990;175:11-16.
[Google Scholar]
Tsumura A., Koezuka H., Ando T., . Macromolecular electronic device: field-effect transistor with a polythiophene thin film. Appl. Phys. Lett.. 1986;49:1210-1212.
[Google Scholar]
Venkataraman L., Klare J.E., Nuckolls C., Hybertsen M.S., Steigerwald M.L., . Dependence of single-molecule junction conductance on molecular conformation. Nature. 2006;442:904-907.
[Google Scholar]
Zaitseva N., Carman L., . Rapid growth of KDP-type crystals. Prog. Cryst. Growth Charact. Mater.. 2001;43:1-118.
[Google Scholar]
Zhang C., Liang W., Chen H., Chen Y., Wei Z., Wu Y., . Theoretical studies on the geometrical and electronic structures of N-methyle-3,4-fulleropyrrolidine. J. Mol. Struct. (TheoChem). 2008;862:98-104.
[Google Scholar]
Zhang J., Kan Y.-H., Li H.-B., Geng Y., Wu Y., Duan Y.-A., Su Z.-M., . Cyano or o-nitrophenyl? Which is the optimal electron-withdrawing group for the acrylic acid acceptor of D-π-A sensitizers in DSSCs? A density functional evaluation. J. Mol. Model.. 2013;19:1597-1604.
[Google Scholar]
Zhu R., Duan Y.-A., Geng Y., Wei C.-Y., Chen X.-Y., Liao Y., . Theoretical evaluation on the reorganization energy of five-ring-fused benzothiophene derivatives. Comp. Theor. Chem.. 2016;1078:16-22.
[Google Scholar]

Appendix A

Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.jksus.2017.03.010.

Appendix A

Supplementary data

Supplementary data 1

Download

Introduction

Computational details

Results and discussion

Geometries
Electro-optical properties
Charge transport parameters
Nonlinear optical properties (NLO)
Fukui indices
Density of states

Conclusions

Fulltext Views
3

PDF downloads
0

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abdullah S.A.K., Asiri M., Nawaz Tahir M., . (2E)-1-(2,5-Dimethyl-3-thienyl)-3-(2-methoxyphenyl)prop-2-en-1-one. Acta Crystallogr. Sect. E Struct.. 2010;66:o2358.
[Google Scholar]

[2] Abdullah S.A.K., Asiri M., Nawaz Tahir M., . (2E)-3-(3,4-Dimethoxyphenyl)-1-(2,5-dimethylthiophen-3-yl)prop-2-en-1-one. Acta Crystallogr. Sect. E. 2010;E66:o2133.
[Google Scholar]

[3] Abdullah S.A.K., Asiri M., Nawaz Tahir M., . (E)-1-(2,5-Dimethyl-3-thienyl)-3-(2,4,5-trimethoxyphenyl)prop-2-en-1-one. Acta Crystallogr. Sect. E. 2010;E66:o2099.
[Google Scholar]

[4] Badan, J., Hierle, R., Perigaud, A., Zyss, J., Williams, D., 1993. NLO properties of organic molecules and polymeric materials. In: American Chemical Society Symposium Series, American Chemical Society Washington, DC.

[5] Chambon S., D'Aleo A., Baffert C., Wantz G., Fages F., . Solution-processed bulk heterojunction solar cells based on BF2-hydroxychalcone complexes. Chem. Commun.. 2013;49:3555-3557.
[Google Scholar]

[6] Chaudhry A.R., Ahmed R., Irfan A., Shaari A., Al-Sehemi A.G., . Effects of electron withdrawing groups on transfer integrals, mobility, electronic and photo-physical properties of naphtho[2,1-b:6,5-b′]difuran derivatives: a theoretical study. Sci. Adv. Mater.. 2014;6:1727-1739.
[Google Scholar]

[7] Chaudhry A.R., Ahmed R., Irfan A., Shaari A., Isa A.R., Muhammad S., Al-Sehemi A.G., . Effect of donor strength of extended alkyl auxiliary groups on optoelectronic and charge transport properties of novel naphtha[2,1-b:6,5-b′]difuran derivatives: simple yet effective strategy. J. Mol. Model.. 2015;21:1-16.
[Google Scholar]

[8] Cvejn D., Achelle S., Pytela O., Malval J.-P., Spangenberg A., Cabon N., Bureš F., Robin-le Guen F., . Tripodal molecules with triphenylamine core, diazine peripheral groups and extended π-conjugated linkers. Dyes Pigm.. 2016;124:101-109.
[Google Scholar]

[9] Delley B., . From molecules to solids with the DMol3 approach. J. Chem. Phys.. 2000;113:7756-7764.
[Google Scholar]

[10] Frisch, M.J., Trucks, G.W., Schlegel, H.B., et al., 2009. In: Gaussian-09, Revision A.1, Gaussian Inc, Wallingford, CT.

[11] García de Arquer F.P., Armin A., Meredith P., Sargent E.H., . Solution-processed semiconductors for next-generation photodetectors. Nat. Rev. Mater.. 2017;2:16100.
[Google Scholar]

[12] Huong V.T.T., Nguyen H.T., Tai T.B., Nguyen M.T., . Π-Conjugated molecules containing naphtho[2,3-b]thiophene and their derivatives: theoretical design for organic semiconductors. J. Phys. Chem. C. 2013;117:10175-10184.
[Google Scholar]

[13] Irfan A., Al-Sehemi A.G., Muhammad S., Zhang J., . Packing Effect on the Transfer Integrals and Mobility in α, α′-bis(dithieno[3,2-b:2′,3′-d]thiophene) (BDT) and its Heteroatom-Substituted Analogues. Aust. J. Chem.. 2011;64:1587-1592.
[Google Scholar]

[14] Irfan A., Kalam A., Chaudhry A.R., Al-Sehemi A.G., Muhammad S., . Electro-optical, nonlinear and charge transfer properties of naphthalene based compounds: a dual approach study, Optik – Intern. J. Light Elect. Optics. 2017;132:101-110.
[Google Scholar]

[15] Y. Itai, 2012. Thin film field effect transistor and display. US8188480 B2, in, 2012.

[16] Ki-Jun H.-S.K., . Hwang, In-Cheol Han, Beom-Tae Kim, Synthesis of Heterocyclic Chalcone Derivatives and Their Radical Scavenging Ability Toward 2,2-Diphenyl-1-Picrylhydrazyl (DPPH) Free Radicals. Bull. Korean Chem. Soc.. 2012;33:2585-2591.
[Google Scholar]

[17] Levine B.F., Bethea C.G., . Second and third order hyperpolarizabilities of organic molecules. J. Chem. Phys.. 1975;63:2666-2682.
[Google Scholar]

[18] Li X.-C., Sirringhaus H., Garnier F., Holmes A.B., Moratti S.C., Feeder N., Clegg W., Teat S.J., Friend R.H., . A highly π-stacked organic semiconductor for thin film transistors based on fused thiophenes. J. Am. Chem. Soc.. 1998;120:2206-2207.
[Google Scholar]

[19] Lin B.C., Cheng C.P., You Z.-Q., Hsu C.-P., . Charge transport properties of tris(8-hydroxyquinolinato)aluminum(III): why it is an electron transporter. J. Am. Chem. Soc.. 2004;127:66-67.
[Google Scholar]

[20] N.I. Makoto Satsuki, Sadaharu Suga, Hisayoshi Fujikawa, Yasunori Taga, 2007. Organic light emitters using coumarin derivative as luminescent agents having efficiency and durability; display panels, in: US7252892 B2.

[21] Marcus R.A., Sutin N., . Electron transfers in chemistry and biology. Biochim. Biophys. Acta Rev. Bioenerg.. 1985;811:265-322.
[Google Scholar]

[22] R.A.I. Materials Studio Modeling, 2004. San Diego, Materials Studio Modeling, Release 3.0.1. (2004) Accelrys Inc., San Diego.

[23] Matthews D., Infelta P., Grätzel M., . Calculation of the photocurrent-potential characteristic for regenerative, sensitized semiconductor electrodes. Sol. Energy Mater. Sol. Cells. 1996;44:119-155.
[Google Scholar]

[24] Maydt D., De Spirt S., Muschelknautz C., Stahl W., Muller T.J., . Chemical reactivity and biological activity of chalcones and other alpha, beta-unsaturated carbonyl compounds. Xenobiotica. 2013;43:711-718.
[Google Scholar]

[25] Mitsui C., Soeda J., Miwa K., Tsuji H., Takeya J., Nakamura E., . Naphtho[2,1-b:6,5-b′]difuran: a versatile motif available for solution-processed single-crystal organic field-effect transistors with high hole mobility. J. Am. Chem. Soc.. 2012;134:5448-5451.
[Google Scholar]

[26] Muhammad S., Irfan A., Shkir M., Chaudhry A.R., Kalam A., AlFaify S., Al-Sehemi A.G., Al-Salami A.E., Yahia I.S., Xu H.L., . How does hybrid bridging core modification enhance the nonlinear optical properties in donor-π-acceptor configuration? A case study of dinitrophenol derivatives. J. Comput. Chem.. 2015;36:118-128.
[Google Scholar]

[27] Muhammad S., Al-Sehemi A.G., Irfan A., Chaudhry A.R., Gharni H., AlFaify S., Shkir M., Asiri A.M., . The impact of position and number of methoxy group (s) to tune the nonlinear optical properties of chalcone derivatives: a dual substitution strategy. J. Mol. Model.. 2016;22:1-9.
[Google Scholar]

[28] Nadykto A.B., Al Natsheh A., Yu F., Mikkelsen K.V., Herb J., . Chapter 21 computational quantum chemistry: a new approach to atmospheric nucleation. In: Michael E.G., Matthew S.J., eds. Adv Quantum Chem.. Academic Press; 2008. p. :449-478.
[Google Scholar]

[29] Naka S., Okada H., Onnagawa H., Yamaguchi Y., Tsutsui T., . Carrier transport properties of organic materials for EL device operation. Synth. Met.. 2000;111:331-333.
[Google Scholar]

[30] Niu C.G., Guan A.L., Zeng G.M., Liu Y.G., Li Z.W., . Fluorescence water sensor based on covalent immobilization of chalcone derivative. Anal. Chim. Acta. 2006;577:264-270.
[Google Scholar]

[31] Oehzelt M., Akaike K., Koch N., Heimel G., . Energy-level alignment at organic heterointerfaces. Sci. Adv.. 2015;1
[Google Scholar]

[32] Oudar J.L., Chemla D.S., . Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment. J. Chem. Phys.. 1977;66:2664-2668.
[Google Scholar]

[33] S.-H. Park, 2014. Method of fabricating liquid crystal display device using a mixture of rubbing alignment material and UV alignment material. U.S.8654289, in, 2014.

[34] Perdew J.P., Chevary J.A., Vosko S.H., Jackson K.A., Pederson M.R., Singh D.J., Fiolhais C., . Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B. 1992;46:6671-6687.
[Google Scholar]

[35] Preat J., Michaux C., Jacquemin D., Perpète E.A., . Enhanced efficiency of organic dye-sensitized solar cells: triphenylamine derivatives. J. Phys. Chem. C. 2009;113:16821-16833.
[Google Scholar]

[36] Preat J., Jacquemin D., Perpète E.A., . Design of new triphenylamine-sensitized solar cells: a theoretical approach. Environ. Sci. Technol.. 2010;44:5666-5671.
[Google Scholar]

[37] Sánchez-Carrera R.S., Coropceanu V., da Silva Filho D.A., Friedlein R., Osikowicz W., Murdey R., Suess C., Salaneck W.R., Brédas J.-L., . Vibronic coupling in the ground and excited states of oligoacene cations†. J. Phys. Chem. B. 2006;110:18904-18911.
[Google Scholar]

[38] Scalmani G., Frisch M.J., Mennucci B., Tomasi J., Cammi R., Barone V., . Geometries and properties of excited states in the gas phase and in solution: theory and application of a time-dependent density functional theory polarizable continuum model. J. Chem. Phys.. 2006;124:094107-094115.
[Google Scholar]

[39] Torruellas W.E., Neher D., Zanoni R., Stegeman G.I., Kajzar F., Leclerc M., . Dispersion measurements of the third-order nonlinear susceptibility of polythiophene thin films. Chem. Phys. Lett.. 1990;175:11-16.
[Google Scholar]

[40] Tsumura A., Koezuka H., Ando T., . Macromolecular electronic device: field-effect transistor with a polythiophene thin film. Appl. Phys. Lett.. 1986;49:1210-1212.
[Google Scholar]

[41] Venkataraman L., Klare J.E., Nuckolls C., Hybertsen M.S., Steigerwald M.L., . Dependence of single-molecule junction conductance on molecular conformation. Nature. 2006;442:904-907.
[Google Scholar]

[42] Zaitseva N., Carman L., . Rapid growth of KDP-type crystals. Prog. Cryst. Growth Charact. Mater.. 2001;43:1-118.
[Google Scholar]

[43] Zhang C., Liang W., Chen H., Chen Y., Wei Z., Wu Y., . Theoretical studies on the geometrical and electronic structures of N-methyle-3,4-fulleropyrrolidine. J. Mol. Struct. (TheoChem). 2008;862:98-104.
[Google Scholar]

[44] Zhang J., Kan Y.-H., Li H.-B., Geng Y., Wu Y., Duan Y.-A., Su Z.-M., . Cyano or o-nitrophenyl? Which is the optimal electron-withdrawing group for the acrylic acid acceptor of D-π-A sensitizers in DSSCs? A density functional evaluation. J. Mol. Model.. 2013;19:1597-1604.
[Google Scholar]

[45] Zhu R., Duan Y.-A., Geng Y., Wei C.-Y., Chen X.-Y., Liao Y., . Theoretical evaluation on the reorganization energy of five-ring-fused benzothiophene derivatives. Comp. Theor. Chem.. 2016;1078:16-22.
[Google Scholar]