On the numerical solution of space fractional order diffusion equation via shifted Chebyshev polynomials of the third kind

N.H. Sweilam; A.M. Nagy; Adel A. El-Sayed

doi:10.1016/j.jksus.2015.05.002

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

28 (

); 41-47

doi:

10.1016/j.jksus.2015.05.002

On the numerical solution of space fractional order diffusion equation via shifted Chebyshev polynomials of the third kind

N.H. Sweilam^{^a}, A.M. Nagy^{^b,⁎}, Adel A. El-Sayed^{^c}

a Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt

b Department of Mathematics, Faculty of Science, Benha University, Benha, Egypt

c Department of Mathematics, Faculty of Science, Fayoum University, Fayoum, Egypt

⁎Corresponding author. abdelhameed_nagy@yahoo.com (A.M. Nagy),

Received: 2015-4-16, Accepted: 2015-5-11, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this paper, we propose a numerical scheme to solve space fractional order diffusion equation. Our scheme uses shifted Chebyshev polynomials of the third kind. The fractional differential derivatives are expressed in terms of the Caputo sense. Moreover, Chebyshev collocation method together with the finite difference method are used to reduce these types of differential equations to a system of algebraic equations which can be solved numerically. Numerical approximations performed by the proposed method are presented and compared with the results obtained by other numerical methods. The results reveal that our method is a simple and effective numerical method.

Keywords

Space fractional order diffusion equation

Caputo derivative

Chebyshev collocation method

Finite difference method

Chebyshev polynomials of the third kind

Show Related Articles from PubMed

1 Introduction

The subject of fractional calculus (that is, calculus of integrals and derivatives of any arbitrary real or complex order) has gained considerable popularity and importance during the past four decades or so, due mainly to its demonstrated applications in numerous seemingly diverse and widespread fields of science and engineering, chemistry and other sciences (Dalir and Bashour, 2010; Kilbas et al., 2006). It does indeed provide several potentially useful tools for solving differential and integral equations, and various other problems involving special functions of mathematical physics as well as their extensions and generalizations in one and more variables (see for instance, Boyd (2001), Bhrawy et al. (2013, 2014a,b), Kilbas et al. (2006), Miller and Ross (1993), Oldham and Spanier (1974), Podlubny (1999), Rossikhin and Shitikova (1997)).

In recent decades, the Chebyshev polynomials are one of the most useful polynomials which are suitable in numerical analysis including polynomial approximation, integral and differential equations and spectral methods for partial differential equations and fractional order differential equations (see, Canuto et al., 2006; Dalir and Bashour, 2010; Mason and Handscomb, 2003; Scalas et al., 2003; Su et al., 2010; Sousa, 2011; Tadjeran et al., 2006 ).

In recent years, one of the attractive concepts in the initial and boundary value problems is the fractional order diffusion equation, it has found its extensive applications in many fields such as, physics, chemistry, engineering, mathematics, it included in a wide variety of practical situations and has emerged as an important area of investigation. For the general theory and applications of fractional diffusion equations see (Canuto et al., 2006; Dalir and Bashour, 2010; Oldham and Spanier, 1974; Podlubny, 1999; Scalas et al., 2003; Su et al., 2010; Sousa, 2011; Tadjeran et al., 2006 ). The fractional order differential equations have been much studied and many aspects of these equations are explored. For some recent work on fractional diffusion equations, we can refer to different publications (see for instance, Azizi and Loghmani (2013, 2014), Meerschaert and Tadjeran (2004, 2006), Saadatmandi and Dehghan (2007, 2006), Sweilam and Khader (2010), Sweilam et al. (2011, 2012, 2015)) and the references therein.

The fractional order (time–space) diffusion equation makes a great role in the mathematical modeling of several phenomena. It is well known that most of fractional differential equations cannot be solved exactly. Therefore, numerical methods would be proposed and investigated to get approximate solutions of these equations. The Chebyshev finite difference method and a semi-discrete scheme with Chebyshev collocation method have been introduced by Azizi and Loghmani (2013, 2014), for approximating the solution of the space fractional diffusion equations (FDEs). Also, Khader (2011) investigated the Chebyshev collocation method together with the finite difference method for solving FDEs. Moreover, Bhrawy et al. (2014b) introduced efficient generalized Laguerre-spectral methods for solving multi-term fractional differential equations on the half line. The authors in Saadatmandi and Dehghan (2006, 2011) have constructed new operational matrix and tau approach for solution of the space fractional diffusion equation. On the other side many researchers used the finite difference method (FDM) for solving FDEs (see, Elbarbary, 2003; Dehghan and Saadatmandi, 2008; Meerschaert and Tadjeran, 2004, 2006 ). Second kind shifted Chebyshev polynomials and Crank-Nicolson FDM are applied for solving fractional order diffusion equation in Sweilam et al. (2012, 2015).

Our fundamental goal of this work is to develop a suitable way to approximate the space fractional order diffusion equation using the shifted Chebyshev polynomials of the third kind with finite difference method together with Chebyshev collocation method. In what follows, we give some necessary definitions and mathematical relations which are used in this paper.

Definition 1

The Caputo fractional derivative operator $D^{μ}$ of order $μ$ is defined as the following form:

(1)

D^{μ} f (x) = \frac{1}{Γ (m - μ)} \int_{0}^{x} \frac{f^{(m)} (t)}{{(x - t)}^{μ - m + 1}} dt, μ > 0,

where

m - 1 < μ \leq m, m \in N, x > 0

. The linear property of the Caputo fractional derivative exists similar to the integer order differentiation:

(2)

D^{μ} (λ f (x) + γ g (x)) = λ D^{μ} f (x) + γ D^{μ} g (x),

where

λ

and

γ

are constants.

For the Caputo derivative we can obtain the following result:

(3)

D^{μ} k = 0, k is a constant,

(4)

D^{μ} x^{n} = \{\begin{matrix} 0, & for n \in N_{0} and n < ⌈ μ ⌉, \\ \frac{Γ (n + 1)}{Γ (n + 1 - μ)} x^{(n - μ)}, & for n \in N_{0} and n \geq ⌈ μ ⌉ . \end{matrix}

The function $⌈ μ ⌉$ is used to denote the smallest integer greater than or equal to $μ$ . Also $N_{0} = {0, 1, 2, \dots}$ . Recall that, for $μ \in N$ the Caputo differential operator coincides with the usual differential operator of integer order. For more details on fractional derivatives definitions, theorems and its properties see Podlubny (1999).

The main aim of this work is to find approximate solution of space fractional order diffusion equation using the shifted Chebyshev polynomials of the third kind. Consider the one-dimensional space fractional order diffusion equation of the form:

(5)

\frac{\partial u (x, t)}{\partial t} = p (x) \frac{\partial^{μ} u (x, t)}{\partial x^{μ}} + q (x, t),

on a finite domain

0 < x < L, 0 < t \leq T

and the parameter

μ

refers to the fractional order of spatial derivative with

1 < μ \leq 2

. The function

q (x, t)

is the source term. We also assume an initial condition:

(6)

u (x, 0) = f (x), 0 < x < L,

and the boundary conditions:

(7)

u (0, t) = v_{0} (t), 0 < t \leq T

(8)

u (L, t) = v_{1} (t), 0 < t \leq T .

In case of

μ = 2

, Eq. (5) is the classical second order diffusion equation:

(9)

\frac{\partial u (x, t)}{\partial t} = p (x) \frac{\partial^{2} u (x, t)}{\partial x^{2}} + q (x, t) .

In this paper, we use shifted Chebyshev polynomials of third kind and recall some important properties and its analytical form. Next we use these polynomials to approximate the numerical solution of (FDE) with the aid of the Chebyshev collocation method together with the finite difference method to convert the system of equations in algebraic equations that can be solved numerically.

For this purpose, organization of paper is expressed as follows. In Section 2, we give some properties of Chebyshev polynomials of the third kind which are of fundamental importance in what follows. In Section 3, we introduce main theorem of our technique for solving space fractional order diffusion equation subject to homogeneous and nonhomogeneous boundary conditions using a shifted Chebyshev polynomials of the third kind. Numerical scheme is given in Section 4. In Section 5, we present numerical examples to exhibit the accuracy and the efficiency of our proposed method where our numerical results are computed by Matlab program. Conclusions are presented in Section 6.

2 Some properties of Chebyshev polynomials of the thirdkind

2.1

2.1 Chebyshev polynomials of the thirdkind

Definition 2

The Chebyshev polynomials $V_{n} (x)$ of the third kind are orthogonal polynomials of degree n in x defined on the $[- 1, 1]$ (see, Mason and Handscomb (2003)) $V_{n} (x) = \frac{\cos (n + \frac{1}{2}) θ}{\cos \frac{θ}{2}},$

where

x = \cos θ

and

θ \in [0, π]

. They can be obtained explicitly using the Jacobi polynomials

P_{k}^{(α, β)} (x)

, for the special case

β = - α = \frac{1}{2}

. These are given by:

(10)

V_{k} (x) = \frac{2^{2 k}}{(\begin{matrix} 2 k \\ k \end{matrix})} P_{k}^{(- \frac{1}{2}, \frac{1}{2})} (x) .

Also, these polynomials

V_{n} (x)

are orthogonal on

[- 1, 1]

with respect to the inner product:

(11)

〈 V_{n} (x), V_{m} (x) 〉 = \int_{- 1}^{1} \sqrt{\frac{1 + x}{1 - x}} V_{n} (x) V_{m} (x) dx = \{\begin{matrix} 0, n \neq m, \\ π, n = m, \end{matrix}

where

\sqrt{\frac{1 + x}{1 - x}}

is weight function corresponding to

V_{n} (x)

. The polynomials

V_{n} (x)

may be generated by using the recurrence relations

V_{n + 1} (x) = 2 x V_{n} (x) - V_{n - 1} (x), n = 1, 2, \dots,

with

V_{0} (x) = 1, V_{1} (x) = 2 x - 1 .

Using Eq. (10) and properties of Jacobi polynomials to obtain the analytical form of the Chebyshev polynomials of the third kind $V_{n} (x)$ of degree n, they are given as:

(12)

V_{n} (x) = \sum_{k = 0}^{⌈\frac{2 n + 1}{2}⌉} {(- 1)}^{k} {(2)}^{n - k} \frac{(2 n + 1) Γ (2 n - k + 1)}{Γ (k + 1) Γ (2 n - 2 k + 2)} {(x + 1)}^{n - k} n \in Z^{+},

where

⌈\frac{2 n + 1}{2}⌉

denotes the integral part of

(2 n + 1) / 2

2.2

2.2 The shifted Chebyshev polynomials of the third kind

Since the range $[0, 1]$ is quite often more convenient to use than the range $[- 1, 1]$ , we sometimes map the independent variable $x \in [0, 1]$ to the variable s in $[- 1, 1]$ by the transformation $s = 2 x - 1$ or $x = \frac{(s + 1)}{2}$ , and this leads to a shifted Chebyshev polynomials of the third kind $V_{n}^{*} (x)$ of degree n in x on $[0, 1]$ given by $V_{n}^{*} (x) = V_{n} (2 x - 1) .$ These polynomials are orthogonal on the support interval $[0, 1]$ as the following inner product:

(13)

〈 V_{n}^{*} (x), V_{m}^{*} (x) 〉 = \int_{0}^{1} \sqrt{\frac{x}{1 - x}} V_{n}^{*} (x) V_{m}^{*} (x) dx = \{\begin{matrix} 0, n \neq m, \\ \frac{π}{2}, n = m, \end{matrix}

where

\sqrt{\frac{x}{1 - x}}

is weight function corresponding to

V_{n}^{*} (x)

and normalized by the requirement that

V_{n}^{*} (1) = 1

. Also,

V_{n}^{*} (x)

may be generated by using the recurrence relations

V_{n + 1}^{*} (x) = 2 (2 x - 1) V_{n}^{*} (x) - V_{n - 1}^{*} (x), n = 1, 2, \dots,

with starting values

V_{0}^{*} (x) = 1, V_{1}^{*} (x) = 4 x - 3 .

The analytical form of the shifted Chebyshev polynomials of the third kind $V_{n}^{*} (x)$ of degree n in x is given by

(14)

V_{n}^{*} (x) = \sum_{k = 0}^{n} {(- 1)}^{k} {(2)}^{2 n - 2 k} \frac{(2 n + 1) Γ (2 n - k + 1)}{Γ (k + 1) Γ (2 n - 2 k + 2)} x^{n - k}, n \in Z^{+} .

In a spectral method, in contrast, the function $g (x)$ , square integrable in $[0, 1]$ , is represented by an infinite expansion of the shifted Chebyshev polynomials of the third kind as follows:

(15)

g (x) = \sum_{i = 0}^{\infty} b_{i} V_{i}^{*} (x),

where

b_{i}

is a chosen sequence of prescribed basis functions. One then proceeds somehow to estimate as many as possible of the coefficients

b_{i}

, thus approximating

g (x)

by a finite sum of

(m + 1)

-terms such as:

(16)

g_{m} (x) = \sum_{i = 0}^{m} b_{i} V_{i}^{*} (x),

where the coefficients

b_{i}, (i = 0, 1, \dots)

are given by

(17)

b_{i} = \frac{1}{π} \int_{- 1}^{1} g (\frac{x + 1}{2}) \sqrt{\frac{1 + x}{1 - x}} V_{i} (x) dx

(18)

b_{i} = \frac{2}{π} \int_{0}^{1} g (x) \sqrt{\frac{x}{1 - x}} V_{i}^{*} (x) dx .

3 Main results

The main approximate formula for the function $g_{m} (x)$ given in (16) is presented in the following theorem.

Theorem 1

Let $g_{m} (x)$ be approximated function in terms of shifted Chebyshev polynomials of the third kind as given in (16), suppose $μ > 0$ then, we obtain:

(19)

D^{μ} (g_{m} (x)) = \sum_{i = ⌈ μ ⌉}^{m} \sum_{k = 0}^{i - ⌈ μ ⌉} b_{i} N_{i, k}^{(μ)} x^{i - k - μ},

where

(20)

N_{i, k}^{(μ)} = {(- 1)}^{k} 2^{(2 i - 2 k)} \frac{(2 n + 1) Γ (2 i - k + 1) Γ (i - k + 1)}{Γ (k + 1) Γ (2 i - 2 k + 2) Γ (i - k + 1 - μ)} .

Proof

Using definition of approximated function $g_{m} (x)$ given in Eq. (16) and the Caputo fractional differentiation properties given in Eq. (2) we obtain:

(21)

D^{μ} (g_{m} (x)) = \sum_{i = 0}^{m} b_{i} D^{μ} (V_{i}^{*} (x)) .

The properties of linearity of the Caputo derivative together with Eqs. (3) and (4) are used to claim that:

(22)

D^{μ} (V_{i}^{*} (x)) = 0, i = 0, 1, \dots, ⌈ μ ⌉ - 1, μ > 0 .

Also, we obtain:

(23)

D^{μ} (V_{i}^{*} (x)) = \sum_{k = 0}^{i} {(- 1)}^{k} 2^{(2 i - 2 k)} \frac{(2 i + 1) Γ (2 i - k + 1)}{Γ (k + 1) Γ (2 i - 2 k + 2)} D^{μ} x^{i - k} .

The above Eq. (23) can be rewritten with the aid of Eqs. (3) and (4) as follows:

(24)

D^{μ} (V_{i}^{*} (x)) = \sum_{k = 0}^{i - ⌈ μ ⌉} {(- 1)}^{k} 2^{(2 i - 2 k)} \frac{(2 i + 1) Γ (2 i - k + 1) Γ (i - k + 1)}{Γ (k + 1) Γ (2 i - 2 k + 2) Γ (i - k + 1 - μ)} x^{i - k - μ} .

By combinations Eqs. (21), (22) and (24) we obtain:

(25)

D^{μ} (g_{m} (x)) = \sum_{i = ⌈ μ ⌉}^{m} \sum_{k = 0}^{i - ⌈ μ ⌉} b_{i} {(- 1)}^{k} 2^{(2 i - 2 k)} \frac{(2 i + 1) Γ (2 i - k + 1) Γ (i - k + 1)}{Γ (k + 1) Γ (2 i - 2 k + 2) Γ (i - k + 1 - μ)} x^{i - k - μ},

the above Eq. (25) can be rewritten as the following form:

(26)

D^{μ} (g_{m} (x)) = \sum_{i = ⌈ μ ⌉}^{m} \sum_{k = 0}^{i - ⌈ μ ⌉} b_{i} N_{i, k}^{(μ)} x^{i - k - μ},

where

(27)

N_{i, k}^{(μ)} = {(- 1)}^{k} 2^{(2 i - 2 k)} \frac{(2 i + 1) Γ (2 i - k + 1) Γ (i - k + 1)}{Γ (k + 1) Γ (2 i - 2 k + 2) Γ (i - k + 1 - μ)} .

Simple test example 1

Consider $g (x) = x^{2}$ with $m = 3$ and $μ = 1.5$ . Using Eq. (4) we obtain: $D^{1.5} x^{2} = \frac{Γ (2 + 1)}{Γ (2 + 1 - 1.5)} x^{(2 - 1.5)} = \frac{Γ (3)}{Γ (1.5)} x^{\frac{1}{2}} = \frac{2}{Γ (\frac{3}{2})} x^{\frac{1}{2}} .$

Then, using the proposed method given in Theorem 1 together with Eqs. (17) we obtain:

(28)

D^{1.5} x^{2} = \sum_{i = 2}^{3} \sum_{k = 0}^{i - 2} b_{i} N_{i, k}^{(1.5)} x^{(i - k - 1.5)} = b_{2} N_{2, 0}^{\frac{3}{2}} x^{\frac{3}{2}} + b_{3} N_{3, 0}^{\frac{3}{2}} x^{\frac{3}{2}} + b_{3} N_{3, 1}^{\frac{3}{2}} x^{\frac{1}{2}},

where, $N_{2, 0}^{\frac{3}{2}} = \frac{32}{Γ (\frac{3}{2})}, N_{3, 0}^{\frac{3}{2}} = \frac{256}{Γ (\frac{3}{2})}, N_{3, 1}^{\frac{3}{2}} = \frac{- 224}{Γ (\frac{3}{2})} .$

The constants $b_{2}$ and $b_{3}$ are computed by using Eq. (17) or (18) and then substituting in Eq. (28) we get: $D^{1.5} x^{2} = \frac{2}{Γ (\frac{3}{2})} x^{\frac{1}{2}} .$

4 Numerical scheme

Consider the space fractional order diffusion equation of the type given in Eq. (5) with initial condition as in Eq. (6) and boundary conditions given in Eqs. (7) and (8) respectively. In order to use the Chebyshev collocation method, let us approximate $u (x, t)$ as follows:

(29)

u_{m} (x, t) = \sum_{i = 0}^{m} u_{i} (t) V_{i}^{*} (x) .

From Eqs. (5), (19) and Theorem 1 we can claim:

(30)

\sum_{i = 0}^{m} \frac{{du}_{i} (t)}{dt} V_{i}^{*} (x) = p (x) \sum_{i = ⌈ μ ⌉}^{m} \sum_{k = 0}^{i - ⌈ μ ⌉} u_{i} (t) N_{i, k}^{(μ)} x^{i - k - μ} + q (x, t) .

Now, we collocate Eq. (30) at

(m + 1 - ⌈ μ ⌉)

points

x_{p}

as follows:

(31)

\sum_{i = 0}^{m} \frac{{du}_{i} (t)}{dt} V_{i}^{*} (x_{p}) = p (x_{p}) \sum_{i = ⌈ μ ⌉}^{m} \sum_{k = 0}^{i - ⌈ μ ⌉} u_{i} (t) N_{i, k}^{(μ)} x_{p}^{i - k - μ} + q (x_{p}, t) .

Using the roots of shifted Chebyshev polynomials of the third kinds

V_{m + 1 - ⌈ μ ⌉}^{*} (x)

to suitable the collocation points. Using Eqs. (18) and (29) in the initial condition, we obtain the constants

(u_{i})

in the initial case at

(t = 0)

, moreover by substituting it in the boundary conditions, we obtain

⌈ μ ⌉

equations. For example by substituting Eq. (29) in Eqs. (7) and (8) respectively, in case of

0 < x < 1

we obtain:

(32)

\sum_{i = 0}^{m} {(- 1)}^{(i)} (2 i + 1) u_{i} (t) = v_{0} (x), \sum_{i = 0}^{m} u_{i} (t) = v_{1} (x) .

Notice that: in case the boundary conditions are zeros Dirichlet conditions Eq. (32) can be rewritten as:

(33)

\sum_{i = 0}^{m} {(- 1)}^{(i)} (2 i + 1) u_{i} (t) = 0, \sum_{i = 0}^{m} u_{i} (t) = 0 .

Eq. (31), together with $⌈ μ ⌉$ equations of the boundary conditions (32), give $(m + 1)$ ordinary differential equations which can be solved numerically to get the unknown $u_{i}, i = 0, 1, \dots, m$ .

5 Numerical experiments and comparison

Example 1

Consider Eq. (5) with $μ = 1.8$ it is given in the following form: $\frac{\partial u (x, t)}{\partial t} = p (x) \frac{\partial^{1.8} u (x, t)}{\partial x^{1.8}} + q (x, t), 0 < x < 1, t > 0,$ with the diffusion coefficient $p (x) = Γ (1.2) x^{1.8},$ the source function $q (x, t) = 3 x^{2} (2 x - 1) e^{- t},$ with the initial condition $u (x, 0) = x^{2} (1 - x),$ and the boundary conditions $u (0, t) = u (1, t) = 0, t > 0 .$ The exact solution of this problem is given by: $u (x, t) = x^{2} (1 - x) e^{- t} .$ Let us consider $m = 3$ then, we have:

(34)

u_{3} (x, t) = \sum_{i = 0}^{3} u_{i} (t) V_{i}^{*} (x) .

Using Eq. (31), we claim:

(35)

\sum_{i = 0}^{3} \frac{{du}_{i} (t)}{dt} V_{i}^{*} (x_{p}) = p (x_{p}) \sum_{i = 2}^{3} \sum_{k = 0}^{i - 2} u_{i} (t) N_{i, k}^{(1.8)} x_{p}^{i - k - 1.8} + q (x_{p}, t), p = 0, 1,

where

x_{p}

are the roots of the shifted Chebyshev polynomial of the third kind

V_{2}^{*} (x)

. Using Eqs. (33) and (35) we obtain the following system of ordinary differential equations:

(36)

u_{0}^{\cdot} (t) + G_{1} u_{1}^{\cdot} (t) + G_{2} u_{3}^{\cdot} (t) = H_{1} u_{2} (t) + H_{2} u_{3} (t) + q (x_{0}, t),

(37)

u_{0}^{\cdot} (t) + G_{11} u_{1}^{\cdot} (t) + G_{22} u_{3}^{\cdot} (t) = H_{11} u_{2} (t) + H_{22} u_{3} (t) + q (x_{1}, t),

(38)

u_{0} (t) - 3 u_{1} (t) + 5 u_{2} (t) - 7 u_{3} (t) = 0,

(39)

u_{0} (t) + u_{1} (t) + u_{2} (t) + u_{3} (t) = 0,

where

G_{1} = V_{1}^{*} (x_{0}), G_{2} = V_{3}^{*} (x_{0}), G_{11} = V_{1}^{*} (x_{1}), G_{22} = V_{3}^{*} (x_{1}),

H_{1} = p (x_{0}) N_{2, 0}^{(1.8)} x_{0}^{2 - 1.8}, H_{2} = p (x_{0}) [N_{3, 0}^{(1.8)} x_{0}^{3 - 1.8} + N_{3, 1}^{(1.8)} x_{0}^{2 - 1.8}],

H_{11} = p (x_{1}) N_{2, 0}^{(1.8)} x_{1}^{2 - 1.8}, H_{22} = p (x_{1}) [N_{3, 0}^{(1.8)} x_{1}^{3 - 1.8} + N_{3, 1}^{(1.8)} x_{1}^{2 - 1.8}] .

Now, we use the finite difference method to solve the system (36)–(39) with the following notations:

T = T_{final}, 0 < t_{j} \leq T

and suppose

Δ t = T / N, t_{j} = j Δ t

, for

j = 0, 1, \dots, N

. Also, we define

u_{i} (t_{n}) = u_{i}^{n}, q_{i} (t_{n}) = q_{i}^{n} .

Then, the system in Eqs. (36)–(39), is discretized in the time and has the following form:

(40)

\frac{u_{0}^{n} - u_{0}^{n - 1}}{Δ t} + G_{1} \frac{u_{1}^{n} - u_{1}^{n - 1}}{Δ t} + G_{2} \frac{u_{3}^{n} - u_{3}^{n - 1}}{Δ t} = H_{1} u_{2}^{n} + H_{2} u_{3}^{n} + q_{0}^{n},

(41)

\frac{u_{0}^{n} - u_{0}^{n - 1}}{Δ t} + G_{11} \frac{u_{1}^{n} - u_{1}^{n - 1}}{Δ t} + G_{22} \frac{u_{3}^{n} - u_{3}^{n - 1}}{Δ t} = H_{11} u_{2}^{n} + H_{22} u_{3}^{n} + q_{1}^{n},

(42)

u_{0}^{n} - 3 u_{1}^{n} + 5 u_{2}^{n} - 7 u_{3}^{n} = 0,

(43)

u_{0}^{n} + u_{1}^{n} + u_{2}^{n} + u_{3}^{n} = 0 .

The above system of Eqs. (40)–(43) can be rewritten as the following matrix form:

(44)

{AU}^{n} = {BU}^{n - 1} + Δ {tq}^{n}, or U^{n} = A^{- 1} {BU}^{n - 1} + Δ {tA}^{- 1} q^{n},

where

A = (\begin{matrix} 1 & G_{1} & - Δ {tH}_{1} & G_{2} - Δ {tH}_{2} \\ 1 & G_{11} & - Δ {tH}_{11} & G_{22} - Δ {tH}_{22} \\ 1 & - 2 & 3 & - 4 \\ 1 & 2 & 3 & 4 \end{matrix}),

B = (\begin{matrix} 1 & G_{1} & 0 & G_{2} \\ 1 & G_{11} & 0 & G_{22} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}),

U^{n} = {(u_{0}^{n}, u_{1}^{n}, u_{2}^{n}, u_{3}^{n})}^{T}

and

q^{n} = {(q_{0}^{n}, q_{1}^{n}, 0, 0)}^{T}

In order to obtain the initial solution $U^{0}$ of Eq. (44) we use the initial condition of the problem, $u (x, 0)$ combining with Eq. (17) or (18). Moreover, the approximation solution in Eq. (34) is obtained by substituting analytical form series of the shifted Chebyshev polynomials of the third kind $V_{i}^{*} (x)$ , $i = 0, 1, 2, 3$ as well as the coefficients ( $u_{i}$ , $i = 0, 1, 2, 3$ ) which are computed in (44).

Table 1, presents the numerical results of Example 1 at $T = 2$ . The results obtained by our method with $Δ t = 0.25 e - 3$ and $Δ t = 0.25 e - 6$ are given in the fourth and the fifth columns respectively. In this table, we have computed the absolute error between the exact and the approximate solutions. In order to validate the accuracy of the proposed method, we have compared the results of the presented method with the previously published data given in Khader (2011) and Saadatmandi and Dehghan (2011). From the results in Table 1, we can derive that the accuracy of the presented method is better than other methods. Also, the computational cost (CPU time) seems for the proposed method faster than other methods because we just need few terms (i.e., $m = 3$ ) to obtain a solution with high accuracy. In Figs. 1 and 2 we have plotted the exact and the numerical solutions at $m = 5, T = 1$ and $m = 7, T = 2$ respectively.

Example 2

Consider Eq. (5) with $μ = 1.8$ as follows: $\frac{\partial u (x, t)}{\partial t} = p (x) \frac{\partial^{1.8} u (x, t)}{\partial x^{1.8}} + q (x, t), 0 < x < 1, t > 0,$ with the diffusion coefficient $p (x) = \frac{Γ (2.2)}{6} x^{2.8},$ the source function $q (x, t) = - (1 + x) x^{3} e^{- t},$ with the initial condition $u (x, 0) = x^{3},$ and the boundary conditions $u (0, t) = 0, u (1, t) = e^{- t}, t > 0 .$ The exact solution of this problem is given by: $u (x, t) = x^{3} e^{- t} .$ From the results of Table 2 and Fig. 3, it is obvious that the presented method gives more accurate results than the results discussed in Sweilam et al. (2015).

Table 1 The absolute error of the methods given in Khader (2011), Saadatmandi and Dehghan (2011) and our method for Example 1, at T = 2 with different values of Δt.

x	In Khader (2011) (m = 5)	In Saadatmandi and Dehghan (2011) (m = 5)	Presented method (m = 3)	Presented method (m = 3)
0	2.74 × 10⁻⁵	0	0	0
0.1	4.20 × 10⁻⁵	4.47 × 10⁻⁶	3.77 × 10⁻⁷	3.79 × 10⁻¹⁰
0.2	3.76 × 10⁻⁵	2.78 × 10⁻⁷	6.25 × 10⁻⁷	6.26 × 10⁻¹⁰
0.3	8.44 × 10⁻⁵	5.81 × 10⁻⁶	7.59 × 10⁻⁷	7.61 × 10⁻¹⁰
0.4	3.27 × 10⁻⁵	1.02 × 10⁻⁵	7.97 × 10⁻⁷	7.99 × 10⁻¹⁰
0.5	3.61 × 10⁻⁵	1.17 × 10⁻⁵	7.58 × 10⁻⁷	7.60 × 10⁻¹⁰
0.6	1.94 × 10⁻⁵	1.08 × 10⁻⁵	6.58 × 10⁻⁷	6.59 × 10⁻¹⁰
0.7	2.95 × 10⁻⁵	8.54 × 10⁻⁶	5.14 × 10⁻⁷	5.16 × 10⁻¹⁰
0.8	4.92 × 10⁻⁵	6.06 × 10⁻⁶	3.45 × 10⁻⁷	3.46 × 10⁻¹⁰
0.9	2.83 × 10⁻⁵	3.76 × 10⁻⁶	1.68 × 10⁻⁷	1.68 × 10⁻¹⁰
1	7.73 × 10⁻⁵	0	0	0

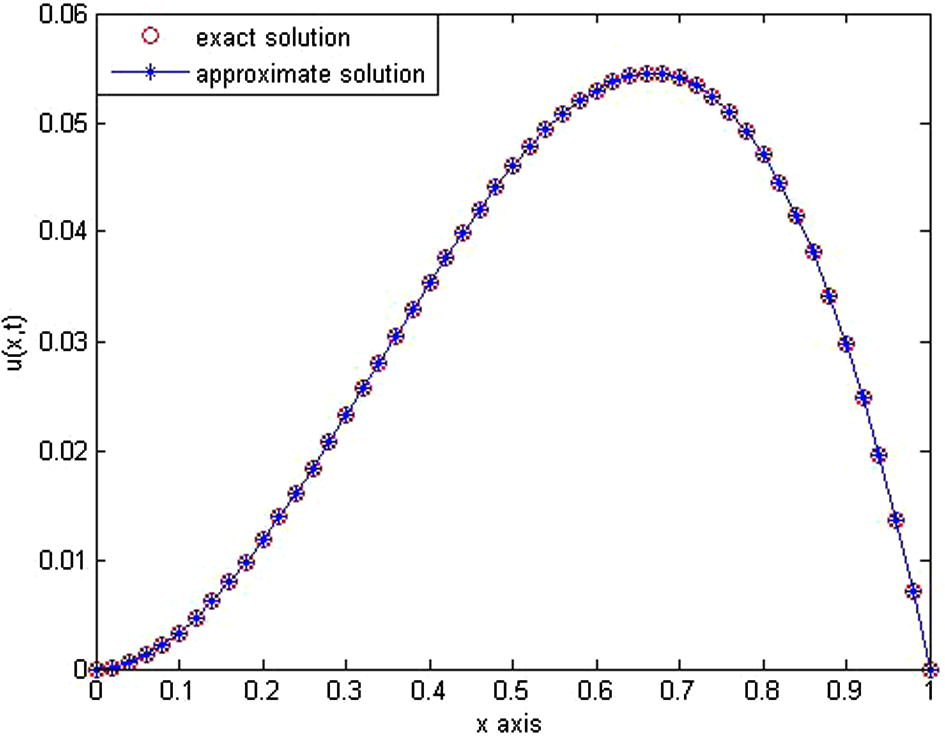
The behavior of exact solution and approximation solution at m = 5 and T = 1 .

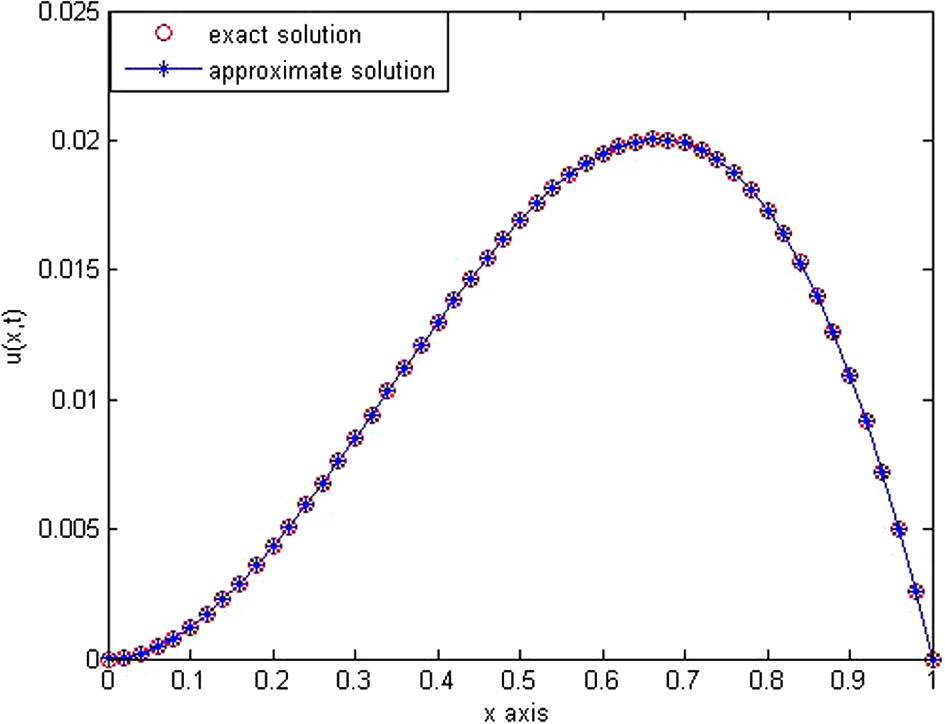
The behavior of exact solution and approximation solution at m = 7 and T = 2 .

Table 2 Comparison of maximum error of the method in Sweilam et al. (2015) and our presented method for Example 2, at m = 3 and T = 1.

Max error (Sweilam et al., 2015)	Max error present method
8.3830 × 10⁻¹⁰	1.008 × 10⁻¹⁰

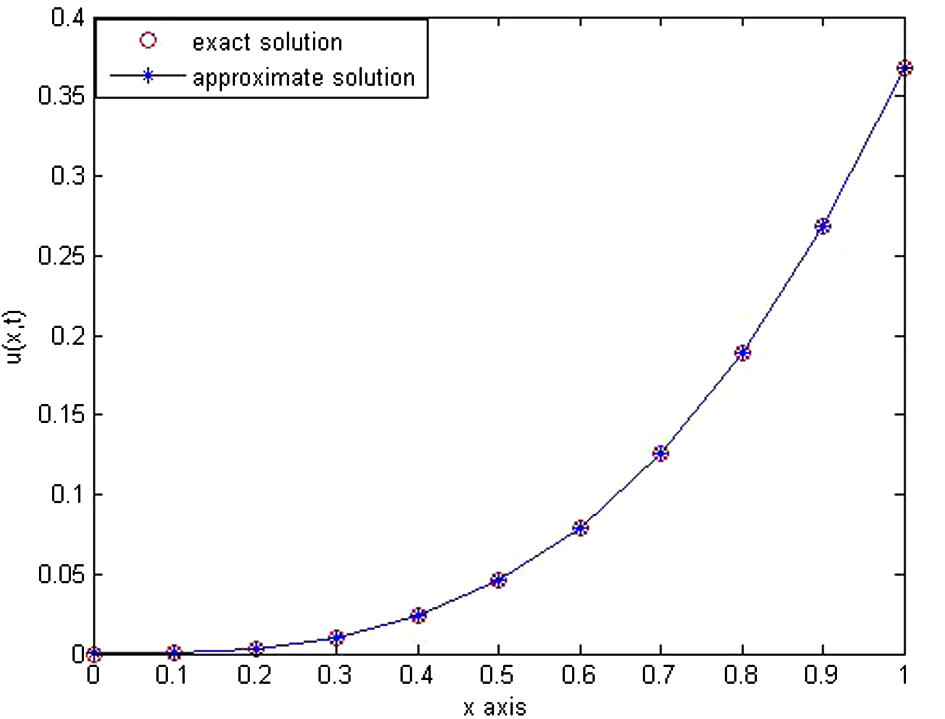
The behavior of exact solution and approximation solution for Example 2 at m = 3 and T = 1 .

6 Conclusions

In this paper, the shifted Chebyshev polynomials of the third kind and its properties together with the Chebyshev collocation method are used to reduce the space fractional order diffusion equation to a system of ordinary differential equations. The fractional derivative is considered in the Caputo sense. The validity and applicability of our presented method are illustrated through some numerical results. These results are compared with other published results in some papers. From the numerical results, it is obvious that our proposed method exhibits good accuracy and efficiency than the other methods. All computed results are obtained using Matlab program.

References

Azizi H., Loghmani G.B., . Numerical approximation for space fractional diffusion equations via Chebyshev finite difference method. J. Fract. Calculus Appl.. 2013;4(2):303-311.
[Google Scholar]
Azizi H., Loghmani G.B., . A numerical method for space fractional diffusion equations using a semi-disrete scheme and Chebyshev collocation method. J. Math. Comput. Sci.. 2014;8:226-235.
[Google Scholar]
Boyd J.P., . Chebyshev and Fourier Spectral Methods (2nd ed.). Mineola: Dover; 2001.
Bhrawy A.H., Alghamdi M.A., Baleanu D., . Numerical solution of a class of functional-differential equations using Jacobi pseudospectral method. Abstr. Appl. Anal. 2013 Article ID 513808, 9 p.
[Google Scholar]
Bhrawy A.H., AlZahrani A., Baleanu D., Alhamed Y., . A modified generalized Laguerre–Gauss collocation method for fractional neutral functional-differential equations on the half-line. Abstr. Appl. Anal. 2014 Article ID 692193, 7 p
[Google Scholar]
Bhrawy A.H., Baleanu D., Assas L.M., . Efficient generalized Laguerre-spectral methods for solving multi-term fractional differential equations on the half line. J. Vibrat. Control. 2014;20(7):973-985.
[Google Scholar]
Canuto C., Quarteroni A., Hussaini M.Y., Zang T.A., . Spectral Methods: Fundamentals in Single Domains. Springer; 2006.
Elbarbary E.M.M., . Chebyshev finite difference approximation for the boundary value problems. Appl. Math. Comput.. 2003;139:513-523.
[Google Scholar]
Dehghan M., Saadatmandi A., . Chebyshev finite difference method for Fredholm integro-differential equation. Int. J. Comput. Math.. 2008;85:123-130.
[Google Scholar]
Dalir M., Bashour M., . Applications of fractional calculus. Appl. Math. Sci.. 2010;4:1021-1032.
[Google Scholar]
Kilbas A.A., Srivastava H.M., Trujillo J.J., . Theory and Applications of Fractional Differential Equations. San Diego: Elsevier; 2006.
Khader M.M., . On the numerical solutions for the fractional diffusion equation. Commun. Nonlinear Sci. Numer. Simul.. 2011;16:2535-2542.
[Google Scholar]
Mason J.C., Handscomb D.C., . Chebyshev Polynomials. New York, NY, Boca Raton: Chapman and Hall, CRC; 2003.
Miller K.S., Ross B., . An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: John Wiley; 1993.
Meerschaert M.M., Tadjeran C., . Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math.. 2004;172(1):65-77.
[Google Scholar]
Meerschaert M.M., Tadjeran C., . Finite difference approximations for two-sided space fractional partial differential equations. Appl. Numer. Math.. 2006;56:80-90.
[Google Scholar]
Oldham K.B., Spanier J., . The Fractional Calculus. New York: Academic Press; 1974.
Podlubny I., . Fractional Differential Equations. New York: Academic Press; 1999.
Rossikhin Y.A., Shitikova M.V., . Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev.. 1997;50(1):15-67.
[Google Scholar]
Saadatmandi A., Dehghan M., . Numerical solution of the one-dimensional wave equation with an integral condition. Numer. Methods Partial Differ. Equ.. 2007;23:282-292.
[Google Scholar]
Saadatmandi A., Dehghan M., . A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl.. 2006;59:1326-1336.
[Google Scholar]
Saadatmandi A., Dehghan M., . A tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl.. 2011;62:1135-1142.
[Google Scholar]
Scalas E., Gorenflo R., Mainardi F., Raberto M., . Revisiting the derivation of the fractional order diffusion equation. Scalling and disordered systems. Fractals. 2003;11(supp1):281-289.
[Google Scholar]
Sweilam N.H., Khader M.M., . A Chebyshev pseudo-spectral method for solving fractional order integro-differential equations. ANZIAM. 2010;51:464-475.
[Google Scholar]
Sweilam N.H., Khader M.M., Nagy A.M., . Numerical solution of two-sided space-fractional wave equation using fnite difference method. J. Comput. Appl. Math.. 2011;235:2832-2841.
[Google Scholar]
Sweilam N.H., Khader M.M., Mahdy A.M.S., . Crank-Nicolson FDM for solving time-fractional diffusion equation. J. Fraction. Calculus Appl.. 2012;2(2):1-9.
[Google Scholar]
Sweilam N.H., Nagy A.M., El-Sayed Adel A., . Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation, Chaos. Solitons Fract.. 2015;73:141-147.
[Google Scholar]
Su L., Wang W., Xu Q., . Finite difference methods for fractional dispersion equations. Appl. Math. Comput.. 2010;216:3329-3334.
[Google Scholar]
Sousa E., . Numerical approximations for fractional diffusion equation via splines. Comput. Math. Appl.. 2011;62 983-944
[Google Scholar]
Tadjeran C., Meerschaert M., Scheffler H.P., . A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys.. 2006;213:205-213.
[Google Scholar]