Translate this page into:
Lévy stable distribution and space-fractional Fokker-Planck type equation
?Corresponding author. duanjs@sit.edu.cn (Jun-Sheng Duan)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The space-fractional Fokker-Planck type equation subject to the initial condition is solved in terms of Fox H functions. The solution as expresses the Lévy stable distribution with the index . From the properties of Fox H functions, the series representation and asymptotic behavior for the solution are also obtained. Lévy stable distribution as describes anomalous superdiffusion and its diffusion velocity is characterized by .
Keywords
Fokker-Planck equation
Laplace operator
Fourier transform
Fox H function
1 Introduction
In recent decades, the theory and applications of the fractional calculus have developed rapidly. The applied fields include viscoelasticity, anomalous diffusion, heat transfer, signal processing, dynamics and control, and so on (Podlubny, 1999; Kilbas et al., 2006). Different definitions and methods have also been proposed (Yang et al., 2013; Yang and Baleanu, 2013; Yang, 2012; Li et al., 2011a,b). Scientists and engineers have found the description of some phenomena is more accurate when the fractional derivative is used. In particular, anomalous diffusion can be characterized by fractional differential equations.
Let random variable
denote the location of diffusing particle with
and
be the probability density function for
. The time-fractional Fokker-Planck type equations are derived and solved in Hilfer (1995) and Rangarajan and Ding (2000); Space-fractional Fokker-Planck type equation is obtained in Compte (1996) and Yanovsky et al. (2000) using statistical methods. One-dimensional case with convective term without asymmetric term reads (Yanovsky et al., 2000)
Space-fractional Fokker-Planck type equations similar to the Eq. (1) are also considered in Chaves (1998) and Chechkin et al. (2002), but therein the exact analytic solutions for the problem (1) and (2) are given only for the cases of and . In the general case of , the solution for the problem (1) and (2) is studied in the sequel. We obtain the exact analytic solution in terms of Fox H functions (Mathai and Saxena, 1978; Srivastava et al., 1982), and its series representation and asymptotic behavior are investigated.
2 Solution to the problem
Taking the Fourier transform for the problem (1) and (2) with respect to x we get
Lévy stable distribution
with index
is defined through the Fourier transform as (Feller, 1971; Fogedby et al., 1992; Zanette, 1997)
In order to obtain the inverse in (7) we rewrite it as
As
, the first expression in Eq. (15) permits
, while the second permits
. Making use of the series expression of Fox functions and the formula
we get the series representations
3 Discussions and conclusions
As
, the Cauchy distribution is obtained from Eqs. (16) and (17)
As
, with the help of the identity
and the expression in Eq. (17), the Gauss distribution is obtained
From Eqs. (16) and (17) we have the following asymptotic expressions
In Figs. 1 and 2, we plot the curves of
versus x for fixed values of t and different values of
. Since for fixed t, the series in (16) converges faster for large
while the second converges faster for small
, the different ranges of x are chosen in Figs. 1 and 2.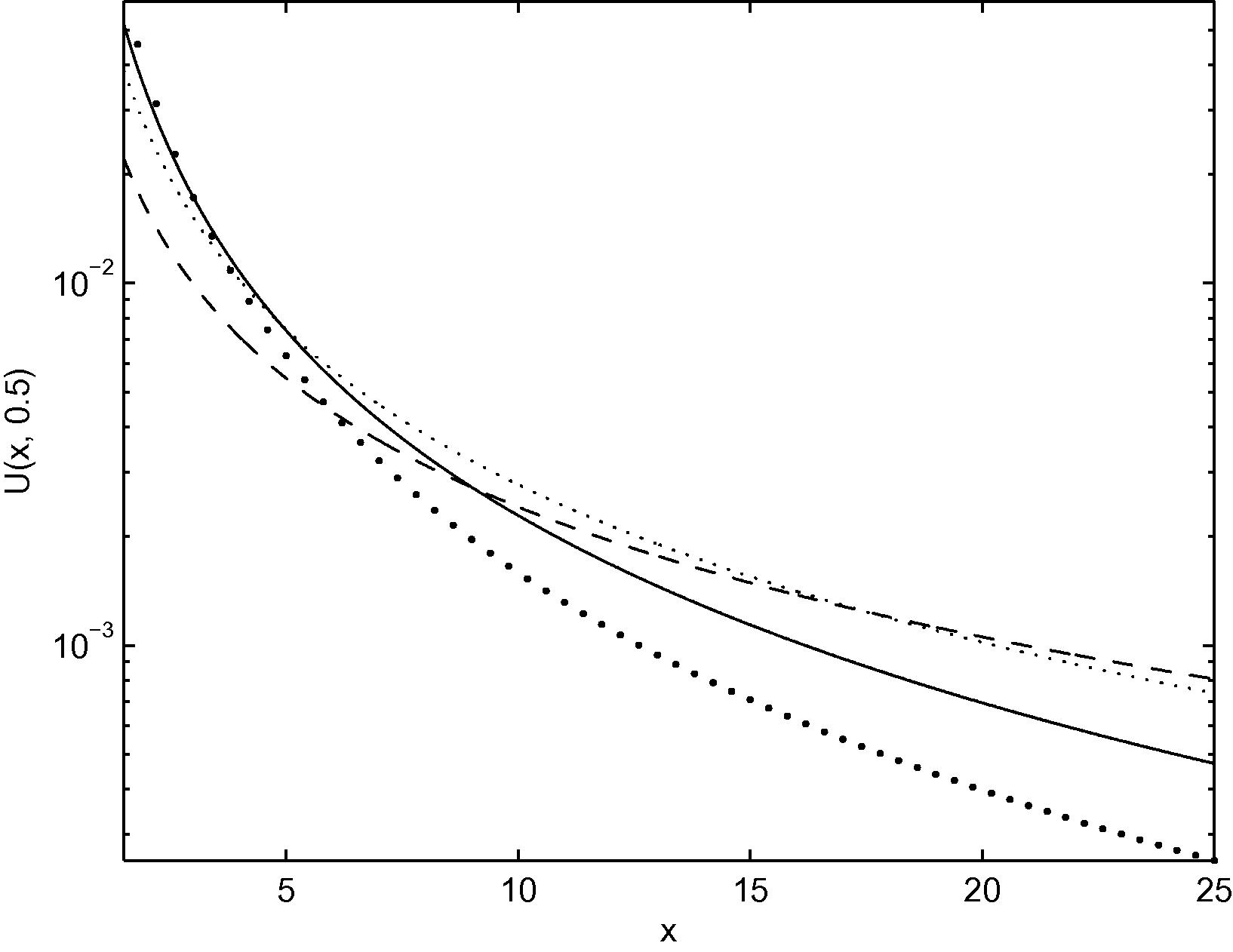
Curves of
versus x on the interval
for
and
(thick dot line), 0.75 (solid line), 0.5 (dot line) and 0.25 (dash line).
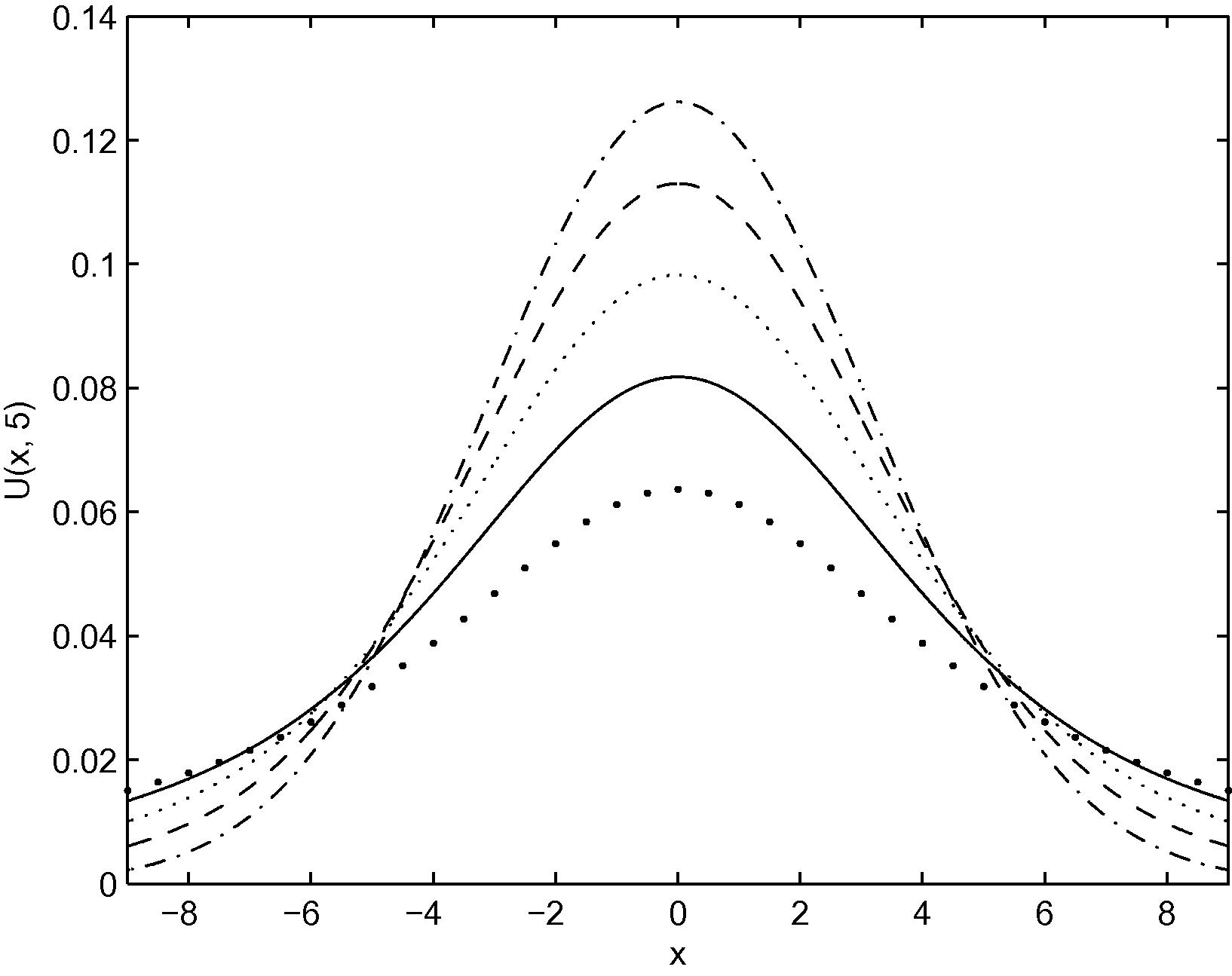
Curves of
versus x on the interval
for
and
(thick dot line), 1.25 (solid line), 1.5 (dot line), 1.75 (dash line) and 2 (dot-dash line).
Inserting Eqs. (15)-(17), (20)-(23) into Eq. (8), we can obtain the Fox function representations, series representations and asymptotic behavior for the probability density .
As , the Gauss distribution (19) describes the standard diffusion process. The mean square displacement is given by . But as , from the asymptotic representation the mean square displacement is infinite. The Lévy stable distribution describes anomalous diffusion (Shlesinger et al., 1993). In order to determine the diffusion velocity we adopt the following method.
Taking a fixed number d
, we investigate
such that
Acknowledgements
This work was supported by the Natural Science Foundation of Shanghai (No. 14ZR1440800), the Innovation Program of the Shanghai Municipal Education Commission (No. 14ZZ161) and the National Natural Science Foundation of China (Nos. 11171295; 11201308).
References
- A fractional diffusion equation to describe Lévy flights. Phys. Lett. A. 1998;239(1-2):13-16.
- [Google Scholar]
- Fractional kinetics for relaxation and superdiffusion in a magnetic field. Phys. Plasmas. 2002;9(1):78-88.
- [Google Scholar]
- Time- and space-fractional partial differential equations. J. Math. Phys.. 2005;46:13504-13511.
- [Google Scholar]
- An Introduction to Probability Theory and Its Applications. New York: Wiley; 1971.
- Fox function representation of Non-Debye relaxation processes. J. Stat. Phys.. 1993;71(3):741-757.
- [Google Scholar]
- Exact solutions for a class of fractal time random walks. Fractals. 1995;3(1):211-216.
- [Google Scholar]
- Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier; 2006.
- Exact solution of impulse response to a class of fractional oscillators and its stability. Math. Probl. Eng.. 2011;2011 (Article ID 657839) 9 p
- [Google Scholar]
- Viewing sea level by a one dimensional random function with long memory. Math. Probl. Eng.. 2011;2011 (Article ID 654284) 13 p
- [Google Scholar]
- The H-function with Applications in Statistics and Other Disciplines. New Delhi: Wiley Eastern Limited; 1978.
- Fractional Differential Equations. San Diego: Academic; 1999.
- First passage time distribution for anomalous diffusion. Phys. Lett. A. 2000;273:322-330.
- [Google Scholar]
- The H-functions of One and Two Variables with Applications. New Delhi/Madras: South Asian Publishers; 1982.
- Advanced Local Fractional Calculus and Its Applications. New York: World Science Publisher; 2012.
- Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci.. 2013;17(2):625-628.
- [Google Scholar]
- Cantor-type cylindrical-coordinate method for differential equations with local fractional derivatives. Phys. Lett. A. 2013;377(28-30):1696-1700.
- [Google Scholar]
- Lévy anomalous diffusion and fractional Fokker-Planck equation. Physica A. 2000;282:13-34.
- [Google Scholar]
- Wave fronts in bistable reactions with anomalous Lévy-flight diffusion. Phys. Rev. E. 1997;55(1):1181-1184.
- [Google Scholar]
Appendix: Fox H function
The Fox H function (Fox function or H function) is defined by the contour integral (Mathai and Saxena, 1978; Srivastava et al., 1982; Glöckle and Nonnenmacher, 1993)
As
and
the asymptotic expansion
We list some properties of the H function:







