A new analytical modelling for nonlocal generalized Riesz fractional sine-Gordon equation

S. Saha Ray

doi:10.1016/j.jksus.2015.03.003

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

28 (

); 48-54

doi:

10.1016/j.jksus.2015.03.003

A new analytical modelling for nonlocal generalized Riesz fractional sine-Gordon equation

S. Saha Ray

National Institute of Technology, Department of Mathematics, Rourkela 769008, India

Received: 2015-2-12, Accepted: 2015-3-8, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this paper, a novel approach comprising the modified decomposition method with Fourier transform has been implemented for the approximate solution of fractional sine-Gordon equation $u_{tt} -^{R} D_{x}^{α} u + \sin u = 0$ where $^{R} D_{x}^{α}$ is the Riesz space fractional derivative, $1 \leq α \leq 2$ . For α = 2, it becomes classical sine-Gordon equation u_tt − u_xx + sin u = 0 and corresponding to α = 1, it becomes nonlocal sine-Gordon equation u_tt − Hu + sin u = 0 which arises in Josephson junction theory, where H is the Hilbert transform. The fractional sine-Gordon equation is considered as an interpolation between the classical sine-Gordon equation (corresponding to α = 2) and nonlocal sine-Gordon equation (corresponding to α = 1). Here the analytic solution of fractional sine-Gordon equation is derived by using the modified decomposition method with Fourier transform. Then, we analyze the results by numerical simulations, which demonstrate the simplicity and effectiveness of the present method.

Keywords

Modified decomposition method with Fourier transform (MDM-FT)

Riesz space fractional derivative

Nonlocal sine-Gordon equation

Hurwitz zeta function

Riemann zeta function

Generalized zeta function

Show Related Articles from PubMed

1 Introduction

The classical sine-Gordon equation (SGE) Wazwaz, 2009 is one of the basic equations of modern nonlinear wave theory and it arises in many different areas of physics, such as Josephson junction theory, field theory, theory of lattices, etc. (Dodd et al., 1982). In these applications the sine-Gordon equation provides the simplest nonlinear description of phenomena under consideration.

The more adequate modelling can be prevailed corresponding to generalization of classical sine-Gordon equation. In particular, taking into account nonlinear effects, such as long–range interactions of particles, complex law of medium dispersion or curvilinear geometry of the initial boundary problem, classical sine-Gordon equation results in nonlocal generalization of SGE.

In this paper, we consider the nonlocal generalization of sine-Gordon equation proposed in Alfimov et al. (2004) as follows:

(1.1)

u_{tt} -^{R} D_{x}^{α} u + \sin u = 0

where the nonlocal operator

^{R} D_{x}^{α}

is the Riesz space fractional derivative,

1 \leq α \leq 2

These similar types of evolution Eq. (1.2) arise in various interesting problems of nonlocal Josephson electrodynamics. These problems were introduced in Ivanchenko and Soboleva (1990), Gurevich (1992), Barone and Paterno (1982), Aliev and Silin (1993), Aliev et al. (1995) and Alfimov and Silin (1995), among these one of the basic model equations is

(1.2)

u_{tt} - H [u_{x}] + \sin u = 0

where H is the Hilbert transform, given by

H [φ] \equiv \frac{1}{π} v . p . \int_{- \infty}^{\infty} \frac{φ (ξ)}{ξ - x} d ξ

and the integral is understood in the Cauchy principal value sense. The evolution Eq. (1.2) was an object of study in a series of papers (Ivanchenko and Soboleva, 1990; Gurevich, 1992; Aliev et al., 1995; Alfimov and Popkov, 1995; Mintz and Snapiro, 1994 ) available in open literature. Other nonlocal sine-Gordon equations were considered in Cunha et al. (1996) and Vázquez et al. (1994).

In this paper, the derived analytical solutions are based on the modified decomposition method with Fourier transform. In this present paper, we employ a new technique such as applying the Fourier transform followed by the decomposition method. This new technique enables derivation of the analytical solutions for the nonlocal fractional sine-Gordon Eq. (1.1).

2 Mathematical preliminaries of fractional calculus

There exist numerous definitions of fractional integrals and fractional derivatives. This paper deals with the Riesz fractional derivative.

2.1

2.1 Definition: Riesz fractional operator

Definition 1

The Riesz fractional operator (Jiang et al., 2012; Samko et al., 2002; Podlubny, 1999 ) for $n - 1 < α \leq n$ , $n \in N$ on the finite interval $0 \leq x \leq L$ is defined as

(2.1.1)

\frac{\partial^{α}}{\partial | x |^{α}} u (x, t) = - c_{α} (_{0} D_{x}^{α} +_{x} D_{L}^{α}) u (x, t)

where

c_{α} = \frac{1}{2 \cos (\frac{π α}{2})}, α \neq 1

_{0} D_{x}^{α} u (x, t) = \frac{1}{Γ (n - α)} \frac{\partial^{n}}{\partial x^{n}} \int_{0}^{x} \frac{u (ξ, t) d ξ}{{(x - ξ)}^{α + 1 - n}}

_{x} D_{L}^{α} u (x, t) = \frac{{(- 1)}^{n}}{Γ (n - α)} \frac{\partial^{n}}{\partial x^{n}} \int_{x}^{L} \frac{u (ξ, t) d ξ}{{(ξ - x)}^{α + 1 - n}}

Lemma 1

For a function u(x) defined on the infinite domain [−∞ < x < ∞], the following equality holds

(2.1.2)

- {(- Δ)}^{\frac{α}{2}} u (x) = - c_{α} (_{- \infty} D_{x}^{α} +_{x} D_{\infty}^{α}) u (x, t) = \frac{\partial^{α}}{\partial | x |^{α}} u (x) for n - 1 < α \leq n, n \in N

Proof

According to Samko et al. (2002), a fractional power of the Laplace operator is defined as follows: $- {(- Δ)}^{\frac{α}{2}} u (x) = - F^{- 1} | x |^{α} F u (x)$ where $F$ and $F^{- 1}$ denote the fourier transform and inverse Fourier transform of u(x), respectively. Hence, we have $- {(- Δ)}^{\frac{α}{2}} u (x) = - \frac{1}{2 π} \int_{- \infty}^{\infty} e^{- ix ξ} | ξ |^{α} \int_{- \infty}^{\infty} e^{i ξ η} u (η) d η d ξ$

Supposing that $u (x)$ vanishes at x = ±∞, we perform integration by parts, $\int_{- \infty}^{\infty} e^{i ξ η} u (η) d η = - \frac{1}{i ξ} \int_{- \infty}^{\infty} e^{i ξ η} u^{'} (η) d η .$

Thus, we obtain $- {(- Δ)}^{\frac{α}{2}} u (x) = - \frac{1}{2 π} u^{'} (η) [i \int_{- \infty}^{\infty} e^{i ξ (η - x)} \frac{| ξ |^{α}}{ξ} d ξ] d η .$

Let $I = i \int_{- \infty}^{\infty} e^{i ξ (η - x)} \frac{| ξ |^{α}}{ξ} d ξ$ , then $I = i [- \int_{0}^{\infty} e^{i ξ (x - η)} ξ^{α - 1} d ξ + \int_{0}^{\infty} e^{i ξ (η - x)} ξ^{α - 1} d ξ]$ for 0 < α < 1, we have $I = i [\frac{- Γ (α)}{{[i (η - x)]}^{α}} + \frac{Γ (α)}{{[i (x - η)]}^{α}}] = \frac{sign (x - η) Γ (α) Γ (1 - α)}{| x - η |^{α} Γ (1 - α)} [i^{α - 1} + {(- i)}^{α - 1}]$

Using $Γ (α) Γ (1 - α) = \frac{π}{\sin (π α)}$ and $i^{α - 1} + {(- i)}^{α - 1} = 2 \sin (\frac{α π}{2})$ , we obtain $I = \frac{sign (x - η) π}{\cos (\frac{α π}{2}) | x - η |^{α} Γ (1 - α)}$

Hence, for 0 < α < 1 $- {(- Δ)}^{\frac{α}{2}} u (x) = - \frac{1}{2 π} \int_{- \infty}^{\infty} u^{'} (η) \frac{sign (x - η) π}{\cos (\frac{α π}{2}) | x - η |^{α} Γ (1 - α)} d η$ $= - \frac{1}{2 \cos (\frac{α π}{2})} [\frac{1}{Γ (1 - α)} \int_{- \infty}^{x} \frac{u^{'} (η)}{{(x - η)}^{α}} d η - \frac{1}{Γ (1 - α)} \int_{x}^{\infty} \frac{u^{'} (η)}{{(η - x)}^{α}} d η]$

Following (Samko et al., 2002; Podlubny, 1999), for 0 < α < 1, the Grünwald–Letnikov fractional derivative in [a, x] is given by $_{a} D_{x}^{α} u (x) = \frac{u (a) {(x - a)}^{- α}}{Γ (1 - α)} + \frac{1}{Γ (1 - α)} \int_{a}^{x} \frac{u^{'} (η)}{{(x - η)}^{α}} d η$

Therefore, if u(x) tends to zero for a → −∞, then we have $_{- \infty} D_{x}^{α} u (x) = \frac{1}{Γ (1 - α)} \int_{- \infty}^{x} \frac{u^{'} (η)}{{(x - η)}^{α}} d η$

Similarly, if u(x) tends to zero for b → +∞, then we have $_{x} D_{\infty}^{α} u (x) = \frac{- 1}{Γ (1 - α)} \int_{x}^{\infty} \frac{u^{'} (η)}{{(η - x)}^{α}} d η$

Hence, if u(x) is continuous and u^′(x) is integrable for $x \geq a$ , then for every α (0 < α < 1), the Riemann–Liouville derivative exists and coincides with the Grünwald–Letnikov derivative. Finally, for 0 < α < 1, we have $- {(- Δ)}^{\frac{α}{2}} u (x) = - \frac{1}{2 \cos (\frac{α π}{2})} [_{- \infty} D_{x}^{α} u (x) +_{x} D_{\infty}^{α} u (x)] = \frac{\partial^{α}}{\partial | x |^{α}} u (x)$ where $_{- \infty} D_{x}^{α} u (x) = \frac{1}{Γ (1 - α)} \frac{\partial}{\partial x} \int_{- \infty}^{x} \frac{u (η) d η}{{(x - η)}^{α}}$ $_{x} D_{\infty}^{α} u (x) = \frac{- 1}{Γ (1 - α)} \frac{\partial}{\partial x} \int_{x}^{\infty} \frac{u (η) d η}{{(η - x)}^{α}}$

Similarly for $1 < α < 2$ , we have $- {(- Δ)}^{\frac{α}{2}} u (x) = - \frac{1}{2 \cos (\frac{α π}{2})} [_{- \infty} D_{x}^{α} u (x) +_{x} D_{\infty}^{α} u (x)] = \frac{\partial^{α}}{\partial | x |^{α}} u (x)$ where $_{- \infty} D_{x}^{α} u (x) = \frac{1}{Γ (2 - α)} \frac{\partial^{2}}{\partial x^{2}} \int_{- \infty}^{x} \frac{u (η) d η}{{(x - η)}^{α - 1}}$ $_{x} D_{\infty}^{α} u (x) = \frac{1}{Γ (2 - α)} \frac{\partial^{2}}{\partial x^{2}} \int_{x}^{\infty} \frac{u (η) d η}{{(η - x)}^{α - 1}}$

Finally, for $n - 1 < α < n$ , we have $- {(- Δ)}^{\frac{α}{2}} u (x) = - \frac{1}{2 \cos (\frac{α π}{2})} [_{- \infty} D_{x}^{α} u (x) +_{x} D_{\infty}^{α} u (x)] = \frac{\partial^{α}}{\partial | x |^{α}} u (x)$ where $_{- \infty} D_{x}^{α} u (x) = \frac{1}{Γ (n - α)} \frac{\partial^{n}}{\partial x^{n}} \int_{- \infty}^{x} \frac{u (ξ) d ξ}{{(x - ξ)}^{α + 1 - n}}$ $_{x} D_{\infty}^{α} u (x) = \frac{{(- 1)}^{n}}{Γ (n - α)} \frac{\partial^{n}}{\partial x^{n}} \int_{x}^{\infty} \frac{u (ξ) d ξ}{{(ξ - x)}^{α + 1 - n}}$ □

Remark

For a function $u (x)$ defined on the finite interval $[0, L]$ , the above equality holds by setting $u^{*} (x) = \{\begin{matrix} u (x) & x \in (0, L) \\ 0 & x \notin (0, L) \end{matrix}$

That is u^∗(x) = 0 on the boundary points and beyond the boundary points.

Definition 2

The Riesz-Feller fractional derivative of order α, $0 < α \leq 2$ , which is given as a pseudo-differential operator with the Fourier symbol −|k|^α, $k \in R$ is defined as in Samko et al. (2002) and Podlubny (1999).

(2.1.3)

\frac{\partial^{α}}{\partial | x |^{α}} u (x) = F^{- 1} [- | k |^{α} \hat{u} (k)] (x)

where

F (u (x)) = \hat{u} (k) = \int_{- \infty}^{\infty} e^{ikx} u (x) dx

3 Analysis of the modified decomposition method with Fourier transform (MDM-FT)

In this article, we apply the MDM (Wazwaz, 1999, 2001; Saha Ray, 2006, 2008; Haziqah et al., 2011 ) to the discussed problem. To show the basic idea let us consider the following fractional SGE (1.1) in the operator form

(3.1)

L_{tt} u -^{R} D_{x}^{α} u + N (u) = 0

where

L_{tt} \equiv \frac{\partial^{2}}{\partial t^{2}}

symbolize the linear differential operators and the notation N symbolize the nonlinear operator.

First we apply Fourier transform to both sides of Eq. (3.1) yielding

(3.2)

L_{tt} \hat{u} + | k |^{α} \hat{u} + F (N (u)) = 0

where

\hat{u} (k, t)

is the Fourier transform of u(x, t) and

F

denotes the Fourier transform respectively.

Now, applying the twofold integration inverse operator $L_{tt}^{- 1} \equiv \int_{0}^{t} \int_{0}^{t} (•) dtdt$ to Eq. (3.2) and using the specified initial conditions yields:

(3.3)

\hat{u} (k, t) = \hat{u} (k, 0) + t \hat{u} (k, 0) - | k |^{α} L_{tt}^{- 1} \hat{u} (k, t) - L_{tt}^{- 1} (F (N (u)))

The Adomian decomposition method (Adomian, 1994) assumes an infinite series solution for unknown function $\hat{u} (k, t)$ given by

(3.4)

\hat{u} (k, t) = \sum_{n = 0}^{\infty} {\hat{u}}_{n} (k, t)

and

N (u) = \sum_{n = 0}^{\infty} A_{n} (u_{0}, u_{1}, . . ., u_{n})

, where A_n is the appropriate Adomian’s polynomial which is generated according to algorithm determined in Adomian (1994). In this specific nonlinearity, we use the general form of formula for

A_{n}

Adomian polynomial as

(3.5)

A_{n} (u_{0}, u_{1}, \dots, u_{n}) = \frac{1}{n!} \frac{d^{n}}{d λ^{n}} {[N (\sum_{k = 0}^{\infty} λ^{k} u_{k})]}_{λ = 0}, n \geq 0

This formula is easy to set computer code to get as many polynomials as we need in calculation of the numerical as well as explicit solutions. For the sake of convenience of the readers, we can give the first few Adomian polynomials for $N (u) = \sin (u)$ of the nonlinearity as $A_{0} = N (u_{0}) = \sin (u_{0})$ $A_{1} = u_{1} \frac{\partial}{\partial u_{0}} N (u_{0}) = u_{1} \cos (u_{0})$ $A_{2} = u_{2} \frac{\partial}{\partial u_{0}} N (u_{0}) + (\frac{u_{1}^{2}}{2!}) \frac{\partial^{2}}{\partial u_{0}^{2}} N (u_{0}) = u_{2} \cos (u_{0}) - \frac{u_{1}^{2}}{2} \sin (u_{0})$ and so on, the rest of the polynomials can be constructed in a similar manner.

Substituting the initial conditions into Eq. (3.3) and identifying the zeroth components ${\hat{u}}_{0}$ , we then obtain the subsequent components by using the following recursive equations of the standard ADM.

(3.6)

{\hat{u}}_{n + 1} (k, t) = - | k |^{α} L_{tt}^{- 1} {\hat{u}}_{n} (k, t) - L_{tt}^{- 1} (F (A_{n})), n \geq 0

Wazwaz (1999) proposed that the construction of the zeroth component of the decomposition series can be defined in a slightly different way. In Wazwaz (1999), he assumed that if the zeroth component ${\hat{u}}_{0} = g$ and the function g is possible to divide into two parts such as g₁ and g₂, the one can formulate the recursive algorithm for u₀ and general term ${\hat{u}}_{n + 1}$ in a form of the modified recursive scheme as follows:

(3.7)

\begin{matrix} {\hat{u}}_{0} = g_{1} \\ {\hat{u}}_{1} = g_{2} - | k |^{α} L_{tt}^{- 1} {\hat{u}}_{0} (k, t) - L_{tt}^{- 1} (F (A_{0})) \\ {\hat{u}}_{n + 1} = - | k |^{α} L_{tt}^{- 1} {\hat{u}}_{n} (k, t) - L_{tt}^{- 1} (F (A_{n})), n \geq 1 \end{matrix}

This type of modification is giving more flexibility in order to solve complicate nonlinear differential equations. In many cases the modified decomposition scheme avoids the unnecessary computation especially in calculation of the Adomian polynomials. The computation of these polynomials will be reduced very considerably by using the MDM.

It is worth noting that once the zeroth components ${\hat{u}}_{0}$ is defined then the remaining components ${\hat{u}}_{n}$ , $n \geq 1$ can be completely determined. As a result, the components ${\hat{u}}_{0}, {\hat{u}}_{1}, . . .,$ are identified and the series solutions thus entirely determined. However, in many cases the exact solution in a closed form may be obtained.

The practical solution will be the n-term approximations $φ_{n}$

(3.8)

φ_{n} = \sum_{i = 0}^{n - 1} {\hat{u}}_{i} (k, t) n \geq 1

with

\lim_{n \to \infty} φ_{n} = \hat{u} (k, t)

Then by applying inverse Fourier transformation we can get the solution for $u (x, t)$ .

In the present analysis, for reducing Riesz space fractional differential equation to ordinary differential equation, we applied here Fourier transform. In this modified decomposition method with Fourier transform (MDM-FT), we finally applied inverse Fourier transform for getting the solution of Riesz space fractional differential equation.

4 Implementation of the MDM-FT method for approximate solution of nonlocal fractional sine-Gordon equation (SGE)

In this section, we first consider two examples for the application of MDM-FT for the solution of nonlocal fractional SGE Eq. (1.1).

4.1

4.1 Example 1

In this example, we shall find analytical approximate solution of the nonlocal fractional SGE Eq. (1.1) with given initial conditions (Wei, 2000; Kaya, 2003; Batiha et al., 2007 )

(4.1.1)

u (x, 0) = 0, u_{t} (x, 0) = 4 \sec h (x)

Then by applying Fourier transform and using Eq. (2.1.3) on Eq. (1.1) and Eq. (4.1.1), we get

(4.1.2)

{\hat{u}}_{tt} (k, t) + | k |^{α} \hat{u} (k, t) + F (\sin u) = 0

with initial conditions

(4.1.3)

\hat{u} (k, 0) = 0, {\hat{u}}_{t} (k, 0) = 2 \sqrt{2 π} \sec h (\frac{k π}{2})

where

F

denotes the Fourier transform and

k

is called the transform parameter for Fourier transform.

Now we apply the modified decomposition method for solving Eq. (4.1.2). Using the scheme of this method given in Eq. (3.7), we can write

(4.1.4)

{\hat{u}}_{0} (k, t) = 0

(4.1.5)

{\hat{u}}_{1} (k, t) = 2 \sqrt{2 π} t \sec h (\frac{k π}{2}) - | k |^{α} L_{tt}^{- 1} {\hat{u}}_{0} (k, t) - L_{tt}^{- 1} (F (A_{0})) = 2 \sqrt{2 π} t \sec h (\frac{k π}{2})

(4.1.6)

{\hat{u}}_{2} (k, t) = - | k |^{α} L_{tt}^{- 1} {\hat{u}}_{1} (k, t) - L_{tt}^{- 1} (F (A_{1})) = - \frac{1}{3} \sqrt{2 π} t^{3} \sec h (\frac{k π}{2}) - \frac{1}{3} \sqrt{2 π} t^{3} | k |^{α} \sec h (\frac{k π}{2})

and so on.

Then by applying inverse Fourier transform of above from Eq. (4.1.4) to Eq. (4.1.6), we have $u_{0} (x, t) = 0$ $u_{1} (x, t) = 4 t \sec h (x)$ $u_{2} (x, t) = \frac{1}{3} t^{3} (- 2 \sec h (x) + 2^{- α} π^{- 1 - α} Γ (1 + α) (- ζ (1 + α, \frac{π - 2 ix}{4 π}) - ζ (1 + α, \frac{π + 2 ix}{4 π}) + ζ (1 + α, \frac{3}{4} - \frac{ix}{2 π}) + ζ (1 + α, \frac{3}{4} + \frac{ix}{2 π})))$ where $ζ (s, a) = \sum_{k = 0}^{\infty} \frac{1}{{(k + a)}^{s}}$ is called Hurwitz zeta function which is a generalization of the Riemann zeta function $ζ (s)$ and also known as the generalized zeta function and so on.

In this manner the other components of the decomposition series can be easily obtained by which $u (x, t)$ can be evaluated in a series form as

(4.1.7)

u (x, t) = u_{0} (x, t) + u_{1} (x, t) + u_{2} (x, t) + \dots = 4 t \sec h (x) + \frac{1}{3} t^{3} (- 2 \sec h (x) + 2^{- α} π^{- 1 - α} Γ (1 + α) (- ζ (1 + α, \frac{π - 2 ix}{4 π}) - ζ (1 + α, \frac{π + 2 ix}{4 π}) + ζ (1 + α, \frac{3}{4} - \frac{ix}{2 π}) + ζ (1 + α, \frac{3}{4} + \frac{ix}{2 π}))) + \dots

4.1.1

4.1.1 Numerical construction of Breather solution

In this present numerical experiment, Eq. (4.1.7) obtained by MDM-FT has been used to draw the graphs as shown in Fig. 1 for $α = 1.75$ . The numerical solutions of Riesz fractional SGE in Eq. (1.1) have been shown in Fig. 1 with the help of 3rd order approximation for decomposition solution of $u (x, t)$ . This represents breather-kink and anti-kink transition associated with fractional order SGE Eq. (1.1).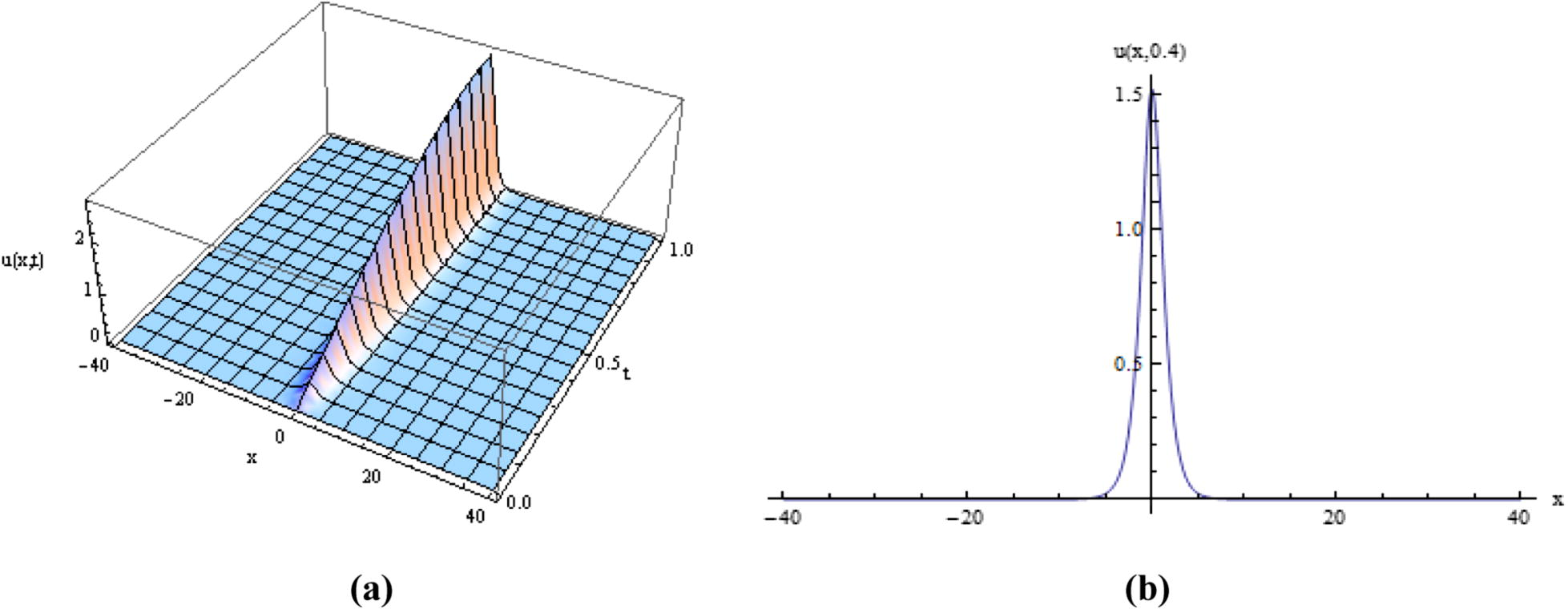

(a) The MDM-FT method solution for u(x, t), (b) corresponding solution for u(x, t) when t = 0.4.

4.2

4.2 Example 2

In this case, we shall find analytical approximate solution of the nonlocal fractional SGE Eq. (1.1) with given initial conditions (Wei, 2000; Kaya, 2003; Batiha et al., 2007 )

(4.2.1)

u (x, 0) = π + ε \cos (μ x), u_{t} (x, 0) = 0

Then by applying Fourier transform and using Eq. (2.1.3) on Eq. (1.1) and Eq. (4.2.1), we get

(4.2.2)

{\hat{u}}_{tt} (k, t) + | k |^{α} \hat{u} (k, t) + F (\sin u) = 0

with initial conditions

(4.2.3)

\hat{u} (k, 0) = \sqrt{2} π^{3 / 2} δ (k) + \sqrt{\frac{π}{2}} ε δ (k - μ) + \sqrt{\frac{π}{2}} ε δ (k + μ), {\hat{u}}_{t} (k, 0) = 0

where

F

denotes the Fourier transform,

k

is called the transform parameter for Fourier transform and δ(.) denotes the Dirac delta function.

Analogous to arguments as discussed in previous Section 4.1. We may obtain the following equations

(4.2.4)

{\hat{u}}_{0} (k, t) = \sqrt{2} π^{3 / 2} δ (k)

(4.2.5)

{\hat{u}}_{1} (k, t) = \sqrt{\frac{π}{2}} ε δ (k - μ) + \sqrt{\frac{π}{2}} ε δ (k + μ) + L^{- 1} (- | k |^{α} {\hat{u}}_{0} (k, t) - F (A_{0})) = \sqrt{\frac{π}{2}} ε δ (k - μ) + \sqrt{\frac{π}{2}} ε δ (k + μ)

(4.2.6)

{\hat{u}}_{2} (k, t) = L^{- 1} (- | k |^{α} {\hat{u}}_{1} (k, t) - F (A_{1})) = (\frac{1}{2} \sqrt{\frac{π}{2}} t^{2} ε δ (k - μ) - \frac{1}{2} \sqrt{\frac{π}{2}} t^{2} ε | k |^{α} δ (k - μ) + \frac{1}{2} \sqrt{\frac{π}{2}} t^{2} ε δ (k + μ) - \frac{1}{2} \sqrt{\frac{π}{2}} t^{2} ε | k |^{α} δ (k + μ))

and so on.

Then by applying inverse Fourier transform of above from Eq. (4.2.4) to Eq. (4.2.6), we have $u_{0} (x, t) = π$ $u_{1} (x, t) = ε \cos (μ x)$ $u_{2} (x, t) = - \frac{1}{2} t^{2} ε \cos (μ x) (- 1 + {(- μ)}^{α} U (- μ) + μ^{α} U (μ))$ where U(.) denotes the Unit Step function and so on.

In this manner the other components of the decomposition series can be easily obtained by which u(x, t) can be evaluated in a series form as

(4.2.7)

u (x, t) = u_{0} (x, t) + u_{1} (x, t) + u_{2} (x, t) + \dots = π + \frac{1}{24} (24 + 12 t^{2} + t^{4}) ε \cos (μ x) + \frac{1}{24} t^{2} ε \cos (μ x) ((- 12 + t^{2} (- 2 + {(- μ)}^{α})) {(- μ)}^{α} U (- μ) + μ^{α} (- 12 + t^{2} (- 2 + μ^{α})) U (μ)) + \dots

4.2.1

4.2.1 Traveling wave solutions and numerical discussions

In this present numerical experiment, Eq. (4.2.7) obtained by MDM-FT has been used to draw the graphs as shown in Fig. 2 for fractional order value α = 1.75. The numerical solutions of fractional SGE Eq. (1.1) have been shown in Fig. 2 with the help of 4th order approximation for the decomposition series solution of u(x, t).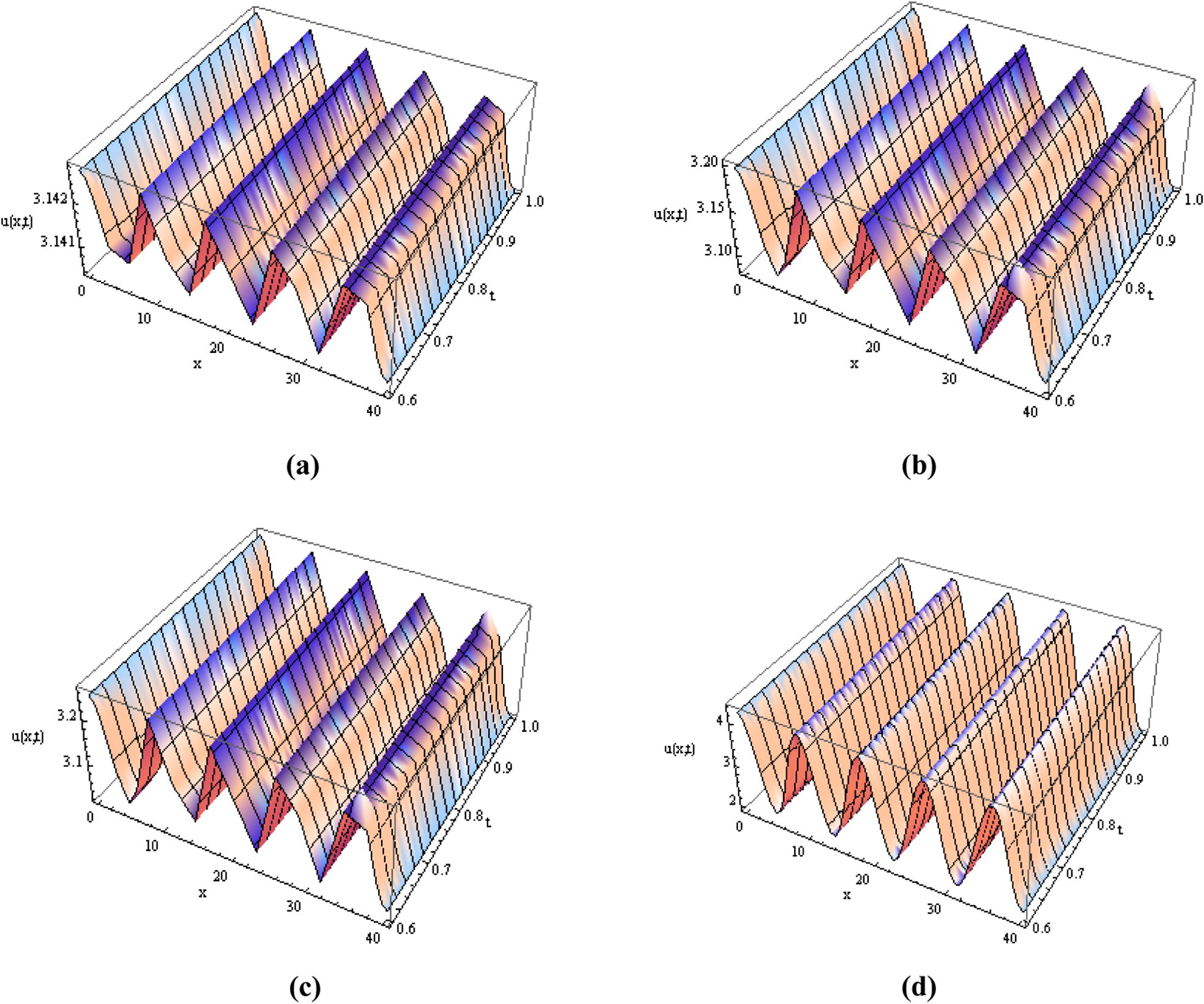

(a) The numerical results for u(x, t) obtained by MDM-FT for (a) ɛ = 0.001, (b) ɛ = 0.05, (c) ɛ = 0.1 and (d) ɛ = 1.0.

5 Conclusion

In this paper, a new analytical technique MDM-FT method has been proposed to obtain the approximate solution of nonlocal fractional SGE. The fractional SGE with nonlocal Riesz derivative operator has been first time solved by the MDM-FT method in order to justify applicability of the above method. The approximate solution to fractional SGE has been calculated by using the MDM without any need for transformation techniques and linearization of the equation. Additionally, it does not need any discretization method to get numerical solution. This method thus eliminates the difficulties and massive computation work. The decomposition method is straightforward, without restrictive assumptions and the components of the series solution can be easily computed using any mathematical symbolic package. Moreover, this method does not change the problem into a convenient one for the use of linear theory.

The proposed MHAM-FT method is very simple and efficient for solving nonlinear fractional sine-Gordon equation with nonlocal Riesz derivative operator.

References

Adomian G., . Solving Frontier Problems of Physics: The Decomposition Method. Boston: Kluwer Academic Publishers; 1994.
Alfimov G.L., Popkov I.D., . Magnetic vortices in a distributed Josephson junction with electrodes of finite thickness. Phys. Rev. B. 1995;52(4503)
[Google Scholar]
Alfimov G.L., Silin V.P., . On small perturbations of stationary states in a nonlinear nonlocal model of a Josephson junction. Phys. Lett. A. 1995;198(105)
[Google Scholar]
Aliev Yu.M., Silin V.P., . Travelling 4π-kink in nonlocal Josephson electrodynamics. Phys. Lett. A. 1993;177(259)
[Google Scholar]
Aliev Yu.M., Ovchinnikov K.N., Silin V.P., Uryupin S.A., . Perturbations of stationary solutions in a nonlocal model of a Josephson junction. J. Exp. Theor. Phys.. 1995;80(551)
[Google Scholar]
Barone A., Paterno G., . Physics and Applications of the Josephson Effect. New York: Wiley; 1982.
Batiha B., Noorani M.S.M., Hashim I., . Numerical solution of sine-Gordon equation by variational iteration method. Phys. Lett. A. 2007;370:437-440.
[Google Scholar]
Cunha M.D., Konotop V.V., Vázquez L., . Small-amplitude solitons in a nonlocal sine-Gordon model. Phys. Lett. A. 1996;221(5):317-322.
[Google Scholar]
Dodd R.K., Eilbeck J.C., Gibbon J.D., Morris H.C., . Solitons and Nonlinear Wave Solutions. London: Academic; 1982.
Alfimov G.L., Pierantozzi T., Vázquaz L., 2004. Numerical study of a fractional sine-Gordon equation. In: Fractional Differentiation and its Applications, FDA 2004, Workshop Preprints/Proceedings, pp. 644–649, 2004–1.
Gurevich A., . Nonlocal Josephson electrodynamics and pinning in superconductors. Phys. Rev. B. 1992;46(3187)
[Google Scholar]
Haziqah C., Hussin C., Kiliçman A., . On the solutions of nonlinear higher-order boundary value problems by using differential transformation method and Adomian decomposition method. Math. Probl. Eng.. 2011;2011 (Article ID 724927, 19 pages)
[Google Scholar]
Ivanchenko Yu.M., Soboleva T.K., . Nonlocal interaction in Josephson junctions. Phys. Lett. A. 1990;147:65-69.
[Google Scholar]
Jiang H., Liu F., Turner I., Burrage K., . Analytical solutions for the multi-term time-space Caputo–Riesz fractional advection–diffusion equations on a finite domain. J. Math. Anal. Appl.. 2012;389(2):1117-1127.
[Google Scholar]
Kaya D., . A numerical solution of the sine-Gordon equation using the modified decomposition method. Appl. Math. Comput.. 2003;143:309-317.
[Google Scholar]
Mintz R.G., Snapiro I.B., . Dynamics of Josephson pancakes in layered superconductors. Phys. Rev. B. 1994;49(6188)
[Google Scholar]
Podlubny I., . Fractional Differential Equation. New York: Academic Press; 1999.
Saha Ray S., . A numerical solution of the coupled sine-Gordon equation using the modified decomposition method. Appl. Math. Comput.. 2006;175:1046-1054.
[Google Scholar]
Saha Ray S., . An application of the modified decomposition method for the solution of the coupled Klein–Gordon–Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul.. 2008;13:1311-1317.
[Google Scholar]
Samko S.G., Kilbas A.A., Marichev O.I., . Fractional Integrals and derivatives: Theory and Applications. London: Taylor and Francis; 2002.
Vázquez L., Evans W.A., Rickayzen G., . Numerical investigation of a non-local sine-Gordon model. Phys. Lett. A. 1994;189(6):454-459.
[Google Scholar]
Wazwaz A., . A reliable modification of Adomian decomposition method. Appl. Math. Comput.. 1999;102(1):77-86.
[Google Scholar]
Wazwaz A.M., . Construction of soliton solutions and periodic solutions of the Boussinesq equation by the modified decomposition method. Chaos, Solitons Fractals. 2001;12(8):1549-1556.
[Google Scholar]
Wazwaz A.M., . Partial Differential Equations and Solitary Waves Theory. Berlin Heidelberg: Springer-Verlag; 2009.
Wei G.W., . Discrete singular convolution for the sine-Gordon equation. Physica D. 2000;137:247-259.
[Google Scholar]