The MLPG with improved weight function for two-dimensional heat equation with non-local boundary condition

1 Introduction

In the past several decades, there has been a growing interest in the development of meshless numerical techniques as alternatives to classical mesh-dependent numerical methods. The MLPG method was first discovered by Atluri and Zhu (1998). This method has been described in textbooks (Atluri, 2004; Liu and Gu, 2005) as allowing for freedom to choose the test function. The method is based on local weak forms and moving least square (MLS) approximation, and obtains the true solution of the problem. The main advantage of the MLPG method is that it only requires nodes and a description of the external and internal boundary conditions, therefore, no element connectivity, neither total nor part, is needed. Effective implementations of meshless methods are a key to success (Katz, 2009; Dehghan, 2005; Liu, 2009; Atluri and Zhu, 1998, 2000; Atluri and Shengping, 2002; Abbasbandy and Shirzadi, 2011; Wu and Tao, 2008).

Finding the numerical solution with a non-local boundary condition is important for research in many fields of science and engineering such as chemical diffusion, diffusion equation, thermoelasticity, heat conduction process, heat transfer, control theory, medical schemes and so on (Martin-Vaquero and Vigo-Aguiar, 2009; Abbasbandy and Shirzadi, 2011; Kazem and Rad, 2012; Bogoya et al., 2012; Syed and Ahmet, 2011; Pisano et al., 2009). It is most widely used and very important in thermoelasticity. In 1963, Cannon (1963) first introduced non-local boundary condition problems, and most investigations developed various problems with one dimension, two dimension, the Dirichlet boundary condition, and the Neumann boundary condition. In 2010, Abbasbandy and Shirzadi (2010, 2011) researched on the MPLG method for the two-dimensional diffusion equation with the Neumann boundary condition and non-classical boundary condition, and a meshless method for the two-dimensional diffusion equation with an integral condition. The proposed method worked very well for the two-dimensional diffusion equations with a non-classical boundary condition, because of its simplicity and high accuracy.

The purpose of this paper is to improve the weight function in the MLS approximation to make the meshless method very efficient for solving the following two-dimensional time-dependent heat equation with non-local boundary conditions, given by Abbasbandy and Shirzadi (2011):

Abbasbandy and Shirzadi (2011) used a meshless local Petrov–Galerkin (MLPG) method to treat parabolic partial differential equations with Dirichlet and Neumann conditions and a non-classical boundary. A difficulty in implementing the MLPG method to impose essential boundary conditions is that the Moving Least Square (MLS) trial functions do not pass through the nodal values. To overcome this difficulty, they used the MLPG method only inside the domain, while at boundaries, they used finite difference schemes in all boundary conditions.

Most and Bucher (2005) presented the application of the MLS interpolation is solved with a new weighting function, which makes the MLS interpolation more attractive especially within a Galerkin method. A new weighting function was designed for meshless shape functions to fulfill these essential conditions with a very high accuracy without any additional effort. Due to the approximative character of this interpolation the obtained shape functions do not fulfill the interpolation conditions, which causes an additional numerical effort for the application of the boundary conditions. This will be clear by pointing out, that the choice of the base polynomial is arbitrary, thus the accuracy can be increased by choosing higher order polynomials.

Yang et al. (2011) used an improved hybrid boundary node method (hybrid BNM) for solving steady fluid flow problems, Miao et al. (2005) used a meshless hybrid boundary-node method for Helmholtz problems, and Wang et al. (2011) used the multi-domain hybrid boundary node method for 3D elasticity. This research used the Hybrid BNM, proposed by Zhang et al. (2002), for potential and elasticity problems which is a new boundary type meshless method and has been developed by Miao et al. (2005). Belytschko et al. (1996) combined MLS approximation and a modified variational principle. It only requires nodes constructed on the boundary of the domain, and does not require any mesh for the interpolation of variables, nor for the integration. The accuracy of the hybrid BNM is rather high. However, shape functions for the classical MLS approximation lack the delta function property, due to which Yang et al. (2011) in their paper used the improved MLS approach in the hybrid boundary node method. They proposed adopting a regularized weight function and used a new weight function that was designed by Most and Bucher. This method leading to the MLS shape functions fulfilling the interpolation condition exactly, enables a direct application of essential boundary conditions without additional numerical effort.

The objective of the present study is to improve the weight function in the classical MLS method. The Gaussian weight function is the most common; however, this kind of shape function does not have the Kronecker delta function property, so the boundary condition cannot be enforced easily and directly. Consequently, a transformation strategy of boundary condition application is inevitable, therefore, additional computational efforts cannot be avoided. In order to remove it, Most and Bucher designed a new weight function that allows for the fulfillment of the MLS interpolation condition with a very high accuracy.

In this paper, we implement the problems under a non-local boundary condition as in Eq. (7). Also, we used the weight function (Most and Bucher, 2005) in our implementation, for which the MLS approximation lacks the Kronecker delta function property, so it should be noted that the weight function leads to the MLS approximation shape functions fulfilling the interpolation condition exactly and enables a direct application of the Dirichlet boundary conditions, where solving the two-dimensional diffusion equation is shown to be accurate and less coding computational expense can be obtained.

The contents of this paper are as follows: Section 2 presents the improved MLS approach, Section 3 discusses the local weak formulation of the problem, Section 4 describes the numerical implementation of the method for the diffusion equation with regular nodes, and finally Section 5 presents the conclusions.

2 The improved MLS approach

Consider a sub-domain Ω_x, the neighborhood of a point x and denoted as the domain of definition of the MLS approximation for the trial function at x, which is located in the problem domain Ω_x. To approximate the distribution of function u in Ω_x, over a number of randomly located nodes x_i, i = 1, 2, …, n, the moving least square approximation u^h(x) of u, ∀x ∈ Ω_x can be defined by

The MLS approximation is well-defined only when the matrix A in (10) is non-singular. It can be seen that this is the case if and only if the rank of P equals m. A necessary condition for a well-defined MLS approximation is that at least m weight functions are non-zero (i.e., n > m) for each sample point x ∈ Ω and that the nodes in Ω_x are not arranged in a special pattern, such as on a straight line. Here, a sample point may be a nodal point under consideration or a quadrature point.

Solving a(x) from (10) and substituting it into (8) gives a relation which may be written in the form of an interpolation function similar to that used in FEM, as:

Usually ϕ_i(x) is called the shape function of the MLS approximation corresponding to nodal point y_i. From (12) and (14), it may be seen that ϕ_i(x) = 0 when w_i(x) = 0. In practical applications, w_i(x) is generally chosen such that it is non-zero over the support of nodal points y_i. The support of the nodal point y_i is usually taken to be a circle of radius r_i, centered at y_i. The fact that ϕ_i(x) = 0, for x not in the support of nodal point y_i, preserves the local character of the moving least square approximation.

Let C^q(Ω) be the space of q^th continuously differentiable functions on Ω. If w_i(x) ∊ C^q (Ω)p_j(x) ∊ C^s(Ω), i = 1, 2, …, n and j = 1, 2, …, m, then φ_i(x) ∊ C^r(Ω) with r = min(q, s).

The partial derivatives of ϕ_i(x) are obtained as

In this paper, we should first choose the weight function in the implementation of the MLS approximation. In the classical MLS method, the Gaussian weight function is the most common. However, this kind of shape function does not have the Kronecker delta function property, so the boundary condition cannot be enforced easily and directly. Consequently, a transformation strategy of boundary condition application is inevitable, therefore, additional computational effort cannot be avoided. In order to remove it, Most and Bucher (2005) designed a new weight function which allows the fulfillment of the MLS interpolation condition with a very high accuracy:

The variable k belongs to the number of supporting points influencing x; s is the normalized distance between the interpolation point and the considered supporting point, $s_i=\frac{\Vert \mathbf{x}-{\mathbf{x}}_i\Vert }{\mathbf{D}}$ and D is the influence radius.

Most and Bucher (2005) recommended the regularization parameter ε, which should be very small, as

3 Local weak formulation

The MLPG method constructs the weak form over local sub-domains such as Ω_s, which is a small region taken for each node in the global domain Ω and may be of any geometric shape and size. In this paper they are taken to be of circular shape. Because the weak form is constructed over local sub-domains, the formulation is called the “local weak formulation”.

The local weak form of (1) for ${\text{x}}_i=(x^i\text{,}{y}^i)\in {\mathrm{\Omega }}_s^i$ can be written as follows:

Substituting trial function $u^h(\mathbf{x}\text{,}t)={\sum }_{j=1}^n{\varphi }_j(\mathbf{x}){\hat{u}}_j(t)$ and $q\equiv \frac{\partial u}{\partial n}$ into (23) yields:

By substituting (13) into (23), the governing equations are transformed in the discretized system, written in a matrix form as

Setting a time-stepping scheme to overcome the time derivative and applying the Crank–Nicolson technique of approximation to (26) yields:

We use the matrix forms in (31) and (34) to compute ${\hat{u}}_i^{k+1}$ and ${\hat{\mu }}^{k+1}$ for nodes located inside the domain and on the Neumann boundary conditions. For nodes on the Dirichlet boundary conditions, we have to impose boundary conditions as follows:

For nodes x^l = (x^l, 1) on the top horizontal boundary $(0⩽x^l⩽1)\text{,}$ using (5), we have

4 Numerical experiments

For the improved MLS approximations, two test problems with regular nodes are presented to illustrate the efficiency and accuracy of the method. The new weight function is used for the MLS approximations, which the regularization parameter ε is chosen as ε = 10⁻⁵. In this paper it is chosen as r₀ = 6h, where h is the distance between nodes in each direction and the analyzed domain is Ω = [0,1] × [0,1]. The errors of u and μ presented in the numerical results are presented by the root mean square (RMS) and N_e errors respectively where $$\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{k=1}^N}{(u({\mathbf{x}}_k)-\hat{u}({\mathbf{x}}_k))}^2}{N}}\text{,}$$ $$N_e=\sqrt{\frac{{\displaystyle \sum _{k=1}^N}{(u({\mathbf{x}}_k)-\hat{u}({\mathbf{x}}_k))}^2}{{\displaystyle \sum _{k=1}^N}u{({\mathbf{x}}_k)}^2}}\text{,}$$ u(x_k) and $\hat{u}({\mathbf{x}}_k)$ are achieved by an exact and approximate solution on x_k points and N is the number of nodes.

The errors of the method for Example 1 at time instant t = 0.5, Δt = 0.1, m = 3 are presented in Table 1 and m = 6 is presented in Table 2. The errors of the method for Example 1 at time instant t = 1, Δt = 0.1, m = 3 are presented in Table 3 and m = 6 is presented in Table 4. The errors of the method for Example 2 at time instant t = 0.5, Δt = 0.1, m = 3 are presented in Table 5 and m = 6 is presented in Table 6. The errors of the method for Example 2 at time instant t = 1, Δt = 0.1, m = 3 are presented in Table 7 and m = 6 is presented in Table 8. The numerical results in these tables show the convergence of the method by increasing the number of nodal points, which can see an increasing accuracy by increasing the number of nodal points. The error with an increasing number of nodes is presented in Figs. 1–4. The results reveal that the error decreases when the number of nodes increase.

Close

Figure 1

The error obtained at time instant t = 0.5 (a), t = 1 (b) and using Δt = 0.1, m = 3 with an increasing number of nodes for Example 1.

Export to PPT

Close

Figure 2

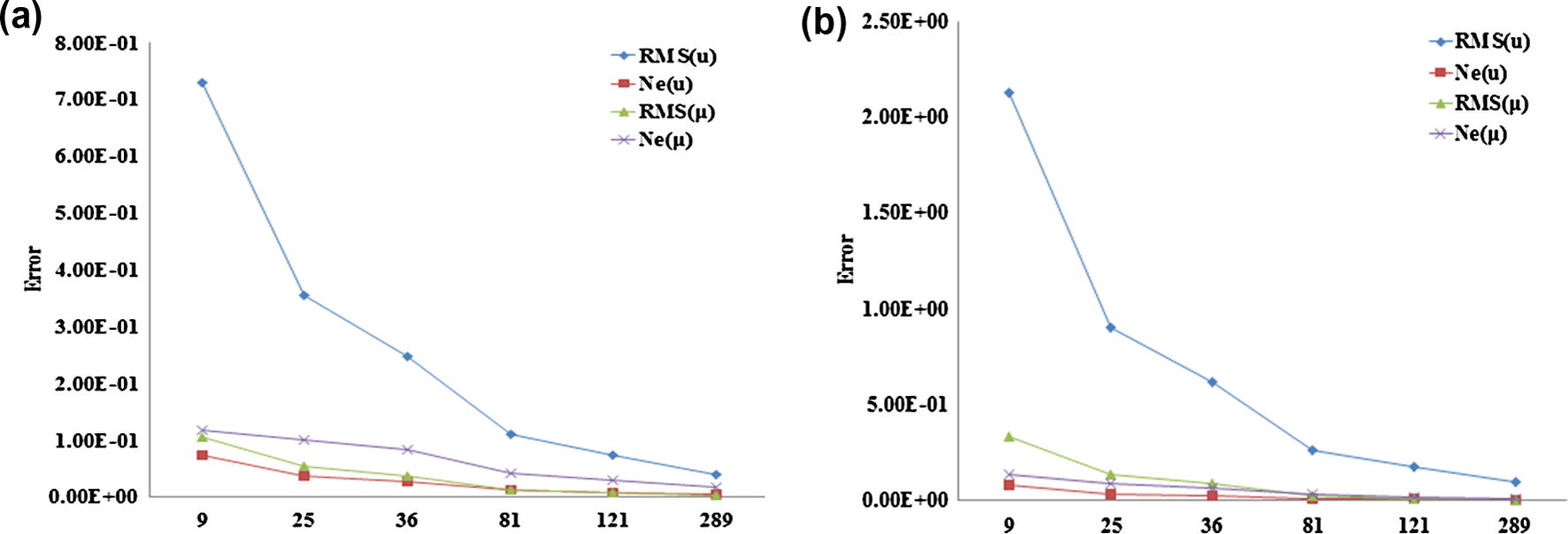
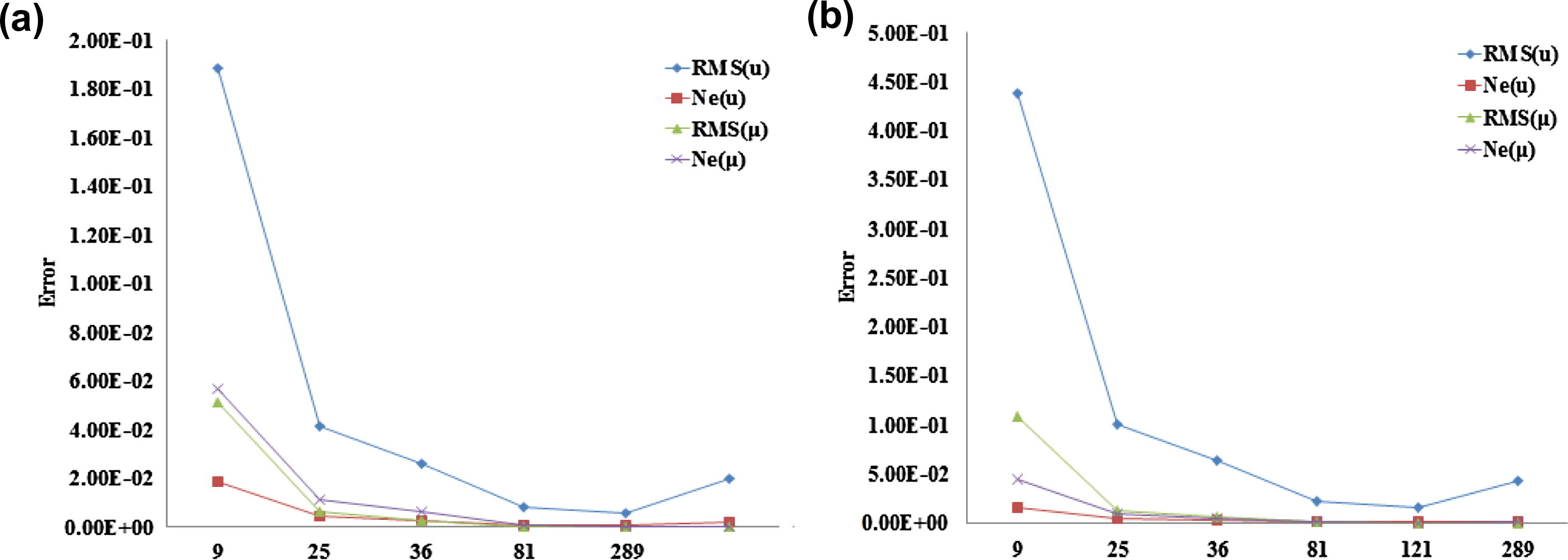
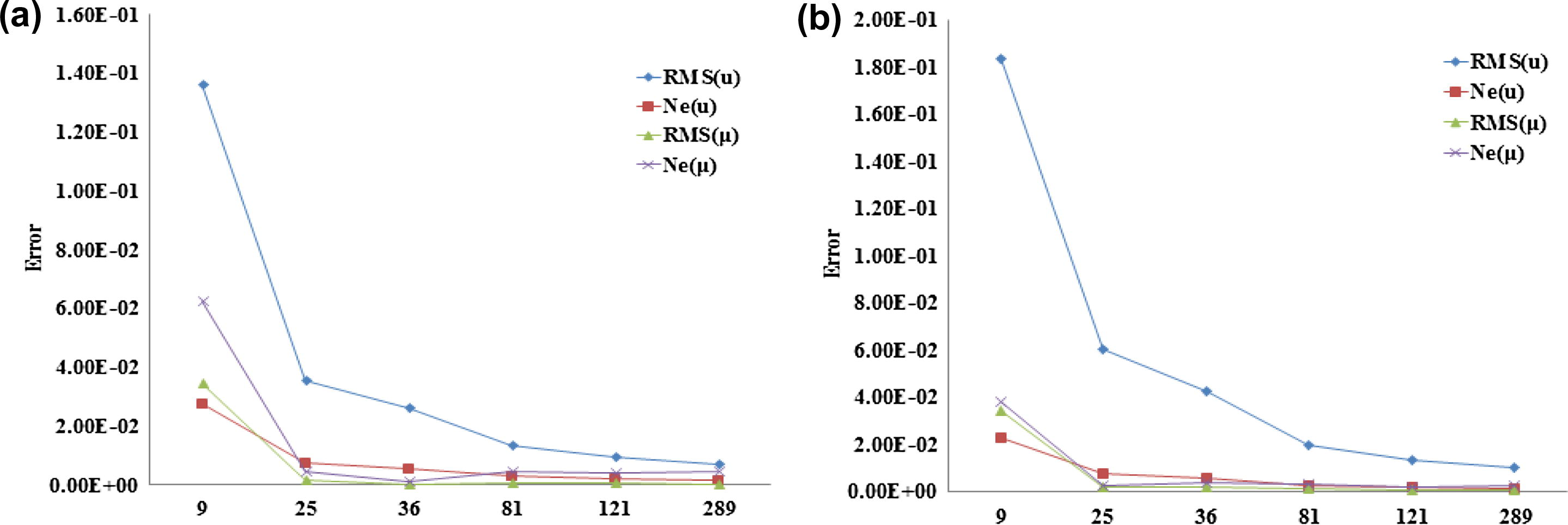
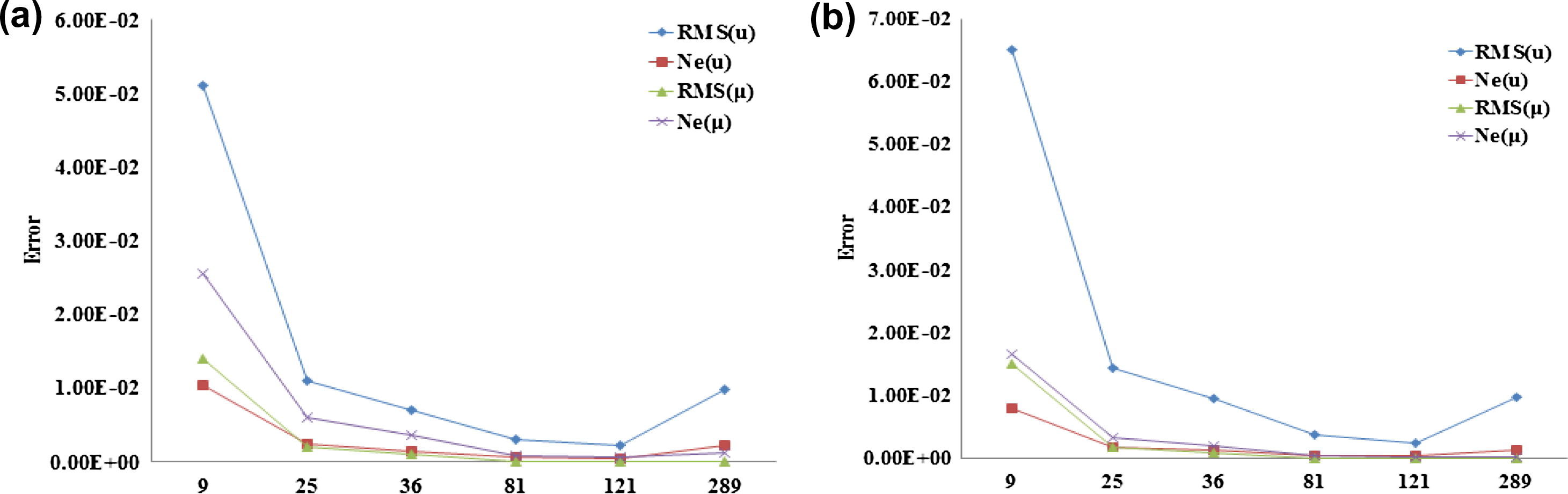
The error obtained at time instant t = 0.5 (a), t = 1 (b) and using Δt = 0.1, m = 6 with an increasing number of nodes for Example 1.

Export to PPT

Close

Figure 3

The error obtained at time instant t = 0.5 (a), t = 1 (b) and using Δt = 0.1, m = 3 with an increasing number of nodes for Example 2.

Export to PPT

Close

Figure 4

The error obtained at time instant t = 0.5 (a), t = 1 (b) and using Δt = 0.1, m = 6 with an increasing number of nodes for Example 2.

Export to PPT

In this paper, we referenced two examples from Abbasbandy and Shirzadi (2011) in a numerical scheme.

5 Conclusions

In this paper, an MLPG method was proposed for the study of two-dimensional heat equation with Dirichlet, Neumann, and non-local boundary conditions on a square domain. This method improved the classic MLS approximation by changing the Gaussian weight function, due to the shape functions constructed in the classical MLS that lack the delta function property so that the boundary condition cannot be enforced directly and a transformation strategy is indispensable. The efficiency has been greatly improved by using the improved MLS approach and the boundary conditions can be enforced easily and directly imposing the Dirichlet boundary conditions and the coding work can also be reduced. Two numerical examples are presented to treat heat equation problems. The numerical results have demonstrated the accuracy, effectiveness of the present method, and the computation expense is decreased slightly since the boundary conditions can be enforced easily and directly imposing the Dirichlet boundary conditions. The values of N_e and RMS errors corroborate the appropriate accuracy of our method. It indicates that the method we introduced in this paper can easily be implemented to other problems.