Approximate analytical solutions of singularly perturbed fourth order boundary value problems using differential transform method

Essam R. El-Zahar

doi:10.1016/j.jksus.2013.01.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

25 (

); 257-265

doi:

10.1016/j.jksus.2013.01.004

Approximate analytical solutions of singularly perturbed fourth order boundary value problems using differential transform method

Essam R. El-Zahar^*,1

Department of Mathematics, College of Sciences and Humanities, Salman Bin Abdulaziz University, P.O. Box 83, Alkharj 11942, Saudi Arabia

*Corresponding author. Tel.: +966 545046828 essam_zahar2006@yahoo.com (Essam R. El-Zahar)

Received: 2012-11-19, Accepted: 2013-1-27, Published: 2013-07-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

1 Permanent address: Department of Basic Engineering Science, Faculty of Engineering, Shebin El-Kom, Menofia University, Egypt

Abstract

In this paper, a reliable algorithm is presented to develop approximate analytical solutions of fourth order singularly perturbed two-point boundary value problems in which the highest order derivative is multiplied by a small parameter. In this method, first the given problem is transformed into a system of two second order ODEs, with suitable boundary conditions and a zeroth-order asymptotic approximate solution of the transformed system is constructed. Then, the reduced terminal value system is solved analytically using the differential transform method. Some illustrating examples are solved and the results are compared with the exact solutions to demonstrate the accuracy and the efficiency of the method. It is observed that the present method approximates the exact solution very well not only in the boundary layer, but also away from the layer.

Keywords

34B05

41A58

65D99

34E05

Analytic approximations

Differential transform method

Singularly perturbed fourth-order boundary-value problems

Asymptotic expansion

1 Introduction

Singularly perturbed boundary value problems (SPBVPs) occur frequently in many areas of applied science and engineering, e.g., heat transfer, fluid dynamics, quantum mechanics, optimal control and chemical reactor theory, etc. These problems have received a significant amount of attention in the past and in recent years due to the fact that the solution exhibits a multiscale character, i.e., there are thin transition layer(s) where the solution varies rapidly, and while away from the layers (s) the solution behaves regularly and varies slowly. Therefore, the numerical treatment of singular perturbation problems presents some major computational difficulties. For the past two decades, many numerical methods have appeared in the literature which cover mostly second order SPBVPs (Kadalbajoo and Patidar, 2002; Kumar et al., 2007). But only few authors have developed numerical methods for higher order SPBVPs. Most notable among these are fitted mesh finite-difference method (Shanthi and Ramanujam, 2002, 2003; Valanarasu and Ramanujam, 2007), exponentially fitted finite difference method (Valarmathi and Ramanujam, 2002a,b; Shanthi and Ramanujam, 2002, 2003, 2004 ), fitted mesh finite element method (Babu and Ramanujam, 2007), fitted Numerov method (Phaneendra et al., 2012), spline method (Siddiqi et al., 2011; Akram and Amin, 2012), Adomain decomposition and homotopy methods (Syam and Attili, 2005) and reproducing Kernel method (Cui and Geng, 2008; Akram and Rehman, 2012). The aim of our study is to employ the Differential Transform Method (DTM) as an alternative to existing methods for solving higher order SPBVPs. The basic idea of DTM was initially introduced by Zhou (1986) who solved linear and nonlinear initial value problems in the electric circuit analysis. It is a semi-numerical and semi-analytic technique that formulizes the Taylor series in a totally different manner. With this technique, the given differential equation and its related boundary conditions are transformed into a recurrence relation that finally leads to the solution of a system of algebraic equations as coefficients of a power series solution. Different applications of DTM can be found in (Jang et al., 2000; Köksal and Herdem, 2002; Abdel-Halim Hassan, 2008; Ayaz, 2004; Arikoglu and Ozkol, 2006; Liu and Song, 2007; Momani and Noor, 2007; Chu and Chen, 2008; El-Shahed, 2008; Momani and Ertürk, 2008; Odibat, 2008; Ravi Kanth and Aruna, 2009; Kuo and Lo, 2009; Al-Sawalha and Noorani, 2009a,b; Ebaid, 2010; Thongmoon and Pusjuso, 2010; Kurulay and Bayram, 2010; Doğan et al., 2011; Alomari, 2011; Demirdag and Yesilce, 2011; Gupta, 2011; Biazar et al., 2012; Gökdoğan et al., 2012 and El-Zahar, 2012, 2013). In this paper, a reliable algorithm is presented to develop approximate analytical solutions of fourth order singularly perturbed two-point boundary value problems in which the highest order derivative is multiplied by a small parameter. In this method, first the given problem is transformed into a system of two second order ODEs, with suitable boundary conditions and a zeroth-order asymptotic approximate solution of the transformed system is constructed. Then, the reduced terminal value system is solved analytically using the DTM. Some illustrating examples are solved and compared with the exact solutions to demonstrate the accuracy and the efficiency of the method. It is observed that the present method approximates the exact solution very well not only in the boundary layer, but also away from the layer.

2 Basic concepts of the DTM

The DTM that has been developed for the analytical solution of ODEs is presented in this section for the systems of ODEs. For this purpose, we consider the following system of ODEs

(1)

\begin{matrix} y_{1}^{'} (t) = f_{1} (t, y_{1}, y_{2}, \dots ., y_{n}), \\ y_{2}^{'} (t) = f_{2} (t, y_{1}, y_{2}, \dots ., y_{n}), \\ ⋮ \\ y_{n}^{'} (t) = f_{n} (t, y_{1}, y_{2}, \dots ., y_{n}), \end{matrix}

subject to initial conditions

(2)

y_{i} (0) = c_{i}, i = 1, 2, \dots, n .

Let [0, L] be the interval over which we want to find the solution of the ODE system (1) and (2). In actual applications of the DTM, the Nth-order approximate solution of the ODE system (1) and (2) can be expressed by the finite series

(3)

y_{i} (t) = \sum_{k = 0}^{N} Y_{i} (k) t^{k} + O (t^{N + 1}), t \in [0, L], i = 1, 2, \dots, n,

where

(4)

Y_{i} (k) = \frac{1}{k!} {[\frac{d^{k} y_{i} (t)}{{dt}^{k}}]}_{t = 0}, i = 1, 2, \dots, n .

which implies that

\sum_{k = N + 1}^{\infty} Y_{i} (k) t^{k}

is negligibly small. Using some fundamental properties of the DTM, (Table 1), the ODE system (1) and (2) can be transformed into the following recurrence relations

(5)

Y_{i} (k + 1) = (F_{i} (k, Y_{1}, Y_{2}, \dots, Y_{n})) / (k + 1), Y_{i} (0) = c_{i}, i = 1, 2, \dots, n,

where F_i(k, Y₁, Y₂, … , Y_n) is the differential transform of the function f_i(t, y₁, y₂, … , y_n), for i = 1, 2, … , n. Solving the recurrence relation (5), the differential transform Y_i(k), k > 0 can be easily obtained .

Table 1 Fundamental operations of DTM.

Original function	Transformed function
y(t) = β(u(t) ± v(t))	Y(k) = βU(k) ± β V(k)
y(t) = u(t)v(t)	$Y (k) = \sum_{ℓ = 0}^{k} U (ℓ) V (k - ℓ)$
$y (t) = \frac{d^{m} u (t)}{{dt}^{m}}$	$Y (k) = \frac{(k + m)!}{k!} U (k + m)$
y(t) = t^m	$Y (k) = δ (k - m) = \{\begin{matrix} 1; & if k = m \\ 0; & if k \neq m \end{matrix}$
y(t) = e^λt	$Y (k) = \frac{λ^{k}}{k!}$
y(t) = sin(ωt)	$Y (k) = \frac{ω^{k}}{k!} \sin (\frac{k π}{2}) = \{\begin{matrix} 0; & k \in even \\ \frac{ω^{k} {(- 1)}^{\frac{k - 1}{2}}}{k!}; & k \in odd \end{matrix}$
y(t) = cos(ωt)	$Y (k) = \frac{ω^{k}}{k!} \cos (\frac{k π}{2}) = \{\begin{matrix} \frac{ω^{k} {(- 1)}^{\frac{k}{2}}}{k!}; & k \in even \\ 0; & k \in odd \end{matrix}$

3 Description of the method

Consider the fourth order linear SPBVP given by:

(6)

- ε y^{iv} (x) - a (x) y^{‴} (x) + b (x) y^{″} (x) - c (x) y (x) = - h (x), x \in T,

(7)

y (0) = p, y (1) = q, y^{″} (0) = - r, y^{″} (1) = - s,

where 0 < ε ≪ 1, a(x), b(x), c(x), and h(x) are sufficiently smooth functions satisfying the following conditions:

(8)

a (x) ⩾ α > 0, b (x) ⩾ β > 0

(9)

0 ⩾ c (x) ⩾ - γ, γ > 0,

(10)

α - γ (1 + δ) ⩾ η > 0 for some η and γ > 0,

and

T = (0, 1), \bar{T} = [0, 1], and y (x) \in C^{(4)} (T) \cap C^{(2)} (\bar{T}) .

The SPBVP (6) and (7) can be transformed into an equivalent system of two second order ODEs of the form

(11)

Ay = H \Leftrightarrow \{\begin{matrix} - y_{1}^{″} (x) - y_{2} (x) = 0, \\ - ε y_{2}^{″} (x) - a (x) y_{2}^{'} (x) + b (x) y_{2} (x) \\ + c (x) y_{1} (x) = h (x), x \in T \\ y_{1} (0) = p, y_{1} (1) = q, \\ y_{2} (0) = r, y_{2} (1) = s \end{matrix},

where y = (y₁(x), y₂(x))^T.

Remark

Here after, the above system (11) is only considered instead of SPBVP (6) and (7). The above conditions (8)–(10) guarantee that it is not a turning point problem and the above system (11), which is equivalent to (6) and (7), is quasi-monotone. For more details about analytical results such as existence, uniqueness, and asymptotic behavior of the solution of (6) and (7) see, (Shanthi and Ramanujam, 2002, 2004).

3.1

3.1 A zeroth-order asymptotic approximate solution

One can look for the asymptotic approximation of the solution of (11) in the form $y (x, ε) = (y_{0} + z_{0}) + ε (y_{1} + z_{1}) + O (ε^{2})$ Using one of the standard perturbation methods (Nayfeh, 1981), one can construct the zeroth-order asymptotic approximate solution y_as = y₀ + z₀ where y₀ = (y₀₁(x), y₀₂(x))^T is a solution of the reduced system of (11) given by

(12)

\begin{matrix} - y_{01}^{″} (x) - y_{02} (x) = 0, y_{01} (0) = p, y_{01} (1) = q, x \in T \\ - a (x) y_{02}^{'} (x) + b (x) y_{02} (x) + c (x) y_{01} (x) = h (x), y_{02} (1) = s \end{matrix}\},

and z₀ is the layer correction given by z₀ = (z₀₁(x), z₀₂(x))^T with

\begin{matrix} z_{01} (x) = 0, \\ z_{02} (x) = (r - y_{02} (0)) (e^{- a (0) x / ε}) . \end{matrix}

Theorem 3.1

The zeroth-order asymptotic approximation y_as of the solution y of (11) satisfies the inequality $‖ y - y_{as} ‖ ⩽ C_{1} ε,$ For proof see (Shanthi and Ramanujam, 2002).

Now, in order to obtain an approximate analytical solution of (11), we only need to obtain an approximate analytical solution to the terminal value system (TVS) (12).

3.2

3.2 The solution of the TVS (12) by DTM

In this section, the DTM is applied to solve the TVS (12). Taking differential transformation to (12) by using the related definitions in Table 1, we obtain the following recurrence relation:

(13)

\begin{matrix} (k + 1) (k + 2) Y_{01} (k + 2) = - Y_{02} (k), \\ \sum_{ℓ = 0}^{k} A (ℓ) (k - ℓ + 1) Y_{02} (k - ℓ + 1) \\ = \sum_{ℓ = 0}^{k} B (ℓ) Y_{02} (k - ℓ) + \sum_{ℓ = 0}^{k} C (ℓ) Y_{01} (k - ℓ) - H (k) \end{matrix}\},

with transformed boundary conditions:

(14)

\sum_{k = 0}^{N} Y_{01} (k) = q, \sum_{k = 0}^{N} Y_{02} (k) = s,

where Y₀₁(k), Y₀₂(k), A(k), B(k), C(k) and H(k) are the transformed functions of y₀₁(x), y₀₂(x), a(x), b(x), c(x) and h(x) respectively.

The recurrence relations (13) with the transformed boundary conditions (14) represent a system of algebraic equations in the coefficients of the power series solution of the system (12). Solving this algebraic system, the differential transform series solution ${\tilde{y}}_{0} = {({\tilde{y}}_{01} (x), {\tilde{y}}_{02} (x))}^{T}$ of (13) is obtained and given by

(15)

\begin{matrix} {\tilde{y}}_{01} (x) = \sum_{k = 0}^{N} Y_{01} (k) x^{k} \\ {\tilde{y}}_{02} (x) = \sum_{k = 0}^{N} Y_{02} (k) x^{k} \end{matrix}\} .

And thus, the approximate analytical solution

y_{ap} = {(y_{ap} (x), y_{ap}^{″} (x))}^{T}

of (11) is obtained and given by

(16)

\begin{matrix} y_{ap} (x) = {\tilde{y}}_{01} (x) \\ y_{ap}^{″} (x) = - {\tilde{y}}_{02} (x) - (r - {\tilde{y}}_{02} (0)) e^{- a (0) x / ε} \end{matrix}\} .

3.3

3.3 The error analysis

The numerical error of the present method has two sources: one from the asymptotic approximation and the other from the analytical approximation by the DTM.

Theorem 3.2

The approximate analytical solution y_ap of (11) satisfies the inequality

(17)

‖ y - y_{ap} ‖ ⩽ C (ε + \frac{1}{(N + 1)!}) .

Proof

Since the DTM is a formalized modified version of the Taylor series method, then we have a bounded error given by $‖ y_{0} - {\tilde{y}}_{0} ‖ ⩽ \frac{M}{(N + 1)!}, M ⩽ ‖y_{0}^{(N + 1)} (ξ)‖, 0 ⩽ ξ ⩽ 1 .$ From Theorem 3.1 and the above bounded error, we have $‖ y - y_{ap} ‖ ⩽ ‖ y - y_{as} ‖ + ‖ y_{as} - y_{ap} ‖ ⩽ ‖ y - y_{as} ‖ + ‖ y_{0} - {\tilde{y}}_{0} ‖ ⩽ C_{1} ε + \frac{M}{(N + 1)!}$ that is $‖ y - y_{ap} ‖ ⩽ C (ε + \frac{1}{(N + 1)!}) □ .$

In more times, the DTM results in the exact solution of the reduced system (12) and the second term of the above error inequality is vanished. The present method works well for singular perturbation problems since the singular perturbation parameter ε is extremely small.

4 Illustrating examples

In this section, three examples are given to demonstrate the accuracy and the efficiency of the method in solving the considered problems. These examples have been chosen because the exact solutions are available for comparison.

Example 1

Consider the following SPBVP with variable coefficients

(18)

- ε y^{iv} (x) - 4 y^{‴} (x) + (1 + x) y^{″} (x) - y (x) = - h (x), x \in [0, 1],

(19)

y (0) = 1, y (1) = 1, y^{″} (0) = - 1, y^{″} (1) = - 1,

where

h (x) = \frac{3 - 4 e^{- 4 / ε} + ε^{2}}{4 (1 - e^{- 4 / ε})} - \frac{(- 16 + ε^{2}) e^{- 4 x / ε}}{64 (1 - e^{- 4 / ε})} - (\frac{1 - 2 e^{- 4 / ε}}{8 (1 - e^{- 4 / ε)}}) x^{2} + (\frac{2}{3} - \frac{ε^{2}}{64} - \frac{- 6 + 9 e^{- 4 / ε} - 2 e^{- 4 x / ε}}{8 (1 - e^{- 4 / ε})}) x - \frac{x^{3}}{24} .

The exact solution of (18) and (19) is given by

y (x) = \{1 + \frac{ε^{2}}{64 (1 - e^{- 4 / ε})} + (\frac{5}{12} - \frac{ε^{2}}{64} - \frac{e^{- 4 / ε}}{(1 - e^{- 4 / ε})}) x - (\frac{3 - 4 e^{- 4 / ε}}{8 (1 - e^{- 4 / ε})}) x^{2} - \frac{ε^{2} e^{- 4 x / ε}}{64 (1 - e^{- 4 / ε})} - \frac{x^{3}}{24}\} .

The equivalent system of (18) and (19) is given by

(20)

\begin{matrix} - y_{1}^{″} (x) - y_{2} (x) = 0, y_{1} (0) = 1, y_{1} (1) = 1 \\ - ε y_{2}^{″} (x) - 4 y_{2}^{'} (x) + (1 + x) y_{2} (x) + y_{1} (x) \\ = h (x), y_{2} (0) = 1, y_{2} (1) = 1 \end{matrix}\},

and the reduced system of (20) is given by

(21)

\begin{matrix} - y_{01}^{″} (x) - y_{02} (x) = 0, y_{01} (0) = 1, y_{01} (1) = 1 \\ - 4 y_{02}^{'} (x) + (1 + x) y_{02} + y_{01} = \frac{3}{4} + \frac{17 x}{12} - \frac{x^{2}}{8} - \frac{x^{3}}{24}, y_{02} (1) = 1 \end{matrix}\} .

Taking differential transformation to (21), we obtain the following recurrence relation

(22)

\begin{matrix} Y_{01} (k + 2) = - Y_{02} (k) / ((k + 1) (k + 2)), \\ Y_{02} (k + 1) = \frac{δ (k - 3) + 3 δ (k - 2) - 34 δ (k - 1) - 18 δ (k)}{96 (k + 1)} \\ + \frac{Y_{01} (k) + \sum_{ℓ = 0}^{k} (δ (ℓ) + δ (ℓ - 1)) Y_{02} (k - ℓ)}{4 (k + 1)} \end{matrix}\} .

with transformed boundary conditions:

(23)

\sum_{k = 0}^{N} Y_{01} (k) = 1, \sum_{k = 0}^{N} Y_{02} (k) = 1 .

Solving the recurrence relation (22) with the boundary conditions (23) results in

\begin{matrix} {\tilde{y}}_{01} (x) = 1 + \frac{5}{12} x - \frac{3}{8} x^{2} - \frac{1}{24} x^{3} \\ {\tilde{y}}_{02} (x) = \frac{3}{4} + \frac{x}{4} \end{matrix}\},

which is the exact solution of (21). Thus we get the following approximate analytical solution of (20)

(24)

\begin{matrix} y_{ap} (x) = 1 + \frac{5}{12} x - \frac{3}{8} x^{2} - \frac{1}{24} x^{3} \\ y_{ap}^{″} (x) = - (\frac{3}{4} + \frac{x}{4} + \frac{1}{4} e^{- 4 x / ε}) \end{matrix}\} .

The results obtained using (24) compare very well with the exact solutions as shown in Fig. 1.

Example 2

Consider the following SPBVP

(25)

- ε y^{iv} (x) - y^{‴} (x) = - \cos (x) + ε \sin (x), x \in [0, 1],

(26)

y (0) = 1, y (1) = 1, y^{″} (0) = 1, y^{″} (1) = \sin (1) .

The exact solution is given by

y (x) = \sin (1) x + ε^{2} x + 1 - \sin (x) + \frac{2 ε^{2} + (x^{2} - x) e^{- 1 / ε} - 2 ε^{2} e^{- x / ε}}{2 (e^{- 1 / ε} - 1)} .

The equivalent system of (25) and (26) is given by

(27)

\begin{matrix} - y_{1}^{″} (x) - y_{2} (x) = 0, y_{1} (0) = 1, y_{1} (1) = 1 \\ - ε y_{2}^{″} (x) - y_{2}^{'} (x) = \cos (x) - ε \sin (x) \\ y_{2} (0) = - 1, y_{2} (1) = - \sin (1) \end{matrix}\},

and the reduced system of (27) is given by

(28)

\begin{matrix} - y_{01}^{″} (x) - y_{02} (x) = 0, y_{01} (0) = 1, y_{01} (1) = 1, \\ - y_{02}^{'} (x) = \cos (x), y_{02} (1) = - \sin (1) . \end{matrix}\} .

Applying differential transform to (28), results in

(29)

\begin{matrix} Y_{01} (k + 2) = - Y_{02} (k) / ((k + 1) (k + 2)) \\ Y_{01} (0) = 1, \sum_{k = 0}^{N} Y_{01} (k) = 1 \\ Y_{02} (k + 1) = \frac{- 1}{k!} \cos (\frac{k π}{2}) / (k + 1) \\ \sum_{k = 0}^{N} Y_{02} (k) = - \sin (1) \end{matrix}\} .

Solving (29), we obtain the following approximate analytical solutions

(30)

\begin{matrix} y_{ap} (x) = 1.0 + (\frac{63433}{241920} - \frac{\sin (1)}{2}) x - (\frac{305353}{725760} - \frac{\sin (1)}{2}) x^{2} \\ + \frac{x^{3}}{6} - \frac{x^{5}}{120} + \frac{x^{7}}{5040} - \frac{x^{9}}{362880} \\ y_{ap}^{″} (x) = (\sin (1) - \frac{305353}{362880}) + x - \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040} \\ + \frac{x^{9}}{362880} + (\sin (1) + \frac{57527}{362880}) e^{- x / ε} \end{matrix}\} .

The results obtained using (30) compare very well with the exact solutions as shown in Fig. 2 .

Example 3

Finally, consider the following nonlinear SPBVP

(31)

- ε y^{iv} (x) - y^{‴} (x) + y^{″} (x) - y {(x)}^{2} = - h (x),

(32)

y (0) = 1, y (1) = 1, y^{″} (0) = 1, y^{″} (1) = \sin (1),

where

h (x) = \cos (x) - (ε + 1) \sin (x) - \frac{e^{- 1 / ε} - e^{- x / ε}}{e^{- 1 / ε} - 1} + {(\sin (1) x + ε^{2} x - \sin (x) + \frac{2 ε^{2} + (x^{2} - x) e^{- 1 / ε} - 2 ε^{2} e^{- x / ε}}{2 (e^{- 1 / ε} - 1)})}^{2} .

The exact solution of (31) and (32) is given by

y (x) = \sin (1) x + ε^{2} x - \sin (x) + 1 + \frac{2 ε^{2} + (x^{2} - x) e^{- 1 / ε} - 2 ε^{2} e^{- x / ε}}{2 (e^{- 1 / ε} - 1)} .

The equivalent system of (31) and (32) is given by

(33)

\begin{matrix} - y_{1}^{″} (x) - y_{2} (x) = 0, y_{1} (0) = 1, y_{1} (1) = 1 \\ - ε y_{2}^{″} (x) - y_{2}^{'} (x) + y_{2} (x) + {(y_{1} (x))}^{2} = h (x) \\ y_{2} (0) = - 1, y_{2} (1) = - \sin (1) \end{matrix}\},

and the reduced system of (33) is given by

(34)

\begin{matrix} - y_{01}^{″} (x) - y_{02} (x) = 0, y_{01} (0) = 1, y_{01} (1) = 1 \\ - y_{02}^{'} (x) + y_{02} (x) + {(y_{01} (x))}^{2} = \cos (x) - \sin (x) \\ + {(1 + \sin (1) x - \sin (x))}^{2} \\ y_{02} (1) = - \sin (1) \end{matrix}\} .

Applying differential transform to (34), results in

(35)

\begin{matrix} Y_{01} (k + 2) = - Y_{02} (k) / ((k + 1) (k + 2)) \\ Y_{01} (0) = 1, \sum_{k = 0}^{N} Y_{01} (k) = 1 \\ Y_{02} (k + 1) = [Y_{02} (k) + \sum_{ℓ = 0}^{k} Y_{01} (ℓ) Y_{01} (k - ℓ) - \frac{1}{k!} (\cos (\frac{k π}{2}) - \sin (\frac{k π}{2})) \\ - \sum_{ℓ = 0}^{k} ((δ (ℓ) + \sin (1) δ (ℓ - 1) - \frac{1}{ℓ!} \sin (\frac{ℓ π}{2})) \\ * (δ (k - ℓ) + \sin (1) δ (k - ℓ - 1) - \frac{1}{(k - ℓ)!} \sin (\frac{(k - ℓ) π}{2})))]/ [k + 1] \\ \sum_{k = 0}^{N} Y_{02} (k) = - \sin (1) \end{matrix}\} .

Solving (35), the approximate analytical solutions are obtained and given by

(36)

\begin{matrix} y_{ap} (x) = 1 - 0.1585290 x + 1.908001 10^{- 9} x^{2} + 0.1666667 x^{3} \\ - {1.9300010}^{- 9} x^{4} - 0.8333333 10^{- 2} x^{5} - 5.90387 10^{- 11} x^{6} \\ + 0.1984127 10^{- 3} x^{7} - 5.414054 10^{- 12} x^{8} - 0.2755730 10^{- 5} x^{9} \\ y_{ap}^{″} (x) = 3.816001 10^{- 9} + x - 2.31000 10^{- 8} x^{2} - 0.1666667 x^{3} \\ - 1.776763 10^{- 9} x^{4} + 0.8333331 10^{- 2} x^{5} + 5.903878 10^{- 11} x^{6} \\ - 0.1984127 10^{- 3} x^{7} + 5.414054 10^{- 12} x^{8} + 0.2755732 10^{- 5} x^{9} \\ + (1 - 3.816001 10^{- 9}) e^{- x / ε} \end{matrix}\} .

Results obtained by the method are compared with the exact solution of each example and the results are listed in Tables 2–4 . The results show that the obtained approximate solutions are in good agreement with the exact solutions not only in the boundary layer, but also away from the layer.

Tables 5–7 present the maximum absolute point wise error for the numerical solution obtained for each previous example at different values of the perturbation parameter, ε, and the DTM order, N. Results in Table 5 show that when N ⩾ 3 the DTM results in the exact solution of the reduced system (21) and the numerical error source is only the asymptotic approximation.

The results in Tables 5–7 show that the accuracy of the approximate solution increases as the order of the DTM increases and the perturbation parameter ε decreases. Moreover, with a constant order of the DTM, the numerical error is maintained at the same level (bold text) for a family of singular perturbation parameter values, where the DTM is the dominant error source, and vice versa when the asymptotic approximation is the dominant error source, which confirm that the numerical results agree closely with the theoretical analysis.

Table 8 presents the processing times used in solving each previous example by DTM at different order values, N, where all calculations are carried out by MAPLE 14 software in a PC with a Pentium 2 GHz and 512 MB of RAM. We can observe that the DTM is a fast and effective tool for solving the considered problems.

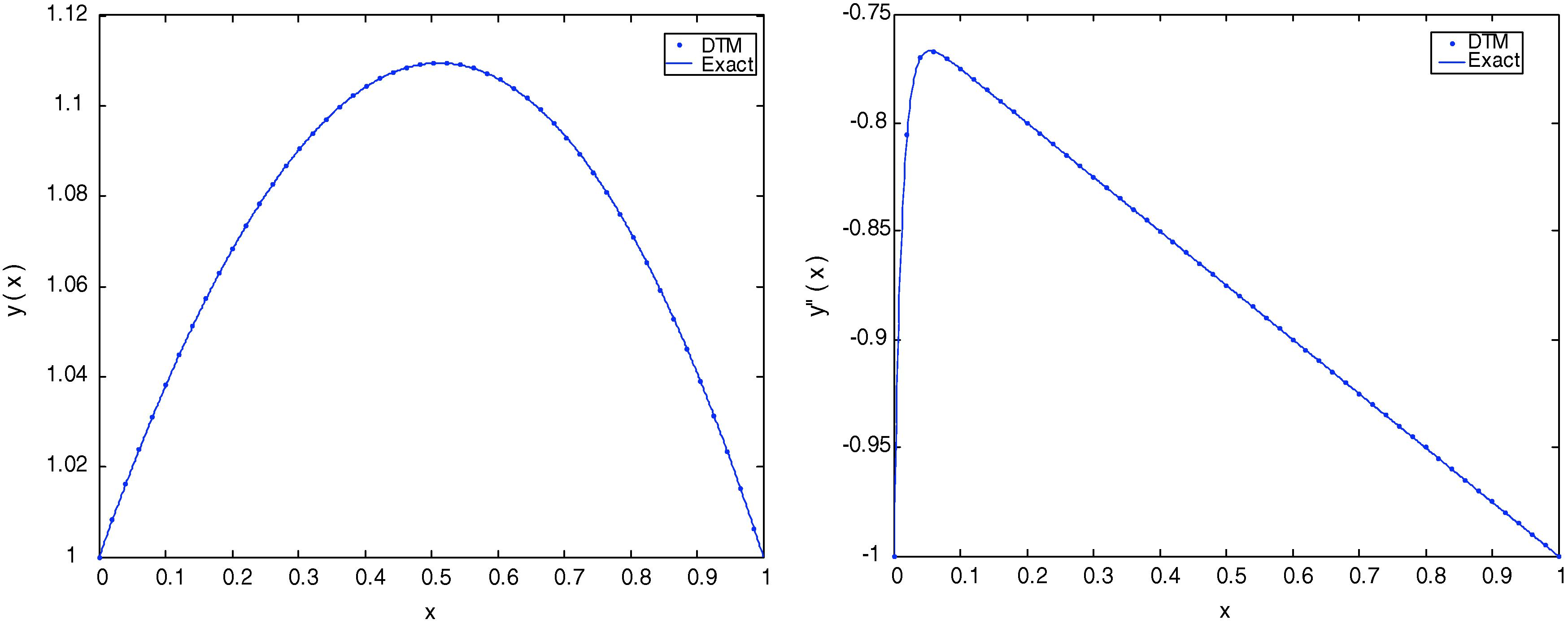
Solution comparison, exact solution of Example 1 (solid line) and (24) solution (doted line) at ε = 0.05.

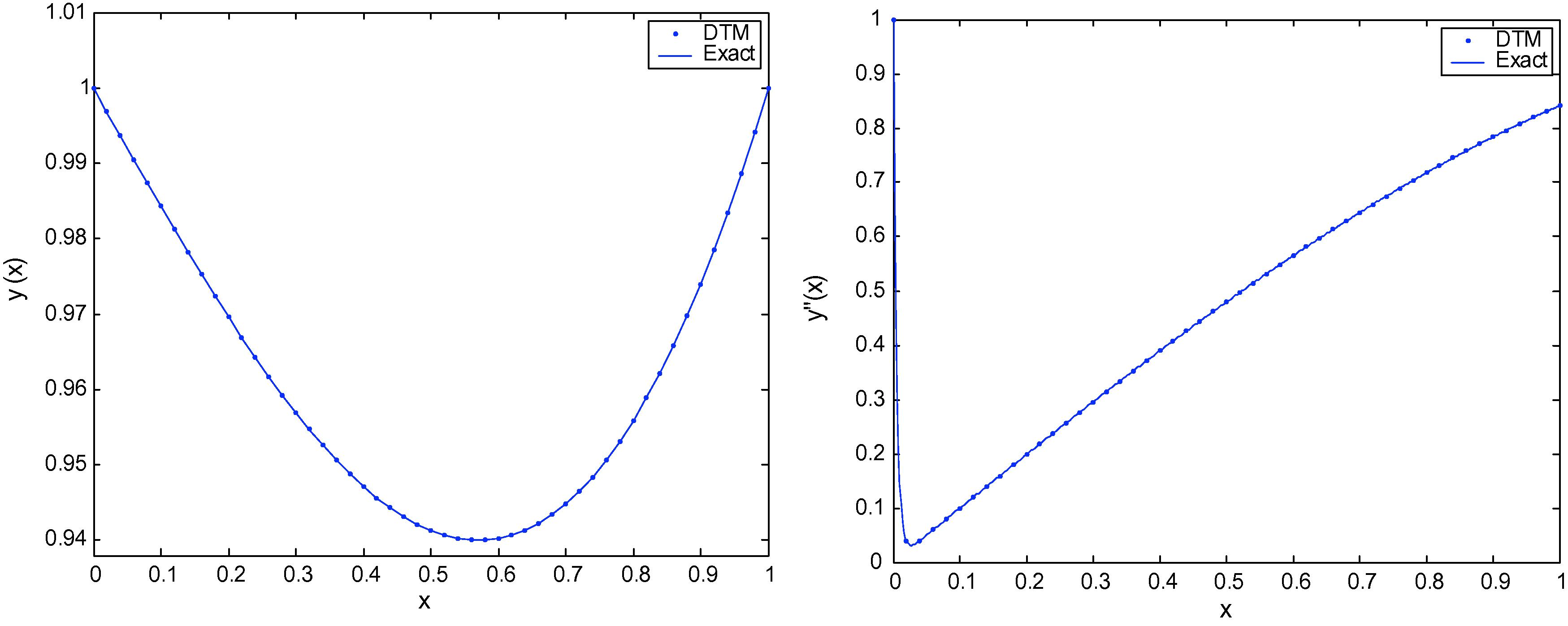
Solution comparison, exact solution of Example 2 (solid line) and (30) solution (doted line) at ε = 0.005.

Table 2 Numerical results of Example 1 (ε = 10⁻⁴).

x	Exact solution y(x)	Approximate solution y_ap(x)	Error	Exact solution y″(x)	Approximate solution $y_{ap}^{″} (x)$	Error
1.0E−06	1.0000e+00	1.0000e+00	6.1264e−12	−9.9020e−01	−9.9020e−01	0.0000e−16
1.0E−05	1.0000e+00	1.0000e+00	5.1511e−11	−9.1758e−01	−9.1758e−01	0.0000e−16
1.0E−04	1.0000e+00	1.0000e+00	1.5337e−10	−7.5460e−01	−7.5460e−01	1.1102e−16
1.0E−03	1.0004e+00	1.0004e+00	1.5609e−10	−7.5025e−01	−7.5025e−01	0.0000e−16
1.0E−02	1.0041e+00	1.0041e+00	1.5469e−10	−7.5250e−01	−7.5250e−01	0.0000e−16
1.0E−01	1.0379e+00	1.0379e+00	1.4062e−10	−7.7500e−01	−7.7500e−01	0.0000e−16
3.0E−01	1.0901e+00	1.0901e+00	1.0937e−10	−8.2500e−01	−8.2500e−01	0.0000e−16
5.0E−01	1.1094e+00	1.1094e+00	7.8125e−11	−8.7500e−01	−8.7500e−01	0.0000e−16
7.0E−01	1.0936e+00	1.0936e+00	4.6875e−11	−9.2500e−01	−9.2500e−01	0.0000e−16
9.0E−01	1.0409e+00	1.0409e+00	1.5625e−11	−9.7500e−01	−9.7500e−01	0.0000e−16
1.0E+00	1.0000e+00	1.0000e+00	1.1102e−16	−.0000e+00	−1.0000e+00	0.0000e−16

Table 3 Numerical results of Example 2 (ε = 10⁻⁴).

x	Exact solution y(x)	Approximate solution y_ap(x)	Error	Exact solution y″(x)	Approximate solution $y_{ap}^{″} (x)$	Error
1.0E−06	1.0000e+00	1.0000e+00	9.9529e−11	9.9005e−01	9.9005e−01	4.9537e−08
1.0E−05	1.0000e+00	1.0000e+00	9.5190e−10	9.0485e−01	9.0485e−01	4.7416e−08
1.0E−04	9.9998e−01	9.9998e−01	6.3239e−09	3.6798e−01	3.6798e−01	3.4050e−08
1.0E−03	9.9984e−01	9.9984e−01	1.0027e−08	1.0454e−03	1.0454e−03	2.4893e−08
1.0E−02	9.9841e−01	9.9841e−01	1.0272e−08	9.9998e−03	9.9998e−03	2.4892e−08
1.0E−01	9.8431e−01	9.8431e−01	1.2609e−08	9.9833e−02	9.9833e−02	2.4892e−08
3.0E−01	9.5692e−01	9.5692e−01	1.7081e−08	2.9552e−01	2.9552e−01	2.4892e−08
5.0E−01	9.4131e−01	9.4131e−01	2.0545e−08	4.7943e−01	4.7943e−01	2.4880e−08
7.0E−01	9.4481e−01	9.4481e−01	2.2544e−08	6.4422e−01	6.4422e−01	2.4398e−08
9.0E−01	9.7400e−01	9.7400e−01	1.6702e−08	7.8333e−01	7.8333e−01	1.7071e−08
1.0E+00	1.0000e+00	1.0000e+00	2.2204e−16	8.4147e−01	8.4147e−01	0.0000e+00

Table 4 Numerical results of Example 3 (ε = 10⁻⁴).

x	Exact solution y(x)	Approximate solution y_ap(x)	Error	Exact solution y″(x)	Approximate solution $y_{ap}^{″} (x)$	Error
1.0E−06	1.0000e+00	1.0000e+00	9.9517e−11	9.9005e−01	9.9005e−01	3.7974e−11
1.0E−05	1.0000e+00	1.0000e+00	9.5178e−10	9.0485e−01	9.0485e−01	3.6318e−10
1.0E−04	9.9998e−01	9.9998e−01	6.3227e−09	3.6798e−01	3.6798e−01	2.4126e−09
1.0E−03	9.9984e−01	9.9984e−01	1.0015e−08	1.0454e−03	1.0454e−03	3.8198e−09
1.0E−02	9.9841e−01	9.9841e−01	1.0150e−08	9.9998e−03	9.9998e−03	3.8537e−09
1.0E−01	9.8431e−01	9.8431e−01	1.1519e−08	9.9833e−02	9.9833e−02	3.9785e−09
3.0E−01	9.5692e−01	9.5692e−01	1.4670e−08	2.9552e−01	2.9552e−01	2.7488e−09
5.0E−01	9.4131e−01	9.4131e−01	1.7908e−08	4.7943e−01	4.7943e−01	8.8606e−10
7.0E−01	9.4481e−01	9.4481e−01	2.0627e−08	6.4422e−01	6.4422e−01	7.0014e−09
9.0E−01	9.7400e−01	9.7400e−01	1.6180e−08	7.8333e−01	7.8333e−01	9.9222e−09
1.0E+00	1.0000e+00	1.0000e+00	3.0317e−10	8.4147e−01	8.4147e−01	3.8417e−10

Table 5 Maximal error comparison for Example 1.

ε	DTM-1	DTM-2	DTM-3	DTM-5	DTM-9
10⁻¹	4.1667e−001	4.1667e−002	1.3793e−004	1.3793e−004	1.3793e−004
10⁻²	4.1667e−001	4.1667e−002	1.5352e−006	1.5352e−006	1.5352e−006
10⁻³	4.1667e−001	4.1667e−002	1.5589e−008	1.5589e−008	1.5589e−008
10⁻⁴	4.1667e−001	4.1667e−002	1.5609e−010	1.5609e−010	1.5609e−010
10⁻⁵	4.1667e−001	4.1667e−002	1.5610e−012	1.5610e−012	1.5610e−012

Table 6 Maximal error comparison for Example 2.

ε	DTM-1	DTM-3	DTM-5	DTM-7	DTM-9
10⁻¹	1.5857e−001	8.1377e−003	6.6434e−003	6.6434e−003	6.6434e−003
10⁻²	1.5853e−001	8.1377e−003	1.9566e−004	9.4397e−005	9.4397e−005
10⁻³	1.5853e−001	8.1377e−003	1.9566e−004	2.7557e−006	9.9235e−007
10⁻⁴	1.5853e−001	8.1377e−003	1.9566e−004	2.7557e−006	4.9537e−08
10⁻⁵	1.5853e−001	8.1377e−003	1.9566e−004	2.7557e−006	4.9537e−08

Table 7 Maximal error comparison for Example 3.

ε	DTM-1	DTM-3	DTM-5	DTM-7	DTM-9
10⁻¹	1.5857e−001	8.1377e−003	6.6434e−003	6.6434e−003	6.6434e−003
10⁻²	1.5853e−001	8.1377e−003	1.9566e−004	9.4396e−005	9.4396e−005
10⁻³	1.5853e−001	8.1377e−003	1.9566e−004	2.7560e−006	9.9226e−007
10⁻⁴	1.5853e−001	8.1377e−003	1.9566e−004	2.7560e−006	2.0627e−008
10⁻⁵	1.5853e−001	8.1377e−003	1.9566e−004	2.7560e−006	1.8500e−008

Table 8 Processing times used in solving Examples 1, 2 and 3.

	DTM-5	DTM-7	DTM-9
Example 1	0.00001	0.00002	0.00002
Example 2	0.00010	0.00011	0.00011
Example 3	0.00009	0.00011	0.00013

5 Conclusions

In this paper, we presented a new and reliable algorithm to develop approximate analytical solutions of fourth order SPBVPs in which the highest order derivative is multiplied by a small parameter. The given fourth order problem is transformed into a system of two second order ODEs, with suitable boundary conditions and a zeroth-order asymptotic approximate solution of the transformed system is constructed. Then, the DTM is applied to solve the terminal value system analytically. The method provides the solutions in terms of convergent series with easily computable components. This approach is simple in applicability as it does not require linearization or discretization like other numerical and approximate methods. We have applied it on three examples and the approximate analytical solutions are presented for each one. Results obtained by the method are compared with the exact solution of each example and are found to be in good agreement with each other not only in the boundary layer, but also away from the layer. Numerical results are presented in figures and tables at different values of the perturbation parameter, ε, and the DTM order N. The results show that the accuracy of the approximate solution increases as the order of the DTM increases and the perturbation parameter ε decreases which agree with the theoretical analysis. The method works successfully in handling the considered fourth order SPBVPs with a high accuracy and a minimum size of computations. This emphasizes the fact that the present method is applicable to other higher order SPBVPs.

Acknowledgements

The author would like to thank the reviewers for their helpful comments which led to improvement of the manuscript.

References

Abdel-Halim Hassan I.H., . Comparison differential transformation technique with Adomian decomposition method for linear and nonlinear initial value problems. Chaos, Solitons & Fractals. 2008;36(1):53-65.
[Google Scholar]
Akram G., Rehman H., . Reproducing kernel method for fourth order singularly perturbed boundary value problem. World Appl. Sci. J.. 2012;16(12):1799-1802.
[Google Scholar]
Akram G., Amin N., . Solution of a fourth order singularly perturbed boundary value problem using quintic spline. Int. Math. Forum.. 2012;7(44):2179-2190.
[Google Scholar]
Alomari A.K., . A new analytic solution for fractional chaotic dynamical systems using the differential transform method. Comput. Math. Appl.. 2011;61:2528-2534.
[Google Scholar]
Al-Sawalha M.M., Noorani M.S.M., . Application of the differential transformation method for the solution of the hyperchaotic Rössler system. Commun. Nonlinear. Sci. Numer. Simul.. 2009;14:1509-1514.
[Google Scholar]
Al-Sawalha M.M., Noorani M.S.M., . A numeric–analytic method for approximating the chaotic Chen system. Chaos, Solitons & Fractals. 2009;42:1784-1791.
[Google Scholar]
Arikoglu A., Ozkol I., . Solution of differential difference equations by using differential transform method. Appl. Math. Comput.. 2006;181(1):153-162.
[Google Scholar]
Ayaz F., . Solutions of the system of differential equations by differential transform method. Appl. Math. Comput.. 2004;147:547-567.
[Google Scholar]
Babu A.R., Ramanujam N., . An asymptotic finite element method for singularly perturbed third and fourth order ordinary differential equations with discontinuous source term. Appl. Math. Comput.. 2007;191:372-380.
[Google Scholar]
Biazar J., Eslami M., Islam M.R., . Differential transform method for special systems of integral equations. J. King Saud Univ. – Science. 2012;24(3):211-214.
[Google Scholar]
Chu H-P., Chen C-Li., . Hybrid differential transform and finite difference method to solve the nonlinear heat conduction problem. Commun. Nonlinear. Sci. Numer. Simul.. 2008;13:1605-1614.
[Google Scholar]
Cui M., Geng F., . A computational method for solving third-order singularly perturbed boundary value problems. Appl. Math. Comput.. 2008;198:896-903.
[Google Scholar]
Demirdag O., Yesilce Y., . Solution of free vibration equation of elastically supported Timoshenko columns with a tip mass by differential transform method. Adv. Eng. Softw.. 2011;42(10):860-867.
[Google Scholar]
Doğan N., Ertürk V.S., Momani S., Akın Ö., Yıldırım A., . Solution of free vibration equation of elastically supported Timoshenko columns with a tip mass by differential transform method. J. King Saud Univ. – Science. 2011;23(2):223-228.
[Google Scholar]
Ebaid A.E.-H., . Approximate periodic solutions for the non-linear relativistic harmonic oscillator via differential transformation method. Commun. Nonlinear. Sci. Numer. Simul.. 2010;15:1921-1927.
[Google Scholar]
El-Shahed M., . Application of differential transform method to non-linear oscillatory systems. Commun. Nonlinear. Sci. Numer. Simul.. 2008;13:1714-1720.
[Google Scholar]
El-Zahar E.R., . Approximate analytical solutions for singularly perturbed boundary value problems by multi-step differential transform method. J. Appl. Sci.. 2012;12(19):2026-2034.
[Google Scholar]
El-Zahar, E.R., 2013. An Adaptive Step-Size Taylor Series Based Method and Application to Nonlinear Biochemical Reaction Model. Trends. Appl. Sci. Res., in press.
Gökdoğan A., Merdan M., Yildirim A., . The modified algorithm for the differential transform method to solution of Genesio systems. Commun. Nonlinear. Sci. Numer. Simul.. 2012;17(1):45-51.
[Google Scholar]
Gupta P.K., . Approximate analytical solutions of fractional Benney–Lin equation by reduced differential transform method and the homotopy perturbation method. Comput. Math. Appl.. 2011;61(9):2829-2842.
[Google Scholar]
Jang M.-J., Chen C.-L., Liy Y.-C., . On solving the initial-value problems using the differential transformation method. Appl. Math. Comput.. 2000;115:145-160.
[Google Scholar]
Kadalbajoo M.K., Patidar K.C., . A survey of numerical techniques for solving singularly perturbed ordinary differential equations. Appl. Math. Comput.. 2002;130 (2–3):457-510.
[Google Scholar]
Köksal M., Herdem S., . Analysis of nonlinear circuits by using differential Taylor transform. Comput. Electr. Eng.. 2002;28:513-525.
[Google Scholar]
Kumar M., Singh P., Mishra H.K., . A recent survey on computational techniques for solving singularly perturbed boundary value problems. Int. J. Comput. Math.. 2007;84:1-25.
[Google Scholar]
Kuo B., Lo C., . Application of the differential transformation method to the solution of a damped system with high nonlinearity. Nonlinear Anal. TMA. 2009;70(4):1732-1737.
[Google Scholar]
Kurulay M., Bayram M., . Approximate analytical solution for the fractional modified KdV by differential transform method. Commun. Nonlinear. Sci. Numer. Simul.. 2010;15(7):1777-1782.
[Google Scholar]
Liu H., Song Y., . Differential transform method applied to high index differential-algebraic equations. Appl. Math. Comput.. 2007;184:748-753.
[Google Scholar]
Momani S., Noor M., . Numerical comparison of methods for solving a special fourth-order boundary value problem. Appl. Math. Lett.. 2007;191(1):218-224.
[Google Scholar]
Momani S., Ertürk V.S., . Solutions of non-linear oscillators by the modified differential transform method. Comput. Math. Appl.. 2008;55:833-842.
[Google Scholar]
Nayfeh A.H., . Introduction to Perturbation Method. New York: Wiley; 1981.
Odibat Z.M., . Differential transform method for solving Volterra integral equation with separable kernels. Math. Comput. Modell.. 2008;48(7–8):144-1149.
[Google Scholar]
Phaneendra K., Reddy Y.N., Soujanya GBSL., . Asymptotic – numerical method for third-order singular perturbation problems. Int. J. Appl. Sci. Eng.. 2012;10(3):241-248.
[Google Scholar]
Ravi Kanth A.S.V., Aruna K., . Differential transform method for solving the linear and nonlinear Klein–Gordon equation. Comput. Phys. Commun.. 2009;180:708-711.
[Google Scholar]
Shanthi V., Ramanujam N., . Asymptotic numerical methods for singularly perturbed fourth-order ordinary differential equations of convection–diffusion type. Appl. Math. Comput.. 2002;133:559-579.
[Google Scholar]
Shanthi V., Ramanujam N., . Asymptotic numerical methods for singularly perturbed fourth-order ordinary differential equations of reaction–diffusion type. Comput. Math. Appl.. 2003;46:463-478.
[Google Scholar]
Shanthi V., Ramanujam N., . A boundary value technique for boundary value problems for singularly perturbed fourth-order ordinary differential equations. Comput. Math. Appl.. 2004;47:1673-1688.
[Google Scholar]
Siddiqi S.S., Akram G., Kanwal A., . Solutions of fifth order singularly perturbed boundary value problems using non-polynomial spline technique. Eur. J. Sci. Res.. 2011;56(3):415-425.
[Google Scholar]
Syam M.I., Attili B.S., . Numerical solution of singularly perturbed fifth order two point boundary value problem. Appl. Math. Comput.. 2005;170:1085-1094.
[Google Scholar]
Thongmoon M., Pusjuso M., . The numerical solutions of differential transform method and the Laplace transform method for a system of differential equations. Nonlinear Anal: Hybrid Syst.. 2010;4:425-431.
[Google Scholar]
Valarmathi S., Ramanujam N., . A computational method for solving boundary value problems for third-order singularly perturbed ordinary differential equations. Appl. Math. Comput.. 2002;129:345-373.
[Google Scholar]
Valarmathi S., Ramanujam N., . An asymptotic numerical method for singularly perturbed third-order ordinary differential equations of convection–diffusion type. Comput. Math. Appl.. 2002;44:693-710.
[Google Scholar]
Valanarasu T., Ramanujam N., . An asymptotic numerical method for singularly perturbed third order ordinary differential equations with weak interior layer, Int. J. Comput. Math.. 2007;84:333-346.
[Google Scholar]
Zhou J.K., . Differential transformation and its applications for electrical circuits. Wuhan, China: Huazhong University Press; 1986. Wuhan, China

Introduction

Basic concepts of the DTM

Description of the method

A zeroth-order asymptotic approximate solution
The solution of the TVS (12) by DTM
The error analysis

Illustrating examples

Conclusions

Fulltext Views
6

PDF downloads
2

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abdel-Halim Hassan I.H., . Comparison differential transformation technique with Adomian decomposition method for linear and nonlinear initial value problems. Chaos, Solitons & Fractals. 2008;36(1):53-65.
[Google Scholar]

[2] Akram G., Rehman H., . Reproducing kernel method for fourth order singularly perturbed boundary value problem. World Appl. Sci. J.. 2012;16(12):1799-1802.
[Google Scholar]

[3] Akram G., Amin N., . Solution of a fourth order singularly perturbed boundary value problem using quintic spline. Int. Math. Forum.. 2012;7(44):2179-2190.
[Google Scholar]

[4] Alomari A.K., . A new analytic solution for fractional chaotic dynamical systems using the differential transform method. Comput. Math. Appl.. 2011;61:2528-2534.
[Google Scholar]

[5] Al-Sawalha M.M., Noorani M.S.M., . Application of the differential transformation method for the solution of the hyperchaotic Rössler system. Commun. Nonlinear. Sci. Numer. Simul.. 2009;14:1509-1514.
[Google Scholar]

[6] Al-Sawalha M.M., Noorani M.S.M., . A numeric–analytic method for approximating the chaotic Chen system. Chaos, Solitons & Fractals. 2009;42:1784-1791.
[Google Scholar]

[7] Arikoglu A., Ozkol I., . Solution of differential difference equations by using differential transform method. Appl. Math. Comput.. 2006;181(1):153-162.
[Google Scholar]

[8] Ayaz F., . Solutions of the system of differential equations by differential transform method. Appl. Math. Comput.. 2004;147:547-567.
[Google Scholar]

[9] Babu A.R., Ramanujam N., . An asymptotic finite element method for singularly perturbed third and fourth order ordinary differential equations with discontinuous source term. Appl. Math. Comput.. 2007;191:372-380.
[Google Scholar]

[10] Biazar J., Eslami M., Islam M.R., . Differential transform method for special systems of integral equations. J. King Saud Univ. – Science. 2012;24(3):211-214.
[Google Scholar]

[11] Chu H-P., Chen C-Li., . Hybrid differential transform and finite difference method to solve the nonlinear heat conduction problem. Commun. Nonlinear. Sci. Numer. Simul.. 2008;13:1605-1614.
[Google Scholar]

[12] Cui M., Geng F., . A computational method for solving third-order singularly perturbed boundary value problems. Appl. Math. Comput.. 2008;198:896-903.
[Google Scholar]

[13] Demirdag O., Yesilce Y., . Solution of free vibration equation of elastically supported Timoshenko columns with a tip mass by differential transform method. Adv. Eng. Softw.. 2011;42(10):860-867.
[Google Scholar]

[14] Doğan N., Ertürk V.S., Momani S., Akın Ö., Yıldırım A., . Solution of free vibration equation of elastically supported Timoshenko columns with a tip mass by differential transform method. J. King Saud Univ. – Science. 2011;23(2):223-228.
[Google Scholar]

[15] Ebaid A.E.-H., . Approximate periodic solutions for the non-linear relativistic harmonic oscillator via differential transformation method. Commun. Nonlinear. Sci. Numer. Simul.. 2010;15:1921-1927.
[Google Scholar]

[16] El-Shahed M., . Application of differential transform method to non-linear oscillatory systems. Commun. Nonlinear. Sci. Numer. Simul.. 2008;13:1714-1720.
[Google Scholar]

[17] El-Zahar E.R., . Approximate analytical solutions for singularly perturbed boundary value problems by multi-step differential transform method. J. Appl. Sci.. 2012;12(19):2026-2034.
[Google Scholar]

[18] El-Zahar, E.R., 2013. An Adaptive Step-Size Taylor Series Based Method and Application to Nonlinear Biochemical Reaction Model. Trends. Appl. Sci. Res., in press.

[19] Gökdoğan A., Merdan M., Yildirim A., . The modified algorithm for the differential transform method to solution of Genesio systems. Commun. Nonlinear. Sci. Numer. Simul.. 2012;17(1):45-51.
[Google Scholar]

[20] Gupta P.K., . Approximate analytical solutions of fractional Benney–Lin equation by reduced differential transform method and the homotopy perturbation method. Comput. Math. Appl.. 2011;61(9):2829-2842.
[Google Scholar]

[21] Jang M.-J., Chen C.-L., Liy Y.-C., . On solving the initial-value problems using the differential transformation method. Appl. Math. Comput.. 2000;115:145-160.
[Google Scholar]

[22] Kadalbajoo M.K., Patidar K.C., . A survey of numerical techniques for solving singularly perturbed ordinary differential equations. Appl. Math. Comput.. 2002;130 (2–3):457-510.
[Google Scholar]

[23] Köksal M., Herdem S., . Analysis of nonlinear circuits by using differential Taylor transform. Comput. Electr. Eng.. 2002;28:513-525.
[Google Scholar]

[24] Kumar M., Singh P., Mishra H.K., . A recent survey on computational techniques for solving singularly perturbed boundary value problems. Int. J. Comput. Math.. 2007;84:1-25.
[Google Scholar]

[25] Kuo B., Lo C., . Application of the differential transformation method to the solution of a damped system with high nonlinearity. Nonlinear Anal. TMA. 2009;70(4):1732-1737.
[Google Scholar]

[26] Kurulay M., Bayram M., . Approximate analytical solution for the fractional modified KdV by differential transform method. Commun. Nonlinear. Sci. Numer. Simul.. 2010;15(7):1777-1782.
[Google Scholar]

[27] Liu H., Song Y., . Differential transform method applied to high index differential-algebraic equations. Appl. Math. Comput.. 2007;184:748-753.
[Google Scholar]

[28] Momani S., Noor M., . Numerical comparison of methods for solving a special fourth-order boundary value problem. Appl. Math. Lett.. 2007;191(1):218-224.
[Google Scholar]

[29] Momani S., Ertürk V.S., . Solutions of non-linear oscillators by the modified differential transform method. Comput. Math. Appl.. 2008;55:833-842.
[Google Scholar]

[30] Nayfeh A.H., . Introduction to Perturbation Method. New York: Wiley; 1981.

[31] Odibat Z.M., . Differential transform method for solving Volterra integral equation with separable kernels. Math. Comput. Modell.. 2008;48(7–8):144-1149.
[Google Scholar]

[32] Phaneendra K., Reddy Y.N., Soujanya GBSL., . Asymptotic – numerical method for third-order singular perturbation problems. Int. J. Appl. Sci. Eng.. 2012;10(3):241-248.
[Google Scholar]

[33] Ravi Kanth A.S.V., Aruna K., . Differential transform method for solving the linear and nonlinear Klein–Gordon equation. Comput. Phys. Commun.. 2009;180:708-711.
[Google Scholar]

[34] Shanthi V., Ramanujam N., . Asymptotic numerical methods for singularly perturbed fourth-order ordinary differential equations of convection–diffusion type. Appl. Math. Comput.. 2002;133:559-579.
[Google Scholar]

[35] Shanthi V., Ramanujam N., . Asymptotic numerical methods for singularly perturbed fourth-order ordinary differential equations of reaction–diffusion type. Comput. Math. Appl.. 2003;46:463-478.
[Google Scholar]

[36] Shanthi V., Ramanujam N., . A boundary value technique for boundary value problems for singularly perturbed fourth-order ordinary differential equations. Comput. Math. Appl.. 2004;47:1673-1688.
[Google Scholar]

[37] Siddiqi S.S., Akram G., Kanwal A., . Solutions of fifth order singularly perturbed boundary value problems using non-polynomial spline technique. Eur. J. Sci. Res.. 2011;56(3):415-425.
[Google Scholar]

[38] Syam M.I., Attili B.S., . Numerical solution of singularly perturbed fifth order two point boundary value problem. Appl. Math. Comput.. 2005;170:1085-1094.
[Google Scholar]

[39] Thongmoon M., Pusjuso M., . The numerical solutions of differential transform method and the Laplace transform method for a system of differential equations. Nonlinear Anal: Hybrid Syst.. 2010;4:425-431.
[Google Scholar]

[40] Valarmathi S., Ramanujam N., . A computational method for solving boundary value problems for third-order singularly perturbed ordinary differential equations. Appl. Math. Comput.. 2002;129:345-373.
[Google Scholar]

[41] Valarmathi S., Ramanujam N., . An asymptotic numerical method for singularly perturbed third-order ordinary differential equations of convection–diffusion type. Comput. Math. Appl.. 2002;44:693-710.
[Google Scholar]

[42] Valanarasu T., Ramanujam N., . An asymptotic numerical method for singularly perturbed third order ordinary differential equations with weak interior layer, Int. J. Comput. Math.. 2007;84:333-346.
[Google Scholar]

[43] Zhou J.K., . Differential transformation and its applications for electrical circuits. Wuhan, China: Huazhong University Press; 1986. Wuhan, China