The homotopy perturbation method for solving neutral functional–differential equations with proportional delays

Jafar Biazar; Behzad Ghanbari

doi:10.1016/j.jksus.2010.07.026

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

24 (

); 33-37

doi:

10.1016/j.jksus.2010.07.026

The homotopy perturbation method for solving neutral functional–differential equations with proportional delays

Jafar Biazar^a, Behzad Ghanbari^a,b,*

a Department of Mathematics, Faculty of Sciences, University of Guilan, P.C. 41938 Rasht, Iran

b Department of nanotechnology, Kermanshah University of Technology, Kermanshah, Iran

*Corresponding author at: Department of Mathematics, Faculty of Sciences, University of Guilan, P.C. 41938 Rasht, Iran b.ghanbary@yahoo.com (Behzad Ghanbari)

Received: 2010-7-3, Accepted: 2010-7-28, Published: 2010-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 12 August 2010

Abstract

The aim of this paper is to apply homotopy perturbation method (HPM) to solve delay differential equations. Some examples are presented to show the ability of the method. The results reveal that the method is very effective and simple.

Keywords

Homotopy perturbation method

Delay differential equations

Show Related Articles from PubMed

1 Introduction

Neutral functional–differential equations with proportional delays represent a particular class of delay differential equation. Such functional–differential equations play an important role in the mathematical modeling of real world phenomena (Bellen and Zennaro, 2003). These equations have been investigated by some authors and several efficient numerical and analytical methods have been designed to approximate their solutions Ishiwata and Muroya used the rational approximation method (Ishiwata and Muroya, 2007) and the collocation method (Ishiwata et al., 2008), Wang et al. obtained approximate solutions by continuous Runge–Kutta methods (Wang et al., 2009) and one-leg θ-methods (Wang and Li, 2007; Wang et al., 2009).

Very recently, Chen and his collaborator applied the variational iteration method for solving a neutral functional–differential equation with proportional delays (Chen and Wang, 2010).

In this paper, we apply the homotopy perturbation method (HPM in short) to solve neutral differential equation with proportional delays as considered in Chen and Wang (2010),

(1)

(u (t) + a (t) u (p_{m} t))^{(m)} = β u (t) + \sum_{k = 0}^{m - 1} b_{k} (t) u^{(k)} (p_{k} t) + f (t), t ⩾ 0,

with the initial conditions

u^{(k)} (0) = λ_{k}, k = 0, 1, \dots, m - 1 .

where a and b_k (k = 0, 1, … , m − 1) are known analytical functions, and β, p_k, c_ik, λ_k are given constants with 0 < p_k < 1 for k = 0, 1, … , m.

This paper is organized as follows: In Section 2, basic idea of HPM is presented. Applying HPM to solving (1) is discussed in Section 3. Section 4 is devoted to numerical comparisons between the results obtained by HPM in this work and some existing methods. Finally, conclusions are stated in the last section.

2 Basic idea of He’s homotopy perturbation method

The topic of the He’s homotopy perturbation method (He, 2004, 2005, 2006 ) has been rapidly growing in recent years. In this method the solution of functional equations is considered as the summation of an infinite series usually converging to the solution.

Considerable research works have been conducted recently in applying this method to a class of linear and nonlinear equations. For example, nonlinear Schrodinger equations (Biazar and Ghazvini, 2007), integral equations (Abbasbandy, 2006), nonlinear oscillators with discontinuities (He, 1999), nonlinear wave equations (He, 2000). To see more applications of this method we refer the interested readers to He (2004, 2005, 2006, 1999, 2000), Biazar and Ghazvini (2007), Abbasbandy (2006) and references therein.

To illustrate the basic ideas of this method, we consider the following nonlinear differential equation:

(2)

A (u) - f (r) = 0, r \in Ω,

with the boundary conditions

B (u, \frac{\partial u}{\partial n}) = 0, r \in Γ,

where A is a general differential operator, B a boundary operator, f(r) a known analytical function and Γ is the boundary of the domain Ω.

The operator A can be divided into two parts, which are L and N, where L is a linear, but N is nonlinear. Eq. (2) can be, therefore, rewritten as follows: $L (u) + N (u) - f (r) = 0 .$ By the homotopy technique, we construct a homotopy U(r, p):Ω × [0,1] → $R$ , which satisfies:

(3)

H (U, p) = (1 - p) [L (U) - L (u_{0})] + p [A (U) - f (r)], p \in [0, 1], r \in Ω,

(4)

H (U, p) = L (U) - L (u_{0}) + pL (u_{0}) + p [A (U) - f (r)], p \in [0, 1], r \in Ω,

where p ∈ [0, 1] is an embedding parameter, u₀ is an initial approximation of Eq. (1), which satisfies the boundary conditions. Obviously, from Eqs. (3) and (4) we will have

\begin{matrix} H (U, 0) = A (U) - L (u_{0}) = 0, \\ H (U, 1) = A (U) - f (r) = 0 . \end{matrix}

The changing process of p form zero to unity is just that of U(r, p) from u₀(r) to u(r). In topology, this is called homotopy. According to the (HPM), we can first use the embedding parameter p as a small parameter, and assume that the solution of Eqs. (3) and (4) can be written as a power series in p:

U = U_{0} + {pU}_{1} + p^{2} U_{2} + p^{3} U_{3} + \dots

Setting p = 1, results in the approximate solution of Eq. (1)

u = \lim_{p \to 1} U = U_{1} + U_{2} + U_{3} + \dots

3 Method of solution

For solving Eq. (1), by homotopy perturbation method we construct a homotopy as follows:

(5)

H (v, p) = (1 - p) [v^{(m)} (t) - u_{0}^{(m)} (t)] + p [v^{(m)} (t) + a (t) v^{(m)} (p_{m} t) - β v (t) - \sum_{k = 0}^{m - 1} b_{k} (t) v^{(k)} (p_{k} t) - f (t)], t ⩾ 0 .

Suppose the solution of Eq. (2) has the form

(6)

v = v_{0} + pv + p^{2} v^{2} + \dots,

where v_i’s are functions yet to be determined.

Whereas series (6) be a convergent series at p = 1, the exact solution of (1), reads as: $v = v_{0} + v_{1} + v_{2} + \dots$ Substituting (6) into (5) and arranging the coefficients powers of p following initial value problems

(7)

\begin{matrix} p^{0} : v_{0}^{(m)} (t) - u_{0}^{(m)} (t) = 0, v_{0}^{(k)} (0) = λ_{k}, k = 0, 1, \dots, m - 1, \\ p^{1} : v_{1}^{(m)} (t) + u_{0}^{(m)} (t) + a (t) u_{0}^{(m)} (p_{m} t) - β u_{0} (t) - \sum_{k = 0}^{m - 1} b_{k} (t) u_{0}^{(k)} (p_{k} t), \\ v_{1}^{(k)} (0) = 0, k = 0, \dots, m - 1, \\ ⋮ \\ p^{n} : v_{n}^{(m)} (t) + a (t) u_{n - 1}^{(m)} (p_{m} t) - β u_{n - 1} (t) - \sum_{k = 0}^{m - 1} b_{k} (t) u_{n - 1}^{(k)} (p_{k} t), \\ v_{n}^{(k)} (0) = 0, k = 0, 1, \dots, m - 1 . \end{matrix}

Identifying the components v_k’s, the nth approximation of the exact solution can be obtained, as:

u_{n} = v_{0} + v_{1} + v_{2} + \dots + v_{n} .

4 Illustrative examples

In this part, some examples are provided to illustrate performance of proposed method. For the sake of comparing purposes, we consider the same examples as used in Chen and Wang (2010).

Example 1

Consider the following first-order neutral functional–differential equation with proportional delay: $\{\begin{matrix} u^{'} (t) = - u (t) + \frac{1}{2} u (\frac{t}{2}) + \frac{1}{2} u^{'} (\frac{t}{2}), t \in [0, 1] \\ u (0) = 1, \end{matrix}$ Exact solution u(t) = e^−t.

In this example, starting with u₀(t) = 1, 7th order of HPM approximate solutions is obtained, as:

(8)

u_{7} (t) = 1 - \frac{127}{128} t + \frac{8001}{16384} t^{2} - \frac{82677}{524288} t^{3} + \frac{1240155}{33554432} t^{4} - \frac{1736217}{268435456} t^{5} + \frac{1736217}{2147483648} t^{6} - \frac{248031}{4294967296} t^{7} .

The graphs of (8) and the exact solution are contained in Fig. 1. Also, we compare the absolute errors of homotopy perturbation method with the ones for the variational iteration method (Chen and Wang, 2010) and the two-stage order-one Runge–Kutta method of Wang et al. (2009) and the one-leg θ-method of Wang and Li (2007), Wang et al. (2009) with θ = 0.8 using h = 0.01, in Table 1.

Example 2

Let us have the following first-order neutral functional–differential equation with proportional delay $\{\begin{matrix} u^{'} (t) = - u (t) + 0.1 u (0.8 t) + 0.5 u^{'} (0.8 t) \\ + (0.32 t - 0.5) \exp (- 0.8 t) + \exp (t), t ⩾ 0 \\ u (0) = 0, \end{matrix}$ which has the exact solution u(t) = te^−t.

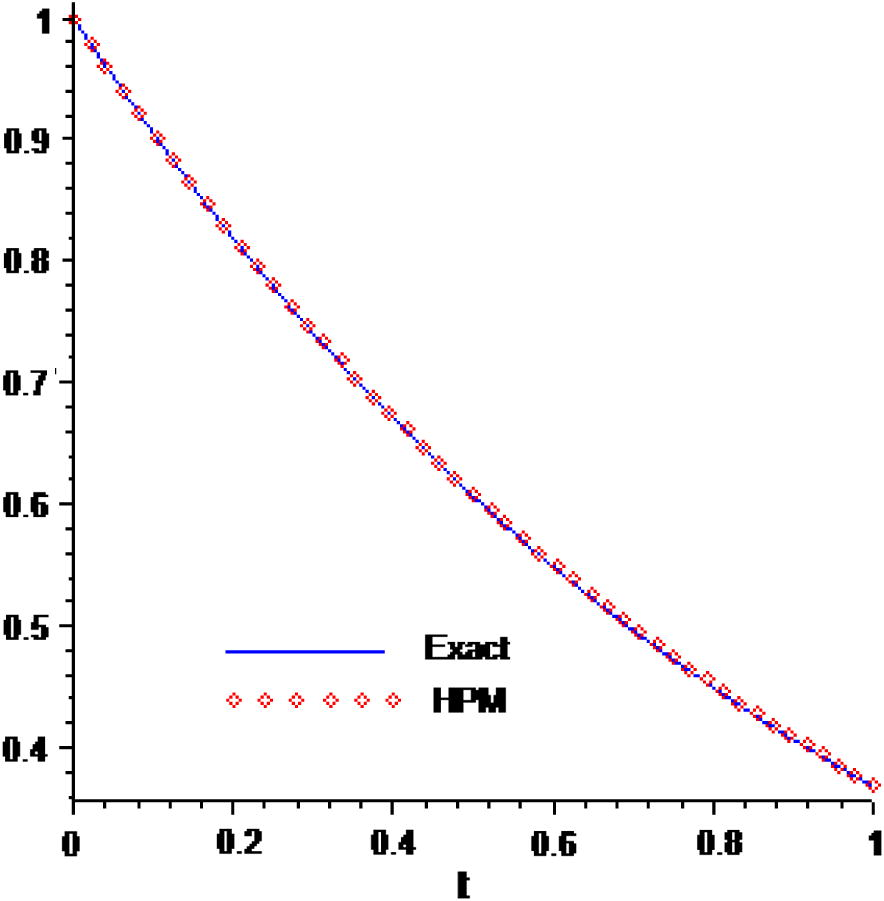
Comparison of the approximate solutions with the exact solution for Example 1.

Table 1 Comparison of the absolute errors for Example 1.

t	Two-stage order-one Runge–Kutta method	One-leg θ-method with θ = 0.8	Variational iterative method		Homotopy perturbation method
t	Two-stage order-one Runge–Kutta method	One-leg θ-method with θ = 0.8	n = 7	n = 8	n = 7	n = 8
0.1	4.55 e−4	2.57 e−3	7.43 e−4	3.72 e−4	6.73 e−4	3.36 e−4
0.2	8.24 e−4	8.86 e−3	1.42 e−3	7.08 e−4	1.16 e−3	5.80 e−4
0.3	1.12 e−3	1.72 e−2	2.02 e−3	1.01 e−3	1.50 e−3	7.50 e−4
0.4	1.35 e−3	2.66 e−2	2.58 e−3	1.29 e−3	1.73 e−3	8.64 e−4
0.5	1.52 e−3	3.63 e−2	3.07 e−3	1.54 e−3	1.86 e−3	9.33 e−4
0.6	1.66 e−3	4.85 e−2	3.52 e−3	1.76 e−3	1.94 e−3	9.68 e−4
0.7	1.75 e−3	5.47 e−2	3.93 e−3	1.97 e−3	1.95 e−3	9.78 e−4
0.8	1.81 e−3	6.29 e−2	4.30 e−3	2.15 e−3	1.93 e−3	9.68 e−4
0.9	1.84 e−3	7.02 e−2	4.64 e−3	2.32 e−3	1.89 e−3	9.44 e−4
1.0	1.85 e−3	7.66 e−2	4.94 e−3	2.47 e−3	1.82 e−3	9.10 e−4

Considering the 5th order of HPM approximate solutions with u₀(t) = 0, we made comparison of such approximation with the exact solution in Fig. 2.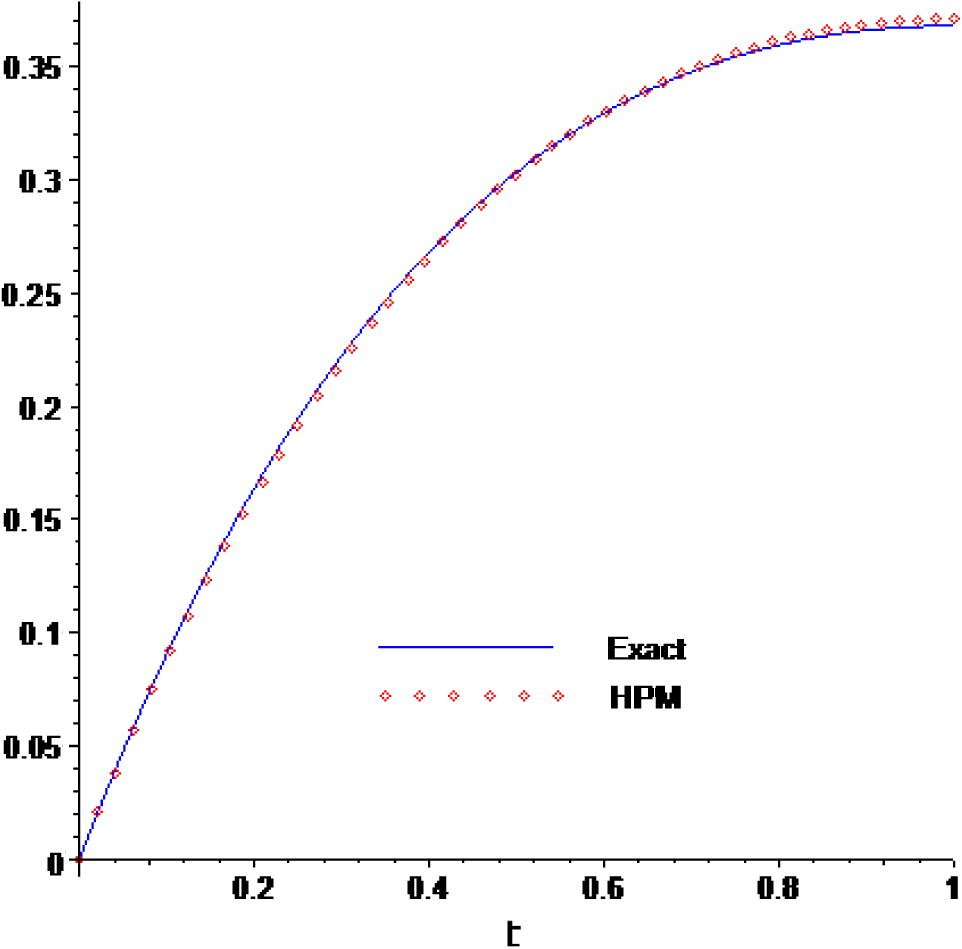

Comparison of the approximate solutions with the exact solution for Example 2.

Comparing Table 2, it can be seen that the approximation solutions by HPM agree with the exact solution.

Example 3

As another example, let us consider the second-order neutral functional–differential equation with proportional delay $\{\begin{matrix} u^{″} (t) = u^{'} (\frac{1}{2} t) - \frac{1}{2} {tu}^{″} (\frac{1}{2} t) + 2, t \in [0, 1] \\ u (0) = 1, u^{'} (0) = 0 . \end{matrix}$

Table 2 Comparison of the absolute errors for Example 2.

t	Two-stage order-one Runge–Kutta method	One-leg θ-method with θ = 0.8	Variational iterative method		Homotopy perturbation method
t	Two-stage order-one Runge–Kutta method	One-leg θ-method with θ = 0.8	n = 5	n = 6	n = 5	n = 6
0.1	8.68 e−4	4.65 e−3	2.62 e−3	1.30 e−3	2.17 e−3	1.06 e−3
0.2	1.49 e−3	1.45 e−2	4.36 e−3	2.14 e−3	2.87 e−3	1.35 e−3
0.3	1.90 e−3	2.57 e−2	5.40 e−3	2.63 e−3	2.63 e−3	1.18 e−3
0.4	2.16 e−3	3.60 e−2	5.89 e−3	2.84 e−3	1.83 e−3	7.61 e−4
0.5	2.28 e−3	4.43 e−2	5.96 e−3	2.83 e−3	7.76 e−4	2.32 e−4
0.6	2.31 e−3	5.03 e−2	5.71 e−3	2.67 e−3	3.33 e−4	2.98 e−4
0.7	2.27 e−3	5.37 e−2	5.23 e−3	2.39 e−3	1.35 e−3	7.64 e−4
0.8	2.17 e−3	5.47 e−2	4.59 e−3	2.04 e−3	2.20 e−3	1.12 e−3
0.9	2.03 e−3	5.35 e−2	3.84 e−3	1.64 e−3	2.82 e−3	1.37 e−3
1.0	1.86 e−3	5.03 e−2	3.04 e−3	1.22 e−3	3.21 e−3	1.50 e−3

Starting with u₀(t) = 1 in (7), we have $\{\begin{matrix} u_{1} (t) = t^{2}, \\ u_{n} (0) = 0, n ⩾ 2 . \end{matrix}$ That is, we obtain u(t) = u₀(t) + u₁(t) = 1 + t², which coincides with the exact solution.

Example 4

In this example, we consider Eq. (1), as: $\{\begin{matrix} u^{″} (t) = \frac{3}{4} u (t) + u (\frac{1}{2} t) + u^{'} (\frac{1}{2} t) \\ + \frac{1}{2} u^{″} (\frac{1}{2} t) - t^{2} - t + 1, t \in [0, 1] \\ u (0) = u^{'} (0) = 0, \end{matrix}$ which enjoys exact solution u(t) = t².

In this example, starting with u₀(t) = 0, 5th order of HPM approximate solutions is obtained, as:

(9)

u_{5} (t) = \frac{31}{32} t^{2} - \frac{31}{3072} t^{3} - \frac{651}{262144} t^{4} - \frac{23095}{37748736} t^{5} - \frac{23095}{37748736} t^{6} + \dots

The approximate solution (9) and exact solution are illustrated in Fig. 3.

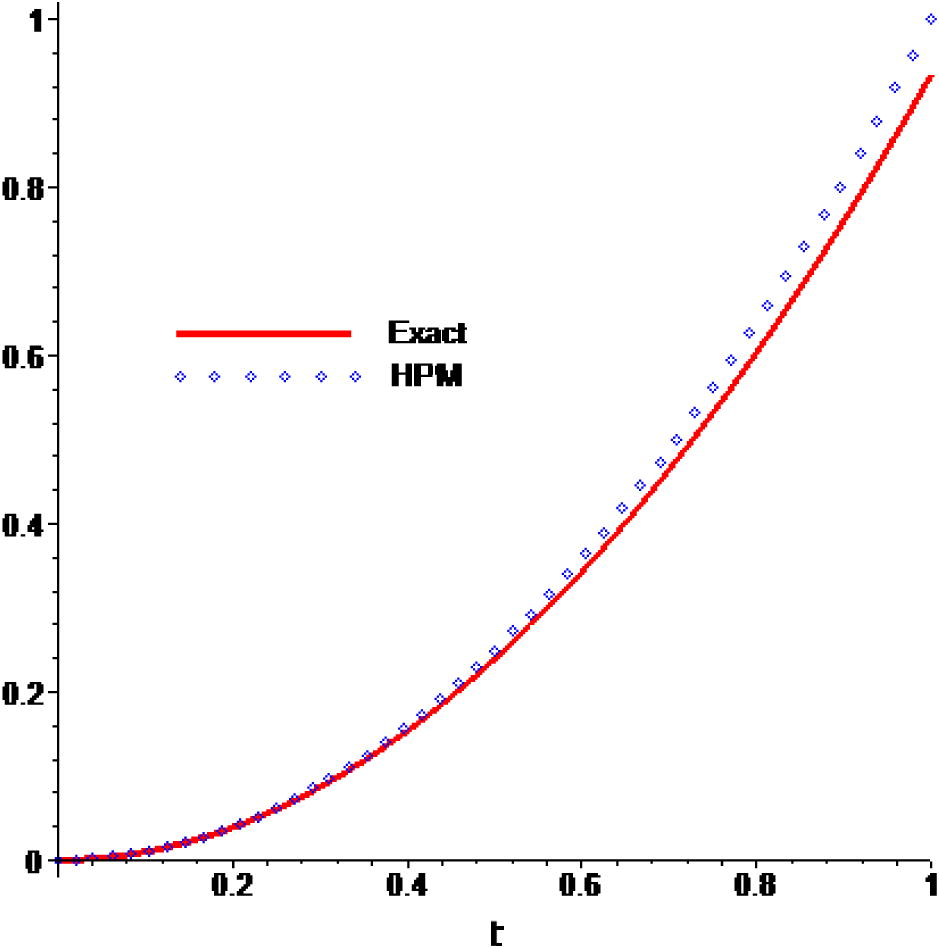
Comparison of the approximate solutions with the exact solution for Example 4.

Similar to above, we compute the absolute errors for different approaches, for example, 4 in Table 3.

Example 5

As last example, let’s try the following third-order case of (1), as: $\{\begin{matrix} u^{‴} (t) = u (t) + u^{'} (\frac{1}{2} t) + u^{″} (\frac{1}{3} t) + \frac{1}{2} u^{‴} (\frac{1}{4} t) - t^{4} \\ - \frac{t^{3}}{2} - \frac{4}{3} t^{2} + 21 t, t \in [0, 1] \\ u (0) = u^{'} (0) = u^{″} (0) = 0, \end{matrix}$

Table 3 Comparison of the absolute errors for Example 4.

t	Two-stage order-one Runge–Kutta method	One-leg θ-method with θ = 0.8	Variational iterative method		Homotopy perturbation method
t	Two-stage order-one Runge–Kutta method	One-leg θ-method with θ = 0.8	n = 5	n = 6	n = 5	n = 6
0.1	8.68 e−3	6.10 e−3	3.34 e−4	1.67 e−4	3.33 e−4	1.67 e−4
0.2	1.49 e−3	2.58 e−2	1.43 e−3	7.15 e−4	1.42 e−3	7.15 e−4
0.3	1.90 e−3	6.47 e−2	2.45 e−3	1.73 e−3	3.44 e−3	1.72 e−3
0.4	2.16 e−3	1.37 e−1	6.58 e−3	3.30 e−3	6.57 e−3	3.30 e−3
0.5	2.28 e−3	2.81 e−1	1.11 e−2	5.55 e−3	1.10 e−2	5.55 e−3

In Fig. 4, we draw the diagrams of the 4th order of HPM approximate results obtained by HPM with u₀(t) = 0 and exact solution u(t) = t².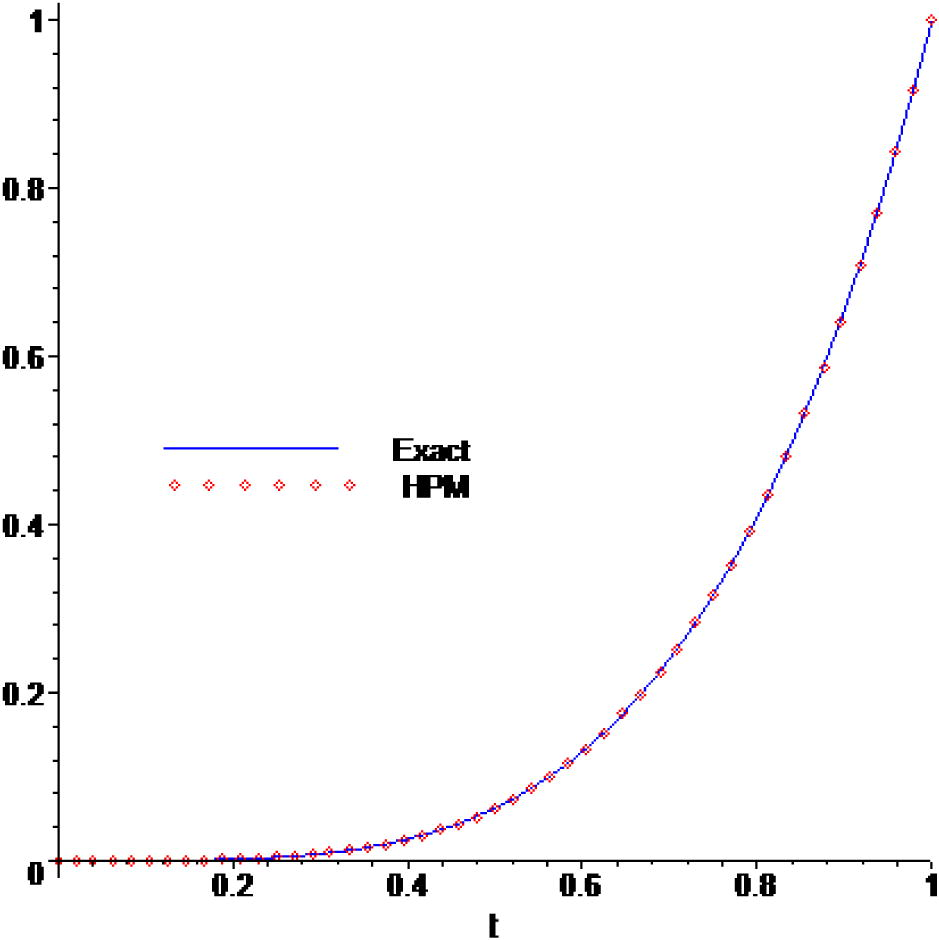

Comparison of the approximate solutions with the exact solution for Example 5.

Furthermore, some result comparisons of this example are reported in Table 4.

Table 4 Comparison of the absolute errors for Example 5.

t	Two-stage order-one Runge–Kutta method	Variational iterative method			Homotopy perturbation method
t	Two-stage order-one Runge–Kutta method	n = 4	n = 5	n = 6	n = 4	n = 5	n = 6
0.1	4.97 e−5	2.46 e−8	3.07 e−9	9.09 e−12	2.50 e−8	3.12 e−9	3.90 e−12
0.2	4.43 e−4	4.03 e−7	5.04 e−8	2.98 e−10	4.09 e−7	5.12 e−8	6.40 e−10
0.3	1.57 e−3	2.09 e−6	2.62 e−7	2.33 e−9	2.12 e−6	2.66 e−7	2.32 e−8
0.4	3.85 e−3	6.80 e−6	8.49 e−7	1.01 e−8	6.90 e−6	8.63 e−7	1.07 e−7
0.5	7.78 e−3	1.71 e−5	2.13 e−6	3.20 e−8	1.73 e−5	2.16 e−6	2.70 e−7
0.6	1.39 e−2	3.64 e−5	4.55 e−6	8.24 e−8	3.69 e−5	4.62 e−6	5.78 e−7
0.7	2.28 e−2	6.96 e−5	8.69 e−6	1.85 e−7	7.06 e−5	8.83 e−6	1.10 e−6
0.8	3.53 e−2	1.23 e−4	1.53 e−5	3.76 e−7	1.24 e−4	1.55 e−5	1.94 e−6
0.9	5.19 e−2	2.03 e−4	2.54 e−5	7.09 e−7	2.06 e−4	2.57 e−5	3.22 e−6
1.0	7.34 e−2	3.21 e−4	4.01 e−5	1.26 e−6	3.25 e−4	4.07 e−5	5.09 e−6

5 Conclusion

In this paper, He’s homotopy perturbation method has been successfully applied to find the solutions of neutral functional–differential equations. The efficiency and accuracy of the proposed decomposition method were demonstrated by some test problems. It is concluded from above tables and figures that the HPM is an accurate and efficient method to solve neutral functional–differential equations.

References

Abbasbandy S., . Numerical solutions of the integral equations: homotopy perturbation method and Adomian’s decomposition method. Applied Mathematics and Computation. 2006;173:493-500.
[Google Scholar]
Bellen Alfredo, Zennaro Marino, . Numerical methods for delay differential equations. In: Numerical Mathematics and Scientific Computation. New York: The Clarendon Press/Oxford University Press; 2003.
[Google Scholar]
Biazar J., Ghazvini H., . Exact solutions for nonlinear Schrodinger equations by He’s homotopy perturbation method. Physics Letters A. 2007;366:79-84.
[Google Scholar]
Chen X., Wang L., . The variational iteration method for solving a neutral functional–differential equation with proportional delays. Computers and Mathematics with Applications 2010
[CrossRef] [Google Scholar]
He J.H., . Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering. 1999;178:257-262.
[Google Scholar]
He J.H., . A coupling method of homotopy technique and perturbation technique for nonlinear problems. International Journal of Non-Linear Mechanics. 2000;35(1):37-43.
[Google Scholar]
He J.H., . The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation. 2004;151:287-292.
[Google Scholar]
He J.H., . Application of homotopy perturbation method to nonlinear wave equations. Chaos, Solitons and Fractals. 2005;26:695-700.
[Google Scholar]
He J.H., . Homotopy perturbation method for solving boundary value problems. Physics Letters A. 2006;350:87-88.
[Google Scholar]
Ishiwata Emiko, Muroya Yoshiaki, . Rational approximation method for delay differential equations with proportional delay. Applied Mathematics and Computation. 2007;187(2):741-747.
[Google Scholar]
Ishiwata Emiko, Muroya Yoshiaki, Brunner Hermann, . A super-attainable order in collocation methods for differential equations with proportional delay. Applied Mathematics and Computation. 2008;198(1):227-236.
[Google Scholar]
Wang WanSheng, Li ShouFu, . On the one-leg θ-methods for solving nonlinear neutral functional–differential equations. Applied Mathematics and Computation. 2007;193(1):285-301.
[Google Scholar]
Wang Wansheng, Zhang Yuan, Li Shoufu, . Stability of continuous Runge–Kutta-type methods for nonlinear neutral delay-differential equations. Applied Mathematical Modelling. 2009;33(8):3319-3329.
[Google Scholar]
Wang Wansheng, Qin Tingting, Li Shoufu, . Stability of one-leg θ-methods for nonlinear neutral differential equations with proportional delay. Applied Mathematics and Computation. 2009;213(1):177-183.
[Google Scholar]