Translate this page into:
A resolvent method for solving mixed variational inequalities
⁎Corresponding author at: Mathematics Department, COMSATS Institute of Information Technology, Islamabad, Pakistan. Tel.: +92 23454027532. noormaslam@hotmail.com (Muhammad Aslam Noor)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 16 July 2010
Peer-review under responsibility of King Saud University.
Abstract
It is well known that the mixed variational inequalities involving the nonlinear term are equivalent to the fixed-point problems. In this paper, we use this alternative equivalent formulation to suggest and analyze a new resolvent-type method for solving mixed variational inequalities. Our results can be viewed as significant extensions of the previously known results for mixed variational inequalities. An example is given to illustrate the efficiency and implementation of the proposed method.
Keywords
Mixed variational inequalities
Self-adaptive rules
Pseudomonotone
Resolvent operator
1 Introduction
Variational inequalities introduced in the early sixties have played a fundamental and significant part in the study of several unrelated problems arising in finance, economics, network analysis, transportation, elasticity and optimization (see Baiocchi and Capelo, 1984; Bnouhachem, 2005; Bnouhachem et al., 2006; Brezis, 1973; Fukushima, 1992; Fu, 2008; Giannessi et al., 2001; Glowinski et al., 1981; Han and Lo, 2002; He and Liao, 2002; He et al., 2004; Kinderlehrer and Stampacchia, 2000; Lions and Stampacchia, 1967; Noor, 1997, 1998, 2000, 2002, 2003a,b, 2004a,b; Noor and Bnouhachem, 2005; Peng and Fukushima, 1999; Solodov and Svaiter, 2000; Stampacchia, 1964; Yang and Bell, 1997) and the references therein. In recent years variational inequalities have been extended in various directions using novel and innovative techniques. A useful and important generation of variational inequalities is the mixed variational inequality containing a nonlinear term. Due to the presence of the nonlinear bifunction, the projection method and its variant forms including the Wiener–Hopf equations technique can not be extended to suggest iterative methods for solving mixed variational inequalities. To overcome these drawbacks, some iterative methods have been suggested for a special cases of the mixed variational inequalities. For example, if the nonlinear term is a proper, convex and lower-semicontinuous function, then one can show that the mixed variational inequalities are equivalent to the fixed point and the resolvent equations. This alternative formulation has played a significant part in the developing various resolvent-type methods for solving mixed variational inequalities. This equivalent formulation has been used to suggest and analyze some iterative methods, the convergence of these methods requires that the operator is both strongly monotone and Lipschitz continuous. Secondly, it is very difficult to evaluate the resolvent of the operator except for very simple cases. Noor (2004b) has used the technique of updating the solution to suggest and analyze some three-step iterative methods for solving some classes of variational inequalities and related optimization problems. It has been shown that three-step iterative methods (Bnouhachem et al., 2006; Fu, 2008) are more efficient than two-step and one-step iterative methods. Inspired and motivated by the research going in this direction. We suggest and analyze a new self-adaptive method for solving mixed variational inequalities by using the resolvent operator and a new step size. We prove the convergence of the proposed method under certain conditions. In numerical experiment, we take a special case of the proposed method and an example is given to illustrate the efficiency of the proposed method.
2 Preliminaries
Let H be a real Hilbert finite-dimensional space, whose inner product and norm are denoted by
and
. Let
be nonlinear operators. Let
denote the subdifferential of a proper, convex and lower-semicontinuous function
. It is well known that the subdifferential
is a maximal monotone operator. We consider the problem of finding
such that
If K is a closed and convex set in H and
is the indicator function of K defined by
then the problem (2.1) is equivalent to finding
such that
(Brezis, 1973) For any maximal operator T, the resolvent operator associated with T, for any
, is defined as
[Brezis, 1973] For a given
and
, the inequality
holds if and only if
, where
is the resolvent operator. It follows from Lemma 2.1 that
If
is the indicator function of a closed convex set
in H, then the resolvent operator
reduces to the projection operator
(see Noor, 1997). It is well known that
is nonexpansive i.e.,
[Noor, 1998]
is solution of the mixed variational inequality (2.1) if and only if
satisfies the relation:
-
T is continuous and pseudomonotone operator on H, that is
-
The solution set of problem (2.1), denoted by , is nonempty.
3 Basic results
In this section, we prove some basic properties, which will be used to establish the sufficient and necessary conditions for the convergence of the proposed method. The following lemmas summarize some basic inequalities with respect to the resolvent operator. We refer to (see, for example, Bnouhachem, 2005) for the complete proof.
Lemma 3.1 Bnouhachem (2005)
For all
and
, it holds that
[Bnouhachem (2005)]If u is not a solution of problem (2.1), then there exist
and
, such that for all
,
and
we have
For any
solution of problem (2.1), we have
From Lemmas 3.2 and 3.3 we have
For a given , find the approximate solution by the following iterative schemes involving the two-steps.
Step 1.
Step 2. The new iterate
is defined by
where
(3.10) implies that
For the convergence analysis of the proposed method, we need the following results.
For given
and
, let
and
satisfy (3.9) and (3.12), then
It follows from (3.13) and (3.16) that Otherwise from (3.10), we have Using Cauchy–Schwartz inequality, we get From the above inequality, we obtain which implies that we obtain the required result.
4 Convergence analysis
In this section, we begin to investigate convergence of the proposed method.
Let be a solution of problem (2.1) and let be the sequence obtained from Algorithm 3.1. Then is bounded and
Let
be a solution of problem (2.1). Then, from (3.11), we have
The following result can be proved by similar arguments as in Bnouhachem et al. (2006). Hence the proof is omitted.
The sequence generated by the proposed method converges to a solution point of problem (2.1).
We now describe the new algorithm as follows.
Step 0. Let and .
Step 1. If , then stop. Otherwise, go to Step 2.
Step 2.
, ,
.
While
, ,
, .
end While
Step 3. Set
,
,
,
,
Step 4.
Step 5. k := k + 1; go to Step 1.
5 Computational results
In this section, we apply the new method to a traffic equilibrium problem, which is a classical and important problem in transportation science (see, for example, He et al., 2004; Yang and Bell, 1997). The numerical results show that the new method is attractive in practice.
Consider a network of nodes N and directed links L, which consists of a finite sequence of connecting links with a certain orientation. Let , etc., denote the links; , etc., denote the paths; denote an origin/destination (O/D) pair of nodes of the network; denotes the set of all paths connecting O/D pair ; represent the traffic flow on path p; denote the traffic demand between O/D pair , which must satisfy where ; and denote the link load on link a, which must satisfy the following conservation of flow equation where
Let A be the path-arc incidence matrix of the given problem and be the vector of the link load. Since u is the path-flow, f is given by
In addition, let
be the row vector of link costs, with
denoting the user cost of traveling link a which is given by
Note that the travel cost on the path p denoted by is
Let P denote the set of all the paths concerned. Let be the vector of (path) travel cost. For given link travel cost vector t, is a mapping of the path-flow u, which is given by
Associated with every O/D pair
, there is a travel disutility
, which is defined as following:
Note that both the path costs and the travel disutilities are functions of the flow pattern u. The traffic network equilibrium problem is to seek the path-flow pattern , which induces a demand pattern , for every O/D pair and each path ,
The problem can be reduced to a variational inequality in the space of path-flow pattern
such that
For the comparison sake, we consider the same example studied in He et al. (2004) and Yang and Bell (1997). The network is depicted in Fig. 1. The free-flow travel cost and the designed capacity of links (5.1) are given in Table 1, the O/D pairs and the coefficient m and q in the disutility function (5.2) are given in Table 2. For this example, there are together 12 paths for the 4 given O/D pairs listed in Table 4.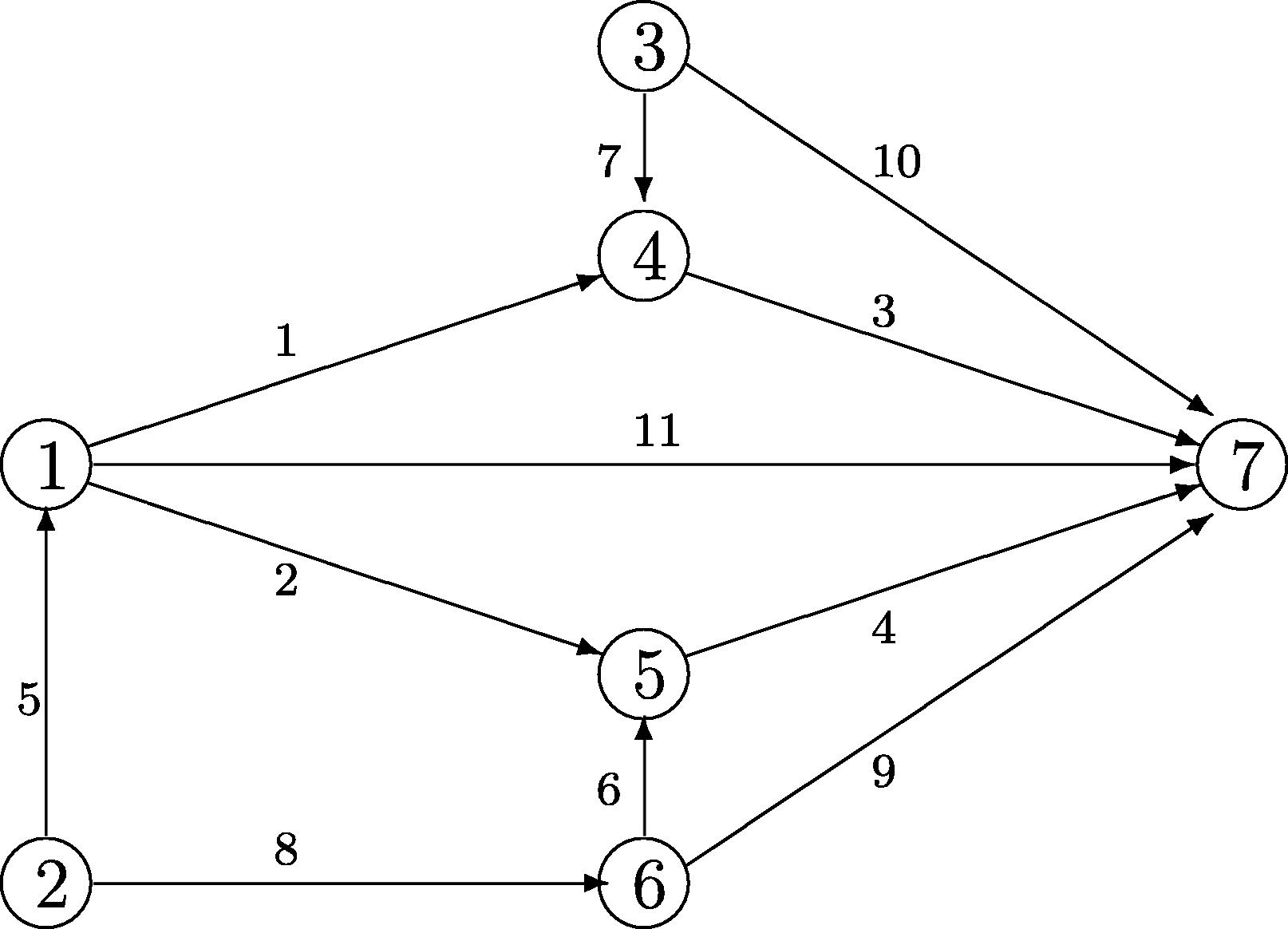
The network used for the numerical test.
Link
Free-flow travel time
Capacity
Link
Free-flow travel time
Capacity
1
6
200
7
5
150
2
5
200
8
10
150
3
6
200
9
11
200
4
16
200
10
11
200
5
6
100
11
15
200
6
1
100
–
–
–
No. of the pair
O/D pair
1
(1, 7)
25
25log 600
2
(2, 7)
33
33log 500
3
(3, 7)
20
20log 500
4
(6, 7)
20
20log 400
In all tests we take
and
. All iterations start with
and
, and stopped whenever
. All codes are written in Matlab and run on a P4-2.00G note book computer. The test results of Algorithm 4.1 and the method in Bnouhachem et al. (2006) for different
are reported in Table 3. k is the number of iterations and l denotes the number of evaluations of mapping T. For the case
, the optimal path-flow and link flow are given in Tables 4 and 5, respectively. The numerical experiments show that the new method is more flexible and efficient to solve the traffic equilibrium problem.
Different ε
Algorithm 4.1
The method in Bnouhachem et al. (2006)
k
l
CPU (Sec.)
k
l
CPU (Sec.)
31
71
0.031
85
185
0.04
35
79
0.047
103
221
0.06
42
96
0.51
120
255
0.07
48
109
0.6
138
291
0.08
54
122
0.72
155
325
0.09
O/D pair
Path No.
Link of path
Optimal path-flow
O/D pair (1, 7)
1
(1, 3)
165.3145
2
(2, 4)
0
3
(11)
138.5735
4
(5, 1, 3)
82.5281
5
(5, 2, 4)
0
O/D pair (2, 7)
6
(5, 11)
55.7871
7
(8, 6, 4)
0
8
(8, 9)
87.0260
O/D pair (3, 7)
9
(7, 3)
19.7549
10
(10)
229.9747
O/D pair (6, 7)
11
(9)
178.5600
12
(6, 4)
0
Link No.
Link flow
Link No.
Link flow
Link No.
Link flow
Link No.
Link flow
1
247.8426
4
0
7
19.7549
10
229.9747
2
0
5
138.3152
8
87.0260
11
194.3606
3
267.5974
6
0
9
265.5860
–
–
Acknowledgements
This research was supported partly by NSFC Grants Nos. 70731002 and 70571034, “The Second Term ‘985’ Engineering-Innovation Center for Computational Laboratory of Evolutionary Economic Theory and its Applications” and “Study on the Evolution of Complex Economic System” at “Innovation Center of Economic Transition and Development of Nanjing University” of Ministry of Education, China.
References
- Variational and Quasi Variational Inequalities. New York: J. Wiley and Sons; 1984.
- A self-adaptive method for solving general mixed variational inequalities. J. Math. Anal. Appl.. 2005;309:136-150.
- [Google Scholar]
- Three-steps iterative algorithms for mixed variational inequalities. Appl. Math. Comput.. 2006;183:436-446.
- [Google Scholar]
- Operateurs Maximaux Monotone et Semigroupes de Contractions dans les Espace d’Hilbert. Amsterdam, Holland: North-Holland; 1973.
- A two-stage prediction–correction method for solving variational inequalities. J. Comput. Appl. Math.. 2008;214:345-355.
- [Google Scholar]
- Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems. Math. Program.. 1992;53:99-110.
- [Google Scholar]
- Equilibrium Problems: Nonsmooth Optimization and Variational Inequality Models. Dordrecht, Holland: Kluwer, Academic Press; 2001.
- Numerical Analysis of Variational Inequalities. Amsterdam, Holland: North-Holland; 1981.
- Two new self-adaptive projection methods for variational inequality problems. Comput. Math. Appl.. 2002;43:1529-1537.
- [Google Scholar]
- Improvement of some projection methods for monotone variational inequalities. J. Optim. Theory Appl.. 2002;112:111-128.
- [Google Scholar]
- An approximate proximal-extragradient type method for monotone variational inequalities. J. Math. Anal. Appl.. 2004;300(2):362-374.
- [Google Scholar]
- An Introduction to Variational Inequalities and their Applications. Philadelphia: SIAM; 2000.
- A new iterative method for monotone mixed variational inequalities. Math. Comput. Model.. 1997;26(7):29-34.
- [Google Scholar]
- An implicit method for mixed variational inequalities. Appl. Math. Lett.. 1998;11:109-113.
- [Google Scholar]
- A class of new iterative methods for general mixed variational inequalities. Math. Comput. Model.. 2000;31:11-19.
- [Google Scholar]
- Proximal methods for mixed quasi variational inequalities. J. Optim. Theory Appl.. 2002;115:447-451.
- [Google Scholar]
- Pseudomonotone general mixed variational inequalities. Appl. Math. Comput.. 2003;141:529-540.
- [Google Scholar]
- Fundamentals of mixed quasi variational inequalities. Int. J. Pure Appl. Math.. 2004;15:137-258.
- [Google Scholar]
- Some developments in general variational inequalities. Appl. Math. Comput.. 2004;152:199-277.
- [Google Scholar]
- Self-adaptive methods for mixed quasi variational inequalities. J. Math. Anal. Appl.. 2005;312:514-526.
- [Google Scholar]
- A hybrid Newton method for solving the variational inequality problem via the D-gap function. Math. Program.. 1999;86:367-386.
- [Google Scholar]
- Error bounds for proximal point subproblems and associated inexact proximal point algorithms. Math. Program. Ser. B. 2000;88:371-389.
- [Google Scholar]
- Formes bilineaires coercivites sur les ensembles convexes. C. R. Acad. Sci. Paris. 1964;258:4413-4416.
- [Google Scholar]
- Traffic restraint, road pricing and network equilibrium. Transp. Res. B. 1997;31:303-314.
- [Google Scholar]







