Translate this page into:
Differential transform method for solving singularly perturbed Volterra integral equations
⁎Corresponding author. ahmet.yildirim@ege.edu.tr (Ahmet Yıldırım)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 15 July 2010
Peer-review under responsibility of King Saud University.
Abstract
In this work, the applications of differential transform method were extended to singularly perturbed Volterra integral equations. To show the efficiency of the method, some singularly perturbed Volterra integral equations are solved as numerical examples. Numerical results show that the differential transform method is very effective and convenient for solving a large number of singularly perturbed problems with high accuracy.
Keywords
Differential transform method
Singularly perturbed problems
Volterra integral equations
1 Introduction
In this paper we consider the singularly perturbed Volterra integral equations (Alnasr et al., 1997, 2000; Lange and Smith, 1988; Angell and Olmstead, 1987)
The aim of our study is to employ the differential transform method (in short, DTM) Pukhov et al., 1980; Zhou et al., 1986 as an alternative to existing methods in solving the singularly perturbed Volterra integral problems and the method is implemented to four numerical examples. The concept of differential transform method was first introduced by Pukhov et al. (1980) and Zhou et al. (1986), who solved linear and nonlinear initial value problems in electric circuit analysis. It is a semi-numerical and semi-analytic technique that formulizes Taylor series in a totally different manner. With this technique, the given differential equation and its related boundary conditions are transformed into a recurrence equation that finally leads to the solution of a system of algebraic equations as coefficients of a power series solution. This method is useful to obtain the exact and approximate solutions of linear and nonlinear differential equations. No need to linearization or discretization, large computational work and round-off errors are avoided. It has been used to solve effectively, easily and accurately a large class of linear and nonlinear problems with approximations. The method is well addressed in Ertürk and Momani (2007), Arıkoğlu and Özkol (2005), Ayaz (2004), Liu and Song (2007), Hassan (2008), Bildik et al. (2006) and Ertürk and Momani (2007).
The paper has been organized as follows. In Section 2, a brief description of the method is presented, while, in Section 3, four numerical examples are solved to demonstrate the applicability of the present method. The discussion on our results is given in Section 4.
2 Differential transform method
Let f (r) be analytic in a domain R and let r = r0 represent any point in R. Then, the function f (r) is represented by a power series whose center is located at r0. The differential transform of the kth derivative of the function f (r) in one variable is defined as follows:
Combining Eqs. (2.1) and (2.2), one may write:
Eq. (2.3) implies that the concept of differential transform method is derived from Taylor series expansion. However, the method does not evaluate the derivatives symbolically. An iterative procedure which is described by the transformed equations of the original functions can be used to calculate the related derivatives. In this study, we use the lower case letter to represent the original function and upper case letter to stand for the transformed function.
In actual applications, the function f (r) is expressed by a finite series and Eq. (2.2) can be written as
Original function
Transformed function
3 Applications and numerical results
In order to illustrate the advantages and the accuracy of differential transform method for solving singularly perturbed Volterra integral equations, we have applied the method to four problems.
We consider the following linear singularly perturbed Volterra integral equation discussed in Alnasr (2000) and Alnasr and Momani (2008):
The exact solution of this problem is known as
According to the operations of differential transformation given in Table 1, we have the following recurrence relation:
Utilizing the recurrence relation in Eq. (3.3), we find
and so on, in this manner
for
can be easily obtained. Therefore, from (2.2), the first few terms of the series solution is as follows:
As the number of terms involved increases, one can observe that the series solution obtained using differential transform method converges to series expansion of the exact solution (3.2). Note that terms are considered in Eq. (3.4) for the numerical results. Comparison of the numerical results with the exact solution (3.2) for and is shown in Table 2.
Consider the following singularly perturbed Volterra integral equation discussed in Alnasr (2000), Alnasr and Momani (2008) and Ibrahim and Alnasr (1998):
The exact solution of this problem is known as
If we apply differential transform to the Eq. (3.5), by using Table 1, we can obtain the following transformed equation:
Consequently, we find
and so on, in this manner
for
can be easily obtained.Therefore, from (2.2), the first few terms of the series solution are as follows:
As the number of terms involved increases, one can observe that the series solution obtained using differential transform method converges to series expansion of the exact solution (3.6). Note that 11 terms are considered in Eq. (3.9) for the numerical results. Comparison of the numerical results with the exact solution (3.6) for and are shown in Table 3.
We consider the following nonlinear singularly perturbed Volterra Integral Equation discussed in Alnasr (2000) and Alnasr and Momani (2008):
One can see that the differential transform of Eq. (3.10) can be evaluated by using Table 1 as follows:
Consequently, we find
and so on, in this manner
for
can be easily obtained. Therefore, from (2.2), the solution of the integral equation (3.10) is given as
The evolution results for the exact solution (3.11) and the approximate solution obtained using differential transform method, for different values of , are shown in Figs. 1–3. Note that 11 terms are considered in Eq. (3.13) for the numerical results.
We consider the following singularly perturbed Volterra integral equation (Kauthen, 1997):
According to the operations of differential transformation given in Table 1, the following recurrence relation is obtained:
Utilizing the recurrence relation in Eq. (3.16), we find
and so on, in this manner
for
can be easily obtained.Therefore, from (2.2), the first few terms of the series solution are as follows:
The evolution results for the exact solution (3.15) and the approximate solution obtained using differential transform method, for and , are shown in Figs. 4 and 5. Note that 90 terms are considered in Eq. (3.17) for the numerical results.
| 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.1 | 0.1 | 0.1 | 0.131207 | 0.131207 | 0.190635 | 0.190635 | 0.347260 | 0.347260 |
| 0.2 | 0.2 | 0.2 | 0.258518 | 0.258518 | 0.364840 | 0.364840 | 0.613003 | 0.613003 |
| 0.3 | 0.3 | 0.3 | 0.382420 | 0.382420 | 0.525594 | 0.525594 | 0.824104 | 0.824104 |
| 0.4 | 0.4 | 0.4 | 0.503338 | 0.503338 | 0.675336 | 0.675336 | 0.998578 | 0.998578 |
| 0.5 | 0.5 | 0.5 | 0.621646 | 0.621646 | 0.816060 | 0.816060 | 1.148500 | 1.148500 |
| 0.6 | 0.6 | 0.6 | 0.737668 | 0.737668 | 0.949403 | 0.949403 | 1.281960 | 1.281960 |
| 0.7 | 0.7 | 0.7 | 0.851690 | 0.851690 | 1.076700 | 1.076700 | 1.404390 | 1.404390 |
| 0.8 | 0.8 | 0.8 | 0.963962 | 0.963962 | 1.199050 | 1.199050 | 1.519430 | 1.519430 |
| 0.9 | 0.9 | 0.9 | 1.074700 | 1.074700 | 1.317350 | 1.317350 | 1.629510 | 1.629510 |
| 1.0 | 1.0 | 1.0 | 1.184100 | 1.184100 | 1.432330 | 1.432330 | 1.736260 | 1.736260 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.1 | 0.104833 | 0.104833 | 0.137510 | 0.137510 | 0.199683 | 0.199683 |
| 0.2 | 0.218669 | 0.218669 | 0.282340 | 0.282340 | 0.397589 | 0.397589 |
| 0.3 | 0.340519 | 0.340519 | 0.433015 | 0.433015 | 0.592269 | 0.592269 |
| 0.4 | 0.469413 | 0.469413 | 0.588175 | 0.588175 | 0.782594 | 0.782594 |
| 0.5 | 0.604405 | 0.604405 | 0.746572 | 0.746572 | 0.967719 | 0.967719 |
| 0.6 | 0.744584 | 0.744584 | 0.907074 | 0.907074 | 1.147046 | 1.147046 |
| 0.7 | 0.889072 | 0.889072 | 1.068664 | 1.068664 | 1.320191 | 1.320191 |
| 0.8 | 1.037037 | 1.037037 | 1.230437 | 1.230437 | 1.486949 | 1.486949 |
| 0.9 | 1.187692 | 1.187692 | 1.391602 | 1.391602 | 1.647272 | 1.647272 |
| 1.0 | 1.340300 | 1.340300 | 1.551470 | 1.551470 | 1.801234 | 1.801234 |
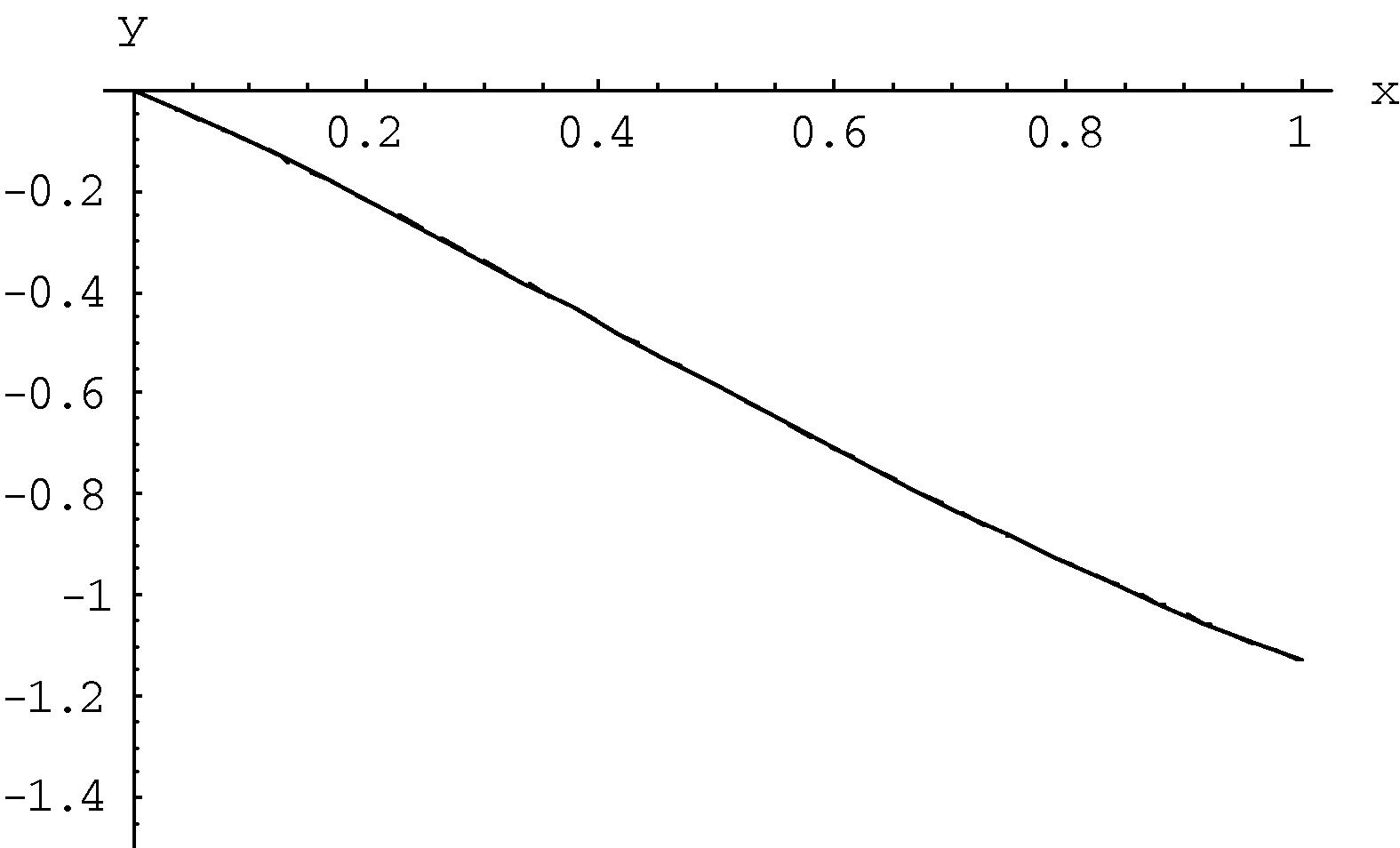
- Plots of Eq. (3.10) when
. Exact solution (___); the approximate solution (---).
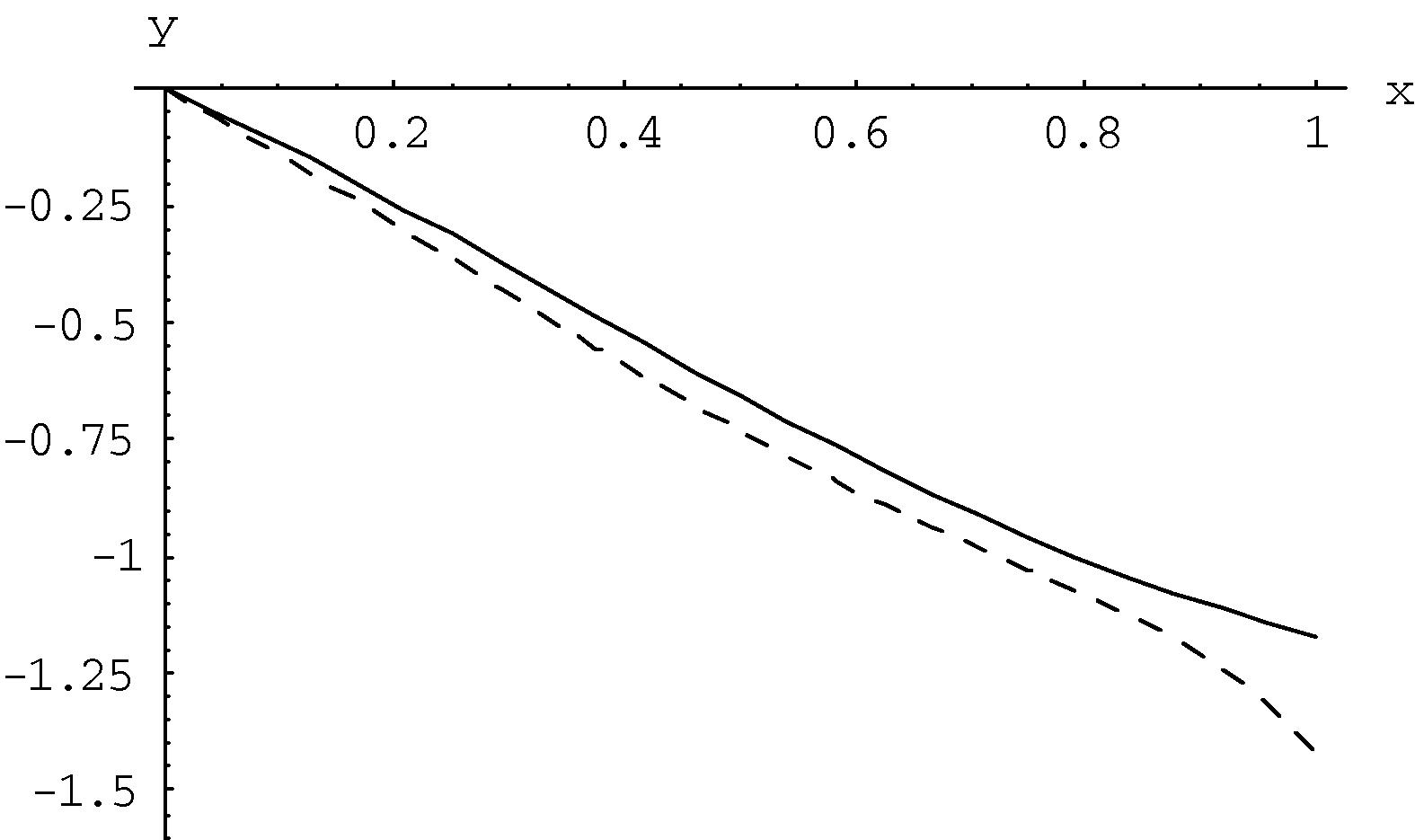
- Plots of Eq. (3.10) when
. Exact solution (___); the approximate solution (---).
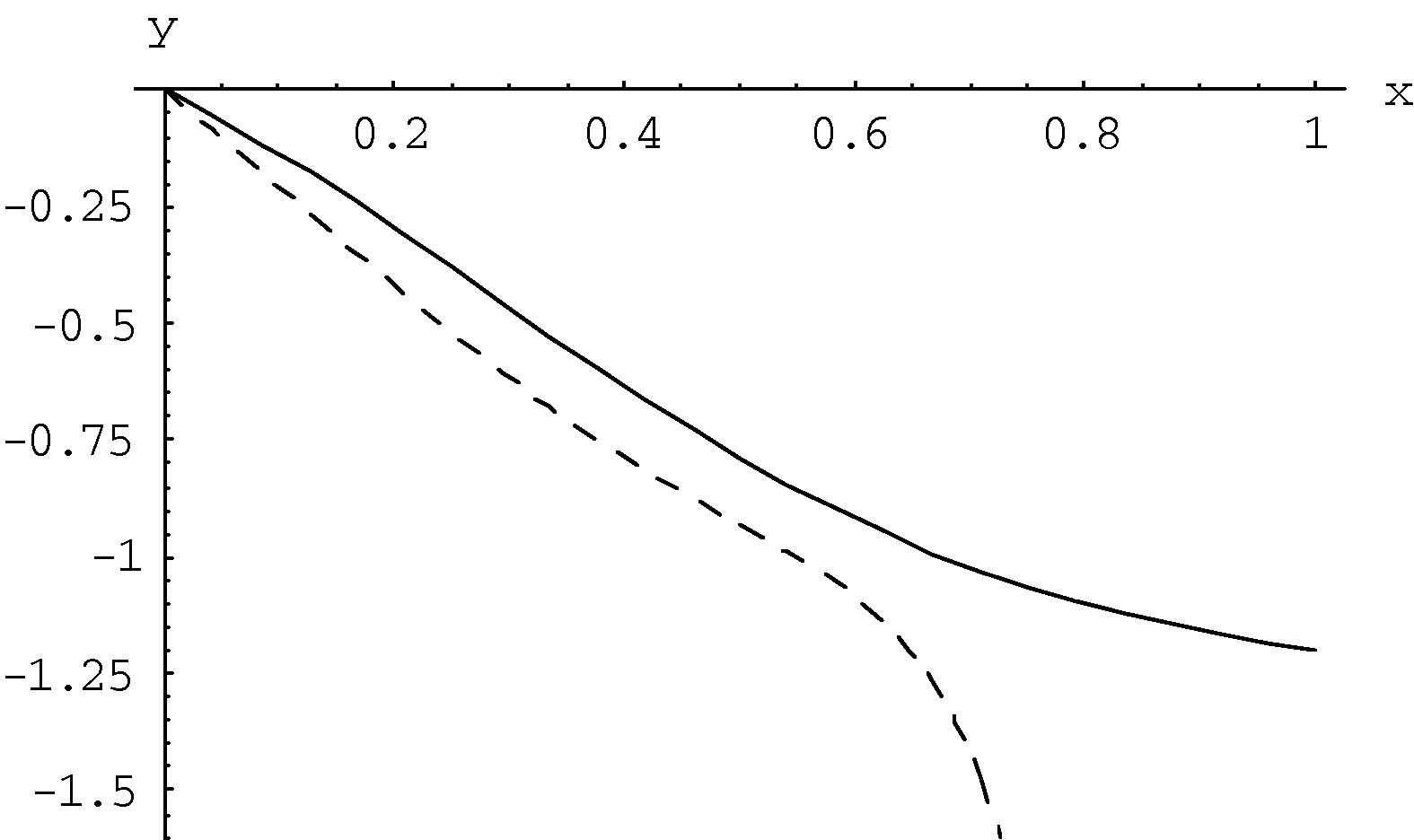
- Plots of Eq. (3.10) when
. Exact solution (___); the approximate solution (---).
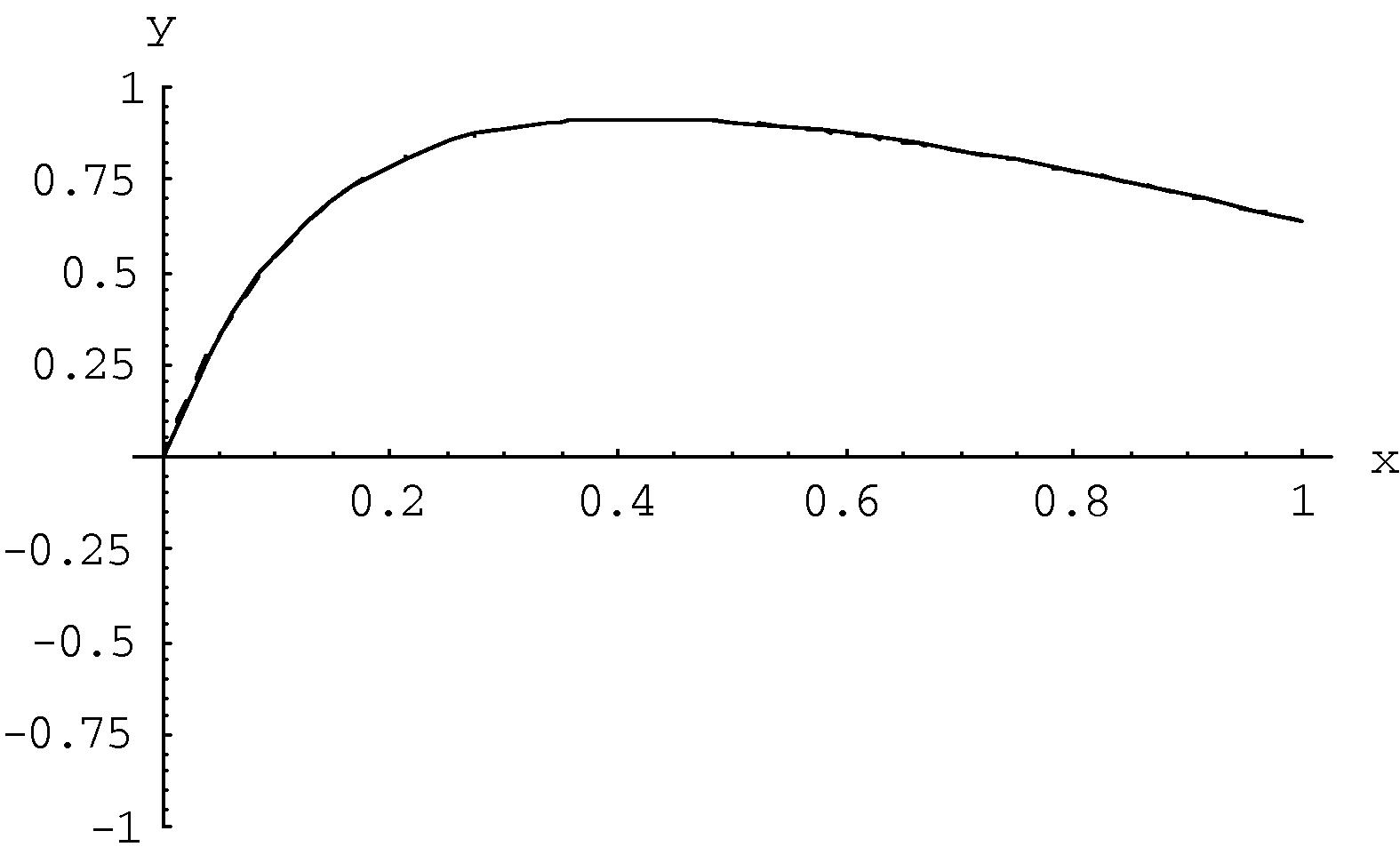
- Plots of Eq. (3.14) when
. Exact solution (___); the approximate solution (---).
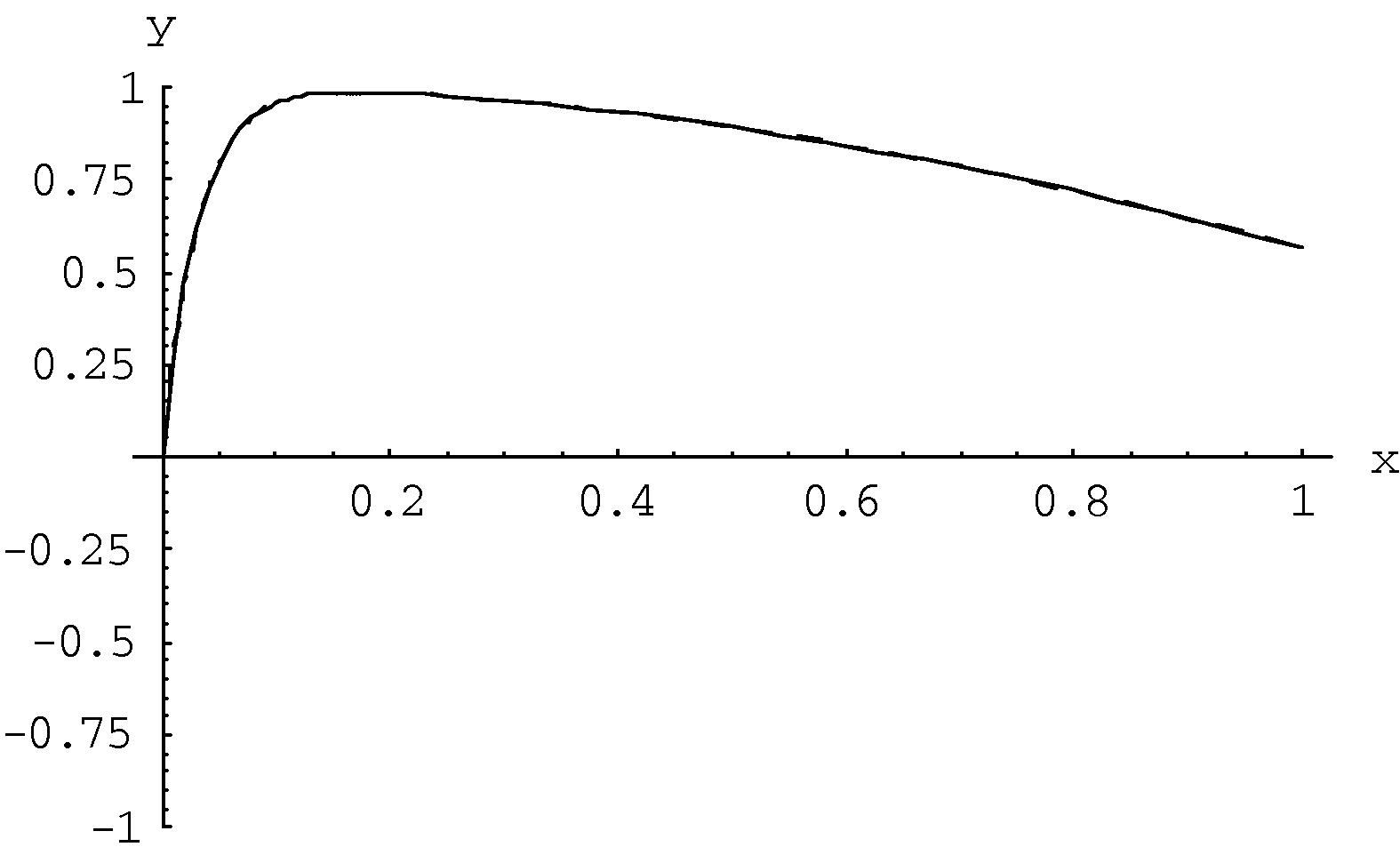
- Plots of Eq. (3.14) when
. Exact solution (___); the approximate solution (---).
4 Conclusion
In this study, Differential transform method is successfully applied to singularly perturbed Volterra integral equations. A symbolic calculation software package, MATHEMATICA is used for all calculations. All the computations show that the approximate solutions are perfectly identical to the exact solutions. Also, the work emphasized our belief that the method is a reliable technique to handle these types of problems. It provides the solutions in terms of convergent series with easily computable components in a direct way without using linearization, discretization or restrictive assumptions.
References
- Modified Multilag methods for singularly perturbed Volterra integral equations. Int. J. Comput. Math.. 2000;75(1):221-233.
- [Google Scholar]
- Application of Homotopy perturbation method to singularly perturbed Volterra integral equations. J. Appl. Sci.. 2008;8(6):1073-1078.
- [Google Scholar]
- Alnasr, M.H., 1997, Numerical Treatment of Singularly Perturbed Volterra Integral Equations. Ph.D. Thesis. Egypt.
- Singularly perturbed Volterra integral equations. Siam J. Appl. Math.. 1987;47(1):1-14.
- [Google Scholar]
- Solution of boundary value problems for integro-differential equations by using differential transform method. Appl. Math. Comput.. 2005;168:1145-1158.
- [Google Scholar]
- Solutions of the system of differential equations by differential transform method. Appl. Math. Comput.. 2004;147:547-567.
- [Google Scholar]
- Solution of different type of the partial differential equation by differential transform method and Adomian’s decomposition method. Appl. Math. Comput.. 2006;172:551-567.
- [Google Scholar]
- The Numerical Solution of Volterra Equations. Amsterdam: CWI; 1986.
- A reliable algorithm for solving tenth-order boundary value problems. Numer. Algorithms. 2007;44(2):147-158.
- [Google Scholar]
- Comparing numerical methods for solving fourth-order boundary value problems. Appl. Math. Comput.. 2007;188:1963-1968.
- [Google Scholar]
- Comparison differential transformation technique with Adomian decomposition method for linear and nonlinear initial value problems. Chaos Solitons Fractals. 2008;36(1):53-65.
- [Google Scholar]
- Quadrature methods with regularization technique for singularly perturbed Volterra integral equations. Int. J. Comput. Math.. 1998;68:285-299.
- [Google Scholar]
- A survey of singularly perturbed Volterra equations. Appl. Numer. Math.. 1997;24:95-114.
- [Google Scholar]
- Singular perturbation analysis of integral equations. Stud. Appl. Math.. 1988;79(11):1-63.
- [Google Scholar]
- Differential transform method applied to high index differential–algebraic equations. Appl. Math. Comput.. 2007;184:748-753.
- [Google Scholar]
- Pukhov, G.E., 1980. Differential Transforms of Functions and Equations. Naukova Dumka (in Russian), Kiev.
- Zhou, J., 1986. Differential Transformation and Its Application for Electrical Circuits. Huazhong University Press (in Chinese).







