Translate this page into:
A note on fuzzy best approximation using Chebyshev’s polynomials
⁎Corresponding author. omidsfard@gmail.com (Omid Solaymani Fard)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 15 July 2010
Peer-review under responsibility of King Saud University.
Abstract
This paper deals with the best approximation for fuzzy valued functions using Chebyshev nodes. We prove a result on the best near-minimax approximation in the fuzzy sense. As an application, Runge’s phenomenon is fuzzified in two different cases, i.e. the best approximation and the best near-minimax approximation.
Keywords
Runge’s Phenomenon
Fuzzy Approximation
Fuzzy Linear Programming
Fuzzy numbers
Fuzzy polynomials
1 Introduction
The problem of best polynomial approximation is a historical problem in applied mathematics. Since the best polynomial approximation problems appear in many different branches, it is important to study this problem from various view points. In this paper, the fuzzy best Chebyshev approximation is discussed. Combining the results in Powell (1981, Chapter 7) and the work of Abbasbany et al. (2007), we intend to introduce the best Chebyshev approximation (best near-minimax approximation) for fuzzy-valued functions. To do this, we use Chebyshev’s nodes and naturally fuzzy Chebyshev’s polynomials to introduce and compute fuzzy best near-minimax approximation.
The structure of the present paper is as follows. In Section 2, the basic concepts of our work are introduced. Section 3 contains a brief description of Chebychev’s nodes, polynomials and approximation. In Section 4, we introduce the fuzzy best near-minimax approximation and a method for obtaining it. In Section 5, For a case study, the fuzzified Runge phenomenon is studied in details. Finally, we have come to conclusion in Section 6.
2 Preliminaries
Here, we recall the basic notations and concepts for fuzzy triangular numbers, fuzzy-valued functions and fuzzy-valued polynomials.
Definition 2.1 Dubois and Prade, 1980, 2000
A fuzzy number is a map , which satisfies:
-
u is upper semi-continuous.
-
outside some interval .
-
There exist real numbers such that , where:
-
–
is monotonic increasing on ,
-
–
is monotonic decreasing on ,
-
–
.
-
Let be the set of all fuzzy numbers, and be the set of all triangular fuzzy numbers with membership function and denote by , where , , and are non-negative real numbers as the left, right spread, and center of the fuzzy number, respectively (Dubois and Prade, 1980).
Also, -cut of a fuzzy number is defined by Dubois and Prade (1980) and Abbasbany et al. (2007)
Definition 2.2 Dubois and Prade, 1980
For and , belonging to , we define a distance by
D is a meter. for more details see Abbasbany et al. (2007).
The norm of a triangular fuzzy number , is
Let . Some results of applying fuzzy arithmetic on fuzzy numbers and are as follows:
-
–
,
-
–
,
-
–
,
-
–
.
A fuzzy number is nonnegative if and only if , and this fuzzy number is non-positive, if and only if .
Denote by , the set of all real-valued polynomials of degree at most N, and by , the set of all nonnegative real-valued piecewise polynomials of degree at most N.
In this study, we employ a class of fuzzy valued polynomials on , and we approximate a fuzzy function , by such fuzzy valued polynomials (Abbasbany et al., 2007; Kaleva (1994)).
For each , the lower and upper spreads of a fuzzy function , on its -cut, are and , respectively, such that, for all
A triangular fuzzy valued polynomial of degree at most N, is a function , which where , also and are positive piecewise polynomials from degree at most N.
The set of all fuzzy valued polynomials is denoted by (Abbasbany et al., 2007; Kaleva (1994)).
3 Chebyshev approximation
We now turn our attention to polynomial interpolation for over based on the nodes . Let be the Lagrange interpolation polynomial of (Mathew and Fink, 2004). Therefore, we have Here, the error function is , where . It is well-known that Chebyshev studied how to minimize the upper bound for . One upper bound can be formed by taking the product of the maximum value of on and the maximum value on . To minimize the statement , Chebyshev discovered that should be chosen so that , where is the polynomial which is generated by Chebyshev’s nodes. Moreover, we have the following well-known theorems and corollary (Philips and Taylor (1980); Powell (1981)).
Assume that N is fixed. Among all possible choices for , and thus among all possible choices for the distinct nodes , where , the polynomial is the unique choice which has the following property
If f is continuous on , there is a unique minimax polynomial approximation of degree at most N for f on .
If f is continuous on , then the minimax approximation to f is an interpolating polynomial on the Chebyshev nodes of .
4 The best near-minimax approximation of fuzzy-valued functions
In this section, we follow Abbasbany et al. (2007) and introduce the best minimax approximation of a fuzzy-valued function on a finite set of distinct points.
Let be a set of distinct points of , and be the value of a fuzzy function at the point , for .
Definition 4.1 Abbasbany et al., 2007
A fuzzy-valued polynomial is the best approximation to on if The problem is referred to the best near-minimax approximation (best Chebyshev approximation), as we use Chebyshev’s nodes.
Suppose that
is a fuzzy number, where
, and
, that is
Taking
Therefore, we get three independent linear programming problems to be solved:
In general, we can use the following definition for the best approximation to
out of
on
, at point x,
Solving 3, 2 and 4, we have three independent polynomials and of degree at most N. But, applying 5, right and left spreads of fuzzy valued polynomial may be piecewise polynomials of degree at most N.
Now, we are ready to state the following theorems which may play dominant roles in the best approximation on Chebyshev’s nodes.
The best approximation of a fuzzy function based on the Chebyshev nodes exists and is unique.
The proof is an immediate consequence of Theorem 4.2.1, p. 99 of Abbasbany et al. (2007).
if and only if the best approximation of a fuzzy-valued function based on the Chebyshev nodes is the best minimax approximation.
Necessity. implies that . Therefore, from (1) we have for , where are the Chebyshev nodes. Hence is the fuzzy interpolating polynomial to on . The rest of the proof follows from Theorem 3.2 and Corollary 3.3, directly.Sufficiency. Suppose that the best approximation of a fuzzy-valued function based on the Chebyshev nodes is the best minimax approximation. Consequently, is immediately derived from the uniqueness of minimax approximation.
5 Runge’s phenomenon
In the field of numerical analysis, Runge’s phenomenon occurs when the polynomials with high degree are applied to approximate the Runge function (Runge, 1901). It was discovered by Runge (1901) when he studied the behavior of errors in the approximation of a certain functions by polynomials. Consider the function (Runng’s function)
The oscillation can be minimized by using Chebyshev nodes instead of the equidistant nodes. In this case, the maximum error is guaranteed to diminish with increasing the degree of polynomial.
In the following, we study this phenomenon numerically when the function
is a fuzzy-valued function. Consider the fuzzy-valued function
Now, the best approximation of function is computed in two different cases for .
-
Case 1.
-
Case 2.
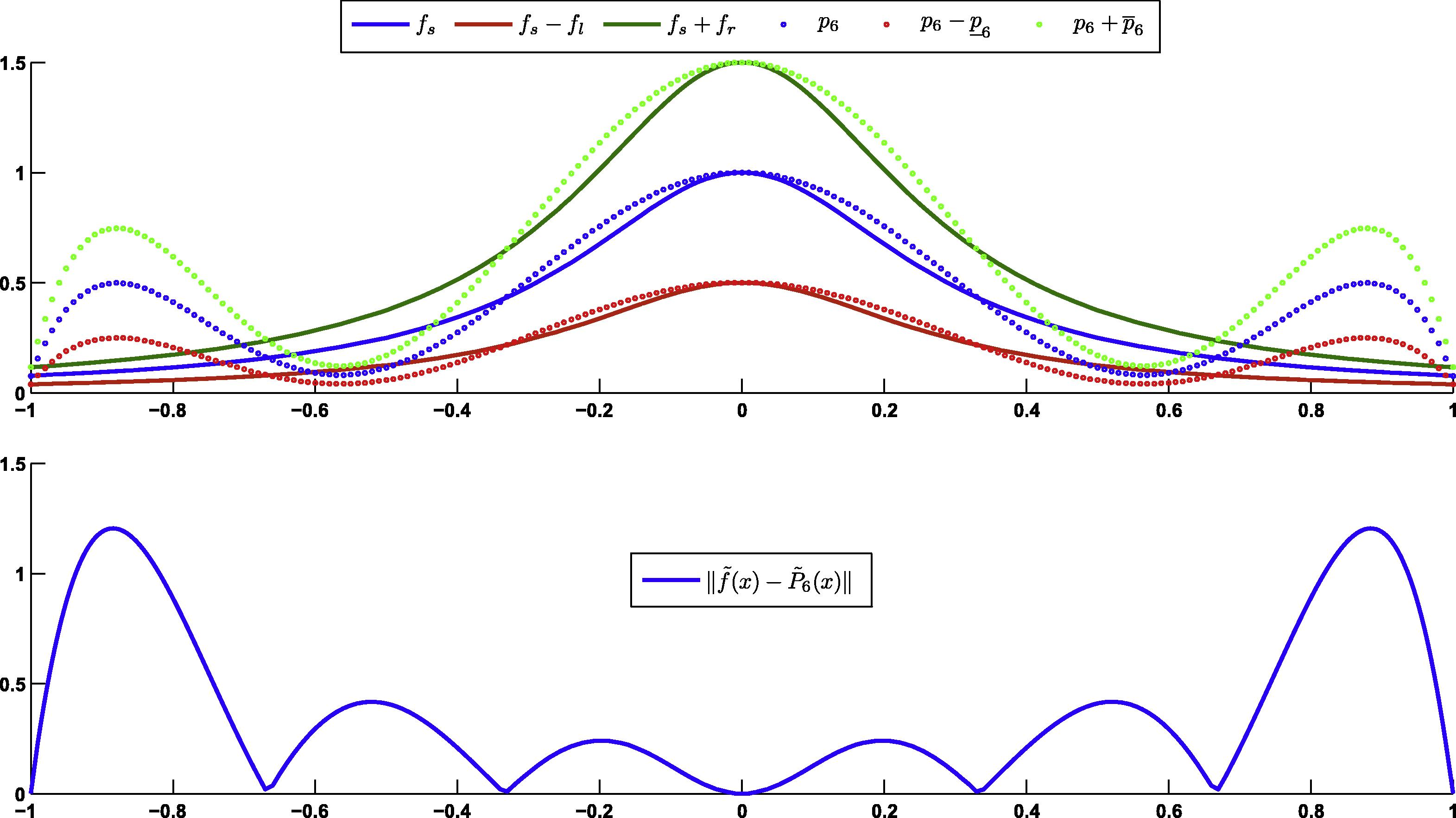
- Results for Case 1.
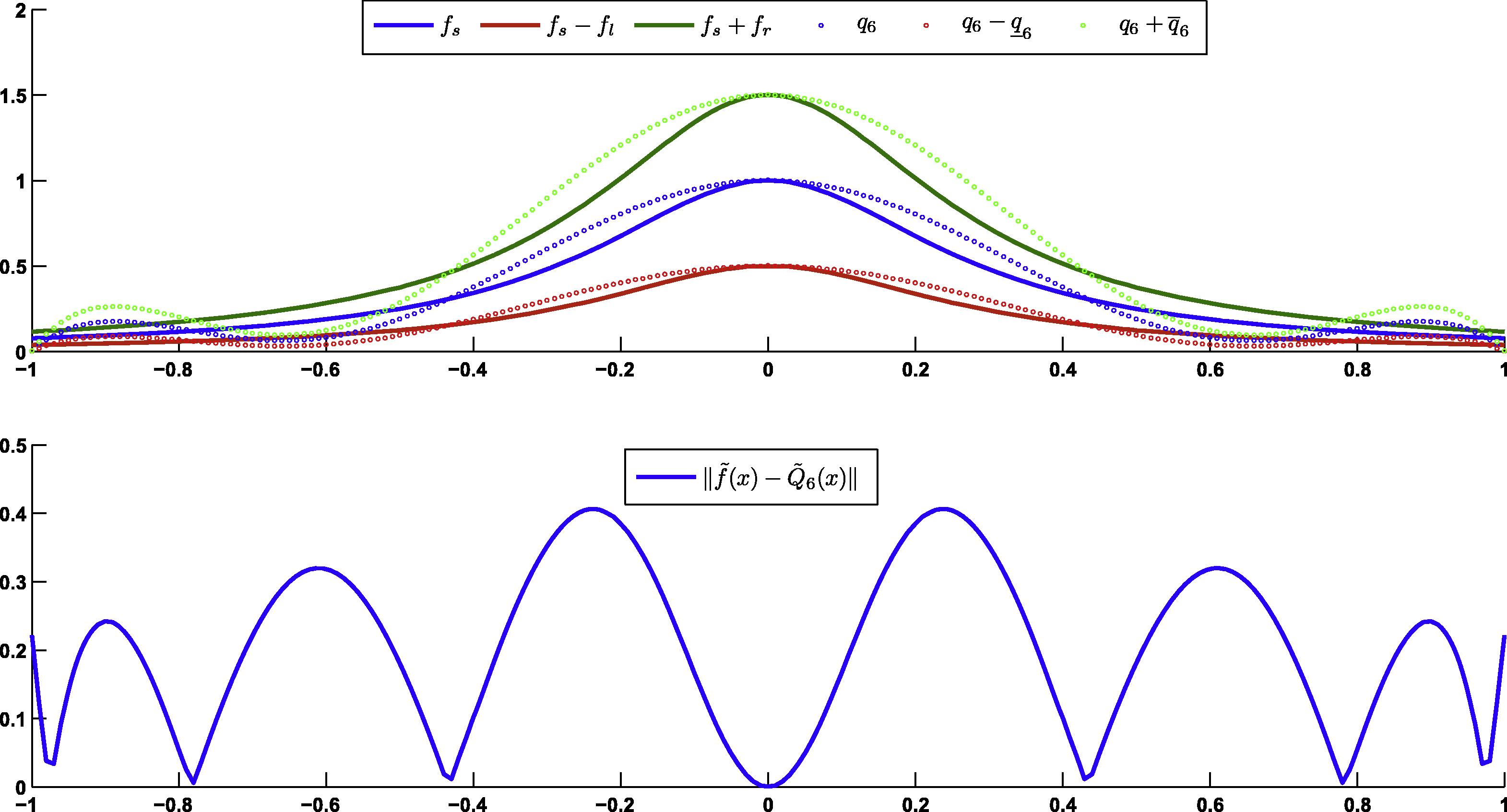
- Results for Case 2.
6 Conclusions
In this study, we proposed a method for finding the best near-minimax approximation of a fuzzy-valued function on a set of Chebyshev nodes. The existence and uniqueness of the best near-minimax approximation of a fuzzy-valued function were also proved. The best near-minimax approximation was compared to the best approximation (Abbasbany et al., 2007) by Runge’s phenomenon in the fuzzy sense.
Acknowledgments
The authors would like to express their sincere appreciations to the anonymous referees for their valuable comments and suggestions which improved the paper.
References
- Fuzzy Sets and Systems: Theory and Application. New York: Academic Press; 1980.
- Numerical Methods Using Matlab. Prentice-Hall Inc.; 2004.
- Theory and Applications of Numerical Analysis. Academic Press; 1980.
- Approximation Theory and Methods. New York: Cambridge University Press; 1981.
- Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten. Zeitschrift fur Mathematische Physik. 1901;246:224-243.
- [Google Scholar]







