Translate this page into:
Series solution of the Smoluchowski’s coagulation equation
⁎Corresponding author. ahmet.yildirim@ege.edu.tr (Ahmet Yıldırım)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 27 July 2010
Peer-review under responsibility of King Saud University.
Abstract
The Smoluchowski coagulation equation is a mean-field model for the growth of clusters (particles, droplets, etc.) by binary coalescence; that is, the driving growth mechanism is the merger of two particles into a single one. In this study, we consider obtaining approximate solutions of the Smoluchowski’s coagulation equation using the homotopy perturbation method. The numerical solutions are compared with the exact solutions. Results derived from our method are shown graphically.
Keywords
The Smoluchowski coagulation equation
Homotopy perturbation method
Approximate solution
Error analysis
Maple software package
1 Introduction
Smoluchowski’s equation is widely applied to describe the time evolution of the cluster-size distribution during aggregation processes. Analytical solutions for this equation, however, are known only for a very limited number of kernels. Therefore, numerical methods have to be used to describe the time evolution of the cluster-size distribution. A numerical technique is presented for the solution of the homogeneous Smoluchowski’s coagulation equation with constant kernel.
In this paper, we will consider the following Smoluchowski’s coagulation equation (Ranjbar et al., in press; Filbert and Laurençot, 2004):
Clusters of masses x and y coalesce by binary collisions at a rate governed by a symmetric kernel K(x, y). The coagulation kernel K(x, y) characterizes the rate at which the coalescence of the two clusters with respective masses x and y produces a cluster of mass x + y and is a non-negative symmetric function
The integral in Eq. (3) accounts for the formation of the cluster of mass x resulting from the merger of two clusters with respective masses y and x − y, y ∈ (0, ∞). The integral in Eq. (4) describes the loss of the cluster of mass x by coagulation with other clusters. Problems involving Smoluchowski’s equation have received a considerable amount of attention in the literature (Drake, 1972). Eq. (1) has been used in a wide range of applications, such as the formation of clouds and smog (Friedlander, 1977), the clustering of planets, stores, galaxies (Silk and White, 1978), the kinetics of polymerization (Ziff, 1980) and even the schooling of fishes (Niwa, 1998) and the formation of marine snow (Kiorbe, 2001). Also, an influential survey article by Aldous summarizes the recent state of affairs (Aldous, 1999). It is well known that during each coagulation event, the total mass of clusters is conserved while the number of clusters decreases. In terms of f, the total number of clusters N(t) and total mass of clusters M(t) at time t ⩾ 0 are obtained by
He (1999, 2003, 2006a) proposed a perturbation technique, so called He’s homotopy perturbation method (HPM), which does not require a small parameter in the equation and takes the full advantage of the traditional perturbation methods and the homotopy techniques. Relatively recent survey on the method and its applications can be found in Dehghan and Shakeri (2008a), Dehghan and Shakeri (2008b), Saadatmandi et al. (2009), Yıldırım (2008a,b, 2009a), Dehghan and Shakeri (2007), Shakeri and Dehghan (2008), Yıldırım (2009b), Koçak and Yıldırım (2009), Yıldırım (2008c, 2009c), and He (2008a,b, 2006b,c).
2 The homotopy perturbation method
Consider the following nonlinear differential equation:
The operator A can, generally speaking, be divided into two parts L and N, where L is linear and N is nonlinear, therefore Eq. (8) can be written as,
By using homotopy technique, one can construct a homotopy
which satisfies
3 Numerical results and comparison with explicit solutions
We first consider Eqs. (1)–(4) with constant kernel K(x, y) = 1 and f0 = exp(−x) (Ranjbar et al., in press),
We now consider Eqs. (1)–(4) with the multiplicative coagulation kernel K(x, y) = xy and f0 = exp(−x)/x (Ranjbar et al., in press),
Similar to previous example, we construct the following homotopy
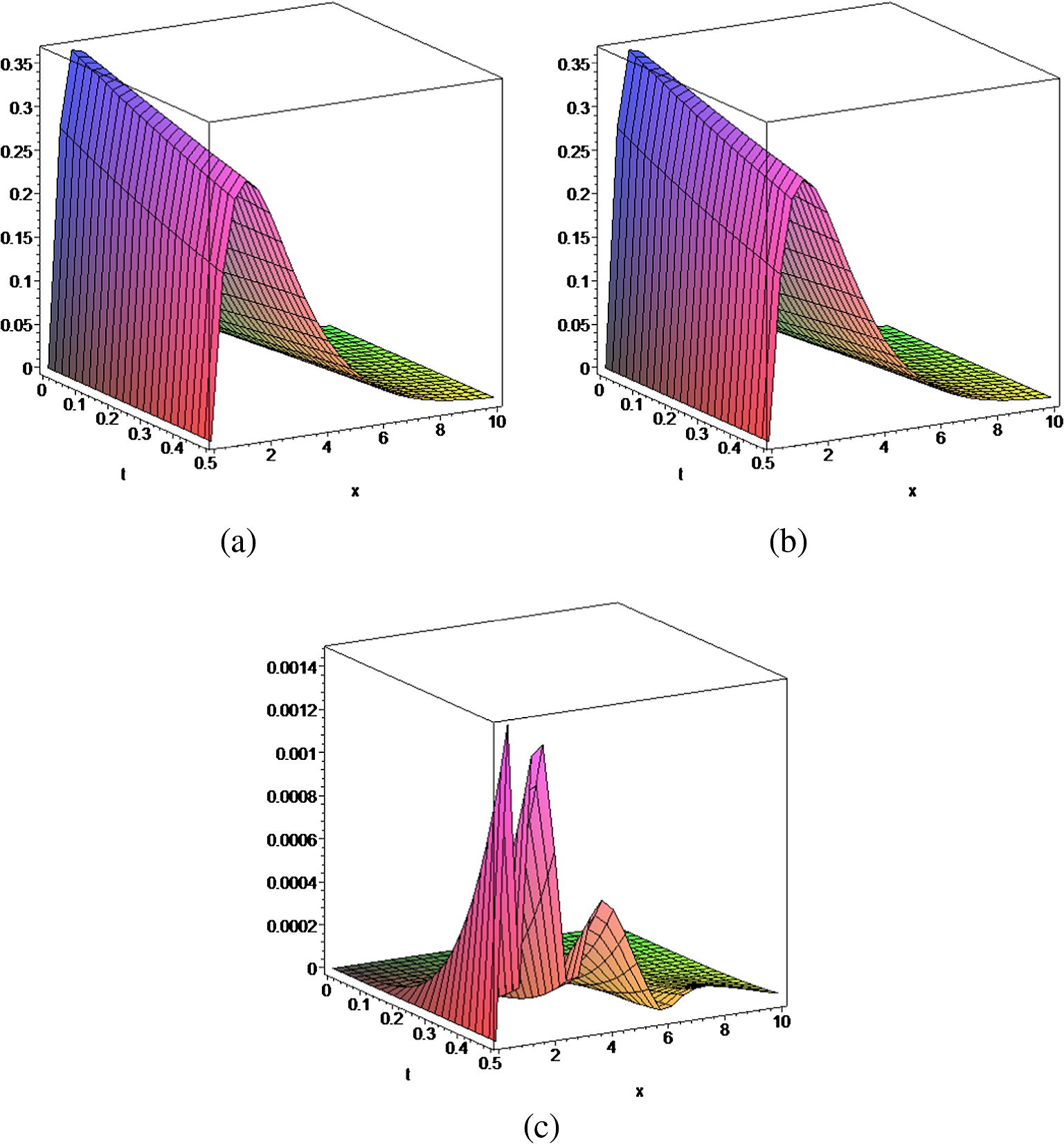
- (a) xf(x, t), (b)
and (c)
.
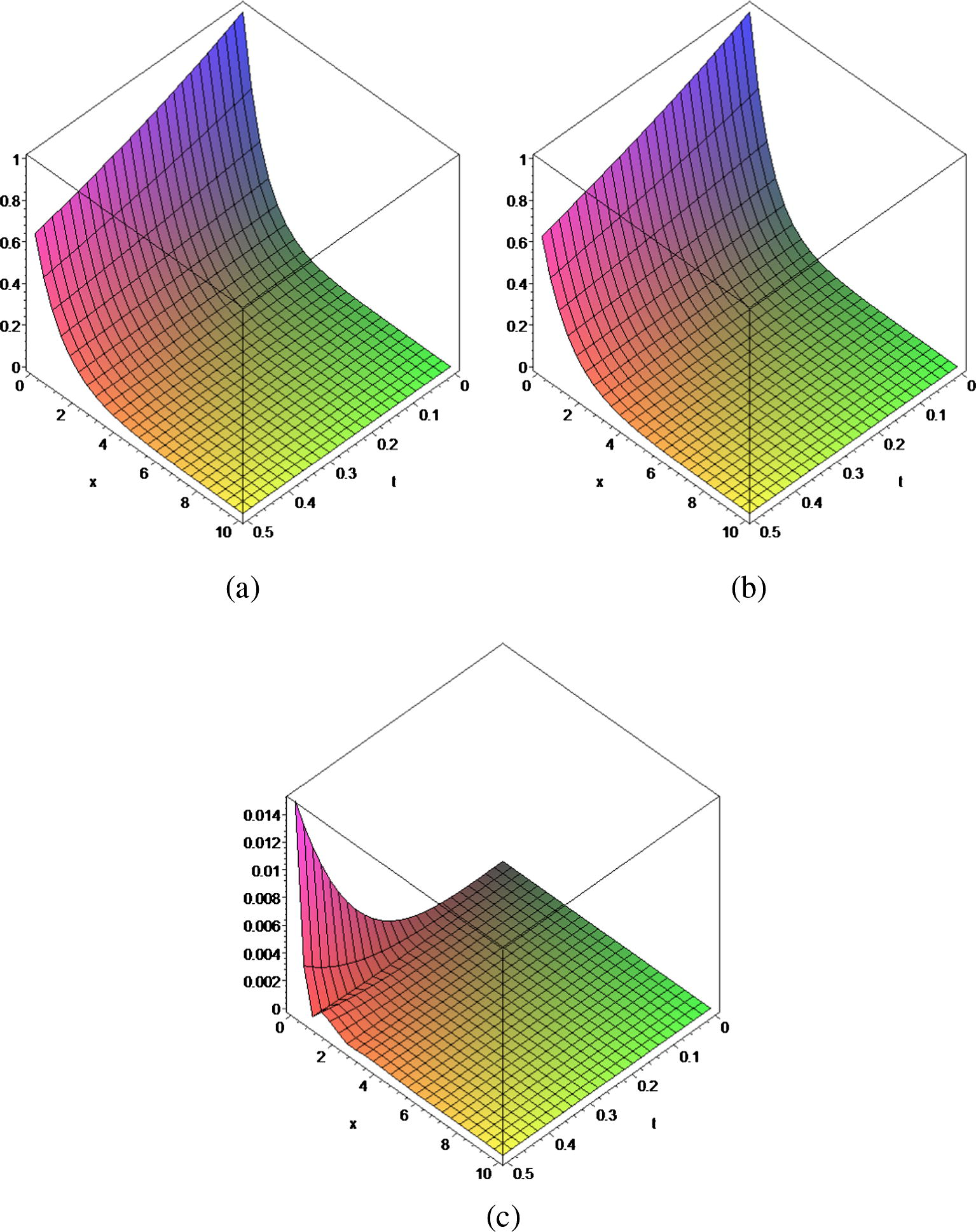
- (a) f(x, t), (b)
and (c)
.
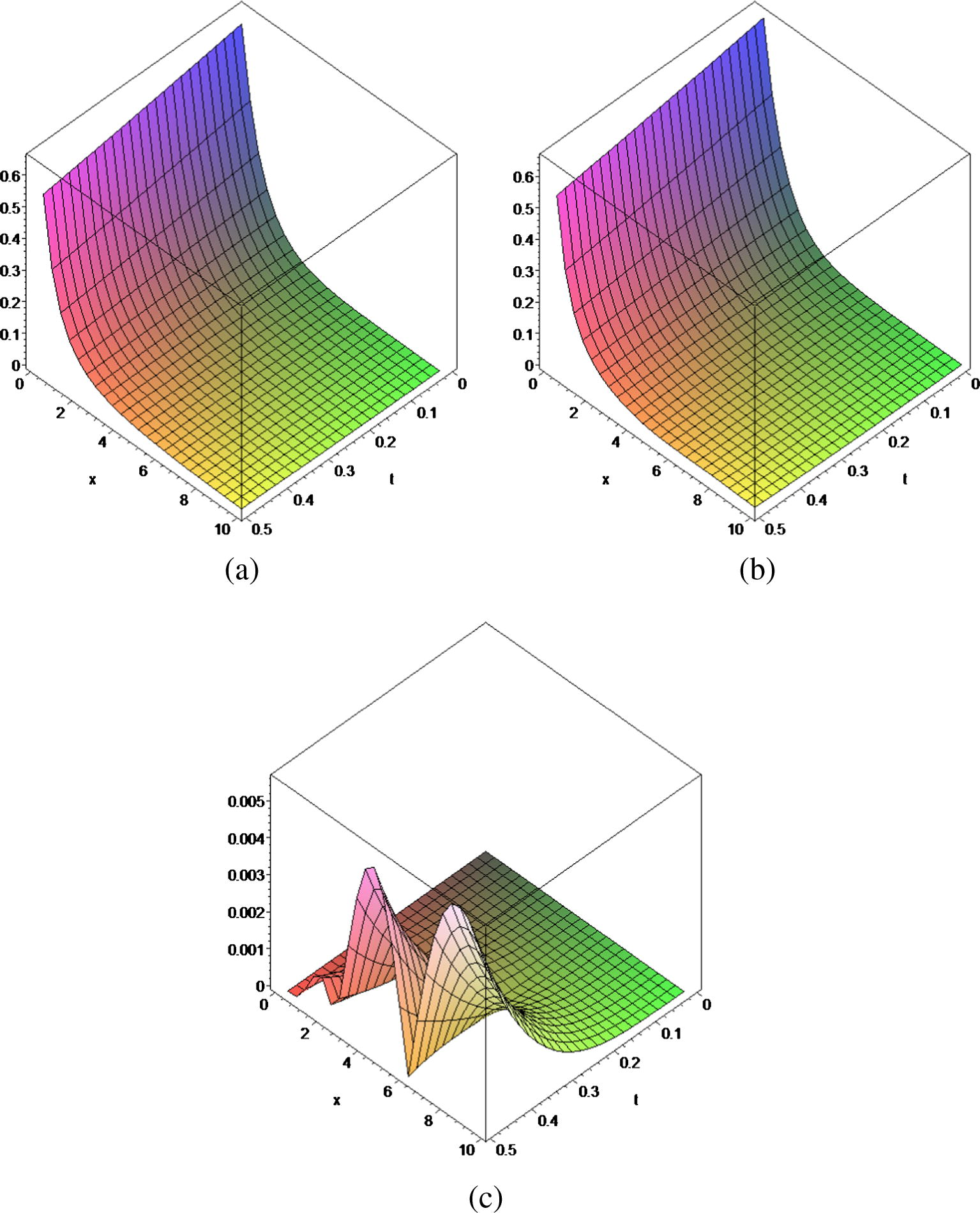
- (a) xf(x, t), (b)
and (c)
.
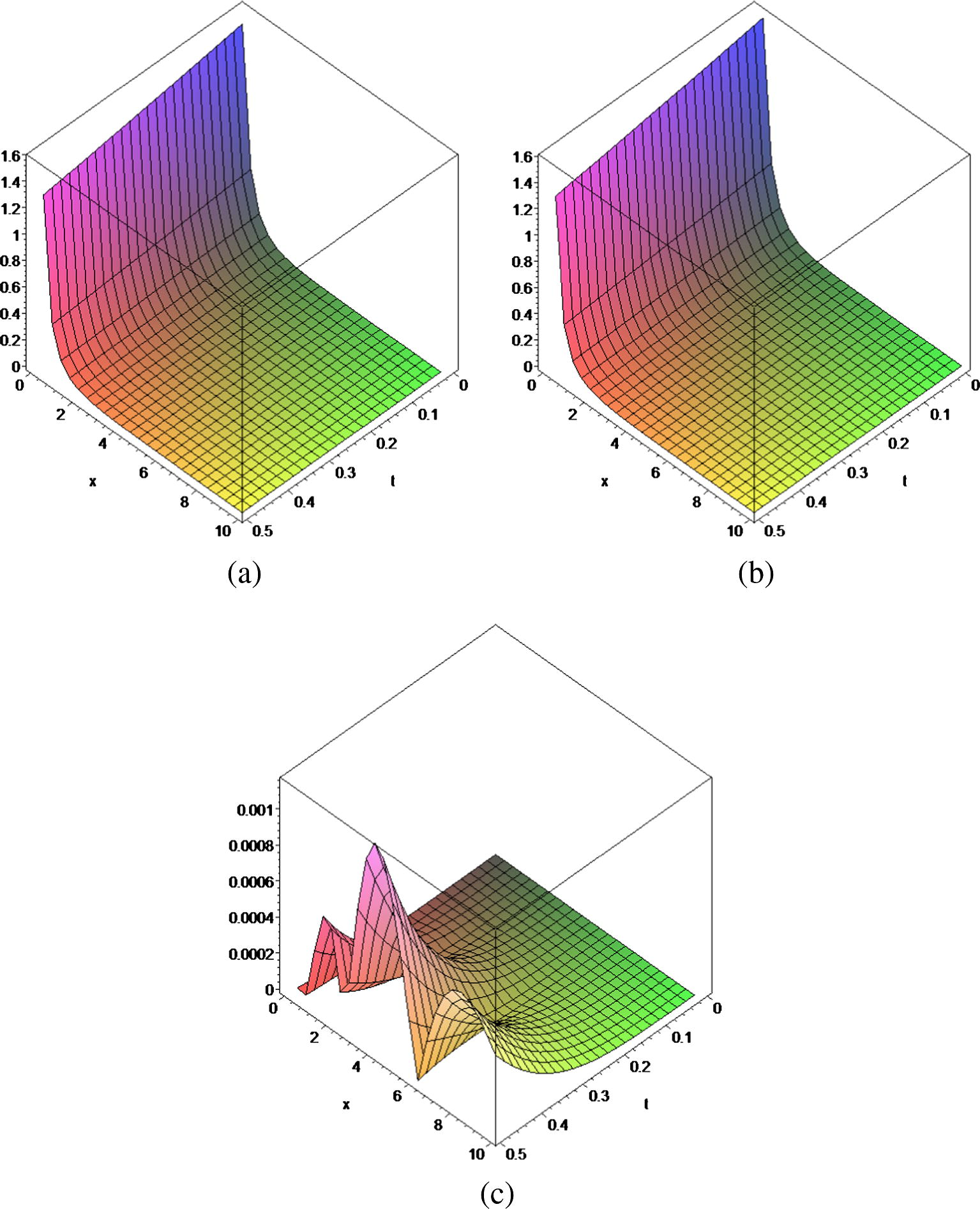
- (a) f(x, t), (b)
and (c)
.
4 Conclusions
In this paper, we used HPM for solving the homogenous Smoluchowski’s coagulation equation with constant kernel. Numerical results obtained show high accuracy of the method as compared with the exact solution. The solution obtained by HPM is valid for not only weakly nonlinear equations but also strong ones. The method gives rapidly convergent successive approximations and handles linear and nonlinear problems in a similar manner.
References
- Deterministic and stochastic models for coalescence (aggregation and coagulation): a review of the mean-field theory for probabilists. Bernoulli. 1999;5:3-48.
- [Google Scholar]
- Solution of a partial differential equation subject to temperature overspecification by He’s homotopy perturbation method. Physica Scripta. 2007;75:778.
- [Google Scholar]
- Solution of an integro-differential equation arising in oscillating magnetic fields using He’s homotopy perturbation method. Progress in Electromagnetic Research (PIER). 2008;78:361-376.
- [Google Scholar]
- Use of He’s homotopy perturbation method for solving a partial differential equation arising in modeling of flow in porous media. Journal of Porous Media. 2008;11:765-778.
- [Google Scholar]
- A general mathematical survey of the coagulation equation. Topics in current aerosol research. In: Hidy G.M., Brock J.R., eds. International Reviews in Aerosol Physics and Chemistry, Part 2. Vol vol. 3. Oxford: Pergamon; 1972. p. :201-376.
- [Google Scholar]
- Coagulation processes with a phase transition. Journal of Colloid Interface Science. 1984;97:266-277.
- [Google Scholar]
- Numerical simulation of the Smoluchowski coagulation equation. SIAM Journal on Scientific Computing. 2004;25:2004-2028.
- [Google Scholar]
- Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics. New York: Wiley; 1977.
- Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering. 1999;178:257-262.
- [Google Scholar]
- Homotopy perturbation method: a new nonlinear analytical technique. Applied Mathematics and Computation. 2003;135:73-79.
- [Google Scholar]
- Homotopy perturbation method for solving boundary value problems. Physics Letters A. 2006;350:87.
- [Google Scholar]
- Some asymptotic methods for strongly nonlinear equations. International Journal of Modern Physics B. 2006;20:1141.
- [Google Scholar]
- New interpretation of homotopy perturbation method. International Journal of Modern Physics B. 2006;20:2561.
- [Google Scholar]
- An elementary introduction to recently developed asymptotic methods and nanomechanics in textile engineering. International Journal of Modern Physics B. 2008;22:3487.
- [Google Scholar]
- Recent development of the homotopy perturbation method. Topological Methods in Nonlinear Analysis. 2008;31:205.
- [Google Scholar]
- Formation and fate of marine snow, small-scale processes with large-scale implications. Scientia Marina. 2001;66:67-71.
- [Google Scholar]
- Numerical solution of 3D Green’s function for the dynamic system of anisotropic elasticity. Physics Letters A. 2009;373:3145-3150.
- [Google Scholar]
- Ranjbar, M., Adibi, H., Lakestani, M., in press. Numerical solution of homogeneous Smoluchowski’s coagulation equation. International Journal of Computer Mathematics. doi:10.1080/00207160802617012.
- Application of He’s homotopy perturbation method for non-linear system of second-order boundary value problems. Nonlinear Analysis: Real World Applications. 2009;10:1912-1922.
- [Google Scholar]
- Solution of the delay differential equations via homotopy perturbation method. Mathematical and Computer Modelling. 2008;48:486.
- [Google Scholar]
- The development of structure in the expanding universe. Astrophysical Journal. 1978;223:L59-L62.
- [Google Scholar]
- Solution of BVPs for fourth-order integro-differential equations by using homotopy perturbation method. Computers and Mathematics with Applications. 2008;56:3175-3180.
- [Google Scholar]
- The homotopy perturbation method for approximate solution of the modified KdV equation. Zeitschrift für Naturforschung A – Journal of Physical Sciences. 2008;63a:621-626.
- [Google Scholar]
- Exact solutions of nonlinear differential-difference equations by He’s homotopy perturbation method. International Journal of Nonlinear Sciences and Numerical Simulation. 2008;9:111-114.
- [Google Scholar]
- Application of He’s homotopy perturbation method for solving the Cauchy reaction–diffusion problem. Computers and Mathematics with Applications. 2009;57:612-618.
- [Google Scholar]
- Homotopy perturbation method for the mixed Volterra–Fredholm integral equations. Chaos, Solitons & Fractals. 2009;42:2760-2764.
- [Google Scholar]
- An algorithm for solving the fractional nonlinear Schrödinger equation by means of the homotopy perturbation method. International Journal of Nonlinear Sciences and Numerical Simulation. 2009;10:445-451.
- [Google Scholar]







