Translate this page into:
An analytical approximation to the solution of chemical kinetics system
⁎Tel./fax: +98 1313233509. hossein.aminikhah@gmail.com (Hossein Aminikhah) aminikhah@guilan.ac.ir (Hossein Aminikhah)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 14 July 2010
Peer-review under responsibility of King Saud University.
Abstract
In this paper, homotopy perturbation method is applied to solve chemical kinetics problem. Theoretical considerations are discussed. Numerical results are presented, to illustrating the efficiently and simplicity of the method.
Keywords
Homotopy perturbation method
Chemical kinetics model
1 Introduction
In every phenomenon in real life, there are many parameters and variables related to each other under the law imperious on that phenomenon. When the relations between the parameters and variables are presented in mathematical language we usually derive a mathematical model of the problem, which may be an equation, a differential equation, an integral equation, a system of integral equations and etc. Consider a model of a chemical process (Butcher, 2003) consisting of three species, which are denoted by
and C. The three reactions are
Homotopy perturbation method has been used by many mathematicians and engineers to solve various functional equations. This method was further developed and improved by He (1999) and applied to nonlinear oscillators with discontinuities (He, 2004), nonlinear wave equations (He, 2005), boundary value problem (He, 2006), limit cycle and bifurcation of nonlinear problems (He, 2005), and many other subjects (He, 1999, 2000, 2004, 2003). It can be said that He’s homotopy perturbation method is a universal one, is able to solve various kinds of nonlinear functional equations. For examples it was applied to nonlinear Schrödinger equations (Biazar and Ghazvini, 2007), to nonlinear equations arising in heat transfer (Ganji, 2006), to the quadratic Riccati differential equation (Abbasbandy, 2006), and to other equations (Odibat and Momani, 2008; Aminikhah and Hemmatnezhad, 2010; Biazar et al., 2009; Aminikhah and Salahi, 2009, 2010; Aminikhah and Biazar, 2010).
The rest of this paper is organized as follows:
In Section 2, the basic idea of homotopy perturbation method is presented. In Section 3, the uses of HPM for solving system of chemical kinetics is presented. And conclusion will be appeared in Section 4.
2 Basic idea of homotopy perturbation method (He, 1999)
To illustrate the basic ideas of the method, we consider the following system of nonlinear differential equations
The operator A can be divided into two parts, which are L and N, where L is a linear, but N is nonlinear. Eq. (4) can be, therefore, rewritten as follows:
3 HPM for system of chemical kinetics
Consider the following nonlinear system of ordinary differential equations (chemical kinetics model) with initial conditions
Substituting Eqs. (15) into (14) and comparing the coefficients of identical degrees of p, for
, we have
x
0
10
5
20
0.5
9.944651132
4.494033438
20.56131543
1
9.880161150
4.098646466
21.02119238
1.5
9.808548358
3.786293183
21.40515846
2
9.731598340
3.550846463
21.71755520
2.5
9.651195643
3.422280269
21.92652409
3
9.569769303
3.494212621
21.93601808
3.5
9.490852205
3.964309224
21.54483857
4
9.419754293
5.187547743
20.39269796
4.5
9.364349610
7.742342740
7.742342740
5
9.335977191
12.50953127
13.15449154
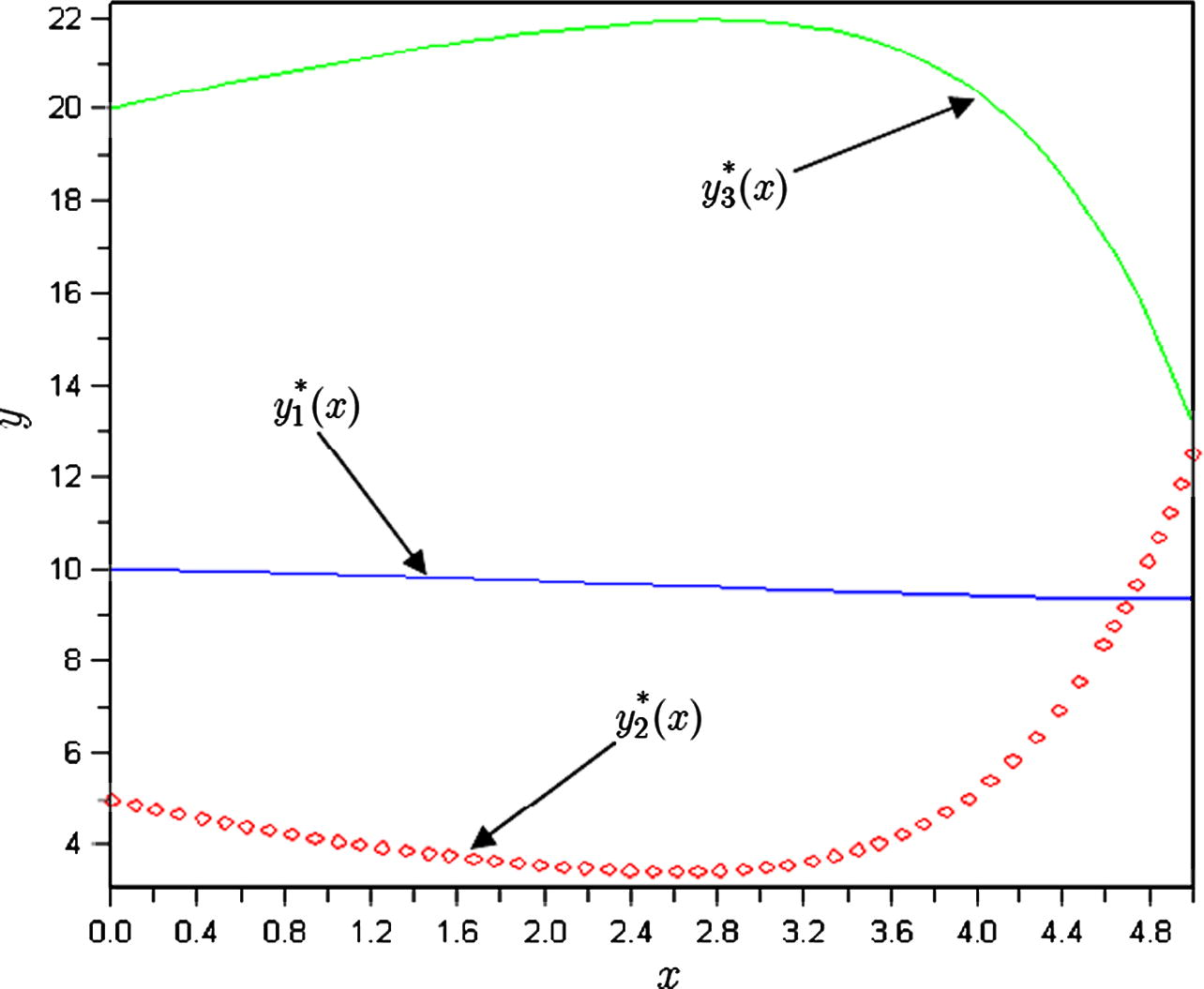
The plots of approximations of chemical kinetics model for
.
If we set,
, therefore, approximations to the solutions with seven terms are as follows
Some numerical results are presented in Table 2 and Fig. 2.
x
0
10
5
20
0.5
10.43503165
4.464605890
20.10036245
1
10.76109494
4.057152920
21.18175214
1.5
11.00402787
3.746196924
20.24977521
2
11.18359480
3.509324189
20.30708101
2.5
11.31487799
3.332706833
20.35241517
3
11.40922038
3.212502512
20.37827711
3.5
11.47471966
3.158098469
20.36718187
4
11.51627359
3.197199938
20.28652648
4.5
11.53517660
3.382762863
20.08206054
5
11.52826765
3.801770988
19.66996136
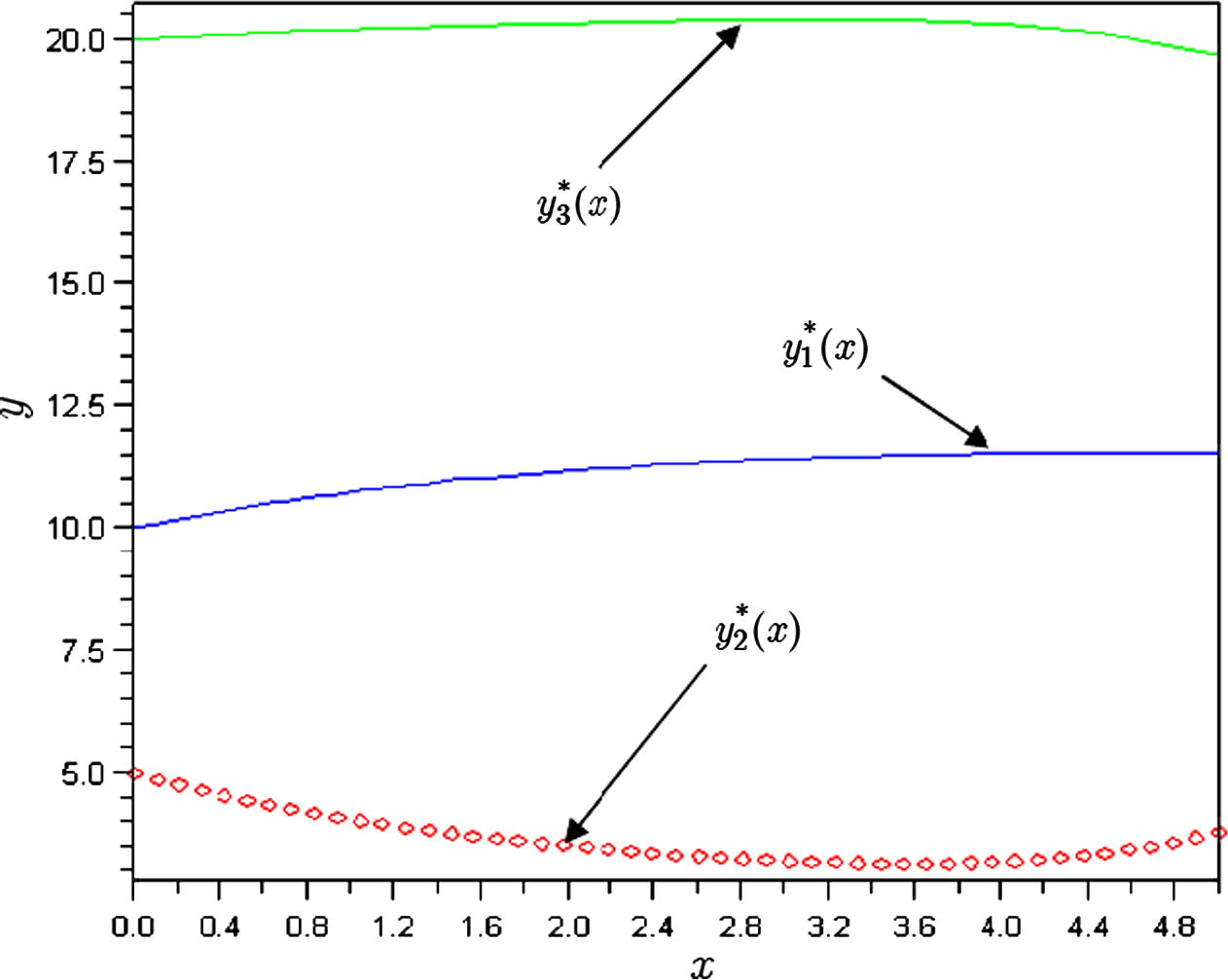
The plots of approximations of chemical kinetics model for
.
4 Conclusions
Homotopy perturbation method has been known as a powerful device for solving many functional equations such as ordinary, partial differential equations, integral equations and so many other equations. In this article, we have applied homotopy perturbation method for solving the nonlinear system of chemical kinetics. Numerical methods such as Runge–Kutta and Euler methods commonly used for solving these equations, either need a lot of computations and have less convergence speed and accuracy or solve only certain types of problems. In many cases one or two terms approximations have enough accuracy, i.e. fast convergence which can be mentioned as an advantage of the homotopy perturbation method. The main advantage of the HPM over ADM. is that this method provides the solution without a need for calculating Adomian’s polynomials (Aminikhah and Salahi, 2010). It can be concluded that He’s homotopy perturbation method is very powerful and efficient technique in finding exact solutions for wide classes of problems.
The computations associated with the examples in this paper were performed using Maple 10.
References
- Numerical solutions of the integral equations: Homotopy perturbation method and Adomian’s decomposition method. Applied Mathematics and Computation. 2006;173:493-500.
- [Google Scholar]
- A new HPM for ordinary differential equations. Numerical Methods for Partial Differential equations. 2010;26(2):480-489.
- [Google Scholar]
- An efficient method for quadratic Riccati differential equation. Communications in Nonlinear Science and Numerical Simulation. 2010;15(4):835-839.
- [Google Scholar]
- A new HPM for integral equations. Applications and Applied Mathematics. 2009;4:122-133.
- [Google Scholar]
- A new homotopy perturbation method for system of nonlinearintegro-differential equations. International Journal of Computer Mathematics. 2010;87(5):1186-1194.
- [Google Scholar]
- Exact solutions for nonlinear Schrödinger equations by He’s homotopy perturbation method. Physics Letters A. 2007;366:79-84.
- [Google Scholar]
- Application of homotopy perturbation method for systems of Volterra integral equations of the first kind. Chaos, Solitons & Fractals. 2009;42(5):3020-3026.
- [Google Scholar]
- Numerical Methods for Ordinary Differential Equations. John Wiley & Sons; 2003.
- The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer. Physics Letters A. 2006;355:337-341.
- [Google Scholar]
- Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering. 1999;178:257-262.
- [Google Scholar]
- Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering. 1999;178:257-262.
- [Google Scholar]
- A coupling method of homotopy technique and perturbation technique for nonlinear problems. International Journal of Non-Linear Mechanics. 2000;35(1):37-43.
- [Google Scholar]
- Homotopy perturbation method: a new nonlinear analytical technique. Applied Mathematics and Computation. 2003;135:73-79.
- [Google Scholar]
- The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation. 2004;151:287-292.
- [Google Scholar]
- Comparison of homotopy perturbation method and homotopy analysis method. Applied Mathematics and Computation. 2004;156:527-539.
- [Google Scholar]
- Application of homotopy perturbation method to nonlinear wave equations. Chaos, Solitons & Fractals. 2005;26:695-700.
- [Google Scholar]
- Limit cycle and bifurcation of nonlinear problems. Chaos, Solitons & Fractals. 2005;26(3):827-833.
- [Google Scholar]
- Homotopy perturbation method for solving boundary value problems. Physics Letters A. 2006;350:87-88.
- [Google Scholar]
- Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. Chaos, Solitons & Fractals. 2008;36(1):167-174.
- [Google Scholar]







