Translate this page into:
Solving a multi-order fractional differential equation using homotopy analysis method
⁎Corresponding author. Tel.: +98 9112113567. jafari@umz.ac.ir (H. Jafari), jafari_h@math.com (H. Jafari),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 1 July 2010
Peer-review under responsibility of King Saud University.
Abstract
In this paper we have used the homotopy analysis method (HAM) to obtain solution of multi-order fractional differential equation. The fractional derivative is described in the Caputo sense. Some illustrative examples have been presented.
Keywords
Fractional differential equation
Homotopy analysis method
Caputo fractional derivative
Riemann-Liouville fractional derivative
1 Introduction
Fractional differential equations have been found to be effective to describe some physical phenomena such as damping laws, rheology, diffusion processes, and so on. Several methods have been used to solve Fractional differential equations, such as Laplace transform method (Podlubny, 1999), Fourier transform method (Kemple and Beyer, 1997), Adomians decomposition method (ADM) (Daftardar-Gejji and Jafari, 2005; Daftardar-Gejji and Jafari, 2007; Jafari and Daftardar-Gejji, 2006), Homotopy analysis method (Liao, 2003; Momani and Odibat, 2008) and so on. For nonlinear FDE, however, one mainly resorts to numerical methods (Diethelm, 1997; Diethelm and Ford, 2002; Diethelm and Ford, 2004; Edwards et al., 2002). These numerical methods involve discretization of the variables, which gives rise to rounding off errors. Another drawback of numerical methods stems from the requirement of large computer memory.
In this paper, the homotopy analysis method (Liao, 1992) is applied to solve the multi-order fractional differential equation studied by Diethelm and Ford (2004): where and denotes Caputo fractional derivative of order .
Liao (1992) employed the basic ideas of the homotopy in topology to propose a general analytic method for nonlinear problems, namely homotopy analysis method (HAM), Liao (1992, 2004, 2003). This method (HAM) (Liao, 2003) provides an effective procedure for explicit and numerical solutions of a wide and general class of differential systems representing real physical problems. Based on homotopy of topology, the validity of the HAM is independent of whether or not there exist small parameters in the considered equation. Therefore, the HAM can overcome the foregoing restrictions and limitations of perturbation techniques so that it provides us with a possibility to analyze strongly nonlinear problems. Jafari and seifi have been solved diffusion-wave equation and partial differential equations and system of nonlinear fractional partial differential equations using homotopy analysis method (Jafari and Seifi, 2009; Jafari and Seifi, 2009). This method has been successfully applied to solve many types of nonlinear problems (Hayat et al., 2004; Momani and Odibat, 2008). These authors have discussed the analytical questions of existence and uniqueness of solutions and investigated how the solutions depend on the given initial data. Further they have presented an algorithm to convert the multi-order FDE into a system of FDE under some conditions and have developed numerical method to solve the system of FDE. In this paper we present an algorithm to convert the multi-order FDE into a system of FDE, without putting any of the restrictions. Thus our algorithm is valid in the most general case and yields fewer number of equations in a system compared to those in Diethelm–Ford algorithm. Consequently the solutions of the system of FDE have been obtained by employing the HAM approach. The paper has been organized as follows. Section 2 describes how to convert a multi-order FDE. In Section 3, HAM is developed to solve the system of FDE. Section 4 presents some illustrative examples. Discussion and conclusions are summarised in the Section 5.
2 Preliminaries
We enlist below some definitions (Luchko and Gorenflo, 1999; Podlubny, 1999) and basic results.
A real function is said to be in the space if there exists a real number such that where . Clearly if .
A function is said to be in the space if .
The (left sided) Riemann-Liouville fractional integral of order
of a function
is defined as:
The (left sided) Riemann-Liouville fractional derivative of
of order
is defined as:
The (left sided) Caputo fractional derivative of
is defined as:
The Mittag-Leffler function
with
is defined by the following series representation valid in the whole complex plane (Mainardi, 1994):
Lemma 2.7 Diethelm and Ford, 2002
Let for some and and let be such that . Then .
3 Multi-order FDE as a system of FDE
Daftardar-Gejji and Jafari have solved multi-order FDE by Adomian decomposition method (Daftardar-Gejji and Jafari, 2007):
Hence the claim. If
, then by Lemma 2.6,
and as
,
Case (ii) Consider
. If
, then define
.
If
, then define
The remark is in order
1. This algorithm is valid in the most general case, because we do not impose any of the restrictions on as mentioned in Eq. (6). We let , whereas in Diethelm and Ford (2004) .
4 Homotopy analysis method and a system of FDE
We can present the multi-order Eq. (5) as system of fractional differential equations:
5 Illustrative Examples
To demonstrate the effectiveness of the method we consider here some multi-order FDE. We transform multi-order FDE to a system of FDE and solve the system of FDE using HAM.
-
Consider the following initial value problem in case of the inhomogeneous Bagley–Torvik equation (Diethelm and Ford, 2002):
(25)In view of the discussion in the Section 3, the Eq. (25) can be viewed as the following system of FDE: Using Eq. (23) we get the following scheme: Thus we get: and hence In view of the above terms, we find and . So is the required solution of (25). -
Consider the following initial value problem,
(26)If we choose and , then Eq. (26) can be reduced to the following system of nonlinear FDE: Applying and to both sides of above system and using HAM Eq. (23) we get the following scheme:(27)Thus So . Hence we find and . Therefore is the required solution. -
Consider the following equation,
(28)Eq. (28) is equivalent to the following system of three FDE only.(29)where . In view of Eq. (29) and HAM we get
In Fig. 1, we draw exact solution
and solution obtained after 3 iterations
.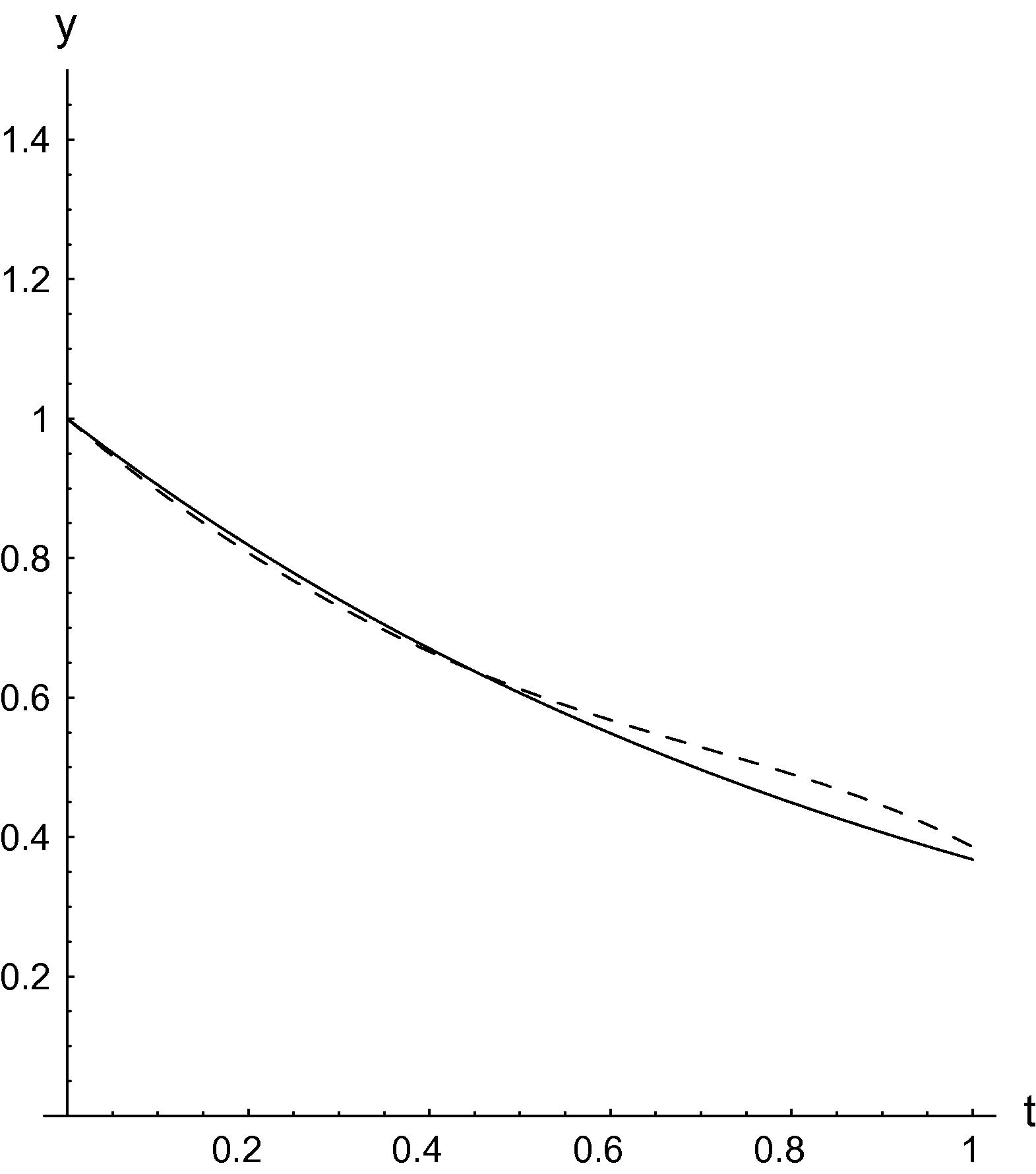
Exact solution (solid line) and HAM solution obtained after 3 iterations (
) (dashed line).
The computations presented here have been carried out with the help of Mathematica 5.
6 Discussion and conclusions
Homotopy analysis method consequently has been utilized to solve the system of fractional differential equations generated by a multi-order fractional differential equation. Thus it has been demonestrated that HAM proves useful in solving linear as well as non linear multi-order fractional differential equations.
References
- Adomian Decomposition: A tool for solving a system of fractional differential equations. J. Math. Anal. Appl.. 2005;301:508-518.
- [Google Scholar]
- Solving a multi-order fractional differential equation using adomian decomposition. J. Math. Anal. Appl.. 2007;189:541-548.
- [Google Scholar]
- An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal.. 1997;5:1-6.
- [Google Scholar]
- Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput.. 2004;154:621-640.
- [Google Scholar]
- The numerical solution of linear multi-term fractional differential equations: systems of equations. J. Comput. Appl. Math.. 2002;148:401-418.
- [Google Scholar]
- Solving linear and non-linear fractional diffusion and wave equations by Adomian decomposition. Appl. Math. Comput.. 2006;180:488-497.
- [Google Scholar]
- Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation. Commun. Non-linear Sci. Numer. Simulat.. 2009;14:2006-2012.
- [Google Scholar]
- Solving a system of nonlinear fractional partial differential equations using homotopy analysis method. Commun. Non-linear Sci. Numer. Simulat.. 2009;14:1962-1969.
- [Google Scholar]
- On the explicit analytic solutions of an Oldroyd 6-constant fluid. Int. J. Eng. Sci.. 2004;42:12335.
- [Google Scholar]
- Kemple, S., Beyer, H., 1997. Global and causal solutions of fractional differential equations. In: Transform Methods and Special Functions: Varna96, Proceedings of 2nd International Workshop (SCTP), Singapore, pp. 210–216.
- Liao, S.J., 1992. The proposed homotopy analysis technique for the solution of nonlinear problems. Ph.D. Thesis, Shanghai Jiao Tong University.
- On the homotopy analysis method for nonlinear problems. Appl. Math. Comput.. 2004;147:499-513.
- [Google Scholar]
- Beyond Perturbation: Introduction to the Homotopy Analysis Method. Boca Raton: CRC Press/Chapman & Hall; 2003.
- An operational method for solving fractional differential equations with the Caputo derivatives. Acta Math. Vietnamica. 1999;24(2):207-233.
- [Google Scholar]
- On the initial value problem for the fractional diffusion-wave equation. In: Rionero S., Ruggeeri T., eds. Waves and stability in continuous media. Singapore: World Scientific; 1994. p. :246-251.
- [Google Scholar]
- A novel method for nonlinear fractional partial differential equations: Combination of DTM and generalized Taylor’s formula. J. Comput. Appl. Math.. 2008;220(1–2):85-95.
- [Google Scholar]
- Fractional Differential Equations, An introduction to fractional derivatives, fractional differential equations, some methods of their solution and some of their applications. SanDiego: Academic Press; 1999.







