Translate this page into:
A reliable algorithm for solving nonlinear Jaulent–Miodek equation
⁎Corresponding author. mostafa.eslami@hotmail.com (Mostafa Eslami)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 1 July 2010
Peer-review under responsibility of King Saud University.
Abstract
Homotopy perturbation method has been applied to solve many functional equations so far. In this work, we propose this method (HPM), for solving Jaulent–Miodek (JM) equation (Kaya and El-Sayed, 2003; Fan, 2003). Numerical solutions obtained by the homotopy perturbation method are compared with the exact solutions. The results for some values of the variables are shown in tables and the solutions are presented as plots as well, showing the ability of the method.
Keywords
A reliable algorithm
Jaulent–Miodek equation
1 Introduction
Large varieties of physical, chemical, and biological phenomena are governed by nonlinear evolution equations. Except a limited number of these problems, most of them do not have precise analytical solutions, so they have to be solved by other methods which lead to closed approximate solutions or numerical solutions. Homotopy perturbation method has been used by many mathematicians and engineers to solve various functional equations. This method continuously deforms the difficult problems under study into a simple problem (He, 2000, 1999). In recent years the application of homotopy perturbation theory has appeared in many researches (He, 2003, 2004, 2005a, b, 2006; Biazar et al., 2007; Ariel et al., 2006; Siddiqui et al., 2006; Odibat and Momani, 2008; Cveticanin, 2006; Ozis and Yildirim, 2007).
2 Solution of system of partial differential equations by homotopy perturbation method
We first consider the system of partial differential equations written in an operator form
To solve system (1) by homotopy perturbation method, we construct the following homotopies:
For simplicity we take
3 Applications
Consider the following Jaulent–Miodek equation
For solving Eq. (7) with initial conditions (8) according to the homotopy perturbation method the following homotopy can be constructed
or
For numerical study four terms approximations have been considered. Suppose
and
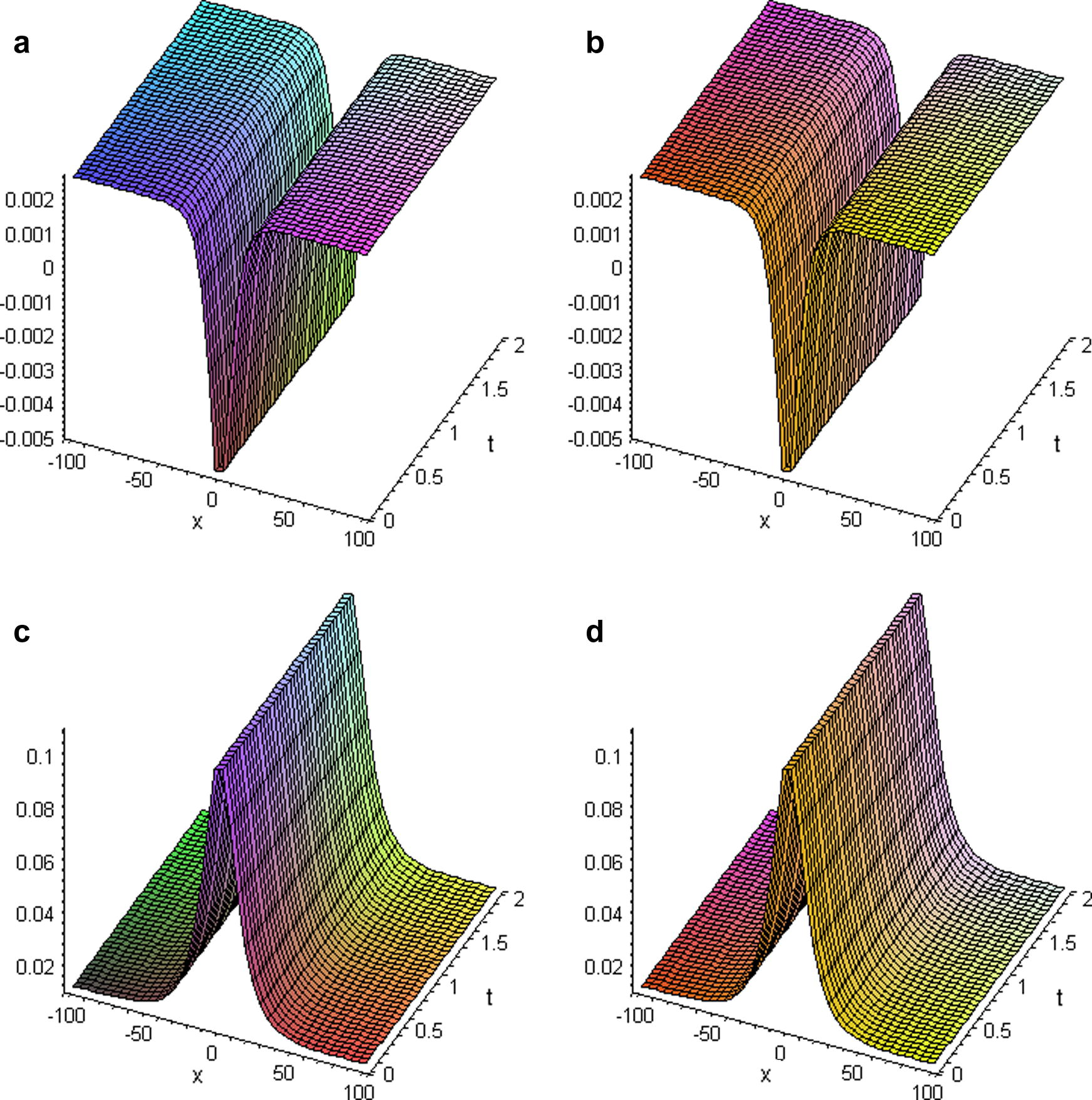
the results are presented in Table 1 and Fig. 1
0.1
0.1
−0.00552421681535966474
0.109994947072326492
0.1
0.15
−0.00552421268119929705
0.109994920399016371
0.15
0.1
−0.00552324416776666749
0.109988671429124380
0.2
0.3
−0.00552185135682729130
0.109979684175985571
0.35
0.25
−0.00551544200337122719
0.109938317095391529
0.45
0.45
−0.00550916080832543826
0.109897761088575401
0.5
0.3
−0.00550553384209772092
0.109874335473663468
0.45
0.7
−0.00550906801481426520
0.109897161826108341
0.4
0.8
−0.00551234934376313588
0.109918350605131830
0.8
0.8
−0.00547508560544371429
0.109677468293014595
0.85
0.95
−0.00546861261467419606
0.109635567784157087
0.9
0.9
−0.00546189829138478970
0.109592087075285587
0.95
0.9
−0.00545477408645114569
0.109545931955545074
1
1
−0.00544719469399408060
0.109496805097819525
4 Conclusions
In this article, we have applied homotopy perturbation method for solving the nonlinear Jaulent–Miodek (JM) equation (Kaya and El-Sayed, 2003; Fan, 2003). The approximate solutions obtained by the homotopy perturbation method are compared with the exact solutions. The results show that the homotopy perturbation method is a powerful mathematical tool for solving systems of nonlinear partial differential equations, which appears in mathematical modeling of different phenomena. This model has been solved by Adomian method, as well (Kaya and El-Sayed, 2003) Homotopy perturbation method in comparison with Adomian’s decomposition method has the advantage of overcoming the difficulty arising in calculating Adomain polynomial in ADM. In our work, we use the maple package to carry the computations.
References
- Homotopy perturbation method and axisymmetric flow over a stretching sheet. International Journal of Nonlinear Science and Numerical Simulation. 2006;7(4):399-406.
- [Google Scholar]
- Homotopy perturbation method for systems of partial differential equations. International Journal of Nonlinear Science and Numerical Simulation. 2007;8(3):411-416.
- [Google Scholar]
- Homotopy-perturbation method for pure nonlinear differential equation. Chaos, Solitons and Fractals. 2006;30:1221-1230.
- [Google Scholar]
- Uniformly constructing a series of explicit exact solutions to nonlinear equations in mathematical physics. Chaos, Solitons and Fractals. 2003;16:819-839.
- [Google Scholar]
- Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering. 1999;178:257-262.
- [Google Scholar]
- A coupling method of homotopy technique and perturbation technique for nonlinear problems. International Journal of Non-Linear Mechanics. 2000;35(1):37-43.
- [Google Scholar]
- Homotopy perturbation method: a new nonlinear analytical technique. Applied Mathematics and Computation. 2003;135:73-79.
- [Google Scholar]
- The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation. 2004;151:287-292.
- [Google Scholar]
- Application of homotopy perturbation method to nonlinear wave equations. Chaos, Solitons and Fractals. 2005;26:695-700.
- [Google Scholar]
- Limit cycle and bifurcation of nonlinear problems. Chaos, Solitons and Fractals. 2005;26(3):827-833.
- [Google Scholar]
- Homotopy perturbation method for solving boundary value problems. Physics Letters A. 2006;350:87-88.
- [Google Scholar]
- A numerical method for solving Jaulent–Miodek equation. Physics Letters A. 2003;318:345-353.
- [Google Scholar]
- Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. Chaos, Solitons and Fractals. 2008;36(1):167-174.
- [Google Scholar]
- A note on He’s homotopy perturbation method for van der Pol oscillator with very strong nonlinearity. Chaos, Solitons and Fractals. 2007;34(3):989-991.
- [Google Scholar]
- Homotopy perturbation method for thin film flow of a fourth grade fluid down a vertical cylinder. Physics Letters A. 2006;352:404-410.
- [Google Scholar]