Validation of Monte Carlo Geant4 code for a 6 MV Varian linac

2.1 Computational hardware resources

The physical structure of the cluster of computers used in this work consists of three nodes: (a) master machine that consists of a Personal Computer (PC) with a single 2.4 GHZ CPU processor and 2 Gbytes of physical memory, where the Geant4 package and other libraries are installed into. The login to the user session, submission of parallel jobs and compilation of user code are managed exclusively by this node. This node has two Ethernet interfaces, one is public called eth1 and the other is private called eth0 used for the private network. (b) Slave machines consist of four dual core Personal Computers having a 2.4 GHZ CPU per processor and a 2 Gbytes of physical memory. Its can act as workhorse nodes and are seen only on the private network. (c) Ethernet Network assures a network connection between the slave machines. Thanks to this device, all these nodes are attached together on the private network.

2.2 Computational user-friendly code

Performing Monte Carlo simulations in a single computer does not seem a good strategy to establish accurate studies of all physics phenomena involved by particles interacting with different components of the linac head, such an operation may take a long CPU time to be finally completed due to the complexity of the relevant geometry and materials that are used for making it, and also the nature of Monte Carlo Geant4 code, especially the concept of the cut production which makes the Geant4 code painfully slow when performing the particles tracking process. This is why we decide to develop a Geant4 user-friendly code that can be run in a flexible way on a cluster of computers.

In this work, a special Geant4 code called G4Linac has been written in C++ language from scratch to perform all mandatory tasks required for validating the Monte Carlo Geant4 code for a 6 MV Varian linac, it consists of two sub-programs namely G4Linac-head and G4Linac-dosecal and has been hosted on GitHub and it can be downloaded freely from: https://github.com/EL-BakkaliJaafar/G4Linac.

Our simulation strategy consists of dividing Monte Carlo simulations into two stages; in the first one we attempt to accurately model the linac head of a 6 MV Varian medical accelerator thanks to the G4Linac-head code that has many features. It includes the construction of model geometry, running multiple simulations at once, performing our one edition of bremsstrahlung splitting technique, recording IAEA Phase-Space data (Capote and Kawrakow, 2009) using G4IAEAPhsp classes (Cortés-Giraldo et al., 2012) and visualizing the whole geometry thanks to the several visualization systems supported by the Geant4 code. Whereas in the second stage, the G4Linac-dosecal has been used for performing dose calculation and has multiple capabilities, its includes simulating dose deposition in a homogeneous water phantom, running multiple simulations at once, reading particle data from the scored phase-space file, generating dosimetric functions of a 6 MV photon beam and visualizing the phantom geometry using several visualization systems. Concerning our Geant4 model, the geometry and materials modeling have been checked carefully and several times, because each component has been coded purely in C++ (codes that can contain several thousand of lines).

All Monte Carlo simulations considered in this work, were performed in a cluster of computers. The Rocks cluster software was used to build and maintain our cluster. The adaptation of Rocks cluster for making a parallel computing environment with Monte Carlo Geant4 was fully presented in our earlier paper (Bakkali et al., 2013).

2.3 Modeling of a 6 MV Varian linac head

Technical drawings of linac head components and related materials data (densities and mixture) for a 6 MV photon beam were provided by the Varian manufacturer against a confidentiality agreement. For these reasons, all these components appear neither with their not real sizes nor with their real positions. The simulated components include:

• Invariant elements: primary collimator, output window, monitors chamber, mirror and mesh.

• Elements which strongly depend on the selected irradiation energy, namely X-ray target and flattening filter.

• Others that depend on the shape of the beam, namely removable jaws.

The coordinates of the treatment head are expressed in a Cartesian coordinate system, the (Oz) axis corresponding to the radiation axis, the origin being located on the upper face of the X-ray target. Fig. 1 shows the linac head components and the water phantom positioned at 100 cm source to the surface distance (SSD).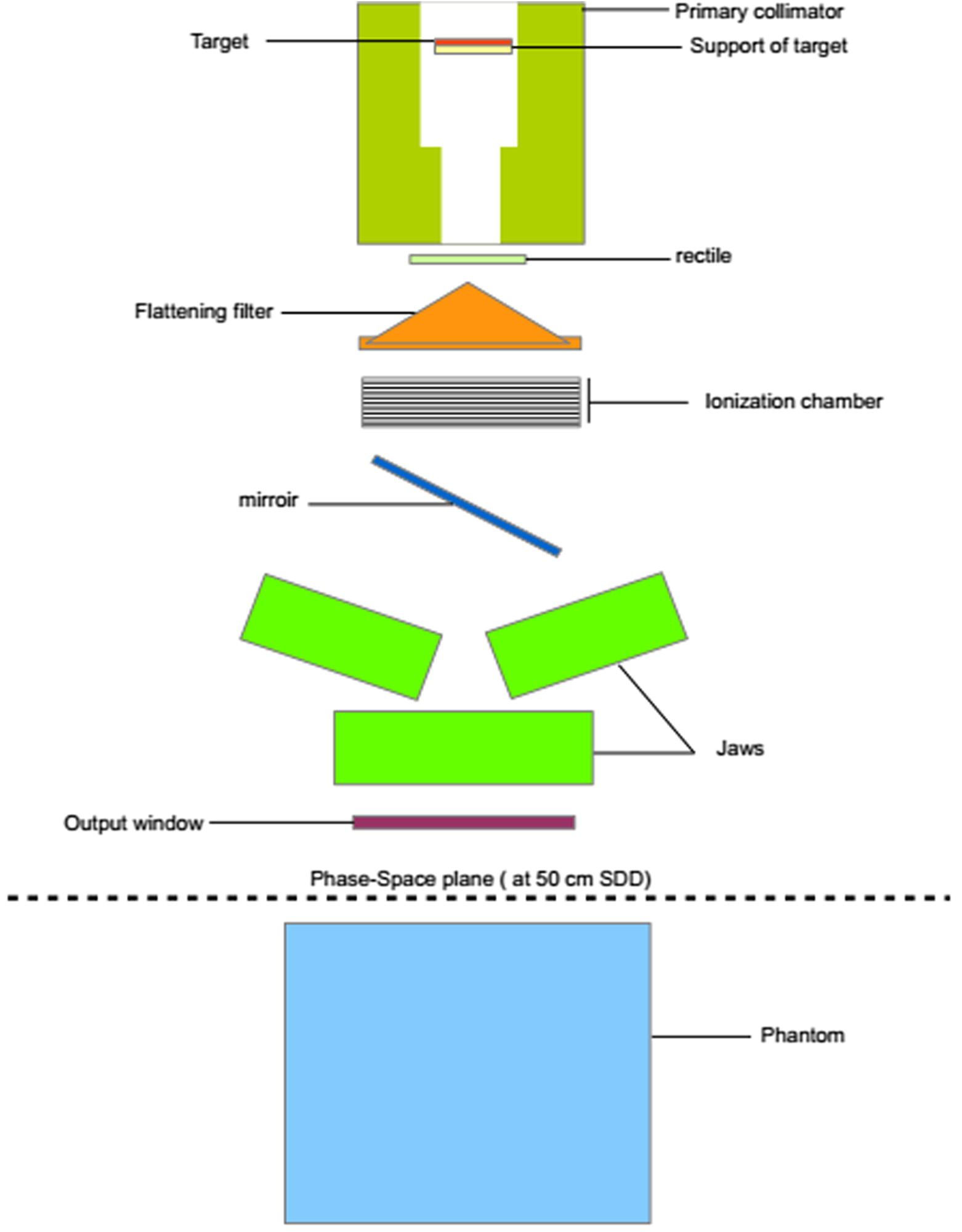

Close

Figure 1

Schematic view of the experimental setup including the simulated geometry of the 6 MV Varian linac head and the simulated geometry of the water phantom.

Export to PPT

The simulation of photons, electrons and positron transportations through the linac head has been done by considering the following interaction processes: Compton Scattering, Gamma Conversion, Photo Electric Effect for photons, Multiple Scattering, Ionization and Bremsstrahlung for electrons and positrons. The Geant4 code provides several physics models, including emstandard_opt0, emstandard_opt1, emstandard_opt2, emstandard_opt3, emlivermore and empenelope. The emstandard_opt2 model has been used in this work because it has been developed specially to model the transport of photons and charged particles for radiotherapy purposes.

With regard to the energy threshold, we used those published in thesis conducted by Zoubair (2012) which are fixed at 60 KeV for all particles. It should be noted here that, the energy threshold adopted by the Geant4 philosophy is defined as production cuts, that is to say, the secondary particles are not generated in the linac head when they have no energy above 60 KeV; but all particles that are living with energies upper than the energy threshold will be generated and tracked until the end of their lives (their kinetic energies drop to zero, artificially killed by the user or they come out of the global volume of simulation).

Regarding the variance reduction techniques, we have firstly incorporated an existing bremsstrahlung splitting technique developed by Tinslay and Koi (2010) in order to enhance artificially the production of bremsstrahlung photons at the X-ray target of a 6 MV Varian linac head. Unfortunately, the obtained results show that this technique alters the physics of the simulated problem and the dosimetric function curves seen to not clone those provided by measurement. With this issue, we decide to make some changes in the implementation of this technique. Thus, our contribution is as follows:

The bremsstrahlung splitting process has been applied strictly for the secondary photons which have been created by the primary electrons hitting X-ray target when the bremsstrahlung interactions occur. In contract, the photons that were created by secondary electrons are kept as they are without splitting.

Taking into consideration that, the factor of splitting is a main parameter which affects our simulation efficiency, we have done many Monte Carlo simulations where this factor was evaluated. On the other hand, we have applied some changes in the physics list class, in particular in it implementation of the emstandard_opt2 model, in order to successfully incorporate the bremsstrahlung splitting process into the G4Linac-head user-friendly code.

2.4 Modeling of a 6 MV photon beam dosimetric functions in a homogeneous water phantom

The calculation of dose distribution functions (PDD and cross beam profile) was carried out in a 40 × 40 × 40 cm³ homogeneous water phantom. The coordinates of the modeled phantom shown in Fig. 1 are expressed in a Cartesian coordinate system; the axis (Oz) corresponds to the axis of bremsstrahlung photon beam and the origin of the phantom is placed at a distance of 120 cm from the upper face of the X-ray target. To calculate dosimetric data at all points where we have their measured values, we have virtually discretized a homogeneous water phantom in small regions called cubic voxels. These voxels all have the same dimensions of 0.5 × 0.5 × 0.5 cm³.

Phase-Space placed at 50 cm from a homogeneous water phantom, has been used as an input to the Monte Carlo simulation of doses deposited by a 6 MV photon beam in this medium. It presented the source of photons created in the X-ray target by bremsstrahlung mechanism, scattered in different linac head components and finally recorded at a square plane defined below jaws components. Indeed, for a given configuration of the incident electron beam, a Phase-Space file previously calculated for this configuration has been considered as a radiation source of the modeled 6 MV photon beam for dose calculation program G4Linac-dosecal.

The modelization of photon, electron and positron transports through phantom have been carried out considering the following interaction processes: Compton Scattering, Gamma Conversion, Photo Electric Effect for photons, Multiple Scattering, Ionization and Bremsstrahlung for electrons and positrons. The emstandard_opt2 model has been chosen to model the physics all phenomenon involved by radiation interaction through a homogeneous water phantom. Concerning the cut production, it value was set to 10 μm for photons as well as for electrons/positrons, with respect to the recommendation of Perrot (2011).

2.5 Methodology followed for optimizing the electron beam configuration

As known, the unknown parameters in a Monte Carlo simulation of the linac head are often the electron source parameters. For the first time we have followed the methodology that was suggested by Verhaegen and Seuntjens (2003) in order to adjust these parameters, but unfortunately we have not arrived to find the best electron beam configuration. Consequently, we have developed our own methodology to adjust all parameters related to the virtual 6 MeV electron source. It consists to make three dependable studies; in each study we compare the calculated dose distributions with those provided by measurement, this by exploiting the Gamma Index comparison method where the tolerance of acceptability was set to 2% for the calculated dose points and 1 mm for the position where we calculate the value of the associated dose points. The proper configuration of the incident electron beam that gives the best Gamma Index results in such a study will be used later as a starting configuration in the next study. It should be noted, that the energy and spatial distributions of the incident electron beam are assumed to be both Gaussian. For each linac head simulation, we considered 25.2 million of independent events to be tracked. To speed-up our Monte Carlo simulation, we conducted eight sub-simulations simultaneously; in each one, we simulate 3.15·10⁶ of independent events in order to produce a Phase-Space file at the end of each run. The CPU time spent by each Monte Carlo simulation is in average 9 h. After these calculations, our Geant4PhspMerger utility (Bakkali, 2012) was exploited to auto-combining these eight Phase-Space files in order to make a single one which will be used later as radiation source for performing dose calculation with the G4Linac-dosecal user-friendly program.

In the first study, we conducted seven Monte Carlo simulations; the configuration that corresponds to a mean energy of 6 MeV, a sigma of 0.5 MeV and a FWHM of 1.18 mm is taken as the starting configuration. The other six configurations have been obtained by decrementing simultaneously the mean energy and the sigma with steps of 0.1 MeV and 0.02 MeV, respectively. It should be noted here, that for all Monte Carlo simulations considered in this work, the calculated data points associated to the dosimetric functions are obtained with statistical uncertainties all less than 1%.

Table 1 gives full details about all configurations of a 6 MeV electron beam selected in the first study.

In the second study, we take the optimal configuration found in the previous study as a starting configuration for this study. This study aims at improving the coincidence between calculation and measurement, thereby repeating the calculation by testing several values of the sigma parameter. In the third study, we keep the optimal electron beam configuration whose parameters were determined in the second study as a starting configuration to conduct this study. The aim is to adjust the value of the FWHM spatial parameter in order to fit much of the measurement. Subsequently, we have attempted to adjust the focal spot size by considering the following four sizes: 0, 0.59, 1.18, 1.77 and 2.36 mm.

3.1 Optimization of splitting factor of the modified bremsstrahlung technique

In this quick study, we test the effectiveness of the modified bremsstrahlung technique on the optimization of the modeling speed of a 6 MV Varian linac. Indeed, we conducted thirteen Monte Carlo simulations in a cluster of computers, this by varying the number of splitting factors (Nsplit) in each simulation, in order to adjust this parameter. For each Monte Carlo simulation, about 2·10³ events were considered. Then, all particle data from the output of each Monte Carlo simulation recorded in a Phase-Space file were analyzed, the most interesting data for our study are the number of particles and the CPU time spent during each Monte Carlo simulation. We define the outflow parameter as being the ratio between the number of the particles stored in a Phase-Space file (captured at 50 cm from the X-ray target) and the CPU time spent by the Monte Carlo simulation. Fig. 2 shows the given results.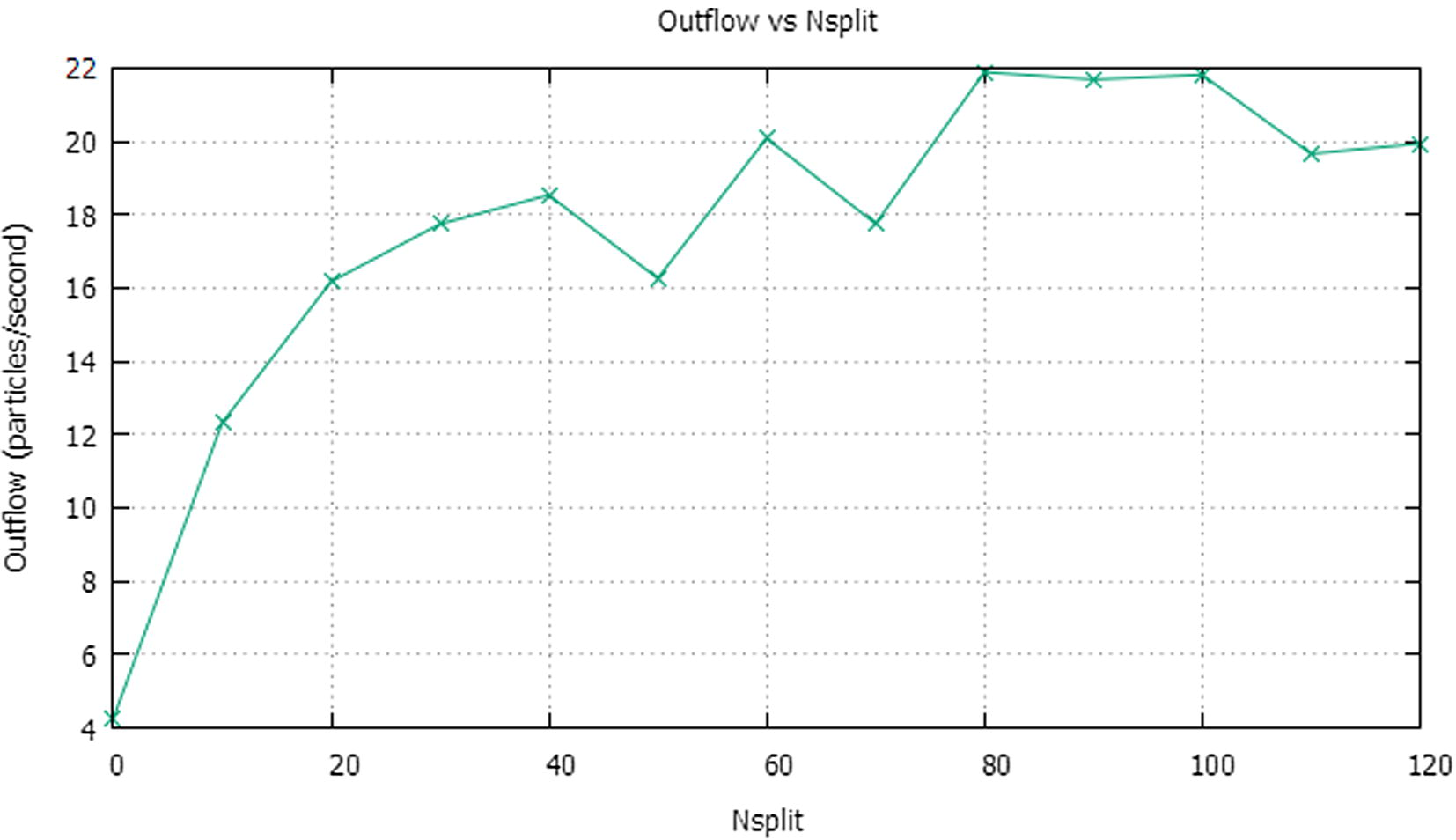

Close

Figure 2

Evolution of the outflow of particles stored in Phase-Space file according to the Nsplit factor.

Export to PPT

According to the above figure, it can be seen that when (Nsplit = 80), there is a maximum outflow (22 particles/second) which is five times higher than the one obtained in analog Monte Carlo simulation (Nsplit = 0). Therefore, a speed-up factor of 5 is achieved for the Monte Carlo simulation of the linac head when the modified version of bremsstrahlung technique is optimized for this machine.

3.2 Results of the first Monte Carlo study

In this study, we modified simultaneously the two parameters that characterize the Gaussian energy distribution namely the mean energy and the sigma. while the focal spot size was fixed at 1.18 mm.

The results of Gamma Index tests relative to the calculated dosimetric functions are summarized in Table 2.

From the table above, we can say that the electron beam configuration with a mean energy of 5.6 MeV, a sigma of 0.42 MeV and a FWHM size of 1.18 mm, is the proper configuration. Indeed, for this configuration the results relative to the Gamma Index tests for PDD indicate that 96.8% of the calculated data points (except the two dose points at the surface dose region) are in good agreement with the measurements. Regarding the calculated cross beam dose profile, the results of Gamma Index tests show that 91.1% of the calculated data points (except the four dose points at the penumbra region) are in good agreement with the measurements.

The dosimetric function curves of the proper configuration obtained after calculation of about three days and the associated Gamma Index results are presented in Fig. 3, and prove the success of our Monte Carlo simulation of a 6 MV Varian linac.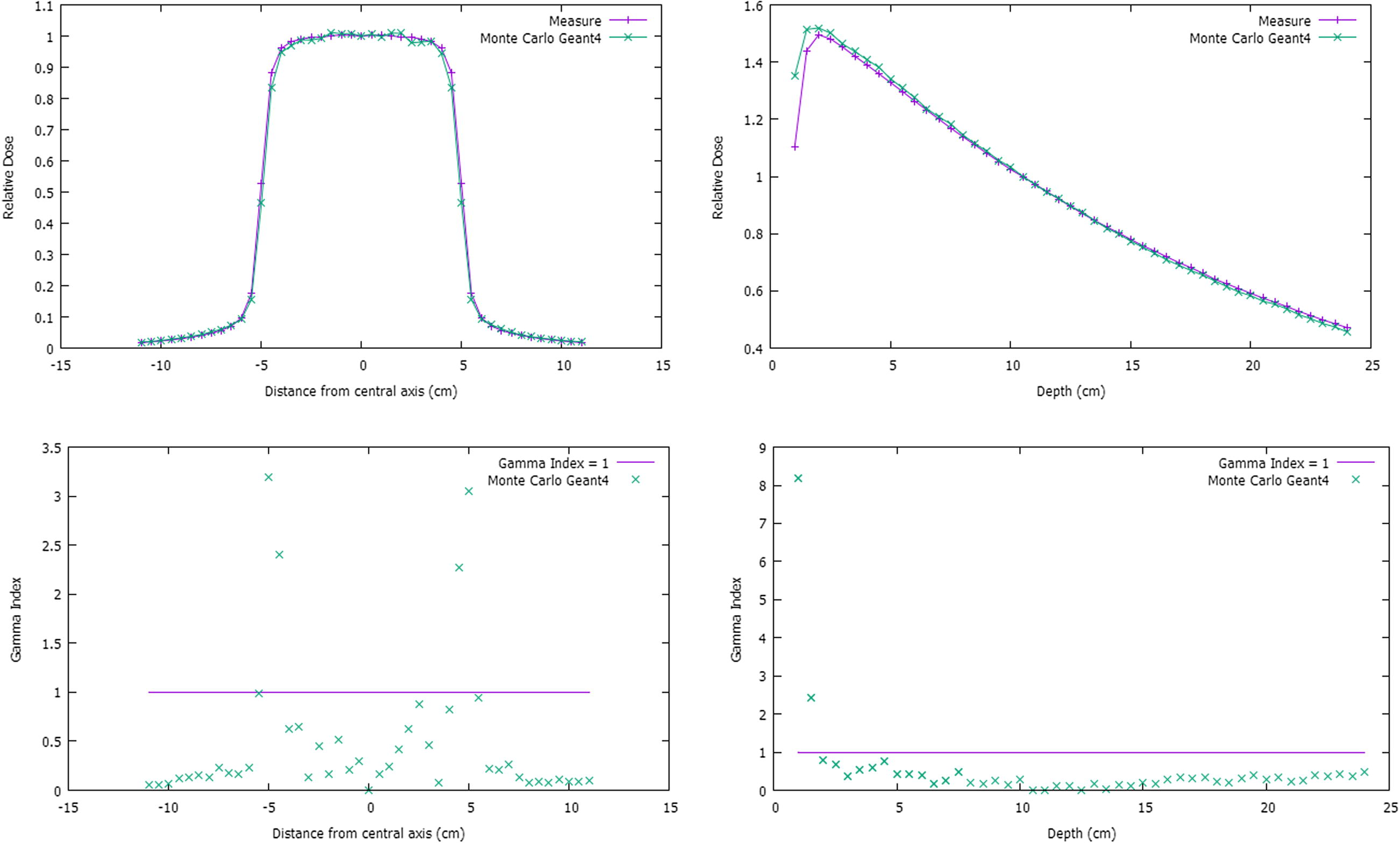

Close

Figure 3

Comparison of calculated and measured dosimetric functions in a homogeneous water phantom for a 6 MV photon beam from the Varian linac head.

Export to PPT

The cross beam profile shown in Fig. 4 consists of three regions, namely the isodose region (doses over 80% of the central beam axis), the penumbra dose regions (defined as the distance between 80% and 20% dose level point on cross beam profile), and dose regions outside the radiation field called umbra (regions under 20% of the central beam dose). The statistical uncertainties associated to the calculated dosimetric functions drawn in Fig. 4 are presented in Fig. 4.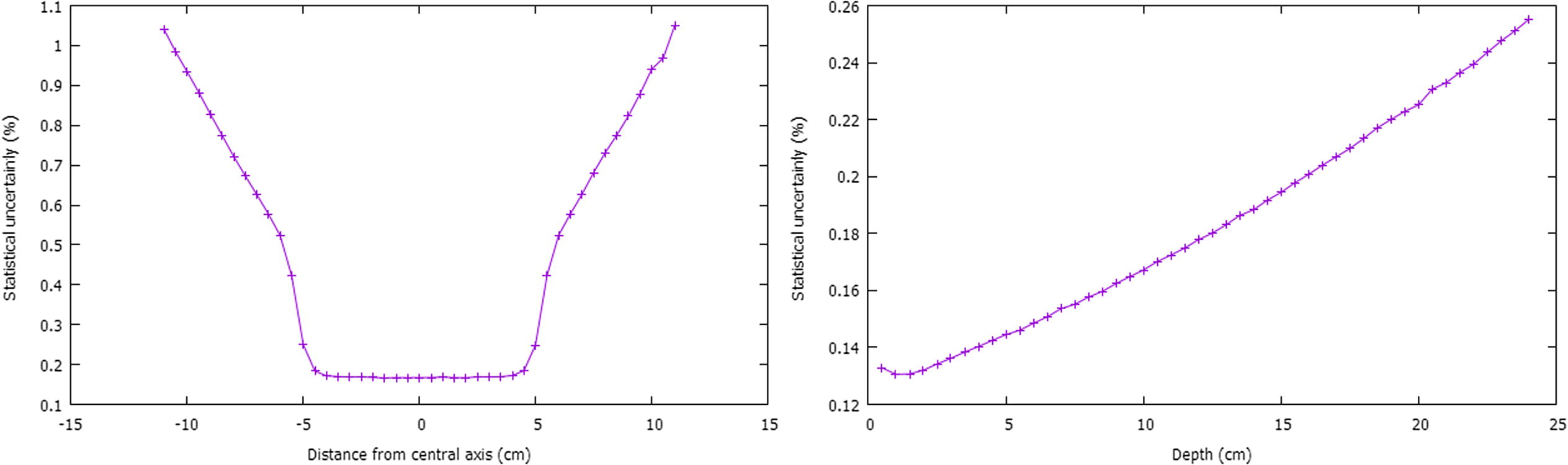

Close

Figure 4

Evolution of statistical uncertainties with the calculated data points associated to the dosimetric functions, namely cross beam profile and PDD.

Export to PPT

From the left side of the above figure, we can see that all calculated dose points located at the isodose region have almost the same statistical uncertainly, due to the fact that same quantity of photons deposit its energies in equal manner in each dose point of the isodose region. Regarding to the penumbra dose regions, the dose decreases rapidly and the scattered bremsstrahlung photons that reach this region are very low due to collimation properties of the jaws components, this explains why the statistical uncertainties have significant values in this region. Whereas in the umbra region, the statistical uncertainly continues to increase due to the fact that the dose in this region outside the radiation field is generally low and results from bremsstrahlung photons transmitted through different linac shielding components.

From the right side of the above figure, the statistical uncertainty associated with each calculated dose point of the PDD dosimetric function increases with the depth; this can be explained by the exponential attenuation law of photons. Thus, the number of photons penetrating through phantom decreases with phantom depth resulting in an increase in statistical uncertainties.

3.3 Results of the second study – effect of the standard deviation of Gaussian energy

To optimize the sigma parameter (related to the Gaussian energy distribution) on modeling of an electron beam source, we have conducted a second Monte Carlo study in which six new electron beam configurations were considered. In fact, for all configurations, we keep the values of the mean energy and the FWHM parameters of the last optimal configuration founded in the first study, whereas the sigma parameter is evaluated. Thus, we have investigated seven values regularly distributed between 0.38 and 0.50 MeV with a step of 0.02 MeV.

In Table 3, we summarize, all obtained results of Gamma Index tests associated to the PDD and cross beam profile dosimetric functions.

We note here, after a deep analysis of the results drawn in the table above, that all calculated PDD curves are seen to be not responsive to a small perturbation of the sigma parameter. In contrast, the cross beam profiles are highly dependent on the variation of this parameter even at a very low value (a step of 0.02 MeV). We can therefore conclude that the sigma parameter related to the incident electron beam which is assumed to be Gaussian, affects only the cross beam profiles and has almost no effect on the calculated PDD produced by a 6 MV photon emitted by Varian linac head.

According to Table 5, it is clear that a value of σ = 0.42 MeV founded during the adjustment step in the first study is still always the optimal value of this parameter. We can conclude, after this second study, the configuration found in the first study is the proper configuration, founded once before. Therefore it remains to investigate the effect of the FWHM parameter on the dose distributions. This is considered the main purpose of the third study.

3.4 Results of the third study – impact of the FWHM parameter on calculated dosimetric functions

We have conducted a third study in which we will seek to evaluate the impact of the FWHM parameter on the calculated dose distributions in a homogeneous water phantom. All configurations included in this study and the results of Gamma Index tests for each configuration, are described in Table 4.

From the table above, it is obvious that the configuration found in previous studies is still always the best one and the optimized value related to the FWHM parameter is still always equal to 1.18 mm. Furthermore, our results show that the PDD and the cross beam dose profile are all very sensitive to a slight variation of the value of the FWHM parameter.

3.5 The effect of the support of the X-ray target

During this study, we simulated only three components of the Varian linac head, namely the primary collimator, the X-ray target and the support of the X-ray target, in order to evaluate the main role of support of the target. In this context, we have considered two Monte Carlo simulations started at the same initial conditions but one with a support of the X-ray target and the other carrier without the support of the target. In fact, we simulated about 2 10³ events representing outgoing electrons from a virtual source. The modified version of bremsstrahlung technique was used and the Nsplit parameter is set to optimal value (Nsplit = 80).

Table 5 shows the obtained results related to this supplementary study which assesses the impact of the support of the X-ray target on the properties of megavoltage photon beam emitted by a Varian linac head.

From the table above, we may well highlight the main role of the support of the X-ray target. One can see that the number of incident electrons leaving the X-ray target was decreased by almost 24% when the support of the copper target is simulated. In addition, the mean energy of electrons is slightly increased while their minimum energy was increased about ten times. So, the main role of the support of the target, according to this study is, to break all low-energy electrons leaving the X-ray target.