Translate this page into:
Unsteady MHD free convective Couette flow between vertical porous plates with thermal radiation
⁎Corresponding author. isahby1973@gmail.com (B.Y. Isah),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This study investigates the unsteady MHD free convective Couette flow of viscous incompressible electrically conducting fluid between two infinite vertical porous plates in the presence of transverse magnetic field and thermal radiation. Solutions for time dependent energy and momentum equations are obtained by the implicit finite difference method. To check the accuracy of the numerical solutions, steady state solutions for energy and momentum equations are obtained by using the perturbation method. The effect of various parameters controlling the physical situation is discussed with the aid of line graphs. Significant results from this study are that both velocity and temperature increase with the increase in thermal radiation parameter and time. A series of numerical experiments show that steady state velocity and temperature occur when the dimensionless time approaches the values of Prandtl number of the fluid. During the course of numerical computation, an excellent agreement was found between unsteady and steady state solutions at large value of time.
Keywords
MHD
Couette flow
Thermal radiation
Free-convective flow
Implicit finite difference
1 Introduction
The literature on steady and unsteady free convective flow phenomenon in vertical plates associated with Couette flow with or without porosity or MHD is numerous. Many studies have been conducted on steady state Couette flow under different physical situations (Tsangaris et al., 2007; Barletta and Magyari, 2008; Chen and Zhu, 2008; Chaughan and Rastogi, 2012) while many others considered their investigation on unsteady Couette flow problems (Dash and Biswal, 1989; Zhu and De Kee, 2007; Raptis, 2011; Salama, 2011; Seth et al., 2012; Jha et al., 2013).
MHD free convective Couette flow has been studied with kin interest due to its possible applications in many industrial problems. For example, in the power industry, among the methods of generating electric power is one in which electrical energy is extracted directly from a moving conducting fluid Ibrahim et al. (2008). Chaughan and Rastogi (2012) studied steady state MHD Couette flow of a viscous, incompressible and electrically conducting fluid flow between two infinite parallel plates in the presence of an inclined magnetic field. Hayat et al. (2004) considered Hydromagnetic Couette flow of an Oldroyd-B fluid in a rotating system of a viscous, incompressible and electrically conducting fluid bounded between two rigid non-conducting parallel plates. Moreover, several authors have studied excellent works on unsteady MHD free-convective flow between vertical parallel porous plates. Hazem (2010a,b) reported unsteady magnetohydromagnetic Couette flow of an electrically conducting incompressible non-Newtonian viscoelastic fluid between two parallel horizontal non-conducting porous plates with heat transfer. Salama (2011) investigated flow formation in Couette motion in magnetohydrodynamics with time varying suction and taking into account the effects of heat and mass transfer. Khem (2012) analyzed MHD Couette motion of an electrically conducting, viscous incompressible fluid through saturated porous medium bounded by two insulated vertical porous plates. Farhad et al. (2012) investigated the hydromagnetic rotating flow of viscous fluid through a porous space under slip condition. Baoku et al. (2012) studied the problem of steady hydromagnetics Couette flow of a high viscous fluid through a porous channel in the presence of an applied uniform transverse magnetic field and thermal radiation.
The present work is motivated to study Unsteady MHD free-convective Couette flow between vertical porous plates with thermal radiation.
2 Mathematical analysis
Consider a time dependent unsteady free convective Couette flow of a viscous, incompressible, electrically conducting and radiating fluid between two infinite vertical parallel porous plates in the presence of transverse magnetic field as shown in Fig. 1. At time,
both the fluid and porous plates are assumed to be at rest at temperature T0. At some time,
the temperature of the porous plate situated at
rises to Tw and starts moving in its own plane with impulsive motion with velocity U while the other porous plate at a distance H from it is fixed and maintained at temperature T0. A uniform magnetic field of strength B0 is imposed normal to the porous plates. The Cartesian (
) co-ordinate systems are taken with x′-axis along the moving porous plate in the vertical upward direction and the y′-axis normal to it. Since the porous plates are of infinite length, the velocity and temperature are functions of y′ and t′ alone. Using Boussinesq’s approximation, the governing equations for the present physical situation in dimensional form are:
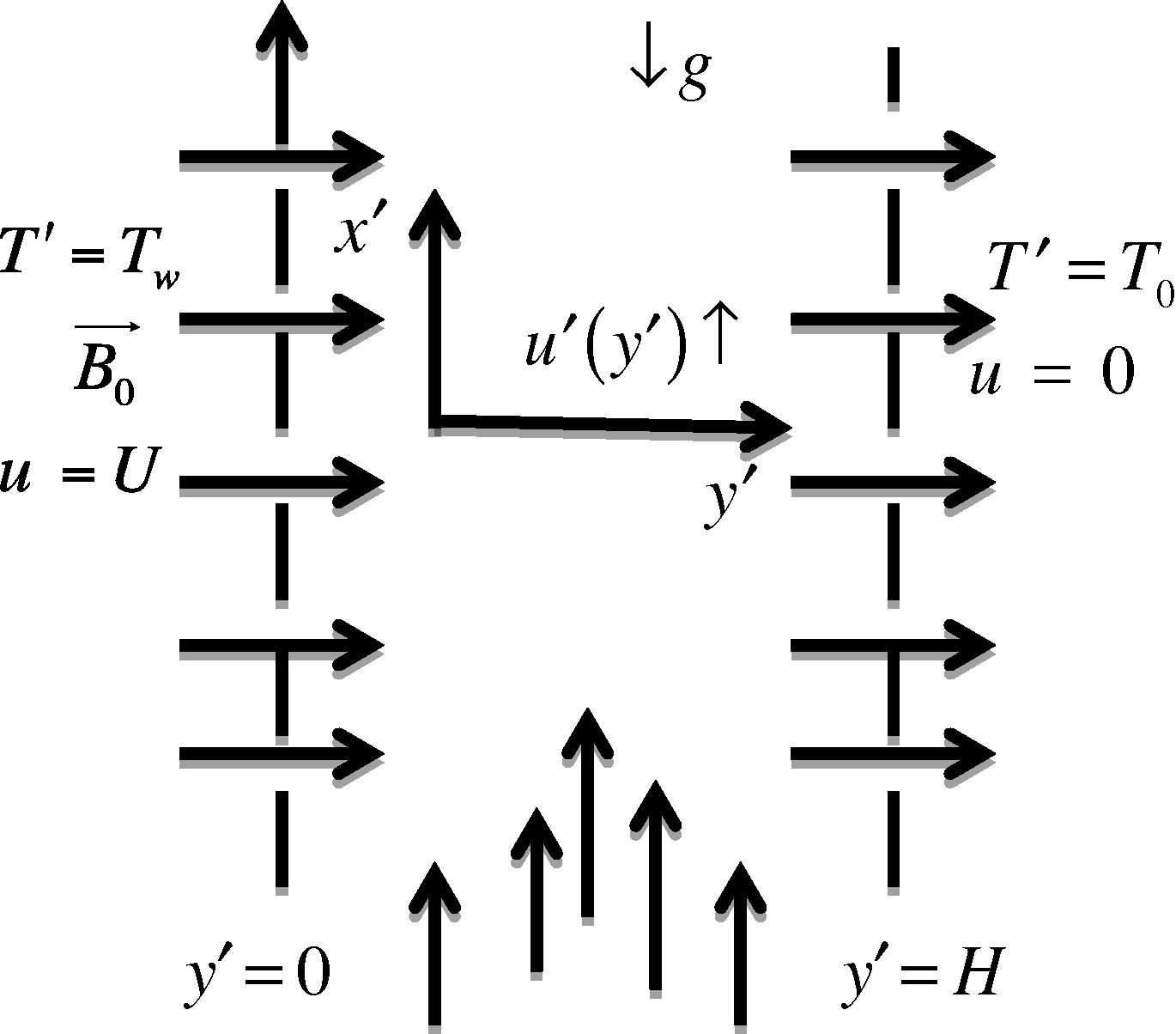
Schematic diagram of the problem.
The quantity qr appearing on the right hand side of Eq. (2) represents the radiative heat flux in the y′-direction where the radiative heat flux in the x′-direction is considered insignificant in comparison with that in the y′-direction. The radiative heat flux term in the problem is simplified by using the Rosseland diffusion approximation for an optically thick fluid according to (Hossaini et al., 1999; Aydin and Kaya, 2009; Rashad, 2009; Ali Agha et al., 2014).
The required initial and boundary conditions to be satisfied are
The dimensionless quantities used in the present problem are
By introducing the dimensionless quantities defined in Eq. (5), Eqs. (1) and (2) in dimensionless form are
3 Analytical solution
The governing equations presented in the previous section are highly nonlinear and exhibited no analytical solutions. In general such solution can be very useful in validating computer routines of complicated time dependent two or three-dimensional free convective and radiating conducting fluid and comparison with experimental data. It is therefore of interest to reduce the governing equations of the present problem to the form that can be solved analytically. A special case of the present problem that exhibits analytical solution is the problem of steady state MHD free-convective Couette flow between vertical porous plates with thermal radiation. The resulting steady state equations and boundary conditions for this special case can be written as
To construct analytical solutions of Eqs. (9) and (10) subject to (11), it is assumed that the radiation parameter is small and taking a power series expansion in the radiation parameter
employs a regular perturbation method.
From (13) the steady-state skin frictions on the boundaries are:
Also from (14) the steady-state Nusselt numbers on the boundaries are:
4 Numerical solution procedure
The nonlinear momentum and energy equations given in (6) and (7) are solved under the appropriate initial and boundary condition (8) by the implicit finite difference method. The transport Eqs. (6), (7) at the grid point (i, j) are expressed in difference form using Taylor’s expansion. The momentum equation reads.
Thus the values of u and θ at grid point t = 0 are known; hence the temperature field has been solved at time
using the known values of the previous time t = ti for all
. Then the velocity field is evaluated using the already known value of temperature field obtained at
. These processes are repeated till the required solution of u and θ is gained at convergence criteria.
The analytical solutions derived in Section 3 are used to check the accuracy and effectiveness of the numerical procedure. For large values of time a steady state condition is reached which corresponds to the steady state solution obtained analytically by using the perturbation technique. A comparison between analytical and corresponding numerical results is presented in Fig. 2.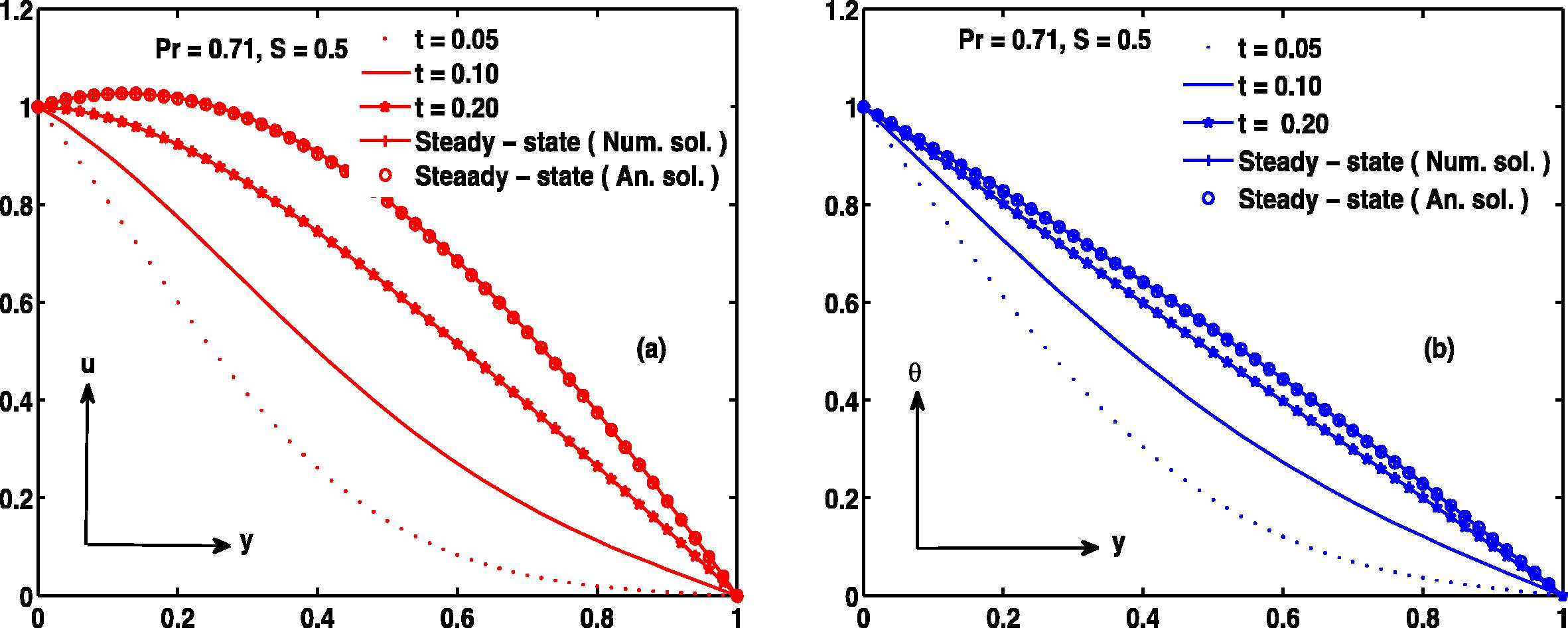
Velocity profile
.
5 Results and discussion
Numerical calculation on velocity field and temperature field using the finite difference method is performed with the help of the dimensionless parameters that govern the flow. The parameters are the magnetic parameter (M), the radiation parameter (R), the temperature difference (CT), the Grashof number (Gr) taken greater than zero that corresponds to external cooling of the moving porous plate, suction/injection parameter (S) simultaneously opposite to porous plates at the same rate and the Prandtl number (Pr) chosen as 0.71 and 7.0 that physically represent two fluids air and water, respectively. Moreover, time is chosen between
so as to capture the transient behavior of both velocity and temperature. In the present numerical computation the numerical values of R are in range of
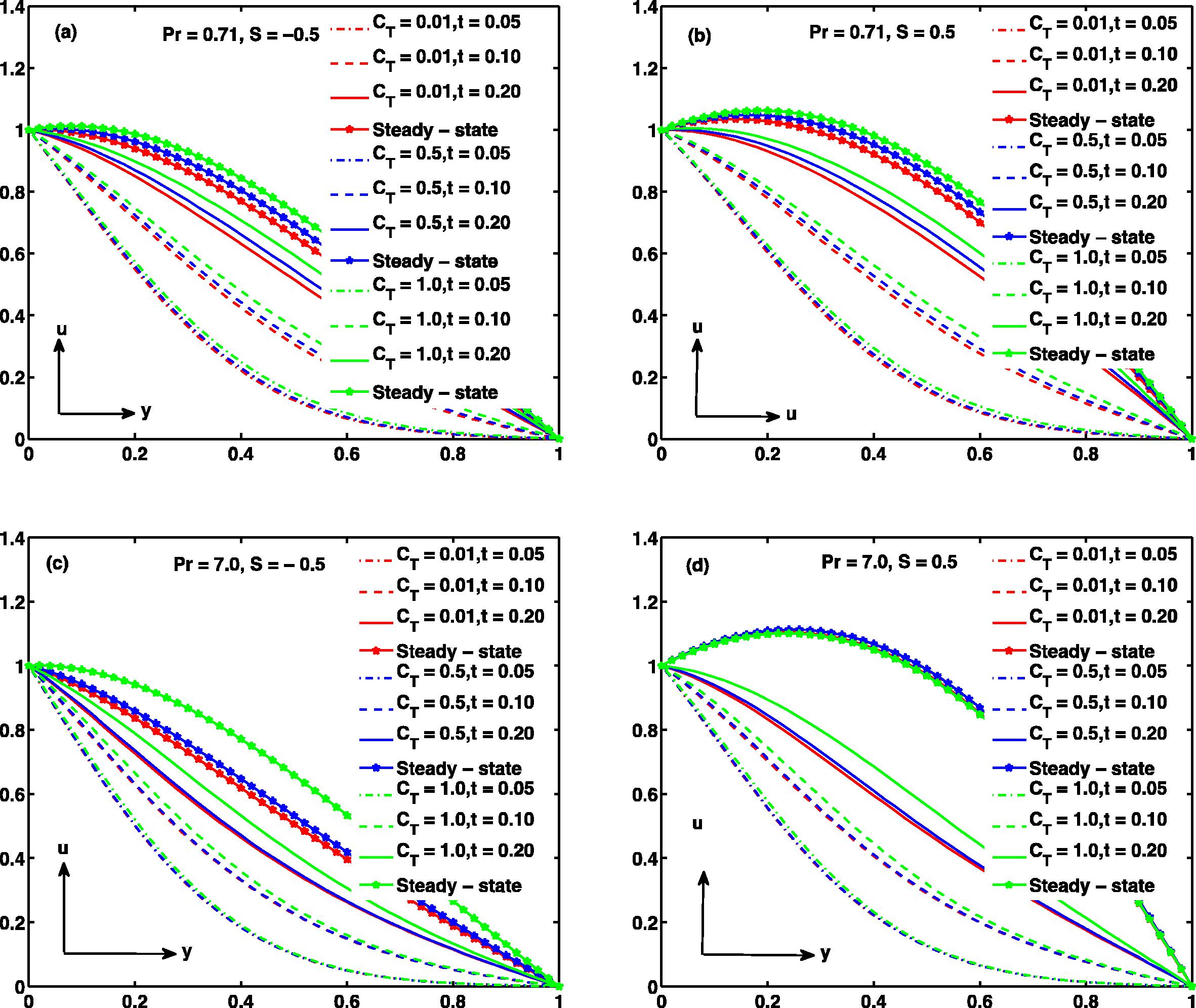
. A large value of, R leads to finite time temperature blow up since the terms associated with R are strong heat sources (Makinde and Chinyoka, 2010). Besides, all other parameters are taken arbitrary. To clearly report the influence of the flow governing parameters on velocity, temperature, skin friction and Nusselt number figures have been shown graphically in Fig. 2 through 24. The numerical scheme was validated using the steady state (perturbation) solution obtained from Eqs. (13) and (14); and our results are found in good agreement between numerical and perturbation solution in a steady state situation as depicted in Fig. 2. Fig. 3a and b describes the influence of S and t on velocity profile. This figure reports that as time increases the velocity (air and water) increases and attains steady state. The figure reveals that when injection (S > 0) takes place at, y = 0 the fluid velocities (air and water) are higher compared with suction (S < 0). Fig. 4 illustrates the effect of Prandtl number (Pr) under the influence of suction and injection respectively. It is observed that the velocity of air (Pr = 0.71) is higher than water (Pr = 7.0) for S < 0 as shown in Fig. 4a while fluid velocity of air (Pr = 0.71) is less than water (Pr = 7.0) for S > 0 as narrated in Fig. 4b. The inspection of the temperature difference parameter CT is drawn in Fig. 5. The result shows that velocity increases with an increase in CT. In Fig. 5d the role of CT is insignificant on velocity in case of water (Pr = 7.0) during steady state with injection at y = 0 and suction at y = 1 which is not true when there is injection at y = 1 and suction at y = 0 as presented in Fig. 5c. However, it is interesting to mention that during steady and unsteady state, the impact of CT is more pronounced in air than water whether suction or injection applied at y = 0 or y = 1 see Fig. 5a and b in comparison with Fig. 5c and d.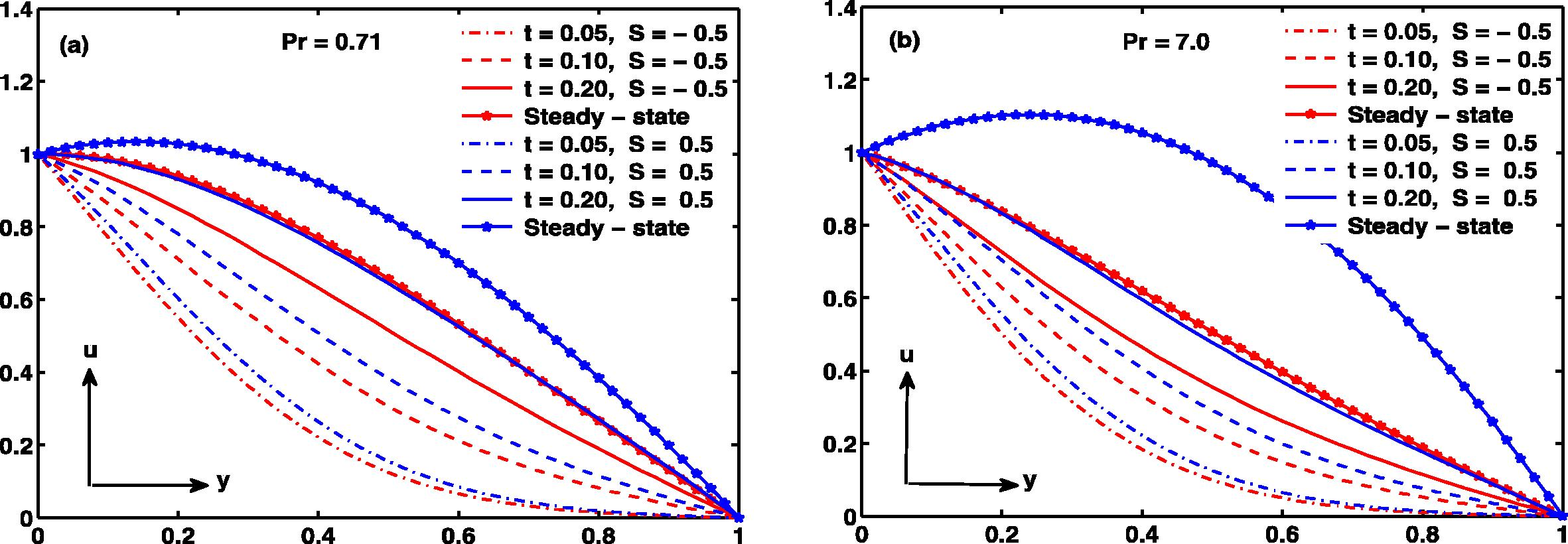
Velocity profile
.
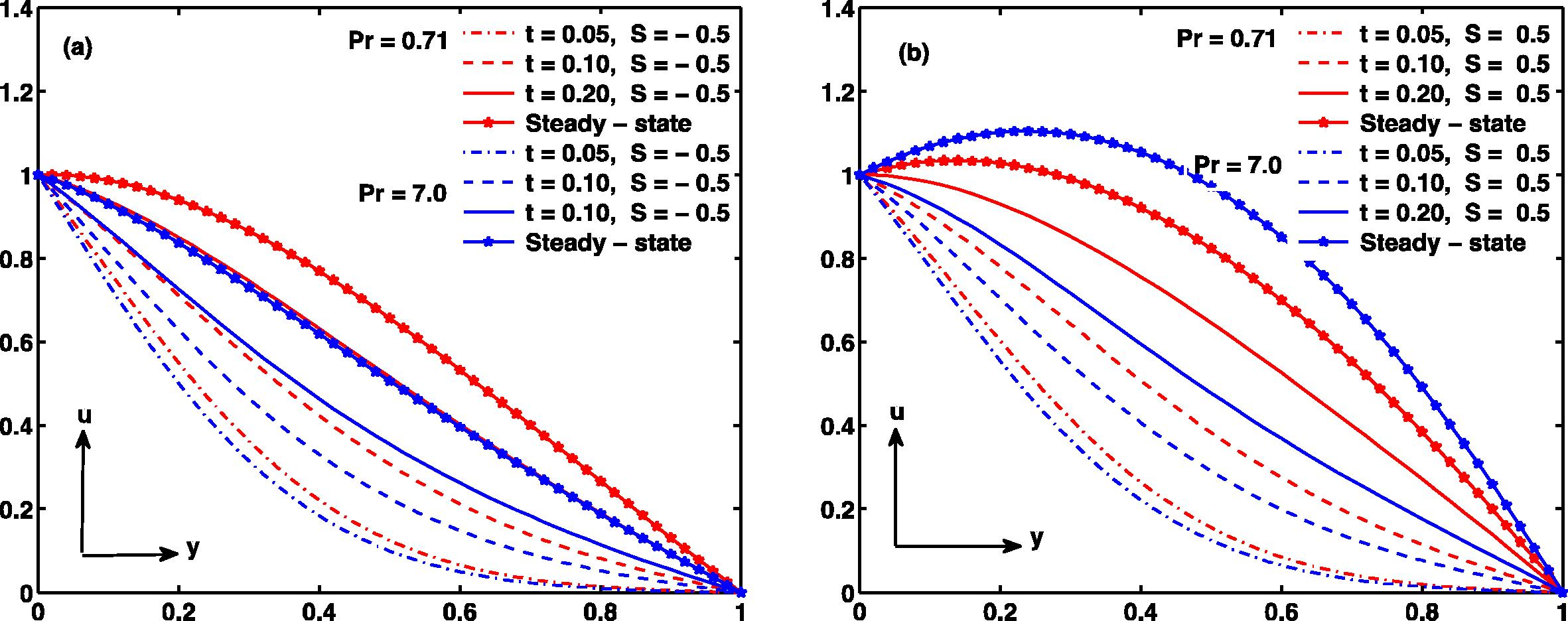
Velocity profile
.
Velocity profile
.
The magnetic parameter M produces resistive force, which acts in the opposite direction to the fluid motion as illustrated in Fig. 6. The impact of this can be clearly seen in Fig. 6a–d respectively, that as magnetic parameter M increases the velocity decreases for both air and water.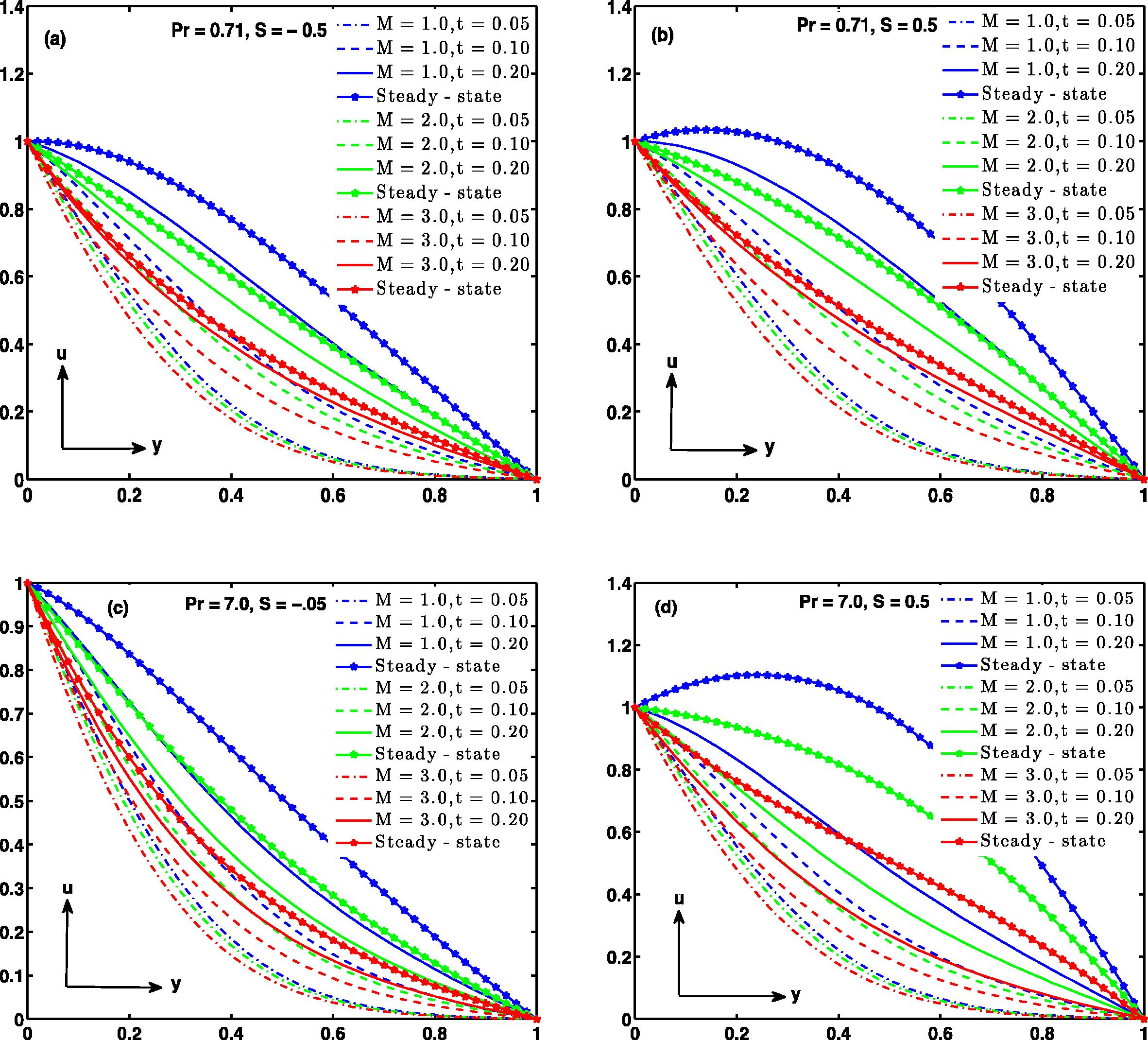
Velocity profile
.
In Fig. 7 velocity increases as radiation parameter increases. Also, it is evident from Fig. 7a–d that the impact of R is more significant incase of air than water.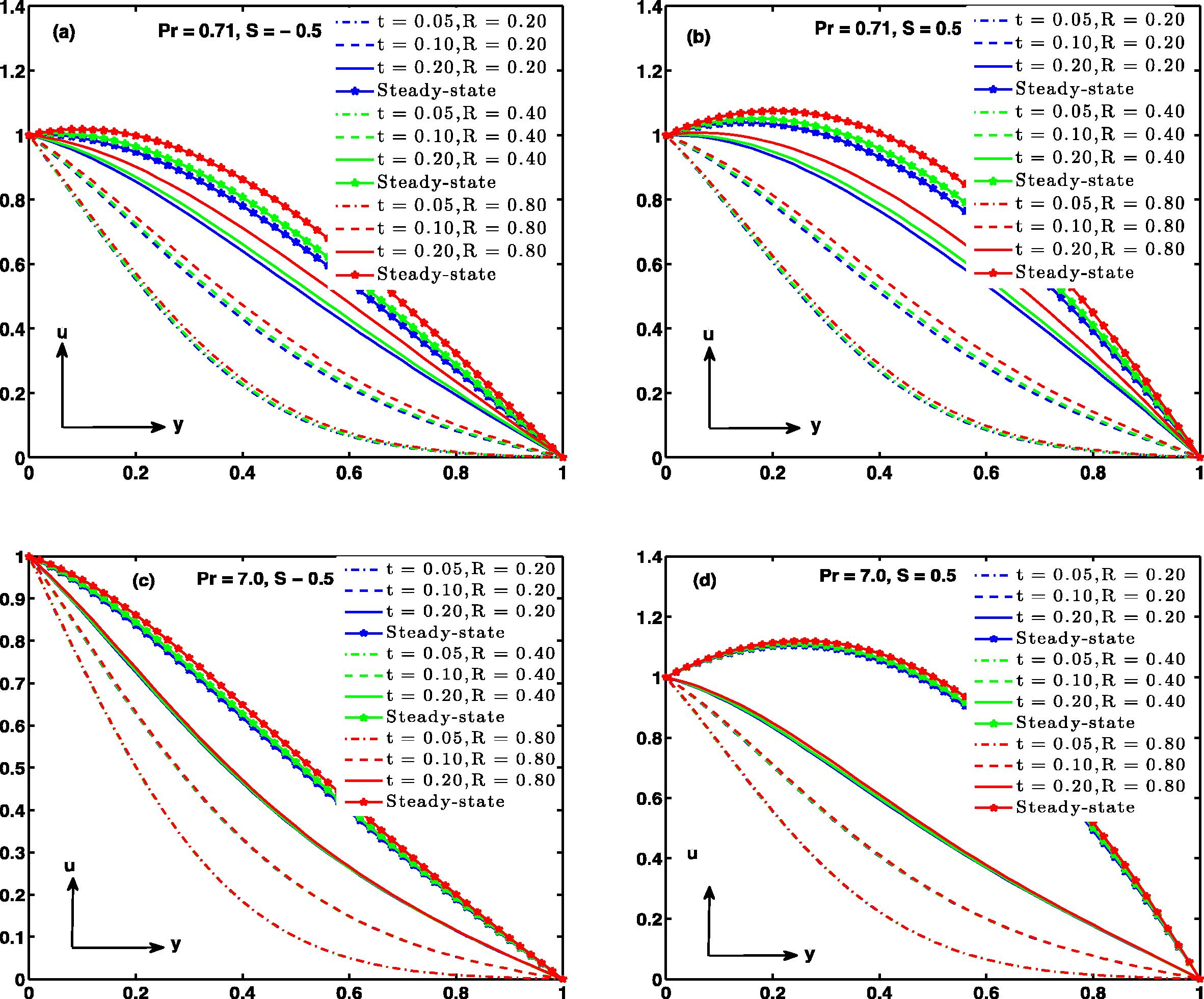
Velocity profile
.
The influence of S and t on temperature profile as seen in Fig. 8(a–d) tells us that as time increases the temperature (air and water) increases and attains steady state value. The figure portrays that when injection (S > 0) takes place at y = 0 the temperature (air and water) is higher compared with suction (S < 0) at y = 0.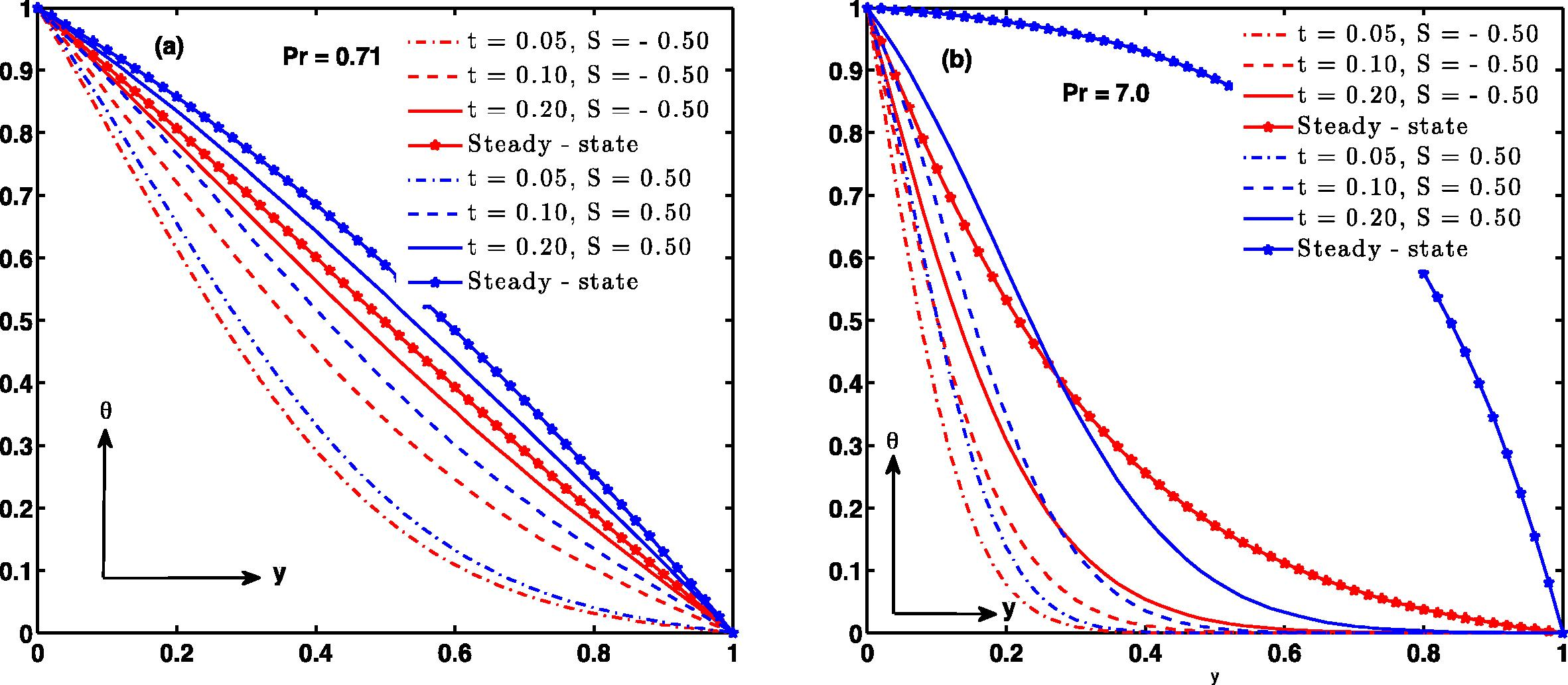
Temperature profile
.
Fig. 9 delineates the effect of Prandtl number (Pr) on temperature profile under the influence of suction and injection respectively. It is observed that the temperature of air (Pr = 0.71) is higher than water (Pr = 7.0) for S < 0 as depicted in Fig. 9a. It is interesting to note that at steady state the temperature is higher for water (Pr = 7.0) in comparison with air (Pr = 0.71) once injection is applied at, y = 0 as illustrated in Fig. 10b which is not true in case of suction. However, during unsteady state the temperature is high incase of air in comparison with water for both suction and injection see Fig. 9a and b respectively. This is due to the physical fact that, as the Prandtl number increases; the thermal diffusivity of the fluid reduces which results in a corresponding decrease in the fluid temperature.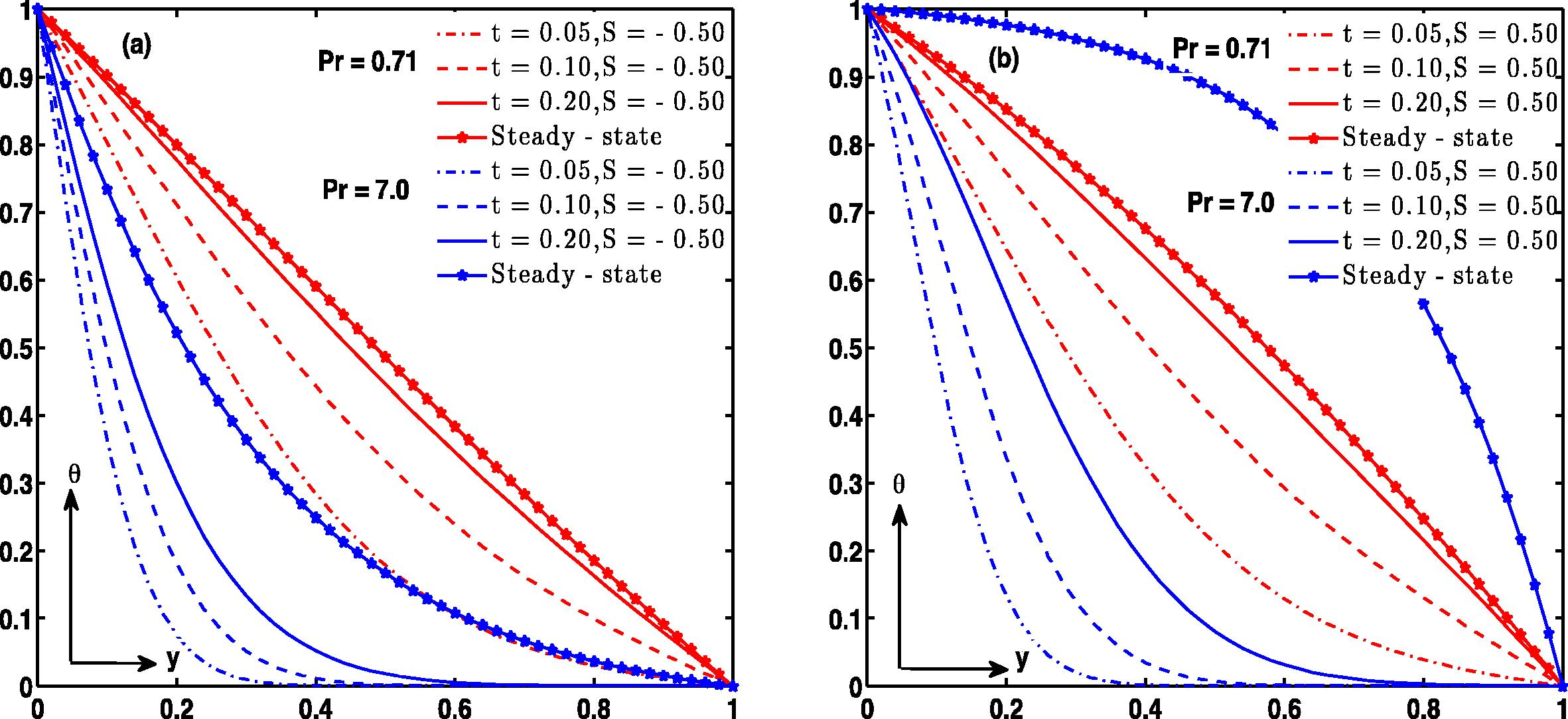
Temperature profile
.
From Fig. 10 it is noted that the temperature increases with time and temperature difference parameter (CT) and finally attains its steady state (see Fig. 10(a–d)). Furthermore, the steady state temperature is higher in case of water (Pr = 7.0) when injection takes place at y = 0 in comparison with suction at y = 0 (see Fig. 10c and d).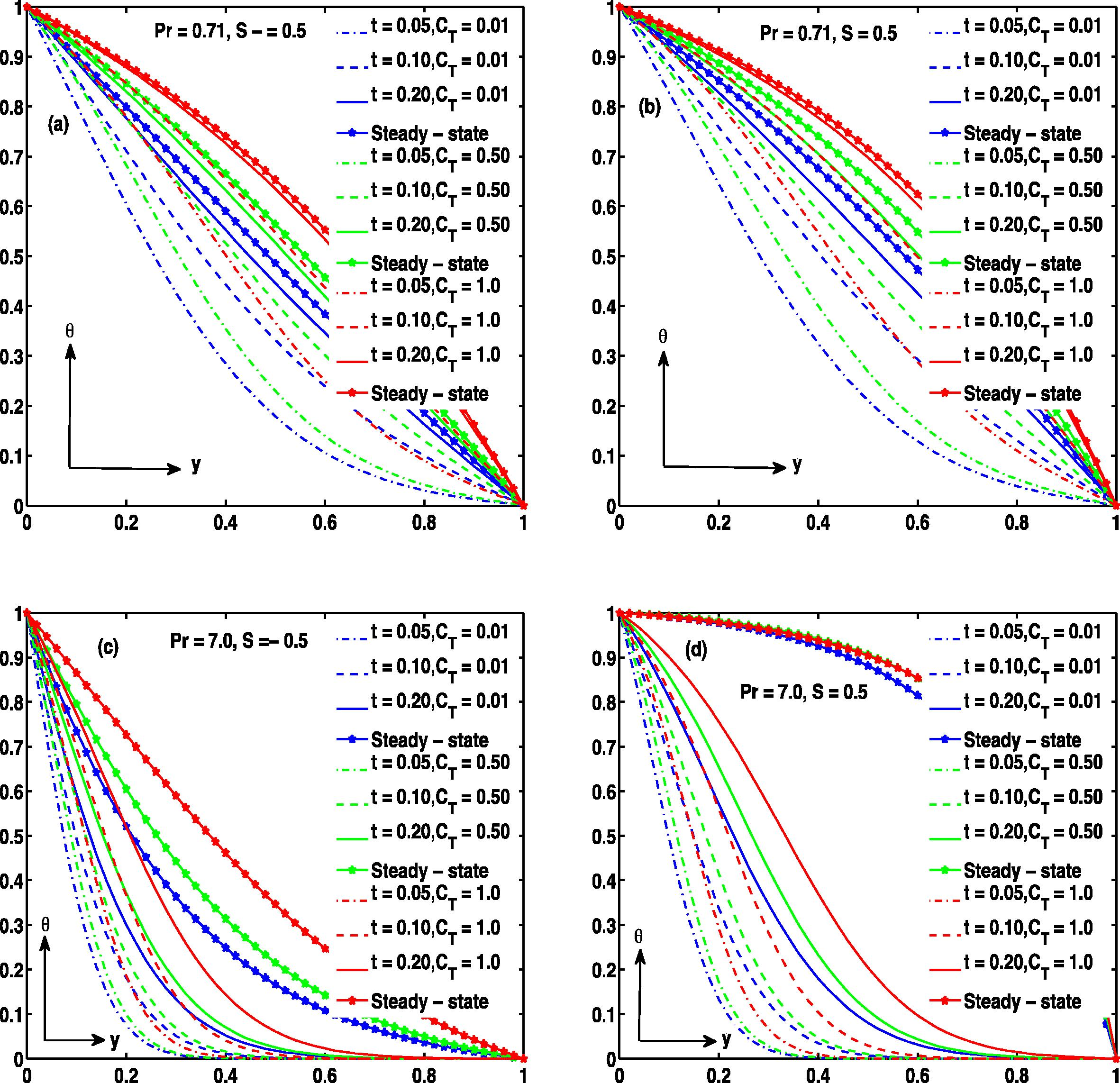
Temperature profile (R = 0.2).
In Fig. 11, the unsteady and steady state temperature distribution for different values of radiation parameter R and time t is outlined. It is recorded that temperature increases significantly as R increases. In addition, there is a strong influence of R on temperature variation specifically in steady situation where injection is imposed at y = 0 in contrast with suction at y = 0 in case of water (Pr = 7.0), as seen in Fig. 11c and d respectively.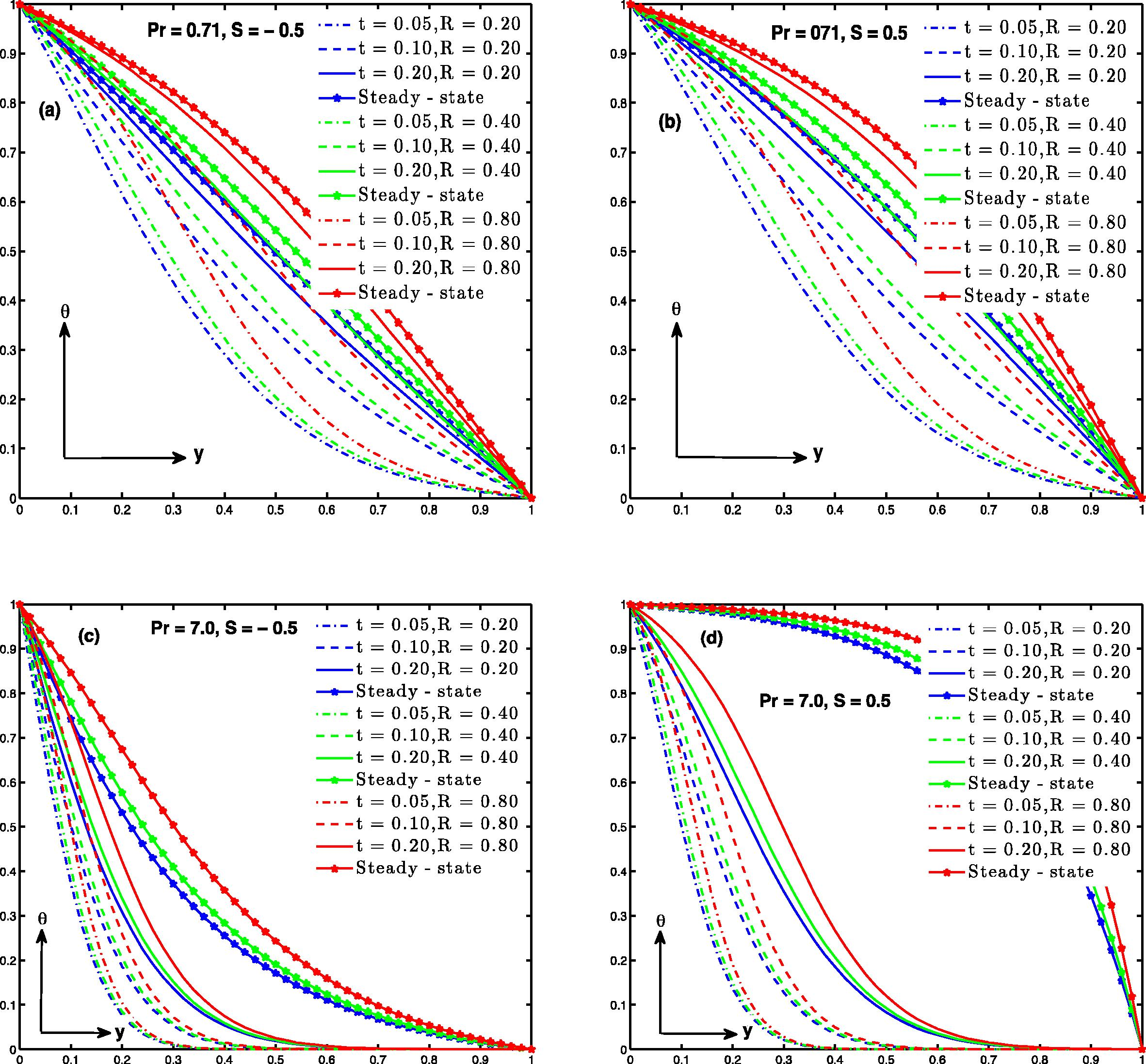
Temperature profile (CT = 0.1).
In Figs. 12 and 13, the variation of skin friction for air (Pr = 0.71) and water (Pr = 7.0) at the plate y = 0 is narrated. Fig. 12 depicts the variation of skin friction with respect to CT and time. From the set out of this figure it is voice-over that the skin friction increases with time and ultimately reaches its steady state value. It is observed from this figure that as CT increases the skin friction increases.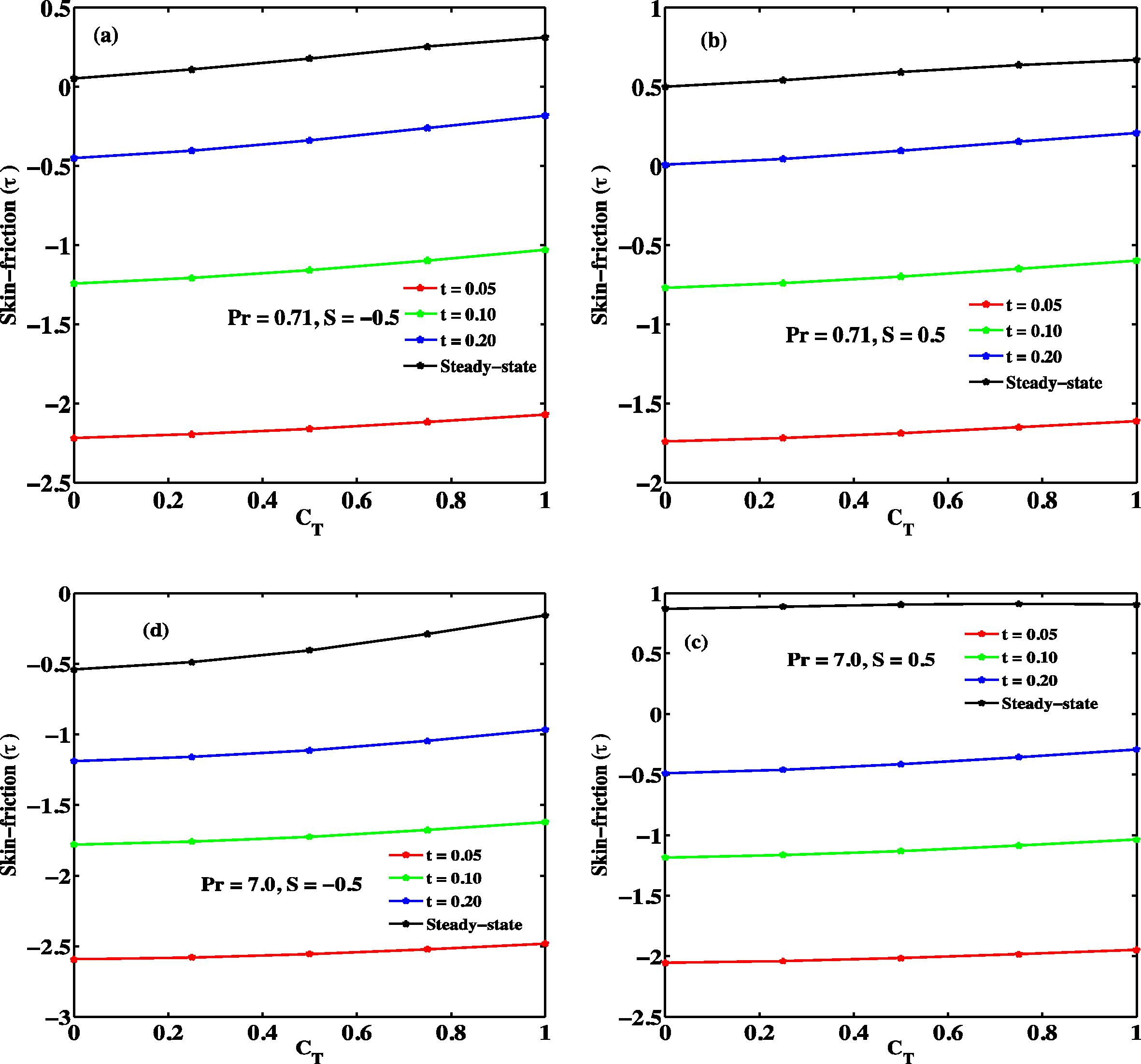
Skin frictions against CT at y = 0.
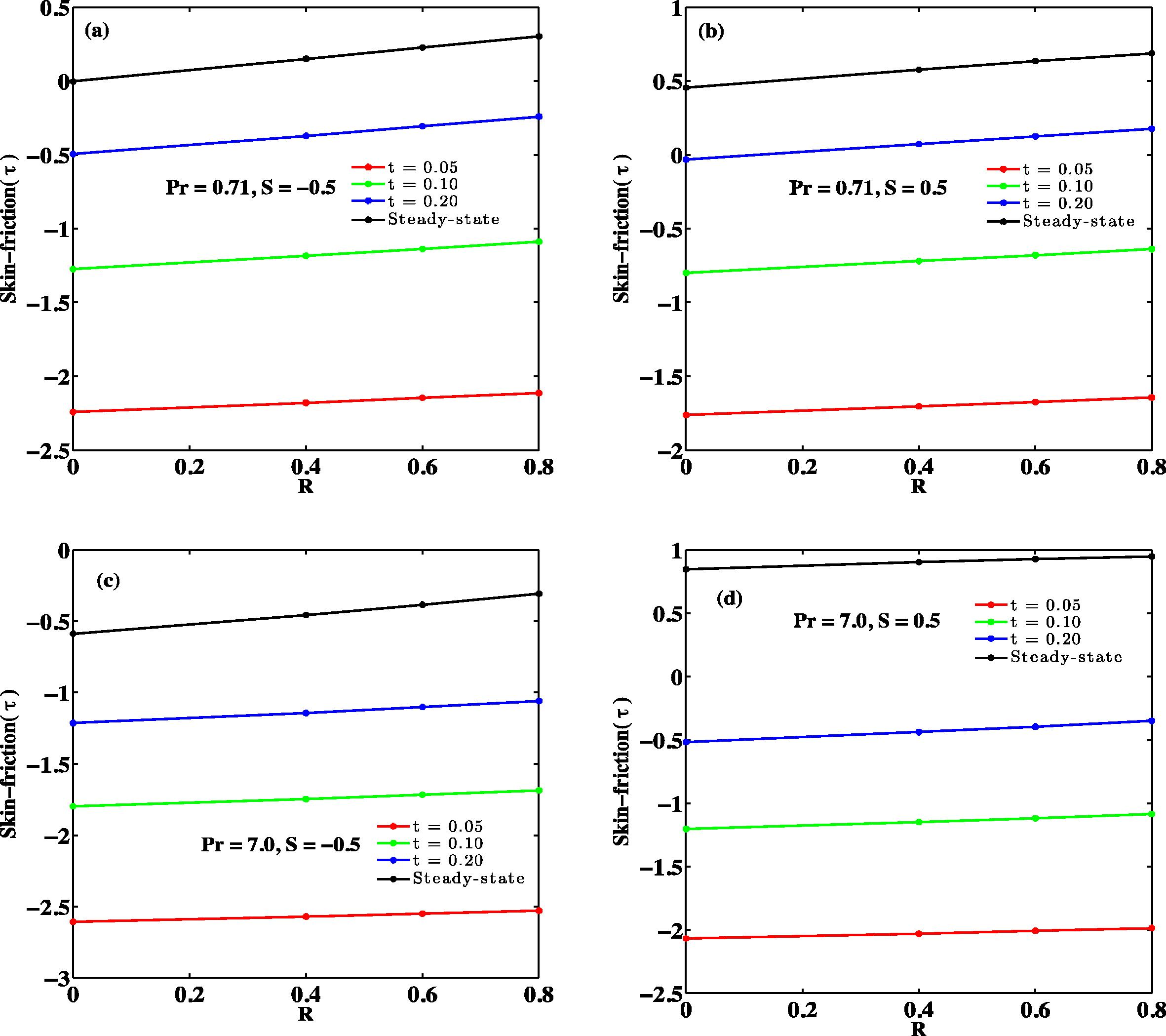
Skin frictions against R at y = 0.
Fig. 13(a–d) shows the description profiles for skin friction for different values of t and radiation parameter R. These figures reflect that, as time increases the skin friction increases until steady state is achieved. It is interesting to emphasize that the numerical value of a skin friction is higher for injection (S > 0) in comparison with suction (S < 0) acting at y = 0. Furthermore, the steady state skin friction values for air (Pr = 0.71) are larger than that of water (Pr = 7.0) in case of suction (S < 0) while it does the reverse in the case of injection (S > 0) acting at y = 0.
Figs. 14 and 15 also sketch out the landmark influence of radiation parameter and temperature difference on Nusselt number (rate of heat transfer) at plates y = 0. In Fig. 14(a–d) and Fig. 15(a–d) as R or CT increases Nusselt number decreases for considered values of, S Pr and t respectively. Furthermore, it is remarkable to point out that the impacts of R and CT on Nusselt number are more prominent due to suction for S < 0 either air or water. From the figures it is also clear that the role of CT and R is more pronounced in case of water (Pr = 7.0) in comparison with air (Pr = 0.71).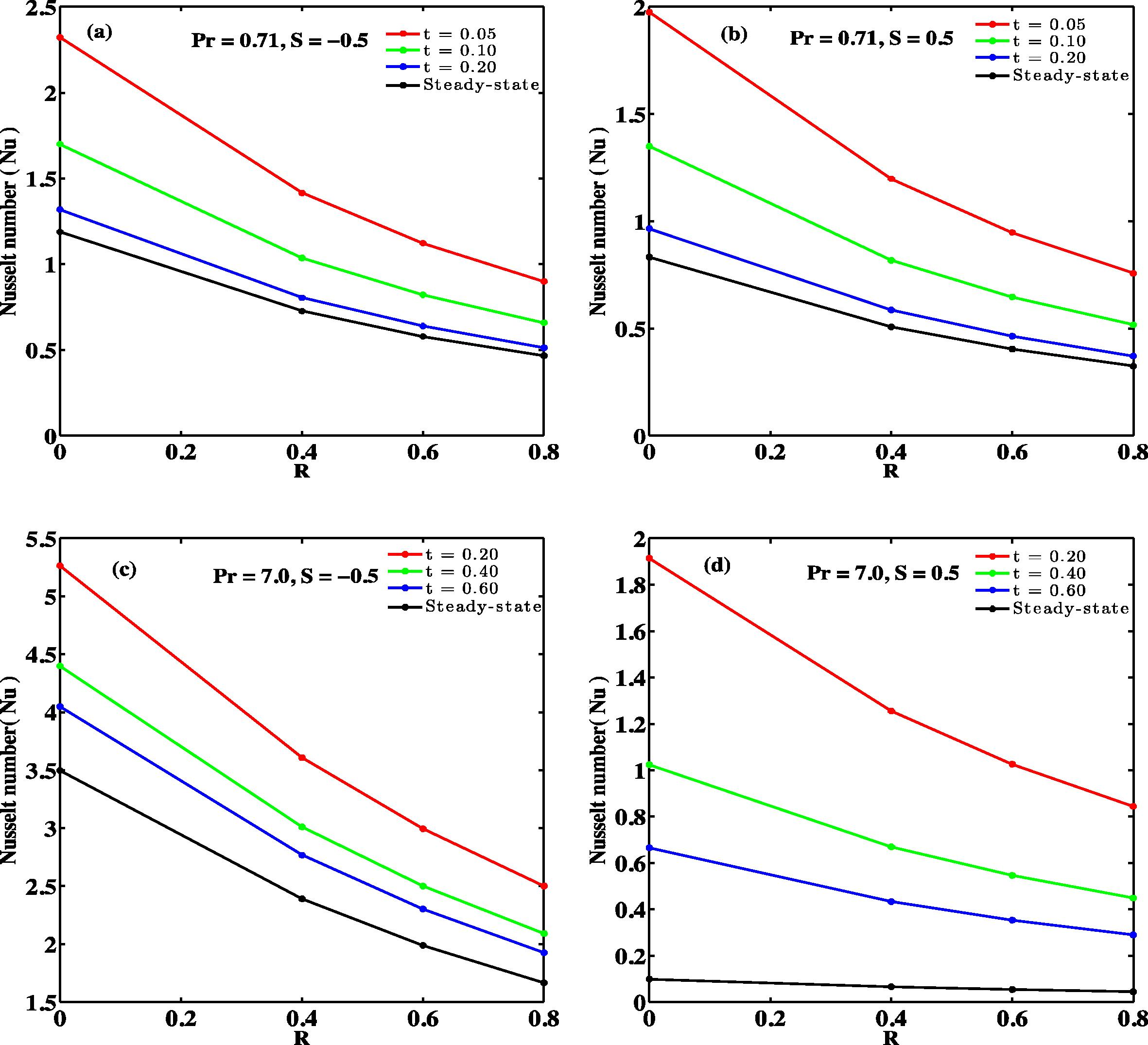
Nusselt numbers against R at y = 0.
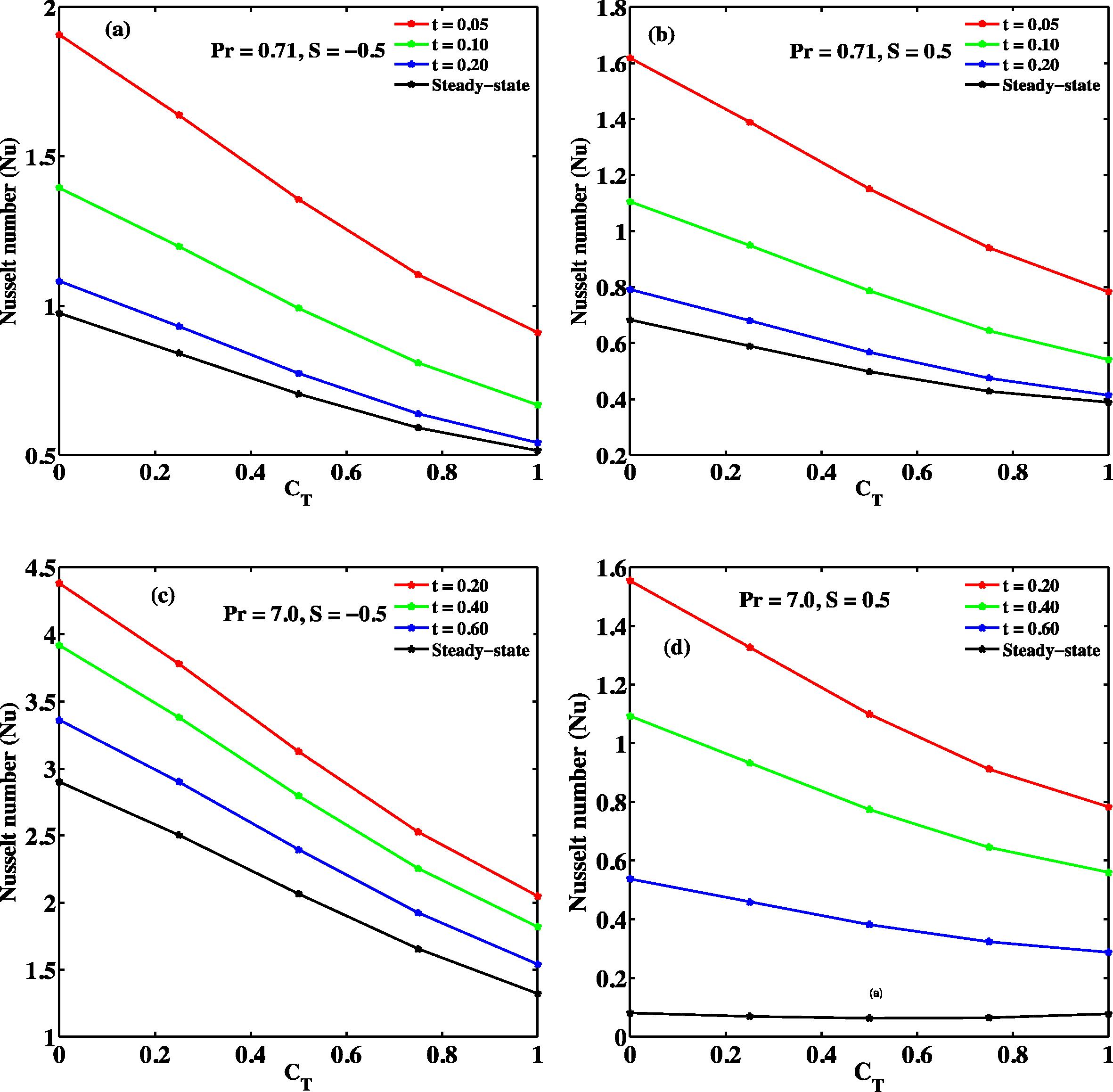
Nusselt numbers against CT at y = 0.
6 Conclusion
The solution of unsteady MHD free-convective Couette flow of a viscous, incompressible and electrically conducting fluid between vertical porous plates with thermal radiation is acquired. The steady state solutions for the non-linear partial differential equations are obtained by the well known perturbation series method while the implicit finite difference technique is used to solve the unsteady equations. The influence of the dimensionless parameters on velocity temperature, skin friction and Nusselt number is demonstrated on figures and discussed. From the results obtained, the findings are:
-
Velocity and temperature field increases with increase in time.
-
Skin-friction increases with increase in time, while Nusselt number decreases with increase in time.
-
Skin friction is always higher in the case of air (Pr = 0.71) in comparison with water (Pr = 7.0) when suction takes place at y′ = 0, while the situation is just reverse with injection at y′ = 0.
-
The rate of heat transfer is higher at porous plate y′ = 0 when suction takes place than injection.
-
Moreover, the time required for the velocity and temperature fields, skin-friction and Nusselt number to attain steady-state strongly rests on the dimensionless parameters M, R, CT, Gr and Pr.
-
The results are found in good agreement between steady state and unsteady solution after some sufficiently large time (t).
-
Also during the numerical computation it is observed that time required to reach steady state is directly proportional to the nature (Prandtl number) of working fluid. Furthermore, convection current is strong as radiation parameter increases.
Acknowledgement
One of the authors Isah B. Yabo is thankful to Usmanu Danfodiyo University, Sokoto for financial support.
References
- Free convection boundary layer flow from a vertical flat plate embedded in a Darcy porous medium filled with a nanofluid: effects of Magnetic field and thermal radiation. Arab J. Sci. Eng.. 2014;39:8331-8340.
- [Google Scholar]
- MHD mixed convective heat transfer flow about an inclined plate. Heat Mass Transfer. 2009;46:129-136.
- [Google Scholar]
- Magnetic field and thermal radiation effects on steady Hydromagnetic Couette flow through a porous channel. Surv. Math. Appl.. 2012;5:215-228.
- [Google Scholar]
- Buoyant Couette–Bingham flow between vertical parallel plates. Int. J. Therm. Sci.. 2008;47(7):811-819.
- [Google Scholar]
- Heat transfer effects on a rotating MHD Couette flow in a channel partially by a porous medium with hall current. J. Appl. Sci. Eng.. 2012;15(3):281-290.
- [Google Scholar]
- Couette–Poiseuille flow of Bingham fluids between two porous parallel plates with slip conditions. J. Nonnewton. Fluid Mech.. 2008;153:1-11.
- [Google Scholar]
- Commencement of Couette flow on Oldroyd with heat sources. Indian J. Pure Appl. Math.. 1989;20(3):267-275.
- [Google Scholar]
- Hydromagnetic rotating flow in a porous medium with slip condition and Hall current. Int. J. Phys. Sci.. 2012;7(10):1540-1548.
- [Google Scholar]
- Hydromagnetic flow of an Oldroyd-B fluid in a rotating system. Int. J. Eng. Sci.. 2004;42:65-78.
- [Google Scholar]
- Unsteady MHD Couette flow of a viscoelastic fluid with heat transfer. Kragujevac J. Sci.. 2010;32:5-15.
- [Google Scholar]
- The effect of suction and injection on unsteady Couette flow with variable properties. Kragujevac J. Sci.. 2010;32:17-24.
- [Google Scholar]
- The effect of radiation on free convection from a porous vertical plate. Int. J. Heat Mass Transf.. 1999;42:181-191.
- [Google Scholar]
- Effect of the chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi infinite vertical permeable moving plate with heat source and suction. Commun. Nonlinear Sci. Numer. Simul.. 2008;13:1056-1066.
- [Google Scholar]
- Unsteady natural convection couette flow of a reactive viscous fluid in a vertical channel. Comput. Math. Model.. 2013;24(3):432-440.
- [Google Scholar]
- Hydromagnetic oscillatory vertical Couette flow of radiating fluid through porous medium with slip and jump boundary conditions. Int. J. Phys. Math. Sci.. 2012;3(1):82-90.
- [Google Scholar]
- Numerical investigation of transient heat transfer to hydromagnetic channel flow with radiative heat and convective cooling. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:3919-3930.
- [Google Scholar]
- Free convective oscillatory flow and mass transfer past a porous plate in the presence of radiation of an optically thin fluid. Therm. Sci.. 2011;15(3):849-857.
- [Google Scholar]
- Perturbation analysis for radiative effect on free convection flows in porous medium in the presence of pressure work and viscous dissipation. Commun. Nonlinear Sci. Numer. Simul.. 2009;14:140-153.
- [Google Scholar]
- Convective heat and mass transfer in a non-newtonian flow formation in a Couette motion in magnetohydrodynamics with time- varying suction. Therm. Sci.. 2011;15(3):749-758.
- [Google Scholar]
- Effects of hall current and rotation on unsteady MHD Couette flow in the presence of an inclined magnetic field. J. Appl. Fluid Mech.. 2012;5(2):67-74.
- [Google Scholar]
- Couette flow of a Bingham plastic in a channel with equally porous parallel walls. J. Nonnewton. Fluid Mech.. 2007;144:42-48.
- [Google Scholar]
- A numerical study for the cessation of Couette flow of non-Newtonian fluids with a yields stress. J. Non-Newtonian Mech.. 2007;143:64-70.
- [Google Scholar]







