Traveling wave solutions of the nonlinear dispersive Klein–Gordon equations

Anjan Biswas; Chaudry Masood Khalique; Abdullahi Rashid Adem

doi:10.1016/j.jksus.2011.05.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

24 (

); 339-342

doi:

10.1016/j.jksus.2011.05.004

Traveling wave solutions of the nonlinear dispersive Klein–Gordon equations

Anjan Biswas^a,*, Chaudry Masood Khalique^b, Abdullahi Rashid Adem^b

a Department of Mathematical Sciences, Delaware State University, Dover, DE 19901-2277, USA

b International Institute for Symmetry Analysis and Mathematical Modeling, Department of Mathematical Sciences, North-West University, Mafikeng Campus, Private Bag X2046, Mmabatho 2735, South Africa

*Corresponding author. Tel.: +1 302 857 7913; fax: +1 302 857 7054. biswas.anjan@gmail.com (Anjan Biswas)

Received: 2011-4-16, Accepted: 2011-5-5, Published: 2011-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 20 May 2011

Peer review under responsibility of King Saud University.

Abstract

In this paper, the traveling wave solutions to the nonlinear dispersive Klein–Gordon equation is obtained. There are five forms of nonlineraity that are studied in this paper. While in each of the cases, the results are in terms of quadratures, the numerical simulation of the solutions are given for completeness.

Keywords

Evolution equations

Solitons

Integrability

Show Related Articles from PubMed

1 Introduction

Klein–Gordon equation (KGE) appears in the study of relativistic Quantum Mechanics (Aguero et al., 2009; Basak et al., 2009; Bawin and Jaminon, 1984; Biswas et al., 2008; Chen, 2005; Cheng, 2011; Comay, 2004; Lakshmi, 2009; Li et al., 2010; Sassaman and Biswas, 2009, 2010a,b, 2011; Yasuk et al., 2006; Zheng and Lai, 2009 ). There are various studies on this equation that has been conducted during the past decades. There are soliton solutions, shock wave solutions are also obtained. In addition, the soliton perturbation theory was also studied for this equation. Later, this equation was extended to (1 + 2) dimensions and in addition the evolution and dispersion terms were generalized (Sassaman and Biswas, 2009, 2010a,b, 2011 ).

The nonlinear dispersive KGE appeared in 2009 (Aguero et al., 2009). In this paper, this nonlinear dispersive KGE will be studied by the aid of traveling wave hypothesis. Traveling wave hypothesis is one of the most fundamental mechanisms of integrating nonlinear evolutions equations. It will be observed that the solutions will be in terms of quadratures. Therefore the numerical simulations will be given for each of these cases. There are five types of nonlinearity that will be taken into consideration.

2 Mathematical analysis

The dimensionless form of the nonlinear dispersive KGE that is going to be studied in this paper is given by (Aguero et al., 2009)

(1)

q_{tt} - k [3 (q_{x})^{2} q_{xx}] + F (q) = 0

Here, in (1), the dependent variable q represents the wave profile, while x and t are the independent variables that represents the spatial and temporal variables, respectively. Also, k is a real valued positive constant. The function F(q) represents the nonlinear function. The function F(q) can be written in terms of the potential function U(q) as (Biswas et al., 2008)

(2)

F (q) = - \frac{\partial U}{\partial q}

This potential function U(q) has at least two minima, q₁ and q₃ and a maxima at q₂ such that

(3)

U (q_{1}) = U (q_{3})

2.1

2.1 Traveling wave solution

The starting traveling wave hypothesis for the solution to (1) is

(4)

q (x, t) = g (x - vt)

where v is the velocity of the wave while the function g represents the shape of the wave profile. Substituting this hypothesis into (1) gives

(5)

v^{2} g^{″} - 3 k (g^{'})^{2} g^{″} + F (g) = 0

Now multiplying both sides of (2) by g′ and integrating yields

(6)

2 v^{2} (g^{'})^{2} - 3 k (g^{'})^{4} + 4 \int g^{'} F (g) d g = 0

which can be solved for g′ once the nonlinear functional F(g) is known.

In this paper there are five types of nonlinearity will be considered. They are (Sassaman and Biswas, 2009, 2010a,b, 2011 )

(7)

F (q) = aq - {bq}^{2}

(8)

F (q) = aq - {bq}^{3}

(9)

F (q) = aq - {bq}^{n}

(10)

F (q) = aq - {bq}^{n} + {cq}^{2 n - 1}

(11)

F (q) = aq - {bq}^{1 - n} + {cq}^{n + 1}

where in (7)–(11), a, b and c are real valued constants. The exponent n in (9)–(11) are positive integers and their further restrictions will be given in the respective subsections. These five forms will be labeled as Forms I–V, respectively.

3 Analytical and numerical solutions

In this section, the analytical and numerical solutions to (3) will be obtained for the five different forms of nonlinearity that are described in the previous section.

3.1

3.1 FORM-I

For the first form, the nonlinear dispersive KGE is given by

(12)

q_{tt} - k [3 (q_{x})^{2} q_{xx}] + aq - {bq}^{2} = 0

In this case, Eq. (6) reduces to

(13)

9 k (g^{'})^{4} - 6 v^{2} (g^{'})^{2} - 6 {ag}^{2} + 4 {bg}^{3} + c_{1} = 0

where c₁ is a constant of integration. Solving for g′ gives

(14)

g^{'} = \frac{1}{\sqrt{3 k}} {[v^{2} - \sqrt{v^{4} - k (4 {bg}^{3} - 6 {ag}^{2} + c_{1})}]}^{\frac{1}{2}}

Separating variables yield

(15)

\frac{x - vt}{\sqrt{3 k}} + c_{2} = \int^{g} \frac{d y}{{[v^{2} - \sqrt{v^{4} - k (4 {by}^{3} - 6 {ay}^{2} + c_{1})}]}^{\frac{1}{2}}}

The following figure shows the profile of the traveling wave where the parameter values are v = k = 1, a = b = −1, while c₁ = c₂ = 0 (Fig. 1).

Figure 1

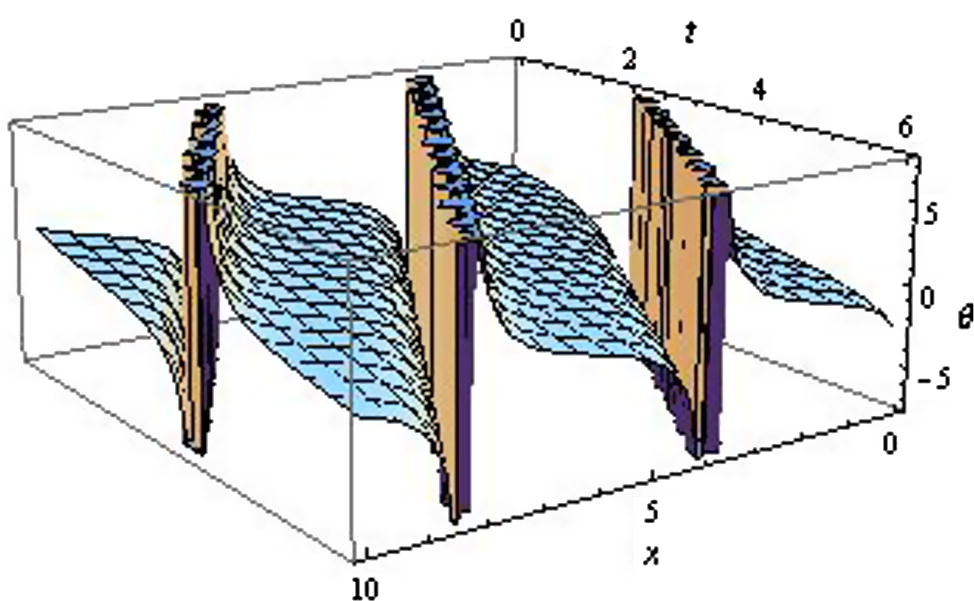
Wave profile for KGE (Form-I).

3.2

3.2 FORM-II

With the second form, the nonlinear dispersive KGE is given by

(16)

q_{tt} - k [3 (q_{x})^{2} q_{xx}] + aq - {bq}^{3} = 0

In this case, Eq. (6) reduces to

(17)

3 k (g^{'})^{4} - 2 v^{2} (g^{'})^{2} - 2 {ag}^{2} - {bg}^{4} + c_{1} = 0

where c₁ is a constant of integration. Solving for g′ gives

(18)

g^{'} = \frac{1}{\sqrt{3 k}} {[v^{2} \pm \sqrt{v^{4} - 3 k ({bg}^{4} - 2 {ag}^{2} + c_{1})}]}^{\frac{1}{2}}

By separation of variables,

(19)

\frac{x - vt}{\sqrt{3 k}} + c_{2} = \int^{g} \frac{d y}{{[v^{2} \pm \sqrt{v^{4} - 3 k ({by}^{4} - 2 {ay}^{2} + c_{1})}]}^{\frac{1}{2}}}

The following figure shows the profile of the traveling wave where the parameter values are v = k = a = b = 1, while c₁ = c₂ = 0 (Fig. 2).

Figure 2

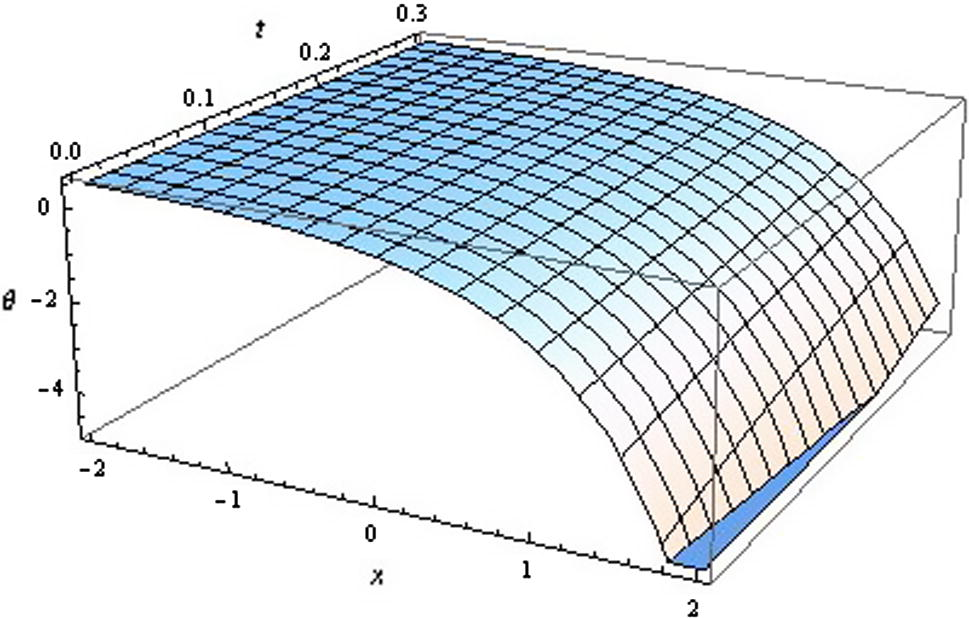
Wave profile for KGE (Form-II).

3.3

3.3 FORM-III

For the third form, the nonlinear dispersive KGE is given by

(20)

q_{tt} - k [3 (q_{x})^{2} q_{xx}] + aq - {bq}^{n} = 0

where n is a positive integer. If n = 1 or 2, this case collapses to the first two forms. Here, Eq. (6) reduces to

(21)

3 (n + 1) k (g^{'})^{4} - 2 (n + 1) v^{2} (g^{'})^{2} - 2 (n + 1) {ag}^{2} + 4 {bg}^{n + 1} + c_{1} = 0

where c₁ is a constant of integration. Solving for g′ gives

(22)

g^{'} = \frac{1}{\sqrt{3 (n + 1) k}} {[(n + 1) v^{2} \pm \sqrt{(n + 1)^{2} v^{4} - 3 (n + 1) k {4 {bg}^{n + 1} - 2 (n + 1) {ag}^{2} + c_{1}}}]}^{\frac{1}{2}}

Once again, separation of variables yield

(23)

\frac{x - vt}{\sqrt{3 (n + 1) k}} + c_{2} = \int^{g} \frac{d y}{{[(n + 1) v^{2} \pm \sqrt{(n + 1)^{2} v^{4} - 3 (n + 1) k {4 {by}^{n + 1} - 2 (n + 1) {ay}^{2} + c_{1}}}]}^{\frac{1}{2}}}

The following figure shows the profile of the traveling wave where the parameter values are v = k = 1, a = b = −1, with n = 2 while c₁ = c₂ = 0 (Fig. 3).

Figure 3

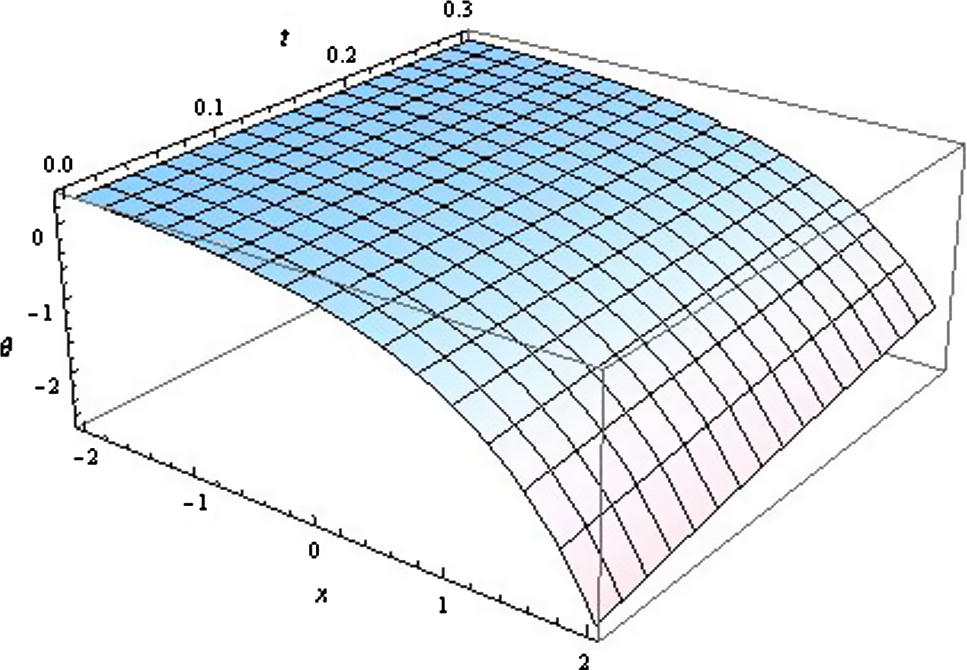
Wave profile for KGE (Form-III).

3.4

3.4 FORM-IV

The fourth form of the nonlinear dispersive KGE is given by

(24)

q_{tt} - k [3 (q_{x})^{2} q_{xx}] + aq - {bq}^{n} + {cq}^{2 n - 1} = 0

where n is a positive integer. If n = 1 or 2, this case collapses to the first two forms. Here, Eq. (6) reduces to

(25)

\begin{matrix} 3 n (n + 1) k (g^{'})^{4} - 2 n (n + 1) v^{2} (g^{'})^{2} \\ - 2 n (n + 1) {ag}^{2} + 4 {nbg}^{n + 1} - 2 (n + 1) {cg}^{2 n} + c_{1} = 0 \end{matrix}

where c₁ is a constant of integration. Solving for g′ gives

(26)

g^{'} = \frac{Q_{1}}{\sqrt{3 n (n + 1) k}}

where

(27)

Q_{1} = {[n (n + 1) v^{2} \pm {(n^{2} (n + 1)^{2} v^{4} - 3 n (n + 1) k \{4 {nby}^{n + 1} - 2 n (n + 1) {ay}^{2} - 2 (n + 1) {cy}^{2 n} + c_{1}\})}^{\frac{1}{2}}]}^{\frac{1}{2}}

By the aid of separation of variables

(28)

\frac{x - vt}{\sqrt{3 n (n + 1) k}} + c_{2} = \int^{g} \frac{d y}{Q_{1}}

The following figure shows the profile of the traveling wave where the parameter values are v = k = 1, a = b = c = 1, with n = 2 while c₁ = c₂ = 0 (Fig. 4).

Figure 4

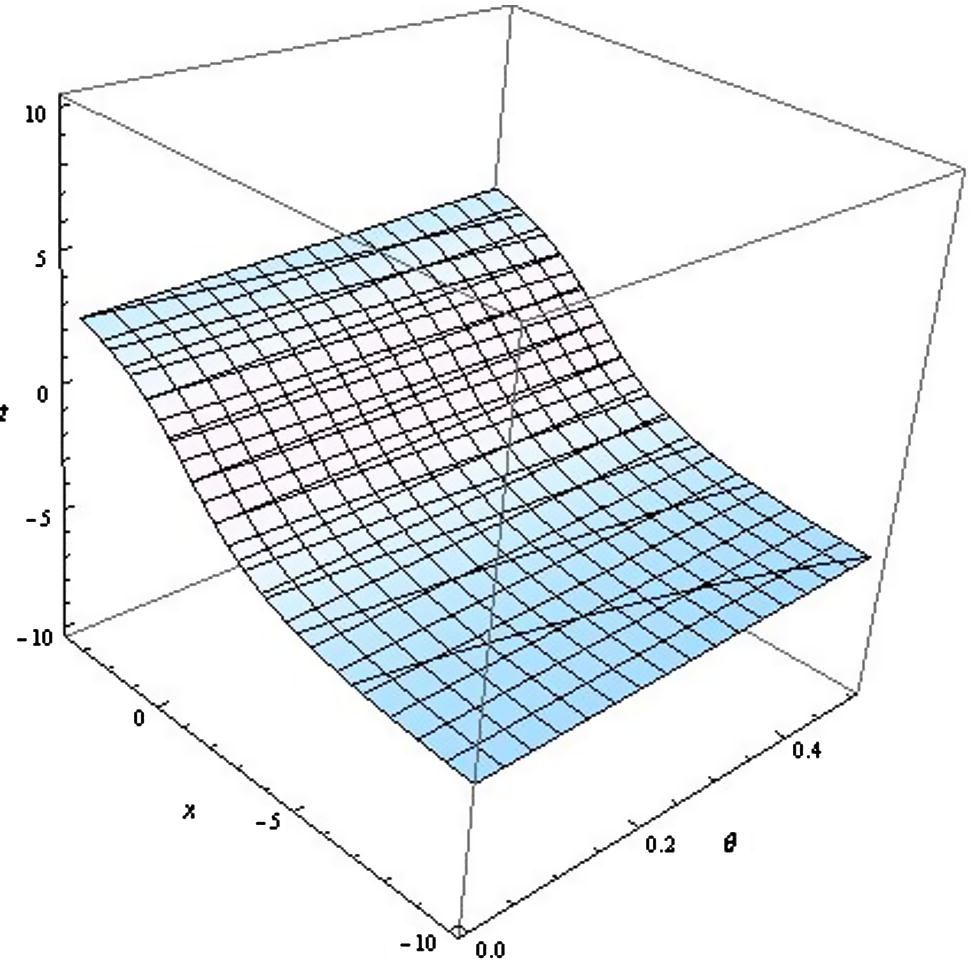
Wave profile for KGE (Form-IV).

3.5

3.5 FORM-V

The fifth and final form of the nonlinear dispersive KGE is given by

(29)

q_{tt} - k [3 (q_{x})^{2} q_{xx}] + aq - {bq}^{1 - n} + {cq}^{n + 1} = 0

where n is a positive integer. If n = 1 or 2, this case collapses to the first two forms. Here, Eq. (6) reduces to

(30)

3 (n^{2} - 4) k (g^{'})^{4} - 2 (n^{2} - 4) v^{2} (g^{'})^{2} - 2 (n^{2} - 4) {ag}^{2} - 4 (n + 2) {bg}^{2 - n} - 2 (n - 2) {cg}^{n + 2} + c_{1} = 0

where c₁ is a constant of integration. Solving for g′ gives

(31)

g^{'} = \frac{Q_{2}}{\sqrt{3 n (n + 1) k}}

where

(32)

Q_{2} = {[(n^{2} - 4) v^{2} \pm {((n^{2} - 4)^{2} v^{4} - 3 (n^{2} - 4) k \{2 (n^{2} - 4) {ay}^{2} + (n + 2) {by}^{2 - n} + 4 (n - 2) {cy}^{n + 2} + c_{1}\})}^{\frac{1}{2}}]}^{\frac{1}{2}}

Thus, separating variables leads to

(33)

\frac{x - vt}{\sqrt{3 n (n + 1) k}} + c_{2} = \int^{g} \frac{d y}{Q_{2}}

The following figure shows the profile of the traveling wave where the parameter values are v = k = a = b = c = 1, with n = 4 while c₁ = c₂ = 0 (Fig. 5).

Figure 5

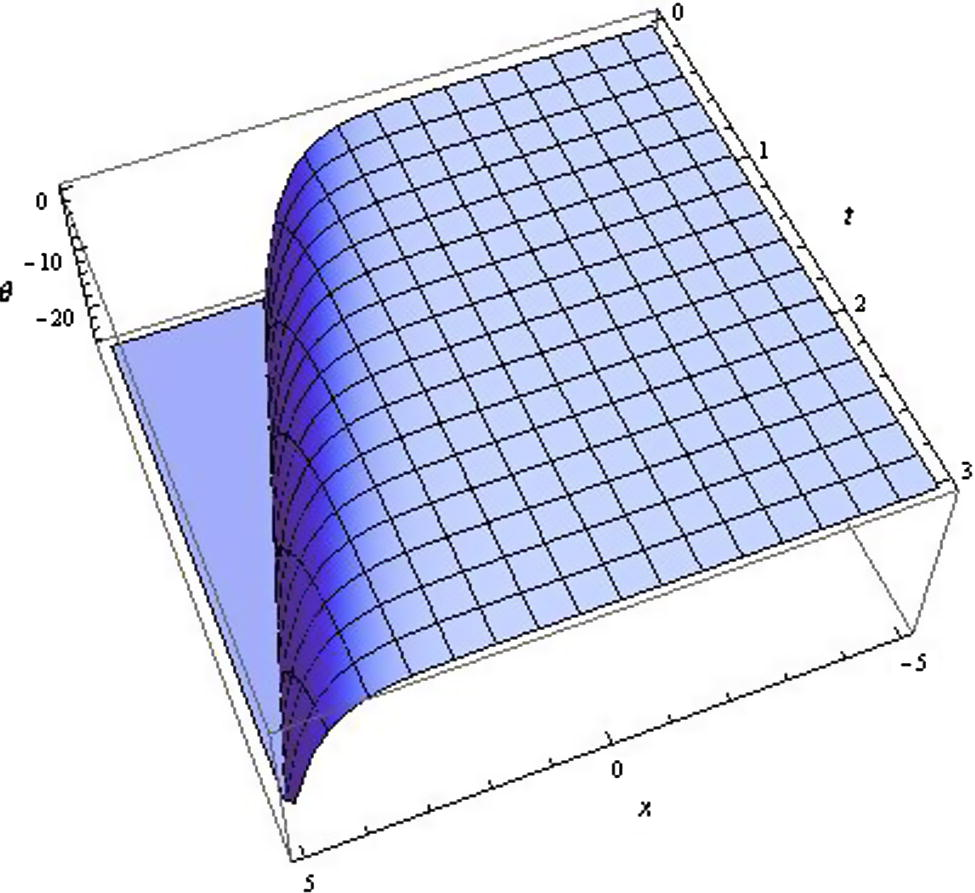
Wave profile for KGE (Form-V).

4 Conclusions

The nonlinear KGE with nonlinear dispersive term is studied in this paper. There are five forms of nonlinearity that are considered. In each of these five cases, the traveling wave solution is obtained. It is observed that the solutions are in terms of quadratures. These integrals cannot be evaluated in terms of known functions. Thus the numerical solutions are given to each of these five cases in order to complete the analysis.

In future, this equation will be further investigated. The conservation laws will be evaluated. The perturbation terms will be taken into account and the adiabatic dynamics of the traveling waves will be evaluated. These results will be reported in future.

References

Aguero M.A., Najera M.L., Aguilar J.A., Sanchez J., . Non-classical traveling wave solutions in a nonlinear Klein–Gordon model. International Journal of Theoretical Physics. 2009;48(7):2098-2111.
[Google Scholar]
Basak K.C., Ray P.C., Bera R.K., . Solution of non-linear Klein—Gordon equation with a quadratic non-linear term by Adomian decomposition method. Communications in Nonlinear Science and Numerical Simulation. 2009;14(3):718-723.
[Google Scholar]
Bawin M., Jaminon M., . Pion form factor and the Klein–Gordon equation. Physical Review C. 1984;30(1):331-334.
[Google Scholar]
Biswas A., Zony C., Zerrad E., . Soliton perturbation theory for the quadratic nonlinear Klein–Gordon equation. Applied Mathematics and Computation. 2008;203(1):153-156.
[Google Scholar]
Chen G., . Solution of the Klein–Gordon for exponential scalar and vector potentials. Physics Letters A. 2005;339(3–5):300-303.
[Google Scholar]
Cheng J-Y., . PT-Symmetric Klein–Gordon oscillator. International Journal of Theoretical Physics.. 2011;50(1):228-232.
[Google Scholar]
Comay E., . Difficulties with the Klein–Gordon equation. Apeiron. 2004;11(3):1-18.
[Google Scholar]
Lakshmi B.S., . On a modified Klein–Gordon equation. Apeiron. 2009;16(4):485-491.
[Google Scholar]
Li K., Wang J., Dulat S., Ma K., . Wigner functions for Klein–Gordon oscillators in non-commutative space. International Journal of Theoretical Physics.. 2010;49(1):134-143.
[Google Scholar]
Sassaman R., Biswas A., . Topological and non-topological solitons of the generalized Klein–Gordon equation. Applied Mathematics and Computation. 2009;215(1):212-220.
[Google Scholar]
Sassaman R., Biswas A., . Topological and non-topological solitons of the Klein–Gordon equation in (1 + 2) dimensions. Nonlinear Dynamics. 2010;61(1-2):23-28.
[Google Scholar]
Sassaman R., Biswas A., . 1-soliton solution of the coupled nonlinear Klein–Gordon equations. Studies in Mathematical Sciences. 2010;1(1):30-37.
[Google Scholar]
Sassaman R., Biswas A., . Soliton solution of the generalized Klein–Gordon equation by semi-inverse variational principle. Mathematics in Engineering, Science and Aerospace. 2011;2(1):99-104.
[Google Scholar]
Yasuk F., Durmus A., Boztosun I., . Exact analytical solution of the relativistic Klein–Gordon equation with noncentral equal scalar and vector potential. Journal of Mathematical Physics. 2006;47:082302.
[Google Scholar]
Zheng Y., Lai S., . A study of three types of nonlinear Klein–Gordon equations. Dynamics of Continuous, Discrete and Impulsive Systems: Series B. 2009;16(2):271-279.
[Google Scholar]