Translate this page into:
Topological aspects of extended Sierpiński structures with help of underlying networks
⁎Corresponding author. m.imran658@uaeu.ac.ae (Muhammad Imran)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Sierpiński networks are the most studied networks of fractal nature with applications in various fields of science. A generalized Sierpiński network is obtained by copying the base network, resulting in the self-similar network. The extended Sierpiński networks are obtained by introducing a new vertex in a generalized Sierpiński network and attaching this vertex with the extreme vertices. Certain network invariants are used to find thermodynamic properties, physio-chemical properties, and biological activities of chemical compounds. These network invariants play a dynamic role in QSAR/QSPR study. In this paper, we discussed Zagreb indices and forgotten topological index for extended Sierpiński networks by using any base network . Moreover, for the studied topological indices, we attained some bounds using different parameters i.e. order, size, maximum and minimum degrees of vertices in network .
Keywords
Zagreb indices
Forgotten index
Extended Sierpiński networks
Extremal networks
1 Introduction
Sierpiński networks are the most studied networks similar to fractals. A fractal is a geometric structure that is self-similar throughout its structure. Fractal models are tremendously common since, nature is full of fractals, for example, plants, canals, coastlines, mountains, clouds, seashells, and tornadoes. Fractals help to study and comprehend key scientific ideas, such as how bacteria grow, freezing water patterns, and brain waves. Sierpiński and Sierpiński type networks are considered in fractal theory (Teplyaev, 1998). Klavžar and Milutinović showed that the Sierpiński networks are similar structure to the Tower of Hanoi (Klavžar and Milutinović, 1997). The Sierpiński networks have many attractive properties for instance coding and metric properties and play an important role in numerous areas of science i.e. dynamic systems, probability, psychology, biology, chemical graph theory, computer networking and physical sciences. For more detail see (Alquran et al., 2020; Naseem et al., 2021; Klavžar et al., 2002; Romik, 2006; Vecchia and Sanges, 1988).
The networks studied in this article assumed to be finite and simple. A network/graph is a collection of set of vertices and set of edges . The order of graph is the cardinality of its vertices, while cardinality of edges is called size and frequently denoted by p and q respectively. The degree of vertex v is known as the number of edges connected to that particular vertex and denoted by . A graph is known as complete if every two vertices are incident to each other. and represent the minimum and maximum degree of a vertex in graph . If = l, then is a l-regular graph. The path, star, cycle and complete graph of order p are represented by and .
In mathematical chemistry, chemical graph theory, and pharmaceutical industry, topological invariants are very important. The physio-chemical properties of chemical structures can be forecasted by using topological invariants. From the last few decades, several topological indices were established and examined in literature (Todeschini and Consonni, 2000), which are applied to attain the facts of numerous characteristics of organic materials which depend on their molecular structures. Wiener a chemist in 1947 introduced the first topological index in order to determine the boiling points of paraffins (Wiener, 1947).
Gutman et al. in Gutman and Trinajstić (1972) and Gutman et al. (1975) introduced the Zagreb indices, which are stated as
Furtula and Gutman (2015) proposed forgotten topological index, stated as
For more detail on topological indices see Liu et al. (2019), Havare (2021), Akhter and Imran (2017), An and Das (2018), Che and Chen (2016), Cristea and Steinsky (2013), Gutman (2013), Horoldagva and Das (2015), Hua and Das (2013), Horoldagva et al. (2016), and Yoon and Kim (2006).
The generalized Sierpiński graph of dimension t is represented by is a graph with vertex set , where . The vertex set is the set of all words of length t, where , two vertices linked by an edge in if and only if there is such that.
-
if .
-
and .
-
and if .
From above definition, it is clear that, if
then
and a word z such that
and
. A vertex of the form
is known as extreme vertex and denoted by
. For a graph
of order
has p extreme vertices. Moreover, extreme vertices have same degree in
as in base graph
and
. Fig. 1 and Fig. 2 represents the generalized and extended Sierpiński graphs respectively, where extended Sierpiński graph is obtained by involving a new vertex x in generalized Sierpiński graph and joining it with extreme vertices. Extended Sierpiński graph is represented by
.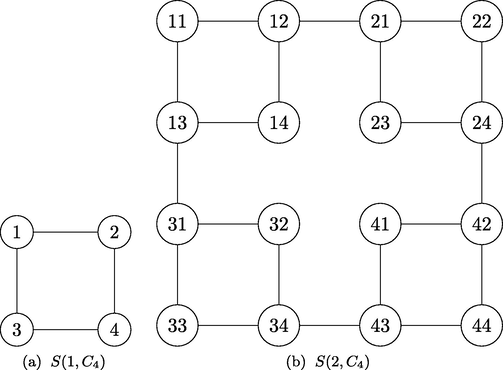
Sierpinski graphs S(1,C4) and S(2,C4).
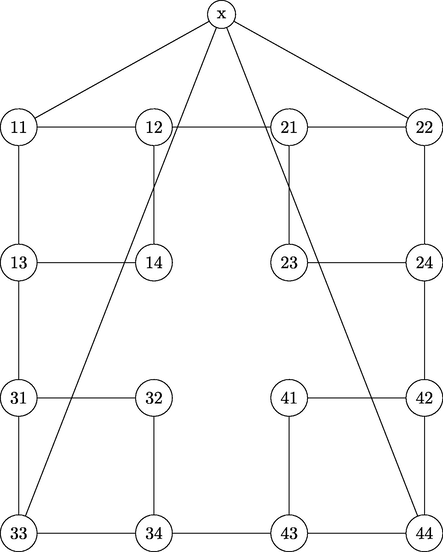
Extended Sierpiński graph
.
For , here represents the degree of v in . For our convenience is represented by in this article. Let is the number of copies of edge with degrees and in . For represents the triangles of having r and s as its vertices, while represents the number of triangles in . For , we have and . We used the function for a graph of order p. Imran and Jamil (2020) calculate the constraints of generalized Sierpiński graphs. We will establish the results for topological properties of extended Sierpiński graph with any base graph . For these topological indices we will obtain some sharp bounds in terms of numerous parameters. In this article, we will select the first Zagreb, second Zagreb and forgotten indices to investigate the invariants of graphs. Following lemmas are helpful in finding the main results of the paper.
Zhou (2004) Let be a graph without triangle having order p, size . Then and equality holds if and only if is a complete bipartite graph.
Zhou (2004) Let be a graph without triangle having size . Then and equality holds if and only if is a union of a complete bipartite graph and isolated vertices.
Das (2003) Let p and be vertices and edges respectively of a graph . Then and left equality holds if and only if is a regular graph and right equality holds if and only if is or .
Zhou (2004) Let be a size of a graph . Then and equality holds if and only if is a union of a complete and isolated vertices.
Estrada-Moreno and Rodríguez-Velázquez (2019) Let p be the order of a graph , for any edge rs and integer , we have
-
-
-
-
.
2 Main results
In this part of paper, we obtained the Zagreb and forgotten topological indices for extended Sierpiński graph by considering any arbitrary graph . Furthermore, we also compute some bounds for . Here represents the degree of extreme vertices and is the degree of new vertex which is introduced in generalized Sierpiński graph in order to obtain throughout this article. By using Lemma 1.5 we can deduce the following result for extended Sierpiński graph.
Let p be the order of a graph , for any edge rs and integer , we have
-
-
-
-
-
.
Let p and q be vertices and edges of a graph . Then first Zagreb index of extended Sierpiński graph of the graph of dimension is .
Let p and q be vertices and edges of a graph . Then the first Zagreb index of can be defined as
Now, by using Lemma 2.1 we have □
From Lemma 1.3 we obtained the next result.
Let p and be vertices and edges respectively of a graph . Then .
The lower bound is obtained if is isomorphic to a regular graph and upper bound is obtained if is isomorphic to or . Lemma 1.1 gives the result for the upper bound of .
Let be a graph without triangle having order p, size and . Then .
Let and be path, star, cycle and complete graphs of order p. Then the first Zagreb index for extended Sierpiński graph with dimension of these graphs is given as
-
-
-
-
.
From Theorem 2.2, we have
Now, by replacing the value of and by taking path, star, cycle and complete graph as a base graph in above equation, then we will obtain □
Let is a base graph with minimum and maximum degree and respectively. Then for extended Sierpiński graphs, we have left equality holds if -regular graph and right equality holds if -regular graph.
Let be a base graph having order p and size q. The first Zagreb index of can be stated as
Now, by using Lemma 2.1 we have,
Since, is the minimum degree in graph , then we obtained and equality holds if -regular graph
Since, is the maximum degree in , then inequality becomes and equality holds if -regular graph. □
Let be the vertices of a regular graph . Then for extended Sierpiński graph, we have the left equality holds if and right equality holds if .
Now, in next theorem we compute the formula of second zagreb index for extended Sierpiński graph.
Let be extended Sierpiński graph with dimension , where having p vertices and q edges. Then second Zagreb index of is .
Let be a graph having p vertices and q edges. The second Zagreb index of can be stated as
Now, by using Lemma 2.1 we have □
Let and be path, star, cycle and complete graphs of order p. Then second Zagreb index for extended Sierpiński graph with dimension of these graphs is given as
.
From Theorem 2.8, we have
Now, by replacing the value of and and by taking path, star, cycle and complete graph as a base graph in above equation, then we will obtain □
Let is a base graph with minimum and maximum degree and respectively. Then for extended Sierpiński graph, we have where left equality holds if -regular graph and right and only if -regular graph.
Let p and q are the order and size respectively of a graph . Then second Zagreb index of can be stated as
Now, by using Lemma 2.1 we have
Since, is the minimum degree of . Then we obtained and equality holds if -regular graph.
As is the maximum degree of . Then we obtained and equality holds if -regular graph. □
If is without triangle, then above result becomes as follow.
Let be a graph without triangle. Then .
Let be the order of a connected regular graph . Then . The left equality holds if and right equality holds if .
The following theorem gives the exact formula of forgotten index of .
Let be extended Sierpiński graph of dimension of base graph with p vertices and q edges. Then the forgotten topological index of is .
Let p and q be order and size of a graph . Then forgotten topological index of can be defined as
Now, by using Lemma 2.1 we have □
Let and be path, star, cycle and complete graphs of order p. Then forgotten topological index for extended Sierpiński graph with dimension of these graphs is given as
.
From Theorem 2.13, we have
Now, by replacing the value of and by taking path, Star, Cycle and complete graph as a base graph in above equation, then we will obtain □
If is a base graph, where and are minimum and maximum degrees respectively. Then for extended Sierpiński graph, we have
left equality holds if -regular graph and right equality holds if -regular graph.
Let p and q be order and size respectively of a graph . Then forgotten topological index of can be stated as
Now, by using Lemma 2.1 we have
As is the minimum degree of graph . Then we have and equality holds if -regular graph
As is the maximum degree of graph . Then we obtained and equality holds if -regular graph. □
Let be the order of a base graph . Then
left equality holds if and right equality holds if .
3 Conclusion
The extended Sierpiński graphs are obtained by introducing a new vertex in generalized Sierpiński graph and attached this vertex with extreme vertices. In this paper, we have compute the Zagreb and forgotten invariants for extended Sierpiński graphs using any base graph . Moreover, for these topological indices of extended Sierpiński graph, we attained some sharp bounds by applying numerous parameters. In future, we want to extend this work by applying other topological indices on extended Sierpiński graphs and attained the fruitful results.
Data availability statements
All the data used to finding the results is included in the manuscript.
Acknowledgments
This research is supported by the University program of Advanced Research (UPAR) and UAEU-AUA grants of United Arab Emirates University (UAEU) via Grant No.G00003271 and Grant No. G00003461.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Computing the forgotten topological index of four operations on graphs. AKCE Int. J. Graphs Combinat.. 2017;14(1):70-79.
- [Google Scholar]
- Embedding (3+1)-dimensional diffusion, telegraph, and Burger’s equations into fractal 2D and 3D spaces: An analytical study. J. King Saud Univ.- Sci.. 2020;32(1):349-355.
- [Google Scholar]
- First Zagreb index, -connectivity, beta-deficiency and -hamiltonicity of graphs. MATCH Commun. Math. Comput. Chem.. 2018;80:141-151.
- [Google Scholar]
- Lower and upper bounds of the forgotten topological index. MATCH Commun. Math. Comput. Chem.. 2016;76:635-648.
- [Google Scholar]
- Distances in Sierpiński graphs and on the Sierpiński gasket. Aequationes Mathematicae. 2013;85(3):201-219.
- [Google Scholar]
- Sharp bounds for the sum of the squares of the degrees of a graph. Kragujevac J. Math.. 2003;25:31-49.
- [Google Scholar]
- On the General Randić index of polymeric networks modelled by generalized Sierpiński graphs. Discrete Appl. Math.. 2019;263:140-151.
- [Google Scholar]
- Graph theory and molecular orbitals, Total -electron energy of alternant hydrocarbons. Chem. Phys. Lett.. 1972;17(4):535-538.
- [Google Scholar]
- Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys.. 1975;62(9):3399-4405.
- [Google Scholar]
- Topological indices and QSPR modeling of some novel drugs used in the cancer treatment. Int. J. Quantum Chem.. 2021;121(24):e26813
- [Google Scholar]
- Sharp lower bounds for the Zagreb indices of unicyclic graphs. Turkish J. Math.. 2015;39:595-603.
- [Google Scholar]
- Complete characterization of graphs for direct comparing Zagreb indices. Discrete Appl. Math.. 2016;215:146-154.
- [Google Scholar]
- The relationship between the eccentric connectivity index and Zagreb indices. Discrete Appl. Math.. 2013;161(16–17):2480-2491.
- [Google Scholar]
- Sharp bounds on certain degree based topological indices for generalized Sierpiński graphs. Chaos Solitons Fractals. 2020;132:109608
- [Google Scholar]
- Graphs and a variant of the Tower of Hanoi problem. Czechoslovak Math. J.. 1997;47:95-104.
- [Google Scholar]
- The hosoya index of graphs formed by a fractal graph. Fractals. 2019;27(8):1950135.
- [Google Scholar]
- Some engineering applications of newly constructed algorithms for one-dimensional non-linear equations and their fractal behavior. J. King Saud Univ.- Sci.. 2021;33(5):101457
- [Google Scholar]
- Shortest Paths in the Tower of Hanoi Graph and Finite Automata. SIAM J. Discrete Math.. 2006;20(3):610-622.
- [Google Scholar]
- Spectral Analysis on Infinite Sierpiński Gaskets. J. Functional Anal.. 1998;159(2):537-567.
- [Google Scholar]
- Todeschini, R., Consonni, V., 2000. Handbook of Molecular Descriptors. Wiley-VCH, Weinheim, Germany.
- A recursively scalable network VLSI implementation. Future Gener. Comput. Syst.. 1988;4(3):235-243.
- [Google Scholar]
- Structural determination of paraffin boiling point. J. Am. Chem. Soc.. 1947;69:17-2.
- [Google Scholar]
- A relationship between bounds on the sum of squares of degrees of a graph. J. Appl. Math. Comput.. 2006;21(1–2):233-238.
- [Google Scholar]







