Translate this page into:
The Stokes’ second problem for nanofluids
⁎Corresponding author. sanam_143_6@hotmail.com (Naeema Ishfaq)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this paper, a nanofluid version of the Stokes’ second problem is investigated. For this purpose, a homogeneous model is considered with nano-sized Cu particles suspended in water. The governing equations are first transformed in dimensionless form and then solved by Laplace transform. Exact solutions corresponding to the dimensionless velocity and temperature due to both cosine and sine oscillations of an infinite flat plate are presented. It is concluded that both skin friction coefficient and density of nanofluids increases with an increase of nanoparticles volume fraction. Also the dimensionless temperature increases by increasing the Eckert number and solid volume fraction of nanoparticles.
Keywords
Nanofluids
Stokes’s second problem
Oscillatory boundary layer
1 Introduction
The Stokes’ second problem is one of the classical boundary layer problems of the unsteady shear flow of a viscous fluid with inertia near a flat plate (see Schilichting, 1968). The flat plate is made to oscillate sinusoidally parallel to itself. This flow model is also referred in the literature as ‘Stokes layer’ or oscillatory boundary layer (Batchelor, 1967; Drazin and Riley, 2006). Such types of models have a wide range of applications in the field of biotechnology, chemical engineering, micro-fluidic devices and nanotechnology (Yakhot and Colosqui, 2007).
Exact solutions for the motion of a viscous incompressible fluid caused by the cosine and sine oscillations of a flat plate have been provided by Erdogan (2000). He has presented the steady-state solutions as well as transient solutions for the flow due to an oscillating plate. Later, analytical solution for a laminar flow of a Johson-Segalman fluid on oscillating plate was reported (Hayat et al., 2004). The effects of Navier slip on the Stokes’ second problem due to an oscillating wall were also studied (Khaled and Vafai, 2004). Furthermore, Stokes’s second problem has been investigated for eight different non-Newtonian fluids with temperature variation near the wall for both sine and cosine oscillations (Ai and Vafai, 2005). The fluid flow generated by an infinite plate in oscillatory motion as reported by Yakhot and Colosqui (2007) in a simple plane oscillator, are shown to be in good agreement with experiments on nano resonators operating in a wide range of pressure and frequency variation in both gases and water. Subsequently, Balmforth et al. (2009) presented a one-dimensional theoretical and experimental study on the effect of viscoplasticity on the Stokes layer. Khan et al. (2010) provided exact solutions of the Stokes second problem for Burgers’ fluid. Numerical solution of Stokes second problem has been analyzed and the corresponding numerical results have been found very close to the analytical results (Sin and Wong, 2010). By extending the study of the numerical solutions, the Stokes’ second problem for a power-law fluid was revisited by Pritchard et al. (2011) obtaining both semi-analytical periodic solutions and COMSOL based numerical solutions. McArdle et al. (2012) presented asymptotical and numerical exploration into the effect of thixotropic or antithixotropic rheology on the oscillatory boundary layer.
In this note, Stokes second problem for nanofluids is considered. However, the Stokes’ first problem (impulsive motion caused by the moment of the plate) for nanofluids has been studied through the combine effects of Brownian motion and thermophoresis on the velocity, temperature and volume fraction of the nanoparticles (Uddin et al., 2013). Most recently, the unsteady flow and heat transfer of the viscous fluid driven by impulsively started infinite flat plate in a nanofluid has been discussed by Rosali et al. (2014).
Here in, for the 1st time, we are examining the Stokes’ second problem for nanofluids. The purpose of the present study is to explore the nanofluid version of the Stokes’ layer and to investigate heat transport and nanoparticles volume fraction over an oscillating flat plate. In addition, the effects of nanoparticles volume fraction, dimensionless time and Eckert number on the dimensionless velocity, temperature distribution as well as on the skin friction has been presented graphically. Exact solutions are also obtained for the system of the non-linear coupled partial differential equations.
2 Model formulation
Let us consider an incompressible, Newtonian nanofluid of constant kinematic viscosity
occupying a semi-finite space
, with the
in the vertical direction, bounded by an impermeable wall at
. This wall is subject to sinusoidal oscillation so that the
velocity on the wall is given by
or
, resulting in the induced nanofluid flow. The velocity decays to zero as
. The half space plate is embedded in a medium saturated with water based nanofluids. The base fluid and the nanoparticles are assumed to be in thermal equilibrium and no slip occurs between them. We also consider the effects of viscous dissipation on the nanofluid temperature. The temperature at the wall
is assumed to be constant and as
the temperature approaches to a constant ambient temperature
. The momentum equation for the proposed unsteady nanofluid flow becomes a diffusion equation inheriting the kinematic viscosity of the nanofluid
The energy equation under the above assumption takes the form
Which are subject to the following initial and boundary conditions:
The thermal conductivity of the nanofluid is represented by is the nanoparticle volume fraction parameter, is the reference density of the fluid fraction, is the density of the solid fraction, is the viscosity of the fluid fraction, is the kinematic viscosity of the fluid fraction, is the thermal conductivity of the fluid fraction, is the specific heat at constant pressure and is the thermal conductivity of the solid volume fraction.
For the governing equations, we introduce the non-dimensional quantities defined by
The dimensionless problem is therefore given by
The physical quantities of interest are also the skin friction or shear stress coefficient
and the local Nusselt number
are defined as
Using variables (5), we get
3 Exact solution
The system of PDEs in Eq. (6) subject to boundary conditions (7) can be solved using integral transforms, see (Spiegel, 1971; Weerakoon, 1994; Khan and Khan, 2008). Here, we state the exact solution directly without going into details.
3.1 For at
The solution of the differential Eq. (6) subject to the cosine oscillating boundary condition is and where
The skin friction and reduced Nusselt number are found to be and
3.2 For at
The solution of the differential Eq. (6) subject to the sine oscillating boundary condition is and
The skin friction and reduced Nusselt number for sine oscillation are found to be and
4 Results and discussion
This section discusses the effects of solid volume fraction
of nanoparticle, dimensionless time
and Eckert number
on the dimensionless velocity, temperature profiles as well as on the skin friction for the nano particle
with water as a base fluid. The thermo-physical properties of water and considered
are listed in Table 1.
Physical properties
Base Fluid (water)
Cu
(J/kg K)
4179
385
(kg/m3)
997.1
8933
(W/mK)
0.613
401
Fig. 1 is plotted to see the effects of volume fraction parameter
and different time points
on the velocity. It is observed that there exist some oscillations near the wall in the velocity profile and far away from the plate it again approaches to zero. Amplitude of the flow increases as volume fraction increases and there is a phase shift in the nanofluid against the regular fluid
Fig. 2 elucidates the influence of
on the temperature field. It is noted that temperature field is an increasing function of
. The effect of viscous dissipation on the dimensionless velocity and temperature is given in Fig. 3. It is important to note that
corresponds to the case when viscous dissipation is absent. Positive value of
corresponds to plate cooling i.e. transfer of heat from plate to fluid; while negative values imply reserve i.e. plate heating where in heat is received by the plate from the fluid. From this Figure it is clear that thermal boundary layer thickness increases by increasing the Eckert number
. This is because of the fact that due to large viscous resistance there is more accumulation of heat energy in the fluid particles near the boundary. In Fig. 4, contours are plotted for different values of solid volume fraction
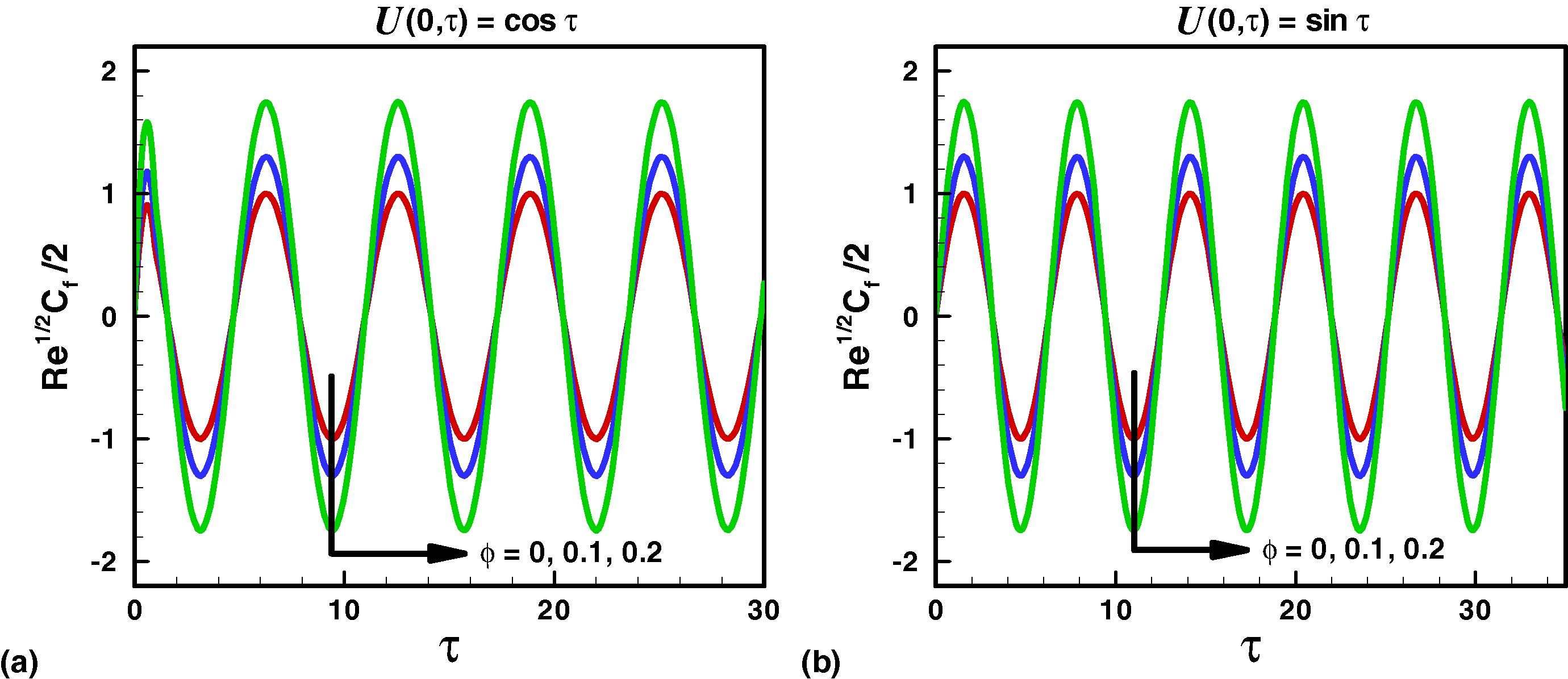
. Variations of skin friction coefficient with
nanoparticles volume fraction can be observed from Fig. 5. It is observed that due to oscillatory motion of the plate the skin friction coefficient also varies periodically. The oscillatory amplitude of skin friction increases with the increase of volume fraction parameter. The density of nanofluids increases with increasing nanoparticle volume fraction. Due to this reason, the skin friction also increases with increasing nanoparticle volume fraction.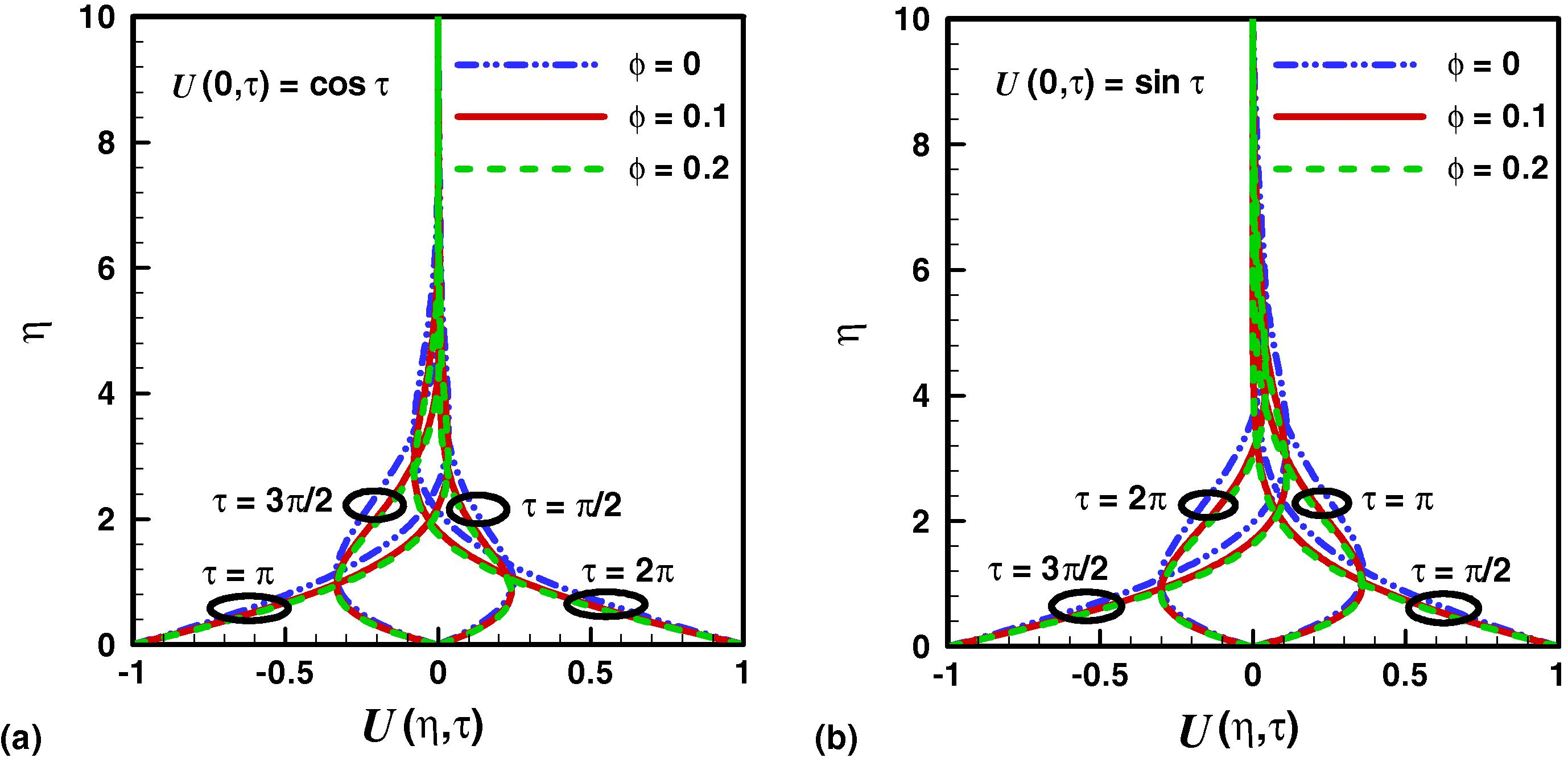
Effects of Cu nanoparticles volume fraction on velocity profile.
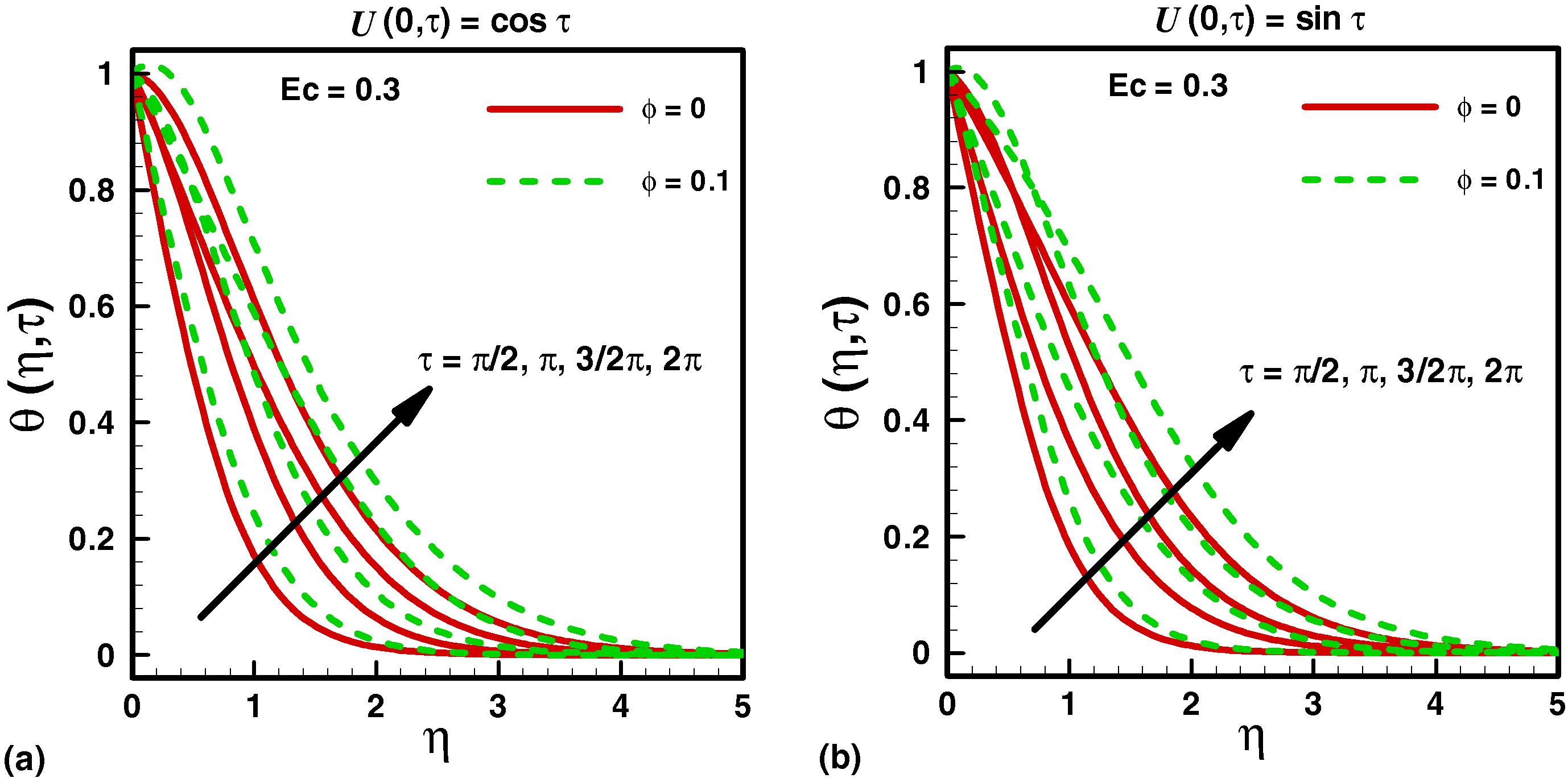
Effects of Cu nanoparticles volume fraction on temperature profile.
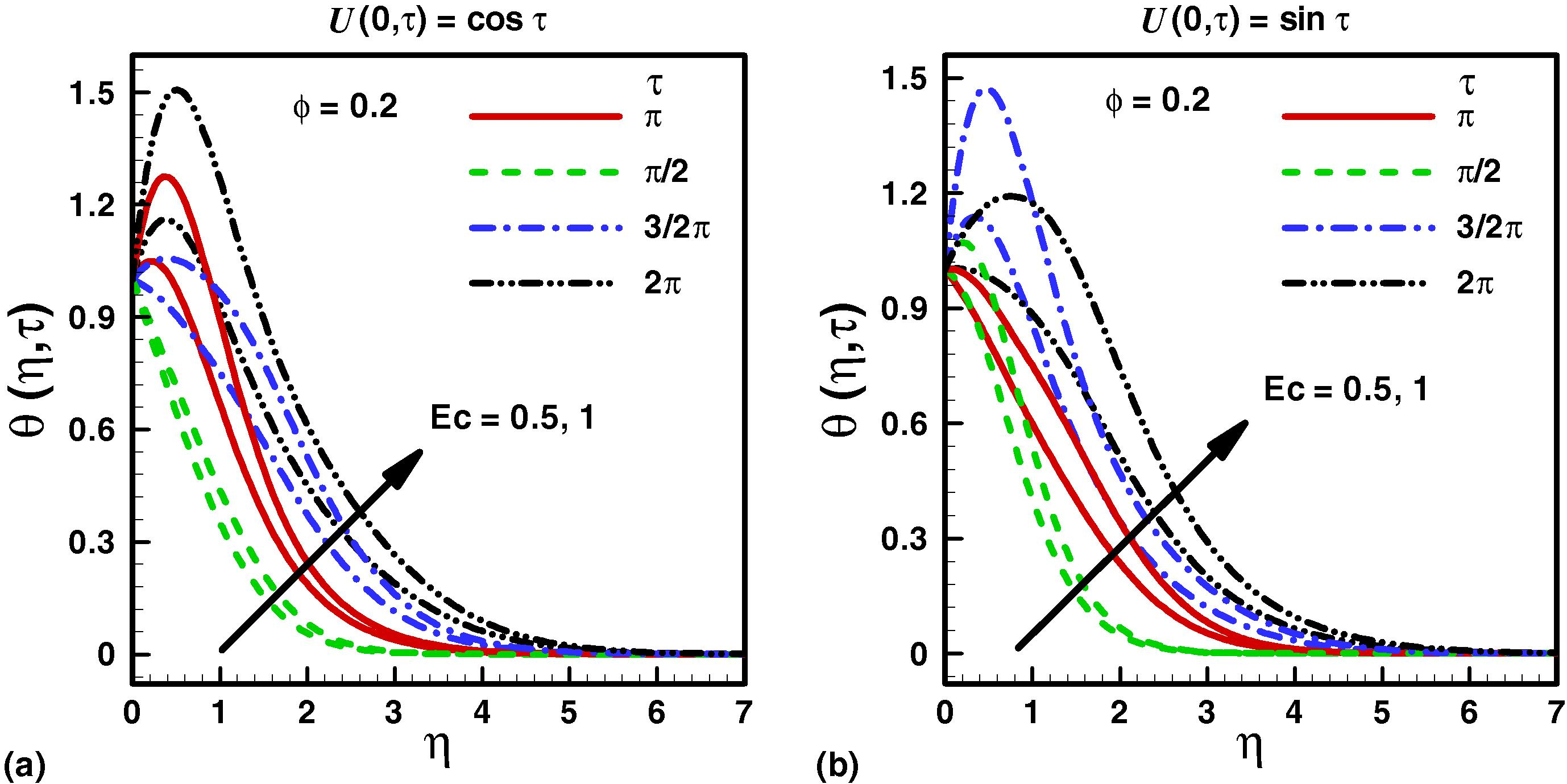
Effects of Eckert number on temperature profile.
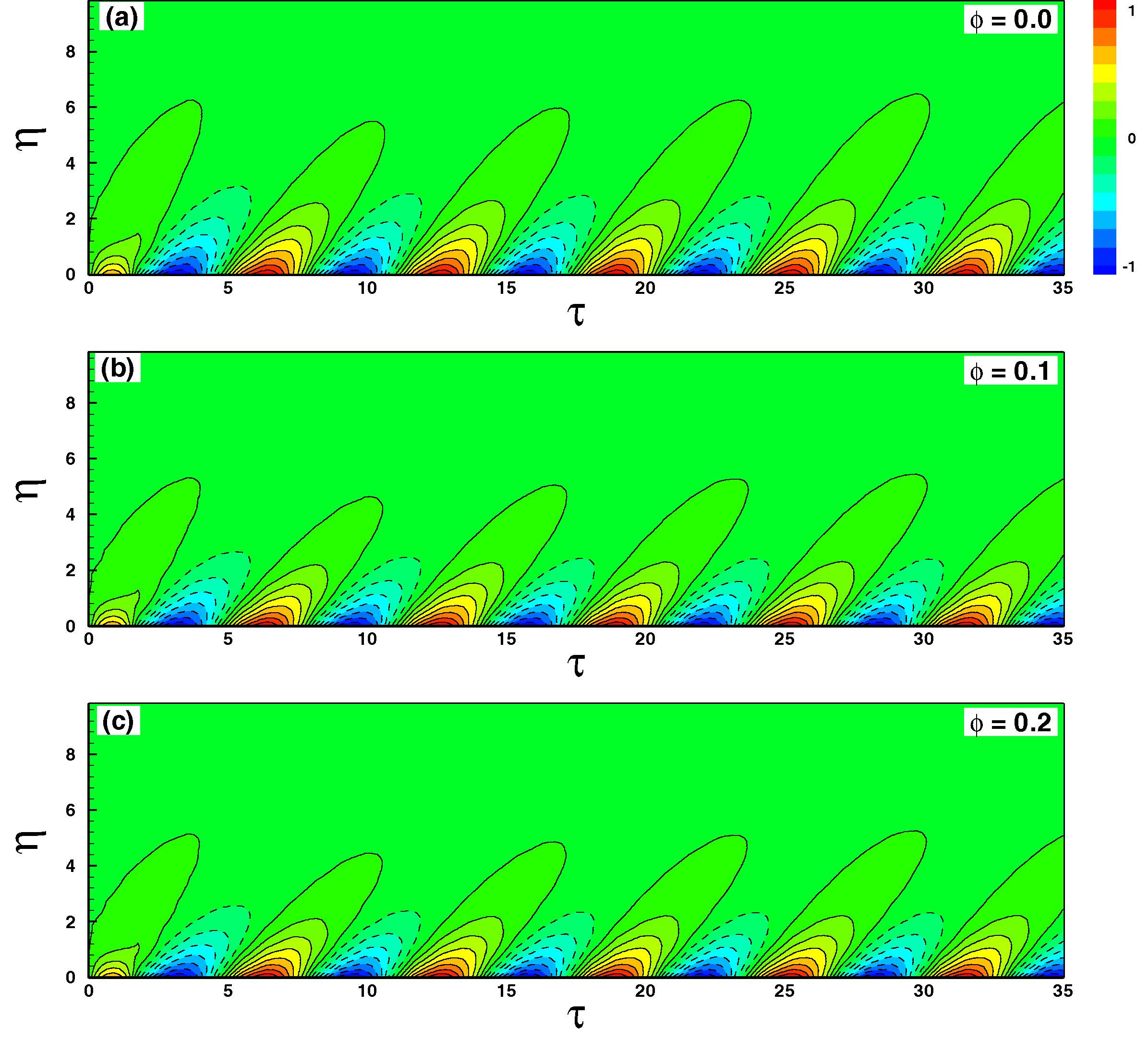
Contour plots.
Variation of skin friction with solid volume fraction of nanoparticles.
5 Conclusions
We have studied the effects of solid nanoparticles fraction on the Stokes layer subject to both cosine and sine oscillations. The governing equations along with imposed initial and boundary conditions are first converted into dimensionless form and then solved by using the Laplace transform technique. It is observed that skin friction coefficient increases with solid volume fraction of nanoparticles. The dimensionless temperature increases by increasing the Eckert number and solid volume fraction of nanoparticles. Moreover, the exact solutions obtained in this study are significant not only because they are solutions of some fundamental flows, but they also serve as accuracy checks for numerical, asymptotic and analytical methods. Hence the contents of present communication add significant advancement to the existing knowledge.
Acknowledgment
This work was supported by National Natural Science Foundation of China.
References
- An investigation of Stokes’ second problem for non-Newtonian fluids. Numer. Heat Transfer Part A – Appl.. 2005;47:955-980.
- [Google Scholar]
- An Introduction to Fluid Dynamics. Cambridge University Press; 1967.
- Drazin, P.G., Riley, N., 2006. The Navier-Stokes equations: a classification of flows and exact solutions, London Mathematical Society Lecture Notes Series, vol. 334, Cambridge University Press.
- A Note on Unsteady Flow of a Viscous Fluid due to an Oscillating Plane Wall. Int. J. Non-Linear Mech.. 2000;35:1-6.
- [Google Scholar]
- Stokes’ second problem for a Johnson-Segalman fluid. Appl. Math. Comput.. 2004;148:697-706.
- [Google Scholar]
- The effect of the slip condition on Stokes and Couette flows due to an oscillating wall: exact solutions. Int. J. Non-Linear Mech.. 2004;39:795-809.
- [Google Scholar]
- On exact solutions of Stokes second problem for a Burgers’ fluid, I. The case γ∗ λ2/4. Z. Angew. Math. Phys.. 2010;61:697-720.
- [Google Scholar]
- The Stokes boundary layer for a thixotropic or antithixotropic fluid. J. Nonnewton. Fluid Mech.. 2012;185:18-38.
- [Google Scholar]
- The Stokes boundary layer for a power-law fluid. J. Non-Newton. Fluid Mech.. 2011;166:745-753.
- [Google Scholar]
- Boundary Layer Theory (sixth ed.). New York: McGraw-Hill; 1968.
- Sin, V.K., Wong, I.K., 2010. Numerical Study of Stokes' Second Flow Problem. International Conference on Computational and Information Sciences, IEEE. 242–245.
- Schaum's outline of advanced mathematics for engineers and scientists. McGraw-Hill; 1971.
- Heat and mass transfer from a suddenly moved plate in nanofluids. Proc. Institut. Mech. Eng. Part N: J. Nanoeng. Nanosyst.. 2013;227:29-37.
- [Google Scholar]
- Application of Sumudu transform to partial differential equations. Int. J. Mathem. Educ. Sci. Technol.. 1994;25:277-283.
- [Google Scholar]
- Stokes' second flow problem in a high-frequency limit: application to nanomechanical resonators. J. Fluid Mech.. 2007;586:249-258.
- [Google Scholar]







